Exploiting Duplications for Efficient Task Offloading in Multi-User Edge Computing

Abstract

The proliferation of IoT applications has pushed the horizon of edge computing, which provides processing ability at the edge of networks. Task offloading is one of the most important issues in edge computing and has attracted continuous research attention in recent years. With task offloading, end devices can offload the entire task or only subtasks to the edge servers to meet the delay and energy requirements. Most existing offloading schemes are limited by the increasing complexity of task topologies, as considerable time is wasted for local/edge subtasks to wait for their precedent subtasks being executed at the edge/local device. This problem becomes even worse when the dependencies among subtasks become complex and the number of end-users increases. To address this problem, our key methodology is to exploit subtask duplications to reduce the inter-subtask delay and shorten the task completion time. Based on this, we propose a Duplication-based and Energy-aware Task Offloading scheme (DETO), which duplicates critical subtasks that have a large impact on the completion time and thus enhances the parallelism between local and edge computing. In addition, among numerous choices of subtask duplications, DETO evaluates the gain/cost ratio for each possible duplication and chooses the most efficient ones. As a result, the extra resource for duplications is greatly reduced. We also design a distributed DETO algorithm to support multi-user, multi-server edge computing. Extensive evaluation results show that DETO can effectively reduce the task completion time (by 12.22%) and improve the resource utilization (by 15.17%), in particular for multi-user edge computing networks.

1. Introduction

The proliferation of IoT applications, e.g., object recognition, vehicular systems and self-driving [1,2,3], have pushed the horizon of a novel computing paradigm—Multi-access Edge Computing (MEC) [4]. In MEC, a number of edge servers are deployed close to the user, and the computation-intensive tasks from end users are uploaded to and processed in the network of edge servers. After that, the results are returned to end user devices [5,6]. As a result, the completion time of services and the energy consumption of end user devices can be reduced.

Traditional offloading schemes [7] upload the entire task to edge servers. These approaches fail to utilize the parallelism between end devices and edge servers. To address this issue, the recent studies [8,9] decompose the task into a number of subtasks and upload some of them to edge servers. In this way, end devices and edge servers can execute their subtasks in parallel, such that the overall completion time is reduced. For example, the authors in [8] synthetically considered the computation workload of subtasks, dependency among subtasks and wireless transmission time. In doing this, the subtasks can be rationally scheduled in the edge server or local devices, and the makespan of applications can be reduced.

However, in the approaches based on task decomposition, more communication delay is introduced as the information exchange among subtasks that are not located in the same processor needs to be done through the wireless links. To better understand the limitations of the existing works and reveal further optimization space, we study an example of task offloading for the object recognition applications [10], as shown in Figure 1.

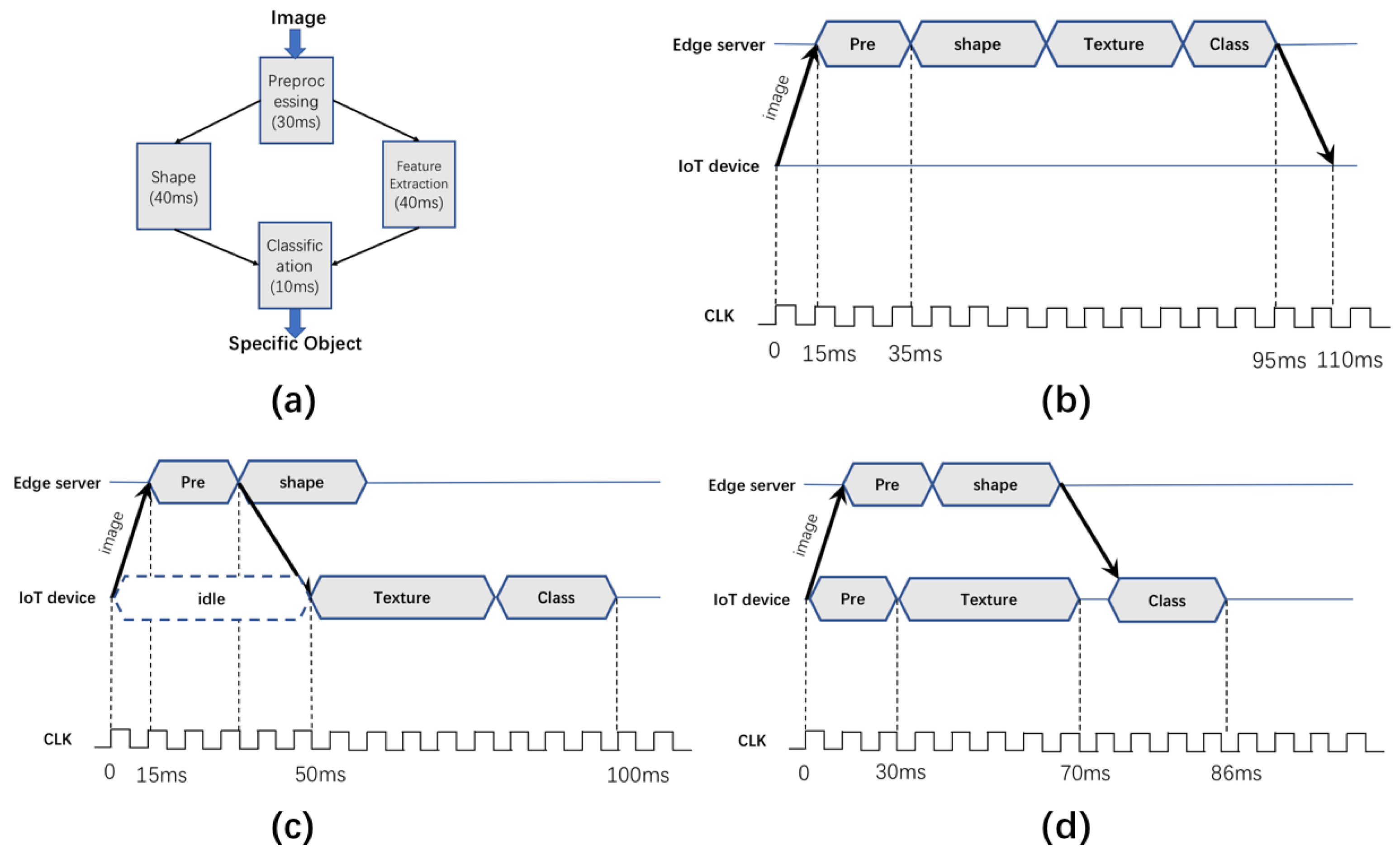
The task topology is depicted as a directed acyclic graph (DAG) as shown in Figure 1a. Each rectangle denotes a subtask with the execution delay labeled. An arrowed line from rectangle A to rectangle B denotes that subtask B depends on the results of subtask A. We can see that the object recognition first inputs the target image to the “Pre-processing” subtask. Based on the results of “Pre-processing”, “Shape” and “Texture” will extract the object shapes and texture, respectively. Based on the extractions, the “Classification” subtask can recognize the object as a specific class of objects.

Figure 1b shows the basic idea of traditional offloading works [7,11,12], which treat the four subtasks as a whole and offload them to edge servers. This approach overlooks the parallelism between users and edge servers. Figure 1c shows the basic idea of the recent works based on task decomposition [8,13], which chooses some of the subtasks to offload, and thus the overall delay is reduced. From

Table 1. The delay comparison.

	Energy Cost (Local Execution Time)	Overall Delay
Figure 1b	0 ms	110 ms
Figure 1c	50 ms	100 ms
Figure 1d	80 ms	86 ms

, through the offloading strategies based on task decomposition, the latency is reduced from 110 to 100 ms due to parallelism.

However, from Figure 1c, we can see that considerable time (from 0 to 50 ms) is wasted in the “idle” slot because the subtask “Texture” needs to wait for the computational results from the subtask “Pre”. The reason is that uploading subtasks requires the information exchange among them to be done through wireless links (an additional communication round is needed from “Pre” to “Texture”). To further reduce the execution delay and fully exploit the parallelism between local devices and edge servers, an intuitive yet reasonable solution is to duplicate the Pre-processing module in the local devices (Figure 1d), and the overall execution delay can be further reduced to 86 ms.

The key idea behind the duplication-based approach is trading the computation resources (CPU cycles required to accomplish task) for reducing communication delay. Considering that wireless interference widely exists in multi-user edge computing networks [14,15] and has a high impact on the overall performance [16,17], trading computation resources for communication efficiency is likely to achieve significant performance gains. However, implementing such an idea in real-world systems is a non-trivial task due to the following challenges:

• How to reveal the duplication and offloading opportunities from complex task topologies. Before trading resources for communication efficiency, we need to first identify which subtasks are the most appropriate to be duplicated and offloaded. Different combinations of the two kinds of subtasks can lead to largely different performances. Considering the diversity and complexity of potential edge applications [10], the searching space can be surprisingly large, as analyzed in Section 3.
• How to coordinate the duplication and offloading strategies among multiple users. Apart from the “actual” execution time, the overall execution time consists of communication delay and task queuing delay. Each user’s duplication and offloading decisions will affect wireless contentions and the subtask scheduling at both local users and edge servers and further affect the communication delay and task queuing delay. As a result, we need to coordinate the duplication and offloading strategies among multiple users to improve the overall system performance.

To address the above challenges, we propose a Duplication-based and Energy-aware Task Offloading scheme (DETO) to find a good tradeoff between resource consumption and communication overhead. DETO has three salient features. First, DETO jointly considers the impact of duplication and offloading to model the tradeoff between resource and communication overhead. Second, from the task DAGs, DETO is able to identify the duplication/offloading opportunities by analyzing the subtask dependencies. Third, we propose a distributed DETO algorithm to establish the coordination between multiple users and multiple servers. We conduct extensive simulation experiments to study DETO’s performance gains. The results show that, under multi-user and multi-server edge networks, the average completion time for tasks with four typical topologies can be reduced by 12.22%.

The major contributions of this paper are summarized as follows:

• We propose a novel duplication-based and energy-aware task offloading algorithm (DETO), which exploits task duplications to enhance the parallelism between users and edge servers. The overall task completion time can be shortened as less time is wasted on the subtask communications.
• We consider the multi-user interference and multi-task scheduling and further design a distributed DETO algorithm, which is able to coordinate the duplication/offloading decisions among multiple users.
• We conduct extensive simulation experiments and the performance results demonstrate that DETO can effectively minimize the overall completion time by 12.22% and improve the resource utilization of the edge servers by 15.17% compared to the existing fine-grained offloading strategy.

The rest of this paper is organized as follows. Section 2 introduces the related work. Section 3 presents the system model and problem formulation. Section 4 introduces the three phases of the energy-aware task duplication-based scheduling algorithm (DETO). Section 5 extends the DETO algorithm to multi-user, multi-server scenarios in a centralized and distributed manner. Section 6 presents the evaluation results.

2. Related Work

Recently, multi-access edge computing was recognized by the European 5G PPP (5G infrastructure public, private partnership) research body as one of the key emerging technologies for 5G networks. There have been numerous works on the computation offloading problem in the literature, and various offloading policies have been proposed, which can be classified into two stages.

For the first stage, the researchers do not distinguish subtasks inside the application and upload the entire task as a whole to the edge servers. In [18], they study the multi-user offloading problem for edge computing in a multi-channel wireless interference environment and prove that this is NP-hard to obtain the optimal solution, and then they adopted a heuristic approach for achieving efficient computation offloading in a distributed manner.

Simulation results show that the proposed algorithm achieves superior computation offloading performance and scales well as the user size increases. Furthermore, the authors [19] studied a distributed offloading scheme for a multi-user and multi-server based on orthogonal frequency-division multiple access in small-cell networks. They formulated a distributed overhead minimization problem and then adopted the potential game theory to prove that their proposed decision is a potential game problem.

Finally, compared with other existing computation algorithms, the simulation results show that this new algorithm can guarantee saving overheads. The other works in the first stage, such as [20,21,22], also consider a multi-user and multi-server scenario and propose a heuristic offloading decision algorithm to assign different tasks to the corresponding channel and server to minimize the average completion time.

With the increasing complexity of applications, the offloading related work comes into the second stage. This task has been considered as DAGs in order to identify a fine-grained offloading opportunity. In [23], the authors considered that the application consists of a series of sequential modules and then decide which module to be offloaded and how these modules should be executed (cloud computing or edge computing). Furthermore, the authors in [8] investigated the problem of fine-grained task offloading in edge computing for low-power IoT systems.

They aim to map the subtasks of different applications onto the heterogeneous server and order their executions so that task-precedence requirements are satisfied and a minimum overall completion time is obtained. Moreover, in order to improve the efficiency of the offloading decisions, they further designed a distributed computation offloading algorithm (DEFO) based on game theory. However, this work introduces extra communication delay between subtasks.

Along a different line, in our work, we utilize the processor idle time to duplicate the predecessor task to further reduce the completion time of services. We duplicate the task selectively only if it helps in improving the performance to avoid superfluous energy consumption. There has been extensive work on a duplication-base clustering algorithm for the datacenter [24,25,26].

Our work has the following main differences: (1) The existing studies mainly target an unbounded number of computing machines in the datacenter. (2) Communications in the edge network are via wireless channels, thus it suffers more severe interference than communications in the datacenter. (3) The duplication-based algorithms in the datacenter will replicate all possible ancestors of a given task. However, it is unreasonable and impractical to consider the resource-constraint character of IoT devices.

This paper is the first of its kind that work proposes a fine granularity duplication-based offloading strategy in the edge network in order to reduce the end-to-end delay of application while considering the energy consumption of the devices.

3. System Model

In our offloading scenario, there are a certain number of heterogeneous servers in the edge network, defined by $\mathcal{M}$ = $[1,2,\dots ,m,\dots ,M]$. We consider a set of $\mathcal{N}$ = $[1,2,\dots ,i,\dots ,N]$ user. Each user has a task to be offloaded to the edge network. The execution procedure of the application of user i can be represented by directed acyclic graphs (DAGs) $G_i=(V_i,E_i)$, where $V_i=[T_{i1},T_{i2},\dots ,T_{ij},\dots ,T_{ie}]$ denotes the set of subtasks to be executed, and $T_{i{j}^{\prime }}$ denotes the possible duplication of $T_{ij}$.

$E_i$ represents the set of directed edges characterizing the dependency between the subtasks, and the weight of each edge $edg{e}_{jk}$ represents the amount of data communication between subtasks, in which the subtask j is one of the immediate predecessors of subtask k. Our problem is to upload and schedule these subtasks and the possible duplication of them from different users on edge servers to minimize the overall completion time of all the applications. A feasible schedule should satisfy the following constraints:

• Constraints on tasks: Considering the low-power character of IoT devices, these devices are always equipped with only one radio. Thus, only one of the edge servers can be selected by an IoT device during the task execution. Furthermore, each subtask cannot be interrupted during the execution.
• Constraints on communication: The subtask cannot start until all its immediate predecessors have been finished, and their results have been received. The transferring time is affected by the size of communication data and the communication rate if these two tasks are not assigned to the same processor.
• Constraints on processors: The processors can only run tasks serially—that is to say, the execution of any two subtasks on the same processor cannot overlap. To facilitate the discussion, we assume that the IoT devices and the edge servers have only one processor.

Since our target is to minimize the average completion time in a multi-user and multi-server edge network scenario under the energy-consumption constrain, the transmission time and the execution time should be considered at the same time. In this section, we first present the communication and execution model, and then we propose the energy-consumption model. Finally, we present our optimization problem. The notations used in this paper are summarized in

Table 2. Notations used in the paper.

Notation	Description
$\mathcal{N}$	The set of user
$\mathcal{M}$	The set of edge servers
${\mathcal{V}}_i$	The set of subtasks of devices i
$T_{i,j}$	The subtask j of the device i
$T_{i,j^{\prime }}$	The duplication of $T_{i,j}$
$edg{e}_{i,j}$	The data communication from subtask i to subtask j
$d_i$	The offloading scheme of device i
$d_{i,j}$	The offloading strategy of subtask $T_{i,j}$
$\mathbf{D}$	A possible offloading scheme of all subtasks in the edge
$Rat{e}_{i,k}$	The communication rate between device i and server k
$t_{i,j,k}$	The execution time of $T_{i,j}$ in processor k
$t_{i,j,k}^D$	The time when all the data is ready for $T_{i,j}$
$t_{i,j}^F$	The actual finish time of subtask $T_{i,j}$
$t_{i,j,k}^S$	The actual starting time of subtask $T_{i,j}$
$C_{j,l}^k$	Data exchange time between subtask j and subtask l
$t_{i,j}^k$	The processor k is available to execute $T_{i,j}$
$E_i^c$	The computation consumption of user devices
$E_i^t$	The transmission consumption of user devices
$E_i^t$	The overall energy consumption of user devices
$I(i,j)$	An indicator of duplicate subtask
$m_{(}i,j)$	The required CPU cycle to accomplish the $T_{i,j}$
$\mathbf{I}$	A possible duplication strategy of all subtasks in the edge

.

3.1. Communication and Computation Model

We consider a multi-access edge network scenario, and each IoT device can select only one edge server to offload its subtask or the possible duplicated subtask. Let $d_i$ be an indicator to denote where IoT device i execute its subtasks:

$$d_i=\left\{\begin{array}{c}-i\mathrm{if}\mathrm{the}\mathrm{application}\mathrm{executed}\mathrm{locally}\hfill \\ k\mathrm{if}\mathrm{it}\mathrm{uploads}\mathrm{the}\mathrm{task}\mathrm{to}\mathrm{server}k\hfill \end{array}\right.$$

(1)

Thus, for any subtask of user i, the offloading scheme $d_{ij}=-i$ means this subtask will be executed locally, $d_{ij}=k$ denotes it will be executed with the help of server k. Especially, if $d_{i{j}^{\prime }}=d_{ij}$ represents that the subtask $T_{i,j}$ has no duplications. We adopt $D_i$ = $\{d_{i,1},d_{i,1^{\prime }},d_{i,2},d_{i,2^{\prime }},\dots ,d_{i,|v_i|}\}$ to represent the a possible offloading decision for all subtasks of device i, so the $\mathbf{D}=D_1$×$D_2$ × $\dots \times D_N$ define a possible offloading strategy of all the users in the edge network. Furthermore, we can compute the wireless communication rate between user i and edge server k for a given offloading decision according to the Shannon Equation:

$$Rat{e}_{i,k}\left(\mathbf{D}\right)=Blo{g}_2(1+\frac{q_i{g}_{i,k}}{\varpi +{\sum }_{j\in N:D_i=D_j}{q}_j{g}_{j,s}})$$

(2)

Here, we can see that the wireless transmission rate is affected by the bandwidth B, the transmission power of the device $q_i$, and most important influence factor is the offloading strategy of the nearby user: ${\sum }_{j\in N:D_i=D_j}{q}_j{g}_{j,s}$. The more users select the same edge server to execute their task. The more drastic interference will be suffered by the users. Thus, we coordinate the offloading strategies (a more reasonable $\mathbf{D}$) of the nearby user devices to obtain the most suitable wireless transmission rate for edge computing. We assume that the users will keep connected with the edge servers during the task execution.

It should be stressed here that the Shannon Equation tells the maximum rate at which data can be transmitted over a communication channel of the specified bandwidth in the presence of noise. The noise includes not only the background noise but also the same-frequency inference. The Shannon Equation can well express the wireless transmission time of physical layer channel access scheme (e.g., CDMA) in cellular communication scenarios. We can also extend our study to some WiFi-like protocols (e.g., CSMA). In this case, the wireless transmission rate can be obtained as follows:

$$Rat{e}_{i,k}\left(\mathbf{D}\right)=R_n\left(\frac{B_n}{B_n+{\sum }_{j\in N:D_i=D_j}{B}_j}\right)$$

(3)

where $R_n$ denotes the data rate of the user if it can transmit the data through the channel all its own. $B_n$ denotes the weight of user n in channel sharing. In this case, the transmission rate of each user depends on the weight ($B_j$) of each user.

The execution time of subtask $T_{i,j}$ in the processor k is easily obtained as:

$$t_{i,j,k}=c_{i,j}/f_k\forall k\in \left\{i\right\}\cup \mathcal{M}$$

(4)

where the $c_{i,j}$ means the CPU cycle required to accomplish the $T_{i,j}$, and the $f_k$ denotes the computation capability of user i or the edge server k.

In our scenario, the actual finish time of subtask $T_{i,j}$ in server k is more complex, as it is affected by three factors: (1) the execution time in server k. (2) The time when all the data needed by subtask has arrived at server k. (3) The scheduling result of server k. The execution time is according to Equation (3). The time when all the data needed for $T_{i,j}$ is ready in server k can be denoted by:

$$t_{i,j,k}^D=\underset{l\in pred\left(j\right)}{max}\{min\{(t_{i,l}^F+C_{j,l}^k),(t_{i,l^{\prime }}^F+C_{j,l^{\prime }}^k\}\}$$

(5)

where the $pred\left(j\right)$ is the immediate predecessor subtasks of subtask j. The ready time of $T_{i,j}$ is determined by the lasted time when all the predecessors have transmitted its result to server k. Furthermore, each predecessor subtask may have a duplication, and thus the inner $min$ block in the equation returns the time when the result of a predecessor subtask has transferred to the $T_{i,j}$ either from the $T_{i,l}$ or its duplication $T_{i,l^{\prime }}$, note that if a subtask has no duplications the $t_{i,l^{\prime }}^F$ is infinite. The $t_{i,l}^F$ denotes the actual finish of the subtask $T_{i,l}$, and it will be defined in the following. Furthermore, the $C_{j,l}^k$ denotes the data exchange time between subtask j and its predecessor subtask l:

$$C_{j,l}^k=\left\{\begin{array}{c}0\mathrm{if}{d}_{i,l}=d_{i,j}\hfill \\ edg{e}_{jl}/Rat{e}_{i,k}\mathrm{otherwise}\hfill \end{array}\right.$$

(6)

After that, we finally obtain the actual finish time of subtask $T_{i,j}$:

$$t_{i,j}^F=\underset{k\in \{-i\}\cup \mathcal{M}}{min}\{t_{i,j,k}^S+t_{i,j,k}\}$$

(7)

$$t_{i,j,k}^S=max\{t_{i,j}^k,t_{i,j,k}^D\}$$

(8)

The $t_{i,j}^k$ denotes the time server k is available to execute $t_{i,j}$, which depends on the scheduling result of all the subtask from nearby devices. From Equation (8), we can see that in order to obtain the starting execution time of a task ($t_{i,j,k}^S$) on a processor, all the data required by the subtask must be received and the processor must be available. Furthermore, the actual finish time of $T_{i,j}$ is to select the minimum time by enumerating all the possible processors. It is worth mentioning that Equations (7) and (8) are also suitable for the possible duplicate subtask, as the dependency relationship of duplication is the same as the original subtask.

3.2. Energy-Consumption Model

In our duplication-based task offloading algorithm, we utilize the processor idle time to duplicate predecessor tasks, This can avoid the transfer of data between edge network and user devices and finally improve the overall completion time of applications. However, extra energy consumption will be caused by the duplicate subtask. Thus, in our work, we maintain the focus on the energy consumption of user devices. The computation consumption ($E_i^c$) and communication consumption($E_i^t$) constituted the main parts of the energy cost of user devices i. The overall energy consumption ($E_i$) is effect by the offloading scheme ($D_i$) and the duplication decision $I_{i,j}$, which is defined as follows:

$$I_{i,j}=\left\{\begin{array}{c}1\mathrm{if}{T}_{i,j}\mathrm{has}\mathrm{a}\mathrm{duplicate}\mathrm{subtask}{T}_{i,j^{\prime }}\hfill \\ 0\mathrm{otherwise}\hfill \end{array}\right.$$

(9)

Furthermore, the $I_i$ = $\{I_{i,1},I_{i,2},\dots ,I_{i,|v_i|}\}$ represents the duplication scheme of user device i, and thus $\mathbf{I}=I_1$×$I_2$ × $\dots \times I_N$ denotes a possible duplication strategy of user devices in the edge network.

The computation consumption depends on the subtasks executed locally:

$$E_i^c=\sum _{j=1:d_{ij}=-i}^{|v_i|}{m}_{i,j}{\delta }_i+\sum _{j=1:d_{ij}\ne -i}^{|v_i|}{I}_{i,j}{m}_{i,j}{\delta }_i$$

(10)

where the $m_{i,j}$ denote the required CPU cycle to accomplish the $T_{i,j}$, and the ${\delta }_i$ denotes the energy consumption per CPU cycle in user devices i.

The transmission consumption is mainly affected by the data exchange between user devices and the edge server. It can be formulated as follows:

$$E_i^t=\sum _{\begin{array}{c}j=2:d_{i(j-1)}=-i\\ d_{ij}\ast d_{i{j}^{\prime }}\ne i^2\end{array}}^{|v_i|}(1-I_{i,j})C_{(j-1),j}^k\times q_i$$

(11)

The $q_i$ is the transmission power of user devices i, and the $C_{(j-1),j}^k$ is the data exchanging time between the $T_{i,(j-1)}$ and $T_{i,j}$. From Equation (11), the essential condition of communication consumption: (1) The predecessor subtask $T_{i,j-1}$ is executed in the local processor. (2) The $T_{i,j-1}$ has no duplicate subtask. (3) Either the subtask $T_{i,j}$ or its duplication is executed in the edge server.

3.3. Optimization Problem

From Equation (8), we can see that the scheduling result of subtasks from different users can also affect the overall completion time. Thus, we define $S_{i,j}^k$ = $\{s_{i,j}^k,\forall k\in \left\{i\right\}\cup \mathcal{M},\forall i\in \mathcal{N},\forall j\in V_i\}$ to denote the scheduling order of subtasks. Our aim is to find a suitable task offloading decision $\mathbf{D}$, duplication scheme $\mathbf{I}$ and a scheduling result $S_{i,j}$ for all the subtasks from different users to minimize total latency while satisfying the energy constraints. The duplication-based energy-aware task offloading problem can be formulated as:

$$\mathbf{Opt}:\underset{\left\{I_{i,j},d_{i,j},s_{i,j}\right\}}{min}\left(\sum _{i=1}^N{t}_{i,|v_i|}^F\right))\forall i\in M\forall k\in \mathcal{N}$$

(12)

$$s.t{E}_i^c+E_i^t\le B\forall i\in N$$

(13)

We need to enumerate all the possible strategies of offloading, duplication and scheduling, to find the one that can minimize the result of completion time of all the users. Note that $t_{i,|v_i|}^F$ denote the actual finish time of the exit subtask, which also represent the completion time of the application. We can easily reduce this problem into 0-1 knapsack problem; thus, this problem is NP-hard. In the following sections, we propose heuristic algorithms to solve our duplication-based and energy-aware task offloading problem efficiently.

4. Duplication-Base Offloading Strategy

In this section, we present an efficient duplication-base and energy-aware task offloading (DETO) algorithm according to the optimization problem defined in Equation (12). In the DETO algorithm, we only consider a single-user MEC system with one edge server, and then we further extend the DETO algorithm to multi-user edge networks in the next section. The DETO algorithm can be divided into three phases: the (1) listing phase, (2) processor selection phase and (3) energy-aware duplication phase.

4.1. Listing Phase

Considering the intricate dependencies of the subtasks in the application. At first, we need to order the subtasks by their priorities, which depend not only on the dependency relations among subtasks but also on the important degrees of the subtask in DAG. In this way, the more critical subtask and its duplication can be assigned to the processor preferentially to reduce the overall completion time.

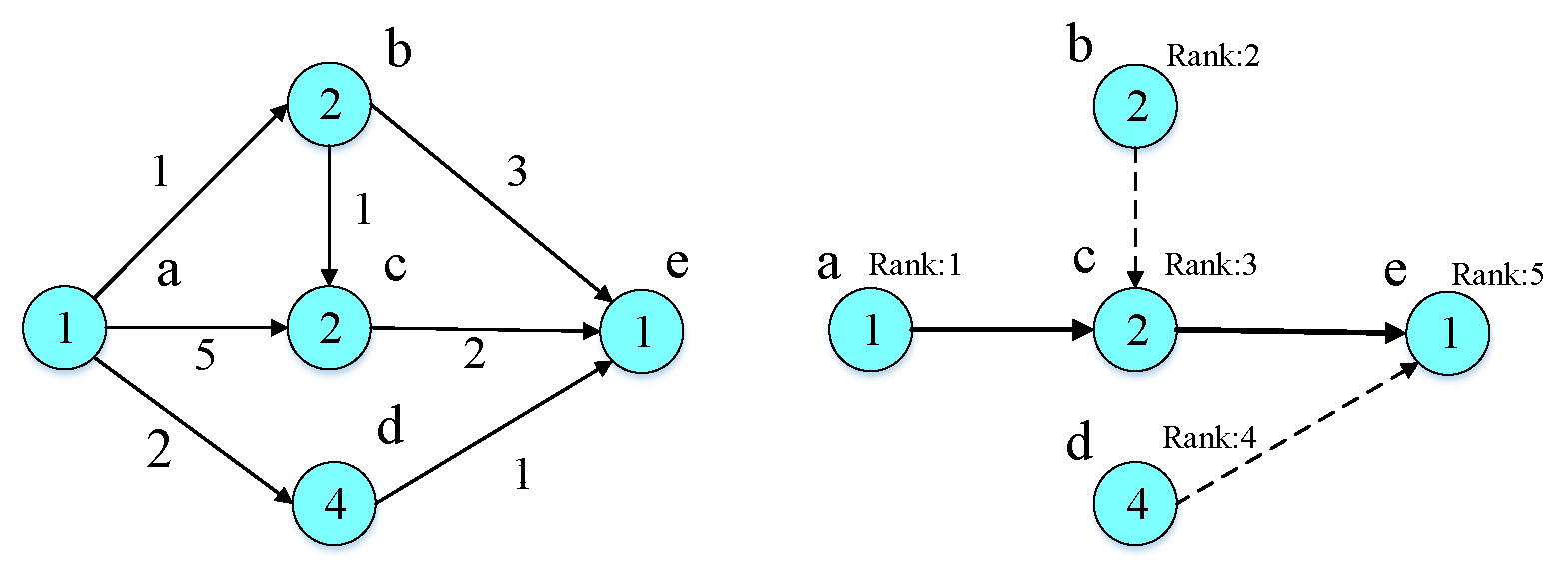
Given an application DAG, as shown in Figure 2, we utilize the average execution time $\overline{t_{i,j}}$ to label the value on each node and use the average transmission $\overline{C_{i,j}}$ to mark the weight on each link. Furthermore, the average earliest start time $\overline{t_{i,j}^{ES}}$ can be computed recursively by traversing the DAG downward, starting from the entry node, where the $\overline{t_{i,1}^{ES}}=0$:

$$\overline{t_{i,j}^{ES}}=\underset{l\in pred\left(j\right)}{max}\left\{\right(\overline{t_{i,l}^{ES}}+\overline{t_{i,l}}+\overline{C_{l,j}}\}$$

(14)

The average latest start time $\overline{t_{i,j}^{LS}}$ can be obtained recursively by traversing the DAG downward, starting from the exit node, where the $\overline{t_{i,|v_i|}^{ES}}=\overline{t_{i,|v_i|}^{LS}}$:

$$\overline{t_{i,j}^{LS}}=\underset{k\in succ\left(j\right)}{max}\left\{\right(\overline{t_{i,k}^{LS}}-\overline{C_{j,k}}\}-\overline{t_{i,k}}$$

(15)

After we obtained $\overline{t_{i,j}^{ES}}$ and $\overline{t_{i,j}^{LS}}$ from these equations, shown in

Table 3. Earliest start/finish time.

	Earliest Start Time	Earliest Finish Time
Node a	0 ms	0 ms
Node b	2 ms	3 ms
Node c	6 ms	6 ms
Node d	3 ms	5 ms
Node e	10 ms	10 ms

, according to the DAG in Figure 2, the DAG is divided into a set of sub-tree. The root of each sub-trees is defined as a critical node (CN), whose $\overline{t_{i,j}^{ES}}$ is equal to the $\overline{t_{i,j}^{LS}}$. The critical nodes are shown by the thick edges connection them, which are node a, node c and node e. The list algorithm starts with critical node (node a) with the minimum value of average earliest time and if the node has parent nodes, assign the highest priority to them. Then, we assign the priority to this critical node. By repeating the above steps, we can obtain the rank of all the nodes shown in Figure 2.

4.2. Processor Selection Phase

After we obtain the priority of each subtask, we need to schedule them and their duplication on its “best” processor. The duplication-based task offloading scheme is described in Algorithm 1. Before that, we give the definition of the $Critical$$Predecessor$ (CP). According to Equation (5), the subtask start time depends on the data arrival time of the predecessor task. Furthermore, the predecessor task from which the data arrives at the latest time is defined as the critical predecessor (CP).

Algorithm 1 The duplication-based task offloading algorithm.

1. Sort all the subtasks in DAG into a $Ran{k}_{list}$ by increasing the order of their rank 2. while there are unscheduled subtasks in the $Ran{k}_{list}$ 3.       select the first unscheduled subtask $T_{i,j}$ in $Ran{k}_{list}$; 4.        Let $E_t=\infty$; 5       For each process $S_1$ in S 6.                compute the $t_{i,j,s_1}^F$ without duplication 7.                if $t_{i,j,s_1}^F$ < $E_t$ 8.                   $E_t=t_{{i,j,s_1}^F}$, save scheduling result to $\mathit{P}$ 9.              end if; 10.              Let $T_{i,l}$ = $CP\left(T_{i,j}\right)$ 11.              For each processor $S_2$ in S 12.              recompute $t_{i,j,s_1}^F$ while duplicating $T_{i,l}$ on $S_2$ 13.                if $t_{i,j,s_1}^F$ < $E_t$ 14.                 $E_t$ = $t_{i,j,s_1}^F$, save scheduling result to $\mathit{P}$ 15.                 Recompute the $T_{i,l}$ = $CP\left(T_{i,j}\right)$ 16.                  Goto $line12$ 17.              end if 18.              end For 19.       end For 20.      Schedule $T_{i,j}$ according to the scheduling result $\mathit{P}$ 21.      Mark $T_{i,j}$ as scheduled 22. end while

In the algorithm, there are three nested loops: (1) In the first loop (step from 2 to 22), all the subtasks and possible duplications will be assigned and scheduled by order of increasing rank value. (2) The second “for loop” (step from 5 to 19) is to consider each processor in P as a potential processor to which the subtask $T_{i,j}$ could be scheduled and will find the “best” processor that minimizes its finish time. (3) Inside the second loop, the third loop (step from 11 to 17) introduces the task duplication into the algorithm. In $line$ 12, we duplicate the critical predecessor of $T_{i,j}$ on each processor to see whether the finish time of $T_{i,j}$ can be further reduced.

Since the critical predecessor is the one from which data will be received the latest by $T_{i,j}$, duplicating other predecessor tasks other than the CP will not decrease the finish time of $T_{i,j}$. In addition, if the duplicate the CP of $T_{i,j}$ will reduce the finish time of $T_{i,j}$, the duplication decision and scheduling result will be saved to P. After the duplication operation, the previously critical node may not be the latest one that transfers the date to the $T_{i,j}$. Thus, in $line$ 14 and $line$ 15, we recompute the critical predecessor and return back the third loop attempt to further reduce the finish time of $T_{i,j}$ by replicating the new critical predecessor.

4.3. Energy-Aware Duplication Phase

From the above duplication-based task offloading algorithm, it can be found that all the subtasks are scheduled by order of its priority, and the optimization objective is the finish time of current subtasks. However, minimizing the finish time of each critical subtask cannot always guarantee the optimization of the overall delay of application. Moreover, an inappropriate duplication may achieve the local optimization solution; however, it may occupy the CPU cycle for successor subtasks, which leads to an increase in the overall completion time and unnecessary energy consumption. Thus, in this subsection, we introduce the energy-aware duplication algorithms (as in Algorithm 2).

Algorithm 2 The energy-aware duplication algorithm.

1. While there are unchecked subtask in $Ran{k}_{list}$ 2.         select the first unchecked subtask $T_{i,j}$ in $Ran{k}_{list}$ 3.         For each duplication $T_{i,j^{\prime }}$ 4.              Reschedule all the subtask after $T_{i,j}$ in                $Ran{k}_{list}$ without $T_{i,j^{\prime }}$ by Algorithm 1. 5.               Compute the time and energy reduction ${\delta }_t$, ${\delta }_e$ 7.             if ${\delta }_t\le 0$ or $\frac{-{\delta }_t}{{\delta }_e}$ ≤ $Ratio$ 8.                Delete $T_i,j^{\prime }$ and save the current rescheduling 9.            else 10.               Rollback the delete operation of $T_i,j^{\prime }$ 11.           end if 12.         end For 13.         Mark $T_{i,j}$ as checked 14. end while

In this algorithm, we remove the duplications that did not help in improving the performance (energy consumption and delay reduction must be comprehensive consideration). Following Algorithm 1, we check each duplication one after another by order of its rank ($line$ 2). Note that in this algorithm, we did not distinguish the duplicate task and an original task, which uniformly called duplication. In the “for loop” ($line$ 3 to $line$ 12), we attempt to remove each subtask to see whether it can improve the performance or not. In ($line$ 7), the metric $Ratio$ can be adjusted based on the remaining energy of a specific user device.

Note that the ${\delta }_e$ only refers to energy reduction in the user devices, and if the duplication the executed in the edge server, the energy cost is equal to 0. It is also worth noting that, once any subtask is removed, the scheduling result of all the succeeded subtasks will be changed (otherwise Algorithm 1 is meaningless), and thus we need to call Algorithm 1 for successor subtasks.

Through the above-mentioned three phases of the algorithm, we finally obtain an efficient duplication-base and energy-aware task offloading algorithm (DETO) in a single-user MEC system with only one server. In the next section, we extend the DETO algorithm to the multi-user and multi-server edge networks.

5. The DETO Algorithm in the Ultra-Dense Network

The explosive number of users in the edge network is challenging for the most advanced fourth-generation network. Furthermore, the ultra-dense network has been considered as a promising candidate for future 5G networks to meet this explosive user demand. The basic idea is to have multiple servers as close as possible to the end users. Furthermore, each user can offload their tasks to either one of them according to the condition of each server (such as the channel condition and the computation load of a server).

However, considering the high dynamic characteristics of the edge scenario, each user has little information about others. Thus, the user cannot estimate the wireless communication rate and the execution time in the server according to Equations (6) and (7). To overcome this dilemma, we use the centralized DETO algorithm in the ultra-dense network (as shown in the Algorithm 3):

Algorithm 3 The centralized DETO algorithm.

1. enumerate all optional offloading decision D = {$d_1$,$d_2$…,$d_n$} 2.    for all server $m\in \mathcal{M}$ do 3.       Create the user group $U_m$, in which $d_i=m$ 4.       integrate $G_i$ of the users in $U_m$ to $G_{u_k}$ 5.      Update the transmission delay $Rat{e}_{i,k}\left(\mathbf{D}\right)$ 6.      Call DETO algorithm to obtain the subtask scheduling, subtask duplication scheme of all users 7.  end for all 8.  find the optimal offloading strategy $\mathbf{D}$ and its related subtask scheduling, subtask duplication scheme for each user

In the centralized DETO scheme, we first enumerate all the possible offloading strategies and then call the DETO algorithm to obtain the subtask scheduling and duplication scheme under a certain offloading strategy. In $line$ 4, we integrate the task of graphs of the users that offload to the same server, and thus the input of Algorithm 1 will be a large DAG, which consists of a series of disconnected subgraphs, and it is impossible for us to find a critical path as shown in $Listing$ $Phase$. Thus, we need to propose a new metric to order the subtasks.

$$rank(i,j)=\overline{t_{i,j}}+\underset{l\in succ\left(j\right)}{max}\{rank(i,l)+\overline{C_{l,j}}\}$$

(16)

The $rank(i,j)$ is the length of the critical path from task j to the exit task. The higher the value is, the higher the priority. For example, in Figure 2, the rank of each node is as follows: rank(a) = 10, rank(b) = 8, rank(c) = 5, rank(d) = 6, rank(c) = 1. In this way, we can rank all the subtasks from the different disconnected subgraphs.

Theorem 1.

The computational complexity of centralized DETO in Algorithm 3 is no less than $O[{(S+1)}^N·(n+2e)]$, where S and N are the numbers of edge servers and IoT devices, respectively. n and e denote the number of subtask and the edge of DAG.

Proof. 

We assume that there are S users who need to offload their tasks to the edge network, which consists of N edge servers. The number of possible optional offloading strategies are:

$$\left(\genfrac{}{}{0pt}{}{0}{N}\right)·S^0+\left(\genfrac{}{}{0pt}{}{1}{N}\right)·S^1+\dots \dots \left(\genfrac{}{}{0pt}{}{N}{N}\right)·S^N=\sum _{i=0}^p\left(\genfrac{}{}{0pt}{}{p}{N}\right)·S^p$$

(17)

where p denotes the number of users who decide to offload their tasks. According to Newton’s binomial theorem:

$$\sum _{i=0}^i\left(\genfrac{}{}{0pt}{}{p}{N}\right)·S^p={(S+1)}^N$$

(18)

Each potential offloading strategy needs to invoke the DETO algorithm to obtain the server scheduling result and its computation delay. The time complexity of the first part in DETO is $O(n+2e)$, and the time complexity of the second step in DETO is $O\left(n\right)$. Therefore, the computational complexity of centralized DETO is no less than $[O{(S+1)}^N·(n+2e)]$. □

From Theorem 1, we find that the centralised DETO algorithm would cause considerable overhead with the increasing number of users and edge servers, as it always enumerates all the optional offloading decisions. Even worse, it would possibly lead to system failure if the centralized controller were involved in hardware failure. In this section, we adopt a game-theoretic approach to address such a challenge. Game theory is a useful framework for designing decentralized scheme, such that user devices in the edge network can self-organize into mutually satisfactory computation offloading and duplication decisions.

In the game-theory-based offloading and duplication strategy in the ultra-dense network, the user can make the decision locally according to the information broadcast by the edge server at each step and make an optimal local decision. After finite steps, none of the users can further improve its execution time by changing its offloading and duplication strategy unilaterally. The details of distributed DETO are described below:

• Initialize step: Each device executes all its subtasks locally to obtain the completion time. The edge servers will broadcast their communication rate and computation capability to all the users.
• Iterative steps:Each user calls the DETO algorithm discussed in Section 4, assuming that if it uploads its task to each server based on the previous information broadcasted by the server. After that, each user will inform the maximum completion time reduction result and corresponding offloading strategy to the edge network. After the edge network receives all the information transferred by the user, they will accept the offloading request of only one device with the greatest gain, and then only the selected user can update its offloading and duplication strategy. Finally, the related server will broadcast the updated information about the transmitting rate and its scheduling result to the network, which then facilitate the users to make further choices in the next iteration.
• Convergence step: After a finite step, when all the user cannot further reduce its own delay by changing strategy unilaterally, the distributed algorithm is terminated.

Although the distributed DETO algorithm may achieve a higher completion time, it has much higher computation efficiency and provides a workable solution in the ultra-dense network. In the distributed DETO algorithm, each IoT device adjusts its own offloading strategies rely solely on the offloading scheme of other users in the lasted international step. Thus, the computational complexity of distributed DETO is $O(n+2e)$, where n and e denote the number of subtasks and edges in DAG.

A possible drawback is that the convergence time may add further overhead to the offloading system. We argue that this process incurs only an initial delay as normally the task DAGs do not change drastically for a given IoT system. Once the process is finished, each IoT device can perform its offloading decisions to reduce the overall task delay.In the next section, we prove the convergence of the distributed DETO by simulation.

6. Evaluation

In this section, we conduct simulations experiments to evaluate the performance of our proposed offloading algorithm. At first, we study the convergence of the Distribute DETO algorithm and then compare our proposed algorithm with the existing work. Finally, we present the computation resource utilization.

6.1. Experiment Settings

We consider an ultra-dense network (UDN) with a certain number of edge servers and users, which are randomly distributed in a 1 × 1 km area with some heterogeneous edge servers. In this multi-access UDN network, many edge servers are in the vicinity of a given IoT device. Thus, each user has various options in making the offloading scheme. Our goal is to find the appropriate offloading strategies for all the users in the UND efficiently. Each user has a task to be completed with the help of an edge network, which consists of inter-dependency subtasks, and their DAG is generated based on some popular user applications, such as object recognition [27], gesture recognition [10] and video navigation application [28].

We also randomly generate some DAG to verify the adaptability of our offloading algorithm, in which the CPU cycles required by subtasks vary from 30 $Megacycle$ to 120 $Megacycle$. Other experimental settings are made as follows: The wireless channel bandwidth is $B=$ 150 kHz. The transmission power is ranged from 100 to 200 mW [29] randomly among different devices, the background noise is set to −120 dBm [30]. We also assume that the CPU frequency of the edge server (30 GHz) is ten times that of user devices (3 GHz) [29].

6.2. The Convergence of Distributed DETO Algorithm

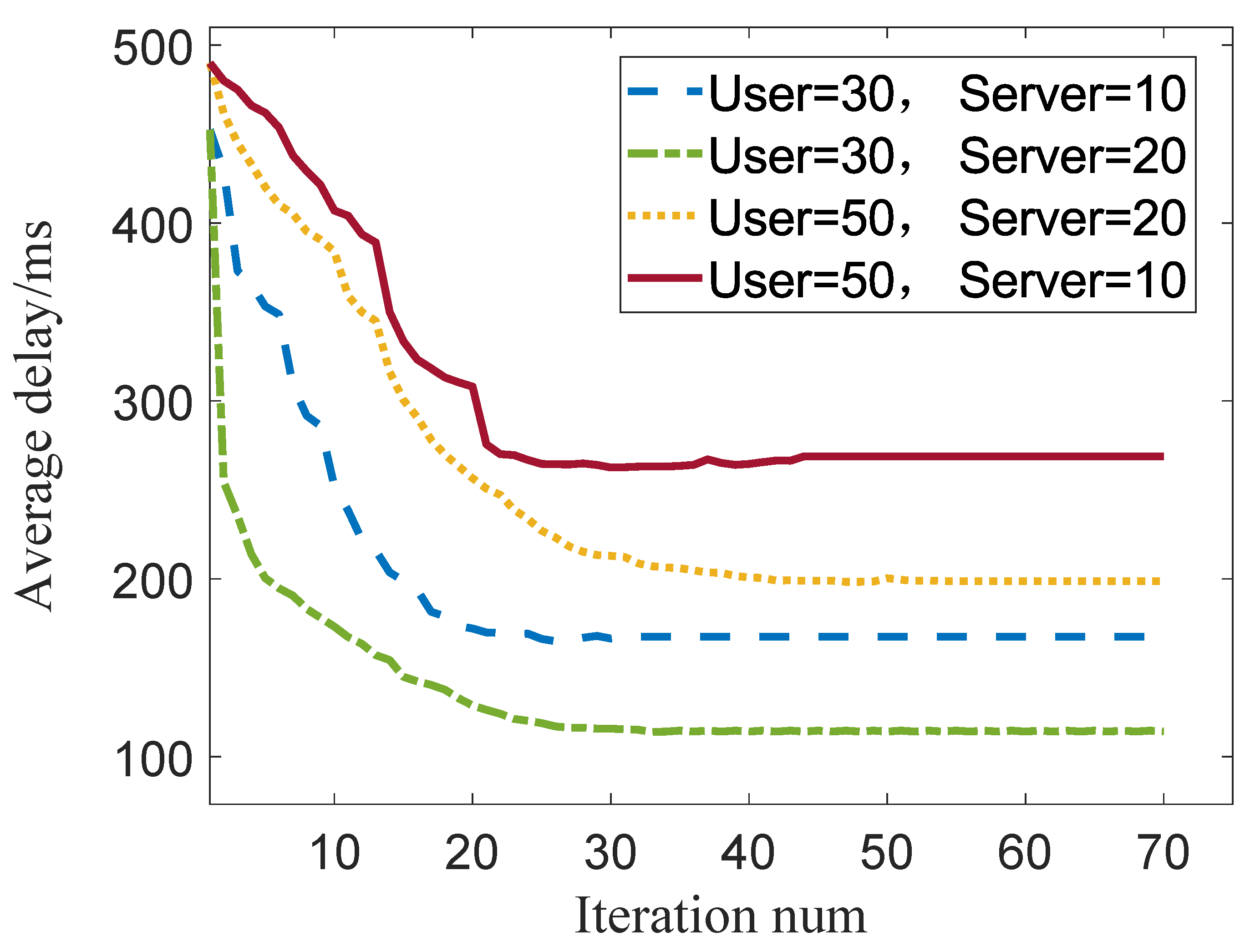
In the multi-user UDN networks, the distributed DETO algorithm is a game-based algorithm; therefore, its convergence must be guaranteed. Figure 3 shows the numerical results of the convergence behavior of distributed DETO algorithm with different number of users and servers.

From this figure, we find that: (1) The distributed DETO algorithm always can reach a Nash equilibrium. (2) The increased number of users will contribute to increasing the convergence time. (3) In a certain number of users, the more edge servers, the lower the average latency, as the user can share more edge computation resources (taking more CPU cycles). However, since the user faces more offloading choices, which comes with the increase in convergence time. (4) The different value of the average delay between the initial step and the convergence step represents the performance gains from edge computing.

6.3. Compared with Existing Work

The distributed DETO algorithm proposed in this work is compared with two different offloading schemes: the PGOA [19] scheme and DEFO [8] scheme.

• PGOA: In [19], they considered the multi-device and multi-MEC scenario of an SCN integrated with MEC and formulated a distributed overhead minimization problem, proposed as the potential game-based offloading algorithm (PGOA), which minimizes the overhead of each user. However, they did not distinguish the subtasks among the applications, and they treated them as an entire task. Thus, they always offloaded these subtasks as a whole to the edge network.
• DEFO: In [8], the author investigated the problem of fine-grained task offloading in edge computing. They proposed a distributed earliest finish time offloading scheme (DEFO) for subtasks from different users, which considered not only the computation workload of the subtask but also the dependency among subtasks in DAG. However, they did not consider utilizing the processor idle time to duplicate predecessor tasks to further reduce the completion time of the application.

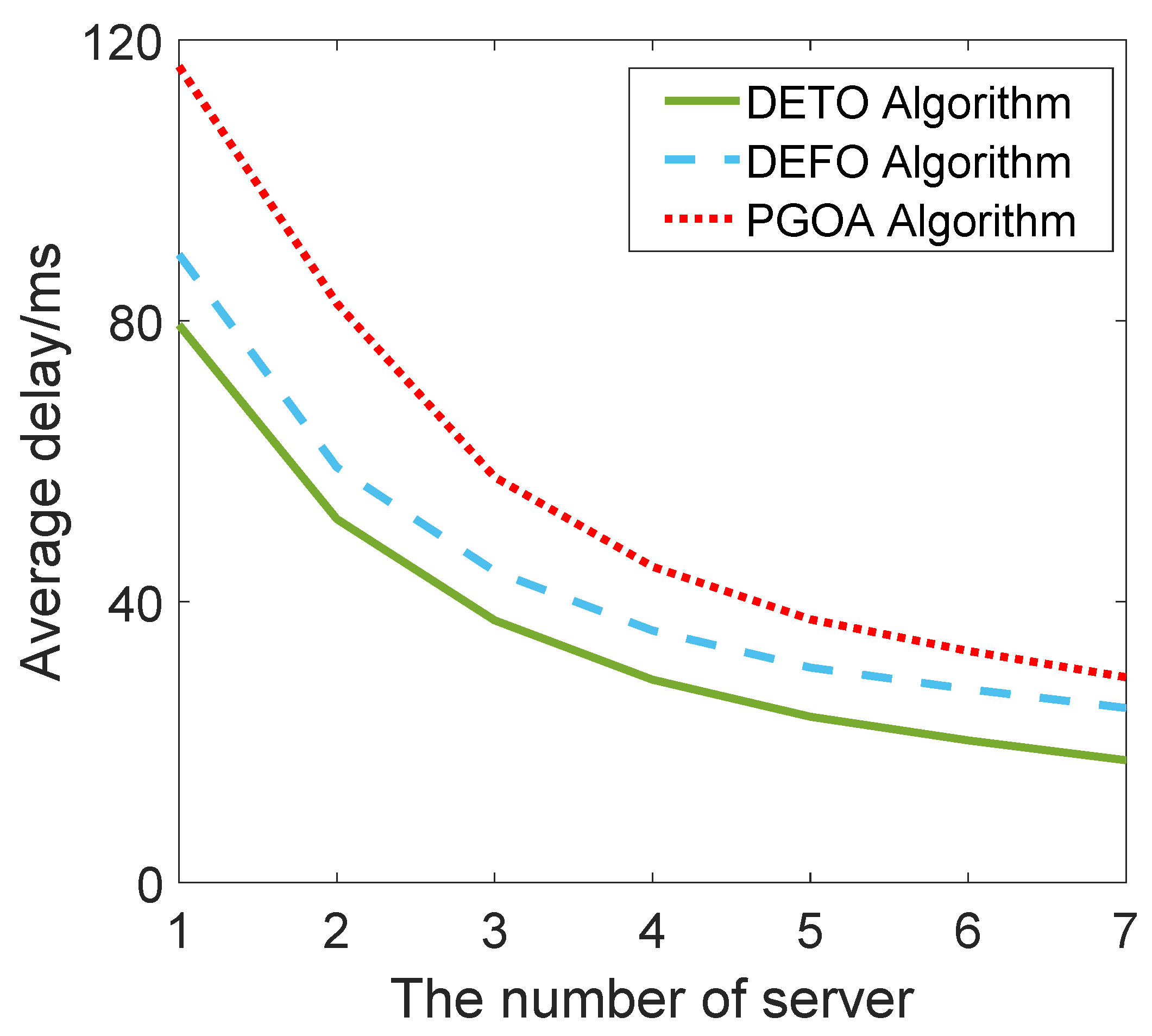
Figure 4 shows the average delay for different network scales in terms of edge servers. The number of edge servers is increased from 1 to 7, and there are twenty users in the edge network. It can be inferred that the average delay will reduce with the increasing number of the server since the users could utilize more edge computation resources (taking more CPU cycles). As the PGOA did not distinguish the subtasks among the application, it always achieves a higher average delay than the fine-grained offloading DEFO and DETO algorithms.

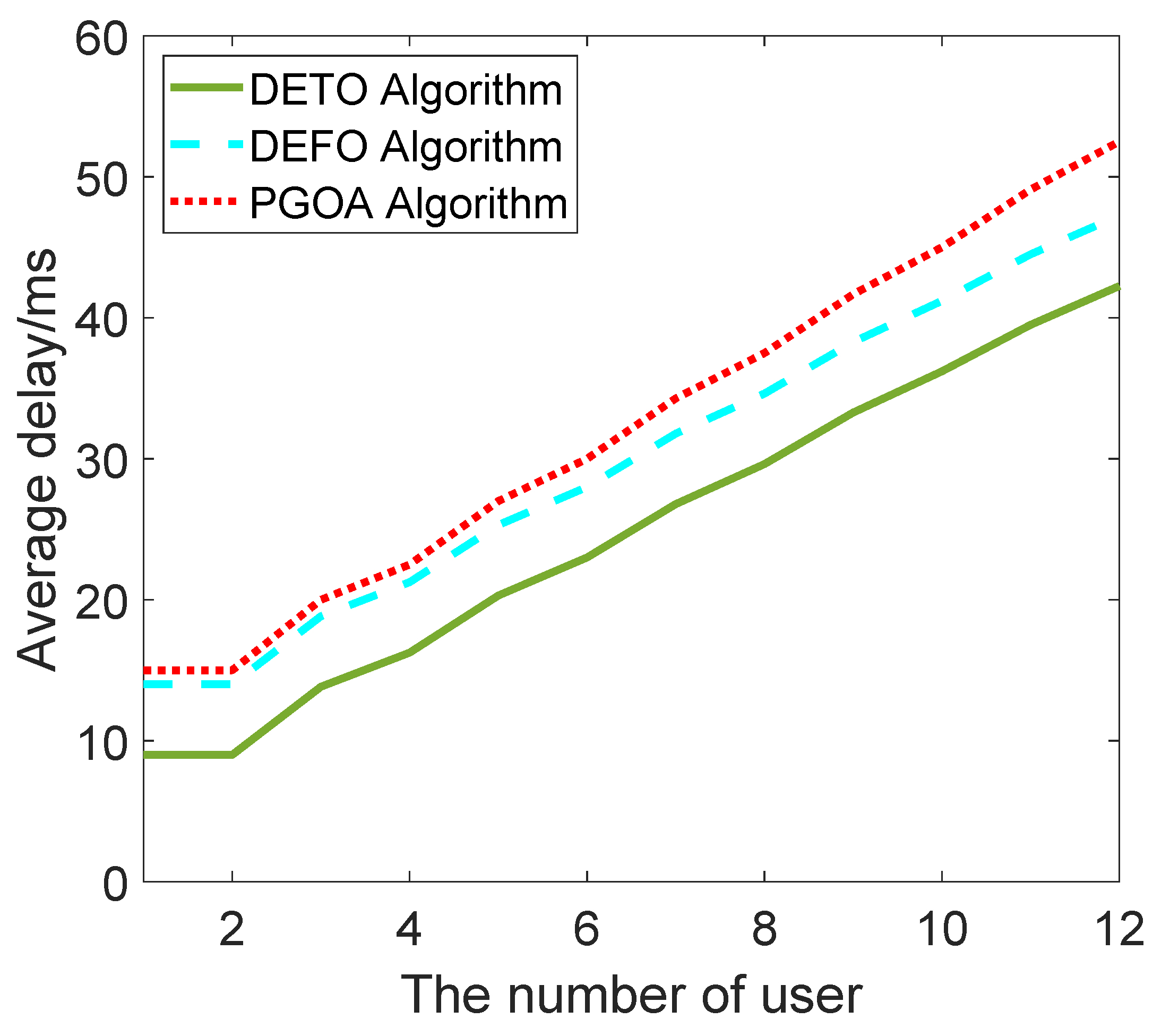
Through utilizing the processor idle time to duplication for certain critical subtasks, our DETO algorithm can further reduce the makespan of all the applications. Figure 5 shows the average delay for the different numbers of users for the same network scale. The number of users grows from 1 to 12, and there are only two edge servers in the network. We find that the average delay will increase with the competing users, and our algorithm can also achieve the minimum delay compared to the other two offloading strategies.

In order to verify the effectiveness of our proposed game-theory-based DETO algorthe ithm, we compare the running time and the average delay with the centralized DETO algorithm.

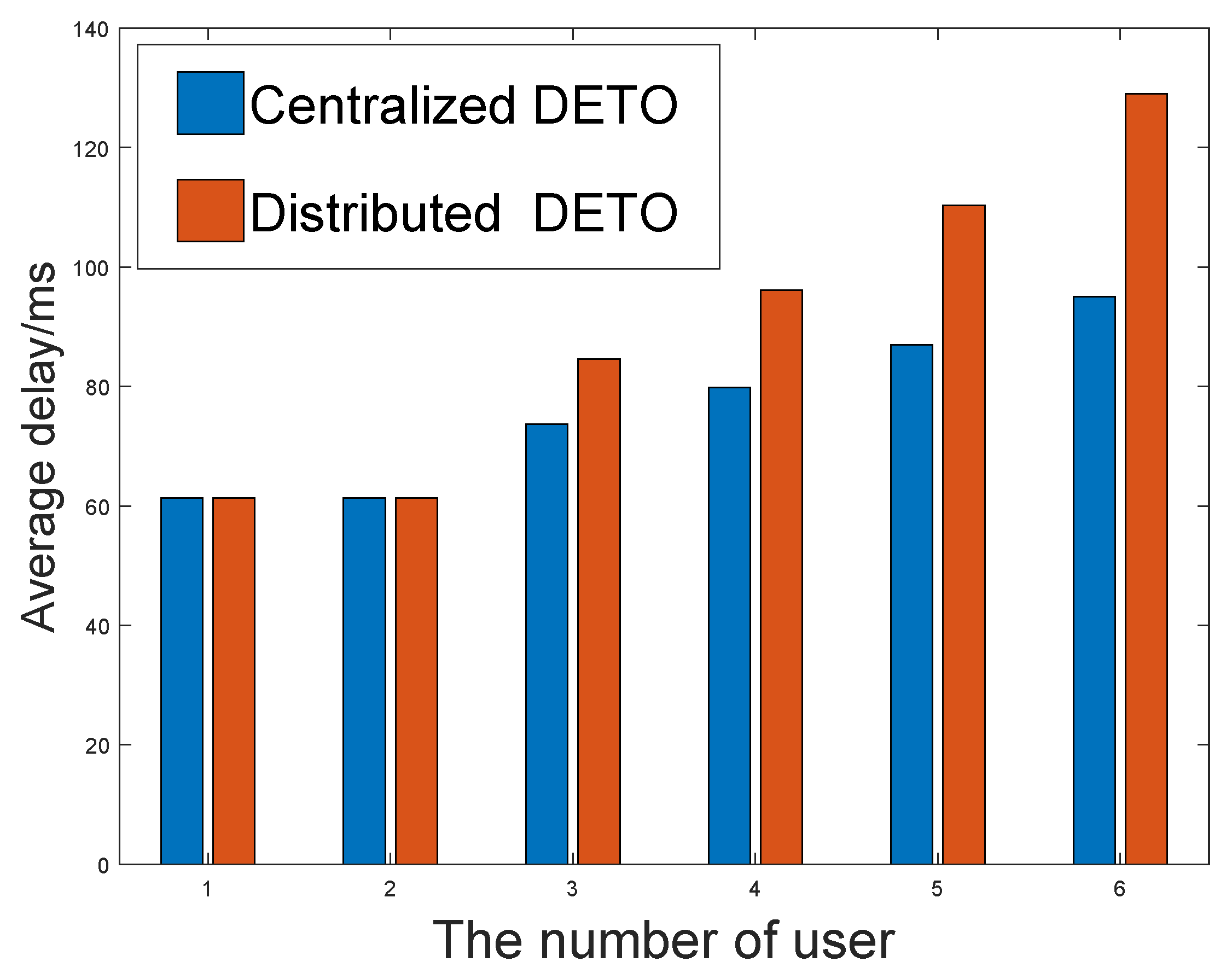
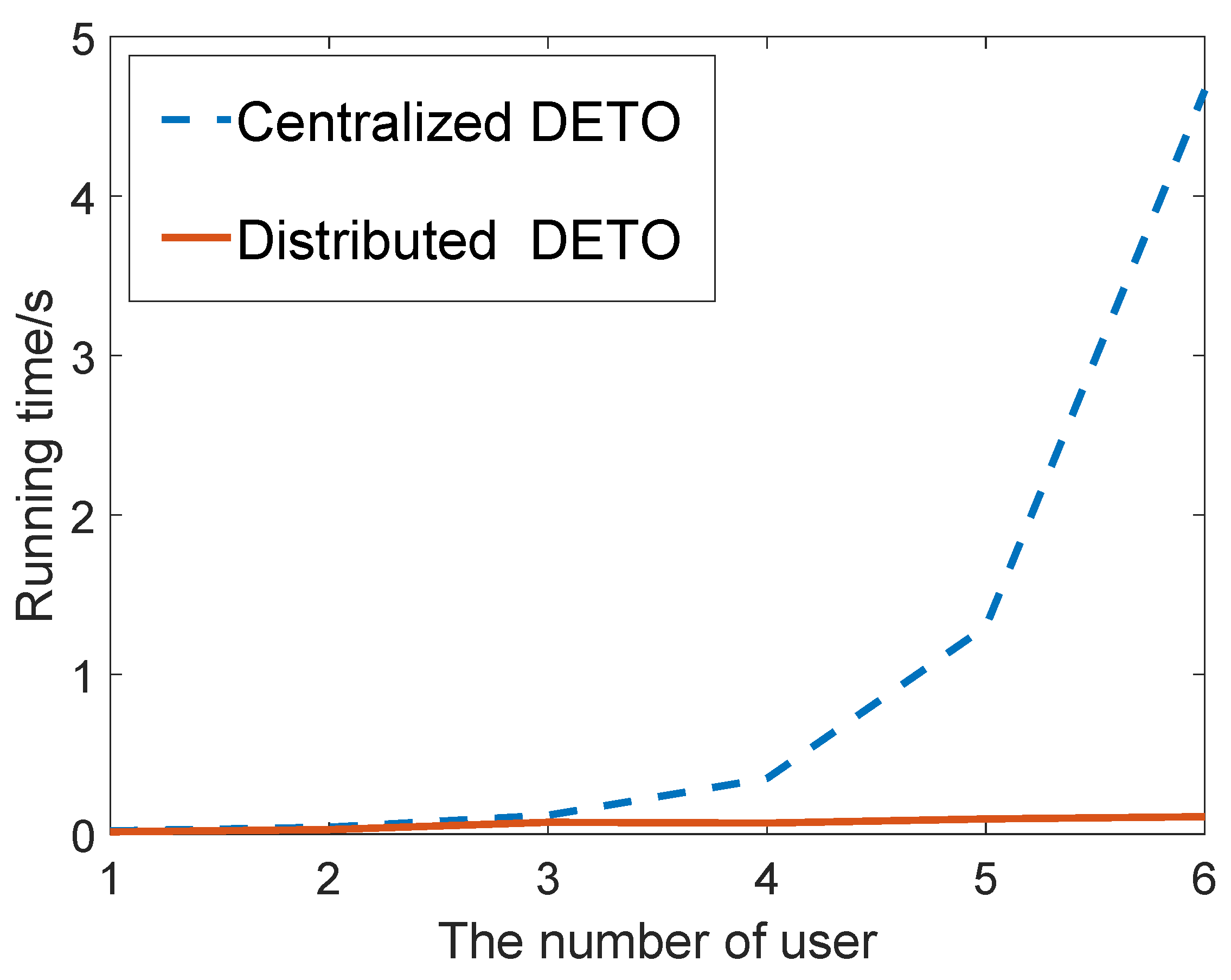
Figure 6 and Figure 7 depict the results and show the comparison between them. The X-axis denotes the number of users. Considering the exponential computational complexity of centralized DETO algorithm, the number of servers is set to 2, and the number of users increases from 1 to 8. As illustrated in these figures, although the centralized algorithm achieves a slightly higher average delay, it has much a higher computation efficiency and provides a workable solution in the ultra-dense network.

6.4. Computation Resource Utilization

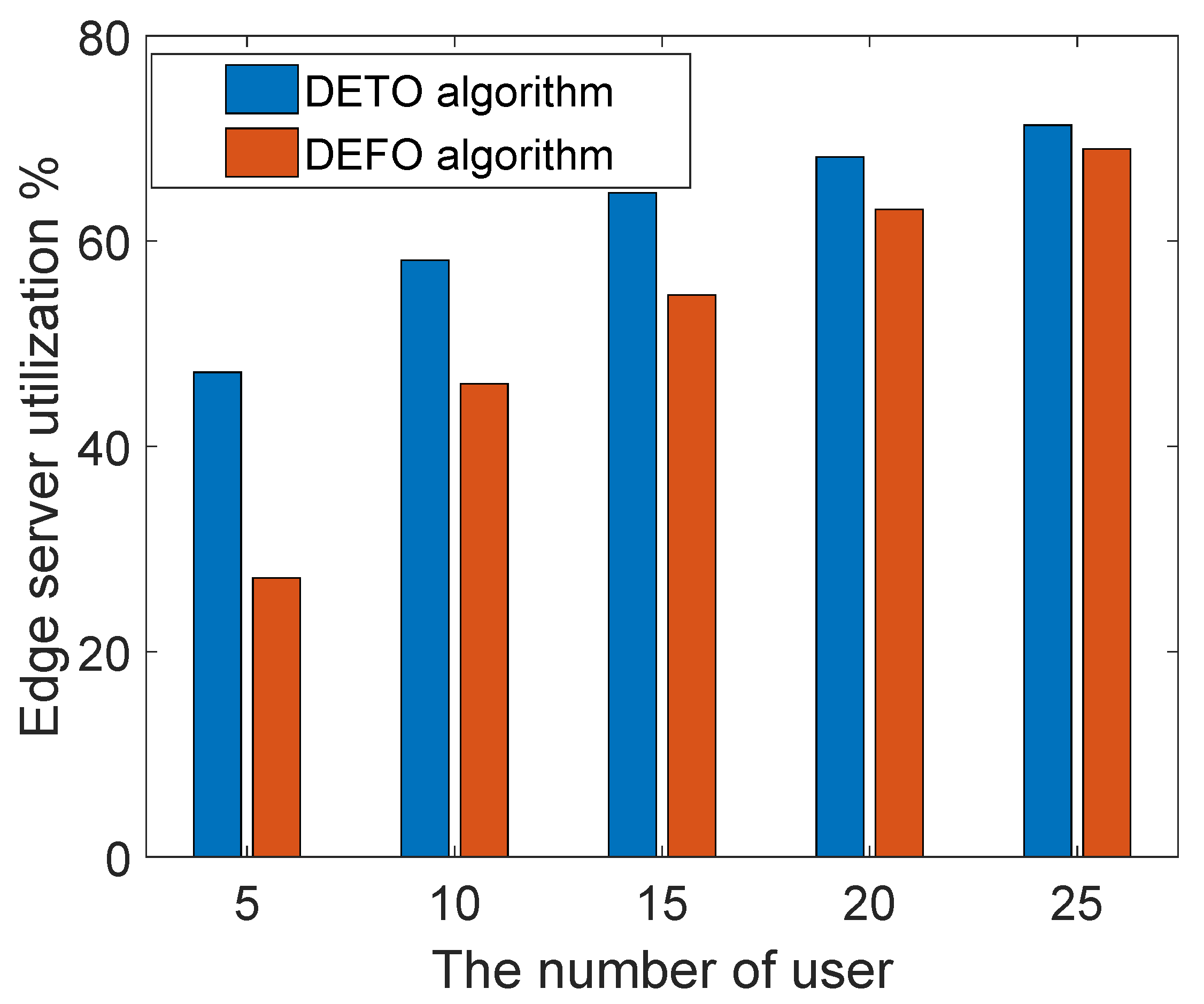
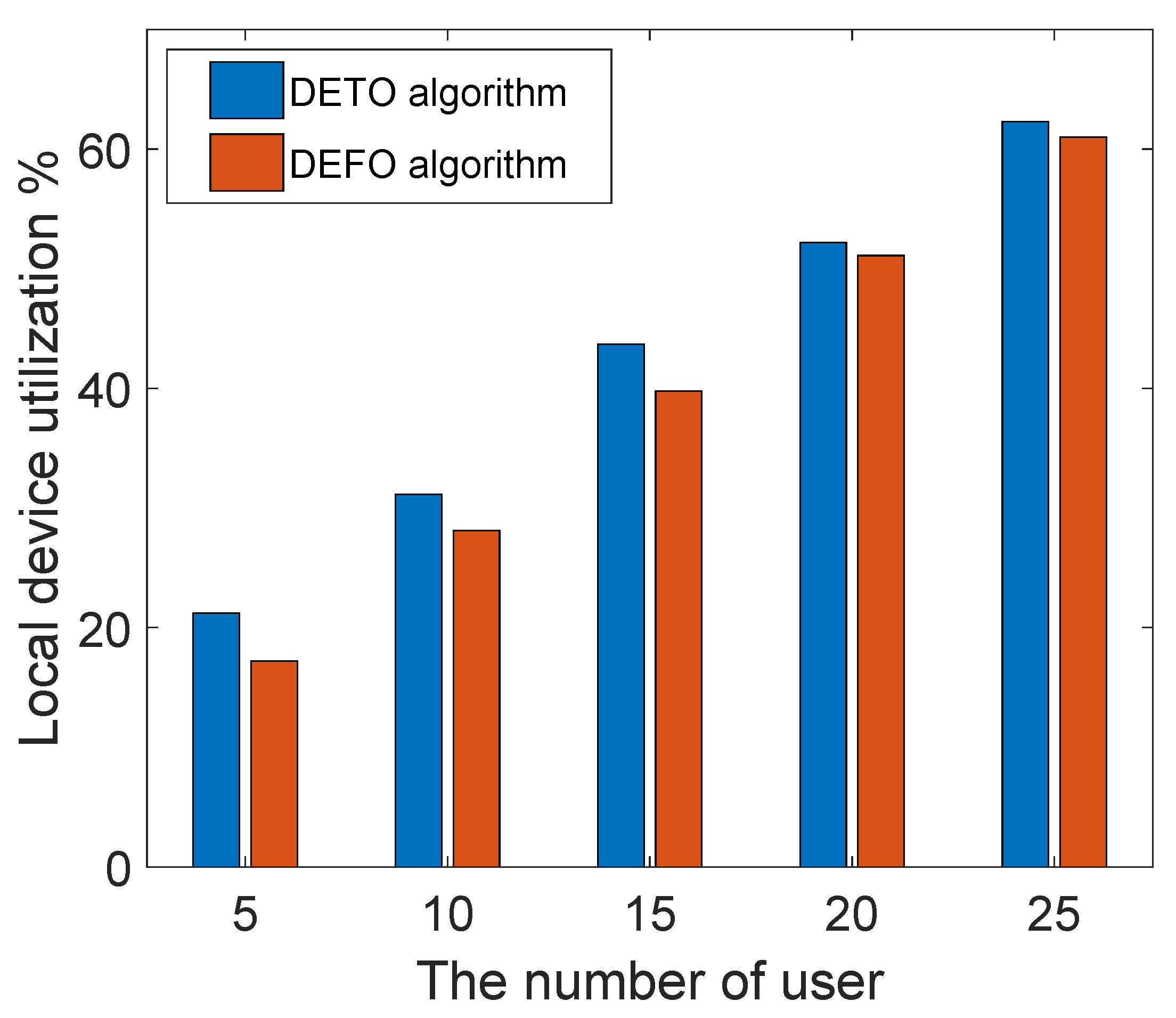
The computation resource utilization mainly refers to CPU utilization, the CPU utilization can be calculated by using the following formula: 100%—(the percentage of time that is spent in idle task). The computation resource utilization is shown in Figure 8 and Figure 9. There are three servers in the edge network, and the number of users increases from 5 to 25. Since our work introduces the duplication subtasks to reduce the completion time, the utilization of the edge server is higher than the DEFO algorithm—that is to say, our offloading scheme reduces the makespan of an application by making full use of the edge server.

As shown in Figure 9, there is a small difference between the local processor utilization of our algorithm and the DEFO algorithm. As in the energy-aware duplication phase, we remove some duplications in the local server if it incurs much extra energy cost. From these figures, with the increasing number of users, the edge computation resource (CPU cycles) comes to the saturation condition, and the user would not offload their task to the edge server. As a result, the computation resource utilization of two different algorithms tends to be the same.

7. Conclusions

In this paper, we first proposed the DETO algorithm, which exploits task duplications to enhance the parallelism between users and edge servers. We then further designed a distributed DETO algorithm, which was able to coordinate the duplication scheme among multiple users. Finally, we conducted extensive simulation experiments, and the performance results showed that DETO can reduce the overall completion and improve the resource utilization of the edge servers.