Fast Motion Model of Road Vehicles with Artificial Neural Networks
Abstract
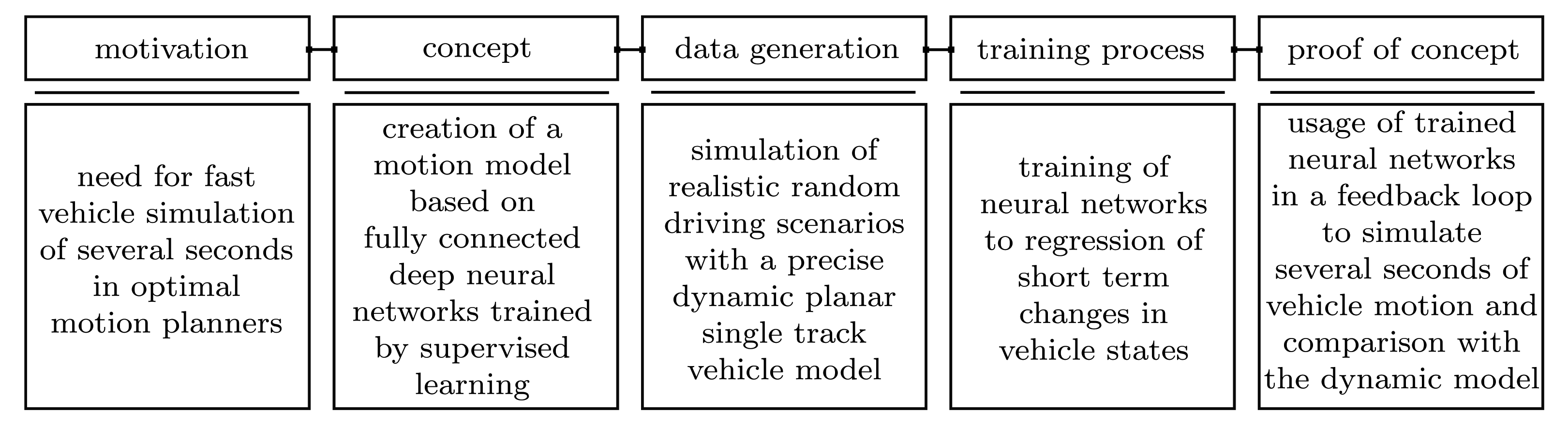
1. Introduction
1.1. Literature Outlook
1.2. Motivation
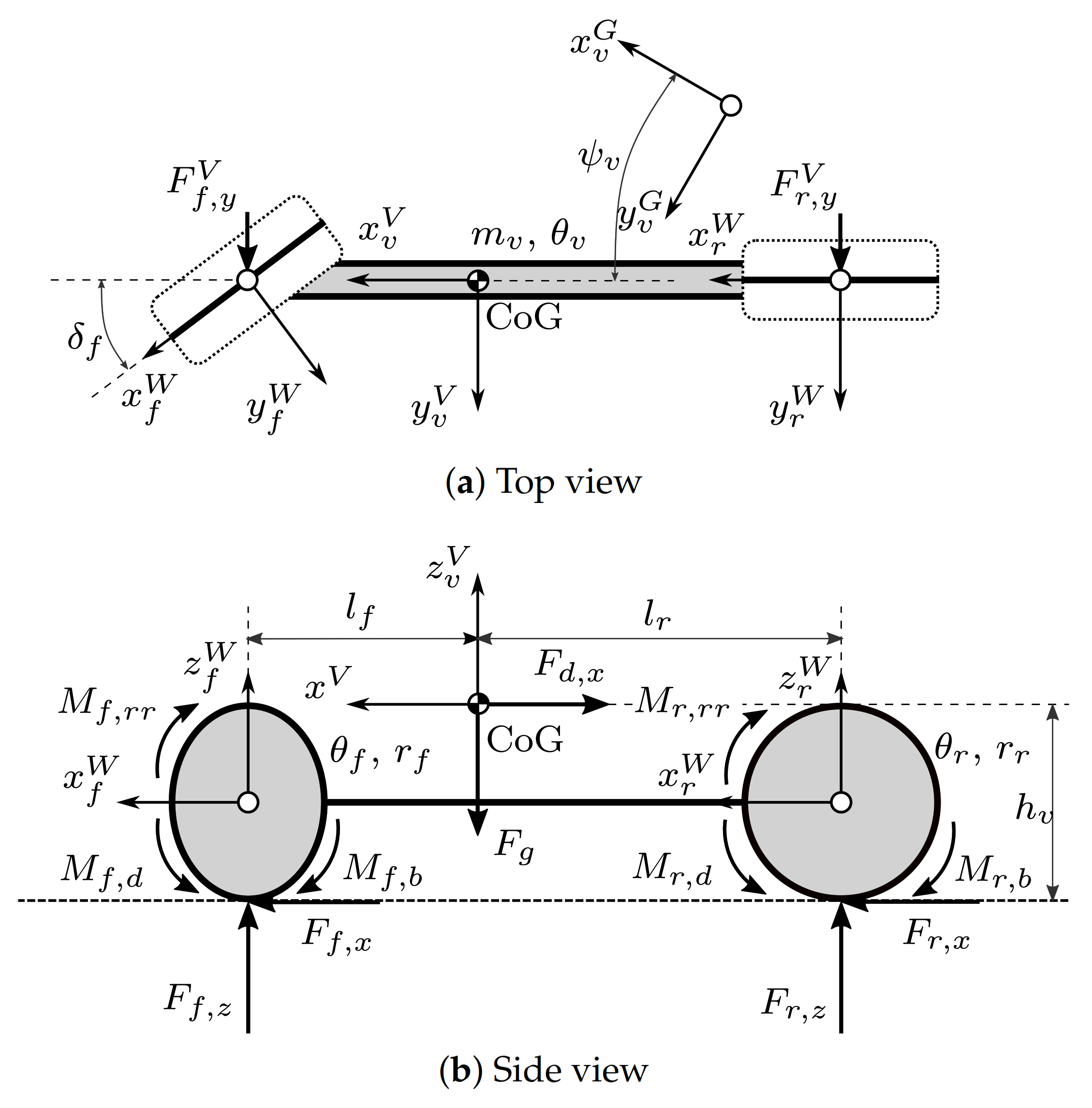
2. Nonlinear Single Track Vehicle Model
2.1. Model Components
2.2. Dynamics of the Chassis
2.3. Dynamics of the Wheels
2.4. Steering Actuation
2.5. Closed Loop Control
2.6. Simulation of Model
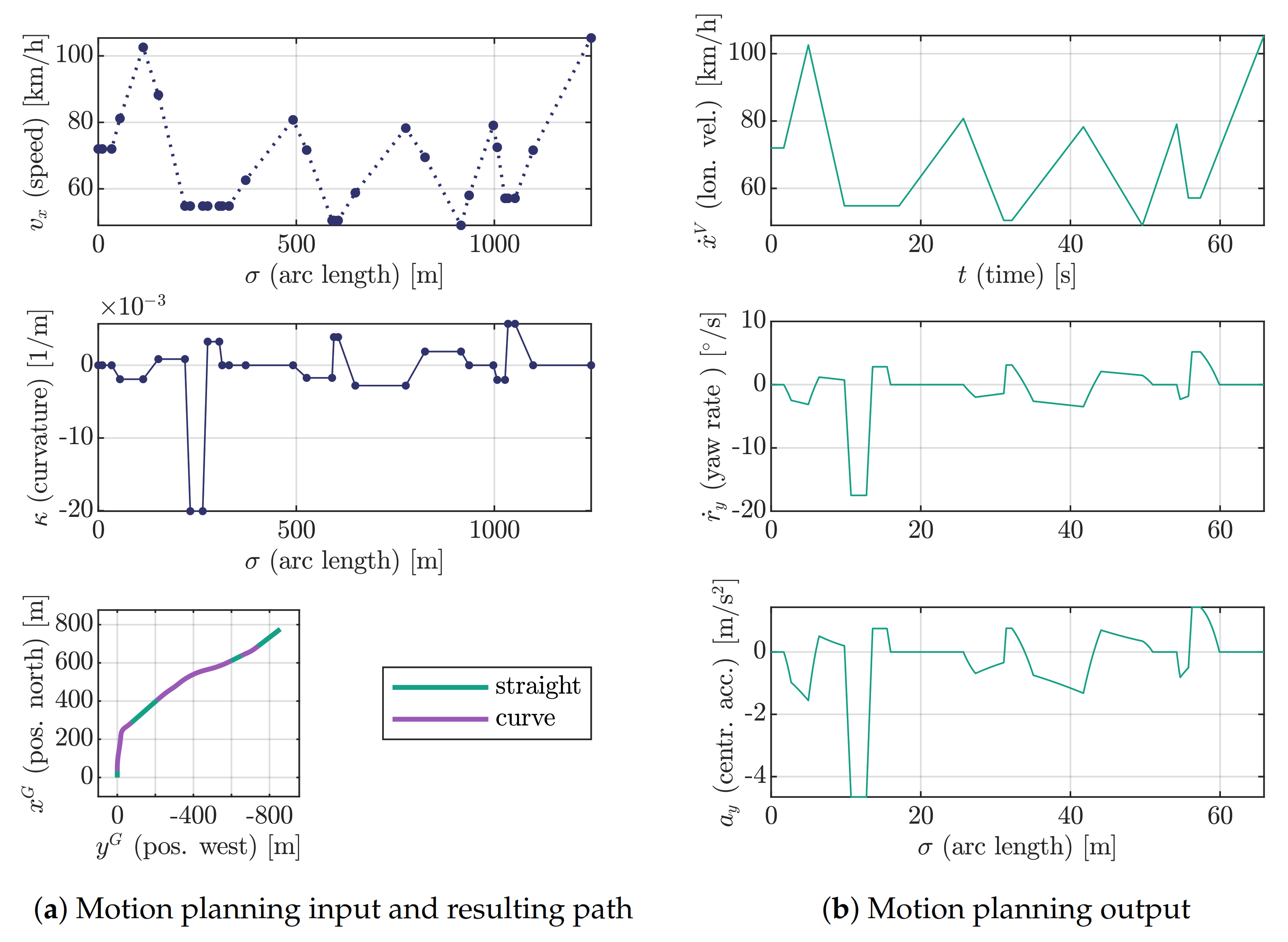
3. Random Trajectory Planning
3.1. Motion Planning Based on Piecewise Linear Curvature and Travel Velocity Functions
3.2. Random Planning
- The knot points of the traveling velocity profile are chosen randomly between allowed lower (10 m/s) and upper (30 m/s) limits.
- Minimal allowed radii are calculated for each section based on maximal allowed lateral acceleration (5 m/s2).
- Radii of each section are chosen randomly in such a way that the values are between and . The factor (10) is a planning parameter.
- Lengths of each section are chosen randomly in such a way that the values are between and . The factors (0.1) and (0.2) are planning parameters.
- Curvature values are calculated, and half of them are inverted to provide left and right turns with equal probability.
- A (0.35) proportion of the curvature values is nulled out to provide straight segments in a way that neighboring straight segments are not allowed.
- Transitions are calculated between each of the previous sections in such way that the proportion of their lengths to the segments lengths (0.4) is given.
- Arc length knot points are calculated by a cumulative sum of segment lengths .
- The curvature and travel velocity profile calculated in 1–8 is then provided to the planner described in Section 3.1 to get the random reference trajectory.
4. Neural Network Based Vehicle Model
4.1. Input–Output Concept
4.2. Learning Sample Generation
4.3. Neural Network Architecture
4.4. Training Process
4.5. Motion Prediction in Feedback Loop
- Input vector is applied to the neural network to compute output . In practice, input and output vectors must be scaled with the scaling vectors in Equations (59) and (60), but this is not reflected to in the equations for the sake of simplicity.
- Vehicle state variables for which estimations are available in the neural network output are calculated byfor general state .
- For variant V0, yaw angle is calculated by numerical integration as
- For variants V0–2, position coordinates are calculated by numerical integration aswhere velocities and are calculated from and by a rotation with −.
- Vehicle state derivative variables for which estimations are available in the neural network output are estimated directly with differencesfor general state .
- Inertial accelerations in momentaneous vehicle frame are evaluated asto take the rotating frame of reference into account.
- Input vector of next step, is assembled from vehicle inputs and results of Equation (62).
- Steps 1–7 are repeated until simulation is finished.
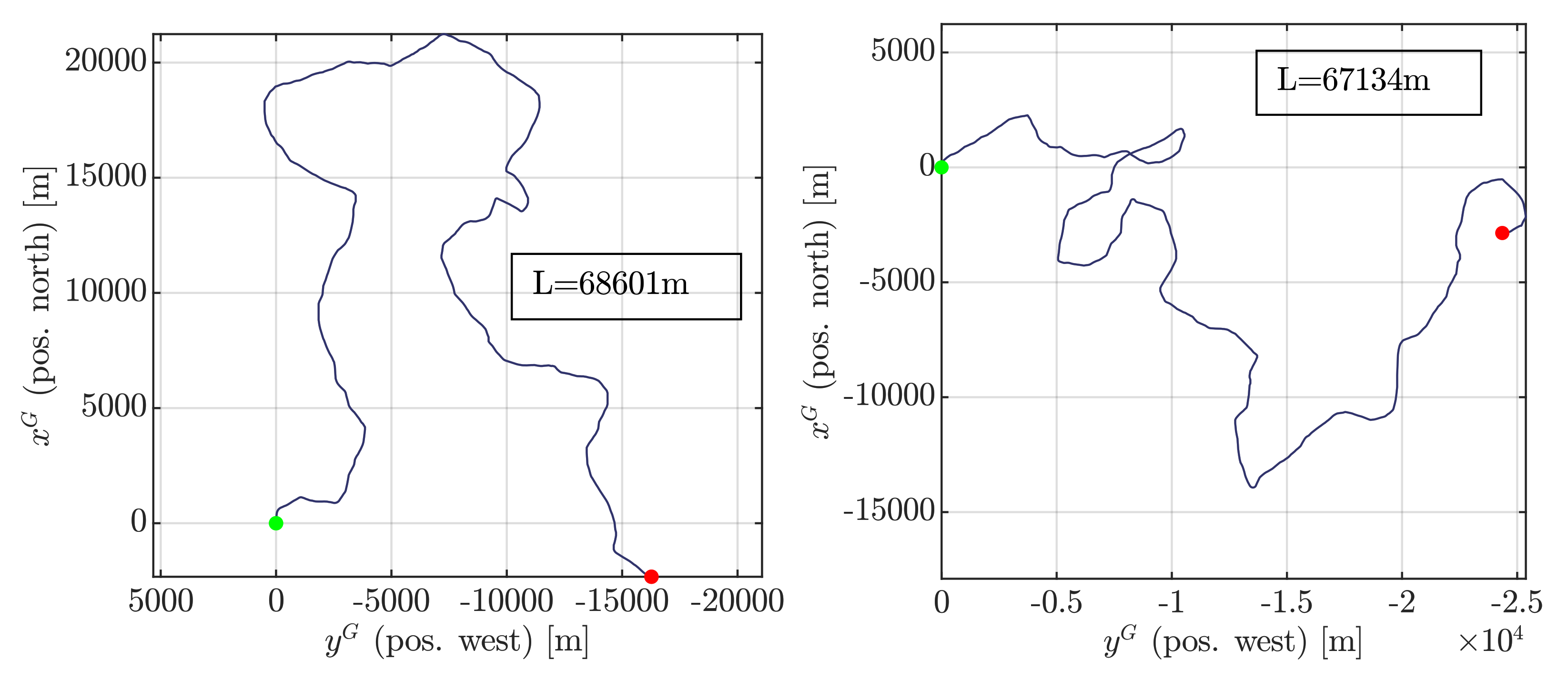
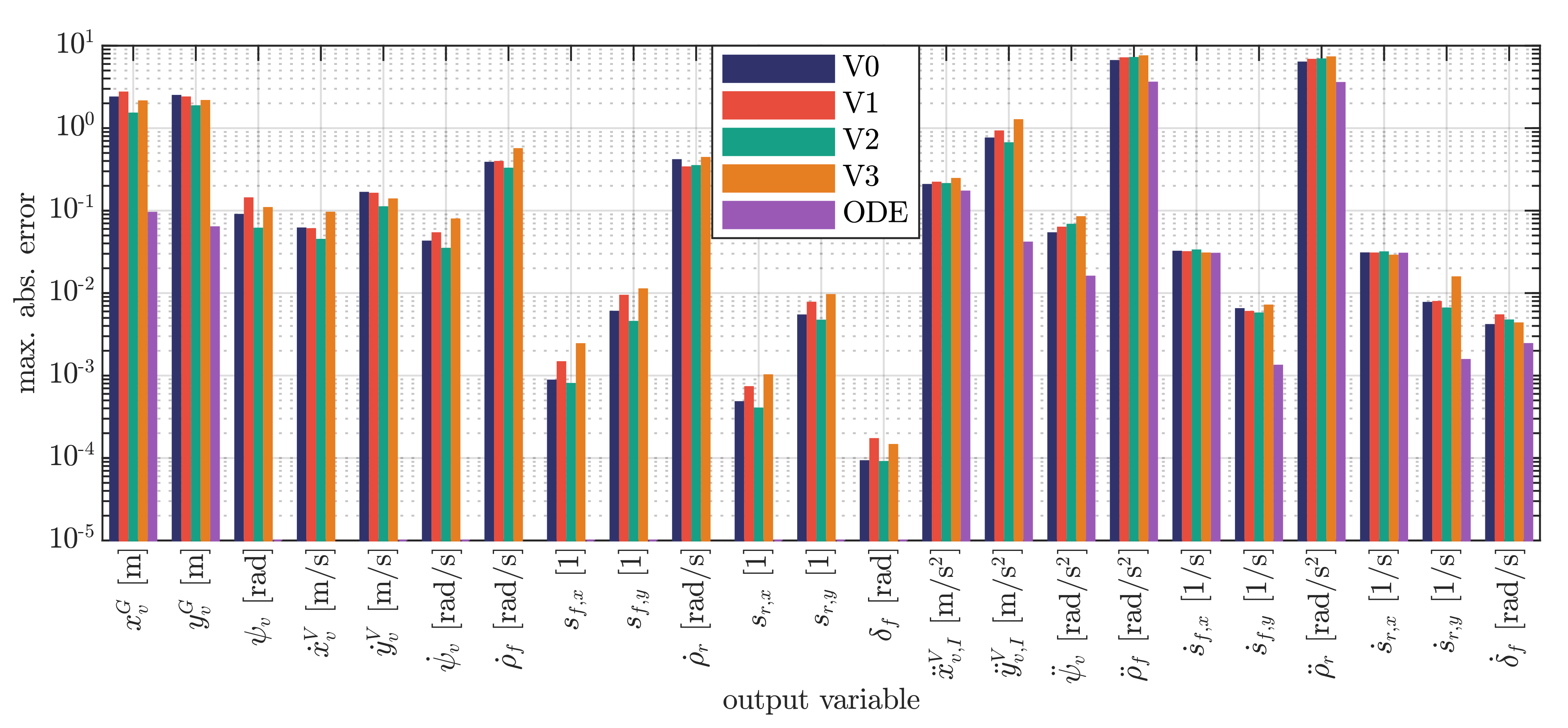
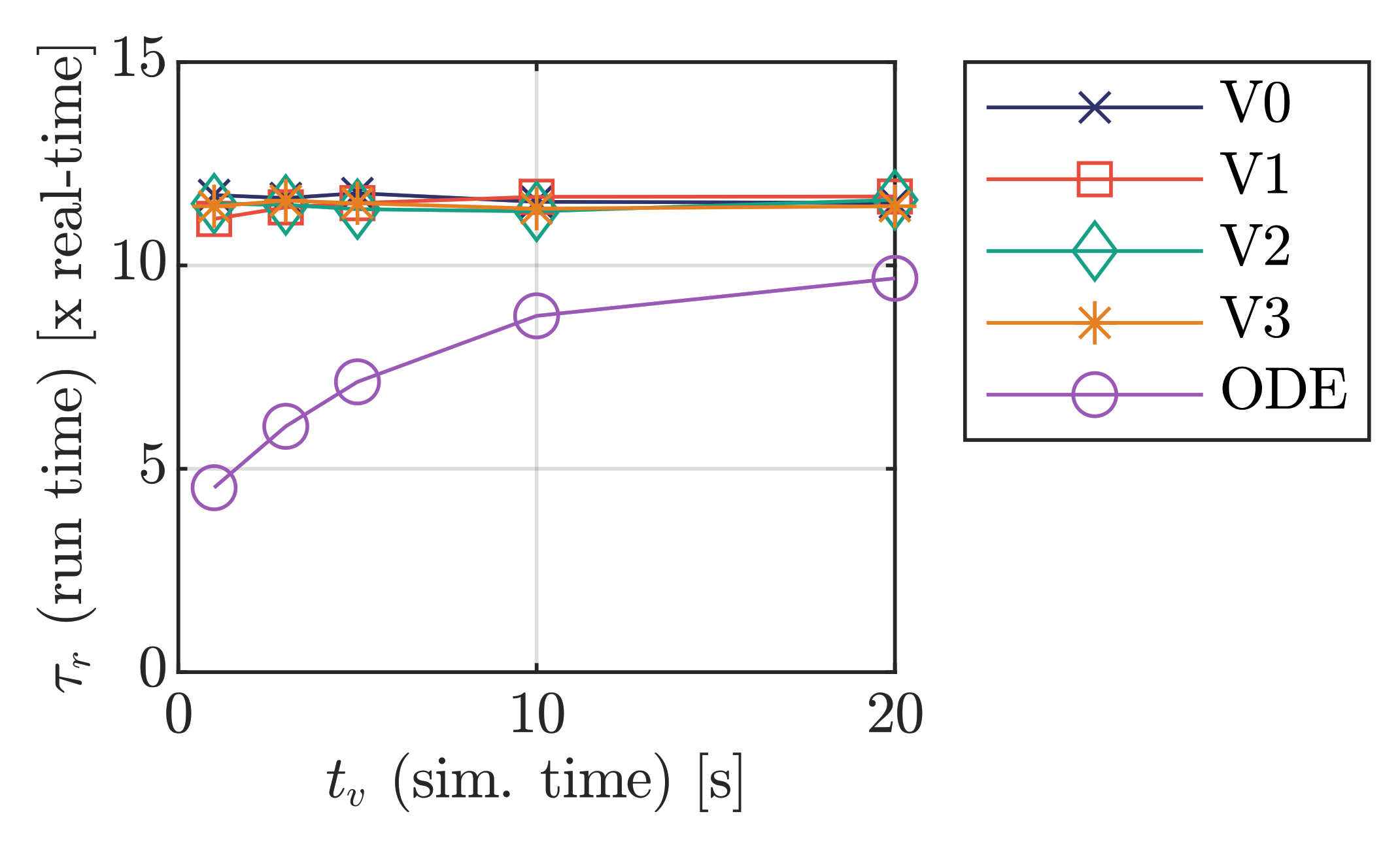
5. Simulation Results
5.1. Regression Fit
5.2. Prediction of Vehicle Motion
5.3. Evaluation of Input–Output Concept
6. Discussion
7. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DDPG | Deep Deterministic Policy Gradient |
| I/O | Input–Output |
| JSON | JavaScript Object Notation |
| MCTS | Monte Carlo Tree Search |
| MAE | Mean Absolute Error |
| MPC | Model Predictive Control |
| NWU | North West Up |
| ODE | Ordinary Differential Equation |
| PBD | Position Based Dynamics |
| PCA | Principal Component Analysis |
| RBFNN | Radial Basis Function Neural Network |
| ReLU | Rectified Linear Unit |
| SELU | Scaled Exponential Linear Unit |
| SMC | Sliding Mode Control |
| Nomenclature | |
| Dynamic quantity in inertial earth-fixed north-west-up coordinate system | |
| Dynamic quantity in rotating vehicle-fixed forward-left-up coordinate system | |
| Dynamic quantity in rotating front or rear wheel-fixed forward-left-up coordinate system | |
| Driving torque (non-negative) [Nm] | |
| Braking torque (non-negative) [Nm] | |
| Steering wheel angle [rad] | |
| , | Position of vehicle center of gravity in x (north), and y (west) directions in earth-fixed coordinate system [m] |
| , | Velocity of vehicle center of gravity in x (north), and y (west) directions in earth-fixed coordinate system [m/s] |
| , | Acceleration of vehicle center of gravity in x (north), and y (west) directions in earth-fixed coordinate system [m/s2] |
| , | Velocity of vehicle center of gravity in x (forward) and y (left) directions in vehicle-fixed coordinate system [m/s] |
| , | Inertial acceleration of vehicle center of gravity in x (forward) and y (left) directions in instantaneous vehicle-fixed coordinate system [m/s2] |
| Yaw angle (rotation angle around up axis) in earth-fixed coordinate system [rad] | |
| Yaw rate (angular velocity in z (up) direction) of vehicle in vehicle-fixed coordinate system [rad/s] | |
| Yaw acceleration (angular acceleration in z (up) direction) of vehicle in vehicle-fixed coordinate system [rad/s2] | |
| Turning angle of front and rear wheels [rad] | |
| Angular velocity of front and rear wheels [rad/s] | |
| Angular acceleration of front and rear wheels [rad/s2] | |
| Slips of front and rear wheels in x (longitudinal) and y (lateral) direction | |
| Slip derivatives of front and rear wheels in longitudinal (x) and lateral (y) direction [1/s] | |
| Steering angle of front wheel [rad] | |
| Steering angle derivative of front wheel [rad/s] | |
| Acting tire forces of front and rear wheels in x (north) and y (west) directions in earth-fixed coordinate system [N] | |
| Acting tire forces of front and rear wheels in x (forward) and y (left) directions in vehicle-fixed coordinate system [N] | |
| Acting tire forces of front and rear wheels in x (longitudinal), and y (lateral) directions in wheel-fixed coordinate systems [N] | |
| Tire forces of front and rear wheels in x (longitudinal), and y (lateral) directions in wheel-fixed coordinate systems in case of pure longitudinal or lateral slip [N] | |
| Tire forces of front and rear wheels in x (longitudinal), and y (lateral) directions in wheel-fixed coordinate systems in case of combined slip [N] | |
| Aerodynamic drag forces in x (north) and y (west) directions in earth-fixed coordinate system [N] | |
| Aerodynamic drag forces in x (forward) and y (left) directions in vehicle-fixed coordinate system [N] | |
| Tire load forces in z (up) direction in vehicle-fixed coordinate system [N] | |
| Driving torques of front and rear wheels [Nm] | |
| , | Intended and acting braking torques of front and rear wheels [Nm] |
| , | Calculated and acting rolling resistance torques of front and rear wheels [Nm] |
| Torque distribution factor to front and rear wheels | |
| , | Center point velocities of front and rear wheels in x (longitudinal) and y (lateral) directions in wheel-fixed coordinate system [m/s] |
| , | Center point velocities of front and rear wheels in x (forward) and y (left) directions in vehicle-fixed coordinate system [m/s] |
| Rolling velocity of front and rear wheels [m/s] | |
| Damped slips of front and rear wheels in x (longitudinal) and y (lateral) direction | |
| Slip stiffness of front and rear wheels in x (longitudinal) and y (lateral) direction | |
| Actual longitudinal slip damping factor | |
| Slip dependent actual relaxation lengths of front and rear tires in x (longitudinal) and y (lateral) direction [m] | |
| State vector of vehicle | |
| Derivative of vehicle state vector | |
| Total mass of vehicle [kg] | |
| Moment of inertia of the vehicle around z (up) axis [kgm2] | |
| Center of gravity height of the vehicle [m] | |
| Horizontal distance of vehicle center of gravity and the front and rear axes [m] | |
| Frontal area of the vehicle [m2] | |
| Aerodynamic drag coefficient of the vehicle | |
| Density of air [kg/m3] | |
| Moment of inertia of the front and rear wheels [kgm2] | |
| Radii of the front and rear wheels [m] | |
| , | Minimal and actual rolling velocity at which braking torque shall be fully applied [m/s] |
| Braking torque dependent factor for [1/Ns] | |
| ,, | Rolling resistance coefficients [1], [s/m], [s2/m2] |
| Rolling velocity at which rolling resistance torque shall be fully applied [m/s] | |
| Maximum values of Magic Formula for front and rear wheels in x (longitudinal) and y (lateral) direction | |
| Shape factors of Magic Formula for front and rear wheels in x (longitudinal) and y (lateral) direction | |
| Stiffness factors of Magic Formula for front and rear wheels in x (longitudinal) and y (lateral) direction | |
| Curvature factors of Magic Formula for front and rear wheels in x (longitudinal) and y (lateral) direction | |
| Coefficient of friction at front and rear wheels | |
| Initial longitudinal slip damping factor | |
| Rolling velocity at which slip damping should switch off | |
| Minimal value of wheels slips at which superposition of forces shall first be considered | |
| , | Initial and minimal relaxation lengths of front and rear tires in x (longitudinal) and y (lateral) direction [m] |
| Steering ratio | |
| Settling time of steering mechanism | |
| Sample time of vehicle model solution [s] | |
| Time of vehicle motion simulation [s] | |
| , | Arc length, arc length knot points [m] |
| , | Curvature of path, curvature profile knot points [1/m] |
| , | Travel speed along path, travel speed profile knot points [m/s] |
| Number of knot points specified for curvature and travel speed profile | |
| Time needed to travel along path section i [s] | |
| Length of path section i [m] | |
| Average travel speed of path section i [m/s] | |
| , | Travel time along path, time needed to reach end of path section i [s] |
| , | Longitudinal acceleration along path, and at path section i [m/s2] |
| , | Yaw rate (angular velocity in z direction) along path, yaw rate output samples [rad/s] |
| Centripetal acceleration along path [m/s2] | |
| , , | Yaw angle (rotation angle around up axis) along path and initially, yaw angle output samples [rad] |
| , , , , | Position in x (north), and y (west) directions in earth-fixed coordinate system along path and initially, position output samples [m] |
| Arc length resolution for numeric calculations [m] | |
| Number of reference trajectory points | |
| Number of road segments | |
| Maximal and minimal allowed travel speed [m/s] | |
| Maximal allowed centripetal acceleration [m/s2] | |
| Radius of path section i [m] | |
| Minimal allowed radius for path section i [m] | |
| Multiplier factor for minimal allowed radii | |
| Multiplier factor path section length in proportion to circumference | |
| Proportion of straight sections compared to curved sections | |
| Proportion of transition section length to normal section length | |
| Prediction time of neural network based vehicle model [s] | |
| General state variable | |
| Change of state variable in time | |
| Input vector of neural network variant VAR | |
| , | Output vector of neural network variant VAR. Element of output vector |
| , | Matrices of training and testing input samples |
| , | Matrices of training and testing output samples |
| Total number of vehicle simulation samples generated for training | |
| Vector of input scales (maximum absolute value of each variable in ) | |
| Vector of output scales (maximum absolute value of each variable in ) | |
| Training loss | |
| Number of elements of output vector | |
| , | Weighting vector for squared error in estimation of . Element of weighting vector |
| , | Estimation of by the neural network. Element of estimation vector |
| , | Time of neural network based vehicle simulation. Time at simulation step j [s] |
| Yaw angle (rotation around up axis) in earth-fixed coordinate system. Computed by neural network based vehicle model [rad] | |
| , | Position of vehicle center of gravity in x (north), and y (west) directions in earth-fixed coordinate system [m]. Computed by neural network based vehicle model |
| , | Inertial acceleration of vehicle center of gravity in x (forward) and y (left) directions in instantaneous vehicle-fixed coordinate system [m/s2]. Computed by neural network based vehicle model |
| Maximum absolute estimation error of neural network | |
| Run time as factor to real-time speed | |
References
- Watzenig, D.; Horn, M. Automated Driving: Safer and More Efficient Future Driving; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Tettamanti, T.; Varga, I.; Szalay, Z. Impacts of Autonomous Cars from a Traffic Engineering Perspective. Period. Polytech. Transp. Eng. 2016, 44, 244–250. [Google Scholar] [CrossRef]
- Barsi, Á.; Csepinszky, A.; Lógó, J.; Krausz, N.; Potó, V. The Role of Maps in Autonomous Driving Simulations. Period. Polytech. Transp. Eng. 2020, 48, 363–368. [Google Scholar] [CrossRef]
- Colan, J.; Nakanishi, J.; Aoyama, T.; Hasegawa, Y. Optimization-Based Constrained Trajectory Generation for Robot-Assisted Stitching in Endonasal Surgery. Robotics 2021, 10, 27. [Google Scholar] [CrossRef]
- Beschi, M.; Mutti, S.; Nicola, G.; Faroni, M.; Magnoni, P.; Villagrossi, E.; Pedrocchi, N. Optimal Robot Motion Planning of Redundant Robots in Machining and Additive Manufacturing Applications. Electronics 2019, 8, 1437. [Google Scholar] [CrossRef]
- Zhang, X.; Ming, Z. Trajectory Planning and Optimization for a Par4 Parallel Robot Based on Energy Consumption. Appl. Sci. 2019, 9, 2770. [Google Scholar] [CrossRef]
- Howard, T.M.; Kelly, A. Optimal rough terrain trajectory generation for wheeled mobile robots. Int. J. Robot. Res. 2007, 26, 141–166. [Google Scholar] [CrossRef]
- Urmson, C.; Anhalt, J.; Bagnell, D.; Baker, C.; Bittner, R.; Clark, M.N.; Dolan, J.; Duggins, D.; Galatali, T.; Ferguson, D.; et al. Autonomous driving in urban environments: Boss and the urban challenge. J. Field Robot. 2008, 25, 425–466. [Google Scholar] [CrossRef]
- Ajanovic, Z.; Lacevic, B.; Shyrokau, B.; Stolz, M.; Horn, M. Search-Based Optimal Motion Planning for Automated Driving. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4523–4530. [Google Scholar] [CrossRef]
- Diachuk, M.; Easa, S.M.; Bannis, J. Path and Control Planning for Autonomous Vehicles in Restricted Space and Low Speed. Infrastructures 2020, 5, 42. [Google Scholar] [CrossRef]
- Hegedus, F.; Bécsi, T.; Aradi, S.; Szalay, Z.; Gáspár, P. Real-time optimal motion planning for automated road vehicles. In Proceedings of the 21th IFAC World Congress, Berlin, Germany, 12–17 July 2020; pp. 15856–15861. [Google Scholar]
- Bender, J.; Müller, M.; Macklin, M. Position-Based Simulation Methods in Computer Graphics. Eurographics 2015. [Google Scholar] [CrossRef]
- Müller, M.; Heidelberger, B.; Hennix, M.; Ratcliff, J. Position based dynamics. J. Vis. Commun. Image Represent. 2007, 18, 109–118. [Google Scholar] [CrossRef]
- Harmon, D.; Zorin, D. Subspace integration with local deformations. ACM Trans. Graph. (TOG) 2013, 32, 1–10. [Google Scholar] [CrossRef]
- von Radziewsky, P.; Eisemann, E.; Seidel, H.P.; Hildebrandt, K. Optimized subspaces for deformation-based modeling and shape interpolation. Comput. Graph. 2016, 58, 128–138. [Google Scholar] [CrossRef]
- Xu, W.; Umetani, N.; Chao, Q.; Mao, J.; Jin, X.; Tong, X. Sensitivity-optimized rigging for example-based real-time clothing synthesis. ACM Trans. Graph. 2014, 33, 107:1–107:11. [Google Scholar] [CrossRef]
- Luo, R.; Shao, T.; Wang, H.; Xu, W.; Chen, X.; Zhou, K.; Yang, Y. NNWarp: Neural network-based nonlinear deformation. IEEE Trans. Vis. Comput. Graph. 2018, 26, 1745–1759. [Google Scholar] [CrossRef]
- Holden, D.; Duong, B.C.; Datta, S.; Nowrouzezahrai, D. Subspace neural physics: Fast data-driven interactive simulation. In Proceedings of the 18th annual ACM SIGGRAPH/Eurographics Symposium on Computer Animation, Los Angeles, CA, USA, 26–28 July 2019; pp. 1–12. [Google Scholar]
- Hu, S.; d’Ambrosio, S.; Finesso, R.; Manelli, A.; Marzano, M.R.; Mittica, A.; Ventura, L.; Wang, H.; Wang, Y. Comparison of Physics-Based, Semi-Empirical and Neural Network-Based Models for Model-Based Combustion Control in a 3.0 L Diesel Engine. Energies 2019, 12, 3423. [Google Scholar] [CrossRef]
- Guarneri, P.; Rocca, G.; Gobbi, M. A Neural-Network-Based Model for the Dynamic Simulation of the Tire/Suspension System While Traversing Road Irregularities. IEEE Trans. Neural Netw. 2008, 19, 1549–1563. [Google Scholar] [CrossRef]
- Liu, X.; Hu, D.; Xiao, J.; Hu, J. Modeling and simulation on movement of air cushion vehicle based on neural network. In Proceedings of the 2017 2nd International Conference on Robotics and Automation Engineering (ICRAE), Shanghai, China, 29–31 December 2017; pp. 513–516. [Google Scholar]
- Swain, S.K.; Rath, J.J.; Veluvolu, K.C. Neural Network Based Robust Lateral Control for an Autonomous Vehicle. Electronics 2021, 10, 510. [Google Scholar] [CrossRef]
- He, Z.; Nie, L.; Yin, Z.; Huang, S. A two-layer controller for lateral path tracking control of autonomous vehicles. Sensors 2020, 20, 3689. [Google Scholar] [CrossRef]
- Song, S.; Chen, H.; Sun, H.; Liu, M. Data Efficient Reinforcement Learning for Integrated Lateral Planning and Control in Automated Parking System. Sensors 2020, 20, 7297. [Google Scholar] [CrossRef]
- Hu, H.; Lu, Z.; Wang, Q.; Zheng, C. End-to-End Automated Lane-Change Maneuvering Considering Driving Style Using a Deep Deterministic Policy Gradient Algorithm. Sensors 2020, 20, 5443. [Google Scholar] [CrossRef]
- Hegedüs, F.; Bécsi, T.; Aradi, S.; Gáspár, P. Motion Planning for Highly Automated Road Vehicles with a Hybrid Approach Using Nonlinear Optimization and Artificial Neural Networks. Stroj. Vestn. J. Mech. Eng. 2019, 65, 148–160. [Google Scholar] [CrossRef]
- Kovári, B.; Hegedüs, F.; Bécsi, T. Design of a Reinforcement Learning-Based Lane Keeping Planning Agent for Automated Vehicles. Appl. Sci. 2020, 10, 7171. [Google Scholar] [CrossRef]
- Hegedüs, F.; Bécsi, T.; Aradi, S.; Gáspár, P. Model based trajectory planning for highly automated road vehicles. IFAC-PapersOnLine 2017, 50, 6958–6964. [Google Scholar] [CrossRef]
- Schramm, D.; Hiller, M.; Bardini, R. Vehicle Dynamics; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Luhua, Z.; Qinggui, C.; Yushan, L.; Naixiu, G. An optimization technique of braking force distribution coefficient for truck. In Proceedings of the 2011 International Conference on Transportation, Mechanical, and Electrical Engineering (TMEE), Changchun, China, 16–18 December 2011; pp. 1784–1787. [Google Scholar]
- Hall, D.E.; Moreland, J.C. Fundamentals of rolling resistance. Rubber Chem. Technol. 2001, 74, 525–539. [Google Scholar] [CrossRef]
- Pacejka, H.B. Tire and Vehicle Dynamics, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 2012; pp. 355–401. [Google Scholar] [CrossRef]
- Snider, J.M. Automatic Steering Methods for Autonomous Automobile Path Tracking; CMU-RITR; Robotics Institute: Pittsburgh, PA, USA, 2009. [Google Scholar]
- Cantisani, G.; Del Serrone, G. Procedure for the Identification of Existing Roads Alignment from Georeferenced Points Database. Infrastructures 2021, 6, 2. [Google Scholar] [CrossRef]
- Parlangeli, G.; Ostuni, L.; Mancarella, L.; Indiveri, G. A motion planning algorithm for smooth paths of bounded curvature and curvature derivative. In Proceedings of the 2009 17th Mediterranean Conference on Control and Automation, Thessaloniki, Greece, 24–26 June 2009; pp. 73–78. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Dong, Y.; Wang, D.; Zhang, L.; Li, Q.; Wu, J. Tightly Coupled GNSS/INS Integration with Robust Sequential Kalman Filter for Accurate Vehicular Navigation. Sensors 2020, 20, 561. [Google Scholar] [CrossRef]
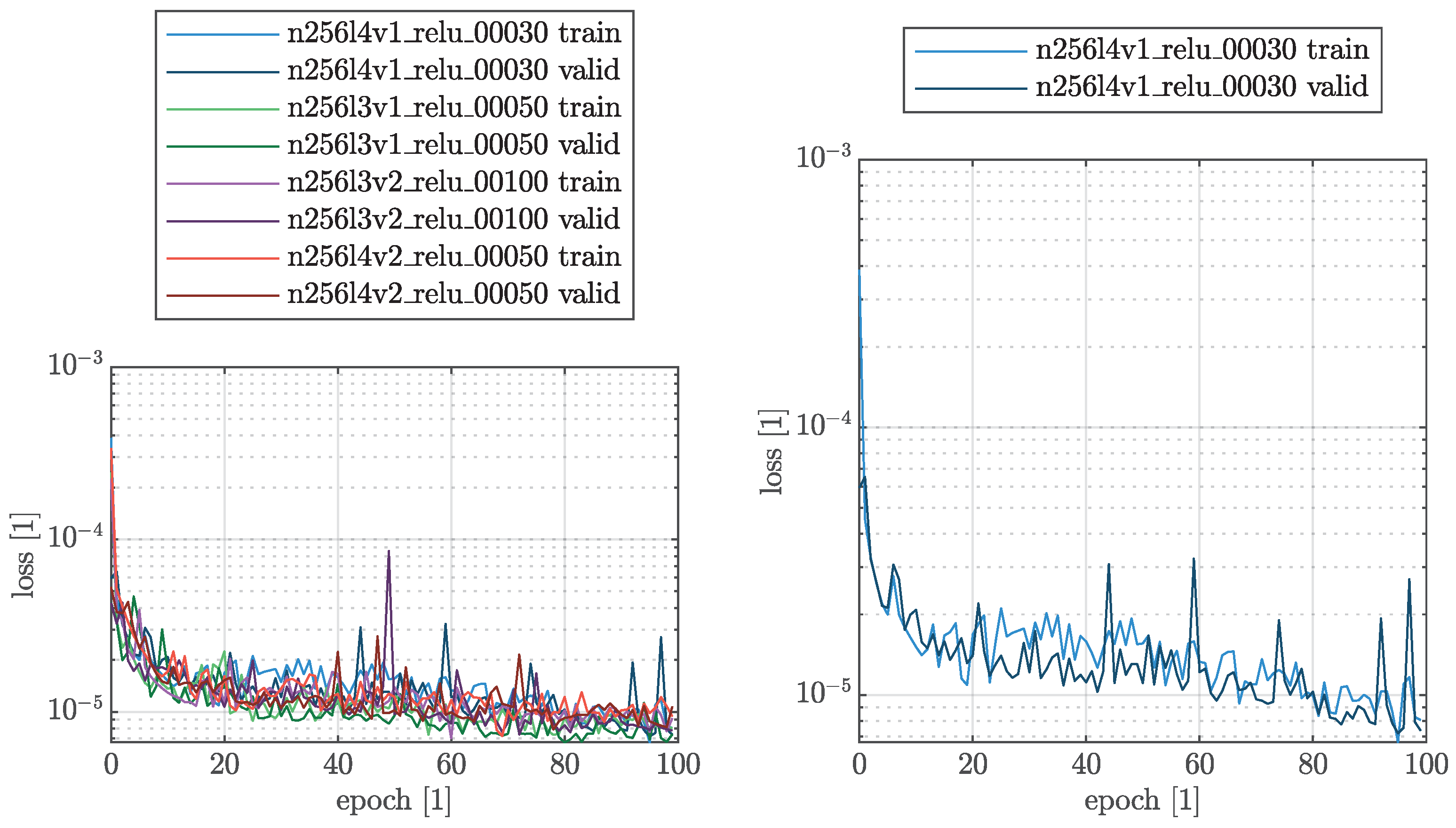
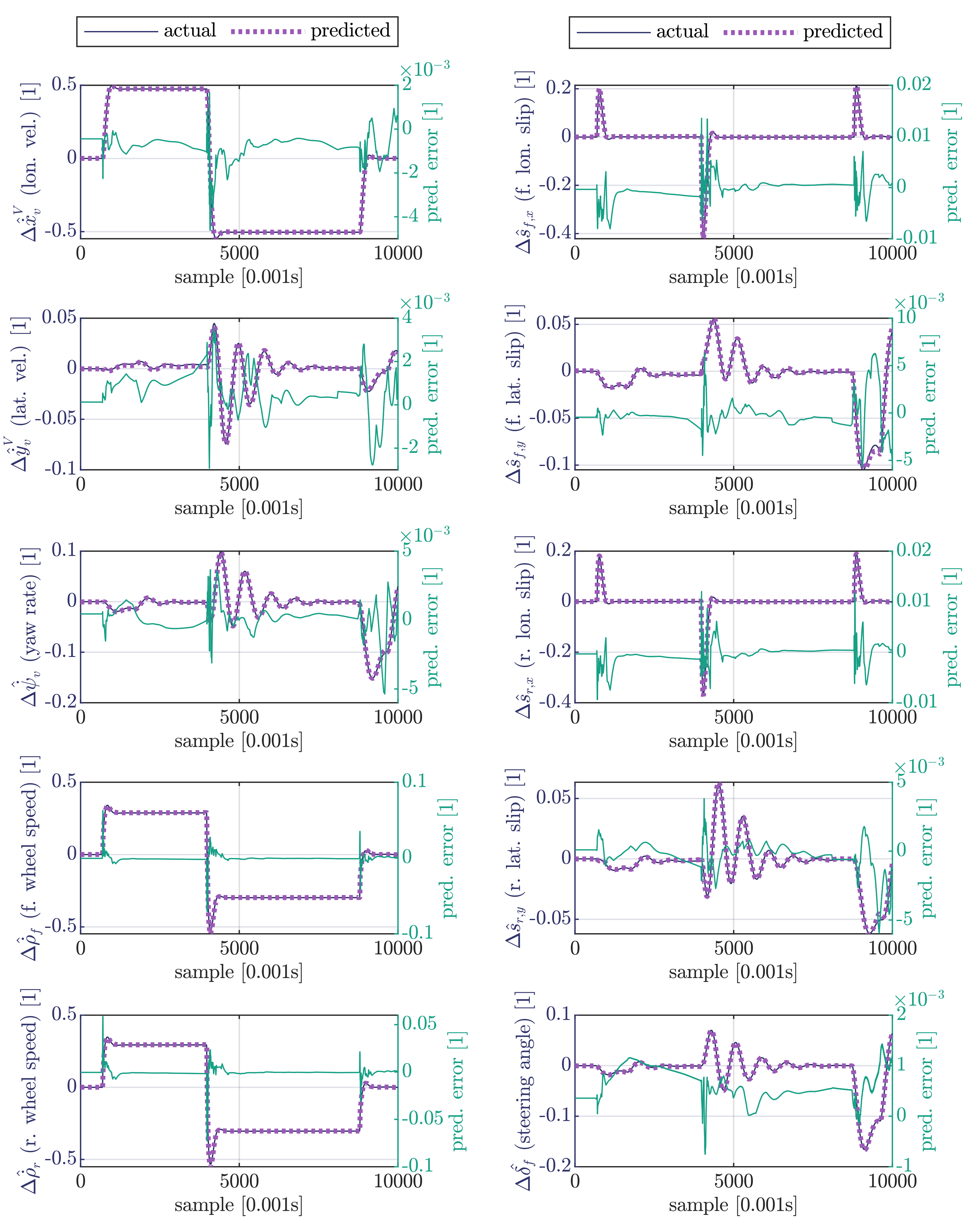
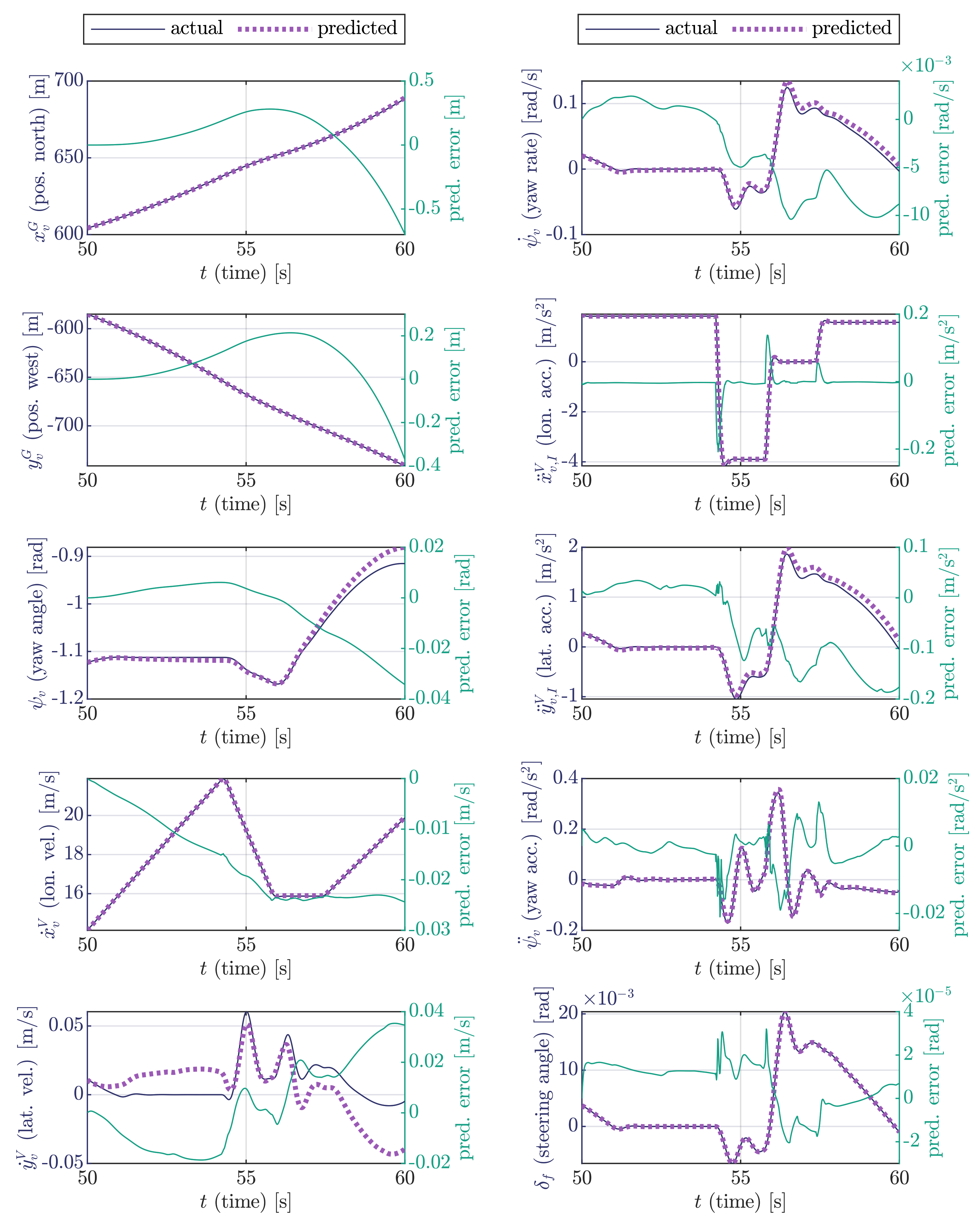
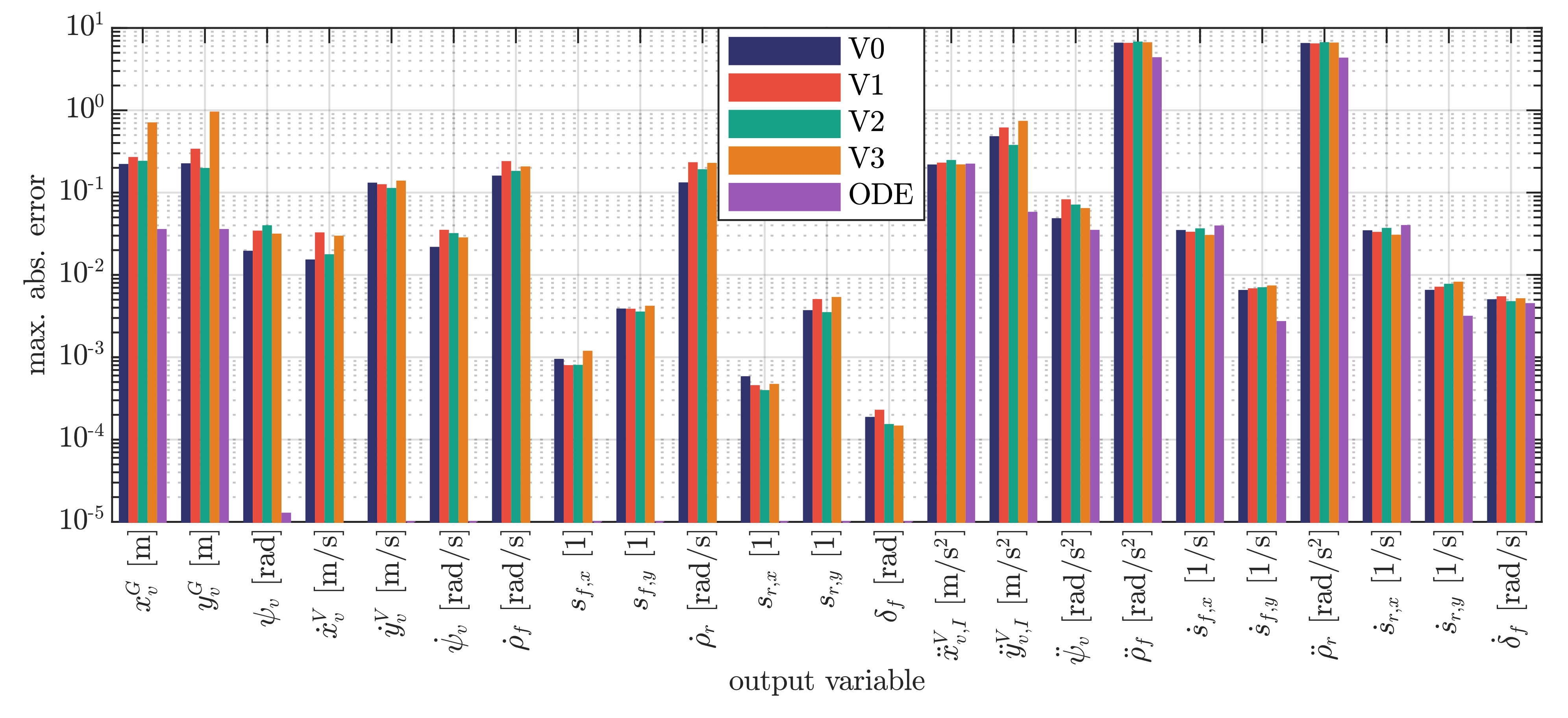
| Name | Layout |
|---|---|
| n256l3v1 | [64, 128, 64] |
| n256l3v2 | [32, 192, 32] |
| n256l4v1 | [32, 96, 96, 32] |
| n256l4v2 | [64, 128, 128, 64] |
| Variable | EMAX | MAE | Variable | EMAX | MAE |
|---|---|---|---|---|---|
| 0.17043 | 0.08441 | 0.93073 | 0.09424 | ||
| 0.16793 | 0.07394 | 0.16374 | 0.08827 | ||
| 0.24512 | 0.08250 | 0.42943 | 0.08377 | ||
| 0.82452 | 0.15126 | 0.13317 | 0.05913 | ||
| 0.51242 | 0.14104 | 0.15871 | 0.04865 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hegedüs, F.; Gáspár, P.; Bécsi, T. Fast Motion Model of Road Vehicles with Artificial Neural Networks. Electronics 2021, 10, 928. https://doi.org/10.3390/electronics10080928
Hegedüs F, Gáspár P, Bécsi T. Fast Motion Model of Road Vehicles with Artificial Neural Networks. Electronics. 2021; 10(8):928. https://doi.org/10.3390/electronics10080928
Chicago/Turabian StyleHegedüs, Ferenc, Péter Gáspár, and Tamás Bécsi. 2021. "Fast Motion Model of Road Vehicles with Artificial Neural Networks" Electronics 10, no. 8: 928. https://doi.org/10.3390/electronics10080928
APA StyleHegedüs, F., Gáspár, P., & Bécsi, T. (2021). Fast Motion Model of Road Vehicles with Artificial Neural Networks. Electronics, 10(8), 928. https://doi.org/10.3390/electronics10080928








