On the VCO/Frequency Divider Interface in Cryogenic CMOS PLL for Quantum Computing Applications
Abstract
:1. Introduction
2. Qubit and Silicon Microelectronics
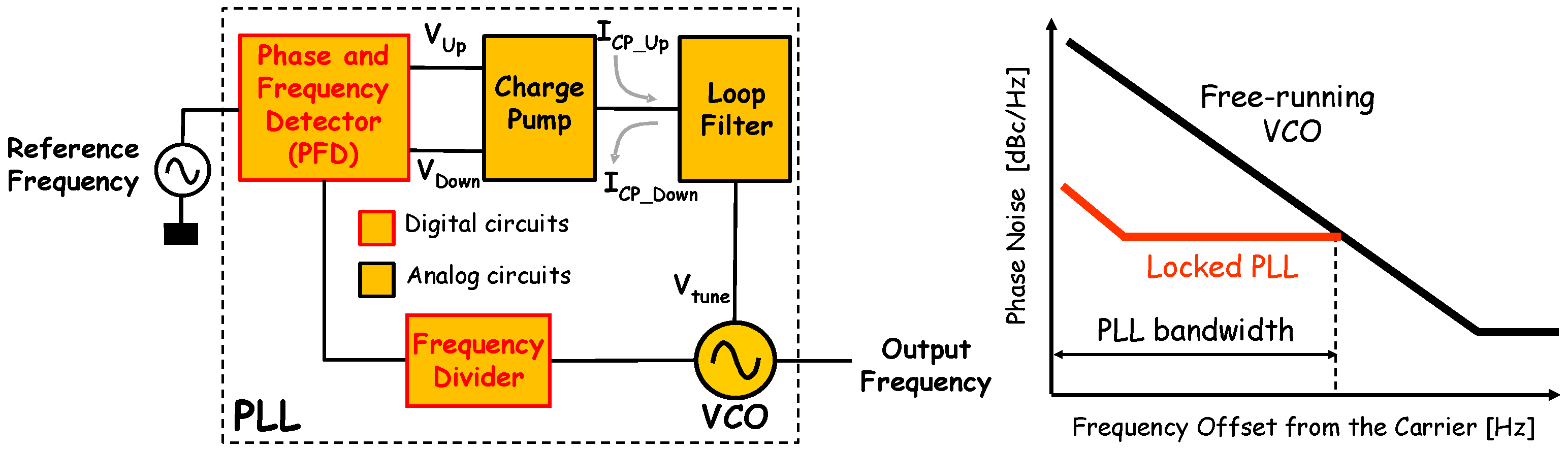
3. PLL/PLO and Quantum Microprocessors
4. Cryogenic Models
5. VCO and Frequency Divider
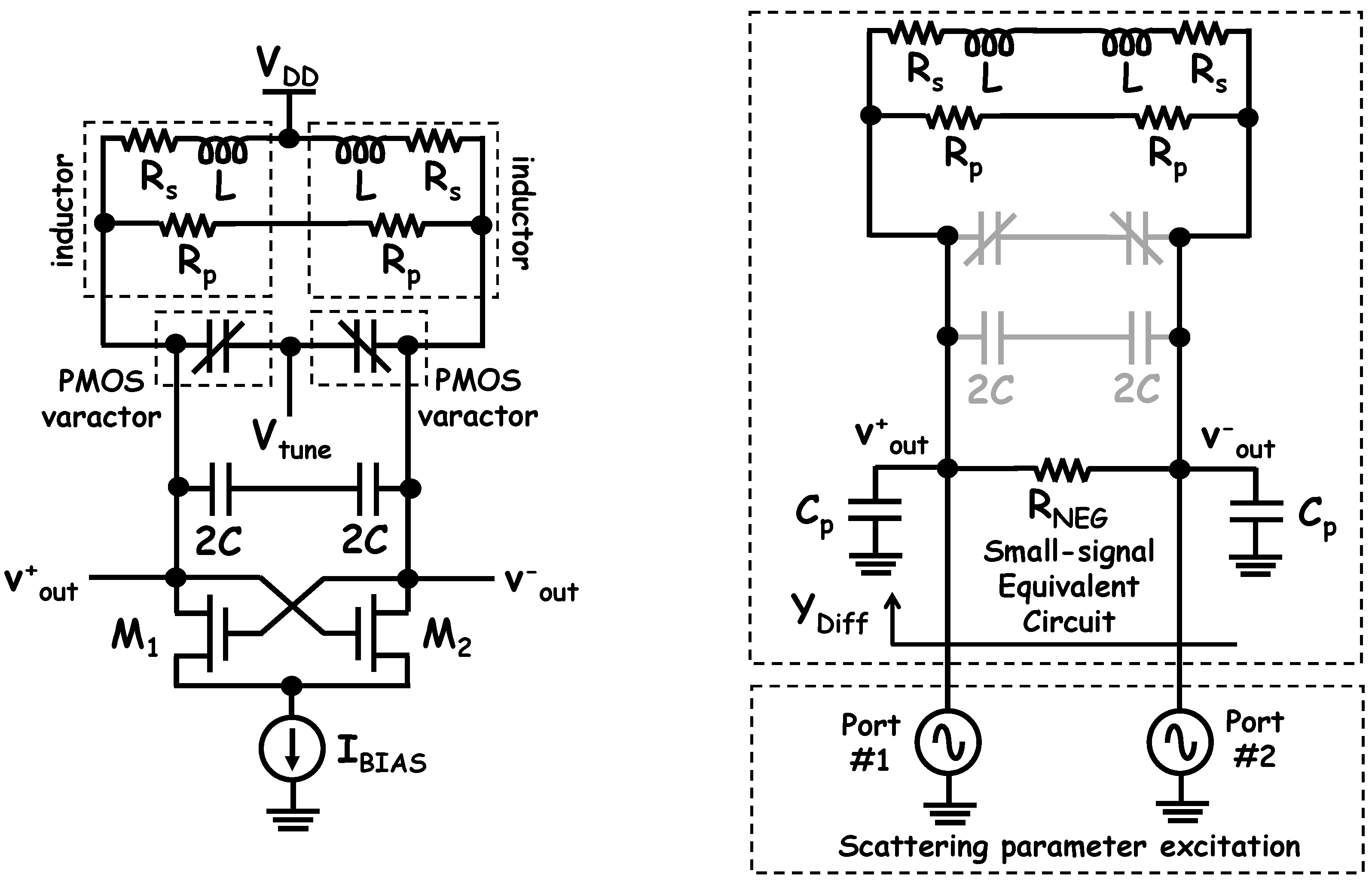
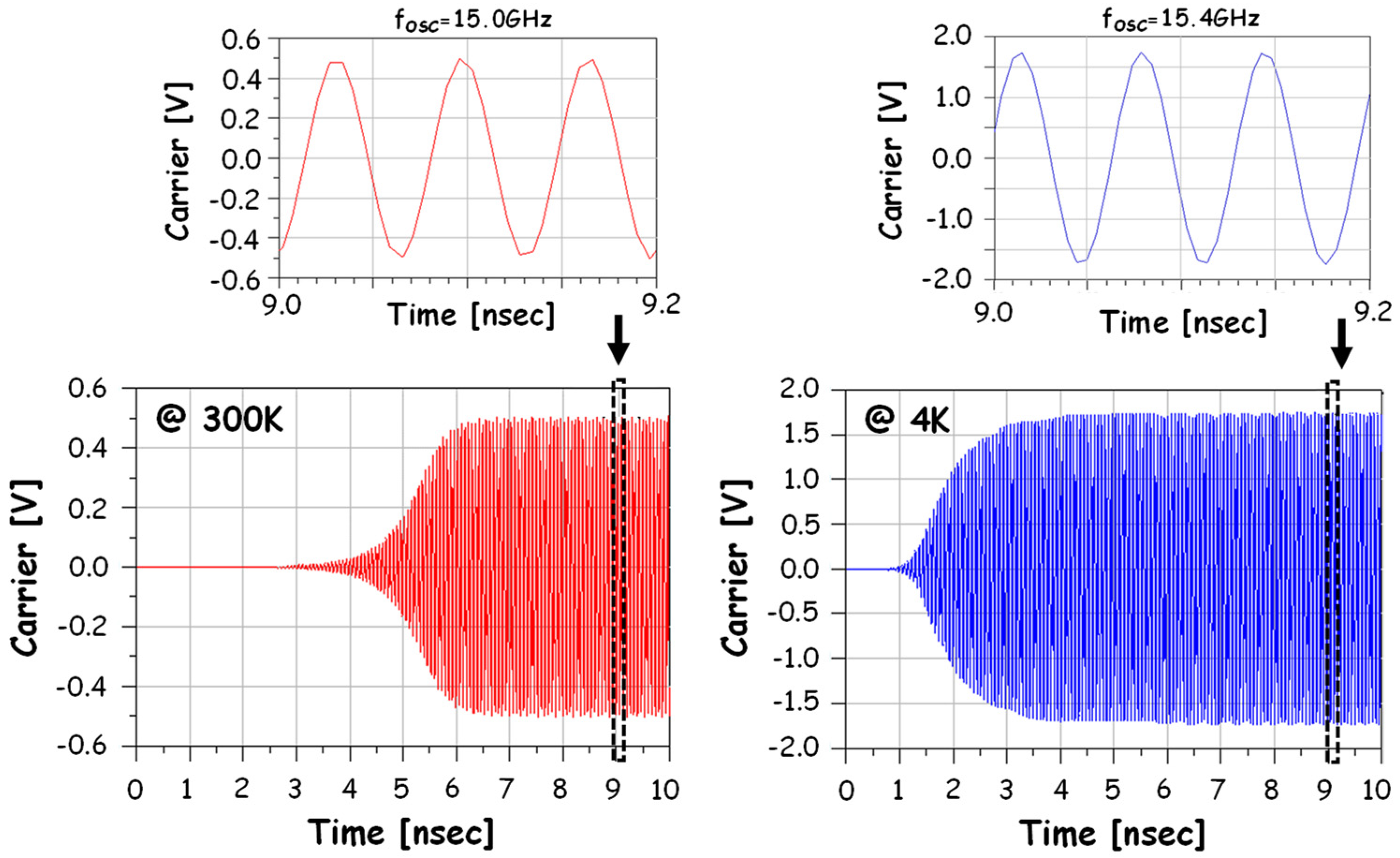
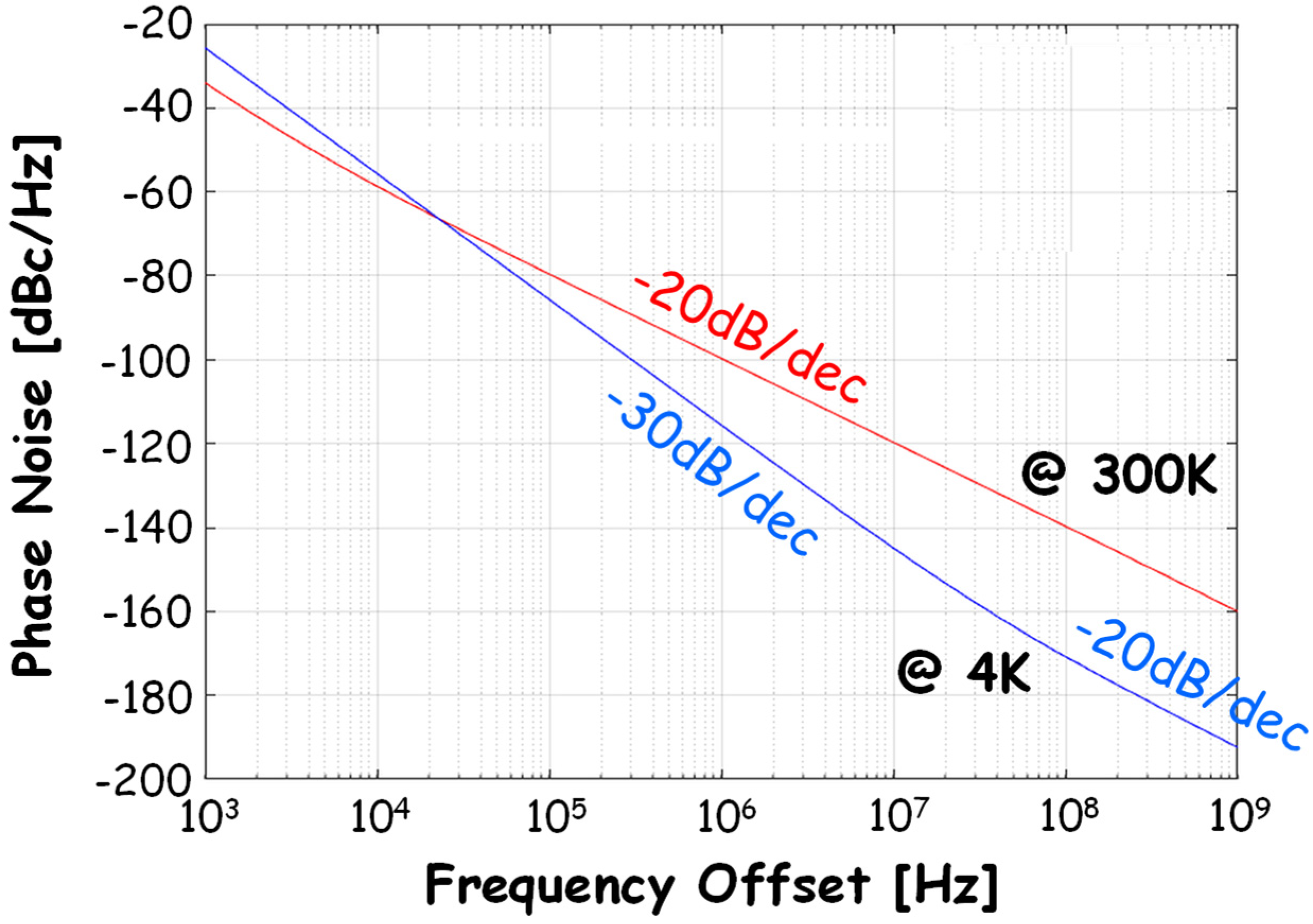
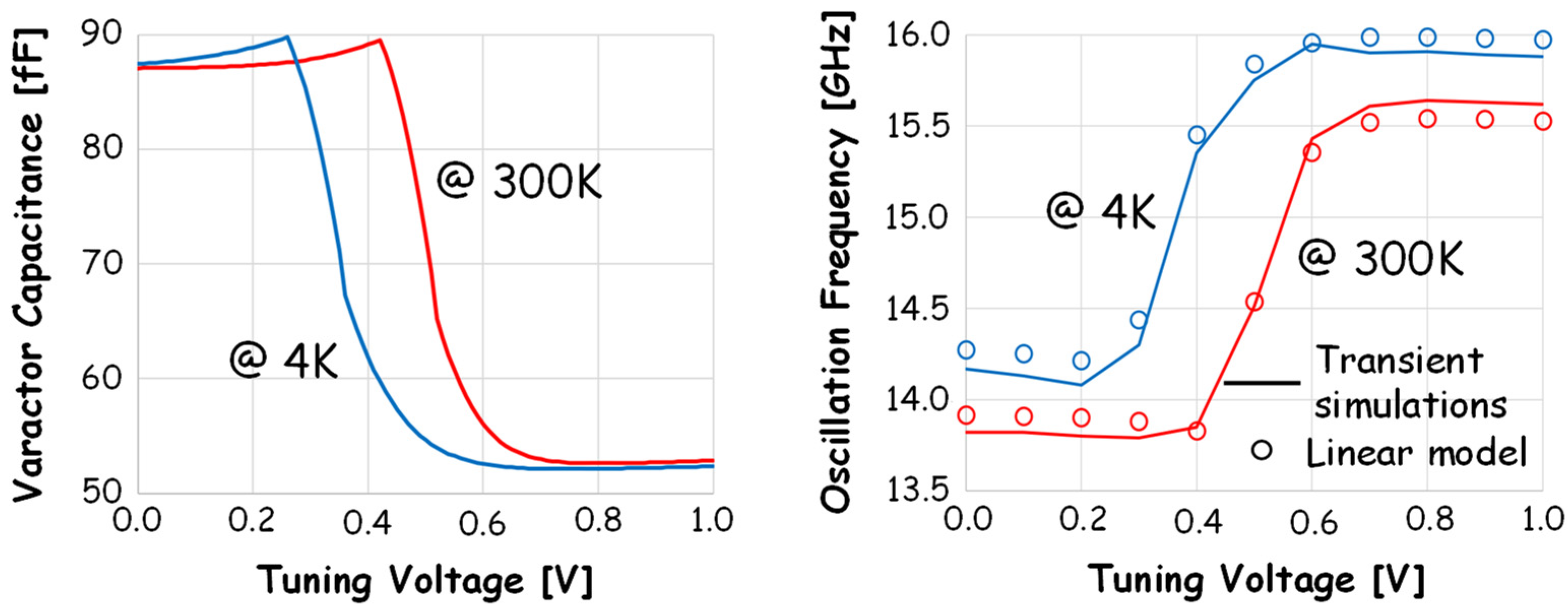
5.1. Voltage Controlled Oscillator: Design and Modeling
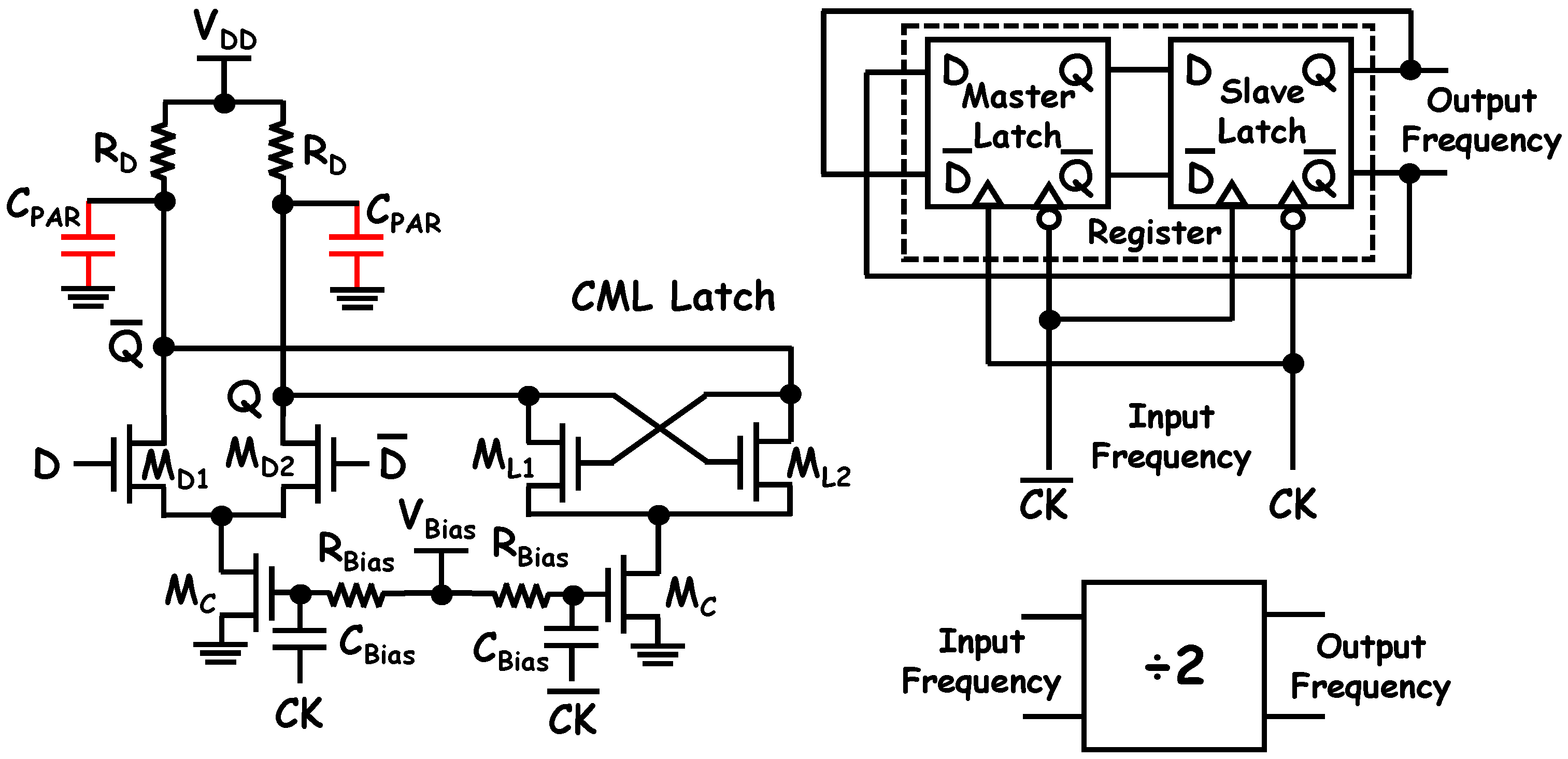
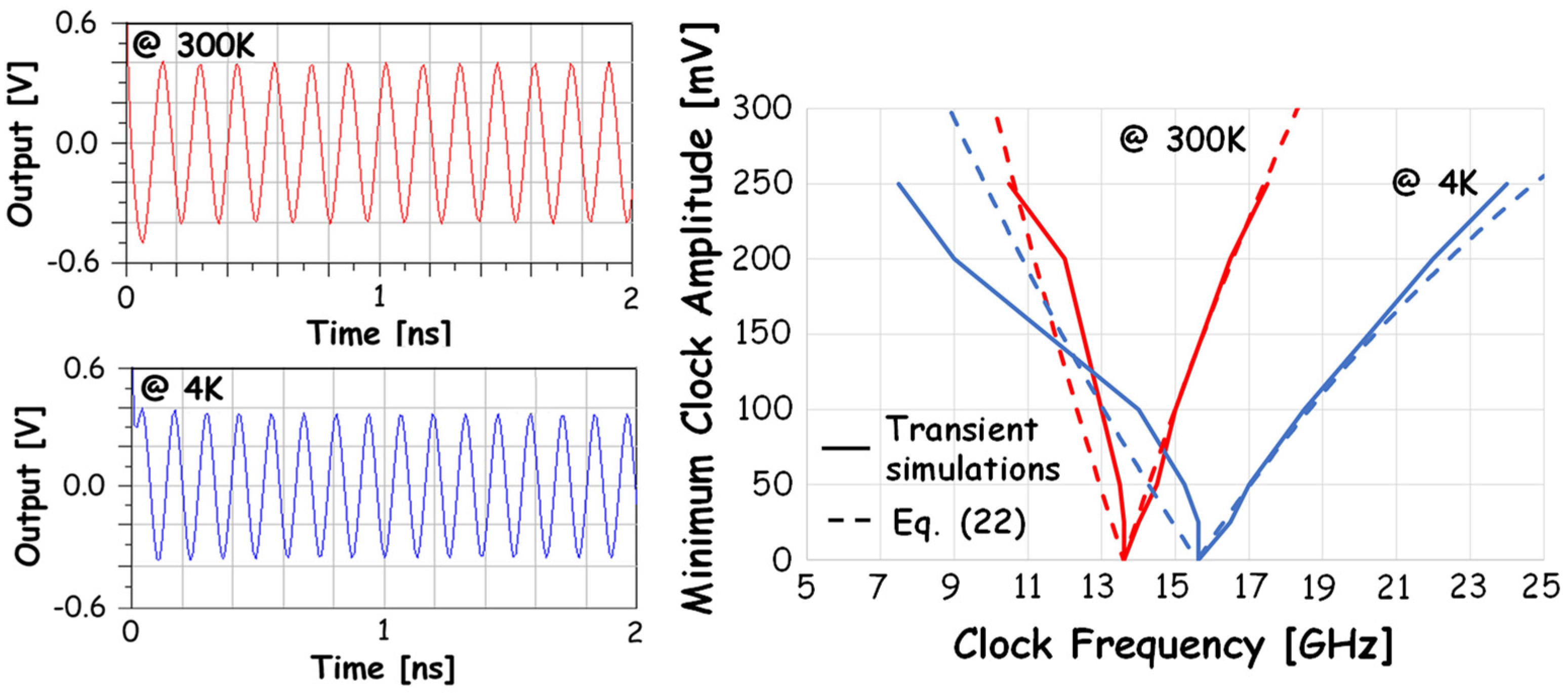
5.2. Frequency Divider: Design and Modeling
6. Design Guidelines
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lojek, B. History of Semiconductor Engineering; Springer: Berlin/Heidelberg, Germany, 2007; ISBN 978-3-642-07064-8. [Google Scholar] [CrossRef]
- Riordan, M.; Hoddeson, L. Crystal Fire: The Birth of the Information Age; Norton & Co.: New York, NY, USA, 1997; ISBN 0-393-04124-7. [Google Scholar]
- McCartney, S. ENIAC: Triumphs and Tragedies of the World’s First Computer; Berkley Publishing Group, Penguin Group: New York, NY, USA, 1999; ISBN 978-0802713483. [Google Scholar]
- Deutsch, D. Quantum theory, the Church-Turing principle and the universal quantum computer. Proc. R. Soc. Lond. 1985, 400, 97–117. [Google Scholar] [CrossRef]
- Kane, B. A silicon-based nuclear spin quantum computer. Nature 1998, 393, 133–137. [Google Scholar] [CrossRef]
- Zwanenburg, F.A.; Dzurak, A.S.; Morello, A.; Simmons, M.Y.; Hollenberg, L.C.L.; Klimeck, G.; Rogge, S.; Coppersmith, S.N.; Eriksson, M.A. Silicon quantum electronics. Rev. Mod. Phys. 2013, 85, 961–1019. [Google Scholar] [CrossRef]
- Russ, M.; Burkard, G. Three-electron spin qubits. J. Phys. Condens. Matter 2017, 29, 1–35. [Google Scholar] [CrossRef] [Green Version]
- Morello, A.; Pla, J.J.; Bertet, P.; Jamieson, D.N. Donor Spins in Silicon for Quantum Technologies. Adv. Quantum Technol. 2020, 3, 1–17. [Google Scholar] [CrossRef]
- Ferraro, E.; Prati, E. Is all-electrical silicon quantum computing feasible in the long term? Phys. Lett. A 2020, 384, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Patra, B.; Incadela, R.M.; van Dijk, J.P.G.; Homulle, H.A.R.; Song, L.; Shahmohammadi, M.; Bodgan Staszewski, R.; Vladimirescu, A.; Babaie, M.; Sebastiano, F.; et al. Cryo-CMOS Circuits and Systems for Quantum Computing Applications. IEEE J. Solid-State Circuits 2018, 53, 309–321. [Google Scholar] [CrossRef] [Green Version]
- Manthena, V.; Miryala, S.; Deptuch, G.; Carini, G. A 1.2-V 6-GHz Dual-Path Charge-Pump PLL Frequency Synthesizer for Quantum Control and Readout in CMOS 65-nm Process. In Proceedings of the IEEE Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (UEMCON), New York, NY, USA, 28–31 October 2020. [Google Scholar]
- Charbon, E.; Sebastiano, F.; Babaie, M.; Vladimirescu, A.; Shahmohammadi, M.; Bodgan Staszewski, R.; Homulle, H.A.R.; Patra, B.; van Dijk, J.P.G.; Incadela, R.M.; et al. Cryo-CMOS Circuits and Systems for Scalable Quantum Computing. In Proceedings of the IEEE International Solid State Circuits Conference, San Francisco, CA, USA, 5–9 February 2017; pp. 264–266. [Google Scholar] [CrossRef]
- Van Dijk, J.P.G.; Charbon, E.; Sebastiano, F. The electronic interface for quantum processors. Microprocess. Microsyst. 2019, 66, 90–101. [Google Scholar] [CrossRef] [Green Version]
- Watson, T.; Philips, S.; Kawakami, E.; Ward, D.; Scarlino, P.; Veldhorst, M.; Savage, D.; Lagally, M.; Friesen, M.; Coppersmith, S. A programmable two-qubit quantum processor in silicon. Nature 2018, 555, 633–636. [Google Scholar] [CrossRef] [Green Version]
- Veldhorst, M.; Eenink, H.G.J.; Yang, C.H.; Dzurak, A.S. Silicon CMOS architecture for a spin-based quantum computer. Nat. Commun. 2017, 8, 1766. [Google Scholar] [CrossRef]
- Nielinger, D.; Christ, V.; Degenhardt, C.; Geck, L.; Grewing, C.; Kruth, A.; Liebau, D.; Muralidharan, P.; Schubert, P.; Vliex, P.; et al. SQUBIC1: An integrated control chip for semiconductor qubits. In Proceedings of the International Workshop on Silicon Quantum Electronics, Sidney, Australia, 13 November 2018. [Google Scholar]
- Bardin, J.C.; Jeffrey, E.; Lucero, E.; Huang, T.; Naaman, O.; Barends, R.; White, T.; Giustina, M.; Sank, D.; Roushan, P.; et al. A 28nm Bulk-CMOS 4-to-8GHz <2mW Cryogenic Pulse Modulator for Scalable Quantum Computing. In Proceedings of the IEEE International Solid State Circuits Conference, San Francisco, CA, USA, 17–21 February 2019; pp. 456–458. [Google Scholar] [CrossRef] [Green Version]
- Charbon, E. Cryo-CMOS: 60 Years of Technological Advances towards Emerging Quantum Technologies. In Proceedings of the Keynote at IEEE 45th European Solid-State Circuit Conference and 49th European Solid-State Device Research Conference, Krakow, Poland, 23–26 September 2019. [Google Scholar]
- Bardin, J. CMOS Integrated Circuits for Control of Transmon Qubits. In Proceedings of the Tutorial at IEEE 45th European Solid-State Circuit Conference, Krakow, Poland, 23–26 September 2019. [Google Scholar]
- Voiginescu, S. Towards monolithic quantum computing processors in production FD-SOI CMOS technology. In Proceedings of the Tutorial at IEEE 45th European Solid-State Circuit Conference and 49th European Solid-State Device Research Conference, Krakow, Poland, 23–26 September 2019. [Google Scholar]
- Sebastiano, F. Cryogenic CMOS interfaces for large-scale quantum computers: From system and device models to circuits. In Proceedings of the Tutorial at at IEEE 45th European Solid-State Circuit Conference and 49th European Solid-State Device Research Conference, Krakow, Poland, 23–26 September 2019. [Google Scholar]
- Mehrpoo, M.; Patra, B.; Gong, J.; Hart, P.A.; van Dijk, J.P.G.; Homulle, H.; Kiene, G.; Vladimirescu, A.; Sebastiano, F.; Charbon, E. Benefits and Challenges of Designing Cryogenic CMOS RF Circuits for Quantum Computers. In Proceedings of the IEEE International Symposium on Circuits and Systems, Sapporo, Japan, 26–29 May 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Meunier, T.; Hutin, L.; Betrand, B.; Thonnart, T.; Pillonet, G.; Billiot, G.; Jacquinot, H.; Cassé, M.; Barraud, S.; Kim, Y.J.; et al. Towards scalable quantum computing based on silicon spin. In Proceedings of the IEEE Symposium on VLSI Technology, Kyoto, Japan, 9–14 June 2019. [Google Scholar] [CrossRef]
- Degenhardt, C.; Artanov, A.; Geck, L.; Grewing, V.; Kruth, A.; Nielinger, D.; Vliex, P.; Zambanini, A.; van Waasen, S. Systems Engineering of Cryogenic CMOS Electronics for Scalable Quantum Computers. In Proceedings of the IEEE International Symposium on Circuits and Systems, Sapporo, Japan, 26–29 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Lehmann, T. Cryogenic Support Circuits and Systems for Silicon Quantum Computers. In Proceedings of the IEEE International Symposium on Circuits and Systems, Sapporo, Japan, 26–29 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Jazaeri, F.; Beckers, A.; Tjalli, A.; Sallese, J.M. A Review on Quantum Computing: From Qubits to Front-end Electronics and Cryogenic MOSFET Physics. In Proceedings of the IEEE International Conference on Mixed Design of Integrated Circuits and Systems, Rzeszow, Poland, 27–29 June 2019; pp. 15–25. [Google Scholar] [CrossRef]
- Van Dijk, J.P.G.; Patra, B.; Subramanina, S.; Xue, X.; Samkharadze, N.; Corna, A.; Jeon, C.; Sheikh, F.; Juarez-Hernandez, E.; Perez Esparza, B.; et al. A Scalale Cryo-CMOS Controller Wideband Frequency-Multiplexed Control of Spin Qubits and Transmons. IEEE J. Solid-State Circuits 2020, 55, 2930–2946. [Google Scholar] [CrossRef]
- Ruffino, A.; Peng, Y.; Yang, T.Y.; Michniewicz, J.; Gonzalez-Zalba, M.F.; Charbon, E. A Fully-Integrated 40-nm 5-6.5GHz Cryo-CMOS System-on-Chip with I/Q Receiver and Frequency Synthesizer for Scalable Multiplexed Readout of Quantum Dots. In Proceedings of the IEEE International Solid-State Circuit Conference, San Francisco, CA, USA, 13–22 February 2021; pp. 210–212. [Google Scholar] [CrossRef]
- Yang, C.H.; Leon, R.C.C.; Hwang, J.C.C.; Saraiva, A.; Tanttu, T.; Huang, W.; Camirand Lemyre, J.; Chan, K.W.; Tan, K.Y.; Hudson, F.E.; et al. Operation of silicon quantum processor unit cell above one Kelvin. Nature 2020, 580, 350–354. [Google Scholar] [CrossRef] [Green Version]
- Petit, L.; Eenink, H.G.J.; Russ, M.; Lawrie, W.I.L.; Hendrickx, N.W.; Philips, S.G.J.; Clarke, J.S.; Vandersypen, L.M.K.; Veldhorst, M. Universal quantum logic in hot silicon Qubits. Nature 2020, 580, 355–359. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hart, P.A.T.; Babaie, M.; Charbon, E.; Vladimirescu, A.; Sebastiano, F. Characterization and Modeling of Mismatch in Cryo-CMOS. IEEE J. Electron Devices Soc. 2020, 8, 263–273. [Google Scholar] [CrossRef]
- Lin, S. Cryogenic Characterization and Modeling of Nanometer CMOS Transistors for Quantum Computing Applications. Thesis in Master of Science in Electrical Engineering. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 30 September 2016. [Google Scholar]
- Akturk, A.; Eng, K.; Hamlet, J.; Ptbhare, S.; Longoria, E.; Young, R.; Peckerar, M.; Gurrieri, T.; Carroll, M.S.; Goldsman, N. Compact Modeling of 0.35um SOI CMOS Technology Node for 4K DC Operating using Verilog-A. Microelectron. Eng. 2010, 87, 2518–2524. [Google Scholar] [CrossRef]
- Beckers, A.; Jazaeri, F.; Enz, C. Cryogenic MOSFET Threshold Voltage Model. In Proceedings of the 49th European Solid-State Device Research Conference (ESSDERC), Krakow, Poland, 23–26 September 2019; pp. 94–97. [Google Scholar] [CrossRef]
- Beckers, A.; Jazaeri, F.; Enz, C. Characterization and Modeling of 28-nm Bulk CMOS Technology Down to 4.2 K. IEEE J. Electron Devices Soc. 2018, 6, 1007–1018. [Google Scholar] [CrossRef]
- Beckers, A.; Jazaeri, F.; Enz, C. Cryogenic MOS Transistor Model. IEEE Trans. Electron Devices 2018, 65, 3617–3625. [Google Scholar] [CrossRef]
- Arora, A. MOSFET Models for VLSI Circuit Simulation: Theory and Practice; Springer: Wien, Austria; New York, NY, USA, 1993; ISBN 978-3-7091-9249-8. [Google Scholar] [CrossRef]
- Carusone, T.C.; Johns, D.A.; Martin, K.W. Analog Integrated Circuit Design; John Wiley & Sons: Singapore, 2013; ISBN 978-0470770108. [Google Scholar]
- Kan, M.; Man-Kang, I.; Shin, H. Extraction and modeling of gate electrode resistance in RF MOSFETs. In Proceedings of the International Conference on Integrated Circuit Design and Technology, Austin, TX, USA, 9–11 May 2005; pp. 207–210. [Google Scholar] [CrossRef]
- PTM Website. Available online: http://ptm.asu.edu/modelcard/LP/45nm_LP.pm (accessed on 23 October 2020).
- Long Channel Models from CMOS Circuit Design, Layout, and Simulation. Available online: https://cmosedu.com/cmos1/cmosedu_models.txt (accessed on 23 October 2020).
- Dierickx, B.; Warmerdam, L.; Simoen, E.R.; Vermeiren, J.; Claeys, C. Model hysteresis and kink behavior of MOS transistors operating at 4.2 K. IEEE Trans. Electron Devices 1988, 35, 1120–1125. [Google Scholar] [CrossRef]
- Razavi, B. Design of CMOS Phase-Locked Loops: From Circuit Level to Architecture Level; Cambridge University Press: Cambridge, UK, 2020; ISBN 978110862620. [Google Scholar] [CrossRef]
- Chang, J.; Viswanathan, C.R. Low frequency noise in CMOSTs at cryogenic temperatures. In Proceedings of the Workshop on Low Temperature Semiconductor Electronics, Burlington, VT, USA, 7–8 August 1989; pp. 133–136. [Google Scholar] [CrossRef]
- Chang, J.; Abidi, A.A.; Viswanathan, C.R. Flicker noise in CMOS transistors from subthreshold to strong inversion at various temperatures. IEEE Trans. Electron Devices 1994, 41, 1965–1971. [Google Scholar] [CrossRef]
- Binkley, D.; Hopper, C.E.; Blalock, B.J.; Mojarradi, M.M.; Cressler, J.D.; Yong, L.K. Noise performance of 0.35-μm SOI CMOS devices and micropower preamplifier from 77–400 K. In Proceedings of the IEEE Aerospace Conference Proceedings, Big Sky, MT, USA, 6–13 March 2004; pp. 2495–2506. [Google Scholar] [CrossRef]
- Gong, M.J.; Alakusu, U.; Bonen, S.; Dadash, M.S.; Lucci, L.; Jia, H.; Gutierrez, L.E.; Chen, W.T.; Daughton, D.R.; Adam, G.C.; et al. Design Considerations for Spin Readout Amplifiers in Monolithically Integrated Semiconductor Quantum Processors. In Proceedings of the IEEE Radio Frequency Integrated Circuits Symposium, Boston, MA, USA, 2–4 June 2019; pp. 111–114. [Google Scholar] [CrossRef]
- Patra, B.; Mehrpoo, M.; Runo, A.; Sebastiano, F.; Charbon, E.; Babaie, M. Characterization and Analysis of On-Chip Microwave Passive Components at Cryogenic Temperatures. IEEE J. Electron Devices Soc. 2020, 8, 448–456. [Google Scholar] [CrossRef]
- Razavi, B. RF Microelectronics, 2nd ed.; Pearson Education: London, UK, 2021; ISBN 978-0-13-713473-1. [Google Scholar]
- Tang, S.D.; Lin, Y.S.; Huang, W.H.; Lu, C.L.; Wang, Y.H. A Current-Mode-Logic-Based Frequency Divider with Ultra-Wideband and Octet Phases. Prog. Electromagn. Res. M 2019, 68, 89–98. [Google Scholar] [CrossRef] [Green Version]
- Hietanen, M.; Aikio, J.; Akbar, R.; Rahkonen, T.; Paerssinen, A. A 28 GHz Static CML Frequency Divider with Back-Gate Tuning on 22-nm CMOS FD-SOI Technology. In Proceedings of the IEEE Proc 19th Topical Meeting on Silicon Monolitic Integrated Circuit in RF Systems, Orlando, FL, USA, 20–23 January 2019; pp. 1–3. [Google Scholar] [CrossRef] [Green Version]
- Luo, J.; Zhang, L.; Wang, Y.; Yu, Z. Behavioral Analysis and Optimization of CMOS CML Dividers for Millimeter-Wave Applications. IEEE Trans. Circuits Syst.—II Express Briefs 2015, 62, 256–260. [Google Scholar] [CrossRef]
- Zhu, M.; Zhao, D. Geometric Analysis and Systematic Design of Millimeter-Wave Low-Power Frequency Dividers in 65 nm CMOS. IEEE Access 2020, 8, 20658–20665. [Google Scholar] [CrossRef]
- Singh, U.; Green, M. Dynamics of High-Frequency CMOS Dividers. In Proceedings of the IEEE International Symposium on Circuits and Systems, Phoenix-Scottsdale, AZ, USA, 26–29 May 2002; pp. 421–424. [Google Scholar] [CrossRef]
- Behagi, A.; Ghanevati, M. Fundamentals of RF and Microwave Circuit Design: Practical Analysis and Design Tools; Chapter 8; Reformed Free Publishing Association: Jenison, MI, USA, 2020; ISBN 9780692948200. [Google Scholar]
- Castaneda-Avina, P.R.; Tlelo-Cuautle, E.; de la Fraga, L.G. Single-Objective Optimization of a CMOS VCO Considering PVT and Monte Carlo Simulations. Math. Comput. Appl. 2020, 25, 76. [Google Scholar] [CrossRef]
- Dani, L.M.; Mishra, N.; Banchhor, S.K.; Miryala, S.; Doneria, A.; Anand, B. Design and Characterization of Bulk Driven MOS Varactor based VCO at Near Threshold Regime. In Proceedings of the IEEE Subthreshold Microelectronics Technology Unified Conference, Burlingame, CA, USA, 15–18 October 2018. [Google Scholar] [CrossRef]
- Maiti, M.; Chakrabartty, S.; Al-Shidaifat, A.; Song, H.; Bhattacharyya, B.K.; Majumder, A. A 90 nm PVT Tolerant Current Mode Frequency Divider with Wide Locking Range. In Proceedings of the IEEE Nordic Circuits and Systems Conference, Oslo, Norway, 27–28 October 2020. [Google Scholar] [CrossRef]
- Deepak, N.; Seshchalam, D.; Raghavendra, K. A 12 GHz Programmable Frequency Divider. Int. J. Electr. Electron. Comput. Sci. Eng. Special Issue. 2016, pp. 199–203. Available online: https://ijeecse.webs.com/91.pdf (accessed on 23 October 2020).
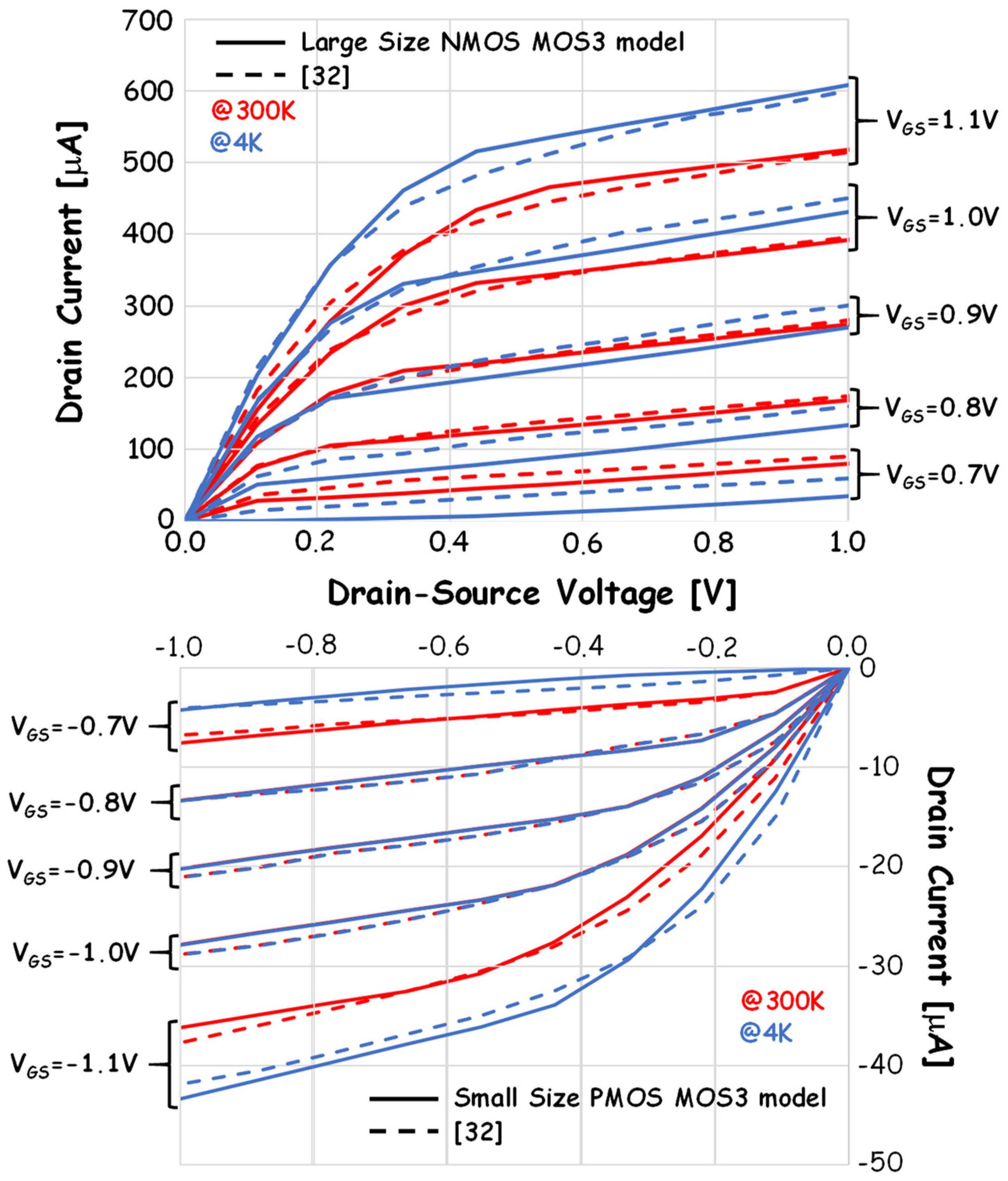
| NMOS Large Size | PMOS Large Size | NMOS Small Size | PMOS Small Size | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | Unit | Temperature [K] | Temperature [K] | Temperature [K] | Temperature [K] | ||||
| 300 | 4 | 300 | 4 | 300 | 4 | 300 | 4 | ||
| PHI | [V] | 0.9579 | 1.156 | 0.9579 | 1.156 | 0.9579 | 1.156 | 0.9579 | 1.156 |
| VTO | [V] | 0.55 | 0.65 | −0.55 | −0.71 | 0.5 | 0.6 | −0.5 | −0.63 |
| KP | [µA/V2] | 200 | 300 | 81 | 131 | 200 | 300 | 81 | 131 |
| ETA | [–] | 0.16 × 10−3 | 0.23 × 10−3 | 0.21 × 10−3 | 0.23 × 10−3 | ||||
| THETA | [V−1] | 1.923 | 1.64 | 1.45 | 0.98 | ||||
| CBD | [F] | 5.4 × 10−16 | 5.4 × 10−17 | 6 × 10−16 | 6 × 10−17 | 5.4 × 10−17 | 5.4 × 10−18 | 6 × 10−17 | 6 × 10−18 |
| CBS | [F] | 5.4 × 10−16 | 5.4 × 10−17 | 6 × 10−16 | 6 × 10−17 | 5.4 × 10−17 | 5.4 × 10−18 | 6 × 10−17 | 6 × 10−18 |
| CGSO | [F/m] | 5 × 10−10 | 5 × 10−10 | 5 × 10−11 | 5 × 10−11 | ||||
| CGDO | [F/m] | 5 × 10−10 | 5 × 10−10 | 5 × 10−11 | 5 × 10−11 | ||||
| KF | [FV2] | 3 × 10−24 | 5.5 × 10−24 | 5.5 × 10−23 | 3 × 10−24 | 5.5 × 10−24 | 5.5 × 10−23 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gira, G.; Ferraro, E.; Borgarino, M. On the VCO/Frequency Divider Interface in Cryogenic CMOS PLL for Quantum Computing Applications. Electronics 2021, 10, 2404. https://doi.org/10.3390/electronics10192404
Gira G, Ferraro E, Borgarino M. On the VCO/Frequency Divider Interface in Cryogenic CMOS PLL for Quantum Computing Applications. Electronics. 2021; 10(19):2404. https://doi.org/10.3390/electronics10192404
Chicago/Turabian StyleGira, Gabriele, Elena Ferraro, and Mattia Borgarino. 2021. "On the VCO/Frequency Divider Interface in Cryogenic CMOS PLL for Quantum Computing Applications" Electronics 10, no. 19: 2404. https://doi.org/10.3390/electronics10192404
APA StyleGira, G., Ferraro, E., & Borgarino, M. (2021). On the VCO/Frequency Divider Interface in Cryogenic CMOS PLL for Quantum Computing Applications. Electronics, 10(19), 2404. https://doi.org/10.3390/electronics10192404







