Abstract
This work presents a new four-dimensional autonomous hyperchaotic system based on Méndez-Arellano-Cruz-Martínez (MACM) 3D chaotic system. Analytical and numerical studies of the dynamic properties are conducted for the new hyperchaotic system (NHS) in its continuous version (CV), where the Lyapunov exponents are calculated. The CV of the NHS is simulated and implemented using operational amplifiers (OAs), whereas the Discretized Version (DV) is simulated and implemented in real-time. Besides, a novel study of the algorithm performance of the proposed DV of NHS is conducted with the digital-electronic implementation of the floating-point versus Q1.15 fixed-point format by using the Digital Signal Processor (DSP) engine of a 16-bit dsPIC microcontroller and two external dual digital to analog converters (DACs) in an embedded system (ES).
Keywords:
hyperchaotic system; DSP; dsPIC; bifurcation diagram; Lyapunov exponent; embedded system; SPI; DAC 1. Introduction
In recent years, the potential applications of chaotic systems have attracted attention as an interesting nonlinear phenomenon, since the chaotic properties are highly desired in several areas of science and engineering such as high sensitivity to initial conditions, high entropy, topology complexity, ergodicity [1,2,3], among others. These properties have an important theoretical value for the academic community and research groups about the study and design of systems that generate chaotic behavior, and they have become a crucial point for engineers with different applications in areas such as biology [4], secure communications [5], chaotic trajectories for autonomous mobile robots [6], experimental network synchronization [7], technology as fingerprint encryption [8], and digital cryptosystems based on chaos [9,10].
In 1963, Lorenz proposed a three-dimensional system with two scrolls, which is recognized as the first chaotic model reported in literature [11]. Subsequently, in 1976 Rössler proposed another chaotic system like Lorenz [12]. In 1979 Rössler proposed the first hyperchaotic system for a model of a particular chemical reaction [13]. Since then, several hyperchaotic systems have been reported, such as temperature fluctuation model [14], with memristive and electronics circuits [15,16], fractional order [17], semiconductor laser system [18], synchronization [19,20], and image encryption [21].
The mathematical definition of a hyperchaotic system is based on a chaotic system with more than one positive Lyapunov exponent, and simultaneously its dynamics are richer and more extended in the phase plane [16]. The hyperchaos has more complex dynamical behaviors than the chaotic system, and it can be found coupling k chaotic systems to obtain a hyperchaotic attractor with n positive Lyapunov exponents; the transition from chaos to hyperchaos shows that the attractor’s dimension increase and the second Lyapunov exponent grow continuously [22]. A hyperchaotic system can be numerically and experimentally generated by adding a simple state feedback controller, e.g., Chua’s circuit [23], Chen system [20], or Lorenz [24].
Recently, the electronic digital implementation of chaotic systems has attracted the attention for the community scientific for the several applications in engineering, e.g., the cryptosystems—where the main encryption process is based on chaos—are designed considering statistical and security tests, even if the cryptosystem has good performance, the computing capacity on embedded systems continues being a challenge for designers [9,10,14,17].
The computing capacity on the embedded systems such as FPGA [25,26,27], system on chip (SOC) [28], DSP [29], and 16 or 32-bit microcontrollers [26,30] continues being a challenge for designers to reproduce a chaotic system considering tools that currently have embedded systems. The algorithm of a chaotic map of discrete time can be directly implemented in an embedded system, whereas the chaotic systems of continuous time need to be discretized by using some numerical solution to be implemented in an embedded system [21]. First, we need to consider the accuracy method and the time complexity to conduct the discrete version (DV) of the chaotic system, and then we need to know the embedded system properties to implement the algorithm, where chaos degradation is unavoidable and can reduce the performance for some application. There are studies that establish techniques to avoid chaos degradation when it is implemented in embedded system [29]. The digital electronic implementation is very limited to meet the requirements as power and performance speed, memory resources, and the time complexity that algorithms based in chaos need to run many computing resources to encrypt and transfer multimedia contents such as ultra-definition video, high-fidelity audio, big-size data files [31], among others.
In this work, we firstly introduce a new 4D hyperchaotic system (NHS) via modifying 3D MACM system inspired by the above works [32]. Two critical parameters, only two nonlinearities, flexible and robust, one unstable equilibrium saddle-point, and low-cost electronic implementation for the continuous and discretized versions are the main novelties of the proposed hyperchaotic system. All these features result in a highly attracting digital implementation, such as low complexity time, high iterations per second (ips) where chaos is preserved, and it may be of great interest for engineering applications such as chaos-based cryptography, biometric systems, telemedicine, and secure communications. According to our best knowledge, the digital implementation of the nonlinear hyperchaotic dynamics in real-time of DV in Q1.15 fixed-point using the DSP engine of the dsPIC have not been reported before.
The paper is organized as follows: Section 2 reports the basic analytical proofs and the extensive numerical tests of the proposed NHS to verify the chaos and hyperchaos existence. Section 3 presents two electronic implementations to reproduce the dynamics of NHS: the first one is implemented by using OAs, the second one is implemented in ES by using dsPIC33FJ and two dual external digital-to-analog converters (DAC). In addition, a digital performance study is conducted taking into consideration the benefits of the dsPIC33FJ’s digital signal processing engine to obtain a Q1.15 fixed-point versus the floating-point versions. Finally, in Section 4 we draw some concluding remarks.
2. Basic Analysis and Characterization of New Hyperchaotic System
In this section, state equations and tests to verify the hyperchaos existence are presented. The NHS system is built by inspecting, modifying, and adding one state to the MACM chaotic system [32]. The proposed NHS is described as follows
The system (1) has ten terms, two quadratic nonlinearities, and four parameters a, b, c, d ∈ +, with c < a + 2, where b and d are characterized as the bifurcation parameters. The nonlinear NHS (1) is hyperchaotic with a = 2, b = 2, c = 0.5, and d = 14.5.
2.1. Symmetry
The system (1) is symmetrical about the z-axis for its invariance under the coordinate transformation (x, y, z, w)→(−x, −y, z, −w). The symmetry is not associated with the a, b, c, d parameters.
2.2. Dissipativity and Existence of Attractor
For a dynamical system, the divergence of 3-dimensional flow is defined by
Therefore, the above analysis proves that our system is dissipative. The exponential contraction rate is calculated as follows
where each volume containing the system trajectory shrinks to zero as t→∞ at an exponential rate of −3.5t. System orbits are ultimately confined into a specific limit set of zero volume, and the asymptotic motion settles onto an attractor. Thereby, the existence of attractor is proved.
The boundness of the chaotic trajectories of system (1) is proved by means of the following theorem. The boundness of NHS by using a similar approach was reported in [33].
Theorem 1.
Suppose that the parameters a, b, c, and d of system (1) are positive. Then, the orbits of system (1) including chaotic orbits are confined in a bounded region.
Proof of Theorem 1.

Consider the candidate Lyapunov function
and the time derivative of V(x,y,z,w) along the trajectories of NHS (1) is given by
Let R0 be the sufficiently large region so that for all trajectories (x,y,z,w) satisfy V(x,y,z,w) = R for R > R0 with the following condition
Consequently on the surface {(x,y,z,w)/V(x,y,z,w)} = R. Since R > R0 we can write = (x,y,z,w) < 0, or the set {(x,y,z,w)/V(x,y,z,w)} ≤ R is a confined region for all the trajectories of chaotic system (1).
The behavior of the system (1) is determined by the number of the equilibrium points and their stabilities. The equilibria of the system (1) can be found by setting = = = = 0 and a, b, c, d > 0, the proposed system (1) has 9 fixed points and . The Jacobean matrix of CV-system (1) is given by
the characteristic polynomial of (4) is as follows:
det(λI − J) = λ4 + (a − c + 2) λ3 + (2a − 2c − ac − bz + 1)λ2
+ (2by2 + a − c − 2ac − 2bz + bcz)λ
+ 2by2 − bz − ac + bcz − 2bcy2 = 0.
+ (2by2 + a − c − 2ac − 2bz + bcz)λ
+ 2by2 − bz − ac + bcz − 2bcy2 = 0.
Evaluating with parameters a = 2, b = 2, c = 0.5, and d = 14.5 in (8), the stability and equilibrium points P0–9 are studied and evaluated. Table 1 shows the stability results of equilibria, where 7 points of NHS (1) are saddle-focus unstable nodes. □

Table 1.
Stability analysis equilibrium points for new hyperchaotic system (NHS).
2.3. Bicurcation Analysis
Figure 1 shows the bifurcation diagram of system (1) with different values of parameter b and d versus y and w state variables by using the initial conditions x0 = y0 = z0 = w0 = 1.
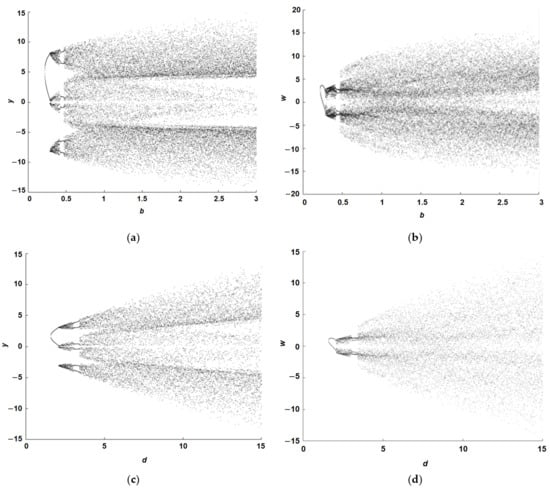
Figure 1.
Bifurcation diagrams of parameters b and d: (a) b versus y state with variations of b = [0.1–3], (b) b versus w state with variations of b = [0.1–3]. (c) d versus y state with variations of d = [1.5–15], and (d) d versus w state with variations of d = [1.5–15].
2.4. Lyapunov Exponents
The behavior of Lyapunov exponents is shown in Figure 2. The initial conditions x0 = y0 = z0 = w0 = 1 and parameter d = 14.5, are considered. Figure 2 shows evolution of Lyapunov exponents L1 = 0.5841, L2 = 0.000127664, L3 = −0.4873, and L4 = −3.5968 considering the variation of bifurcation parameter d = [1.5–15]; the system (1) exhibits two positive Lyapunov exponents L1, L2 > 0, which means that NHS has hyperchaotic behavior.
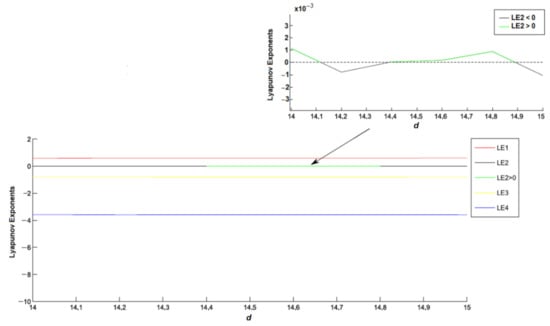
Figure 2.
Lyapunov exponents of system (1) with the variation of bifurcation parameter d = [14–15].
The fractal dimension, commonly known as the Kaplan-Yorke dimension DKY, of this system is:
2.5. Numerical Simulations
Figure 3 shows the temporary states x, y, z, and w, the phase planes and phase space with the strange attractor of system (1) by using the initial conditions x0 = y0 = z0 = w0 = 1 and the parameters a = 2, b = 2, c = 0.5, and d = 14.5.
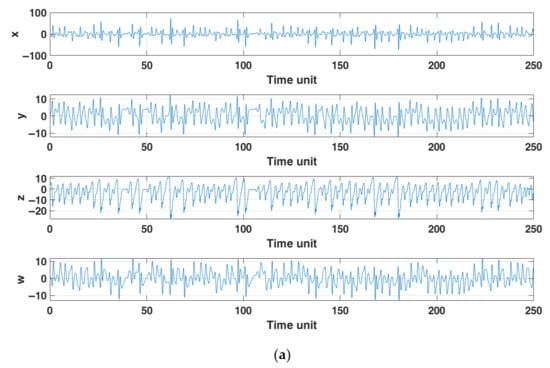
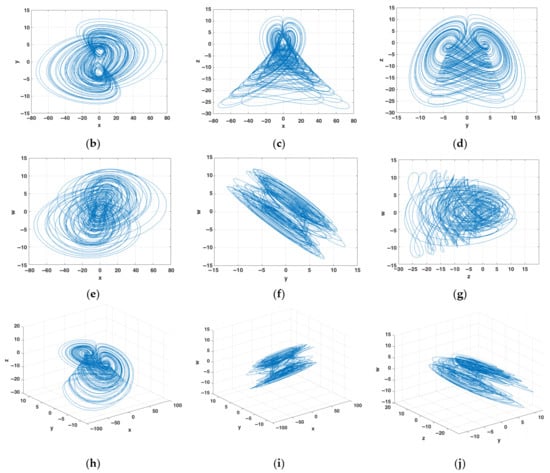
Figure 3.
Hyperchaotic attractor of system (1): (a) time evolution of states x, y, z and w; (b) phase plane x versus y; (c) phase plane x versus z; (d) phase plane y versus z; (e) phase plane x versus w; (f) phase plane y versus w; (g) phase plane z versus w; (h) phase space x versus y versus z; (i) phase space x versus y versus w; and (j) phase space y versus z versus w.
3. Electronic Implementations
In this section, the electronic simulation and implementation of the NHS are presented in their continuous and discretized versions. All the hardware simulation used in NHS are conducted using the Proteus Virtual System Modeling (VSM) software. The continuous version was implemented by means of a circuit designed using TL84 operational amplifiers [32,34]. The discretized version was conducted using the Proteus VSM which has Microchip libraries that include the 16-bit dsPIC33FJ microcontroller and external DACs, the numerical and experimental methods, described in [26,32], are carried out in the electronic implementation of the discretized versions of NHS in floating-point and fixed-point Q1.15.
3.1. Continuous Version and Its Electronic Circuit Design
To implement the electronic continuous version of system (1), the normalized model is regarding with the attenuation factor of 20 for each state variables, i.e., x = 20o, y = 20p, z = 20q, w = 20r are defined. Replacing the new variables on system (1), we obtain the following system:
Replacing the state variables again for o = x, p = y, q = z, r = w, the circuit equivalent representation of system (10) is defined by
where the values of components are: C1 = C2 = C3 = C4 = 100 pF, R = R7 = 1 MΩ, R10 = 1 MΩ R1 = 500 kΩ, R4 = R5 = R8 = R9 = R12 = R13 = 10 kΩ, R14 = 94 kΩ, R2 = 47 kΩ, R3 = R6 = 2 MΩ, the control parameter is fixed in d = 14.5 with R11 = 4.2 MΩ, and the circuit (10) is supply with +Vcc = 18 V and −Vcc = −18 V. To see a change in the dynamical behavior of system (10), is recommend represent the critical parameter d with a variable resistor to R11(VAR) = [0–5 MΩ]. The electronic version of system (11) is implemented using operational amplifiers TL084 and multipliers AD633. Figure 4 shows the equivalent circuit of system (11).
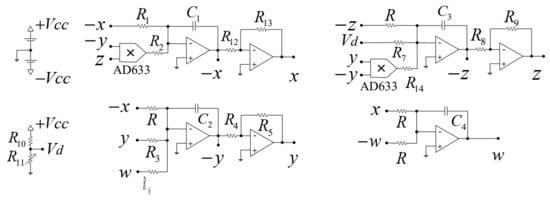
Figure 4.
Schematic diagram of the equivalent circuit of system (11).
In order to compare the experimental results of the system (11), Figure 5 shows the electronics implementation using Proteus VSM simulation and Figure 6 shows the electronic circuit implementation assembly shown in Figure 4. We can see that the corresponding attractors are highly similar with respect to those shown in Figure 3.
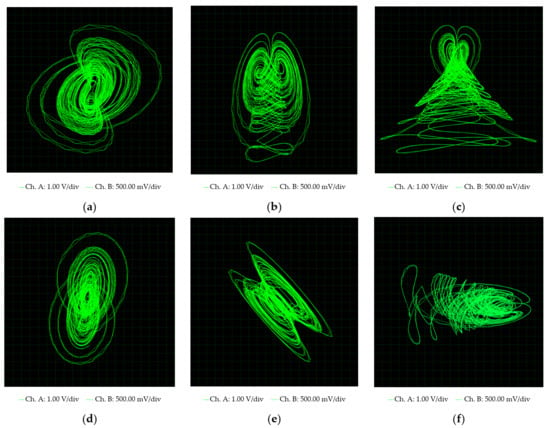
Figure 5.
Electronic simulation of system (11) using Proteus VSM: (a) phase plane x versus y; (b) phase plane x versus z; (c) phase plane y versus z; (d) phase plane x versus w; (e) phase plane y versus w; (f) phase plane z versus w.
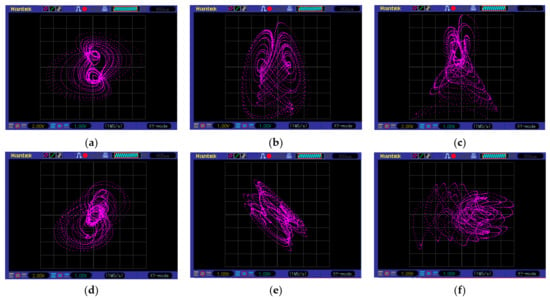
Figure 6.
Electronic circuit implementation of system (11): (a) phase plane x versus y; (b) phase plane x versus z; (c) phase plane y versus z; (d) phase plane x versus w; (e) phase plane y versus w; (f) phase plane z versus w.
3.2. Discretized Version and Embedded System Design
The Euler’s method allows discretizing a continuous system, which is derived from the expansion of Taylor’s series where the quadratic and upper order term are truncated. The Euler method is used to approximate the ordinary differential equations (ODEs) and it is described by
is given by
where τ is the step size and n is the iteration that represents the time in discrete version. The Matlab simulations are carried out using the same parameter and initial conditions (i.e., x0 = y0 = z0 = w0 = 1) considering τ = 0.005 and n = 30000. The Euler algorithm requires less arithmetic operations because it presents just one step, and it is easy to implement [35]. The Euler’s discretization (13) is used to represent the DV of system (1) as follows
x(n + 1) = x(n) + τf(x(n)),
x(n + 1) = x(n) + τ(−ax(n) − by(n)z(n)),
y(n + 1) = y(n) + τ(−x(n) + cy(n) + cw(n)),
z(n + 1) = z(n) + τ(d − y(n)2 − z(n)),
w(n + 1) = w(n) + τ(x(n) − w(n)).
y(n + 1) = y(n) + τ(−x(n) + cy(n) + cw(n)),
z(n + 1) = z(n) + τ(d − y(n)2 − z(n)),
w(n + 1) = w(n) + τ(x(n) − w(n)).
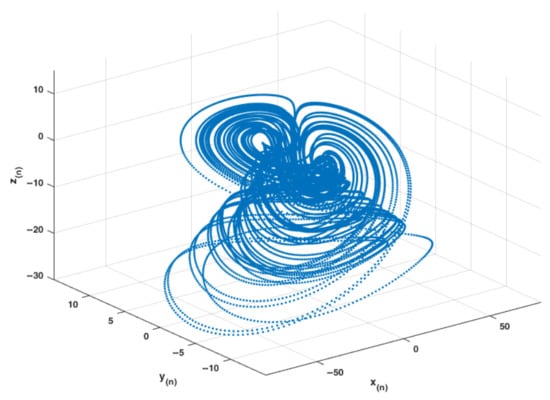
Figure 7.
Hyperchaotic attractor of DV-system (14) projected on x(n) versus y(n) versus z(n).
3.2.1. Circuit Design of an Embedded System
An important attribute of Matlab software and Mikro C for dsPIC compiler is that both have the IEEE-754 standard, numerical results are equivalent to represents the simulation and implementation of the discretized system (14), the numerical data are implemented in 16-bits floating-point format, and fixed-point Q1.15 [36]. The dsPIC architecture allows fast calculation in comparison with 16-bit microcontrollers because it has a DSP engine, therefore it is an important attribute for the implementation of this embedded system. Table 2 describes the peripherals used for this embedded system, where all operations are performed by a 16-bit dsPIC microcontroller dsPIC33FJ and DACs MCP4922 (Microchip Technology, Chandler, AZ, USA) with multiple output of 12-bit resolution, both are energized with Vdd = Vcc = 3.3 V.

Table 2.
Data bus description of embedded system (ES).
In the ES implementation, the SPI protocol is used because it contemplates easy configuration using low-quantity lines and fast serial data bus transmission with the external peripherals. U1 is configured as a master mode, and U2 and U3 as slave, the data serial is 16-bit mode and quick communication of 16.6 Mbps.
The data bus description of the embedded system is described in Table 3. From U1, the control lines SDO, SCK, EDAC1, EDAC2, and LDAC are generated to control U2 and U3 for depict the state variables x(n), y(n), z(n), and w(n) synchronized for each n iteration. The schematic circuit design of the embedded system is shown in Figure 8.

Table 3.
Data bus description of ES.
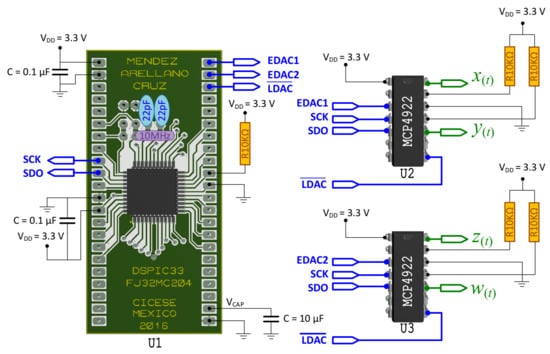
Figure 8.
Schematic of the implementation of system (14) in embedded system.
The maximum number of n iterations generated in one second is referred to the total quantity of iterations QT, and it is represented in time units (tu), the NHS has four dimensions, i.e., N = 4 dimensions, and the QT representation is given by
where the time period TTd is considered as the total-decoding-time that the algorithm needs to reproduce an iteration n, and fTd represents the maximum number of iterations n that the ES generates in one second (ips); the frequency fTd is the reciprocal of TTd. The time complexity tc is the time that numerical algorithm (NA) needs to reproduce one iteration n by using U1; the total-graphic time tTg is the time that the two DACs U2–U3 required to represent the four state variables x(t), y(t), and z(t), w(t), respectively. The tTdac is the time required for each DAC which represents two state variables, and the ES design illustrates, at the same time, the state variables x(t), y(t), z(t), and w(t) for each n sample.
In the next subsection we will analyze two electronic implementations, using a numerical format for each. Specifically, we are using the proposed parameters of Equation (15) to denote the system (14) in floating-point with the sub index 1, and the same system (14)—with some numerical variable changes—in fixed-point with the sub index 2.
3.2.2. Implementation of the DV of NHS in Floating-Point
The flow chart of the electronic/digital implementation process of the DV of NHS (14) is shown in Figure 9. The description of each step is described below.
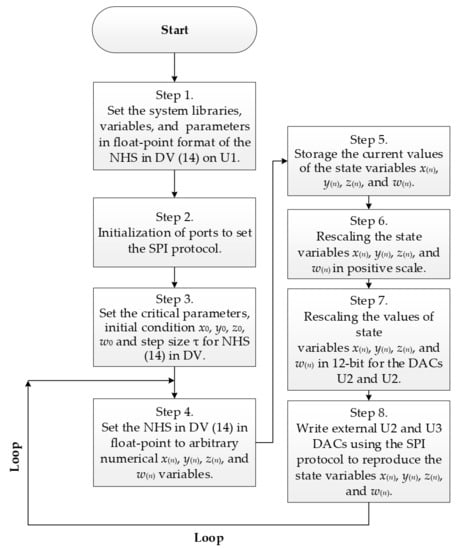
Figure 9.
Flow chart of the electronic/digital implementation process in floating-point version of NHS (14).
From Figure 9, the steps 1–3 describe the process to set the numerical conditions to initialize the ports, system libraries, variables, parameters, and set the initial conditions of the DV of NHS (14) in floating-point. Subsequently, the steps 4–6 describe all the entire loop-process to store, and rescaling the state variables in positive scale. Finally, the steps 7–8 describe the rescaling process to write the U2 and U3 DACs of the system (14) for specific n iteration.
Figure 10 and Table 4 show the implementation results of the DV of the NHS (14) to exemplify (15). We obtained QT1 = 221.22 considering τ = 0.02 using the proposed ES.
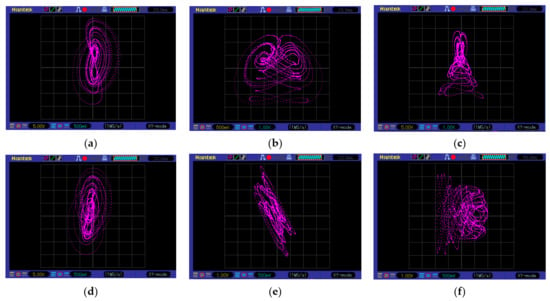
Figure 10.
Electronic circuit implementation of system (11): (a) phase plane x(n) versus y(n); (b) phase plane x(n) versus z(n); (c) phase plane y(n) versus z(n); (d) phase plane x(n) versus w(n); (e) phase plane y(n) versus w(n); (f) phase plane z(n) versus w(n).

Table 4.
Implementation results of DV-system (14) on the proposed ES.
This study is focused on computing the numerical results, considering only the capability that the embedded system has to run the NA of system (14) and dismissing the graphic results tTg1 = 0, which means that only can be considered tc1 = 56 µs—the numerical conversions to set and write the 12-bit DACs U2 and U3 are ignored, and the algorithm (14) is only implemented in U1. We obtained TTd1 = 56 µs, which means that the NA has a performance of fTd1 = 17857 ips.
3.2.3. Implementation of the DV of NHS in Fixed-Point Q1.15
The dsPIC microcontroller includes DSP proficiencies; it is a 16-bit microcontroller with high-performance and a high computation speed. The DSP libraries of MikroC PRO for dsPIC Compiler (MikroElektronika, Belgrade, Serbia) are based on fixed-point, and their routines work with fractional Q1.15 format [35]. The coefficients, the step size, and state variables of discretized system (14) must be arrangement in fractional Q1.15 format to not excess the numerical limits (−1, 1). The same numerical attenuation used in system (10) and electronics implementation of system (11) is used in the DV of system (14). The attenuation factor 20 is proposed for each x = 20o, y = 20p, z = 20q, and w = 20r state variables, replacing in system (14), the following system is obtained,
evaluating τ = 0.02, and with the corresponding parameters, we have
o(n + 1) = o(n) − aτo(n) − bτp(n)q(n),
p(n + 1) = p(n) − τo (n) + cτp(n) + cτr(n),
q(n + 1) = q(n) + dτ − τp(n)2 − τq(n),
r(n + 1) = r(n) + τo (n) − τr(n),
p(n + 1) = p(n) − τo (n) + cτp(n) + cτr(n),
q(n + 1) = q(n) + dτ − τp(n)2 − τq(n),
r(n + 1) = r(n) + τo (n) − τr(n),
o(n + 1) = 0.96o(n) − 0.8p(n)q(n),
p(n + 1) = − 0.02o(n) + 0.505p(n) + 0.505p(n) + 0.01r(n),
q(n + 1) = 0.0145 + 0.98q(n) − 0.4p(n)2,
r(n + 1) = 0.02o (n) + 0.98r(n).
p(n + 1) = − 0.02o(n) + 0.505p(n) + 0.505p(n) + 0.01r(n),
q(n + 1) = 0.0145 + 0.98q(n) − 0.4p(n)2,
r(n + 1) = 0.02o (n) + 0.98r(n).
The vector multiplication function and vector dot function of the DSP system libraries are used to build the algorithm of system (17). First, the vector dot function is used to multiply the two nonlinearities p(n)q(n) and p(n)2 by separation, after the vector dot function is used for the representation of each equation of the DV of system (17), the results obtained are represented in fixed-point Q1.15. In Figure 11, we illustrate the flow chart of the electronic/digital implementation process of the DV of NHS (17), the steps 1–3 describe the process to set the numerical conditions to initialize the ports, system libraries, variables, parameters, and set the initial conditions converted in fixed-point. Subsequently, the steps 4–6 describe all the entire loop-process to store and rescale the state variables in a positive scale. Finally, steps 7–8 describe the rescaling process to write the U2 and U3 DACs of the system (17) for specific n iteration.
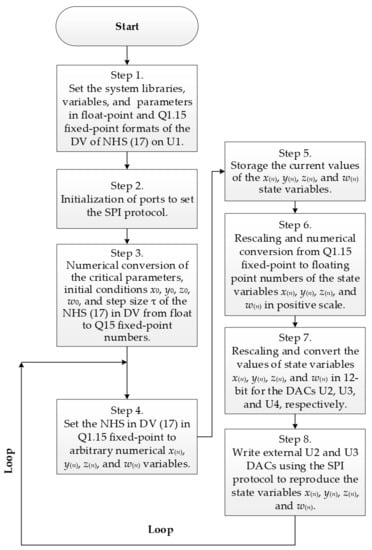
Figure 11.
Flow chart of the electronic/digital implementation process in Q1.15 fixed-point version of NHS (17).
Figure 12 and Table 5 show the implementation results in fixed-point of the DV of the NHS (17) to exemplify (15). We obtained more QT2 = 495.04, considering the same τ = 0.02 from system (14) and implementing it in the proposed ES.
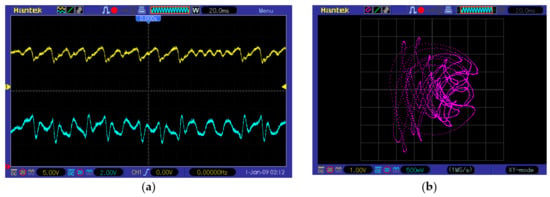
Figure 12.
Hyperchaotic system (17) implemented in fixed-point: (a) time evolution of states z(n) and w(n); (b) phase plane z(n) versus w(n).

Table 5.
Implementation results in fixed-point of the DV of system (17) on the proposed ES.
The system (17) is implemented in the embedded system and the graphic results are dismissed tTg2 = 0, which means that only tc2 = 6 µs is computed. We obtained TTd2 = 6 µs, which means that the NA has a performance of fTd2 = 166666 ips.
3.2.4. Comparison of the Digital Implementations of the DV of NHS Algorithm in dsPIC
For better comparison between the performance algorithms of the DV of the NHS in the dsPIC, Table 6 summarizes the electronic implementation using the ES with different numerical representation of system (14) and system (17), in Table 4 and Table 5, respectively. The electronic implementation of system (17) is based on Q1.15 fixed-format and it shows better TTd2 = 6 µs and fTd2 = 166666 ips performance versus the floating-point format used in the system (14), which shows TTd1 = 56 µs and fTd1 = 17857 ips, which means that there is 89% improvement in the ips reproduction by using the same algorithm.

Table 6.
Implementation results of the DV of NHS system (14) versus DV of system NHS (17) on the ES.
The proposed hardware of the ES allows comparison of the performance of the system algorithm (14) versus the system algorithm (17). The algorithm of the system (17) was based on the fixed-point format Q1.15, and it had better performance for digital applications because it provides 166.6 kHz iterations per second, which means that it is very attractive as a base system for encryption applications and electronics implementations, e.g., to encrypt high-fidelity audio such as Compact Disk quality 44.1 kHz or DVD audio quality 48 kHz, data-transfer, and even for low-resolution video applications or image, among others.
4. Conclusions
This work presented analytical and numerical studies of a new hyperchaotic system (NHS) that produces chaos and hyperchaos, varying only two parameters. The analysis includes tests of symmetry, dissipativity, equilibria and stability, bifurcation analysis, and Lyapunov exponents. The results showed that new hyperchaotic attractor presents two positive Lyapunov exponents, an unstable equilibrium saddle-point at the origin, and it is flexible and robust which allows obtaining different hyperchaotic and chaotic behavior.
The simulation results of the NHS in its continuous version (CV) and discretized version (DV) were conducted using Proteus Virtual System Modeling (VSM), and the experimental electronic results were carried out using operational amplifiers for CV. In addition, a novel study to implement the DV of the NHS in an embedded system was presented, which is very useful in digital implementation. In general, we can mention that the digital implementation has some benefits versus the electronic implementation of the analog systems, which is the typical aging, and tolerance of the components, which means that chaotic systems are highly attractive in the electronic digital implementation if the chaos quality condition is preserved.
The ES has a simple hardware design, easy connection with low-cost of implementation (only $6 USD dsPIC33FJ plus two DACs 4922) and is friendly for digital electronic implementation. The DSP-engine numerical properties of the dsPIC microcontroller allowed validation of the numerical performance of the DV of the NHS, and its algorithm was implemented and compared in floating-point versus fractional Q1.15 versions. The Q1.15 fractional version showed very good performance in the DV of NHS, it has the capability to run over 166k iteration per second (ips), and it is very attractive as a main algorithm, e.g., to implement a digital cryptosystem based in chaos, where a high quantity of iteration per second is essential to encrypt multimedia applications and to transfer cryptograms of digital audio of high fidelity, files, pictures, or even compressed video of low-resolution.
As future work, complementary studies will carry out the NHS with encryption and synchronization applications. Other techniques for representation of discretized version will be incorporated as the fractional and fixed-point computation on an embedded system in 32-bit microcontroller.
Author Contributions
Conceptualization, R.D.M.-R. and A.A.-D.; methodology, R.D.M.-R. and C.C.-H.; software, R.D.M.-R. and M.A.M.-E.; validation, R.D.M.-R., A.A.-D., and C.C.-H.; formal analysis, M.A.M.-E. and A.A.-D.; investigation, R.D.M.-R. and M.A.M.-E.; writing—original draft preparation, R.D.M.-R. and A.A.-D.; writing—review and editing M.A.M.-E. and C.C.-H.; supervision, C.C.-H.; funding acquisition, C.C.-H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the CONACYT, México, under Research Grant 166654 (A1-S-31628).
Data Availability Statement
The data used to support the findings of this study are included within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| 3D | Three-dimensional |
| 4D | Four-dimensional |
| MACM | Méndez-Arellano-Cruz-Martínez |
| NHS | New hyperchaotic system |
| CV | Continuous version |
| OA | Operational amplifiers |
| DV | Discretized Version |
| DSP | Digital Signal Processor |
| DACs | Digital-to-analog converters |
| ES | Embedded System |
| NA | Numerical algorithm |
References
- Eckmann, J.-P.; Ruelle, D. Ergodic theory of chaos and strange attractors. Rev. Mod. Phys. 1985, 57, 617–656. [Google Scholar] [CrossRef]
- May, R.M. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef] [PubMed]
- Alligood, K.T.; Sauer, T.D.; Yorke, J.A. Chaos: An Introduction to Dynamical Systems; Springer: Berlin, Germany, 1996. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; Perseus Books: Boston, MA, USA, 1994. [Google Scholar]
- Liu, J.; Wang, Z.; Shu, M.; Zhang, F.; Leng, S.; Sun, X. Secure Communication of Fractional Complex Chaotic Systems Based on Fractional Difference Function Synchronization. Complexity 2019, 2019, 7242791. [Google Scholar] [CrossRef] [Green Version]
- Nakamura, Y.; Sekiguchi, A. The chaotic mobile robot. IEEE Trans. Robot. Autom. 2001, 17, 898–904. [Google Scholar] [CrossRef]
- Arellano-Delgado, A.; López-Gutiérrez, R.; Cruz-Hernández, C.; Posadas-Castillo, C.; Cardoza-Avendaño, L.; Serrano-Guerrero, H. Experimental network synchronization via plastic optical fiber. Opt. Fiber Technol. 2016, 19, 93–98. [Google Scholar] [CrossRef]
- Murillo-Escobar, M.A.; Cruz-Hernández, C.; Abundiz-Pérez, F.; López-Gutiérrez, R.M. A robust embedded biometric authentication system based on fingerprint and chaotic encryption. Expert Syst. Appl. 2015, 42, 8198–8211. [Google Scholar] [CrossRef]
- Méndez-Ramírez, R.; Arellano-Delgado, A.; Cruz-Hernández, C.; Abundiz-Perez, F.; Martinez-Clark, R. Chaotic digital cryptosystem by using SPI protocol and its dsPICs implementation. Front. Inf. Technol. Electron. Eng. 2018, 19, 165–179. [Google Scholar] [CrossRef]
- Méndez-Ramírez, R.; Arellano-Delgado, A.; Murillo-Escobar, M.; Cruz-Hernández, C. Multimedia contents encryption using the chaotic MACM system on a smart-display. In Cryptographic and Information Security Approaches for Images and Videos; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2019; 10th chapter. [Google Scholar]
- Lorenz, E. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Rössler, O.E. An equation for continuous chaos. Phys. Lett. A 1976, 57, 397–398. [Google Scholar] [CrossRef]
- Rössler, O.E. An equation for Hyperchaos. Phys. Lett. A 1979, 71, 155–157. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Rajagopal, K.; Sambas, A.; Kacar, S.; Cavusoglu, U. A new hyperchaotic temperature fluctuations model, its circuit simulation, FPGA implementation and an application to image encryption. Int. J. Simul. Process. Model. 2018, 13, 281–296. [Google Scholar] [CrossRef]
- Kamdem Kuate, P.D.; Lai, Q.; Fotsin, H. Complex behaviors in a new 4D memristive hyperchaotic system without equilibrium and its microcontroller-based implementation. Eur. Phys. J. Spec. Top. 2019, 228, 2171–2184. [Google Scholar] [CrossRef]
- Rajagopal, K.; Vaidyanathan, S.; Karthikeyan, A.; Srinivasan, A. Complex novel 4D memristor hyperchaotic system and its synchronization using adaptive sliding mode control. Alex. Eng. J. 2018, 57, 683–694. [Google Scholar] [CrossRef]
- Rajagopal, K.; Karthikeyan, A.; Duraisamy, P. Hyperchaotic Chameleon: Fractional Order FPGA Implementation. Complexity 2017, 16, 8979408. [Google Scholar] [CrossRef] [Green Version]
- Vicente, R.; Daudén, J.; Colet, P.R. Toral Analysis and Characterization of the Hyperchaos Generated by a Semiconductor Laser Subject to a Delayed Feedback Loop. IEEE J. Quantum Electron. 2005, 41, 541–548. [Google Scholar] [CrossRef] [Green Version]
- Panga, S.; Liu, Y. A new hyperchaotic system from the Lü system and its control. J. Comput. Appl. Math. 2011, 235, 2775–2789. [Google Scholar] [CrossRef] [Green Version]
- Li-Xin, J.; Hao, D.; Meng, H. A new four-dimensional hyperchaotic Chen system and its generalized synchronization. Chin. Phys. B 2010, 19, 100501. [Google Scholar] [CrossRef]
- Ding, L.; Ding, Q. A Novel Image Encryption Scheme Based on 2D Fractional Chaotic Map, DWT and 4D Hyper-chaos. Electronics 2020, 9, 1280. [Google Scholar] [CrossRef]
- Kapitaniak, T.; Maistrenko, Y.; Popovych, S. Chaos-hyperchaos transition. Phys. Rev. E 2000, 62, 1972. [Google Scholar] [CrossRef] [Green Version]
- Li, G.L.; Chen, X.Y.; Liu, F.C.; Mu, X.M. Hyper-chaotic Canonical 4-D Chua’s Circuit. In Proceedings of the 2009 International Conference on Communications, Circuits and Systems, Milpitas, CA, USA, 23–25 July 2009; p. 10879007. [Google Scholar]
- Wang, X.; Wang, M. A hyperchaos generated from Lorenz system. Phys. A Stat. Mech. Appl. 2008, 387, 3751–3758. [Google Scholar] [CrossRef]
- Chen, B.; Yu, S.; Chen, P.; Xiao, L. Design and Virtex-7-Based Implementation of Video Chaotic Secure Communications. Int. J. Bifurc. Chaos 2020, 30, 24. [Google Scholar] [CrossRef]
- Méndez-Ramírez, R.; Arellano-Delgado, A.; Murillo-Escobar, M.; Cruz-Hernández, C. Degradation Analysis of Chaotic Systems and their Digital Implementation in Embedded Systems. Complexity 2019, 22, 9863982. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L. Fixed-point FPGA model-based design and optimization for Henon map chaotic generator. In Proceedings of the 2017 IEEE 8th Latin American Symposium on Circuits & Systems (LASCAS), Bariloche, Argentina, 20–23 February 2017; p. 16964391. [Google Scholar]
- Flores-Vergara, A.; Inzunza-González, E.; García-Guerrero, E.E.; López-Bonilla, O.; Rodríguez-Orozco, E.; Hernández-Ontiveros, J.M.; Cárdenas-Valdez, J.R.; Tlelo-Cuautle, E. Implementing a Chaotic Cryptosystem by Performing Parallel Computing on Embedded Systems with Multiprocessors. Entropy 2019, 21, 268. [Google Scholar] [CrossRef] [Green Version]
- Chuan Qin, K.S.; Shaobo, H. Characteristic Analysis of Fractional-Order Memristor-Based Hypogenetic Jerk System and Its DSP Implementation. Electronics 2021, 10, 841. [Google Scholar] [CrossRef]
- Mendez-Ramirez, R.; Arellano-Delgado, A.; Cruz-Hernandez, C.; Lopez-Gutierrez, R.M. Degradation analysis of generalized Chua’s circuit generator of multi-scroll chaotic attractors and its implementation on PIC32. In Proceedings of the Future Technologies Conference (FTC), San Francisco, CA, USA, 6–7 December 2016; pp. 1034–1039. [Google Scholar]
- Koulamas, C.; Lazarescu, M.T. Real-Time Embedded Systems: Present and Future. Electronics 2018, 7, 205. [Google Scholar] [CrossRef] [Green Version]
- Méndez-Ramírez, R.; Cruz-Hernández, C.; Arellano-Delgado, A.; Martínez-Clark, R. A new simple chaotic Lorenz-type system and its digital realization using a TFT touch-screen display embedded system. Complexity 2017, 2017, 6820492. [Google Scholar] [CrossRef] [Green Version]
- Nik, H.S.; Golchaman, M. Chaos Control of a Bounded 4D Chaotic System. Neural Comput. Applic. 2014, 25, 683–692. [Google Scholar]
- Qinghai, S.; Hui, C.; Yuxia, L. Complex Dynamics of a Novel Chaotic System Based on an Active Memristor. Electronics 2020, 9, 410. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.Y.; Cao, W.; Chung, T.-S.; Morris, J. Applied Numerical Methods Using Matlab; John Wiley and Sons Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Microchip Technology Inc. 16-Bit Language Tools Libraries, Reference Manual; Microchip Technology Inc.: Chandler, AZ, USA, 2014; DS0001456J.1–155. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).