Abstract
The 5G and beyond future wireless networks aim to support a large variety of services with increasing demand in terms of data rate and throughput while providing a higher degree of reliability, keeping the overall system complexity affordable. One of the key aspects regarding the physical layer architecture of such systems is the definition of the waveform to be used in the air interface. Such waveforms must be studied and compared in order to choose the most suitable and capable of providing the 5G and beyond services requirements, with flexible resource allocation in time and frequency domains, while providing high spectral and power efficiencies. In this paper, several beyond 5G waveforms candidates are presented, along with their transceiver architectures. Additionally, the associated advantages and disadvantages regarding the use of these transmission techniques are discussed. They are compared in a similar downlink transmission scenario where three main key performance indicators (KPIs) are evaluated. They are the peak-to-average power ratio, the overall system spectral efficiency (wherein the out of band emissions are measured, along with the spectral confinement of the power spectral density of the transmitted signals) and the bit error rate performance. Additionally, other KPIs are discussed.
1. Introduction
Over the past recent years, the fifth generation (5G) of wireless communication systems and networks has been researched, engineered and deployed. This introduces a new paradigm that will change and define the future generations of telecommunication standards, revolutionizing the way people interact, work and live [1,2]. The continuous growth of mobile devices and applications, with increasing bandwidth demands, will force the 5G and beyond technology to be able to support enormous volume of data, while being more energy efficient than the previous generation [3]. Therefore, 5G and beyond generations are envisioned to improve major key performance indicators (KPIs), including data rates, spectral efficiency, power consumption, transceiver complexity, connection density, latency, and mobility [4,5]. This can be done by exploring different methods for achieving a higher capacity of exchanging information with enhanced coverage potential, reliability and availability [2,6].
In general, three different types of services are to be supported in 5G: Enhanced Mobile Broadband (eMBB), massive machine-type communication (mMTC) which includes massive Internet of Things (IoT), and Ultra-Reliable and Low-Latency Communication (URLLC). Regarding eMBB, the KPIs driven from [7] include peak data rates of 20 Gb/s for the downlink (DL) and 10 Gb/s for the uplink (UL), spectral efficiencies of DL 30 bits/Hz and UL 15 bits/Hz, mobility up to 500 km/h and system bandwidth support up to 1 GHz. Regarding mMTC, the number of devices to be connected is enormous, requiring relaxed synchronization and low-cost devices [8]. Therefore, the KPIs include a density of 1 million devices per km2, an area traffic capacity of about 10 Mbits/s/m2, coverage of 164 dB and user equipment (UE) battery life up to 15 years. The URLLC implies a high reliability upon the transmission of a packet from the transmitter to the receiver, i.e., with a low probability of error (1 packet loss out of 100 million packet), no mobility interruption time and less than 1 ms latency [9].
In order to accomplish such ambitious requirements, the 5G and beyond networks will rely on an intelligent combination of several complementary factors and integration of advanced technologies [10] which includes:
- More flexible and efficient use of the current spectrum available in sub-6 Ghz bands, which may include the aggregation of non-contiguous and fragmented under-utilized spectrum bands for different network deployment scenarios [11];
- Expand the operation of 5G and beyond mobile network to consider also carrier frequencies above 6 GHz, enabling high capacity and high throughput services with low latency [12];
- The use of milli-meter (mm)-wave systems [13,14] to deliver an unprecedented level of service to the end user while dealing with new challenges, especially regarding high penetration loss, strong Doppler effects, sparsity and directionality [6,12];
- Enhanced higher-order modulations, frame structure, multiple access and coding schemes;
- The concept of network slicing, which uses resources when and where needed, that are after released [15].
Another way of improving the efficiency of the wireless 5G and beyond networks consists on densification by either increasing the number of antennas per site or by adding more base stations (BSs) and access points (APs) allowing for better spatial reuse of the spectrum. However, the network efficiency can also be improved by using more spectrum or by improving the spectral efficiency, i.e., the number of bits that can be transmitted per second in each unit of bandwidth [16]. One viable approach of grating a considerable increase in the network spectral efficiency consists into the use of multiple antennas at the transmitter and the receiver, also known as multiple-input-multiple-output (MIMO). Massive MIMO (m-MIMO) [17] deploys a massive number of transmitter antennas on the BS and serves a cell with a large number of terminals in the same time-frequency resource, separated in the spatial domain by receiving very directive signals [18]. In addition, it explores multipath propagation in order to boost overall data rates. Therefore, it represents one of the key technologies deployed in 5G wireless communication standards, providing high diversity and beamforming gains and spatial multiplexing of users and, hence, granting an increase on the throughput, reliability, and spectral and energy efficiency with simple signal processing, while reducing the inter-cell interference [19,20]. In [21] are presented in more detail the five disruptive technologies that can lead to both architectural and component design changes in 5G systems.
From the physical layer (PHY) perspective, modulation and waveform design is one of the most important aspects that plays a major role in fulfilling the 5G and beyond systems requirements. Because the current 4G long term evolution (LTE) communication systems are limited and cannot fully meet the previously mentioned objectives, an highly flexible air interface design must be identified, being capable of supporting mixed services with different waveform parameters [22,23]. Therefore, tremendous research and development of new suitable candidate waveforms for future cellular networks have been performed.
The goal of this paper is to provide a fair comparison between several candidates waveforms that are expected to be implemented in the next generation of wireless communications, 6G. After a brief introduction to the waveforms, the evaluation is performed by measuring some KPIs in a similar downlink transmission scenario. The main contributions of this paper are then:
- To provide a detailed overview of some promising multi-carrier waveforms.
- To perform an analysis between these waveforms regarding the peak-to-average power ratio (PAPR), power spectral density (PSD) and computation complexity.
- To derive a performance comparison between the waveforms in typical channel models.
The outline of this paper is as follows. Section 2 lists and explains the 5G and beyond network requirements that must be fulfilled by candidate waveforms. Section 3 presents a detailed description of the transceiver architecture of the main candidate waveforms being proposed for beyond 5G, while in Section 4 these are compared. Section 5 concludes the paper, drawing the main conclusions.
Throughout this paper the following notation will be employed: capital bold lettering (e.g., ) is used to refer a block/vector of samples at the frequency domain, and lower-case bold lettering (e.g., ) to denote a block/vector of samples at the time domain, while non-bold capital (e.g., ) or lower-case lettering (e.g., ) are used to denoted the symbols/samples of each of those block/vectors, respectively.
2. Waveform Key Performance Indicators for 5G and beyond Communications
A candidate waveform that defines physical shape of the signal that carries the modulated information through a wireless communication channel, should fulfill the following KPIs [22]:
- High Spectral Efficiency: Spectral efficiency is an important parameter since it indicates the achievable amount of bits that can be transmitted per second and per unit of bandwidth (bits/s/Hz), thus defining the maximum attainable bit rate given the available bandwidth. It is crucial to transmit the maximum amount data, using the minimum bandwidth that is possible, due to both licensing requirements and the spectrum scarcity resulting from the increasing transmission bandwidth requirement with demand for any time. Low spectral efficiency waveform formats can lead to high spectral amplitude outside the allocated bandwidth. This is known as out of band (OOB) radiation, which causes multiplexed services being transmitted on adjacent frequency channels to interfere with each other, a phenomena known as inter-channel interference (ICI) [6].
- Peak-to-average-power-ratio: The PAPR indicates the ratio between the maximum peak and the average transmitted power of the signal. A high PAPR results from the large fluctuations of the signal’s envelope and it is associated to a high power consumption at the base station’s terminals front-end, decreasing transmission energy efficiency. This is mainly due to the need of using linear power amplifiers, that are poorly efficient and is even lower when they are operated with some amount of back-off in order to avoid amplifier’s saturation and signal distortion (which can lead to spectral regrowth and higher bit error rates (BERs)) [24,25].
- Processing delay: Directly related to the URLLC 5G requirement, a waveform format with high complexity and large block processing delays increases the overall latency. The processing delay can be controlled by reducing the symbol temporal duration or period or increasing the sub-carrier spacing, which can be performed by efficient algorithms and signal processing techniques [4,6].
- Robustness to frequency-selective channels: When the transmitted signal travels through a wireless channel, it travels trough several paths with varied length, with multiple echos of the signal reaching the receiver. This causes an effect denoted as multipath fading [26]. The several copies of the waves that carry the transmitted signal arrive at the receiver with random amplitudes, frequencies and phases and can be combined constructively and destructively, interfering with one another. This leads to a temporal dispersion of the signal which can induce inter-symbol interference (ISI), impacting severely the transmission. Therefore, waveforms must be designed in order to be robust to this impairment.
- Robustness to time-selective channels: In wireless environments, transmitter and receiver mobility and, consequently, time-varying channels are still an open issue. The waveform transceiver system must be design in order to be robust to time-selective channels, by taking into account the channel coherence time, related to changes in the amplitudes, delays and the number of multipath components are observed. In fact, larger transmitted blocks can lead to higher sensibility to both carrier frequency offset (CFO) and Doppler effects [6].
- Massive Asynchronous Transmission: In 5G and beyond systems, a high number of communicating nodes will be communicating at a given time. In order to efficiently utilize network resources, asynchronous multiple access is essential. Thus, waveforms designs that are well localized in a multiplexed domain by allowing asymmetric and dynamic allocation of both time and frequency resources, as in frequency division duplex (FDD) and time division duplex (TDD), can achieve higher throughput through more efficient channel utilization [6].
- Complexity: The hardware and computation complexity represent a critical metric. It mainly depends on the the number of operations required at the transmitter or receiver, which may include windowing, filtering operations, as well as interference cancellation algorithms. The overall system complexity will influence the cost and the energy efficiency of the system and can represent a bottleneck upon selecting and determining the most suitable waveform candidate to be implemented for a certain type of applications [4].
- High flexibility, reliability and MIMO friendless: The ideal waveform should also be able to support the coexistence of different numerologies and multi-numerology to enable several services, while allowing dynamic allocation of bandwidth for these (numerologies/services) [9]. An extremely high reliability is also necessary. This means that the evaluated BER performances for the chosen waveform should be better, or at least, similar to previous standard waveforms. The new waveform should support and be extended to MIMO (especially massive-MIMO), without requiring much additional effort.
- Filtering/Windowing: The waveform should allow a filtering and/or windowing operation to be performed in both the transmission and reception stages, in order to manage the OOB emissions and latency. On the one hand, a wide filter bandwidth, which results in shorter filter length (in time domain), can control the system latency. However they are not very efficient at lowering the OOB emissions. On the other hand, a narrow filter implies very low OOB emissions but results in a long filter length (in time domain) which increases the system latency. Hence, there must be a trade-off between low OOB emissions and low latency [6].
3. Candidate Waveforms
The general waveform formats can be mainly classified as single-carrier (SC) and multi-carrier (MC) waveforms. In conventional SC modulation techniques, a high rate data stream occupy a large portion of the available spectrum. A wireless channel is usually a frequency selective channel, i.e., different frequency components are faded differently by the channel, being characterized by its coherence bandwidth, i.e., the frequency range over with the frequency response of the channel is approximately flat [26]. In high rate transmission scenarios, the low coherence bandwidth of the channel makes the SC systems require complex equalization schemes to deal with ISI.
Alternatively, in MC systems, a high rate stream of data is divided into several lower rates streams where independent data are modulated on different sub-channels, multiplexed in the frequency domain. This means that each sub-channel now occupies only a fraction of the overall bandwidth, allowing each sub-carrier experiences frequency flat-fading [27]. Nevertheless, a guard band is required between each adjacent sub-channel to eliminate any ICI.
3.1. Orthogonal Frequency Division Multiplexing
In order to fulfill the 5G and beyond KPI requirements [28], a new radio interface has been suggested by 3rd Generation Partnership Project (3GPP) for 5G systems [29]. The choice of the waveform for 5G New Radio culminated in the adoption of Orthogonal Frequency Division Multiplexing (OFDM) [27] added by a cyclic prefix (CP) for the underlying PHY technology in mobile broadband systems, regarding DL transmissions, as in 4G LTE systems.
OFDM is a MC modulation technique that can be implemented based on the numerology parametrization (number of sub-carriers, sub-carrier spacing and CP length) [10]. An OFDM signal consists on a group of N adjacent and orthogonal sub-carriers spaced, at frequency domain. The sub-carrier spacing depends on aspects such as radio-channel frequency selectivity, rate of channel variations, phase noise and Doppler effect [12,30].
Figure 1 represents the scheme of an OFDM transceiver. The bitstream is bit-interleaved and channel coded before mapping the resulting bitstream into constellation symbols. These symbols are drawn from a M-ary constellation, are mapped into each sub-carriers and simultaneously transmitted in an overlapping and parallel approach, with the transmitted signal being given by
where is a unitary rectangular pulse, allowing a considerable gain in spectral efficiency, saving up to 50% of the used spectrum [27]. The sub-carries spacing grants a degree of orthogonality, allowing an efficient demodulation free from interference from other sub-carriers [31] and exhibiting robustness against ICI. OFDM presents other interesting advantages, such as, the easy implementation of the transmitters based on inverse fast Fourier transform (IFFT) algorithm, as can be perceived from (1).
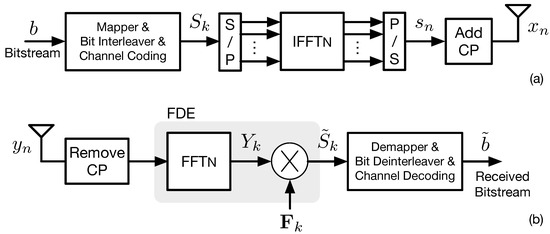
Figure 1.
OFDM transmitter (a) and receiver (b).
The receivers include the CP removal, followed by a frequency domain equalization (FDE) procedure, resulting in (denoting the estimated symbol sequence) Finally, the demapper, bit-deinterleaver and channel decoding operations are applied to the symbol sequence, resulting in the estimated bitstream, . e based on its inverse transform, i.e., the fast Fourier transform (FFT), allowing an efficient and low complexity FDE. It also enables the possibility of adapting the transmitted power and the modulation cardinality and an easy integration with MIMO technology, both at the transmitter and receiver, and a simple channel estimation [32,33].
Since the individual user’s channel delay spread is not taken into consideration [4] and due to different time delays upon reception of an OFDM symbol, ISI can occur, where the last part of the current symbol adds with the first part of the time delayed symbol. In order to avoid ISI, associated with multipath fading, in each OFDM symbol, it is necessary to add a cyclic extension of the symbol itself, called a CP, which is a copy of the tail of a symbol placed at its beginning [24], resulting in . Its duration is required to be greater than the impulse response of the transmission channel, which, in turn, is related to the channel delay spread. This also allows transforming the linear convolution that occurs in the transmission channel, in a cyclic convolution at the level of the individual processing of each OFDM symbol, enabling the implementation of a simple receiver based on the FFT. However the use of a CP per OFDM symbol increases the transmission overhead, by adding redundancy since the same content is transmitted twice as the CP. This lowers the effective throughput of the CP-OFDM system as well as its spectral efficiency, since the duration of the CP often represents a considerable percentage of the period of the symbol(which can reach up to 7–33%) [24]. Another aspect is related to the power wasted to transmit the CP, which reduces the power efficiency of OFDM transceivers.
The high amplitude of OFDM’s spectrum outside the allocated bandwidth is due to the sharp transitions of the rectangular pulse used in the signal generation, whose spectrum is a sinc. This way, the PSD of OFDM signal is a superposition sum of sinc shaped spectra, each one associated to a sub-carrier and centered in the corresponding frequency. These lateral lobes, of considerable amplitude add together giving rise to considerable OOB emissions [4,34], producing a decrease in the spectral efficiency of the system since they may cause interference on any adjacent channel.
Besides the restricted spectral efficiency, time domain transmitted signals in an OFDM system can have high peak values since the instantaneous amplitude of each sub-carrier that form the OFDM symbol is added by the IFFT operation. Therefore, OFDM systems are also conditioned by the ratio of high peak power vs. average power ratio, i.e., PAPR, which grows proportionally to the number of sub-carriers employed on the transmission and is usually evaluated through its complementary cumulative distribution function (CCDF) [25]. Such a high PAPR demands that the power amplifier must operate with a large output backoff in order to amplify the signal within its linear range and avoid amplifier’s saturation (which can lead to signal distortion), but that decreases amplifier power efficiency [27].
As can be concluded, OFDM does not fully meet some of the requirements for future wireless communication and further enhancements in this field can be made. This brought the need for the development of new techniques as alternatives to CP-OFDM, with greater spectral and power efficiency. Within the context of 5G and further generations of wireless communications, many alternative waveforms have been the subject of many recent studies [4,11,12,34,35,36,37,38,39,40], with several techniques being proposed as Generalized Frequency Division Multiplexing (GFDM) [41,42,43], Filtered-OFDM (F-OFDM) [44,45], the Time Interleaved Block Windowed Burst Orthogonal Frequency Division Multiplexing (TIBWB-OFDM) technique [46,47,48] and its variant with windowing time overlapping (WTO) [49,50].
3.2. Filtered Orthogonal Frequency Division Multiplexing
The F-OFDM waveform is still one of the most promising waveform candidates for 5G and beyond. It is based on OFDM, allowing to share some of the properties with OFDM-based designs, such as MIMO friendliness, PAPR reduction techniques based on discrete Fourier transform (DFT) precoding, and low complexity channel equalization in the receiver, since it relies on a CP and does not require any interference cancellation algorithm [44]. However, F-OFDM relies on sub-band based splitting and filtering, allowing the co-existence of different time-frequency granularities, where independent OFDM systems can co-exist in the assigned bandwidth [45]. This way, this system allows inter-sub-band asynchronous transmission to optimize the communication based on the different channel conditions and enabling diverse applications by adopting different numerologies (sub-carrier spacing, CP length, transmission time interval) in different sub-bands. Also, global synchronization is no longer a requirement.
In Figure 2 it is presented the basic transmitter and receiver architecture of F-OFDM. In each sub-band, a filter is applied in order to obtain lower OOB emission and to suppress the inter-sub-band interference. This is made of the expanse of losing of the time domain orthogonality between consecutive OFDM symbols in each sub-band [45], inducing inter sub-band interference (ITSBI). In general, the sub-bands do not overlap with each other and a guard interval is employed between sub-bands to mitigate ITSBI. One of the main drawbacks F-OFDM, compared with OFDM, is its relatively high complexity due to the filtering operation [9]. Furthermore, by supporting asynchronous transmission with flexible sub-band numerology, inner-sub-band interference (INSBI) may arise along with the aforementioned ITSBI. These two interference classes depend on many factors, such as the timing offset between the different interfering users, the guard band length and the filters employed in each sub-band [51].
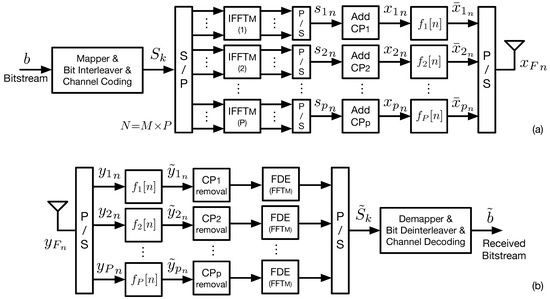
Figure 2.
F-OFDM transmitter (a) and receiver (b).
2
3.2.1. F-OFDM Transmitter and Filter Design
The F-OFDM transmitter generates the sub-band OFDM based signals, by assigning M consecutive sub-carriers in an OFDM symbol. This number M can be different for different sub-bands. However, for the sake of clarity, in the following description of F-OFDM, all the OFDM sub-band symbols are considered to have the same number of carriers. This means that the transmitter performs P IFFTs of size M, with P sub-band OFDM symbols being included within an OFDM symbol period, . Afterwards, each one of these new P “symbols” are added with a different CP of length, [44].
Figure 2 shows the schematic of a F-OFDM transceiver. Each one of the OFDM sub-band based signals is given by
where denote the modulated symbol from an constellation carried by the kth sub-carrier, from the assigned sub-carrier range. Each is added a CP adding a total of samples, resulting in . The overall N-sized OFDM, , signal is written in vector (3) and includes all the P sub-band signals, ,
The F-OFDM transmitted signal is obtained by filtering the CP-OFDM sub-signals, , through an appropriately designed spectrum shaping filter, , resulting in . In other words, in each sub-band the rectangular window, , is replaced by a filter , as follows
These filters are centered around the assigned sub-carriers with a bandwidth able to cover all the sub-carriers M assigned for that sub-band, and its time duration is a fraction of an OFDM symbol duration [44]. The overall F-OFDM signal, can, thus, be written as
Usually, these filter can be different for each sub-band, with their sizes being dependent on M. The filter design is one the most critical aspects of this technique, involving a trade-off between the time and frequency domain characteristics and complexity [45]. Usually, the the filter length is also allowed to exceed the CP length to achieve a better balance between the frequency and time localization [44].
The ideal prototype filter has a rectangular frequency response, i.e., a sinc time domain impulse response which causes no distortion in the pass-band and no OOB radiation [44]. For practical implementations, the sinc impulse response is soft-truncated with a window, such as the Hanning or root raised cosine (RRC) windows. In this paper, the Hanning window was employed in the filtering stage. More details on filter design can be found in [52]. By adopting this approach, the impulse response of the obtained filters will have smooth transitions, avoiding abrupt jumps at the edges, presenting only a limited time domain energy spread [9], which limits considerably the ISI introduced between consecutive OFDM symbols [45].
3.2.2. F-OFDM Receiver
The F-OFDM receiver for each sub-band is similar to the CP-OFDM receiver. However each sub-band received signal is first filtered with the respective matched filter used upon transmission, i.e., , resulting in the estimated signal, . This is followed by the CP (with length) removal and then the FDE (that performs an M-sized FFT operation) and finally the detection of the data symbols, , and bitstream, .
3.3. Generalized Frequency Division Multiplexing
The GFDM waveform concept introduces additional degrees of freedom when compared to traditional OFDM, by allowing a more flexible multi-carrier transmission regarding time-frequency structure design [42]. The main difference between GFDM and OFDM is that, in GFDM, the total number of modulated constellation symbols per frame is , using sub-symbols with different time-slots and N sub-carriers [53]. The basic architecture of a GFDM transmitter and receiver is presented in Figure 3.
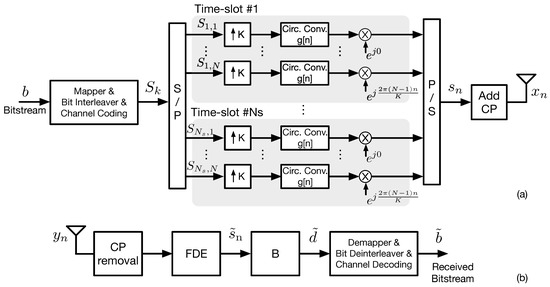
Figure 3.
GFDM transmitter (a) and receiver (b).
3.3.1. GFDM Transmitter
In a GFDM transmitter, every stream is firstly upsampled by , filtered, and then shifted to its carrier frequency. In the filtering stage the sub-carriers are circularly convoluted with a prototype filter, , such as the RRC [53]. A GFDM symbol is obtained through superposition of the filtered data symbols belonging to all sub-carriers and time slots and can be represented as follows [42]
where is the complex modulated symbol on the kth sub-carrier and mth sub-symbol, and denotes the prototype filter. The choice of can lead to lower ISI but higher ICI, which in turn deteriorates with higher roll-off [53].
Equation (6) can also be written as
where is a vector of data symbols, and is a complex valued modulation matrix with elements based on the parameters , K, N and , whose elements can be represented as [54]
for and .
Among the main characteristics of GFDM is characterized by the following:
- The adjustable filters used for pulse shaping are circularly convoluted over a defined number of symbols. This can result in non-orthogonal sub-carriers and both ISI and ICI might arise [4,43].
- Since GFDM is a MC technique it can exhibit high PAPR values, although with the inclusion of adjustable pulse shapes, along with the possibility of employing a filter-bank, equivalent to a DFT-OFDM signal, these values can be reduced [4,55,56].
- The possibility of adjusting the sub-carrier spacing allows a reduction on the OOB emissions.
- In the GFDM block construction, the overhead needed to avoid IBI is relatively small. Instead of adding a CP to every symbol like CP-OFDM schemes, the GFDM transmitter includes the addition of a single CP for an entire block that includes multiple sub-symbols [43], resulting in . Windowing techniques can also be employed in the GFDM multi-symbols in order to avoid discontinuities due to tail-biting.
Therefore, GFDM can achieve higher spectral efficiency than OFDM systems, at the expanse of self-introduced interference between sub-symbols and higher transceiver complexity. Additionally, the need for long filter lengths (narrow filter bandwidth) requires higher block processing which can lead to higher latency [6]. Several transmitter and receiver architectures have been proposed to reduce the overall system complexity, in order to address the needs of future wireless communication networks, such as in [43] which proposes a low complexity transmitter implementation based on the IFFT/FFT approach, just like OFDM, or in [54] which presents a receiver architecture that presents a sparse representation of the pulse-shaping filter in frequency domain, which also simplifies any interference cancellation algorithm.
3.3.2. GFDM Receiver
If we assume that the CP inserted in the GFDM multi-symbol is larger than the channel’s delay spread, the GFDM received symbol at frequency domain can be expressed as
where denotes the channel frequency response at kth sub-carrier and represents the complex additive white Gaussian noise (AWGN) sample with variance , while the total length of is . In order to compensate the influence of the channel on the received signal, a FDE method can be applied to the received signal [43]. Assuming perfect channel estimation and synchronization of the received signal, the minimum mean square error (MMSE) algorithm can be employed as follows [43]
where denotes the signal-to-noise (SNR) ratio.
Afterwards, a -sized inverse DFT (IDFT) is applied to the estimated signal (included in the FDE in Figure 3b), resulting in . Thereafter, the time domain signal is fed into a detector as follows:
with being the detection matrix and is the resulting vector which contains the estimated data symbols.
Furthermore, as a consequence of self-created interference between adjacent sub-carries and time-slots, worse BER performances are observed [54]. Thus, it is necessary to cancel this interference to achieve an acceptable performance [57]. Recently, it has been proposed many equalization and self-cancellation techniques that aim to tackle this multi-user interference in several realistic scenarios [58,59,60].
In [61], a double sided successive interference cancellation (DSSIC) method was proposed and applied on the detected symbols, subtracting the interference to adjacent sub-carriers in an iterative fashion.
Four set of different detectors have been proposed, materialized in a different matrix. The ones mentioned in this paper follow the ones presented in [43,53] and more details can be found in these references. They are divided as:
- Match Filtering (MF), where the same filter included in the transmitter is now applied to each received block, i.e., , where H is the Hermitian operator (conjugate and transpose). This maximizes the SNR ratio per sub-carrier, but introduces self-interference when a non-orthogonal transmit pulse is employed [43].
- Zero Forcing (ZF), where the inverse of matrix , presented in (7), is applied to recover the data symbols, i.e., . This approach completely removes any ICI at the cost of enhancing the influence of the noise in the detected symbols.
- DSSIC, which although being based on the MF detector, tries to minimize the ICI between neighboring sub-carriers. The basic idea is to subtract the ICI presented in the received signal at kth sub-carrier and caused by th and th sub-carriers. More details can be found in [43,53,61].
- SIC, which is similar to DSSIC but only the interference from the th sub-carrier is compensated.
3.4. Time Interleaved Block Windowed Burst Orthogonal Frequency Division Multiplexing
3.4.1. TIBWB-OFDM
The TIBWB-OFDM was proposed in [46,47] and is based on BWB-OFDM [62]. This new waveform allows a better spectral efficiency, by employing transmitted signals with a PSD as compact as F-OFDM schemes and a better power efficiency when compared to conventional CP-OFDM schemes [62]. The greater spectral efficiency is obtained by increasing the spectral confinement and lowering the OOB emissions of the signal transmitted through the use of windowing techniques. The increase in power efficiency is obtained by concatenating a number of OFDM symbols, to which a single prefix of zeros is added, thereby eliminating the need of a CP [47]. Furthermore, this modulation technique performs a time-interleave operation between the samples of the various OFDM symbols that make up the overall BWB-OFDM multi-symbol [62]. Figure 4a depicts the TIBWB-OFDM transmitter. The time interleave operation is performed after the cyclic extension and windowing operation and causes the compression and replication of the spectral data over the occupied bandwidth, creating a diversity effect in the frequency domain, thus increasing the robustness of the method against deep fading of the communication channel, by allowing partial data recover from eventual unaffected spectrum replicas [46,47].
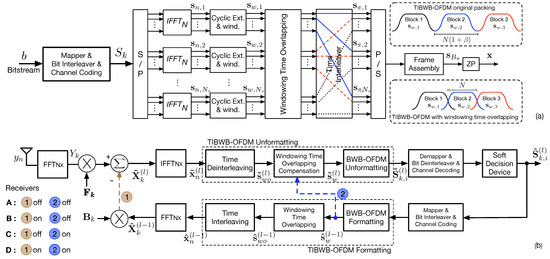
Figure 4.
TIBWB-OFDM with WTO transmitter (a) and receiver (b). Conventional TIBWB-OFDM is obtained by removing the WTO block in transmitter and WTO compensation in receivers A and B.
The TIBWB-OFDM original packing consists into the juxtapotion of a set of N sub-carrier windowed OFDM-based symbols, generated according to a N-sized IFFT operation , where denote the modulated symbol from an m-ary constellation carried by the kth sub-carrier, , of the ith OFDM symbol, .
Afterwards, the cyclic extension and windowing operations is applied to each one of , to perform spectral shaping [46]. Windowing employs a square root raised cosine (SRRC) pulse shape where represents the window roll-off as in [46,47].
Consequently, the new windowed symbol are expressed by
where the operator ⊙ represents a point-wise Hadamard multiplication. The tailing zeros from the windowing operation are then discarded, resulting in (12) being a vector with length . The simple time domain juxtaposition of the component OFDM symbols forms a BWB-OFDM multi-symbol [62]. As mentioned, the TIBWB-OFDM approach performs a time domain interleaving operation between the samples of the BWB-OFDM multi-symbol [46,47], resulting in a set of interleaved symbols, as follows
making up the TIBWB-OFDM multi-symbol, where is the time-interleaved matrix with period of size , where the cth column has a “one” at row .
The final step of Figure 4a includes the insertion of a single -sized zero-pad (ZP), acting as a guard interval in order to deal with channel’s delay spread and avoid ISI. This results in the transmitted block, with a total length of .
3.4.2. TIBWB-OFDM Packing with WTO
Although the TIBWB-OFDM technique already tackles some of the disadvantages inherent to the use of the OFDM, while being easily applied to MIMO and mMIMO systems [48,63], it also brings interesting challenges. The promised spectral and power efficiency increases proposed by the method are limited by the growth of the windowed OFDM-based blocks and also due to their juxtaposition. Even though performing the windowing operation with higher roll-off improves the spectral confinement of the transmitted signal, when juxtaposing the component blocks, the overall length of the TIBWB-OFDM multi-symbol increases proportionally to (1 + ). Consequently, the achieved spectral efficiency of this technique is limited, by either:
- improving spectral confinement by reducing OOB emission when using a larger roll-off. This however, results in greater multi-symbol length, which increases the required bandwidth, in order to keep transmission rate [49].
- by improving symbol rate when conventional rectangular window is used since a sole ZP is used per group of packed OFDM-based blocks. This results in very high OOB emissions, just like typical OFDM schemes [49].
Furthermore, the windowing operation employed in the transmission is responsible for the decrease in the average signal power, due to the low amplitude of the window tails. As a consequence, the overall PAPR of the TIBWB-OFDM multi-symbol tends to grow as the window roll-off increases [50].
Additionally, in Figure 4a, an alternative packing structure is also presented within the original art of TIBWB-OFDM block construction. It includes a partial overlap between the adjacent windowed OFDM symbols that form the TIBWB-OFDM multi-symbol, in time domain, to keep original transmission rate and spectrum occupancy [49,50]. This constitutes the basis of the TIBWB-OFDM with WTO waveform, whose transmitter is based on the previously mentioned operations, followed by an overlapping procedure, as suggested by Figure 4a.
The overlapping operation precedes the time interleaving block, and, therefore, instead of simply juxtaposing the OFDM symbols, they are partially tailed overlapped, in time domain, i.e., the last samples of the current symbol are added with the first samples of the next symbol, with the overlap signal samples being given by
The remaining steps that generate the WTO signal are the same that are included within the original transmitter, as in [46,47]. The only difference is that, before ZP insertion, (13) now becomes
The number of overlapped samples can be regulated, as in [49]. However, the most interesting scenario is when the temporal expansion of the overall signal is mitigated, meaning that the overlapped windowed OFDM symbols maintain a total length of N samples (except for the first and last one). The total length of the TIBWB-OFDM with WTO multi-symbol is now . It is clear that the temporal expansion of the overall signal is , thus meaning that is negligible when compared to packing conventional OFDM blocks with rectangular windowing. This way we can increase the spectral efficiency of the system [49]. This alternative packing also improves the power efficiency of the system by creating a flatter waveform with fewer transitions, increasing the average power of the transmitted signal, and thus reducing on the signal’s PAPR [49,50].
3.4.3. Receivers for TIBWB-OFDM with WTO
In order to cope with both channel impairments and the additional interference introduced between adjacent OFDM component blocks of the TIBWB-OFDM multi-symbol, a different set of receivers must be developed. The TIBWB-OFDM with WTO receivers must be entail both channel equalization and inter-block interference cancellation (IBIC). Linear or iterative FDE can be applied to the received signal aiming to cancel out channel impairments, as for conventional TIBWB-OFDM without WTO. In order to mitigate inter-block interference, a two-way (i.e., simultaneously forward and backward) interference successive cancellation (ISC) is employed. While ISC can also be made iterative enabling better interference cancellation when combined with linear FDE, the IBIC procedure can be simplified after the initial iteration when this is combined with iterative FDE [64].
The TIBWB-OFDM is also seen as an hybrid modulation technique [47], since in the receiver side, the signal can be interpreted as block-based SC-FDE and each data stream is equalized with a single tap equalizer, as shown in [46]. The basic block diagram of a TIBWB-OFDM receiver is given by receiver A (without the WTO compensation block) presented in Figure 4b. The received signal is converted to frequency domain by the means of a -sized DFT, resulting in , with for the TIBWB-OFDM original packing and for the TIBWB-OFDM with WTO. The signal in the frequency domain can be written as in (9). In order to obtain an estimate of the transmitted signal, , linear FDE algorithms can be employed, such as the MMSE equalization [46] as in (10) (for this case, in both equations and are replaced with and , respectively). Afterward, the estimated signal is then converted to time domain, , through a -sized IDFT, the ZP is removed and the block is deinterleaving resulting in the estimated BWB-OFDM block whose unformatting follows [47,49,62].
The channel equalization can also include non-linear iterative FDEs, such as the iterative block decision feedback equalizer (IB-DFE) [65,66], which was included in the TIBWB-OFDM receiver in [64] and is shown in Figure 4b.
At this point, in order to cancel out the interfering resulting from the WTO operation, an IBIC algorithm must be employed. In [64], four different receiver embodiments are presented for a TIBWB-OFDM with WTO transmission, where iterative and non-iterative strategies can be used for both channel FDE and IBIC. They are all presented in Figure 4, depending on whether the links 1 and 2 are on or off. These receivers are divided as:
- Receiver A (Link 1—off; Link 2—off): It consists on the linear MMSE FDE technique, presented in (10) to deal with channel impairments and an MMSE ISC algorithm to cancel WTO interference.
- Receiver B (Link 1—on; Link 2—off): It consists on the non-linear IB-DFE FDE [47] and MMSE ISC algorithms. Each iteration allows an improvement in BER performance since the ISC algorithm is applied iteratively.
- Receiver C (Link 1—off; Link 2—on): This receiver is similar to A since it includes the linear MMSE FDE scheme. However, instead of applying the MMSE ISC algorithm per iteration, an iterative IBIC algorithm is employed, assuming perfect reconstruction.
- Receiver D (Link 1—on; Link 2—on): This receiver is a combination of both receivers B and C, wherein the IB-DFE FDE technique and the iterative IBIC algorithm are employed.
More details on the developed ISC algorithm can be found in [49,64], while the iterative IBIC version along with the receivers are presented in [64].
4. Performance Results and Discussion
In this section we perform a comparison between the candidate waveforms mentioned in previous section, regarding the PAPR and PSD/spectral efficiency of the transmitted signal, BER performance and implementation complexity. For the TIBWB-OFDM with and without WTO cases we consider that OFDM component sub-symbols with sub-carriers and the number of packed OFDM blocks per TIBWB-OFDM block is . For the CP-OFDM and F-OFDM cases, in order to perform a fair comparison, the total number of carriers was chosen in a way that the overall signal’s length is similar to the length of the TIBWB-OFDM block. This way, the total number of carriers for these cases is . Also, for GFDM, the same procedure was applied and the number of time-slots employed in transmission was adjusted to . The carrier multiplication factor and the number of time-slots is (and not 63) in order to provide the same conditions regarding channel coding. Quadrature phase shift keying (QPSK) modulation with a Gray coding rule are applied upon bits carried on each carrier. Furthermore, for all the transmission scenarios, the transmission channel is a severely time dispersive channel with 32 symbol-spaced multipath components with uncorrelated Rayleigh fading.
4.1. PAPR
The PAPR of a time domain signal, , is expressed by
where corresponds to the conjugate of and the operator represents the mathematical expectation or mean value.
As mentioned, the PAPR is evaluated by its CCDF, which can be expressed by
where is the PAPR of the symbol and is a PAPR threshold.
The transmitted signal’s PAPR’s CCDF for the different waveforms are presented in Figure 5, wherein is depicted for dB. For the TIBWB-OFDM with and without WTO and GFDM cases, the SRRC window is employed with a roll-off of . As we can observe all the waveforms presented in this figure present relatively high PAPR values, since they all are MC modulation techniques. We can clearly observe that the waveform that provides the worst PAPR behaviour is the TIBWB-OFDM. As mentioned, the high PAPR values are result of the windowing operation performed in the transmitter, which is responsible for decreasing the average power of the transmitted signal, increasing the PAPR as in (17). Additionally, the PAPR of the TIBWB-OFDM waveform tends to increase as the roll-off increases [50]. On the contrary, for the WTO case, the time overlapping operation allows the reduction of the PAPR by creating a waveform without the low amplitude of the symbol’s tails, which in turn, opposes the decrease in the average signal power and, consequently, reducing the PAPR. In this operation, only the tails of the windowed OFDM symbols are overlapped, thus, the increase of the peak power is negligible. The F-OFDM candidate presents similar performance as OFDM since the only difference is regarding the filtering stage and the simulation was performed assuming large OFDM and F-OFDM signals with a total length equal to a TIBWB-OFDM multi-symbol. Therefore, although the Hanning window presents smooth transitions, it does not affect the PAPR considerably in this analysis. Hence, the high PAPR values still occur since the transmission scheme is based on the IFFT operation, wherein the instantaneous amplitude of each sub-carrier that form the OFDM sub-symbol are added. GFDM falls into the same category, however, in this case, the SRRC window employed with makes the PAPR to increase slightly when compared to OFDM.
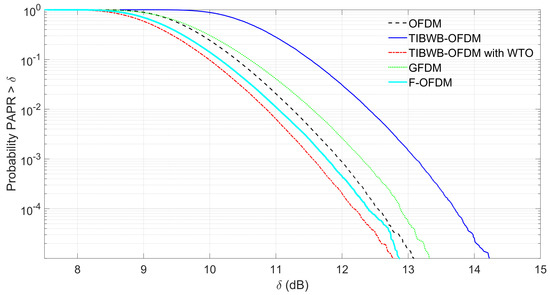
Figure 5.
PAPR’s CCDF of the OFDM, TIBWB-OFDM with and without WTO, GFDM and F-OFDM.
In brief, from the point of view of this KPI, the only waveform that is not recommended is the TIBWB-OFDM.
4.2. PSD and Spectral Efficiency
In order to compare the waveforms regarding their spectral efficiency, we will evaluate the required bandwidth taking as reference the total transmission time of the overall symbol sequence, i.e., the useful bit-rate , assuming that all the sub-carriers are modulated by symbols from the same constellation. This means that the waveforms that transmit a signal with larger overhead require a larger bandwidth in order to achieve the same total transmission of the symbol sequence.
For the TIBWB-OFDM with WTO waveform, the overhead includes the temporal extension of the sub-blocks and the ZP, but this is negligible when compared to the total signal length. This means that the total bandwidth required is proportional , where denotes the symbol rate and relates to the bit-rate by .
On the other hand, the standard TIBWB-OFDM, although providing a higher degree of spectrum confinement, does not deal with the temporal extension of the sub-symbols and the overhead in this case is proportional to the window roll-off, , leading to an increase of the required bandwidth, .
A similar analysis can be made to GFDM since the overall overhead includes a single CP. However, the CP is only added per GFDM block and then can be discarded. This way, the total required bandwidth is also proportional can also be approximated by the symbol rate i.e., .
The CP-OFDM and F-OFDM cases the overhead will include the CP per symbol, which in these cases, represents a significant percentage of the overall signal, granting an increase of the required bandwidth proportional to the CP percentage, i.e., .
Table 1 presents a resume of the total bandwidth for arbitrary values of the CP and window roll-off, while in Figure 6 it is presented a comparison on the PSD normalized to the information bit rate , of CP-OFDM, F-OFDM, GFDM and TIBWB-OFDM with and without WTO, assuming a baseband QPSK-modulated transmitted symbol sequence. Once more, the strict window is considered for both the TIBWB-OFDM and GFDM cases, and the CP employed in CP-OFDM and F-OFDM techniques is assumed to be 25% of the overall signal’s length.

Table 1.
Required bandwidth for the different waveforms.
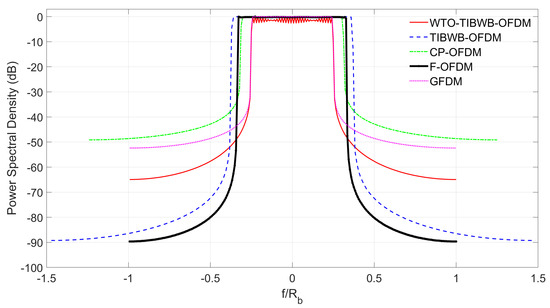
Figure 6.
PSD of CP-OFDM, GFDM, F-OFDM and TIBWB-OFDM with and without WTO.
From Figure 6, it is clear the considerable improve on spectral efficiency gains of the new proposed TIBWB-OFDM with WTO against all the other techniques. Although the F-OFDM waveform is the one that provides the lowest OOB radiation due to the employment of the filtering operation, it relies on a CP (just like OFDM) to deal with the channel’s impairments and also requires a large ZP (in the order of the filter length), which limits its spectral efficiency. A similar OOB radiation to F-OFDM is obtained with the conventional TIBWB-OFDM, but also in this case the spectral efficiency is limited due to the temporal extension of the symbols due to the windowing operation. Regarding GFDM this presents a poor OOB rejection, that compares to CP-OFDM schemes [42]. The amount of spectrum saved for the TIBWB-OFDM with WTO (when compared to conventional TIBWB-OFDM) is proportional to the temporal growth of the OFDM-based blocks, i.e., to . Also, the use of a ZP per group of OFDM-based symbols allows this technique to save spectrum when compared to CP-OFDM and F-OFDM schemes.
In summary, the TIBWB-OFDM with WTO and GFDM, from the point of view of spectrum demand, are the most spectrally efficient waveforms, since they require the least amount of signal overhead. On the other hand, the waveforms that provide a higher degree of spectrum confinement are the TIBWB-OFDM and F-OFDM, while TIBWB-OFDM with WTO still provides considerably low OOB emissions. All things considered, the TIBWB-OFDM with WTO is among all the one that with the better spectral efficiency, presenting a good trade-off between effective throughput, while still achieving low OOB radiation.
4.3. BER Performance
Figure 7 compare the BER performances of TIBWB-OFDM waveforms with and without WTO, GFDM, F-OFDM and with conventional CP-OFDM. In order to provide a fair comparison in a realistic scenario, the same amount of CP, considered in Section 4.2, is employed in CP-OFDM and F-OFDM transmissions. The four receiver embodiments proposed in [64] are employed for the TIBWB-OFDM with WTO waveform. Furthermore, the conventional TIBWB-OFDM results are presented for the linear MMSE and IB-DFE receivers, as in [47]. Regarding OFDM, F-OFDM and GFDM a FDE MMSE algorithm is employed at the early stage of the receiver. However four different interference cancellation methods are considered in the GFDM receiver. The MF, ZF and DSSIC detectors mentioned in the previous section are included, along with the simpler version of the DSSIC detector (the GFDM SIC detector) which subtracts the ICI presented in the signal at kth sub-carrier and caused only by the th sub-carrier [43,53]. Perfect synchronization and channel estimation is assumed at reception. The channel code employed is a (128,64) LDPC code and bit-interleaving is applied over 21 consecutive coded words for the TIBWB-OFDM and OFDM cases. For GFDM and F-OFDM, since the number of time-slots is higher the bit-interleave operation is applied over 32 consecutive coded words. For a fair comparison results are also presented as function of the ratio energy per information bit to noise spectral density added to the required amount of back-off taking as reference PAPR at . Additionally, the CP power penalty is also considered.
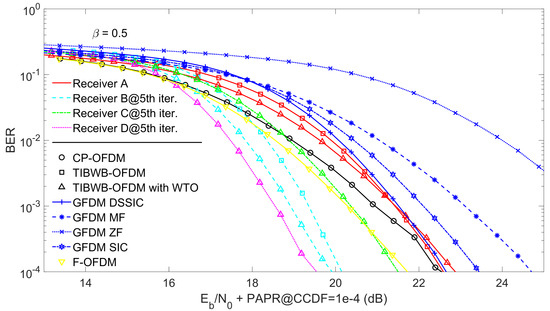
Figure 7.
BER performance of 25% CP-OFDM and F-OFDM together with GFDM and TIBWB-OFDM with and without WTO considering the different proposed receivers when .
More specifically, Figure 7 includes the performance for the different techniques for , with results for the iterative receivers being presented for the 5th iteration. Clearly, by analyzing this figure, we can conclude that the TIBWB-OFDM receiver D has the best performance when back-off associated to the PAPR is considered, with almost no added complexity when compared to receiver B. Also, we can conclude that the GFDM detectors SIC, but mainly, DSSIC can really improve the BER performance of GFDM standard MF and ZF receivers, while exhibiting a similar performance when compared to standard TIBWB-OFDM case with receiver A. It is worth stating that the SIC algorithms were applied only for 1 iteration. Furthermore, although the TIBWB-OFDM with WTO (regarding receivers B and D) is a waveform that have interference levels that must be dealt in the receiver, they present better BER performances than standard OFDM and TIBWB-OFDM (regarding receiver B) cases, due to its much lower PAPR owing to the windowing and packing with overlap operation. Finally, we can also conclude that F-OFDM presents a slightly better performance (less than 1 dB) than CP-OFDM due to the large ZP that is added in the last stage of the transmitter.
To sum up, with the employing of more efficient and complex receiver equalization techniques, the TIBWB-OFDM and TIBWB-OFDM with WTO are able to provide a satisfactory performance, outperforming OFDM and F-OFDM in terms of reliability. GFDM presents the overall worst BER performance, however it is possible to enhance the receiver’s interference cancellation algorithms in order to provide a more acceptable performance.
4.4. Computational Complexity
The next figure of merit that is included in this paper is the computational complexity regarding the implementation of the different transceiver presented for every waveform. In order to perform a fair comparison the complexity is evaluated in terms of the number of complex multiplications for each MC scheme. The same signal conditions, regarding sub-carriers N and sub-symbols employed in transmission are assumed in this analysis.
Table 2 shows the computational complexity of the 5G and beyond candidate waveforms in terms of total number of complex multiplication employed in transmission and reception. It is clear that most of the complexity effort comes from the receiver operations.

Table 2.
Transceiver complexity for the different waveforms.
The complexity of OFDM schemes comprises the IFFT and FFT complexity employed at the transmitter and receiver, respectively. For the F-OFDM waveform, the overall complexity includes the multiplication operations performed in OFDM added by complexity due to transmit and receive filters. It is assumed that the filtering operation employed in transmission is performed once for the CP samples [67].
The complexity analysis of GFDM transmitter is based on the low complexity transmitter implementation proposed in [42], where the first term originates from the -sized FFTs of N sub-carriers, the second one arises from the filtering operation of N sub-carriers and the last one from the -sized IFFT that converts the signal back to time domain. The receiver complexity analysis is based on [54] and includes the multiplications presented in both the MF operation and the SIC algorithm.
In [64] the TIBWB-OFDM with WTO receivers complexity was analysed and it was concluded that:
- Receiver A includes only a direct path, where includes a -sized FFT upon signal reception, a MMSE equalization algorithm and BWB-OFDM unformatting with WTO compensation.
- Receivers B and D include the direct path but instead of MMSE equalization, the IB-DFE algorithm is employed. The feedback path wherein the BWB-OFDM block formatting is performed is also included. For L iterations, the number of multiplications will increase proportionally by L in the direct path and in the feedback path.
- Receiver C is similar to receiver A in the first iteration, performing all the operation in the direct path, while including the BWB-OFDM formatting operation in the feedback path. For , the direct path only includes the BWB unformatting with WTO compensation and the feedback path includes the BWB-OFDM formatting.
The TIBWB-OFDM receivers A and B are identical to the ones explained for the TIBWB-OFDM with WTO with the only difference being the removal of the WTO compensation block. Therefore the multiplications employed in this block are not considered in these cases.
Table 2 presents the overall transceiver complexity for the same number of carriers, sub-symbols and roll-off employed in previous subsections. Also in this case we considered that the filter length is , the number of iterations is and (we can discard the ZP here since it represents only a very small fraction of the overall signal). The number of multiplications for the TIBWB-OFDM standard case can be considered discarding the term and considering that . The complexity regarding the simpler GFDM receivers with the MF and ZF detectors can be obtained by discarding the term .
Concluding, for DL transmissions, where this KPI is the most critical, due to the low processing capabilities of mobile terminals, the most suitable waveform is F-OFDM, since, when compared to OFDM, it only requires the sub-band filtering operations. On the other hand, GFDM and TIBWB-OFDM with and without WTO rely on transmission/reception of large signals with multiple OFDM-based sub-symbols and may include iterative interference cancellation algorithms. Therefore, along with the filtering and windowing operations, respectively, multiple FFTs and IFFTs must be employed to recover the original data, increasing significantly the receiver complexity.
4.5. Further KPI Discussion
In this subsection, other KPI for each waveform are compared and analyzed in further detail:
- Processing delay and filtering/windowing: These KPI are directly related. GFDM relies on a CP insertion and performs the filtering operation by sub-carrier, after an upsample operation, requiring a long filter length (narrow bandwidth). Thus, the overall block processing delay will be high [4,6]. Both TIBWB-OFDM with and without WTO perform the filtering operating per sub-band, and thus, they use shorter filter length (wide bandwidth). However, the overall system delay is still high because the systems require that each one of the OFDM-based sub-symbol go through several operations. Besides, FFT modulation formats involving a relatively high duration multi-symbols are employed. Therefore, the overall block processing delay will be high for all these waveforms and they are not suitable for low latency applications. Additionally, F-OFDM schemes use shorter filter lengths and although including large CP lengths, the overall symbol duration remains low, compared to the previous waveforms. Thus, from the point of view of this KPI, the most suitable waveforms are OFDM and F-OFDM.
- Robustness to frequency-selective channels: Overall, all the MC waveforms are robust to the frequency selectivity of the wireless channel. The OFDM principle is to divide the transmission channel’s bandwidth into narrowband sub-carriers, by transforming a broadband frequency selective channel into multiple narrowband flat-fading sub-channels. Therefore, deep fadings will affect only a few sub-carriers. F-OFDM is based on OFDM schemes and GFDM can be seen as a generalization of OFDM [68], with both presenting the same robustness as OFDM, regarding multipath propagation. Both TIBWB-OFDM with and without WTO go beyond that and allow a deeper level of robustness against deep fading [46], due to the inclusion of the time interleave/deinterleave operations in their transceiver design, granting a higher degree of diversity in the frequency domain and robustness upon transmission under deep inband channel fades. Thus, from the point of view of this KPI, the most suitable waveforms are TIBWB-OFDM with and without WTO.
- Robustness to time-selective channels: When the user mobility is taken into account, the changes of the transmission channel can cause ICI, affecting all the MC waveforms. F-OFDM is as robust as OFDM regarding this KPI. However, in [38,47] it is shown, respectively, that both GFDM and TIBWB-OFDM waveforms are MC schemes that are relatively robust regarding this impairment. In GFDM the use of very well localised pulse shapes in the frequency domain allows a certain degree of CFO resilience [38]. Additionally, in TIBWB-OFDM, the large multi-symbol length can also allow a more accurate estimation of the CFO or Doppler drift based on the IB-DFE principle [47]. This way, GFDM and TIBWB-OFDM with and without WTO are the most suitable waveforms to be considered in a mobile transmission/reception environment.
- High flexibility and efficient MIMO implementation: All of the waveform contenders presented in this paper are flexible with the possibility of employing multiple numerology parameters since they are based on OFDM scheme. A friendly MIMO adaptation is directly related to the implementation complexity regarding the channel equalization techniques that are employed in the system [6]. In general, OFDM-based waveforms (F-OFDM and TIBWB-OFDM) allow an efficient MIMO implementation since the transceiver architecture allows a simplification in the FDE with only one equalization iteration per sub-carrier with simple channel estimation techniques. Also, in [63], it is shown that the TIBWB-OFDM waveform is also easily integrated in MIMO systems. GFDM is an exception since the sub-carrier superposition is performed in frequency domain causing ICI that must be dealt in the receiver, requiring a channel estimation in each sub-symbol [6]. However, in TIBWB-OFDM with WTO the interference is added locally between adjacent sub-symbols in time domain. Hence, concerning this KPI, the only waveform that is not recommended is GFDM.
4.6. Final Discussion
To sum up this discussion, Table 3 summarizes and grades the different MC waveform formats analyzed throughout this paper for each KPI. This table considers the simulation results from previous subsections and the grades are presented taking into consideration a performance comparison between each waveform candidate and OFDM.

Table 3.
Comparison of different MC schemes.
There are three categories of traffic types in 5G and beyond, which exhibit different characteristics under different propagation scenarios. They are eMBB, mMTC and URLLC.
eMBB mainly focuses on high transmission bit rate and spectral efficiency. Therefore, the main positive KPIs that a waveform contender should have is regarding the spectral efficiency, OOB emissions, robustness to both time and frequency selectivity and efficient MIMO implementation. From this perspective, by analyzing Table 3, the most suitable waveforms to be the heir of OFDM are GFDM and TIBWB-OFDM with WTO, due to their ability to provide a very high spectral efficiency, with relatively low OOB emissions, along with a considerable robustness upon transmission in time and frequency selective channels (although MIMO implementations in GFDM transceivers require more complex channel equalization schemes).
Concerning the mMTC service requirements, the used waveform should support a huge number of devices, with simple synchronization and low power consumption. Hence, waveforms with low PAPR and computation complexity, along with an efficient MIMO implementation should prevail. Pure MC waveforms always exhibit high PAPR values. However, F-OFDM is the most fitting candidate to replace OFDM in DL transmissions since its characteristics are better adapted to fulfill the UE receiver’s low complexity requirement. If we consider UL transmissions, TIBWB-OFDM with WTO is a suitable candidate to replace current OFDM systems, since it presents a similar transmitter’s complexity to OFDM with much better power and spectral efficiencies, and because the receiver’s computation complexity criteria is less critical at BS.
Regarding URLLC, service requirements include high reliability and low latency as the main focus. Thus, the KPIs that a waveform should have are an acceptable BER performance, low computation complexity and low processing delay. From Table 3, F-OFDM is the most suitable waveform when the main issue is the latency. This is typically observed in real time applications, such as online gaming or video applications. However, if the main focus is on reliability, the TIBWB-OFDM with and without WTO are the main contenders, due to their ability to provide reasonable BER performances.
5. Conclusions
This paper addressed the main KPI regarding the 5G and beyond candidates waveforms and also discussed the challenges they present in order to fulfill the diverse set of requirements for future wireless communications. It also described in the detail the advantages and disadvantages of each waveform, while providing a detailed overview of the transceiver architecture of each MC scheme.
Ultimately, we can state that there is no ideal waveform that can fit all requirements, and trade-offs must be beared in mind. Therefore, in order to select the most suitable waveform formats for a specific scenario, future wireless systems must be flexible by taking into account the different 5G and beyond services requirements and propagation conditions. An alternative solution consists of choosing and adapting the waveform format that suits the most service requirements for a specific type of application.
Author Contributions
Conceptualization, F.C.; methodology, F.C.; software, A.S. and D.C.; validation, M.G., V.S., R.D., A.S. and D.C.; formal analysis, F.C., M.G., V.S., R.D., A.S. and D.C.; investigation, F.C., M.G., V.S., R.D., A.S. and D.C.; resources, M.G. and V.S.; Software, A.S. and D.C.; data curation, F.C., M.G., V.S. and R.D.; writing–original draft preparation, F.C.; writing–review and editing, M.G., V.S., R.D., A.S. and D.C.; visualization, F.C. and M.G.; supervision, M.G., V.S., R.D., A.S. and D.C.; project administration, M.G., V.S., R.D., A.S. and D.C.; funding acquisition, M.G., V.S., R.D., A.S. and D.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work is funded by FCT/MCTES under the projects MASSIVE5G (POCI-01-0145-FEDER-030588) and UIDB/50008/2020-UIDP/50008/2020.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DFT | Discrete Fourier Transform |
| KPI | Key Performance Indicator |
| eMBB | Enhanced Mobile Broadband |
| mMTC | Massive Machine-Type Communication |
| CCDF | Complementary Cumulative Distribution Function |
| URLLC | Ultra-Reliable and Low-Latency Communication |
| GFDM | Generalized Frequency Division Multiplexing |
| FDE | Frequency Domain Equalization |
| TIBWB-OFDM | Time Interleaved Block Windowed Burst OFDM |
| MIMO | Multiple-Input-Multiple-Output |
| MMSE | Minimum Mean Square Error |
| IBIC | Inter-Block Interference Cancellation |
| ISC | Interference Successive Cancellation |
| AWGN | Additive White Gaussian Noise |
| ICI | Inter-Channel Interference |
| SRRC | Square Root Raised Cosine |
| IB-DFE | Iterative Block Decision Feedback Equalizer |
| DSSIC | Double Sided Interference Cancellation |
| PAPR | Peak-to-Average-Power-Ratio |
| IFFT | Inverse Fast Fourier Transform |
| WTO | Windowing Time Overlapping |
| FDD | Frequency Division Duplex |
| ITSBI | Inter Sub-Band Interference |
| OFDM | Orthogonal Frequency Division Multiplexing |
| 3GPP | 3rd Generation Partnership Project |
| S/P | Serial to Parallel |
| DL | Downlink |
| ISI | Inter-Symbol Interference |
| PSD | Power Spectral Density |
| IoT | Internet of Things |
| 5G | Fifth Generation |
| UL | Uplink |
| F-OFDM | Filtered-OFDM |
| UE | User Equipment |
| CFO | Carrier Frequency Offset |
| OOB | Out of Band |
| AP | Access Point |
| mm | Milli-Meter |
| PHY | Physical Layer |
| BS | Base Station |
| SNR | Signal-to-Noise Ratio |
| LTE | Long Term Evolution |
| BER | Bit Error Rate |
| MF | Match Filtering |
| ZF | Zero-Forcing |
| SC | Single-Carrier |
| TDD | Time Division Duplex |
| MC | Multi-Carrier |
| CP | Cyclic Prefix |
| INSBI | Inner Sub-Band Interference |
References
- Strinati, E.C.; Barbarossa, S.; Gonzalez-Jimenez, J.L.; Kténas, D.; Cassiau, N.; Dehos, C. 6G: The Next Frontier. arXiv 2019, arXiv:1901.03239. [Google Scholar]
- Chin, W.H.; Fan, Z.; Haines, R. Emerging technologies and research challenges for 5G wireless networks. IEEE Wirel. Commun. 2014, 21, 106–112. [Google Scholar] [CrossRef]
- Norp, T. 5G Requirements and Key Performance Indicators. J. ICT 2018, 6, 15–30. [Google Scholar] [CrossRef]
- Demir, A.F.; Elkourdi, M.; Ibrahim, M.; Arslan, H. Waveform Design for 5G and Beyond. In 5G Networks: Fundamental Requirements, Enabling Technologies, and Operations Management; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2018; pp. 51–76. [Google Scholar]
- Andrews, J.G.; Buzzi, S.; Choi, W.; Hanly, S.; Lozano, A.; Soong, A.C.K.; Zhang, J.C. What Will 5G Be? IEEE J. Sel. Areas Commun. 2014, 32, 1065–1082. [Google Scholar] [CrossRef]
- Santacruz, J.P.; Rommel, S.; Johannsen, U.; Jurado-Navas, A.; Monroy, I.T. Candidate Waveforms for ARoF in Beyond 5G. Appl. Sci. 2020, 10, 3891. [Google Scholar] [CrossRef]
- International Telecommunications Union-Radiocommunications Sector (ITU-R). IMT Vision—Framework and Overall Objectives of the Future Development of IMT for 2020 and Beyond; Technical Report M.2083-0; ITU: Geneva, Switzerland, 2015. [Google Scholar]
- Wunder, G.; Kasparick, M.; ten Brink, S.; Schaich, F.; Wild, T.; Gaspar, I.; Ohlmer, E.; Krone, S.; Michailow, N.; Navarro, A.; et al. 5GNOW: Challenging the LTE Design Paradigms of Orthogonality and Synchronicity. In Proceedings of the 2013 IEEE VTC Spring, Dresden, Germany, 2–5 June 2013; pp. 1–5. [Google Scholar]
- Zhang, X.; Chen, L.; Qiu, J.; Abdoli, J. On the Waveform for 5G. IEEE Commun. Mag. 2016, 54, 74–80. [Google Scholar] [CrossRef]
- Balint, C.; Budura, G. OFDM-Based Multi-Carrier Waveforms Performances in 5G. In Proceedings of the 2018 International Symposium on Electronics and Telecommunications (ISETC), Timisoara, Romania, 8–9 November 2018; pp. 1–4. [Google Scholar]
- Gerzaguet, R.; Bartzoudis, N.; Baltar, L.G.; Berg, V.; Doré, J.B.; Kténas, D.; Font-Bach, O.; Mestre, X.; Payaró, M.; Färber, M.; et al. The 5G candidate waveform race: A comparison of complexity and performance. EURASIP J. Wirel. Commun. Netw. 2017, 2017, 13. [Google Scholar] [CrossRef]
- Zaidi, A.A.; Luo, J.; Gerzaguet, R.; Wolfgang, A.; Zaidi, A.A.; Weiler, R.J.; Vihriäla, J.; Svensson, T.; Qi, Y.; Halbauer, H.; et al. A Preliminary Study on Waveform Candidates for 5G Mobile Radio Communications above 6 GHz. In Proceedings of the 2016 IEEE 83rd Vehicular Technology Conference (VTC Spring), Nanjing, China, 15–18 May 2016; pp. 1–6. [Google Scholar]
- Dehos, C.; Gonzalez, J.; Domenico, A.; Ktenas, D.; Dussopt, L. Millimeter-Wave Access and Backhauling: The Solution to the Exponential Data Traffic Increase in 5G Mobile Communications Systems. IEEE Commun. Mag. 2014, 52, 88–95. [Google Scholar] [CrossRef]
- Tesanovic, M.; Nekovee, M. mmWave-Based Mobile Access for 5G: Key Challenges and Projected Standards and Regulatory Roadmap. In Proceedings of the 2015 IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015; pp. 1–6. [Google Scholar]
- Kukliński, S.; Tomaszewski, L. Key Performance Indicators for 5G network slicing. In Proceedings of the 2019 IEEE Conference on Network Softwarization (NetSoft), Paris, France, 24–28 June 2019; pp. 464–471. [Google Scholar]
- Marzetta, T.; Larsson, E.; Yang, H.; Ngo, H. Fundamentals of Massive MIMO; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Björnson, E.; Larsson, E.G.; Marzetta, T.L. Massive MIMO: Ten myths and one critical question. IEEE Commun. Mag. 2016, 54, 114–123. [Google Scholar] [CrossRef]
- Interdonato, G.; Björnson, E.; Ngo, H.; Frenger, P.; Larsson, E. Ubiquitous Cell-Free Massive MIMO Communications. EURASIP J. Wirel. Commun. Netw. 2019, 2019, 197. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, S.; Lin, Y.; Zheng, J.; Ai, B.; Hanzo, L. Cell-Free Massive MIMO: A New Next-Generation Paradigm. IEEE Access 2019, 7, 99878–99888. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Ashikhmin, A.; Yang, H.; Larsson, E.G.; Marzetta, T.L. Cell-Free Massive MIMO Versus Small Cells. IEEE Trans. Wirel. Commun. 2017, 16, 1834–1850. [Google Scholar] [CrossRef]
- Boccardi, F.; Heath, R.W.; Lozano, A.; Marzetta, T.L.; Popovski, P. Five disruptive technology directions for 5G. IEEE Commun. Mag. 2014, 52, 74–80. [Google Scholar] [CrossRef]
- Zaidi, A.A.; Baldemair, R.; Tullberg, H.; Bjorkegren, H.; Sundstrom, L.; Medbo, J.; Kilinc, C.; Da Silva, I. Waveform and Numerology to Support 5G Services and Requirements. IEEE Commun. Mag. 2016, 54, 90–98. [Google Scholar] [CrossRef]
- Wunder, G.; Jung, P.; Kasparick, M.; Wild, T.; Schaich, F.; Chen, Y.; Brink, S.T.; Gaspar, I.; Michailow, N.; Festag, A.; et al. 5GNOW: Non-orthogonal, asynchronous waveforms for future mobile applications. IEEE Commun. Mag. 2014, 52, 97–105. [Google Scholar] [CrossRef]
- Rohde & Schwarz. 5G Waveform Candidates. Tech. Rep. June 2016. Available online: https://www.rohde-schwarz.com/nl/applications/5g-waveform-candidates-application-note56280-267585.html (accessed on 7 December 2020).
- Rahmatallah, Y.; Mohan, S. Peak-To-Average Power Ratio Reduction in OFDM Systems: A Survey and Taxonomy. IEEE Commun. Surv. Tutor. 2013, 15, 1567–1592. [Google Scholar] [CrossRef]
- Rappaport, T.S. Wireless Communications: Principles and Practice; Dorling Kindersley: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Chiueh, T.D.; Tsai, P.Y. OFDM Baseband Receiver Design for Wireless Communications; Wiley Publishing: Singapore, 2007. [Google Scholar]
- Maziar, N.; Yue, W.; Milos, T.; Shangbin, W.; Yinan, Q.; Mohammed, A. Overview of 5G Modulation and Waveforms Candidates. J. Commun. Inf. Netw. 2016, 1, 44–60. [Google Scholar] [CrossRef]
- Study on Scenarios and Requirements for Next Generation Access Technologies; 3rd Generation Partnership Project (3GPP), Tech. Rep. 38 913; ETSI: Sophia Antipolis, France, 2017.
- Poornima, T.; Dhinesh, K.; Sudhakar, R. Waveform candidates for 5G mobile communications. In Proceedings of the 2017 2nd IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT), Bangalore, India, 19–20 May 2017; pp. 856–860. [Google Scholar]
- Nee, R.V.; Prasad, R. OFDM for Wireless Multimedia Communications, 1st ed.; Artech House, Inc.: Norwood, MA, USA, 2000. [Google Scholar]
- Hazareena, A.; Mustafa, B.A. A Survey: On the Waveforms for 5G. In Proceedings of the 2018 Second International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 29–31 March 2018; pp. 64–67. [Google Scholar]
- Banelli, P.; Buzzi, S.; Colavolpe, G.; Modenini, A.; Rusek, F.; Ugolini, A. Modulation Formats and Waveforms for 5G Networks: Who Will Be the Heir of OFDM?: An overview of alternative modulation schemes for improved spectral efficiency. IEEE Signal Process. Mag. 2014, 31, 80–93. [Google Scholar] [CrossRef]
- Doré, J.; Gerzaguet, R.; Cassiau, N.; Ktenas, D. Waveform contenders for 5G: Description, analysis and comparison. Phys. Commun. 2017, 24, 46–61. [Google Scholar] [CrossRef]
- Schaich, F.; Wild, T. Waveform contenders for 5G—OFDM vs. FBMC vs. UFMC. In Proceedings of the 2014 6th International Symposium on Communications, Control and Signal Processing (ISCCSP), Athens, Greece, 21–23 May 2014; pp. 457–460. [Google Scholar]
- Jebbar, H.; Hassani, S.E.; Abbassi, A.E. Performance study of 5G multicarrier waveforms. In Proceedings of the 2017 International Conference on Wireless Networks and Mobile Communications (WINCOM), Rabat, Morocco, 1–4 November 2017; pp. 1–6. [Google Scholar]
- Liu, Y.; Chen, X.; Zhong, Z.; Ai, B.; Miao, D.; Zhao, Z.; Sun, J.; Teng, Y.; Guan, H. Waveform Design for 5G Networks: Analysis and Comparison. IEEE Access 2017, 5, 19282–19292. [Google Scholar] [CrossRef]
- Tiwari, S.; Chatterjee, S.; Das, S.S. Comparative analysis of waveforms for fifth generation mobile networks. In Proceedings of the 2016 IEEE International Conference on Advanced Networks and Telecommunications Systems (ANTS), Bangalore, India, 6–9 November 2016; pp. 1–6. [Google Scholar]
- Kaur, R.; Kaur, N.; Kansal, L. Comprehensive study of future waveforms for 5G. Int. J. Pure Appl. Math. 2018, 118, 4663–4672. [Google Scholar]
- Khan, B.; Velez, F.J. Multicarrier Waveform Candidates for Beyond 5G. In Proceedings of the 2020 12th International Symposium on Communication Systems, Networks and Digital Signal Processing (CSNDSP), Porto, Portugal, 20–22 July 2020; pp. 1–6. [Google Scholar]
- Fettweis, G.; Krondorf, M.; Bittner, S. GFDM—Generalized Frequency Division Multiplexing. In Proceedings of the VTC Spring 2009—IEEE 69th Vehicular Technology Conference, Barcelona, Spain, 26–29 April 2009; pp. 1–4. [Google Scholar]
- Michailow, N.; Gaspar, I.; Krone, S.; Lentmaier, M.; Fettweis, G. Generalized frequency division multiplexing: Analysis of an alternative multi-carrier technique for next generation cellular systems. In Proceedings of the 2012 International Symposium on Wireless Communication Systems (ISWCS), Paris, France, 28–31 August 2012; pp. 171–175. [Google Scholar]
- Michailow, N.; Matthé, M.; Gaspar, I.S.; Caldevilla, A.N.; Mendes, L.L.; Festag, A.; Fettweis, G. Generalized Frequency Division Multiplexing for 5th Generation Cellular Networks. IEEE Trans. Commun. 2014, 62, 3045–3061. [Google Scholar] [CrossRef]
- Abdoli, J.; Jia, M.; Ma, J. Filtered OFDM: A new waveform for future wireless systems. In Proceedings of the 2015 IEEE 16th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Stockholm, Sweden, 28 June–1 July 2015; pp. 66–70. [Google Scholar]
- Zhang, X.; Jia, M.; Chen, L.; Ma, J.; Qiu, J. Filtered-OFDM—Enabler for Flexible Waveform in the 5th Generation Cellular Networks. In Proceedings of the 2015 IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015; pp. 1–6. [Google Scholar]
- Fernandes, T.; Gomes, M.; Silva, V.; Dinis, R. Time-Interleaved Block Windowed Burst OFDM. In Proceedings of the 2016 IEEE 84th Vehicular Technology Conference (VTC-Fall), Montreal, QC, Canada, 18–21 September 2016; pp. 1–5. [Google Scholar]
- Fernandes, T.; Pereira, A.; Gomes, M.; Silva, V.; Dinis, R. A new hybrid multicarrier transmission technique with iterative frequency domain detection. Phys. Commun. 2018, 27, 7–16. [Google Scholar] [CrossRef]
- Pereira, A.; Bento, P.; Gomes, M.; Dinis, R.; Silva, V. TIBWB-OFDM: A Promising Modulation Technique for MIMO 5G Transmissions. In Proceedings of the 2018 IEEE 88th Vehicular Technology Conference (VTC-Fall), Chicago, IL, USA, 27–30 August 2018; pp. 1–5. [Google Scholar]
- Conceição, F.; Gomes, M.; Silva, V.; Dinis, R. Highly efficient TIBWB-OFDM waveform for broadband wireless communications. In Proceedings of the 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 25–28 May 2020; pp. 1–5. [Google Scholar]
- Conceição, F.; Gomes, M.; Silva, V.; Dinis, R. Time Overlapping TIBWB-OFDM Symbols for Peak-To-Average Power Ratio Reduction. In Proceedings of the 11th Conference on Telecommunications (ConfTele 2019), Lisbon, Portugal, 26–28 June 2019. [Google Scholar]
- Chen, H.; Hua, J.; Li, F.; Chen, F.; Wang, D. Interference Analysis in the Asynchronous f-OFDM Systems. IEEE Trans. Commun. 2019, 67, 3580–3596. [Google Scholar] [CrossRef]
- Huawei, HiSilicon. f-OFDM Scheme and Filter Design. In Proceedings of the 3GPP TSG RAN WG1 Meeting 85, R1-165425, Nanjing, China, 23–27 May 2016. [Google Scholar]
- Alves, B.; Mendes, L.; Guimarães, D.; Gaspar, I. Performance of GFDM over Frequency-Selective Channels—Invited Paper. Telecomunicações 2013, 15, 1–9. [Google Scholar]
- Gaspar, I.; Michailow, N.; Navarro, A.; Ohlmer, E.; Krone, S.; Fettweis, G. Low Complexity GFDM Receiver Based on Sparse Frequency Domain Processing. In Proceedings of the 2013 IEEE 77th Vehicular Technology Conference (VTC Spring), Dresden, Germany, 2–5 June 2013; pp. 1–6. [Google Scholar]
- Barba-Maza, L.M.; Dolecek, G.J. PAPR reduction of GFDM system using Xia pulse and OPTS scheme. In Proceedings of the 2020 IEEE 63rd International Midwest Symposium on Circuits and Systems (MWSCAS), Springfield, MA, USA, 9–12 August 2020; pp. 774–777. [Google Scholar]
- Michailow, N.; Fettweis, G. Low peak-to-average power ratio for next generation cellular systems with generalized frequency division multiplexing. In Proceedings of the 2013 International Symposium on Intelligent Signal Processing and Communication Systems, Naha, Japan, 11–12 November 2013; pp. 651–655. [Google Scholar]
- Kassam, J.; Miri, M.; Magueta, R.; Castanheira, D.; Pedrosa, P.; Silva, A.; Dinis, R.; Gameiro, A. Two-Step Multiuser Equalization for Hybrid mmWave Massive MIMO GFDM Systems. Electronics 2020, 9, 1220. [Google Scholar] [CrossRef]
- Dias, W.D.; Mendes, L.L.; Rodrigues, J.J.P.C. Low Complexity GFDM Receiver for Frequency-Selective Channels. IEEE Commun. Lett. 2019, 23, 1166–1169. [Google Scholar] [CrossRef]
- Lim, B.; Ko, Y. Multiuser Interference Cancellation for GFDM With Timing and Frequency Offsets. IEEE Trans. Commun. 2019, 67, 4337–4349. [Google Scholar] [CrossRef]
- Mohammadian, A.; Tellambura, C.; Valkama, M. Analysis of Self-Interference Cancellation Under Phase Noise, CFO, and IQ Imbalance in GFDM Full-Duplex Transceivers. IEEE Trans. Veh. Technol. 2020, 69, 700–713. [Google Scholar] [CrossRef]
- Datta, R.; Michailow, N.; Lentmaier, M.; Fettweis, G. GFDM Interference Cancellation for Flexible Cognitive Radio PHY Design. In Proceedings of the 2012 IEEE Vehicular Technology Conference (VTC Fall), Quebec City, QC, Canada, 3–6 September 2012; pp. 1–5. [Google Scholar]
- Nunes, J.; Bento, P.; Gomes, M.; Dinis, R.; Silva, V. Block-Windowed Burst OFDM: A High-Efficiency Multicarrier Technique. Electron. Lett. 2014, 50, 1757–1759. [Google Scholar] [CrossRef]
- Pereira, A.; Bento, P.; Gomes, M.; Dinis, R.; Silva, V. MIMO Time Interleaved Block Windowed Burst OFDM with Iterative Frequency Domain Equalization. In Proceedings of the 2018 15th International Symposium on Wireless Communication Systems (ISWCS), Lisbon, Portugal, 28–31 August 2018; pp. 1–6. [Google Scholar]
- Conceição, F.; Gomes, M.; Silva, V.; Dinis, R. An OFDM-Based Waveform with High Spectral Efficiency. IEEE Commun. Lett. 2020, 24, 2614–2618. [Google Scholar] [CrossRef]
- Souto, N.; Dinis, R.; Correia, A.; Reis, C. Interference-Aware Iterative Block Decision Feedback Equalizer for Single-Carrier Transmission. IEEE Trans. Veh. Technol. 2015, 64, 3316–3321. [Google Scholar] [CrossRef]
- Dinis, R.; Montezuma, P.; Souto, N.; Silva, J. Iterative Frequency-Domain Equalization for general constellations. In Proceedings of the 2010 IEEE Sarnoff Symposium, Princeton, NJ, USA, 12–14 April 2010; pp. 1–5. [Google Scholar]
- Ijaz, A.; Zhang, L.; Xiao, P.; Tafazolli, R. Analysis of Candidate Waveforms for 5G Cellular Systems; InTech: Rijeka, Croatia, 2016. [Google Scholar]
- Michailow, N. Integration of a GFDM Secondary System in an Existing OFDM System. Ph.D. Thesis, Technische Universitat Dresden, Dresden, Germany, 2010. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).