Agent-Based Model for End-of-Life Product Flow Analysis
Abstract
1. Introduction
1.1. Solid Waste Management
1.2. Behavioral Theories
1.3. Simulation of Waste Management Operations
2. Objective and Methodology
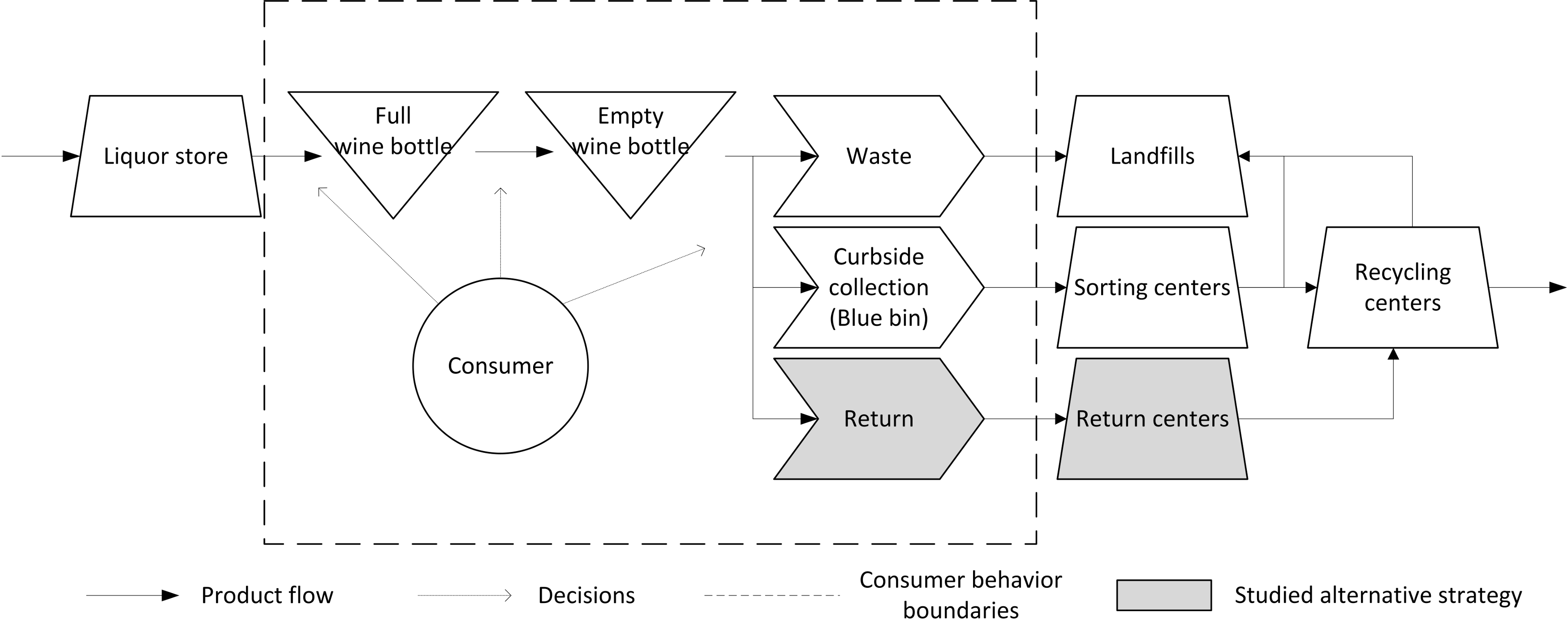
3. The Model
3.1. Behavior and Decision-Making
3.2. Attitude: Opinions and Incentives
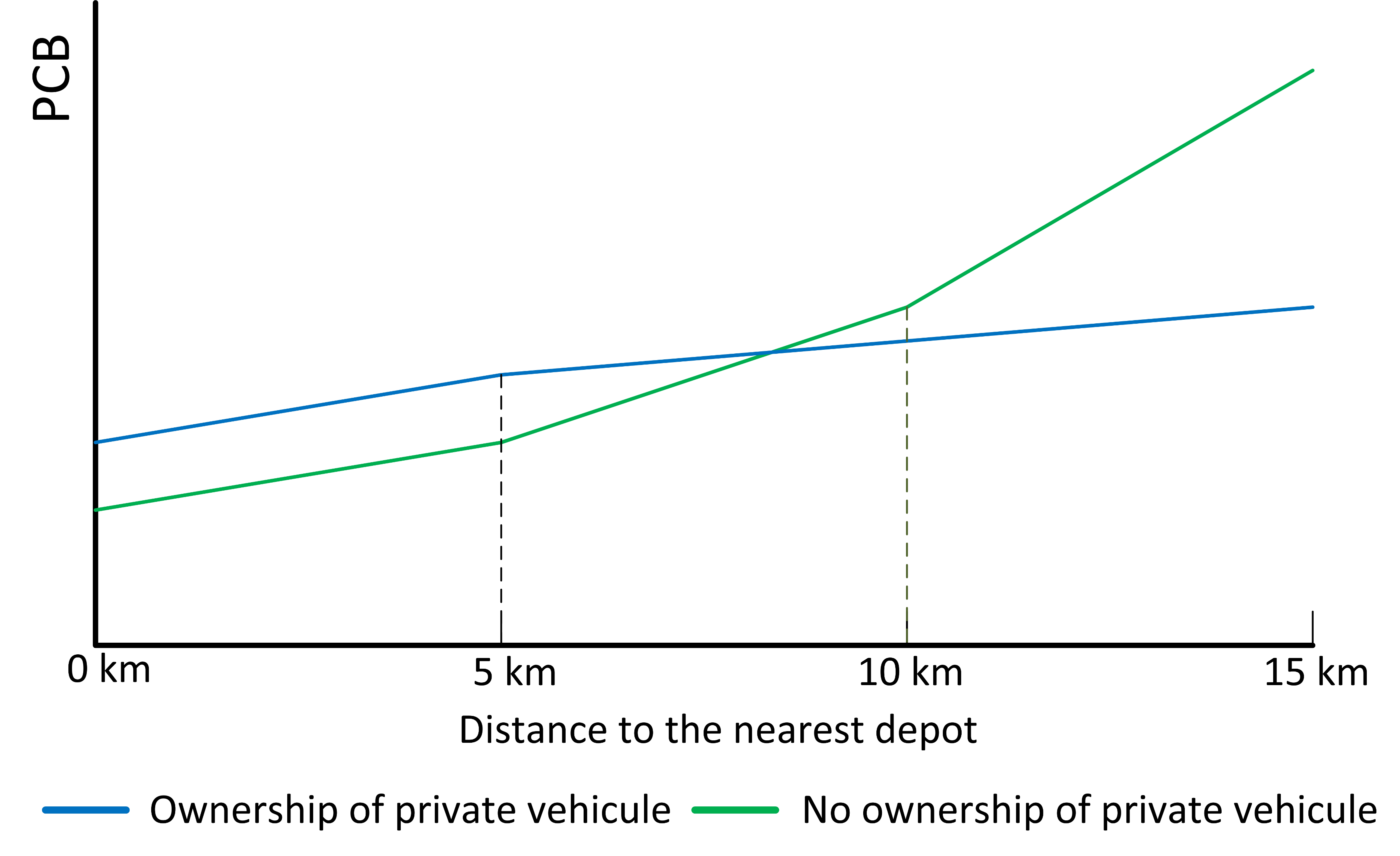
3.3. The Perceived Behavioral Control
4. Results
4.1. Model Calibration
4.2. Model Validation
4.3. Experiments
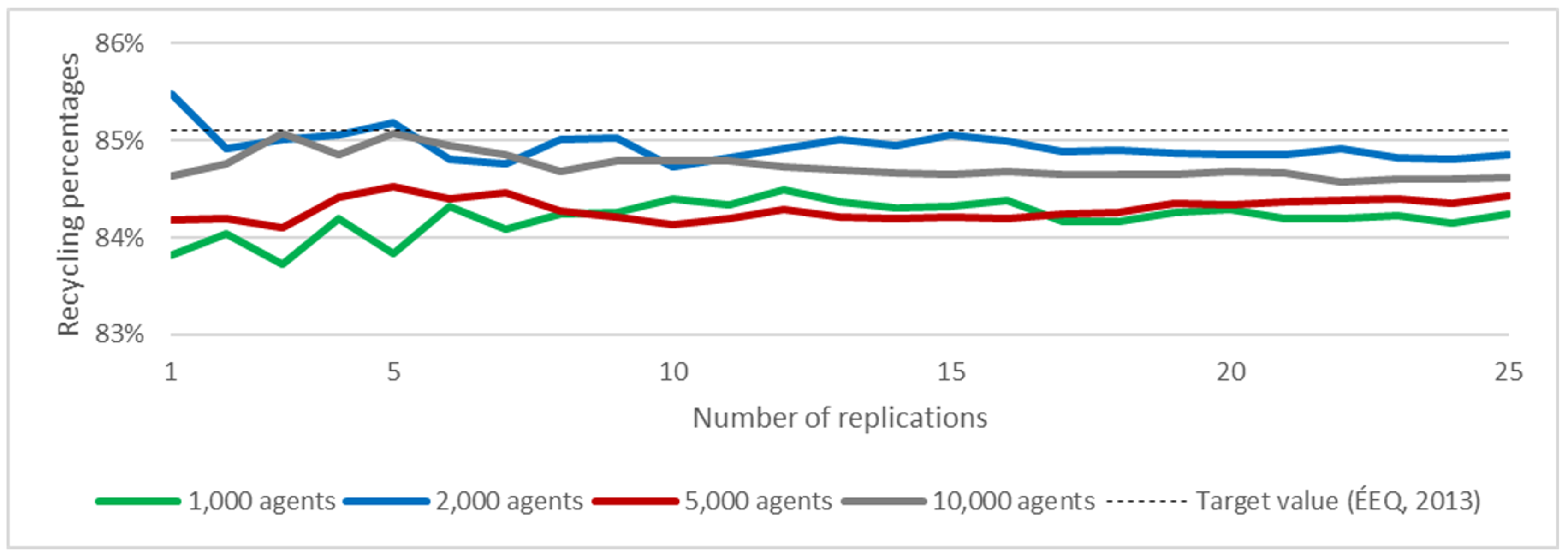
4.3.1. Model Stability
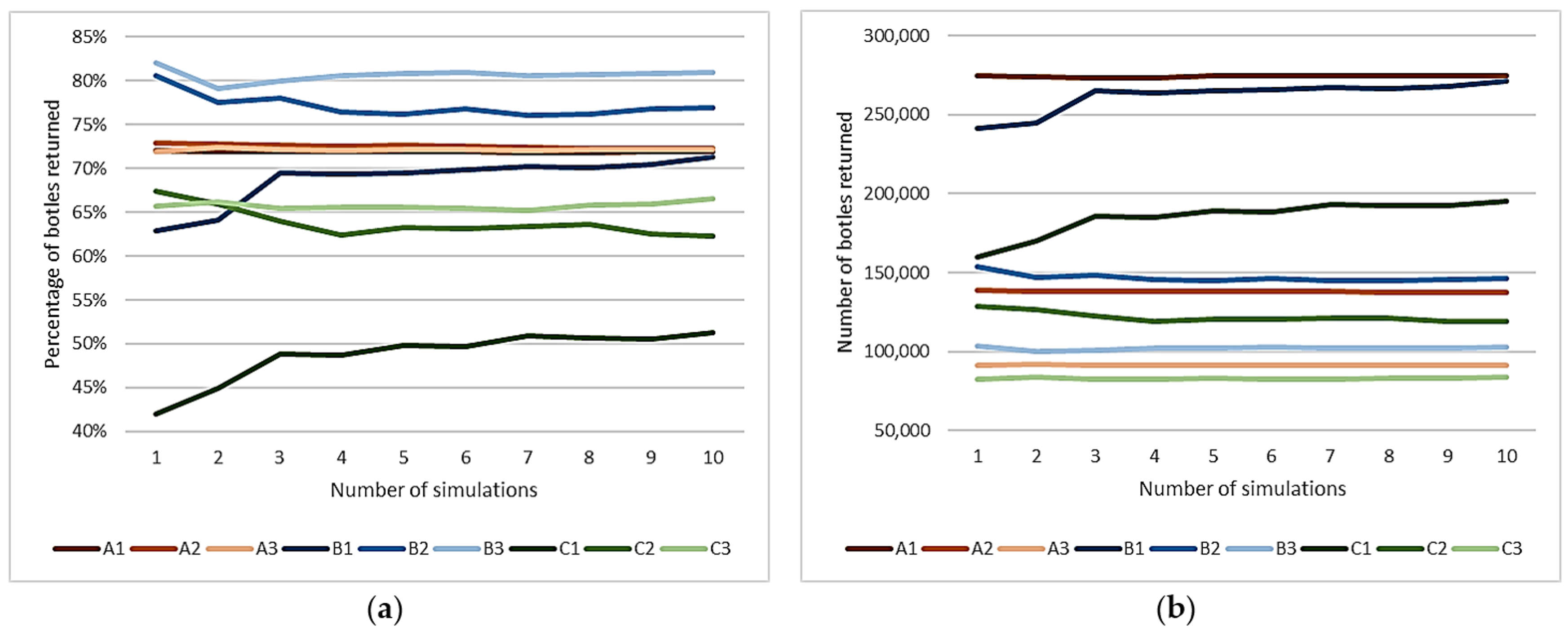
4.3.2. Bottle Returns Percentages
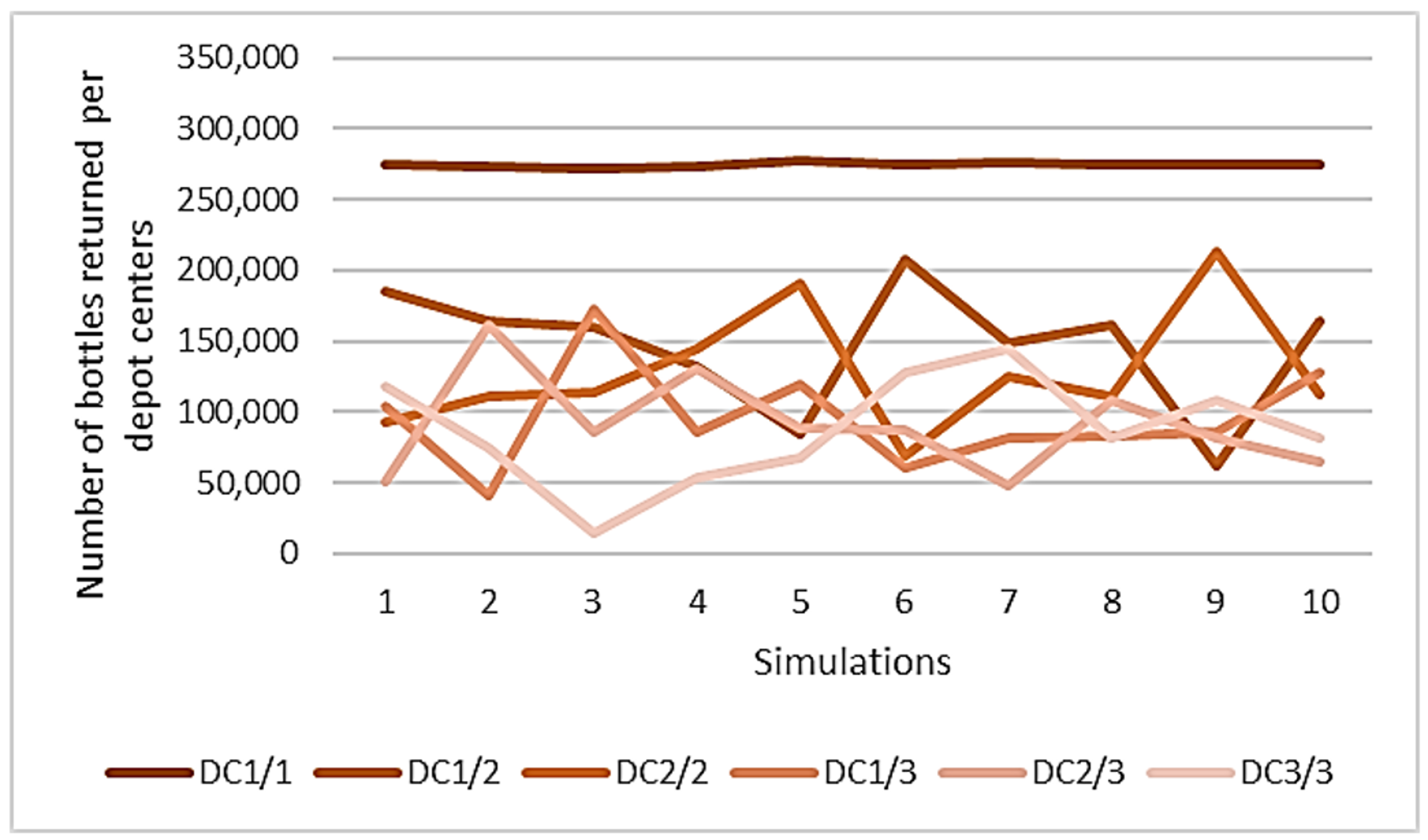
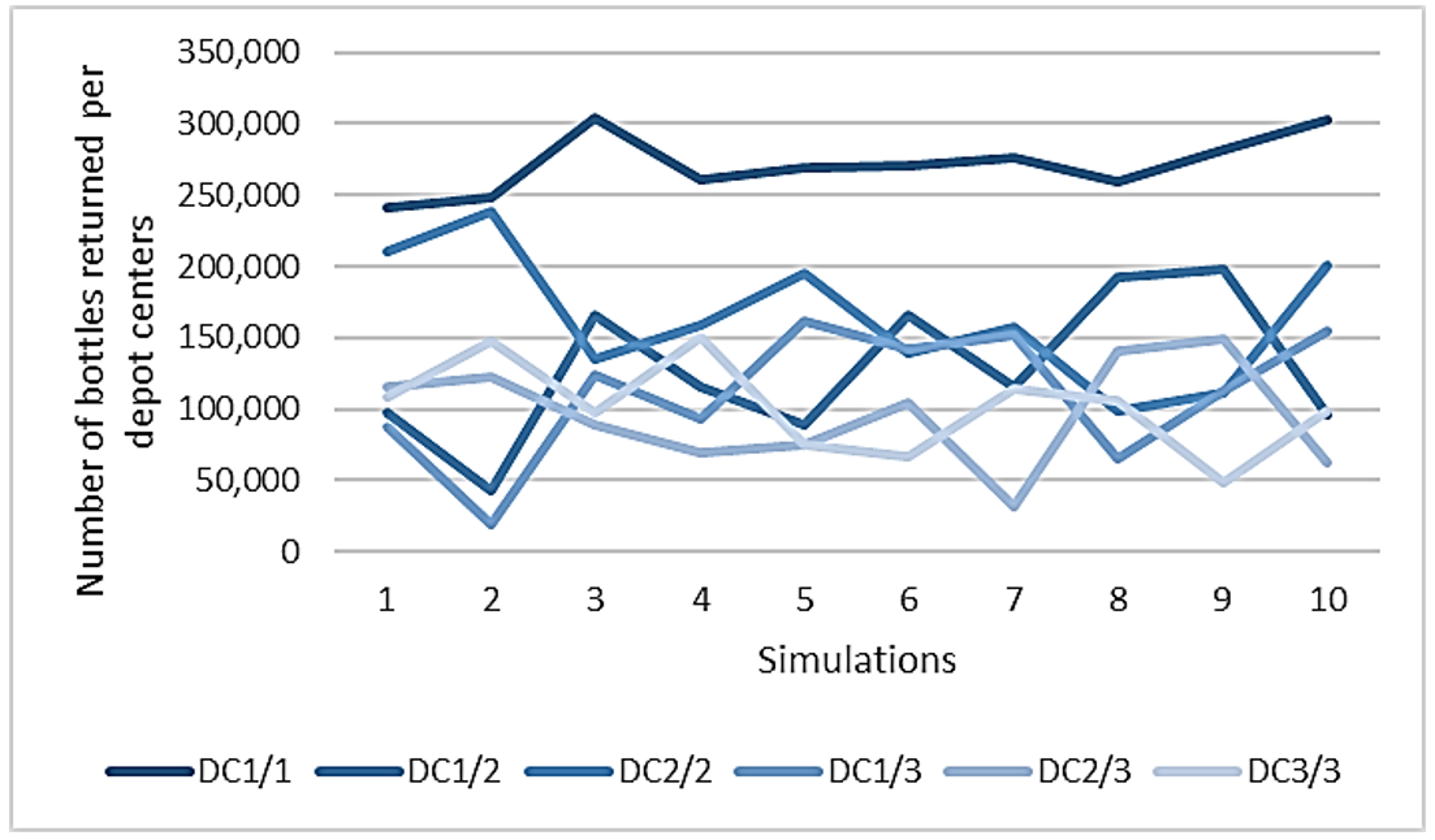
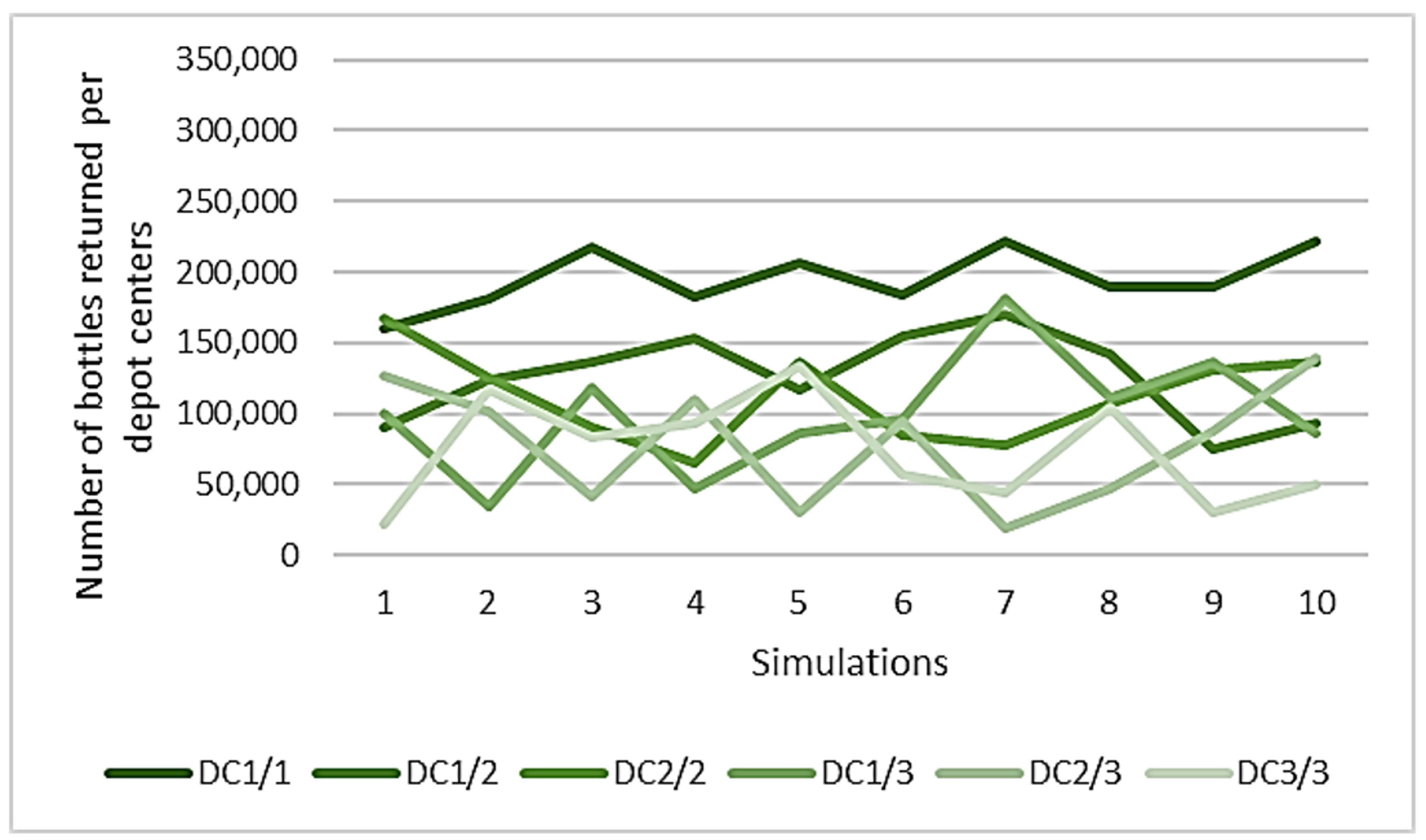
4.3.3. Number of Bottles Returned in Depot Center
5. Discussion
5.1. General Insights
5.2. Model Limitations and Future Works
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Graphical Representations of the Scenarios Produced with AnyLogic


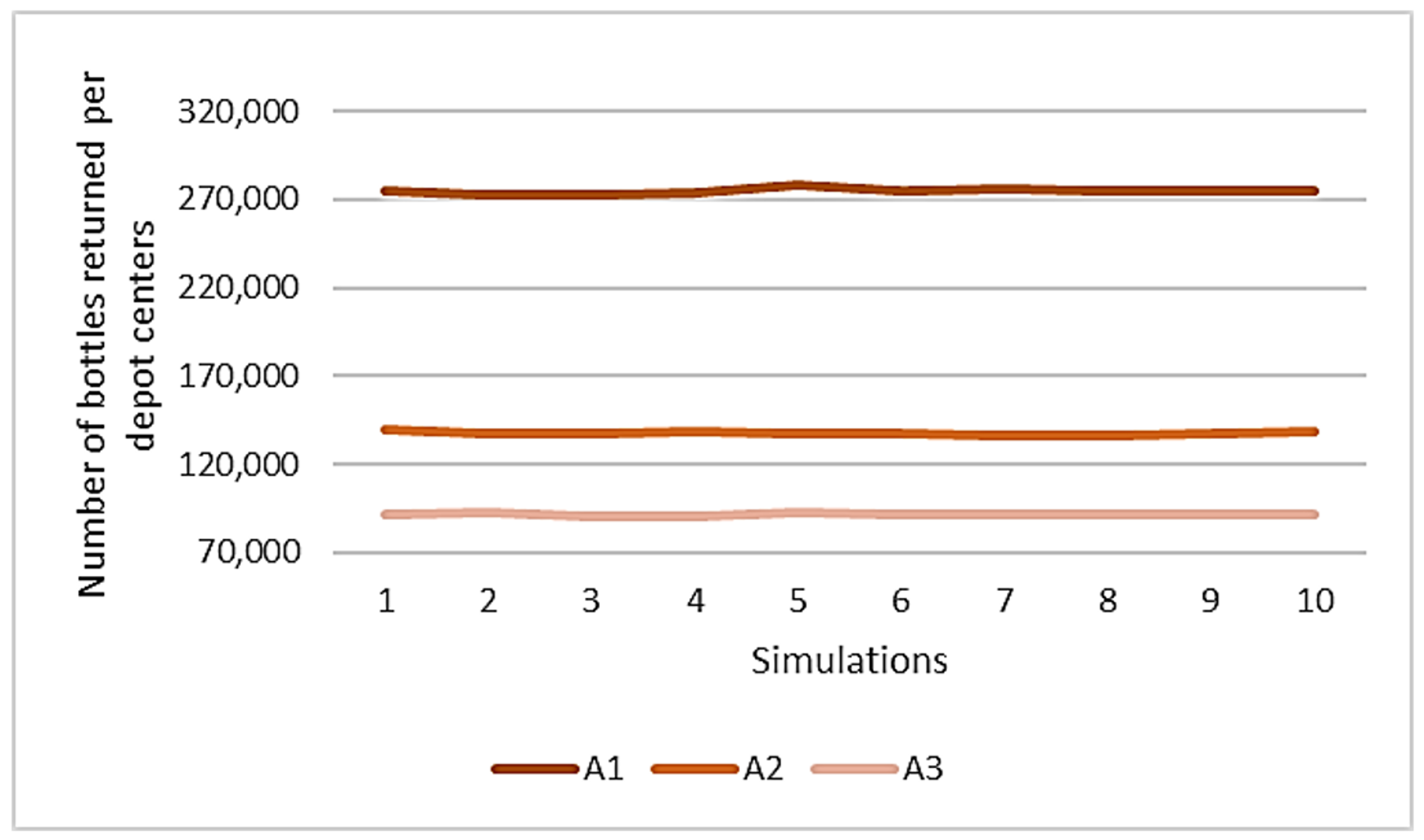
Appendix B. Average Number of Bottles Returned Per Depot Center for Each Simulation Run
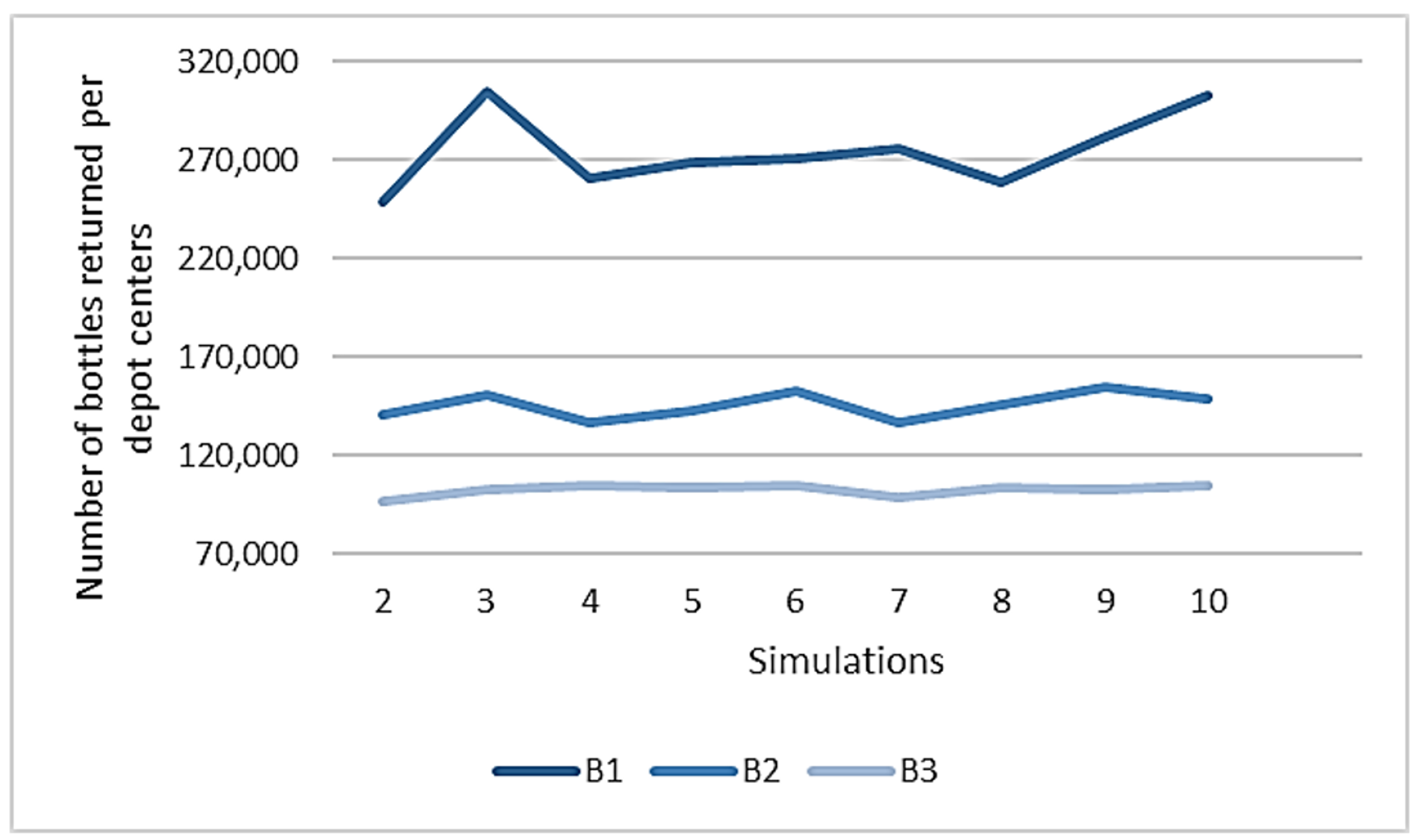
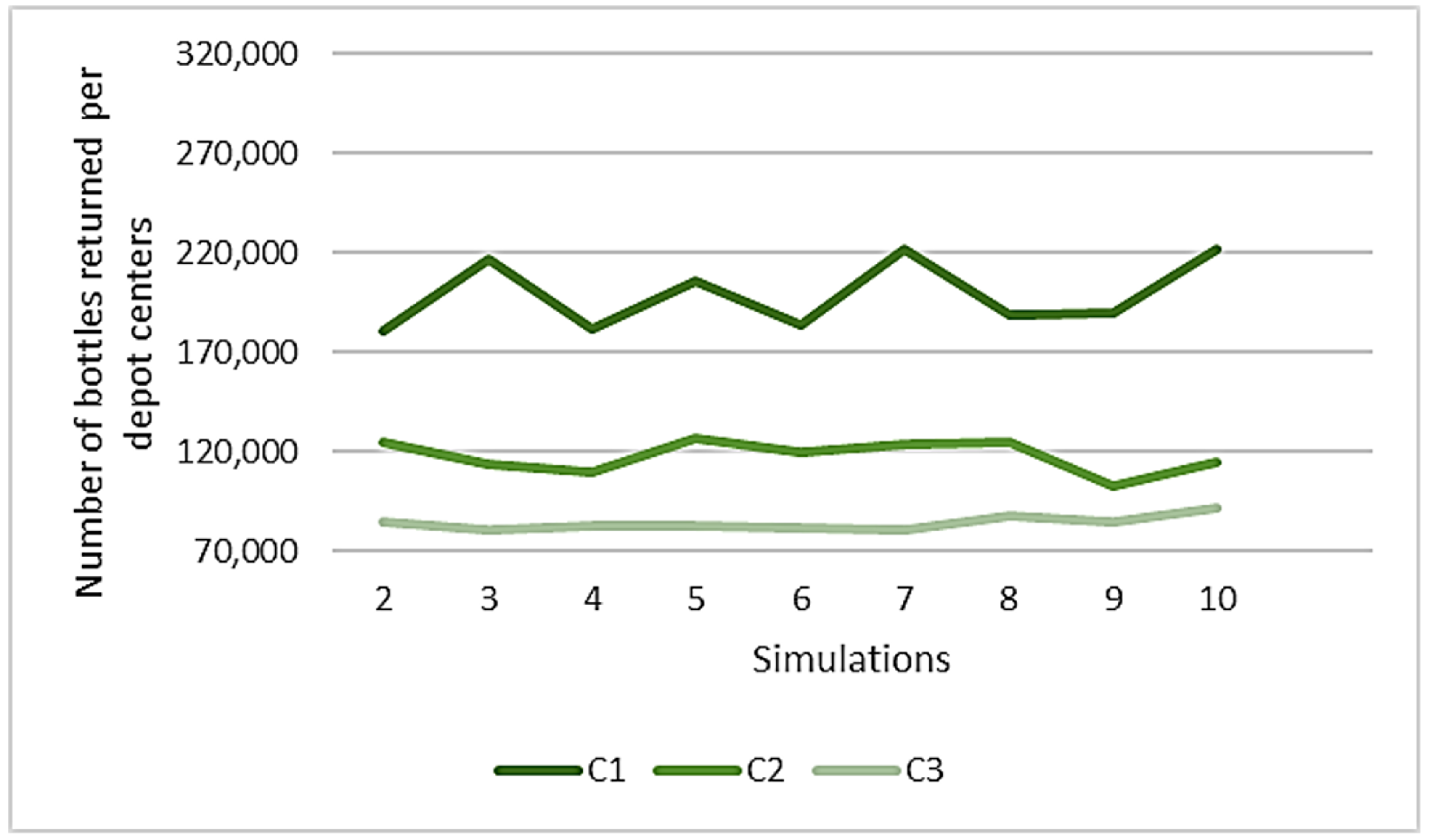
Appendix C. Number of Bottles Returned Per Depot Center for Each Simulation Run
References
- Zaman, A.U. A comprehensive study of the environmental and economic benefits of resource recovery from global waste management systems. J. Clean. Prod. 2016, 124, 41–50. [Google Scholar] [CrossRef]
- Karmperis, A.C.; Aravossis, K.; Tatsiopoulos, I.P.; Sotirchos, A. Decision support models for solid waste management: Review and game-theoretic approaches. Waste Manag. 2013, 33, 1290–1301. [Google Scholar] [CrossRef] [PubMed]
- Soltani, A.; Hewage, K.; Reza, B.; Sadiq, R. Multiple stakeholders in multi-criteria decision-making in the context of municipal solid waste management: A review. Waste Manag. 2015, 35, 318–328. [Google Scholar] [CrossRef] [PubMed]
- Borshchev, A. The Big Book of Simulation Modeling: Multimethod Modeling with AnyLogic 6; AnyLogic North America: Chicago, IL, USA, 2013. [Google Scholar]
- Goddard, H.C. The benefits and costs of alternative solid waste management policies. Resour. Conserv. Recycl. 1995, 13, 183–213. [Google Scholar] [CrossRef]
- Bohm, R.A.; Folz, D.H.; Kinnaman, T.C.; Podolsky, M.J. The costs of municipal waste and recycling programs. Resour. Conserv. Recycl. 2010, 54, 864–871. [Google Scholar] [CrossRef]
- Lakhan, C. Diversion, but at what cost? The economic challenges of recycling in Ontario. Resour. Conserv. Recycl. 2015, 95, 133–142. [Google Scholar] [CrossRef]
- Cleary, J. Life cycle assessments of municipal solid waste management systems: A comparative analysis of selected peer-reviewed literature. Environ. Int. 2009, 35, 1256–1266. [Google Scholar] [CrossRef] [PubMed]
- De Feo, G.; Malvano, C. The use of LCA in selecting the best MSW management system. Waste Manag. 2009, 29, 1901–1915. [Google Scholar] [CrossRef] [PubMed]
- Fitzgerald, G.C.; Krones, J.S.; Themelis, N.J. Greenhouse gas impact of dual stream and single stream collection and separation of recyclables. Resour. Conserv. Recycl. 2012, 69, 50–56. [Google Scholar] [CrossRef]
- Simon, B.; Amor, M.B.; Földényi, R. Life cycle impact assessment of beverage packaging systems: Focus on the collection of post-consumer bottles. J. Clean. Prod. 2016, 112, 238–248. [Google Scholar] [CrossRef]
- Komly, C.E.; Azzaro-Pantel, C.; Hubert, A.; Pibouleau, L.; Archambault, V. Multiobjective waste management optimization strategy coupling life cycle assessment and genetic algorithms: Application to PET bottles. Resour. Conserv. Recycl. 2012, 69, 66–81. [Google Scholar] [CrossRef]
- Vellini, M.; Savioli, M. Energy and environmental analysis of glass container production and recycling. Energy 2009, 34, 2137–2143. [Google Scholar] [CrossRef]
- Ghinea, C.; Drăgoi, E.N.; Comăniţă, E.D.; Gavrilescu, M.; Câmpean, T.; Curteanu, S.; Gavrilescu, M. Forecasting municipal solid waste generation using prognostic tools and regression analysis. J. Environ. Manag. 2016, 182, 80–93. [Google Scholar] [CrossRef] [PubMed]
- Thøgersen, J. Recycling and morality: A critical review of the literature. Environ. Behav. 1996, 28, 536–558. [Google Scholar] [CrossRef]
- Stern, P.C. New environmental theories: Toward a coherent theory of environmentally significant behavior. J. Soc. Issues 2000, 56, 407–424. [Google Scholar] [CrossRef]
- Sidique, S.F.; Joshi, S.V.; Lupi, F. Factors influencing the rate of recycling: An analysis of Minnesota counties. Resour. Conserv. Recycl. 2010, 54, 242–249. [Google Scholar] [CrossRef]
- Sidique, S.F.; Lupi, F.; Joshi, S.V. The effects of behavior and attitudes on drop-off recycling activities. Resour. Conserv. Recycl. 2010, 54, 163–170. [Google Scholar] [CrossRef]
- López-Mosquera, N.; Lera-López, F.; Sánchez, M. Key factors to explain recycling, car use and environmentally responsible purchase behaviors: A comparative perspective. Resour. Conserv. Recycl. 2015, 99, 29–39. [Google Scholar] [CrossRef]
- Babaei, A.A.; Alavi, N.; Goudarzi, G.; Teymouri, P.; Ahmadi, K.; Rafiee, M. Household recycling knowledge, attitudes and practices towards solid waste management. Resour. Conserv. Recycl. 2015, 102, 94–100. [Google Scholar] [CrossRef]
- Bissing-Olson, M.J.; Fielding, K.S.; Iyer, A. Experiences of pride, not guilt, predict pro-environmental behavior when pro-environmental descriptive norms are more positive. J. Environ. Psychol. 2016, 45, 145–153. [Google Scholar] [CrossRef]
- Tucker, P. Normative influences in household waste recycling. J. Environ. Plan. Manag. 1999, 42, 63. [Google Scholar] [CrossRef]
- Steg, L.; Vlek, C. Encouraging pro-environmental behaviour: An integrative review and research agenda. J. Environ. Psychol. 2009, 29, 309–317. [Google Scholar] [CrossRef]
- Best, H.; Mayerl, J. Values, beliefs, attitudes: An empirical study on the structure of environmental concern and recycling participation. Soc. Sci. Q. 2013, 94, 691–714. [Google Scholar] [CrossRef]
- Gifford, R.; Nilsson, A. Personal and social factors that influence pro-environmental concern and behaviour: A review. Int. J. Psychol. 2014, 49, 141–157. [Google Scholar] [CrossRef] [PubMed]
- Kormos, C.; Gifford, R. The validity of self-report measures of proenvironmental behavior: A meta-analytic review. J. Environ. Psychol. 2014, 40, 359–371. [Google Scholar] [CrossRef]
- Morren, M.; Grinstein, A. Explaining environmental behavior across borders: A meta-analysis. J. Environ. Psychol. 2016, 47, 91–106. [Google Scholar] [CrossRef]
- Ajzen, I. The theory of planned behavior. Organ. Behav. Hum. Decis. Process. 1991, 50, 179–211. [Google Scholar] [CrossRef]
- Tonglet, M.; Phillips, P.S.; Read, A.D. Using the Theory of Planned Behaviour to investigate the determinants of recycling behaviour: A case study from Brixworth, UK. Resour. Conserv. Recycl. 2004, 41, 191–214. [Google Scholar] [CrossRef]
- White, K.M.; Hyde, M.K. The role of self-perceptions in the prediction of household recycling behavior in Australia. Environ. Behav. 2012, 44, 785–799. [Google Scholar] [CrossRef]
- Chan, L.; Bishop, B. A moral basis for recycling: Extending the theory of planned behaviour. J. Environ. Psychol. 2013, 36, 96–102. [Google Scholar] [CrossRef]
- Rhodes, R.E.; Beauchamp, M.R.; Conner, M.; Bruijn, G.J.D.; Kaushal, N.; Latimer-Cheung, A. Prediction of depot-based specialty recycling behavior using an extended theory of planned behavior. Environ. Behav. 2015, 47, 2. [Google Scholar] [CrossRef]
- Botetzagias, I.; Dima, A.-F.; Malesios, C. Extending the theory of planned behavior in the context of recycling: The role of moral norms and of demographic predictors. Resour. Conserv. Recycl. 2015, 95, 58–67. [Google Scholar] [CrossRef]
- Tucker, P.; Murney, G.; Lamont, J. Predicting recycling scheme performance: A process simulation approach. J. Environ. Manag. 1998, 53, 31–48. [Google Scholar] [CrossRef]
- Tucker, P.; Smith, D. Simulating household waste management behaviour. J. Artif. Soc. Soc. Simul. 1999, 2, 31. [Google Scholar]
- Bonabeau, E. Agent-based modeling: Methods and techniques for simulating human systems. Proc. Natl. Acad. Sci. USA 2002, 99 (Suppl. 3), 7280–7287. [Google Scholar] [CrossRef] [PubMed]
- Kiesling, E.; Günther, M.; Stummer, C.; Wakolbinger, L.M. Agent-based simulation of innovation diffusion: A review. Cent. Eur. J. Oper. Res. 2012, 20, 183–230. [Google Scholar] [CrossRef]
- Scalco, A.; Ceschi, A.; Shiboub, I.; Sartori, R.; Frayret, J.M.; Dickert, S. The implementation of the theory of planned behavior in an agent-based model for waste recycling: A review and a proposal. In Agent-Based Modeling of Sustainable Behaviors; Springer: Berlin/Heidelberg, Germany, 2017; pp. 77–97. [Google Scholar]
- Schwarz, N.; Ernst, A. Agent-based modeling of the diffusion of environmental innovations—An empirical approach. Technol. Forecast. Soc. Chang. 2009, 76, 497–511. [Google Scholar] [CrossRef]
- Kaufmann, P.; Stagl, S.; Franks, D.W. Simulating the diffusion of organic farming practices in two New EU Member States. Ecol. Econ. 2009, 68, 2580–2593. [Google Scholar] [CrossRef]
- Ceschi, A.; Dorofeeva, K.; Sartori, R.; Dickert, S.; Scalco, A. A Simulation of Householders’ Recycling Attitudes Based on the Theory of Planned Behavior. In Trends in Practical Applications of Agents, Multi-Agent Systems and Sustainability; Springer: Berlin/Heidelberg, Germany, 2015; pp. 177–184. [Google Scholar]
- Ghali, M.R.; Frayret, J.-M.; Ahabchane, C. Agent-Based Model of Self-Organized Industrial Symbiosis. J. Clean. Prod. 2017, 161, 452–465. [Google Scholar] [CrossRef]
- Shi, X.; Thanos, A.E.; Celik, N. Multi-objective agent-based modeling of single-stream recycling programs. Resour. Conserv. Recycl. 2014, 92, 190–205. [Google Scholar] [CrossRef]
- Wang, B.; Brême, S.; Moon, Y.B. Hybrid modeling and simulation for complementing Lifecycle Assessment. Comput. Ind. Eng. 2014, 69, 77–88. [Google Scholar] [CrossRef]
- Armitage, C.J.; Conner, M. Efficacy of the theory of planned behaviour: A meta-analytic review. Br. J. Soc. Psychol. 2001, 40, 471–499. [Google Scholar] [CrossRef] [PubMed]
- Rai, V.; Robinson, S.A. Agent-based modeling of energy technology adoption: Empirical integration of social, behavioral, economic, and environmental factors. Environ. Model. Softw. 2015, 70, 163–177. [Google Scholar] [CrossRef]
- Maki, A.; Burns, R.J.; Long, H.; Rothman, A.J. Paying people to protect the environment: A meta-analysis of financial incentive interventions to promote proenvironmental behaviors. J. Environ. Psychol. 2016, 47, 242–255. [Google Scholar] [CrossRef]
- CROP. Comportements des Québécois Dans L'éventualité d'un Élargissement de la Consigne; CROP: Montreal, QC, Canada, 2015. [Google Scholar]
- Sidique, S.F.; Lupi, F.; Joshi, S.V. Estimating the demand for drop-off recycling sites: A random utility travel cost approach. J. Environ. Manag. 2013, 127, 339–346. [Google Scholar] [CrossRef] [PubMed]
- SOM. Portrait des Comportements et Attitudes des Citoyens Québécois à L’égard des 3RV; SOM: Montreal, QC, Canada, 2015. [Google Scholar]
- Éco-Entreprise Québec (ÉEQ). Caractérisation des Matières Résiduelles du Secteur Résidentiel au Québec 2012–2013; Éco-Entreprise Québec: Montreal, QC, Canada, 2013. [Google Scholar]
- CM Consulting. Who Pays What: An Analysis of Beverage Container Collection and Costs in Canada; CM Consulting: Barcelona, Spain, 2014. [Google Scholar]
- CM Consulting. Who Pays What: An Analysis of Beverage Container Collection and Costs in Canada; CM Consulting: Barcelona, Spain, 2016. [Google Scholar]
- CREATE. Étude Comparative des Systèmes de Récupération des Contenants de Boisson au Québec; CREATE: Montreal, QC, Canada, 2015. [Google Scholar]
- SAQ. Rapport Annuel 2016; SAQ: Montreal, QC, Canada, 2016. [Google Scholar]
- Éduc-Alcool. Les Québécois et L'alcool 2017; Éduc-Alcool: Montreal, QC, Canada, 2017. [Google Scholar]
- Institut de la statistique du Québec. Recensement et Enquête Nationale Auprès des Ménages de 2011; Statistique Canada: Ottawa, ON, Canada, 2011. [Google Scholar]
- Turcotte, M. % of Population Aged 18 and over Making All Trips by Car (as a Driver or Passenger) on the Reference Day, by Census Metropolitan Area (CMA); Statistique Canada: Ottawa, ON, Canada, 2008.
- Roque, D.; Masoumi, H.E. An analysis of car ownership in Latin American cities: A perspective for future research. Periodica Polytechnica. Transp. Eng. 2016, 44, 5. [Google Scholar]
- Pyddoke, R.; Creutzer, C. Household Car Ownership in Urban and Rural Areas in Sweden 1999–2008; Centre for Transport Studies: Stockholm, Sweden, 2014. [Google Scholar]
- LIDD. Présentation du Rapport Final (Sommaire Exécutif); LIDD: Montreal, QC, Canada, 2015. [Google Scholar]




| Groups | Populations | Population Density (hab./km2) | Private Car Ownership (%) | Deposit Value ($) | Number of Depot Centers |
|---|---|---|---|---|---|
| 1 | (A) Urban | 3500 | 45 | 0.15 | 1, 2 and 3 |
| (B) Suburban | 1000 | 70 | |||
| (C) Rural | 200 | 80 | |||
| 2 | (A) Urban | 3500 | 45 | 0.35 | |
| (B) Suburban | 1000 | 70 | |||
| (C) Rural | 200 | 80 |
| Population | Number of Depot Centers | Average (%) | Standard Deviation | Min (%) | Max (%) |
|---|---|---|---|---|---|
| Urban (A) | 1 | 71.92 | 0.31 | 71.28 | 72.34 |
| 2 | 72.23 | 0.49 | 71.35 | 72.84 | |
| 3 | 72.22 | 0.47 | 71.56 | 72.80 | |
| Suburban (B) | 1 | 71.77 | 5.38 | 62.85 | 80.04 |
| 2 | 76.89 | 3.55 | 71.52 | 81.29 | |
| 3 | 81.01 | 2.01 | 76.20 | 82.46 | |
| Rural (C) | 1 | 51.33 | 5.23 | 42.02 | 58.09 |
| 2 | 62.31 | 4.24 | 53.99 | 67.35 | |
| 3 | 66.59 | 2.77 | 63.79 | 72.59 |
| Population | Number of Depot Centers | Average | Standard Deviation | Min | Max |
|---|---|---|---|---|---|
| Urban (A) | 1 | 274,587 | 1568 | 272,275 | 278,084 |
| 2 | 137,704 | 917 | 136,262 | 139,091 | |
| 3 | 91,512 | 656 | 90,003 | 92,232 | |
| Suburban (B) | 1 | 271,327 | 20,729 | 241,391 | 304,499 |
| 2 | 146,143 | 6902 | 136,311 | 154,599 | |
| 3 | 102,685 | 2739 | 96,336 | 104,880 | |
| Rural (C) | 1 | 195,079 | 20,607 | 159,608 | 221,672 |
| 2 | 118,841 | 8463 | 102,805 | 128,791 | |
| 3 | 84,070 | 3294 | 80,925 | 91,537 |
| Population | Number of Depot Centers | Average | Standard Deviation | Min | Max |
|---|---|---|---|---|---|
| Urban (A) | 1 | 274,587 | 1568 | 272,275 | 278,084 |
| 2 | 137,704 | 43,795 | 62,468 | 206,999 | |
| 3 | 91,512 | 35,804 | 14,971 | 172,254 | |
| Suburban (B) | 1 | 271,327 | 20,729 | 241,391 | 304,499 |
| 2 | 146,143 | 50,375 | 43,246 | 197,962 | |
| 3 | 102,685 | 37,975 | 18,752 | 161,188 | |
| Rural (C) | 1 | 195,079 | 20,607 | 159,608 | 221,672 |
| 2 | 118,841 | 31,816 | 65,393 | 170,538 | |
| 3 | 84,070 | 41,121 | 18,854 | 180,556 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Labelle, A.; Frayret, J.-M. Agent-Based Model for End-of-Life Product Flow Analysis. Resources 2018, 7, 42. https://doi.org/10.3390/resources7030042
Labelle A, Frayret J-M. Agent-Based Model for End-of-Life Product Flow Analysis. Resources. 2018; 7(3):42. https://doi.org/10.3390/resources7030042
Chicago/Turabian StyleLabelle, Alexandre, and Jean-Marc Frayret. 2018. "Agent-Based Model for End-of-Life Product Flow Analysis" Resources 7, no. 3: 42. https://doi.org/10.3390/resources7030042
APA StyleLabelle, A., & Frayret, J.-M. (2018). Agent-Based Model for End-of-Life Product Flow Analysis. Resources, 7(3), 42. https://doi.org/10.3390/resources7030042




