Improving the Performance of Turbo-Coded Systems under Suzuki Fading Channels

Abstract

In this paper, the performance of coded systems is considered in the presence of Suzuki fading channels, which is a combination of both short-fading and long-fading channels. The problem in manipulating a Suzuki fading model is the complicated integration involved in the evaluation of the Suzuki probability density function (PDF). In this paper, we calculated noise PDF after the zero-forcing equalizer (ZFE) at the receiver end with several approaches. In addition, we used the derived PDF to calculate the log-likelihood ratios (LLRs) for turbo-coded systems, and results were compared to Gaussian distribution-based LLRs. The results showed a 2 dB improvement in performance compared to traditional LLRs at ${10}^{-6}$ of the bit error rate (BER) with no added complexity. Simulations were obtained utilizing the Matlab program, and results showed good improvement in the performance of the turbo-coded system with the proposed LLRs compared to Gaussian-based LLRs.

1. Introduction

Rayleigh distribution has been widely used in wireless communication as an amplitude distribution for small-scale faded channels [1,2,3,4]. On the other hand, distribution for large-scale faded channels due to shadowing is represented by log-normal distribution [5,6]. However, it is more convenient to combine both distributions in land mobile communication to express both fading effects [7,8]. Suzuki probability density function (PDF) was introduced in Reference [9] to undertake such a task. Many articles considered the Suzuki channel model in their analysis. In Reference [10], outage probability was addressed for device-to-device (D2D) communications in the environment of Suzuki distribution. Due to the complexity in calculating integrals resulting from this distribution, two nonanalytic approximating approaches were used to derive closed forms for outage probability in the presence of additive white Gaussian noise (AWGN).

The statistical properties of ultrareliable low-latency communication (URLLC) were analyzed in Reference [11] for several channel fading models, including Suzuki distribution. Outage probability and performance were also analyzed utilizing power-law approximation for the maximum ratio-combiner (MRC) detector. In Reference [12], a new approach was introduced to develop a nonstationary complex-channel model that has an envelope similar to Suzuki distribution to address both small- and large-scale fading. In addition, it derived and analyzed Doppler power spectral density (PSD) and local power delay profile (PDP).

In Reference [13], separating slow and fast fading was considered, utilizing a moving average filter in which Rayleigh and log-normal distributions were individually used to analyze the effects of multipath fading and shadowing, respectively. An efficient and novel method was proposed in Reference [14] to implement Weibull, log-normal, and Suzuki fading channels that utilize CORDIC technology that does not require a multiplier.

The work in the literature shows that the LLRs used in calculating the soft bits for the decoder are approximated using Gaussian distribution without taking into consideration the effect of channel equalization.

Linear detectors such as zero-forcing equalizers (ZFE) and minimum-mean-square error (MMSE) reduced complexity compared to more sophisticated detectors. In addition, the tendency of wireless-communication systems is to reduce detection complexity and to improve bit error rate (BER) performance.

According to that, we considered the ZFE detector to equalize the channel effect at the receiver. The noise PDF after the ZFE is derived for Suzuki fading channels analytically and theoretically with proposed approximations. In addition, the derived PDFs are utilized in the calculation of the log-likelihood ratios (LLRs) to be used in the soft decoding of the turbo decoder. The results showed improvement in the performance of the coded system with the proposed LLRs compared to Gaussian-based LLRs.

The rest of this paper is organized as follows. Section 2 demonstrates the system model, and Section 3 shows the derivation of the noise PDF, including the proposed approximations. Section 4 is used to discuss the results obtained in this paper. Finally, Section 5 concludes the study.

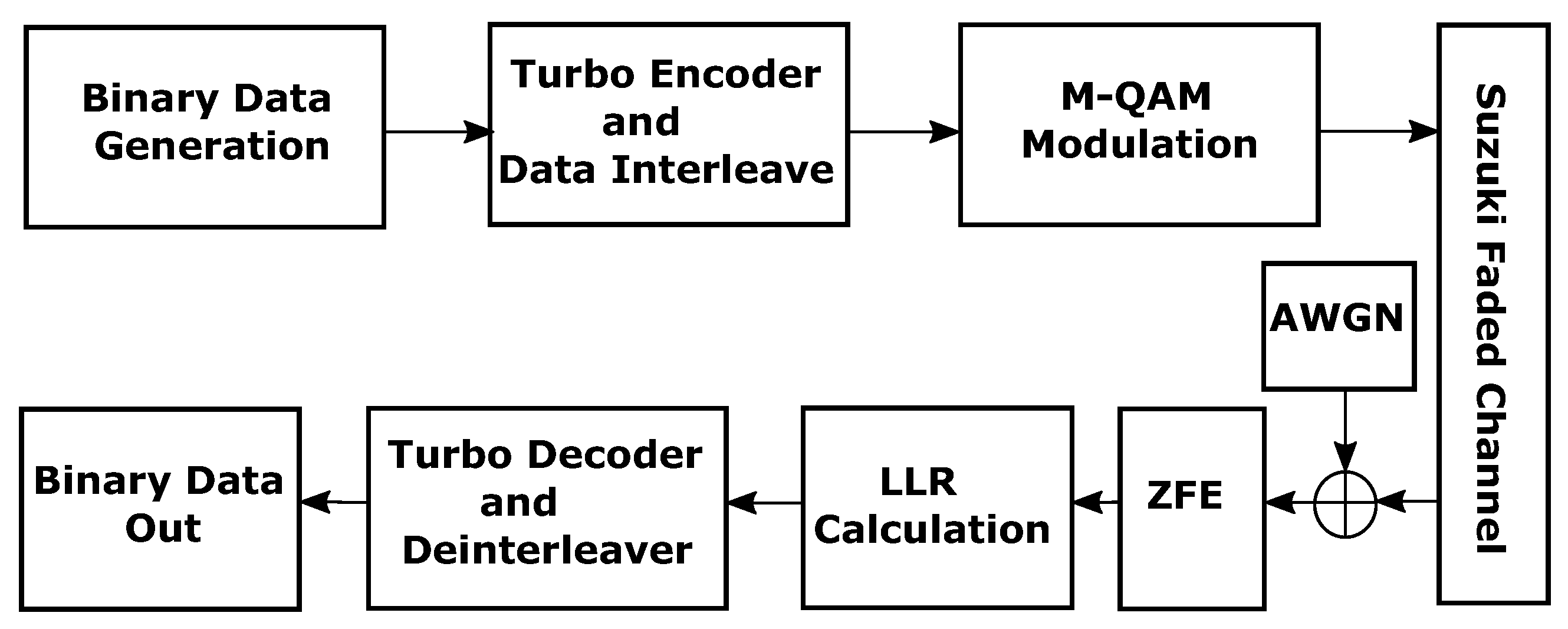
2. System Model

The system model of Figure 1 was considered in the analysis of this paper. The binary generated data are encoded, with a $1/3$- and $1/2$-rate turbo encoder with a codeword length of 4096 bits. Binary codewords were converted to equivalent symbols and modulated with M-quadrature amplitude modulation (M-QAM) to be transmitted via a Suzuki faded channel. The data were received in the presence of AWGN, such that

$$\mathbf{y}=\mathbf{h}\mathbf{x}+\mathbf{w},$$

(1)

where $\mathbf{y}\in {\mathbb{C}}^{1\times N}$ and $\mathbf{x}\in {\mathbb{C}}^{1\times N}$ are the received and transmitted vectors with length N, while $\mathbf{h}\in {\mathbb{C}}^{1\times N}$ and $\mathbf{w}\in {\mathbb{C}}^{1\times N}$ are the channel and the AWGN parameters, respectively. The received signal was equalized utilizing the ZFE, such that

$$\widehat{\mathbf{x}}=\mathbf{x}+\widehat{\mathbf{w}},$$

(2)

where $\widehat{\mathbf{x}}=\mathbf{x}/\mathbf{h}$ and $\widehat{\mathbf{w}}=\mathbf{w}/\mathbf{h}$ are the equalized received signal and noise, respectively. The LLRs were calculated based on the noise PDF that is proposed in this work utilizing ratio distribution $\mathbf{w}/\mathbf{h}$, which we describe in Section 3. Finally, the turbo decoder generates the binary data using these LLRs. It is worth mentioning that the channel parameters were assumed to be known at the receiver side.

3. Noise Distribution

3.1. AWGN Distribution

The Gaussian distribution can be written as [15,16]:

$$p(w)=\frac{1}{\sqrt{2\pi {\sigma }_w^2}}exp(-\frac{{(w-{\mu }_w)}^2}{2{\sigma }_w^2}),$$

(3)

where, ${\sigma }_w^2$ and ${\mu }_w$ are the variance and the statistical mean of Gaussian random variable w. The complex AWGN RV is represented using $\mathbf{w}={\mathbf{w}}^I+{\mathbf{w}}^Q$, where superscripts I and Q are denoted for the in-phase and the quadrature part of the complex AWGN signal.

3.2. Suzuki Distribution

Suzuki distribution is a combination of Rayleigh and log-normal distributions, such that [14,17]:

$$p(h)={\int }_0^{\infty }\frac{h}{\sqrt{2\pi }{\sigma }_h{\alpha }^3}exp(-\frac{h^2}{2{\alpha }^2})exp(-\frac{{(ln(\alpha )-{\mu }_h)}^2}{2{\sigma }_h^2})d\alpha ,$$

(4)

where ${\sigma }_h$ and ${\mu }_h$ represent the channel variance and mean. There is no analytic solution to Equation (4). Instead, numerical methods are widely used to find an approximate value of this integration. In our analysis, we utilize this integral to derive noise distribution after the ZFE.

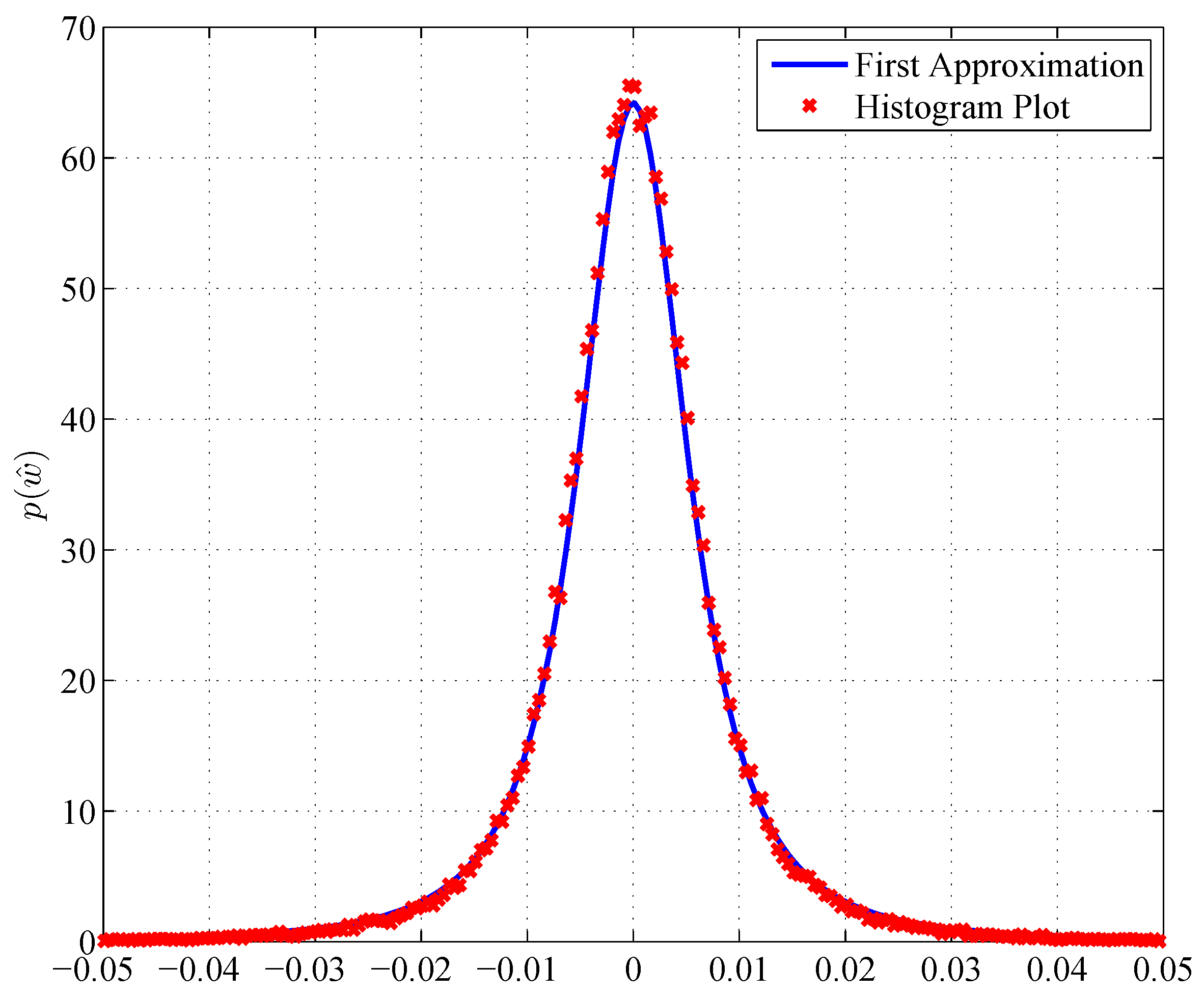
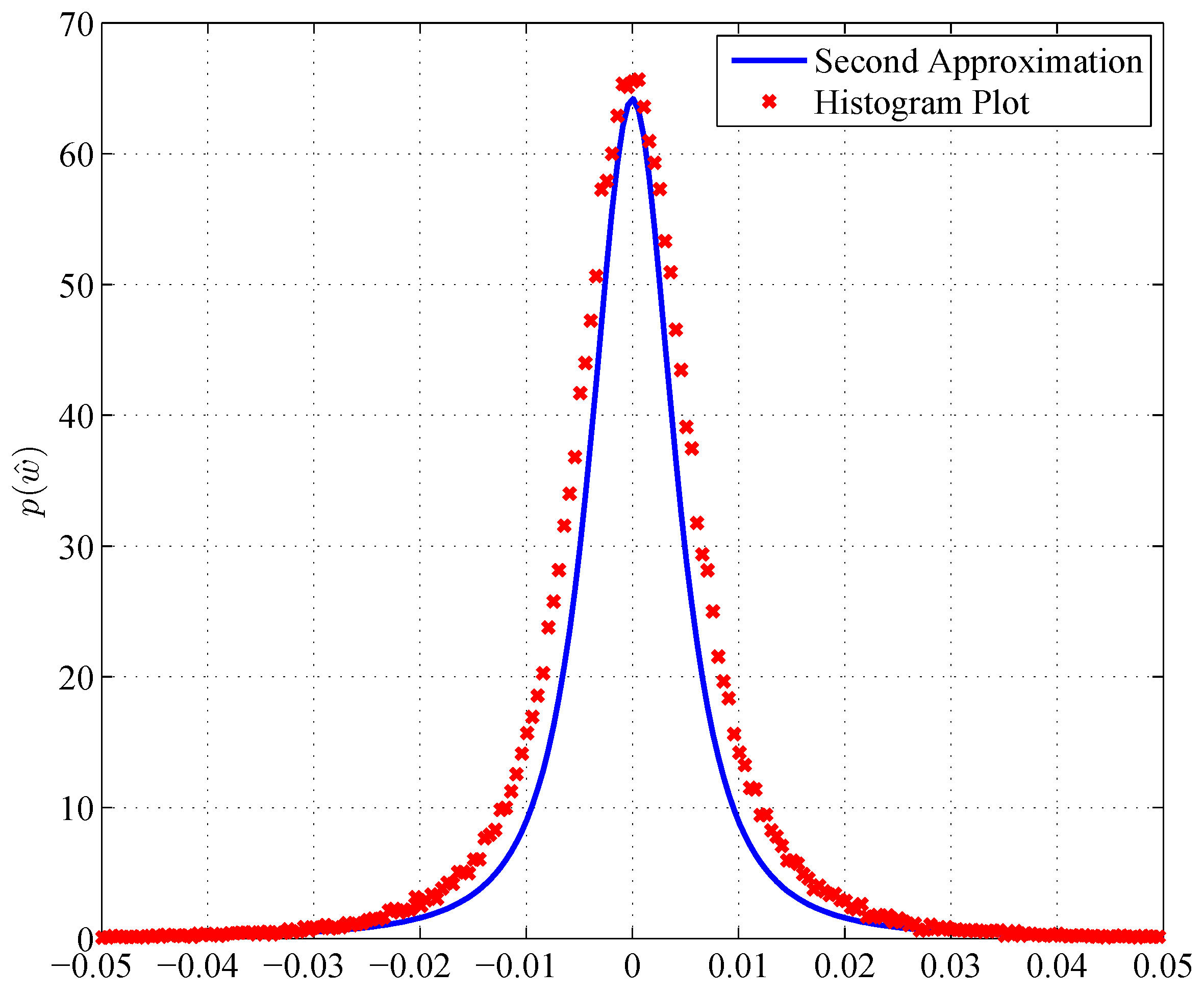
3.3. Ratio Distribution

The equalized noise random variable can be written as

$${\widehat{w}}_k=w_k/h_k,$$

(5)

where subscript k represents the elementwise operation; hence, k is eliminated from subsequent operations to maintain simplicity. In addition, channel distribution is assumed to be zero mean, which means substituting $\mu =0$ in Equation (4).

Assuming uncorrelated noise and channel PDFs, the ratio distribution of Equation (5) can be calculated using [18]:

$$p(\widehat{w})={\int }_0^{\infty }\left|h\right|p(h,w)dh,$$

(6)

where $p(h,w)$ represents the joint PDF of channel h and the AWGN w random variables. By substituting Equations (3) and (4) in Equation (6), the PDF of the ratio can be written as:

$$\begin{array}{ccc}\hfill p(\widehat{w})& =& {\int }_0^{\infty }\left|h\right|p(h,h\widehat{w})dh,\hfill \\ & =& {\int }_0^{\infty }{\int }_0^{\infty }\frac{h^2}{2\pi {\sigma }_h{\sigma }_w{\alpha }^3}exp(\frac{-{\widehat{w}}^2{h}^2}{2{\sigma }_w^2})exp(\frac{-h^2}{2{\alpha }^2})exp(\frac{-{ln}^2(\alpha )}{2{\sigma }_h^2})dhd\alpha .\hfill \end{array}$$

(7)

To solve this integration, first we integrate for h, which reduces the integration into the following formula [19]:

$$\begin{array}{ccc}\hfill I_1& =& {\int }_0^{\infty }{h}^{2}exp(-h^2\frac{({\sigma }_w^2+{\widehat{w}}^2{\alpha }^2)}{2{\alpha }^2{\sigma }_w^2})dh,\hfill \\ & =& \frac{\sqrt{2\pi }{\alpha }^3{\sigma }_w^3}{2{({\sigma }_w^2+{\alpha }^2{\widehat{w}}^2)}^{1.5}},\hfill \end{array}$$

(8)

by substituting this formula into Equation (7), it reduces into

$$\begin{array}{c}\hfill p(\widehat{w})=\frac{{\sigma }_w^2}{2\sqrt{2\pi }{\sigma }_h}{\int }_0^{\infty }\frac{exp(\frac{-{ln}^2(\alpha )}{2{\sigma }_h^2})}{{({\sigma }_w^2+{\widehat{w}}^2{\alpha }^2)}^{1.5}}d\alpha .\end{array}$$

(9)

Factor $1/{({\sigma }_w^2+{\widehat{w}}^2{\alpha }^2)}^{1.5}$ can be written in the form of a series, such that

$${({\sigma }_w^2+{\widehat{w}}^2{\alpha }^2)}^{-1.5}=\sum _{n=0}^{\infty }\frac{{\widehat{w}}^n{\alpha }^n}{{\sigma }_w^{n+3}}\left(\genfrac{}{}{0pt}{}{-\frac{3}{2}}{\frac{n}{2}}\right).$$

(10)

Substituting Equation (10) in Equation (9) results in the following formula:

$$\begin{array}{c}\hfill p(\widehat{w})=\frac{{\sigma }_w^2}{2\sqrt{2\pi }{\sigma }_h}\sum _{n=0}^{\infty }\frac{{\widehat{w}}^n}{{\sigma }_w^{n+3}}\left(\genfrac{}{}{0pt}{}{-\frac{3}{2}}{\frac{n}{2}}\right){\int }_0^{\infty }{\alpha }^{n}exp(\frac{-{ln}^2(\alpha )}{2{\sigma }_h^2})d\alpha .\end{array}$$

(11)

The integration of this formula can be calculated as:

$$\begin{array}{c}\hfill p(\widehat{w})=\frac{1}{2{\sigma }_w}\sum _{n=0}^{\infty }{(\frac{\widehat{w}}{{\sigma }_w})}^n\left(\genfrac{}{}{0pt}{}{-\frac{3}{2}}{\frac{n}{2}}\right)exp(\frac{{\sigma }_h^2}{2}{(n+1)}^2)\end{array}$$

(12)

This result represents the noise PDF after the ZFE for Suzuki faded channel in series form. However, it is not very useful to use this formula in the current form. Therefore, we further simplified and approximated this formula in two ways:

• The first approximation assumes ${(n+1)}^2\approx (n+1)$, and the PDF can be written as,

  $$\begin{array}{c}\hfill p(\widehat{w})=\frac{exp({\sigma }_h^2/2){\sigma }_w^2}{2({\sigma }_w^2+|\widehat{w}{{|}^{2}exp({\sigma }_h^2))}^{1.5}}.\end{array}$$

  (13)
• The second approximation assumes the power of exponential ${(n+1)}^2\approx 2n+1$, and the simplified formula can be written as:

  $$\begin{array}{c}\hfill p(\widehat{w})=\frac{exp({\sigma }_h^2/2){\sigma }_w^2}{2({\sigma }_w^2+|\widehat{w}{{|}^{2}exp(2{\sigma }_h^2))}^{1.5}}.\end{array}$$

  (14)

To verify the close match between the derived PDFs and the histogram plot, we used the Kolmogorov–Smirnov (KS) goodness-of-fit test [20,21]. At a 5% significance level, the decision of the KS test for the first approximation was 0, implying that we cannot reject the null hypothesis that both vectors have the same PDFs. On the other hand, the KS test for the second approximation was 1, which implies that we must reject the null hypothesis, and the two PDFs are not the same.

4. Numerical Results

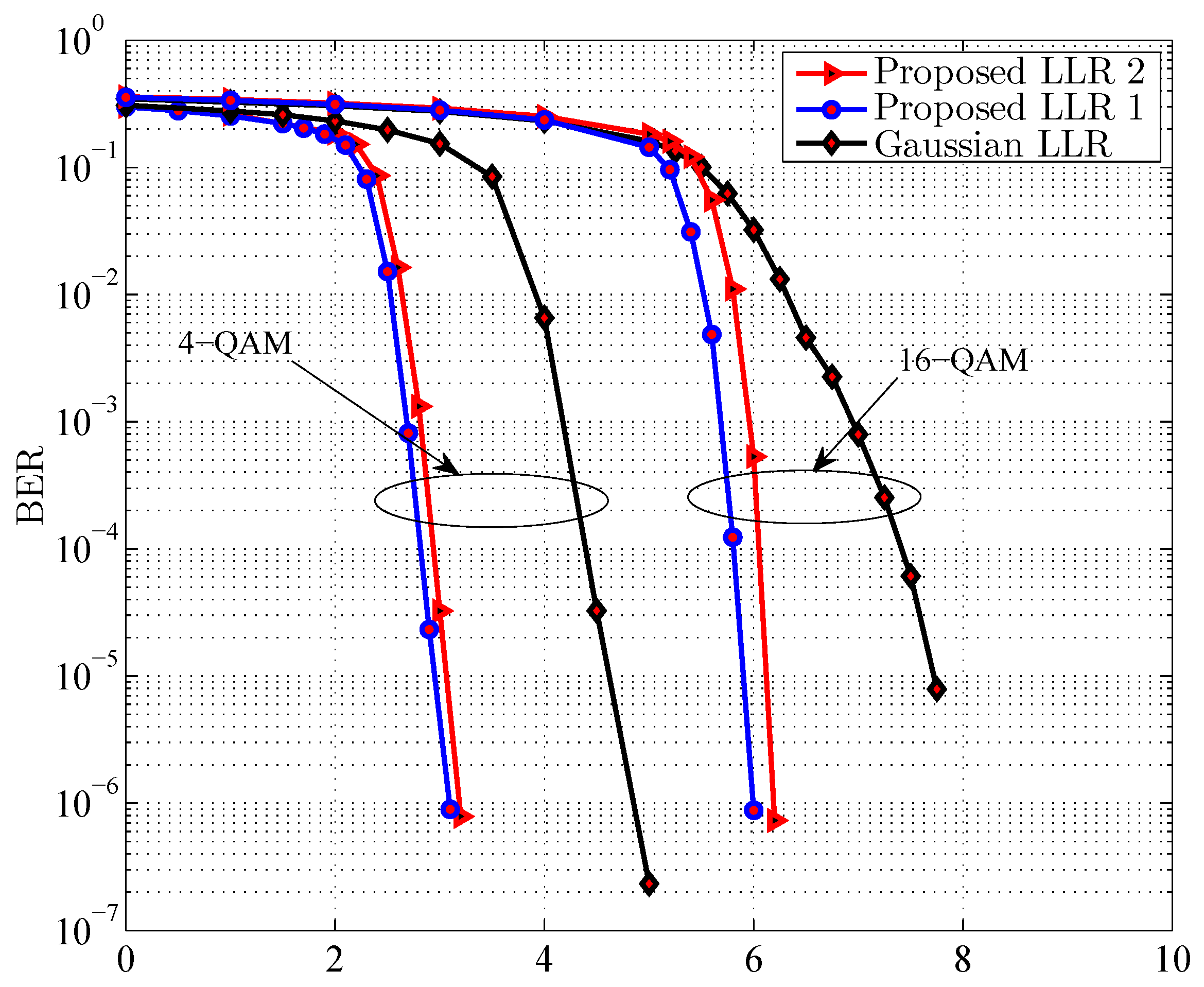
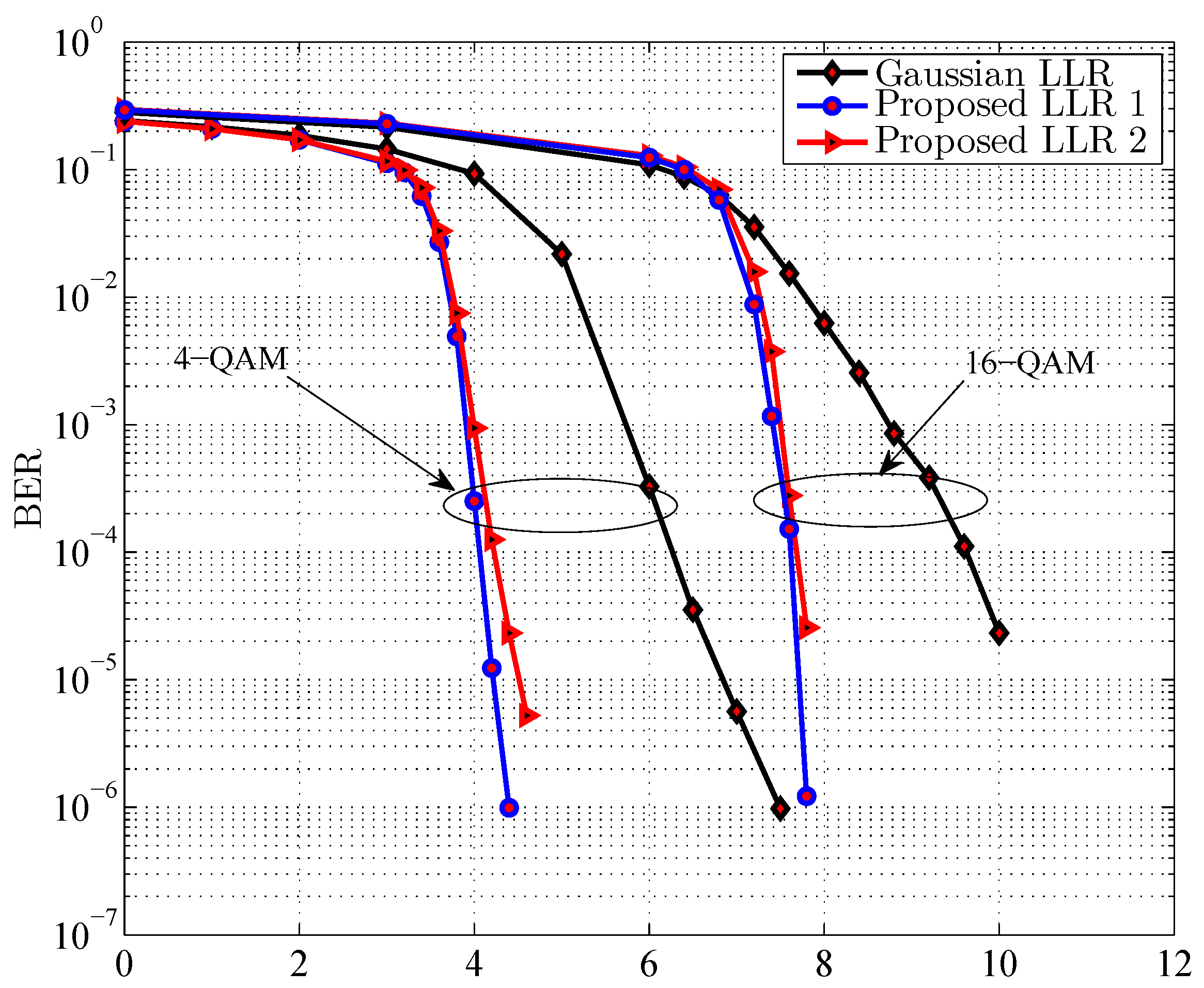
4.1. LLR Calculations

The noise PDFs that are derived in Equations (13) and (14) are utilized in this section to calculate the LLR equations for the coded system, such that

$$\begin{array}{c}\hfill b_0={log}_e\left(\frac{p({\widehat{w}}^I{|}_{{\widehat{x}}^I=1})}{p({\widehat{w}}^I{|}_{{\widehat{x}}^I=-1})}\right),\end{array}$$

(15)

$$\begin{array}{c}\hfill b_1={log}_e\left(\frac{p({\widehat{w}}^Q{|}_{{\widehat{x}}^Q=1})}{p({\widehat{w}}^Q{|}_{{\widehat{x}}^Q=-1})}\right).\end{array}$$

(16)

where, superscripts I and Q are used to denote the in-phase and quadrature parts of the signal. Equations (15) and (16) represents the LLRs for the 4-QAM scheme of the modulation. Similar equations can be calculated for the 16-QAM scheme with 4 LLR levels, such that signals ${\widehat{x}}^I$ and ${\widehat{x}}^Q$ take four values, and such that (−3, −1, +1, +3), with $b_0,b_1,b_2,b_3$ being the soft LLR for the coded system.

4.2. Performance Improvement

In this section, the numerical results are discussed to verify the accuracy of the derived PDFs. First, it is observed from Figure 2 that both the first approximation and the histogram PDFs exhibit the same distribution. In addition, the KS test showed a close match between the two distributions, as demonstrated in the previous section. However, Figure 3 did not show a close match between the derived approximation and the histogram plot, which was also proofed by the KS test in Section 3.

Figure 4 and Figure 5 compared the performance of the turbo-coded system with the proposed LLRs that was derived utilizing both Equation (13) and (14) PDFs and the Gaussian based-LLRs for rates $1/3$ and $1/2$, respectively. It was observed that the proposed LLRs with the first approximation improved the performance of the turbo-coded system by more than 2 dB at BER = ${10}^{-5}$ for both modulation constellations and for both ratios. On the other hand, the second approximation also improved the performance of the coded system with a small degradation in performance compared to the first approximation, as demonstrated with the red line of the simulation.

4.3. Complexity Calculations

In this section, the number of operations required to calculate the derived noise distribution and the corresponding LLRs are calculated utilizing the $gaxpy$ algorithm [22]. The complexity of calculating Equations (13)–(16), and the Gaussian PDF and its LLRs is illustrated in

Table 1. Number of required operations.

Methods	Add./Sub.	Multip./Div.	Power/Sqrt	Exp./Log
Equation (13)	1	5	2	2
Equation (14)	1	6	2	2
Equations (15) and (16)	2	5	2	3
Gaussian PDF	0	5	2	1
Gaussian LLR	3	2	2	0

.

It is observed from Table 1 that the number of operations required to calculate the PDFs and the LLRs for the proposed detector compared to Gaussian PDF are relatively low and cost-effective for implementation with regards to the improvement in BER performance.

Practically, we selected four SNR values to calculate the running time of the simulations, such that SNR = 0, 1, 1.5, and 2 dB, while data size was $2\times {10}^6$ bits. As a result, the simulation time required for utilizing Gaussian LLRs was 198.9063 s, while it was 217.2656 s for the proposed LLRS considering the 4-QAM scheme. As a result, the cost for improvement in the BER of 2 dB increases running time by factor

$$\frac{217.2656-198.9063}{198.9063}=9.23\%.$$

5. Conclusions

In conclusion, this paper proposed a novel approach to analytically calculate noise distribution after the ZFE. The derived PDF was approximated utilizing series representations to reduce the complexity of calculations. The first approximation showed a close match to the histogram plot of noise distribution. In addition, both PDFs were utilized to implement the LLR equations for the turbo-coded system. It was observed that the proposed LLRs improved the performance of the coded system compared to the Gaussian-based LLR, with a small degradation for the second approximation compared to the first approximation. It was also observed that the complexity of both approximations and their LLRs slightly increased the number of operations compared to Gaussian receivers. The increase in running time of $9.23\%$ results in a 2 dB improvement to the BER of the proposed system, which is regarded as an effective receiver compared to Gaussian-based receiver.