Power and Area Efficient Clock Stretching and Critical Path Reshaping for Error Resilience

Abstract

Energy efficient semiconductor chips are in high demand to cater the needs of today’s smart products. Advanced technology nodes insert high design margins to deal with rising variations at the cost of power, area and performance. Existing run time resilience techniques are not cost effective due to the additional circuits involved. In this paper, we propose a design time resilience technique using a clock stretched flip-flop to redistribute the available slack in the processor pipeline to the critical paths. We use the opportunistic slack to redesign the critical fan in logic using logic reshaping, better than worst case sigma corner libraries and multi-bit flip-flops to achieve power and area savings. Experimental results prove that we can tune the logic and the library to get significant power and area savings of 69% and 15% in the execute pipeline stage of the processor compared to the traditional worst-case design. Whereas, existing run time resilience hardware results in 36% and 2% power and area overhead respectively.

1. Introduction

Cost effective variation tolerance is hard to achieve in nanometer scale technology nodes [1,2]. Manufacturing process limitations in advanced nodes cause random dopant fluctuations and line edge roughness [3,4,5] which require additional process margins. High device density in nanoscale chips results in an increase in dynamic voltage and temperature variations [6,7] which widens the design margins further. As a result, the chip life cycle has shrunk tremendously. Dynamic variations are random in nature and depend heavily on the workload. Moreover, the magnitude of delay variations in the near- threshold regime is exponential with respect to supply voltage. Traditional variation tolerance techniques use worst case design margins which results in huge wastage of chip resources. We need novel error tolerance techniques that can improve the performance, power and area of chips without affecting the chip reliability. The proposed Variation Tolerant Design (VTD) improves the above design parameters for the same reliability margins as the Worst-Case Design (WCD) as shown in Figure 1.

Post-silicon tuning [8] and adaptive techniques help to recover fixed design margins to combat process variability. Sensor and monitor-based techniques generate a hardware signature of the variation which is then used in higher abstraction layers to tune the operating condition [9,10]. However, sensor response is not fast enough to dynamic variations, which limits the amount of design margin improvement. This prevents the use of sensors in better than worst case (BTWC) design techniques. In addition, sensor calibration, to determine the safe region of operation, contributes to the post-silicon testing costs.

Performance variations, whether static or dynamic, are manifested as timing errors in the critical paths. Critical path replica [11] is a non-intrusive technique which duplicates and monitors the critical path to detect variations. Although this helps to avoid data corruption by short paths, they will not be able to detect the actual variation encountered by the critical path under consideration. In-situ error resilience techniques compare the input data with a delayed version to decide whether a timing error has happened. The operating point of the silicon is then tuned dynamically to regain the design margins until the error rate exceeds the threshold limit. Here, the error detection window decides the design margin improvement. Max delay constraint of the flip-flop is relaxed by the error detection window and the min delay constraint is tightened by the same amount to prevent short paths from corrupting the data and the error signal. This max delay min delay trade-off is a major design challenge when using in-situ error resilience. Razor I [12] uses a flip-flop as data path and a latch in shadow path to generate timing error signal. It suffers from meta-stability issues since the data changes too close to the clock edge. Meta-stability detector, short path buffer and MUX overheads make this technique power hungry. In Razor II [13] the meta-stability issue is avoided using a latch based data path. But latch makes the data path transparent to glitches and spurious transitions. In addition, hold buffers and duty cycle control overheads are significant. Double sampling with time borrowing (DSTB) [14] is similar to Razor I with flip-flops as the data path. Transition detection with time borrowing (TDTB) is similar to Razor II with latches as the data path. Another approach Bubble razor [15] breaks the dependency between speculation window and minimum delay using a two-phase latch implementation. However, it has area and power penalties. In-situ techniques correct errors in the architecture level using instruction replay or counter flow pipelining. This adds a latency of few clock cycles for error recovery and makes the error path design constraints very stringent. Also, they suffer from sharp design margin deterioration with increasing error rate due to the error correction latency to recover from the critical wall of the slack behavior.

In-situ methods like soft edge flip-flops [16] and TIMBER [17] masks the error by borrowing time from the next pipeline stage. Compared to error detection methods, there is no latency overhead for error masking, which makes it a good candidate for performance-driven designs. Soft edge flip-flops are able to reclaim only small fixed design margins. Here the clock control circuit is internal to the flip-flop which limits the degree of softness attained. TIMBER uses discrete time borrowing coupled with error propagation to detect multistage timing errors. Here the design margin reduction is limited because the time borrow window is divided into smaller intervals to deal with multistage errors. Also, they suffer from significant error propagation and hold buffer overheads.

Better than worst case design (BTWC) techniques [18,19,20,21] can be used to tune the operating corner of the chip to the typical corner together with error resilience elements in the critical path to detect and correct the dynamic errors. Processor pipelines have the critical wall of slack behavior [22]. This results in many critical paths which makes the cost of resilience even higher. Razor techniques deal with high error rates by adjusting the system frequency. TIMBER shares a fixed design margin among multiple pipeline stages. Also, the system frequency needs to be halved to recover from multistage errors beyond three stages.

Cost-effective alternatives like EVAL (Environment for Variation Afflicted Logic) [23] uses adaptive body bias and supply voltage scaling to optimize slow paths and fast paths. Blue Shift [24] varies the timing constraints and bias voltage to optimize selected critical paths. Power-aware slack distribution (SlackOptimizer) [24] sizes the cell to distribute slack evenly in a power and cost-efficient manner. Selective End Point Optimization (SEOpt), Clock Skew Optimization (SkewOpt) and Combined Optimization (CombOpt) [25,26] inserts additional margins and thus reduce the cost of resilience by replacing error tolerant registers with conventional ones. They need significant design time and computational complexity.

Our work utilizes the slack imbalances inherent in processor pipelines to strengthen the critical paths. We use static timing analysis (STA) to find positive slack paths which immediately succeeds the critical paths. We use a simple clock stretched flip-flop (CSFF) to redistribute this slack to the critical stage. This enables us to redesign the combinational fan-in of the critical path proportionate to the extra slack margin. The relaxed slack margins result in power and area savings in the critical fan-in logic cone. In this paper, we propose two power optimization techniques to redesign the critical stages of a 40nm processor pipeline. One approach uses path optimization directives to adjust the timing slack during the synthesis stage. The second approach uses BTWC sigma corner library to resign critical modules with sufficient consecutive slack in the processor pipeline. The slack apportioning is done in such a way that pessimistic design margins are maintained with respect to the stretched clock edge. The whole scheme is non-speculative and does not involve any runtime voltage or frequency scaling. This guarantees power and area savings without high error rates associated with speculative techniques. Timing is closed at design time keeping the worst design margins relative to the delayed clock edge which avoids any meta-stability issues in the design.

Table 1. Comparison of Error Resilience Techniques.

Feature	Design Level Optimization	Sequential Optimization Based on Error Detection	Combinational & Sequential Optimization	Sequential Optimization Based on Error Masking	Proposed
Speculation Mechanism	ABB, ASV, OSB, PCT	Adaptive voltage/frequency scaling	Adaptive voltage/frequency scaling	Adaptive voltage/frequency scaling	Non-speculative, based on cell downsizing and BTWC library
Error Handling	Duplicate paths	Duplicate Latch/FFs	Duplicate Latch/FFs	Duplicate Latch/FFs	No error
Clock Tree Loading	No	Yes	Yes	Yes	No
Short Path Padding	No	Yes	Yes	Yes	Yes
Sequential Overhead	Large	Large	Large	Large	None
Combinational Overhead	Small	Small	Small	Small	None
Meta-stability	Yes	Yes	Yes	Yes	No
Techniques	EVAL, Blueshift	Razor I, Razor II, Bubble Razor DSTB, TDTB	Slack Optimizer, Skew Optimizer, CombOpt	TIMBER, soft edge flip-flop	Clock stretched flip-flop

MS = Meta stability, T_w = error detection window, T_ck = clock period.

summarizes the features of the different error resilience techniques discussed so far.

The major contributions of this paper are as follows.

(1)

We propose a simple clock stretcher to borrow slack available in the processor pipeline stage. Timing closure with pessimistic design margins with respect to the delayed clock prevents meta-stability and critical operating point behavior issues in the pipeline.

(2)

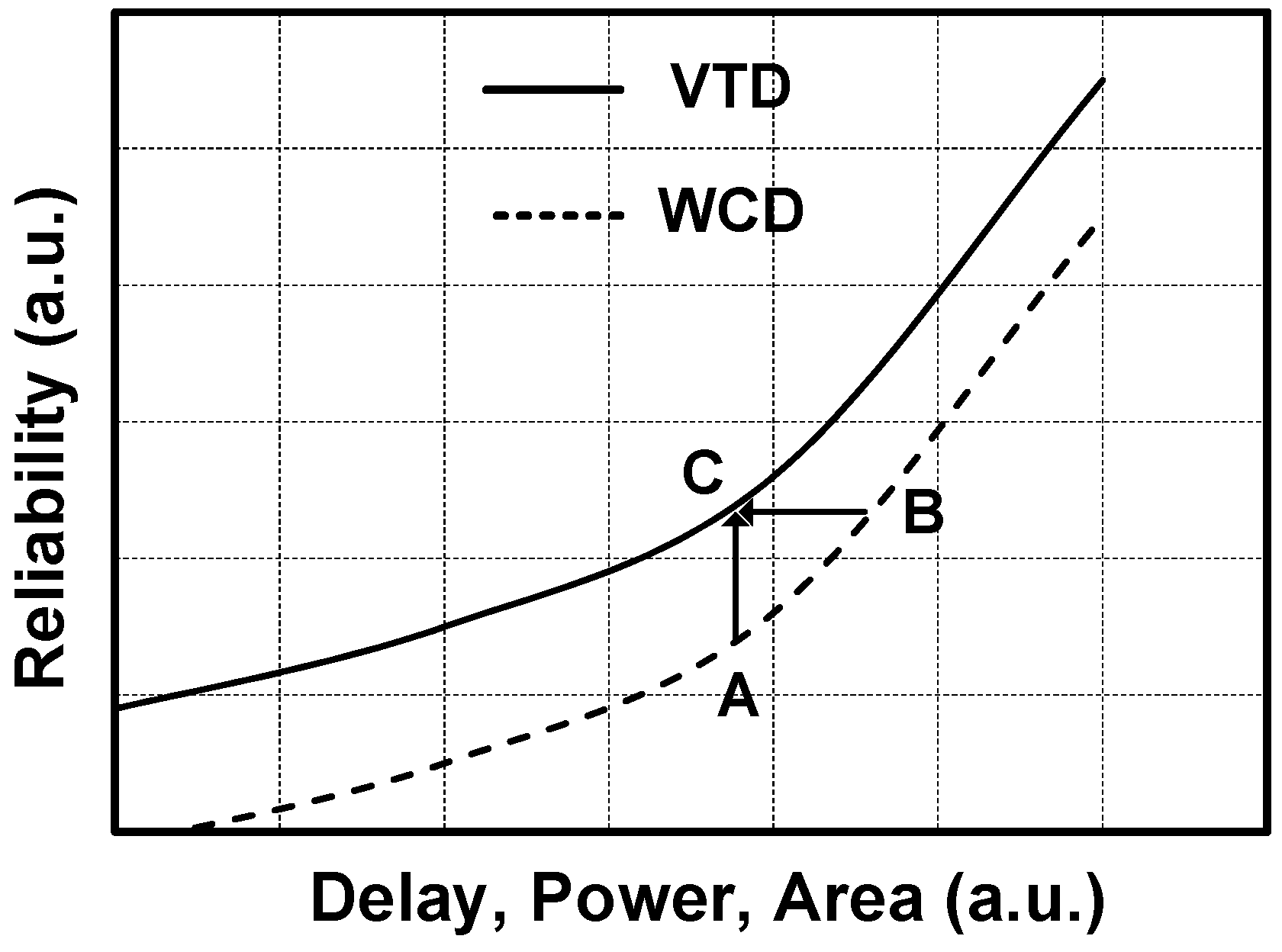
We come up with two critical path reshaping techniques to convert the extra slack margins created by the clock stretcher into power and area savings as shown in Figure 2b,c. The first approach relaxes the slack margins and redesigns the logic based on the new slack. The second approach replaces the logic library with BTWC sigma corner library.

(3)

The proposed approaches downsize the short path logic along with the critical paths, which removes hold buffer overheads. The non-speculative nature of our approach removes error management and latency overheads which minimizes the cost for error resilience.

The rest of this paper is organized as follows. Section 2 details the motivation to use the proposed technique. Section 3 explains the proposed design methodology. Section 4 describes our proposed power optimization techniques and experimental results are shown in Section 5. Finally, conclusions are summarized in Section 6.

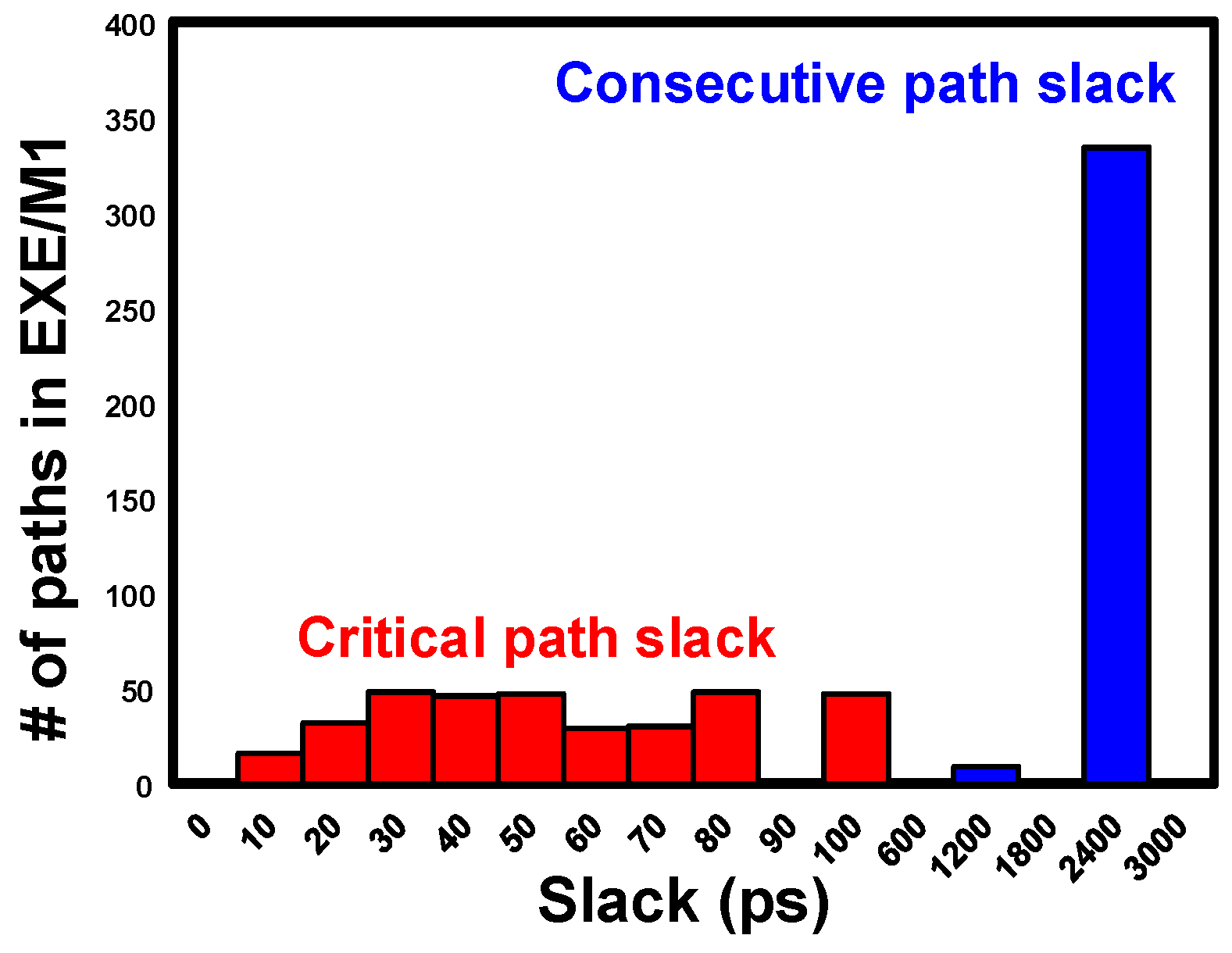
2. Motivation

Typical processor pipelines are highly unbalanced with respect to the slack present in various combinational logic stages. Traditional logic synthesis tools optimizes the combinational logic and do not support any optimization between the combinational paths separated by sequential elements. Sequential optimizations like retiming may introduce additional power and area overheads. Figure 3 shows the effect of retiming on the processor pipeline. It is obvious that the number of critical endpoints has doubled after retiming and there is hardly any slack improvement. In contrast to the existing techniques, we come up with a design-time optimization which is energy efficient and reliable. We use a 40 nm processor core with 26 K logic gates and 7000 flip-flops. We chose the critical endpoints with slack less than 2% of the clock period. Based on our investigation, we see that for most of the timing paths in the near critical slack region (pipe_1 slack) there is sufficient consecutive stage slack (pipe_2 slack) as shown in Figure 3. Results show that 85% of the critical paths get a mean slack improvement of 42× if they borrow slack from the consecutive stage. We leverage this slack to relax the design margins of the critical paths and the delayed inputs are sampled using a clock stretched flip-flop. We reshape the combinational logic along the critical paths to get power and area savings. The proposed approach under designs the critical logic of the pipeline instead of reducing design margins at runtime. This approach minimizes the speculative overheads associated with a typical error resilience techniques. Also, the design margin improvement helps the pipeline to be more variation tolerant. Worst case design margins are still met with respect to the delayed clock edge of the flip-flop. This helps to eliminate all the timing speculation overheads and critical wall of slack issues related to adaptive in-situ error correction schemes. Unlike a fixed speculation window, the proposed method uses an elastic window which allows timing speculation proportional to the available slack.

3. Proposed Design Methodology

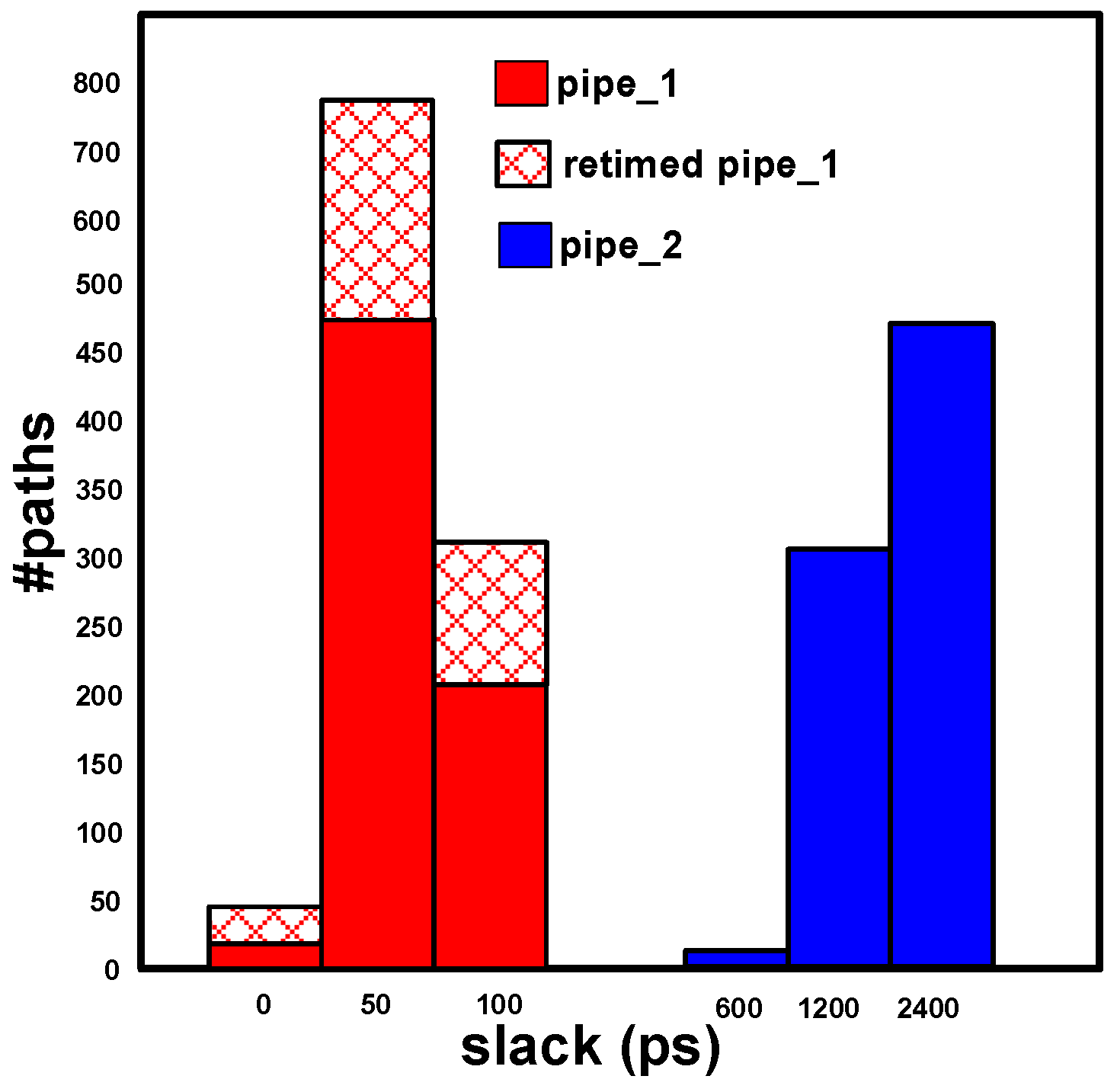
3.1. Slack Balancing

To explain the proposed slack balancing technique [27,28,29] we consider the pipeline shown in Figure 4 with four registers. Combinational path (d, b) is the critical path with minimum feasible clock period T = 11. Path (d, b) can borrow time from the consecutive stage (b, d) whose delay is 9. So, we replace the flip-flop b by a clock stretched flip-flop with a clock delay 2. Now we have an extra margin of 2 in the critical path (d, b) which is used to under design the logic for power and area savings. We use two techniques to under design the critical path logic. The first one relaxes the critical path slack by the extra slack margin available and redesigns the logic with smaller cell equivalents from the same logic library. The second technique identifies modules with sufficient consecutive path slacks and swaps the critical path logic library with a BTWC sigma corner library. Thus, we trade-off the extra slack margin for power and area savings using the slower cells in the sigma corner library.

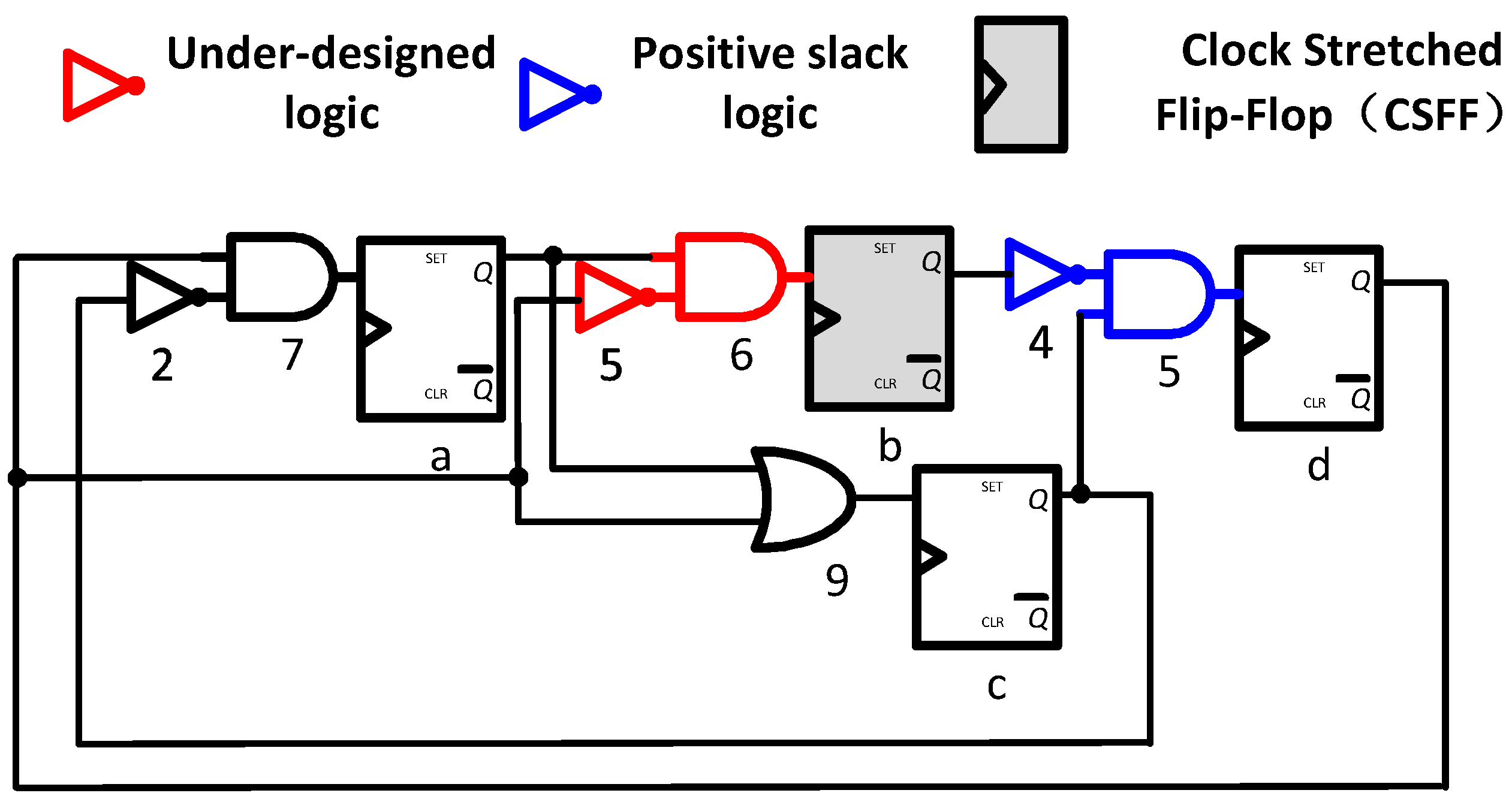
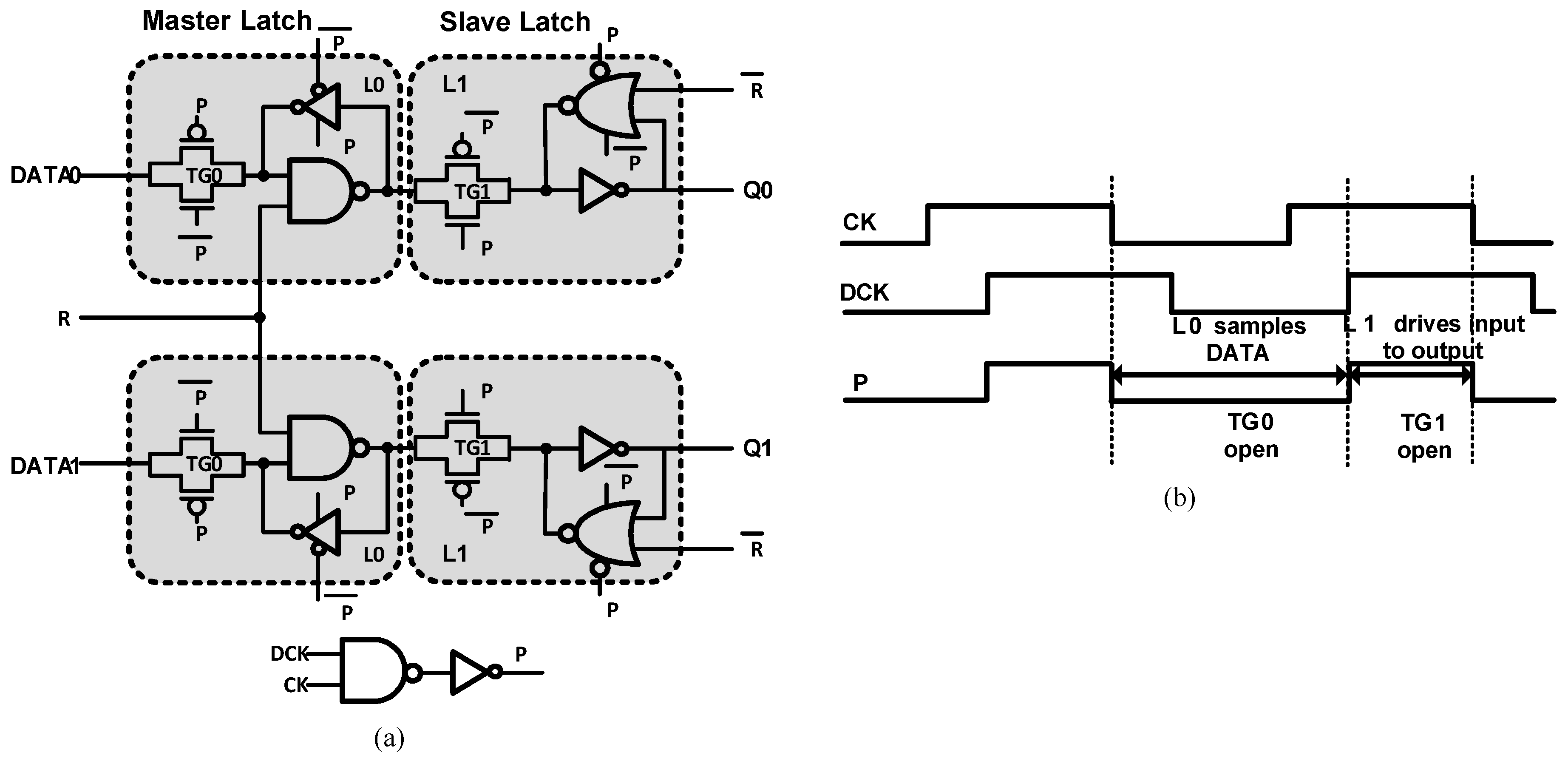
3.2. Clock Stretched Flip-Flop (CSFF)

In this section, we will explain the proposed clock stretching flip-flop [27] to relax the design margins on the critical paths. As shown in Figure 5a, the flip-flop architecture is similar to master slave flip-flop with the additional clock control signal P. The stretched clock P allows delayed transition of data. P is derived from the original clock CK and the delayed clock DCK. We also propose a multi bit flip-flop structure as shown in Figure 5a to combine the individual flip-flop data paths which gives additional power and area savings as detailed in the results section. As shown in Figure 5b, during the low phase of P, transmission gate TG0 is open whereas TG1 is closed and master latch L0 samples the input data. During the high phase of P, transmission gate TG1 is open and TG0 closed and the shadow latch L1 sample the data to output. The transparency window for the master latch L0 determines the time borrowed from the consecutive stage. The time borrowed TB is equal to the phase difference between CK and DCK. We choose four TBs which are multiples of T_ck/8 for each critical end point register based on the available slack in the consecutive stage, where T_ck is the clock period. Our approach has no redundant data sampling and error handling circuitry compared to other resilience circuits because we relax a fixed amount of slack at each end point during design time. The data input D is timed in such a way it maintains pessimistic design margins with the clock edge P which avoids meta-stability overheads in the design. The transistor count of the proposed error resilience flip-flop is half of that of other error resilient architectures resulting in considerable area and power savings.

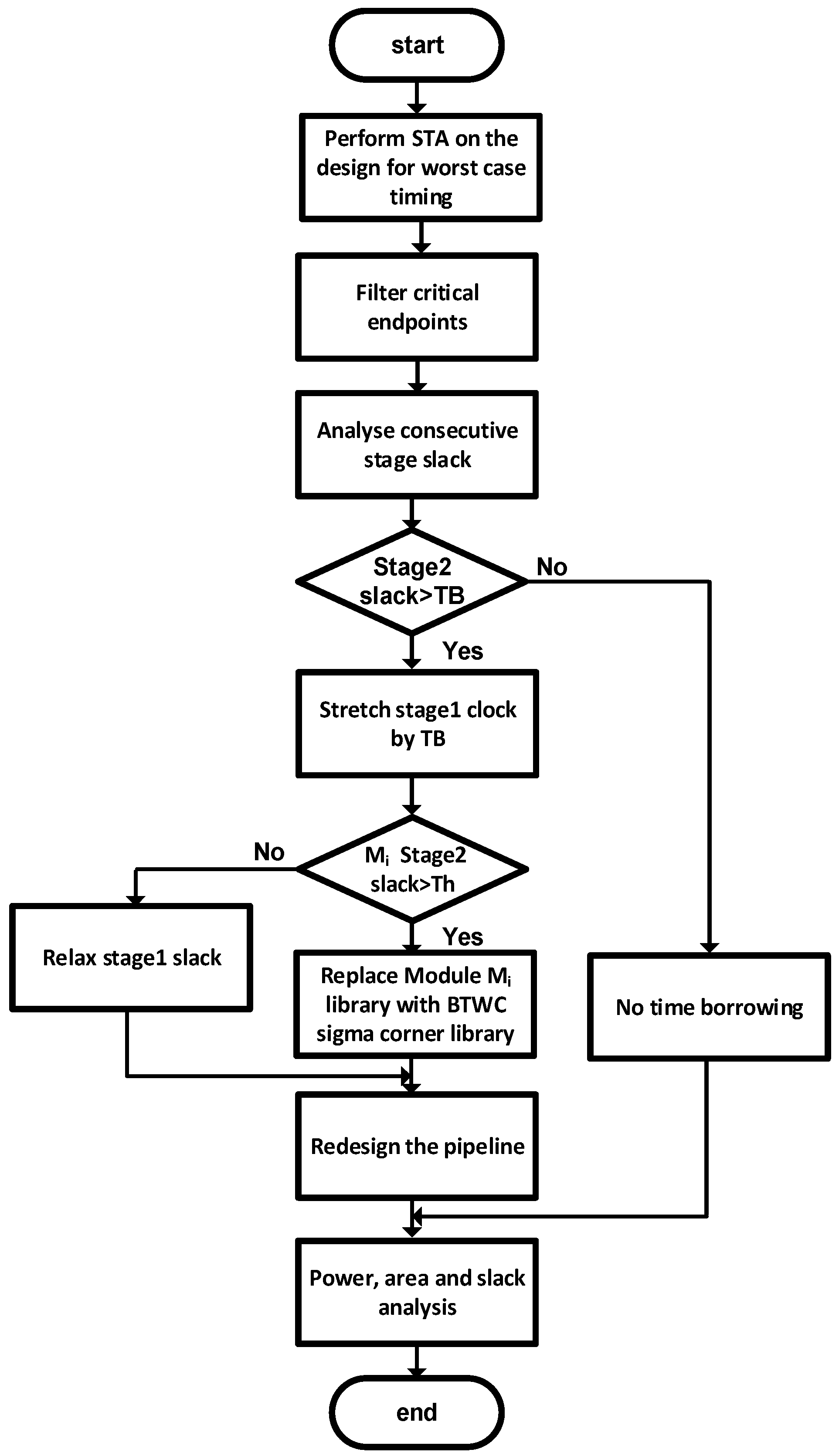
3.3. Design Flow

The proposed design flow using CSFF is shown in Figure 6. We take the processor design through Cadence RTL Compiler synthesis run and did the placement and optimization in Encounter. The design signed off at worst corner is taken as the baseline. We used the critical endpoints report and the slack report to filter those paths whose slack is below threshold T_h. After this, we analyze the consecutive stage slack of these critical endpoints and categorize them with a time borrowing window TB based on the slack available. This is followed by their clocks being stretched by DCK which is phase shifted by TB. In the next step, we optimize the combinational fan-in logic of those endpoints whose slack is relaxed. The logic modules for which all the critical paths have sufficient consecutive slack is filtered. The logic library of those modules is replaced by a BTWC sigma corner library and the pipeline is redesigned with the new library. For the other critical endpoints outside the module, the individual slacks are relaxed and the pipeline is re-synthesized based on the new slack. For benchmarking, we characterized 16 flavors of TIMBER [17] flip-flops using Cadence Liberate to compare the results of our approach with typical error resilience circuits. The BTWC sigma corner libraries were developed using Cadence Variety. We used Cadence Multi-bit flow to combine the flip-flops using add-on scripts during the synthesis phase.

4. Power Optimization Algorithm

The design complexity is high for advanced technology nodes. We need to tackle the power performance trade-offs in a more efficient way. In the previous works [27,28] we had already introduced the individual concepts of clock stretching and logic optimizations based on sigma corner and logic reshaping. In this paper we uncover how the effective combination of these techniques help in power and area savings. We introduce the combination of clock stretching with sigma corner optimization and we arrived at a strategy where every module uses either size based or sigma based optimization in order to achieve best savings. Once the design is reinforced with clock stretching circuits, we use custom logic power optimization techniques to achieve power and area savings without compromising the reliability. In this paper, we use logic reshaping and BTWC sigma corner libraries for power optimization.

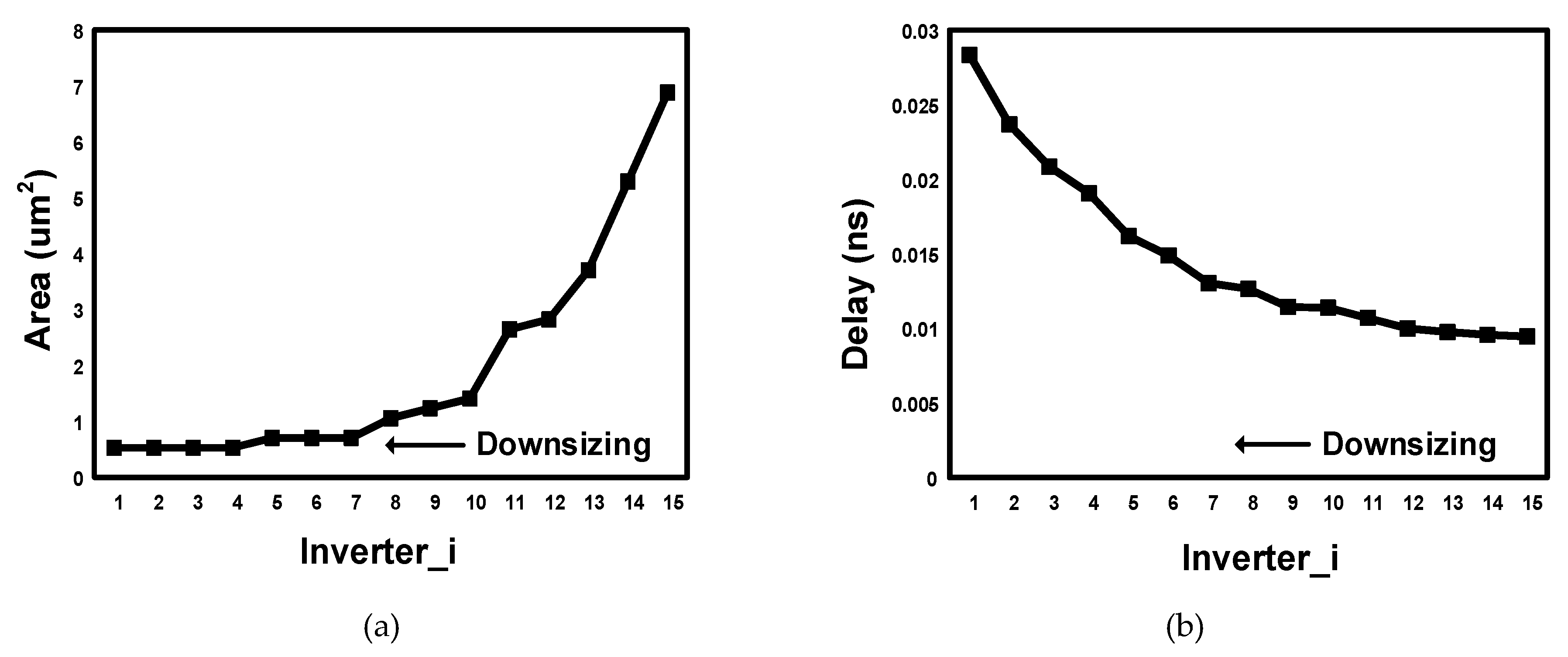
4.1. Power Optimization by Logic Reshaping (SizeOpt)

The critical path logic of typical worst case corner designs is made up of power and area hungry cells to meet the delay requirements. With rising design margins in advanced nodes, more power is spent on optimizing this logic to meet the guard bands. We propose a technique [27] to utilize available slack and redistribute it to the critical path logic using CSFF. This creates extra slack margins in the combinational paths preceding the critical endpoints. We leverage this slack to relax the path timing constraints. Once we relax the path slacks, we re-synthesize the pipeline. The synthesis tool picks smaller cell equivalents from the logic library which leads to smaller and fewer cells in the critical path resulting in power and area savings. The area reduction and delay increase resulting from the downsizing is depicted in Figure 7a,b respectively. The horizontal axis denotes the inverter serial number with different drive strengths. The extra slack margin helps to downsize the logic at the expense of cell delay increase. Algorithm 1 shows the pseudo code (SizeOpt) for the slack analysis and critical path reshaping. P represents the critical paths and S represents the corresponding consecutive slacks. For each critical path in P, we choose a DCK phase shift from TB = {TB1, TB2, TB3 or TB4}. We fix the TB value as a multiple of T_ck/8, with TB1 = T_ck/8, TB2 = T_ck/4, TB3 = 3T_ck/8 and TB4 = Tck/2 for our experiments. For reshaping, we relax the timing margin on selected paths by TB and resynthesize the logic so as to get power and area savings. This process relaxes the short paths as well as long path slacks in the critical fan-in. Thus, the short paths get the same delay increase as the long path. This prevents the need for additional buffers along the short paths.

Algorithm 1. Slack analysis & Downsizing (SizeOpt)

1.  ProcedureSizeOpt (Initial Netlist) 2.  Run STA to find critical paths P and consecutive slacks 3.  P ← Φ 4.  for all timing endpoints p in the netlist do 5.       if slack(p) < Th then 6.          P ← P U {p} 7.       end if 8.  end for 9.  for all TB = TB4, TB >= TB1, TB = TB − TB1 do 10.       for all p ∈ P do 11.          if consecutive slack (p) >= TB and < 2TB then 12.             Replace register CLK with stretched CLK, with DCK = TB 13.             Relax fan-in logic timing by TB 14.                 end if 15.          end for 16.  end for 17.  Redesign the pipeline and close timing 18.  Calculate Power and Area savings 19.       return (netlist)

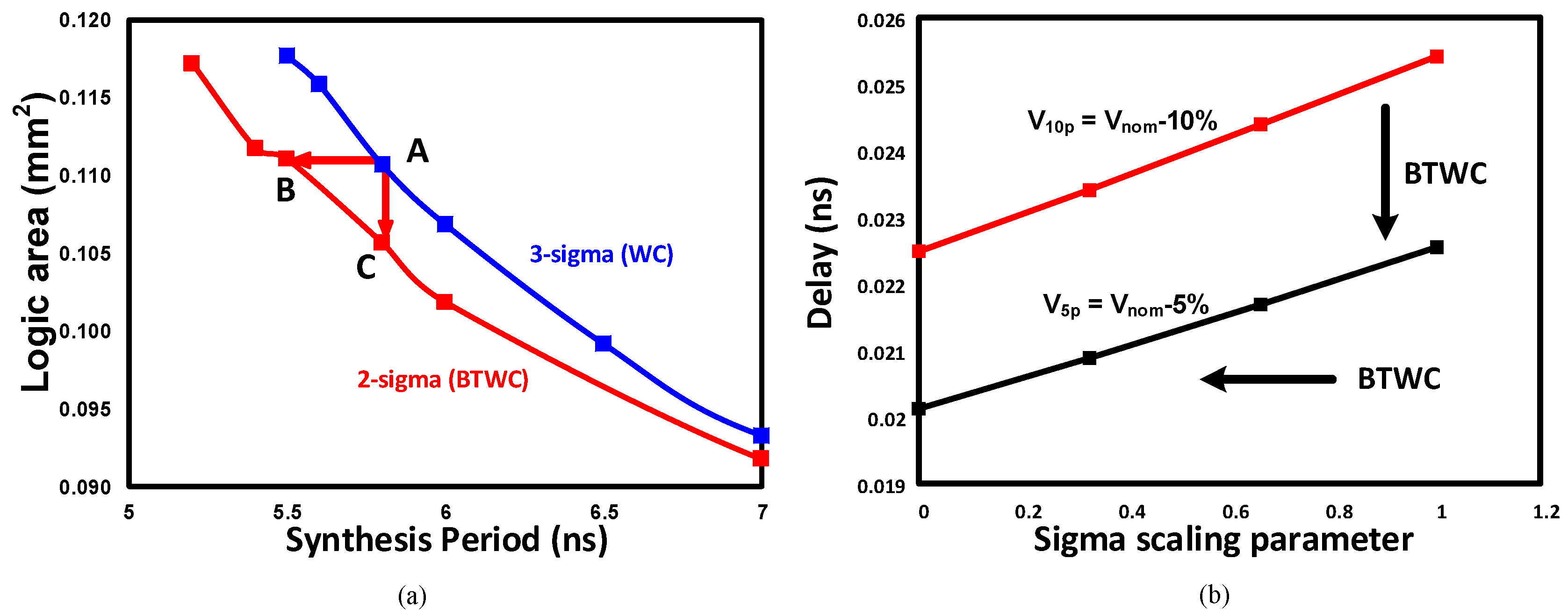
4.2. Power Optimization by Library Tuning (SigmaOpt)

In conventional design flows, we use worst-case libraries for timing sign off, which results in power and area overheads. So, we developed a BTWC sigma corner library with relaxed process and voltage corners. We used this library to synthesis design modules which has extra slack presence. After investigating the three-stage processor pipeline, we see that we have a module in the execute (EXE) pipeline stage in which all the critical paths (~390) have considerable slack in the consecutive stage as shown in Figure 8. We used the BTWC sigma corner library to design that logic module. Figure 9a shows the area speed trade-off for a typical processor pipeline for the worst case (WC) 3-sigma and a BTWC 2-sigma process library. The results show that for the same logic area, a BTWC design can be signed off at a higher frequency B than the 3-sigma design frequency A. Also for the same synthesis period, a 2-sigma design consumes a lesser logic area C compared to the logic area A of a 3-sigma design. This proves the area as well as power reduction capabilities of a BTWC sigma library design.

We characterized the libraries using different sigma parameters ranging from 0 to 1. The sigma parameter of 1 represents Sigma3 which is the worst-case corner with pessimistic design margins. Sigma2, Sigma1 and Sigma0 have scaling parameters of 0.66, 0.33 and 0, respectively, while Sigma0 is the optimistic library corner. Figure 9a shows the area and speed gain for Sigma2 compared to Sigma3. Each sigma corner library was characterized using two sets of voltage corners. The V_10p library variant represents the WC voltage corner and the V_5p version represents the BTWC voltage corner with relaxed voltage margins. Figure 9b shows the delay values of a standard inverter cell for the different library variants. As we sweep the sigma values right to left from WC sigma corner to BTWC corner, the inverter delay reduces. Also, when we tune the voltage from V_10p to V_5p corner, the inverter delay reduces. Thus, we achieve faster timing closure with fewer resources to meet the design margins. We use the BTWC corner libraries for power optimization while leveraging CSFFs for pessimistic worst-case variations in real silicon. Based on this, we propose an algorithm BTWC sigma library cell swap (SigmaOpt) for power optimization as shown in Algorithm 2. The procedure takes an Initial Netlist designed for worst case corners. The procedure runs static timing analysis and filters the paths P with slack less than a predetermined threshold Th. In our experiments, we mark paths with less than 2% slack margin as critical paths. The procedure looks for design modules M_i which can be relaxed by TB = {TB1, TB2, TB3 or TB4}. We use TB1 = T_ck/8, TB2 = T_ck/4, TB3 = 3T_ck/8 and TB4 = Tck/2 for our experiments. Once we find a module M_i which can be relaxed by TB, we use the clock stretcher to delay their clocks by TB. This is followed by swapping the critical fan in logic with a BTWC sigma corner library and redesigning the pipeline for power and area savings. Once a module is relaxed with the chosen sigma corner library, we look for other modules which satisfy the same consecutive slack criteria. This procedure generates a netlist netlist_sigma for the sigma corner input library set.

Algorithm 2. BTWC sigma library cell swap (SigmaOpt)

1.  ProcedureSigmaOpt (Initial Netlist) 2.  Run STA to find critical paths P and consecutive slacks 3.  P ← Φ 4.  for all timing endpoints p in the netlist do 5.          if slack(p) < Th then 6.             P ← P U {p} 7.          end if 8.  end for 9.  for all sigma = 0, sigma <= 2, sigma = sigma + 1 do 10.        for all I = 0, i <= m, i = i + 1 do 11.             if module Mi consecutive slack (Pi) >= TB then 12.                Replace register CLK with stretched CLK, with DCK = TB 13.                Swap the logic library with sigma library 14.                   end if 15.             end for 16.  Redesign the pipeline and close timing 17.  Calculate Power and Area savings 18.   return (netlistsigma) 19.  end for

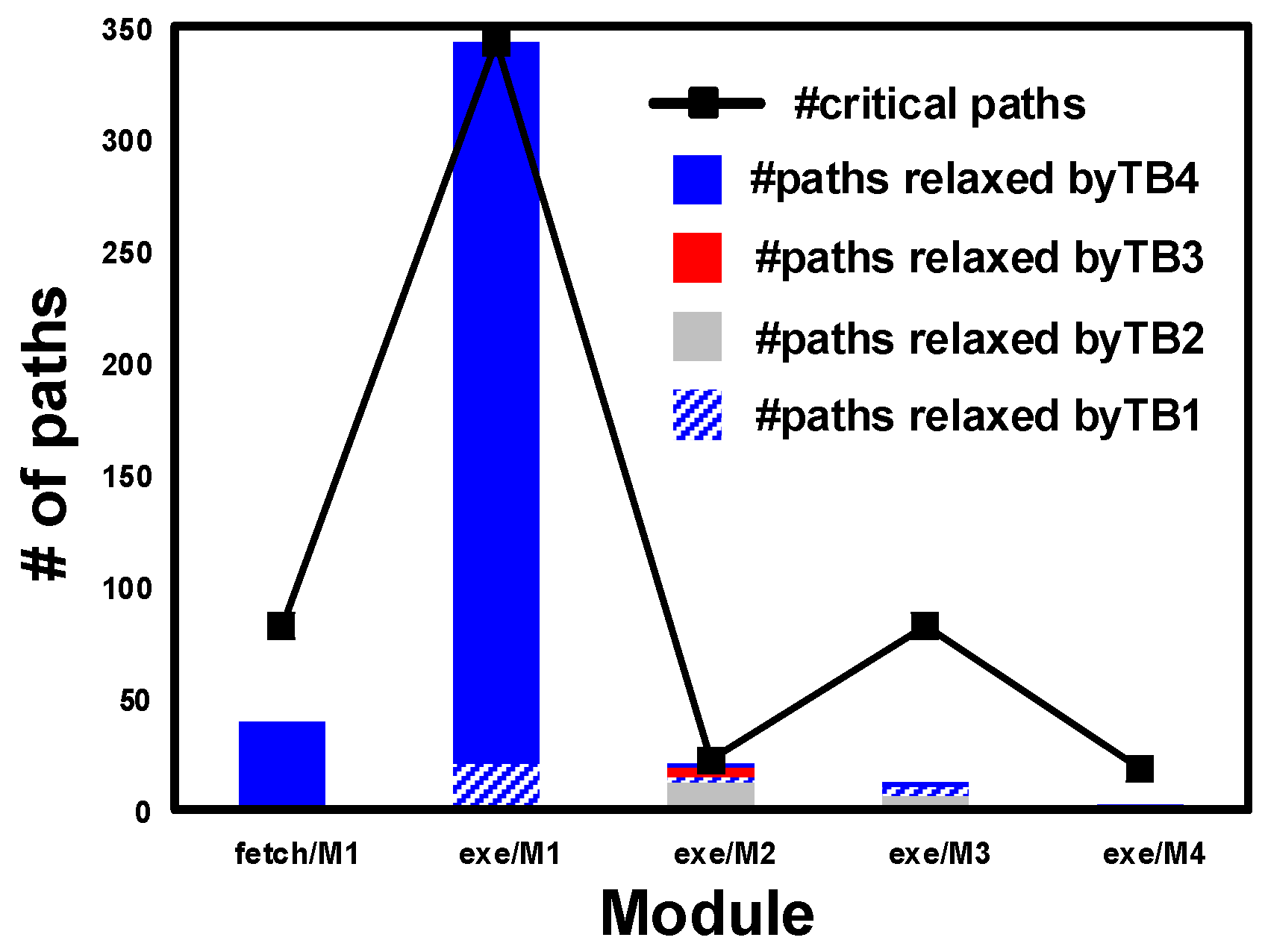
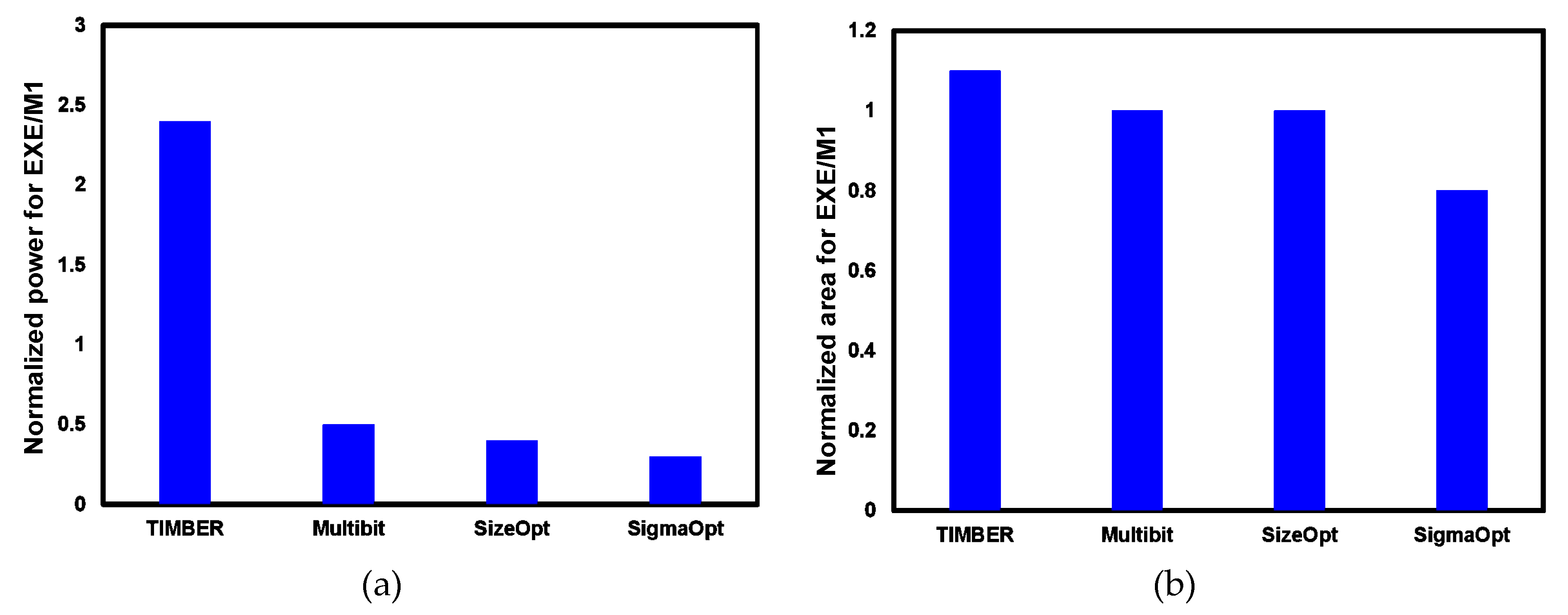
5. Results and Analysis

5.1. Flip-Flop Level Savings

We use a simplified flip-flop structure to balance the slack between different pipeline stages. Compared to the reference TIMBER [17] flip-flop, the proposed circuit is similar to a standard master-slave flip-flop which makes it easy for the design tools to use it in the design flow. An area reduction of 60% compared to TIMBER is attained per flip-flop for the proposed scheme.

Table 2. Power and Delay Savings of Proposed Circuit.

Variables	TIMBER FF	Proposed
C to Q delay rising	91.62ps	77.5ps
C to Q delay falling	91.83ps	80.67ps
Max power@ 1.1V	3.21uW	2.608uW
Min [email protected]	1.857uW	1.478uW

shows the flip-flop level savings in terms of C to Q delay, minimum power and maximum power compared to TIMBER. We get a rising C to Q delay reduction of 18.21%, falling C to Q delay reduction of 13.83%, maximum power saving of 23% and minimum power saving of 25.6% compared to the reference TIMBER flip-flop.

5.2. Chip-Level Savings

The proposed methodology is used to design the critical pipeline stages of an industrial processor. Power and area comparisons are being done against the baseline designed for worst case and with a TIMBER based error resilient architecture. The reference design (WC) used worst case 3-sigma process corner and 10% voltage variation (P_3sigma, V_10p) with normal MSFFs. TIMBER [17] based pipeline used the same worst process and voltage corner (P_3sigma, V_10p). Three power optimization techniques were used to achieve power and area savings against the worst-case baseline design. The Multibit technique combined the individual flip-flops in the design into dual bit and quad bit flip-flops. As shown in Figure 10, the fetch stage has 39 critical paths with sufficient consecutive slack and execute stage has 377 paths with sufficient slack. Module M1 in EXE stage has sufficient consecutive slack present in all the 343 critical paths. The SizeOpt technique used clock stretching and combinational logic reshaping along the critical paths with sufficient slack using the worst case 3-sigma process corner and 10% voltage variation (P_3sigma, V_10p). The SigmaOpt technique used clock stretching and 1-sigma process corner with 5% voltage variation (P_1sigma, V_5p) to design module M1 in the EXE pipeline stage.

Table 3. Power Savings of the Proposed Design Methodologies.

Power (µW)	Baseline			TIMBER			Multibit			SizeOpt			SigmaOpt
	Leakage	Dynamic	Total	Leakage	Dynamic	Total	Leakage	Dynamic	Total	Leakage	Dynamic	Total	Leakage	Dynamic	Total
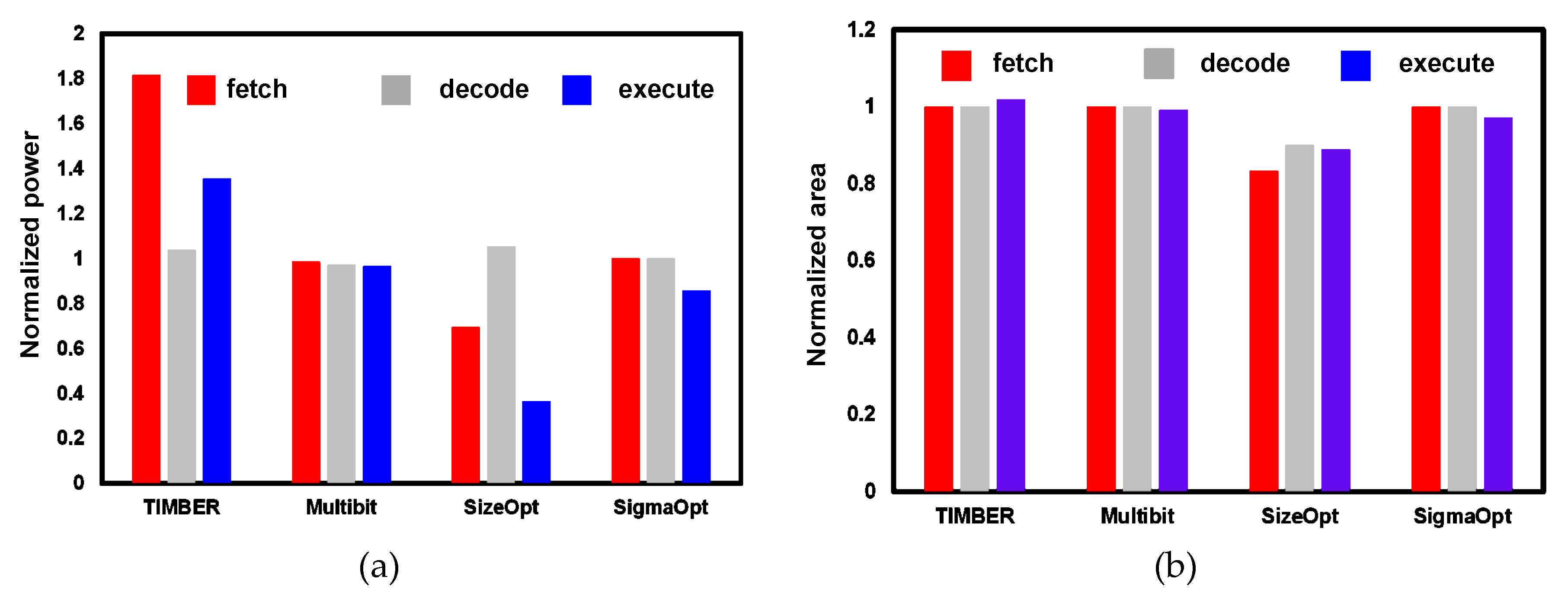
Fetch	1.5	265.1	266.6	1.5	482.4	483.9	1.5	261.2	262.7	1.1	184	185.1	1.5	265.1	266.6
Dec.	0.9	149.1	150	0.8	154.8	155.6	0.9	144.9	145.8	0.7	157.3	158	0.9	149.1	150
Exe.	14.8	1307.9	1322.7	14.7	1777.4	1792.2	14.8	1262.2	1277	11.2	471.7	482.9	15.5	1118.6	1134.1

shows the power comparison results between WC baseline, TIMBER and the proposed Multibit, SizeOpt and SigmaOpt schemes in the pipeline stages.

Table 4. Area Savings of the Proposed Design Methodologies.

Area (mm2)	Baseline				TIMBER				Multibit				SizeOpt				SigmaOpt
	#Cells	Cell	Net	Total	#Cells	Cell	Net	Total	#Cells	Cell	Net	Total	#Cells	Cell	Net	Total	#Cells	Cell	Net	Total
Fetch	1976	0.005	0.007	0.012	2014	0.005	0.007	0.012	1920	0.005	0.007	0.012	1751	0.004	0.006	0.01	1976	0.005	0.007	0.012
Dec.	1874	0.003	0.007	0.01	1900	0.003	0.007	0.01	1867	0.003	0.007	0.01	1796	0.003	0.006	0.009	1874	0.003	0.007	0.01
Exe.	16414	0.045	0.063	0.108	16356	0.047	0.063	0.11	15964	0.045	0.062	0.107	15053	0.038	0.058	0.096	15734	0.043	0.061	0.105

shows the area comparison between baseline, TIMBER and proposed schemes. Figure 11a,b shows the normalized power and area comparisons between TIMBER and the proposed schemes with respect to the worst case baseline. Power comparison results show 81% power overhead for TIMBER, 1.4% power savings for Multibit and 31% power savings for the SizeOpt in the fetch stage against the WC baseline design. In the execute pipeline stage, TIMBER has a power overhead of 36% compared to the baseline whereas the proposed schemes give a power saving of 3.5%, 63% and 37% for the Multibit, SizeOpt and SigmaOpt respectively. Area comparisons in the EXE stage show an area overhead of 2% for TIMBER and a saving of 1%, 11% and 3% respectively for the Multibit, SizeOpt and SigmaOpt schemes against the baseline.

The individual power and area comparison results in Figure 12a,b for module M1 in the EXE stage, shows the effectiveness of SigmaOpt in that module to reduce power and area. So in this work, we came up with an optimization strategy which use a combination of the individual techniques introduced in the previous literature [27,28]. The combined optimizations with multibit flip-flops, size optimization as well as sigma corner library represented by CombOpt gives an overall power and area savings as shown in

Table 5. Power Savings of the Proposed Design Methodologies.

Power (µW)	Baseline				TIMBER				CombOpt
	# of Cells	Leakage	Dynamic	Total	# of Cells	Leakage	Dynamic	Total	# of Cells	Leakage	Dynamic	Total
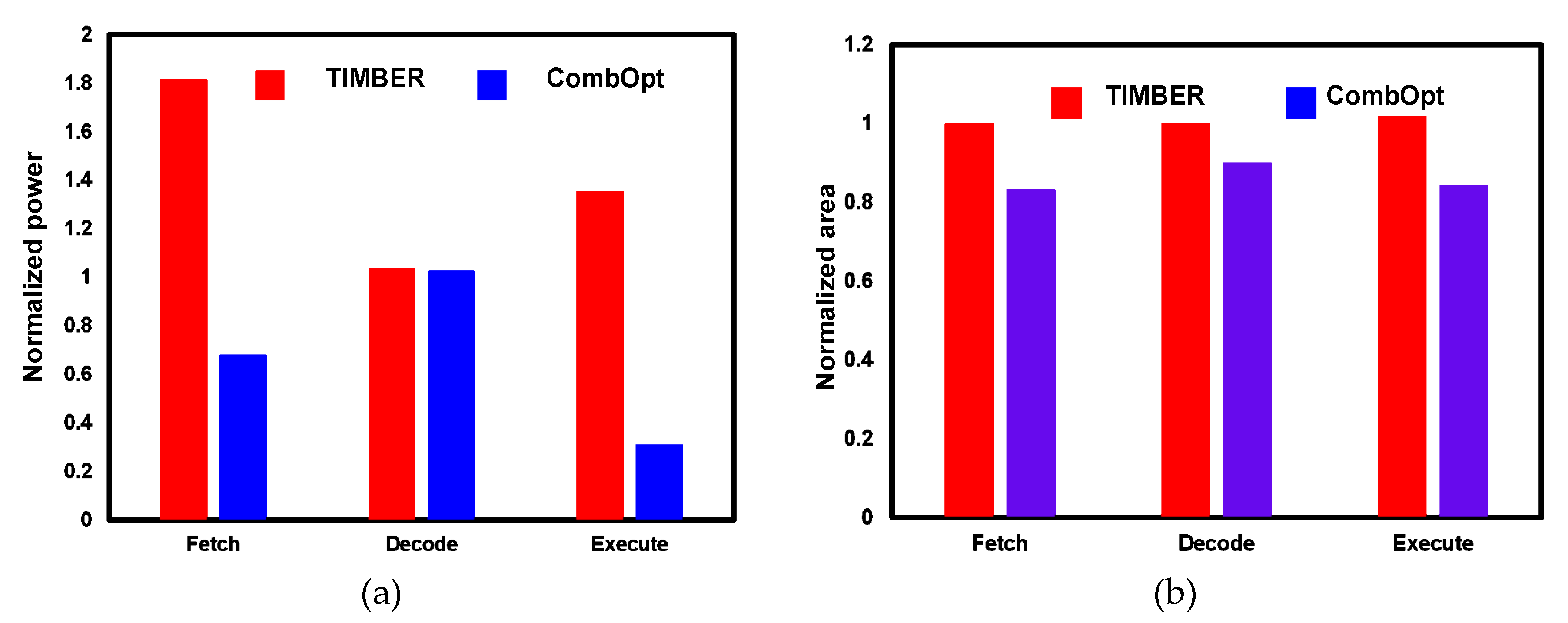
Fetch	1976	1.5	265.1	266.6	2014	1.5	482.4	483.9	1695	1.1	180.1	181.2
Dec.	1874	0.9	149.1	150	1900	0.8	154.8	155.6	1789	0.7	153.1	153.8
Exe.	16414	14.8	1307.9	1322.7	16356	14.7	1777.4	1792.2	14012	11.968	396.947	408.915

and

Table 6. Area Savings of the Proposed Design Methodologies.

Area (mm2)	Baseline				TIMBER				CombOpt
	# of Cells	Cell Area	Net Area	Total	# of Cells	Cell Area	Net Area	Total	# of Cells	Cell Area	Net Area	Total
Fetch	1976	0.005	0.007	0.012	2014	0.005	0.007	0.012	1695	0.004	0.006	0.01
Dec.	1874	0.003	0.007	0.01	1900	0.003	0.007	0.01	1789	0.003	0.006	0.009
Exe.	16414	0.045	0.063	0.108	16356	0.047	0.063	0.11	14012	0.035	0.056	0.091

respectively. Figure 13a,b shows the normalized power and area comparisons between TIMBER and the combined optimizations with respect to the worst case baseline. The combined optimizations give a power savings of 32% and 69% in the fetch and execute stages respectively. It also gives an area savings of 15% in the execute stage.

6. Conclusions

The proposed methodology retains the throughput advantages of error masking circuits and at the same time reduce the power/area overheads compared to TIMBER. The margins reclaimed by the slack aware clock stretching during design time is used to reshape the combinational circuits for power/area savings. The best optimization strategy is selected for the individual modules which results in best overall power and are savings from the combined optimizations. Experimental results show a power and area saving of 32% and 16% respectively in the fetch pipeline stage. In the execute stage we get a power and area saving of 69% and 15% respectively. On the other and speculative techniques like TIMBER have power and area overhead of 36% and 2% respectively in the execute pipeline stage. Timing closure is done at design time with respect to the stretched clock which removes meta-stability overheads. The combinational logic reshaping is done in such a way that it adds delay to the short paths as well which prevents the need for additional hold buffers. Moreover, the proposed technique does not exhibit the critical operating point behavior which makes it a reliable option for error resilience and power savings.