Abstract
A simple optimization strategy for the computation of 3D finite-differencing kernels on many-cores architectures is proposed. The 3D finite-differencing computation is split direction-by-direction and exploits two level of parallelism: in-core vectorization and multi-threads shared-memory parallelization. The main application of this method is to accelerate the high-order stencil computations in numerical relativity codes. Our proposed method provides substantial speedup in computations involving tensor contractions and 3D stencil calculations on different processor microarchitectures, including Intel Knight Landing.
1. Introduction
Numerical relativity (NR) is the art of solving Einstein’s equations of general relativity using computational physics techniques. The typical NR application is the simulation of strong-gravity astrophysical phenomena like the collision of two black holes or two neutron stars, and the core-collapse and explosion of massive stars. Those simulations are of primary importance for fundamental physics and high-energy astrophysics, including the emerging field of gravitational-wave and multi-messenger astronomy [,,]. Some of the open problems in the simulation of strongly gravitating astrophysical sources demand the modeling of the dynamical interaction between supranuclear-density, high-temperature matter [], and neutrino radiation in complex geometries []; the resolution of magnetohydrodynamical instabilities in global simulations [,]; and the production of accurate gravitational waveforms for many different physical settings [,].
Addressing these challenges will require significant computational resources and codes able to efficiently use them. For example, in the case of neutron star mergers, typical production simulations use few hundreds cores and require CPU-h to cover the dynamical timescale of the last orbits ( milliseconds of evolution). However, to fully capture hydromagnetic instabilities in the merger remnant, necessary to predict the electromagnetic signature of mergers, it would be necessary to increase the resolution in these simulations by more than a factor of ten. With current technologies, a simulation at this scale would require one billion CPU-hrs. Clearly, exascale resources are needed to perform these simulations.
Exascale high-performance computing, based on energy-efficient and heterogeneous architectures, offers the possibility to tackle some of the scientific challenges of relativistic astrophysics in the strong-gravity regime. On the technological side, the Intel Knight Landing (KNL) processor brings up most of the features required for the upcoming exascale computing, such as power efficiency, with large GFLOPS per watt ratios, and high peak performance, provided by the many-core architecture and by large vector instructions []. The KNL many-core architecture allows users to approach exascale systems with the standard MPI/OpenMP programming model that is standard for NR codes. More recently, Intel released the Skylake (SKL) processor microarchitecture that succeeds the Intel Broadwell (BDW) architecture and supports the same AVX-512 instruction set extensions as the KNL one. Vectorization has a key role since it introduces an increasing speedup in peak performance, but existing NR codes do require refactoring or even the introduction of new programming paradigms and new algorithmic strategies for the solution of Einstein equations.
This work discusses the first steps towards the implementation of a highly scalable code that will be dedicated to NR simulations for gravitational wave astronomy and relativistic astrophysics. The primary focus is on the vectorization of the basic kernels employed for the discretization of the spacetime’s metric fields. We consider the optimization of the computation of finite-differencing derivatives on a spatially uniform, logically Cartesian patch using high-order-accurate stencils in 3D. The problem has been discussed rarely since high-order finite-differencing operators are peculiar to NR applications, e.g., [,,,], but not often employed in other branches of relativistic astrophysics (but see [,] for an optimization discussion). Here, we propose an optimization strategy based on the use of OpenMP 4.0 PRAGMA and on two levels of parallelism: in-core vectorization and multi-threads shared memory parallelization.
2. Method
The general relativistic description of the spacetime (metric fields) plus matter and radiation fields reduces to solving an initial-boundary value problem with nonlinear hyperbolic partial differential equations (PDEs) in three spatial dimensions plus time (3 + 1 D).
A toy model equation for the metric fields, , is the tensor wave equation,
obtained by linearizing Einstein equations around a reference background , i.e., assuming with . In the above equations, are the spatial indices, the metric perturbation, the extrinsic curvature, and the Ricci tensor. The latter takes the form
where is the inverse background metric and a sum on k is understood (Einstein’s summation convention).
An even simpler toy model retaining all the key features is the 3D scalar wave equation,
The PDE system in Equation (1) is in a first-order-in-time and second-order-in-space form and mimics the conformal BSSNOK and Z4 free evolution schemes for general relativity [,,,]. Note that the basic operations of the right-hand side (RHS) of Equation (1) are derivatives, metric inversion, and contractions (i.e., multiplications, divisions, and sums).
The numerical solution of Equations (1) and (2) is based on finite differencing. The 3D flat space is discretized with a uniform Cartesian mesh of grid spacing and of size (n is hereafter referred as block-size). We indicate with the grid indices in the three directions and with the corresponding grid-node. Each component of the fields on a given grid-node is denoted by . The derivatives on the RHS, e.g., in the y-direction, are approximated by
where S is the size of the stencil, and are the finite-differencing coefficients reported in Table 1, and the error terms scale as . Similar expressions hold for the other directions. Mixed derivatives are approximated by the successive application of 1D finite differencing operators. The method of lines and standard explicit integration algorithms are then used to time-update the state vector , composed of all the field components, with evolution equations in the form . Our work focuses on the optimization of the finite differencing kernel and tensor contractions for the computation of the RHS of these equations.

Table 1.
Coefficients of 1D finite differencing stencils for the evaluation of first (, top) and second (, bottom) derivatives according to Equation (3), up to a stencil size . Stencils are symmetric with respect to 0.
Our global strategy for the RHS computation is composed of two levels: (i) in-core vectorization, that takes advantage of single instruction multiple data (SIMD) parallelism on aligned memory; and (ii) multi-thread and shared-memory parallelism of the outer loops. The second level splits RHS evaluations in block of operations (derivatives, contractions, etc.) in order to fit instructions and data cache. We expect the latter optimization to be particularly important for the Einstein equations, where the RHS evaluation involves accessing tens of grid functions.
The x-direction is the only one where elements are contiguous in memory; thus, SIMD parallelization is only possible along its fastest running index. The other two directions are accessed as u[ijk + s*dj] or u[ijk + s*dk], where dj and dk . Thus, for the approximation of the derivatives in the y- and z-directions, stridden memory access is unavoidable. Instead of using vector instructions to evaluate Equation (3), we vectorize the code by grouping together points in the x-direction, i.e., the derivatives in the y-direction are computed as:
where V is the size of the vector register, e.g., 8 on KNL nodes when computing in double precision. This simple in-core parallelization strategy is then combined with threading for out-of-core, but in-node parallelism using the OpenMP library. Note that our implementation requires the additional storage of 1D arrays with temporary data. However, for typical block-sizes ( or larger), the additional memory requirements are negligible, even when storing hundreds of grid functions.
A pseudo code of our RHS implementation is the following:

To ensure optimal performance of our code, we perform aligned memory allocation at 64 bit boundaries and we ensure that the block-size is a multiple of the vector size. This avoids the need for and the use of remainder loops. Note that avoiding reminder loops is also necessary to ensure the exact reproducibility of the calculations. The block-size is fixed and set at a compilation stage.
3. Experimental Setup
The above method is tested on BDW, KNL and SKL nodes of the Marconi cluster at CINECA, and on BDW and KNL nodes of the High-Performance-Computing (HPC) data center at the University of Parma. The characteristics of the nodes are listed in Table 2.

Table 2.
Characteristics and performance of the BDW, KNL, and SKL nodes used for the tests.
We consider independent implementations of the scalar wave and linearized Einstein equations and exploit the auto-vectorization capabilities of the Intel compiler combined with the introduction of the PRAGMA SIMD statement. This approach strikes a balance between performance and code portability. The specific options for auto-vectorization that we employed with Intel C/C++ compiler v.17.0.2 are:
icc -O3 -xCORE-AVX2, # do Vectorization on BDW,
icc -O3 -xCORE-AVX512, # do Vectorization on SKL,
icc -O3 -xMIC-AVX512, # do Vectorization on KNL,
icc -O3 -no-vec -no-simd, # do not Vectorize.
Note that, in order to completely disable vectorization, we use the options -no-vec for compiler auto-vectorization and -no-simd to disable the PRAGMA SIMD statements.
While our main results focus on the Intel compiler, Appendix A reports some early tests performed with the GNU compiler.
The data is stored in contiguous arrays of float or double precision data types. In this work, we use double precision, as commonly done in current production codes to avoid issues due to the accumulation of floating point errors over the timesteps of a typical simulation. Appendix B reports results comparing float and double precision data types.
4. Results
4.1. Wave Equation
We explore the performance of our method on BDW, KNL and SKL architectures using the wave equation implementation. Comparative tests on a single core/thread on those architectures are first considered for variable block-sizes, up to points, and with focus on vectorization performance. Multi-thread performance and strong OpenMP scaling are then analyzed with a fixed block-size of points. The speed of our implementation is measured in terms of Million cells updates per second. The results of this section refer to the speed of the whole program that is dominated by the RHS evaluation.
The results relative to the single core optimization are shown in Figure 1. Without vectorization, the speed on the KNL core is about a factor 3 smaller than on the BDW core; and the speed on the latter is about 20% smaller than that on the SKL core. When vectorization is enabled, we find a speedup of 1.5 on BDW, of 2 on SKL, and of 4 on KNL. This in-core optimization results are about half the theoretical maximal speedup of a single core due to the vectorization: 8× for KNL/SKL and 4× for BDW.
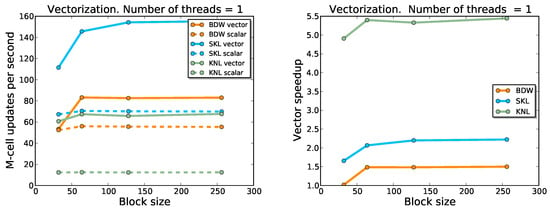
Figure 1.
Single-core performances (left panel) and speedup (right panel) for variable block-sizes and different node architectures, in the case of the wave equation with stencil size . The tests have been executed with vectorization enabled (solid lines) or disabled (dashed lines). The best performance is obtained for vectorized kernel on SKL nodes.
We stress that all data fit in the L3 cache memory on the considered architectures. Moreover, the vectorization efficiency improves even for smaller block-sizes, which fit the L2 and/or L1 cache. As a consequence, the sub-optimal performance of our implementation cannot be ascribed to the memory speed alone, at least in the single thread case (see below for a discussion of possible memory access inefficiencies in the multi-threaded case).
Table 3 reports speedup measurements on the two main operations of the RHS (contraction and derivatives). Such numbers differ by about a factor 2 or more from the potential speedup reported by the compiler at compilation time (also reported in the table). Performances are stable for variable block-sizes as long as the number of floating point operations dominates the computation (). Our results are in line with those reported by Intel in a similar test [].

Table 3.
Vectorization speedup on single cores for the wave equation with stencil size . The block-size is . The table shows the Intel compiler report information (obtained with the -qopt-report options) and the measured speedup (ratio between non-vectorized and vectorized execution time). The measured speedup differs by about a factor 2 or more from the potential speedup.
The results relative to the multi-thread optimization are shown in Figure 2. The block-size employed for these tests is .
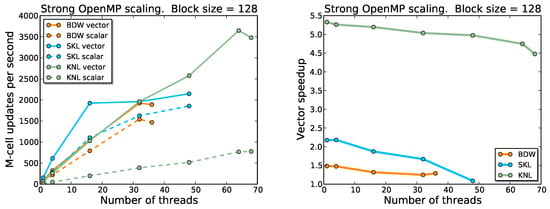
Figure 2.
Multi-thread performances (left panel) and speedup (right panel) for block-size as a function of the number of threads and for different node architectures, in the case of the wave equation with stencil size . Solid and dashed lines refer to enabled and disabled vectorization, respectively. The KNL node demonstrates better speedup, overall performance and scalability, especially in case of large block-sizes.
Scaling on BDW and SKL nodes is close to ideal until 16 threads; then, we observe a drop of the performance even when running on 32 physical cores. On the other hand, the KNL node shows a sustained speedup (about 4×) up to 64 physical cores, and performance remains good also with hyper-threading enabled (not shown in the figure). The use of the KNL node can, in principle, speedup computations by more than a factor of 2 with respect to BWD and SKL architectures when the kernel works on sufficiently large block-sizes. Note, however, that the use of is unrealistic for numerical relativity application since one would be memory limited in that case.
Strong scaling with multiple threads of our vectorized code depends mainly on the available memory bandwidth when accessing data requested by the stencil code. A high data re-use rate would hit the local L1 or L2 cache, with high memory bandwidth. In order to optimize the re-use of data in cache, we used the KMP_AFFINITY environment variable to bind adjacent threads to adjacent cores on the same socket. On the KNL node, we used the Scatter mode since the hyper-threading was enabled (see Figure 3). On SKL and BDW nodes, we used the Compact mode.
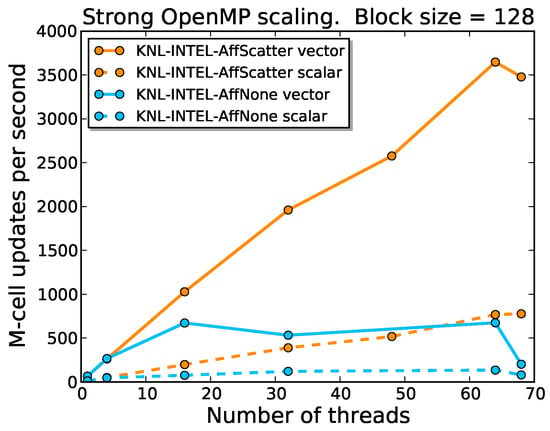
Figure 3.
Effect of pinning threads to KNL cores. The affinity is controlled by the KMP_AFFINITY environment variable. Cyan lines refer to KMP_AFFINITY=none, orange lines to KMP_AFFINITY=scatter.
Although the L2 cache on the KNL architecture can host the allocation of the vectorized x-direction (the memory pattern amounts to bytes), an L2 cache miss can happen when processing stencil data with different x-values.
In this case, data belonging to other tiles can be found in the L2 cache through the Caching/Home Agent (CHA) architecture or in the Multi-Channel Dynamic Random-Access Memory (MCDRAM), depending on the configured Cluster Mode and on the total memory, which amount to bytes. The MCDRAM can be used as a cache memory if the node is configured in Cache Mode. If the node is in Flat Mode, it is possible to allocate data on MCDRAM through the High-Bandwidth Memory (HBM) library or through the memory affinity control provided by the numactl tool. We tested different MCDRAM modes achieving the same results since the MCDRAM is rarely involved.
The optimal KNL multi-thread scalability with respect to the BDW and SKL cases, presented in Figure 2, is due to the good performance in the L2 cache miss management through the CHA architecture. These results are obtained using the omp for directive with the following clauses:
#pragma omp for collapse(1) schedule(static,1).
The reason for this choice is that adjacent x-arrays (i.e., arrays in the y-direction) are processed simultaneously by adjacent cores and this guarantees a fast data communication for this type of L2 cache miss. Furthermore, in our production codes, OpenMP is employed on Cartesian blocks of fixed size given by distributed paralleization; dynamical OMP allocation is not effective in that context.
4.2. Linearized Einstein Equations
Let us now discuss the results on linearized Einstein equations.
Besides stencil operations, the numerical solution of Einstein’s equations also requires the evaluation of many tensor operations, such as the contraction of tensor indices and the inversion of small 3 × 3 or 4 × 4 matrices. Since these operations are local to each grid point and involve the multiple re-use of data already in cache, they can be more efficiently vectorized. The linearized Einstein equations are not as algebraically complex as their fully nonlinear counterpart, but can give an indication of the speedup that could be achieved with vectorization in a production simulation.
We perform a study of the performance of our vectorization and threading strategies for the linearized Einstein equations using the same compiler options as in Section 4.1. The tests are performed using a single KNL node on CINECA Marconi. Our results are summarized in Figure 4 and Figure 5.
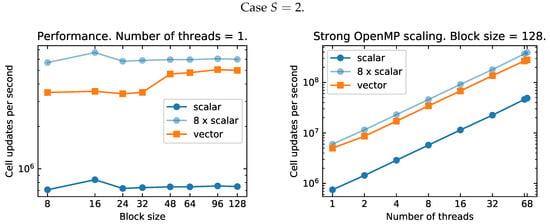
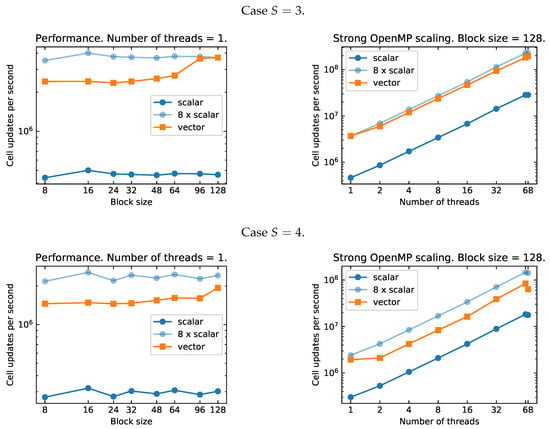
Figure 4.
Single-core performance on the KNL architecture, as a function of the block-size (left panels), and strong scaling with OpenMP, as a function of the number of threads (right panels), for the linearized Einstein equations with different stencil sizes (top: , middle: , bottom: ). We find nearly ideal vector speedup and scaling for large block-sizes. However, the code performances appear inconsistent when using all the 68 physical cores on the node, possibly because of the effect of system interrupts.
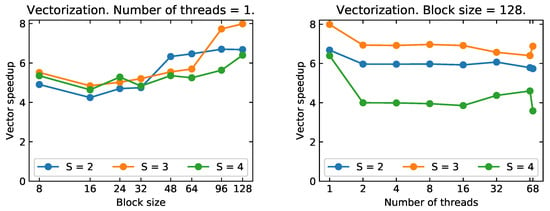
Figure 5.
Vectorization speedup for the linearized Einstein equations for , , and stencil sizes on the KNL architecture. Left panel: single core vector speedup. Right panel: vector speedup for increasing thread count. Good vector efficiency is achieved for large block-sizes, even though the speedup due to vectorization shows an unclear trend with S. The results when using 68 threads might be affected by system interrupts.
The single core performances are very encouraging, especially for large block-sizes. Indeed, on a single core, the vectorized code can achieve close to a factor speedup over the non-vector version of our code. This is the theoretical maximum speedup for double precision calculations if fused math-addition operations are not used. Even for smaller block-sizes, down to , we achieve a speedup factors of . This shows that vectorization would be very beneficial also for production simulations, where the block-sizes are typically or smaller.
When multi-threading, the speedup due to vectorization is somewhat worse. On the one hand, this is expected because each thread operates on a smaller sub-block of the data. On the other hand, when comparing vector speedups with threading to those obtained in an equivalently smaller single core case, we typically find worse speedups in the former case (see Figure 5). This might indicate that the default tiling employed by OpenMP is not efficient. Improvements could be obtained either by tuning the tiling, or by switching to a coarse grained parallelization strategy also for OpenMP. The latter could be, for example, to map threads to individual (small) blocks.
We extended our OpenMP scaling tests all the way up to 68 cores, thus using all of the physical cores on a KNL node. However, we find the results with 68 threads to be somewhat inconsistent between runs: sometimes running on 68 threads yields a speedup and sometimes a slowdown. We find that leaving four physical cores dedicated to OS and IO tasks result in more predictable performances. Consequently, we do not plan to perform simulations using more than 64 OpenMP threads on the KNL architecture. Nevertheless, in Figure 4 and Figure 5, we show the results obtained with 68 threads for completeness.
5. Conclusions
Motivated by the future need of developing a highly scalable code for NR application on exascale computing resources, we have introduced and tested an optimization strategy to calculate 3D finite-differencing kernels on different many-core architectures, including BDW, KNL and SKL. The proposed method can be implemented with a minimal programming effort on existing NR codes. It gives substantial speedup of both contraction and 3D stencil computations on BDW, KNL and SKL architectures.
Our optimization of finite differencing kernels employing auto-vectorization delivers results comparable to those reported by Intel experts in []. The latter work proposes similar strategies, although the best performances are obtained by heavily using intrinsic instructions. This approach would, however, hinder the portability of the code to other architectures, and make the codebase less easily accessible to numerical relativists and astrophysicists lacking formal training in computer science.
Tensor contractions could be further optimized with the use of dedicated libraries, e.g., [,,,]. As noted in [,], however, the performance improvement is neither obvious nor guaranteed because compilers optimization are very effective on explicitly coded loops. Additionally, such libraries are typically optimized for simple operations on tensors with large dimensions. On the contrary, in NR, the tensors’ dimensions are small (), but the expressions are algebraically complex. Furthermore, those tensor libraries do not appear to be sufficiently mature to be used as the central building block of large multi-physics software packages.
Future work will be also focused on improving the multi-thread performances of our approach. For example, the introduction of the loop tiling technique would guarantee a better exploitation of the cache. In particular, an appropriate tile size would maximize the number of hits in the L1 cache.
Author Contributions
S.B. and D.R. conceived and designed the project; A.R. performed the analysis of the wave equation code at CINECA and Parma; S.B. implemented the wave equation code; D.R. implemented the linearized Einstein code and performed the analysis of the linearized Einstein code at CINECA; A.P. performed the analysis of the wave equation code at CINECA; and all authors contributed to discussion and paper writing.
Funding
This research was funded by European Research Council Starting Grant number BinGraSp-714626.
Acknowledgments
D.R. acknowledges support from a Frank and Peggy Taplin Membership at the Institute for Advanced Study and the Max-Planck/Princeton Center (MPPC) for Plasma Physics (NSF PHY-1523261). Computations were performed on Marconi/CINECA (PRACE proposal 2016153522 and ISCRA-B project number HP10B2PL6K), and on the HPC facility of the University of Parma, Italy.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GFLOPS | Billion FLoating Point Operations Per Second |
| BDW | Intel Broadwell architecture |
| CHA | Caching/Home Agent |
| KNL | Intel Knight Landing architecture |
| HBM | High-Bandwidth Memory library |
| HPC | High-Performance-Computing |
| MCDRAM | Multi-Channel Dynamic Random-Access Memory |
| MPI | Message Passing Interface |
| NR | Numerical Relativity |
| OpenMP | Open Multiprocessing |
| RHS | Right-hand side |
| SIMD | Single Instruction Multiple Data |
| SKL | Intel Skylake architecture |
Appendix A. Results with GNU Compiler
We report on comparative tests between the Intel C++ Compiler and the GNU Compiler Collection on the KNL architecture.
The tests employ the wave equation implementation with block-size . The options used with GNU Compiler Collection v.6.1.0 are:
gcc -O3 -mavx512f -mavx512cd -mavx512er -mavx512pf, # do Vectorization on KNL,
gcc -fno-tree-vectorize, # do not Vectorize.
In both cases, we used the OpenMP thread affinity environment variables:
OMP_PROC_BIND=true,
OMP_PLACES=cores.
The same code is executed using different compilers on a variable number of threads and vector speedup results are reported in the left panel of Figure A1.
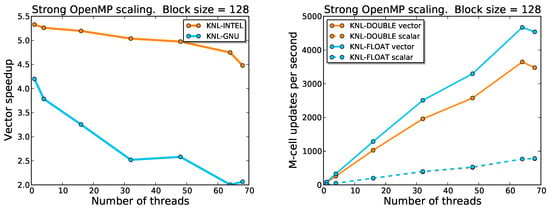
Figure A1.
Left panel: Comparative performance on vectorization and OpenMP parallelization between GNU and Intel compilers on KNL nodes. The speedup is the ratio between non-vectorized and vectorized execution time. Right panel: Strong scaling with multiple threads using single and double precision floating-point numbers. Dashed lines, corresponding to non-vectorized runs, are overlapping. In the case of vectorized runs, the speedup with single precision floating-point numbers is about 30% better than with double precision ones.
Speedup and overall performance with the GNU compiler are worse than with Intel. Exploiting auto-vectorization efficiently with the GNU compilers on KNL architectures seems to require more work; for this reason, we have first decided to focus on Intel compilers. We stress that this does not represent an actual limitation since Intel compilers are usually used in production runs on Intel machines rather than GNU compilers.
Appendix B. Results with Float Data Types
Although in current production codes blocks are stored using double precision floating-point numbers (see Section 2), we evaluated the additional speedup when using float data type. The right panel of Figure A1 shows that, for float data type, the speedup is 30% larger than the speed up obtained with double data type. This result is partially explained by the larger number of vectors (16 instead of 8).
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. 2017, 848, L12. [Google Scholar] [CrossRef]
- Radice, D.; Bernuzzi, S.; Del Pozzo, W.; Roberts, L.F.; Ott, C.D. Probing Extreme-Density Matter with Gravitational Wave Observations of Binary Neutron Star Merger Remnants. Astrophys. J. 2017, 842, L10. [Google Scholar] [CrossRef]
- Perego, A.; Rosswog, S.; Cabezon, R.; Korobkin, O.; Kaeppeli, R.; Arcones, A.; Liebendoerfer, M. Neutrino-driven winds from neutron star merger remnants. Mon. Not. R. Astron. Soc. 2014, 443, 3134–3156. [Google Scholar] [CrossRef]
- Radice, D. General-Relativistic Large-Eddy Simulations of Binary Neutron Star Mergers. Astrophys. J. 2017, 838, L2. [Google Scholar] [CrossRef]
- Kiuchi, K.; Kyutoku, K.; Sekiguchi, Y.; Shibata, M. Global simulations of strongly magnetized remnant massive neutron stars formed in binary neutron star mergers. arXiv, 2017; arXiv:1710.01311. [Google Scholar]
- Bernuzzi, S.; Nagar, A.; Thierfelder, M.; Brügmann, B. Tidal effects in binary neutron star coalescence. Phys. Rev. 2012, D86, 044030. [Google Scholar] [CrossRef]
- Bernuzzi, S.; Nagar, A.; Dietrich, T.; Damour, T. Modeling the Dynamics of Tidally Interacting Binary Neutron Stars up to the Merger. Phys. Rev. Lett. 2015, 114, 161103. [Google Scholar] [CrossRef] [PubMed]
- Sodani, A.; Gramunt, R.; Corbal, J.; Kim, H.S.; Vinod, K.; Chinthamani, S.; Hutsell, S.; Agarwal, R.; Liu, Y.C. Knights Landing: Second-Generation Intel Xeon Phi Product. IEEE Micro 2016, 36, 34–46. [Google Scholar] [CrossRef]
- Brügmann, B.; Gonzalez, J.A.; Hannam, M.; Husa, S.; Sperhake, U.; Tichy, W. Calibration of Moving Puncture Simulations. Phys. Rev. 2008, D77, 024027. [Google Scholar] [CrossRef]
- Husa, S.; González, J.A.; Hannam, M.; Brügmann, B.; Sperhake, U. Reducing phase error in long numerical binary black hole evolutions with sixth order finite differencing. Class. Quantum Gravity 2008, 25, 105006. [Google Scholar] [CrossRef]
- Radice, D.; Rezzolla, L.; Galeazzi, F. Beyond second-order convergence in simulations of binary neutron stars in full general-relativity. Mon. Not. R. Astron. Soc. 2014, 437, L46–L50. [Google Scholar] [CrossRef]
- Bernuzzi, S.; Dietrich, T. Gravitational waveforms from binary neutron star mergers with high-order weighted-essentially-nonoscillatory schemes in numerical relativity. Phys. Rev. 2016, D94, 064062. [Google Scholar] [CrossRef]
- Borges, L.; Thierry, P. 3D Finite Differences on Multi-Core Processors. 2011. Available online: https://software.intel.com/en-us/articles/3d-finite-differences-on-multi-core-processors (accessed on 23 May 2018).
- Andreolli, C. Eight Optimizations for 3-Dimensional Finite Difference (3DFD) Code with an Isotropic (ISO). Intel Software On-Line Documentation. 2014. Available online: https://software.intel.com/en-us/articles/eight-optimizations-for-3-dimensional-finite-difference-3dfd-code-with-an-isotropic-iso) (accessed on 23 May 2018).
- Baumgarte, T.W.; Shapiro, S.L. On the numerical integration of Einstein’s field equations. Phys. Rev. 1999, D59, 024007. [Google Scholar] [CrossRef]
- Nakamura, T.; Oohara, K.; Kojima, Y. General Relativistic Collapse to Black Holes and Gravitational Waves from Black Holes. Prog. Theor. Phys. Suppl. 1987, 90, 1–218. [Google Scholar] [CrossRef]
- Shibata, M.; Nakamura, T. Evolution of three-dimensional gravitational waves: Harmonic slicing case. Phys. Rev. 1995, D52, 5428–5444. [Google Scholar] [CrossRef]
- Bernuzzi, S.; Hilditch, D. Constraint violation in free evolution schemes: Comparing BSSNOK with a conformal decomposition of Z4. Phys. Rev. 2010, D81, 084003. [Google Scholar]
- Landry, W. Implementing a high performance tensor library. Sci. Program. 2003, 11, 273–290. [Google Scholar] [CrossRef]
- Solomonik, E.; Hoefler, T. Sparse Tensor Algebra as a Parallel Programming Model. arXiv, 2015; arXiv:1512.00066. [Google Scholar]
- Huang, J.; Matthews, D.A.; van de Geijn, R.A. Strassen’s Algorithm for Tensor Contraction. arXiv, 2017; arXiv:1704.03092. [Google Scholar]
- Lewis, A.G.M.; Pfeiffer, H.P. Automatic generation of CUDA code performing tensor manipulations using C++ expression templates. arXiv, 2018; arXiv:1804.10120. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).