A 4.1 W/mm² Hybrid Inductive/Capacitive Converter for 2–140 mA-DVS Load under Inductor ^†

Abstract

This work presents a fully integrated hybrid inductive/capacitive converter maintaining high efficiency for a load range of 2 mA to 140 mA (70×) suitable for the dynamic voltage scaling (DVS) based loads. This high efficiency is achieved by using an inductive converter for higher loads (15–140 mA, 0.50–0.9 V) and a capacitive converter for lighter loads (2–5 mA, 0.40–0.55 V) with a 50 mV hysteresis margin. A digital state machine activates the appropriate converter based on the power efficiency and enables the converter hand-over. The functional feasibility of implementing digital circuits as representative loads under the inductor is shown thereby increasing the peak converter power density from 0.387 W/mm² to 4.1 W/mm² with only a minor hit on the efficiency. The maximum measured efficiency is achieved in inductive mode of operation and decreases from 76.4% to 71% when digital circuits are present under the inductor. The design was fabricated in IBM’s 32 nm SOI technology.

1. Introduction

The demand for smaller form factors coupled with longer battery operation places stringent requirements on the power dissipation of integrated circuits in battery powered devices. Due to the comparatively slower improvement in the ampere-hour capacity of batteries, there is increased pressure on circuit designers to achieve greater battery life from existing battery technology. Device scaling reduces the parasitic capacitance being switched and hence reduces dynamic power dissipation. However, scaling has led to packing more and more processing power in a single die which exacerbates power management problem [1]. Dynamic voltage frequency scaling (DVFS) is one of the most widely used techniques to reduce power dissipation in digital circuits [2]. The power savings achieved in a DVFS based system becomes evident when we observe the that the power has a cubic dependence on the supply voltage [3] as shown in Equation (1).

$$P=C_{tot}{V}_{DD}^2\frac{I}{C_{tot}{V}_{DD}}\propto V_{DD}^{\sim 2-3}$$

(1)

Increased device leakage is becoming more and more serious with scaling [4]. Leakage in digital circuits can be reduced to a great extent by reducing the supply voltage [5]. Additionally, the frequent state change from standby mode to active mode and the small durations spent in each mode necessitates rapid transition times. The above application space sets the goals for a voltage regulator powering digital circuits. The regulator along with being highly efficient needs to have fast transient response and wide output power range. Research in the field of computer architecture has shown that power savings is achieved by applying DVFS in a fine grained manner [6,7]. This adds additional constraint on the power delivery network design to be able to support multiple independent voltage domains. Though on-board discrete component based regulators are highly efficient they are not well suited to support more than a few independent domains. Figure 1 shows the primary motivation for developing fully integrated DC-DC conversion solutions which are able to cater to a high output power range while maintaining both high efficiency and high power densities in DVFS loads. The regulator is also required to be area efficient and provide high power density to make the solution cost effective.

Previous work in this area [3,8,9,10,11,12,13,14] have attempted to achieve this goal but either had limited output power ranges or displayed degraded efficiency at lower output voltages. Other works such as [15,16] have shown very high power densities but need additional fabrication steps to build the inductor in the interposer or the package substrate which increases the cost of the overall system. Recently, capacitive converters using high density trench capacitors have shown very high power density and efficiency [17]. However, in a capacitor converter the capacitor size has to increase linearly with load current for a given maximum operating frequency [18]. In contrast, we use a switched inductor converter for high power and switched capacitor converter for low powers. We show in Section 2 that an inductor can be placed above the digital circuits, hence achieving high power density.

Some details of this fully integrated hybrid converter for DVS loads were presented in [19]. Also some variations of hybrid converter had been reported in works [20,21,22]. In this design for a DC-DC converter a capacitive converter is used to support lighter loads while an inductive converter is used to support higher loads as shown in Figure 2. In order to effectively utilize the large area under the inductor of the inductive converter, we propose to place digital load circuits under the inductor as shown in Figure 3. In this paper, we will first present the architecture of the hybrid converter in Section 2 where we will also explain the results from a testchip to understand the interaction between the digital circuits and power inductor placed above the digital circuits. Then we will present the capacitive and inductive converters which are connected in parallel to form the hybrid converter along with a prototype implementation details. The test setup used to characterize the hybrid converter is described in Section 3. Measurement results from the prototype testchip is reported in Section 4. Finally we will summarize this work in Section 5.

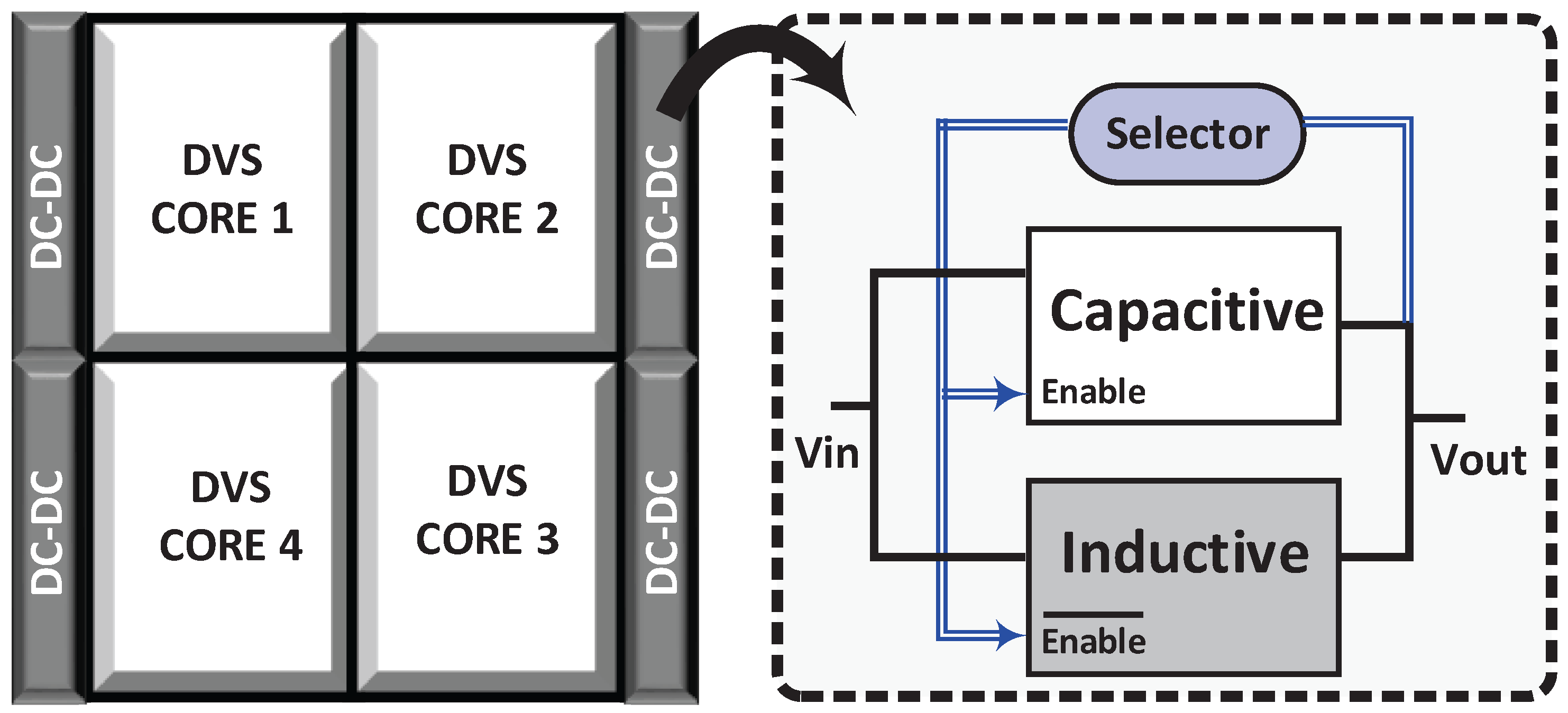
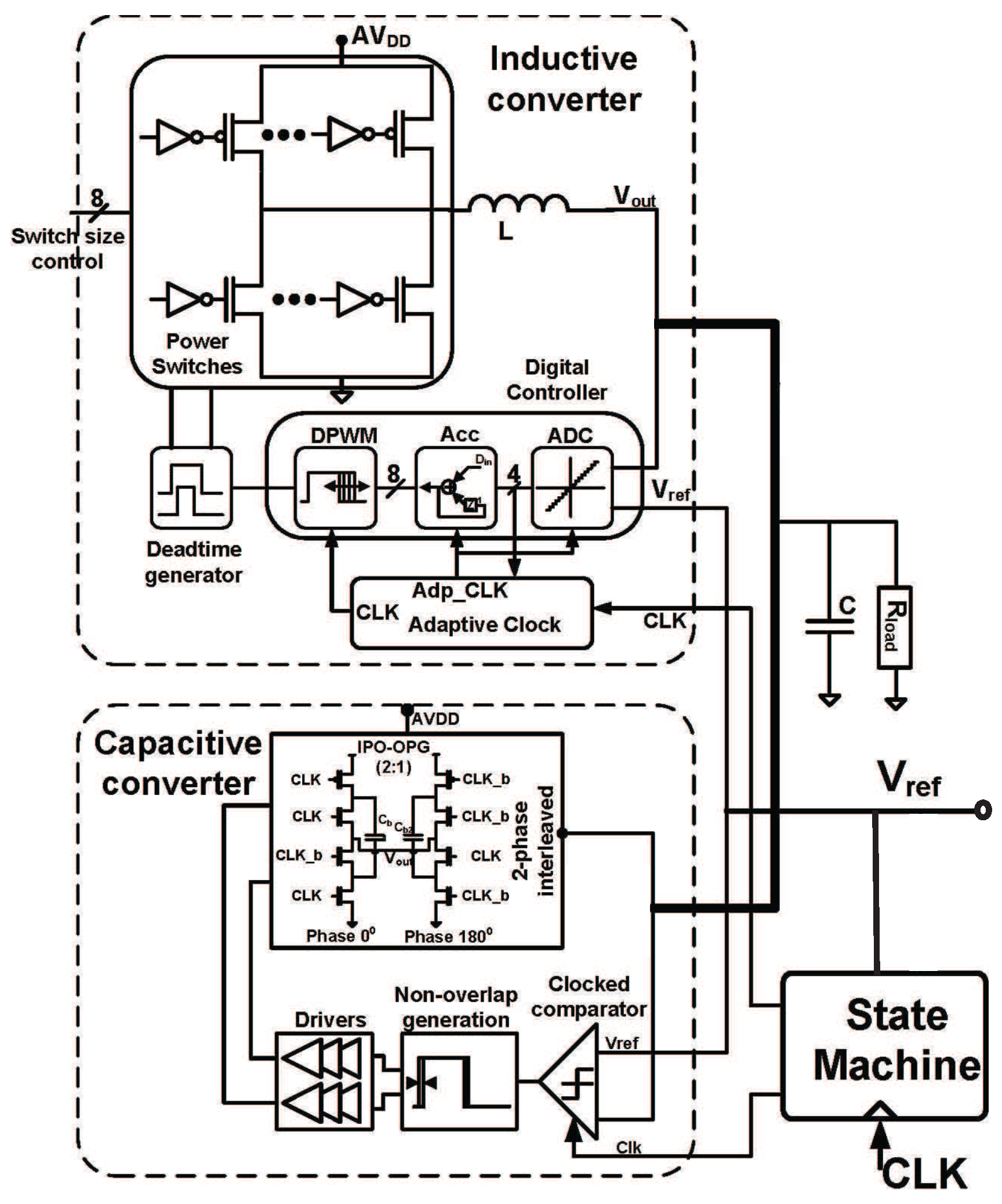
2. Architecture

Figure 2 provides the motivation for combining the two converters to achieve higher efficiency across a wide output power range. Here, to maintain high power efficiency, shown on the Y-axis, capacitive converters are used at low powers and inductive converters are used at high powers. We note that by changing the voltage conversion ratio of capacitive converter, higher efficiency at low power operation can be performed. But the increase in capacitance value for higher power outputs puts practical limitations on capacitive converters for higher loads in DVS based systems. On the other hand inductive converters are able to support higher loads. Thus a hybrid of both these converters can achieve a wide output power range.

The details of the hybrid converter are provided later (Figure 14). However, both converters are connected in parallel but only one is switched on at any one time. The switching between the converters is done when the efficiency achieved by one exceeds that achieved by the other. The switching between the converters is done on the basis of voltage sensing to optimize efficiency. This transition voltage can be estimated for a given load condition and is modeled in the following analysis. The switch-over point between the two converters can be decided by considering when the efficiencies of both converters are equal.

We know that at the time of switching $V_{out,cap}$ = $V_{out,ind}$ thus the ratio of converter efficiencies, α, is given by Equation (2).

$$\alpha =\frac{{\eta }_{ind}}{{\eta }_{cap}}=\frac{\left[\frac{V_{out,ind}\times I_{out,ind}}{V_{in,ind}\times I_{in,ind}}\right]}{\left[\frac{V_{out,cap}\times I_{out,cap}}{V_{in,cap}\times I_{in,cap}}\right]}=\frac{I_{in,cap}}{I_{in,ind}}$$

(2)

The switch over from capacitive to inductive converter is done when the ratio α is greater than one and from inductive to capacitive when it is less than one. We can identify the transition voltage, $V_{sw}$, if we plug in the values of the two converter currents [3,23] in Equation (2), we get

$$\alpha =\frac{\frac{1}{k}·\frac{V_{max}-V_{out}}{R_{out}}}{\frac{V_{out}·I_{out}}{V_{in}}+\frac{I_{out}^2·(R_L+R_{Switch})}{V_{in}}}$$

(3)

where $V_{max}$ is the no load output voltage of the capacitive converter, $R_L$ is the series parasitic resistance of the integrated inductor, $R_{Switch}$ is the on-resistance of the MOS switches.

The above relation can be used to estimate $V_{sw}$ for any kind of load. Figure 4 shows the variation of $\alpha ={\eta }_{ind}/{\eta }_{cap}$ with output voltage for our design for a 10 Ω load on the left (blue line) and a digital load (DVS 25 [email protected] V) on the right (red line). The dotted line corresponds to $\alpha =1$. The transition voltage for the digital load in this plot is 0.5 V and the transition voltage for the 10 Ω resistive load is 0.44 V. Increasing the resistive load current or the digital load current would move the optimal transition voltage to a lower value as indicated in the figure.

To avoid limit cycling between the two converters it is necessary to add some hysteresis margin to the transitions between the two converters. Increasing this hysteresis margin reduces the probability of limit cycles but unfortunately also reduces the overall conversion efficiency as the less efficient converter is allowed to operate for a longer period. However, making this hysteresis margin too small would result in “hunting”. In particular, the hysteresis margin should be made larger than the sum of the ripple voltage and the noise at the decision point. For our prototype design the ideal transition voltage is 0.55 V and the measured ripple voltage is 35 mV around the transition point. Using a little bit of a safety margin we operate the capacitive converter from 0.4 V to 0.55 V and operate the inductive from 0.9 V to 0.5 V, i.e., we use a 50 mV hysteresis margin.

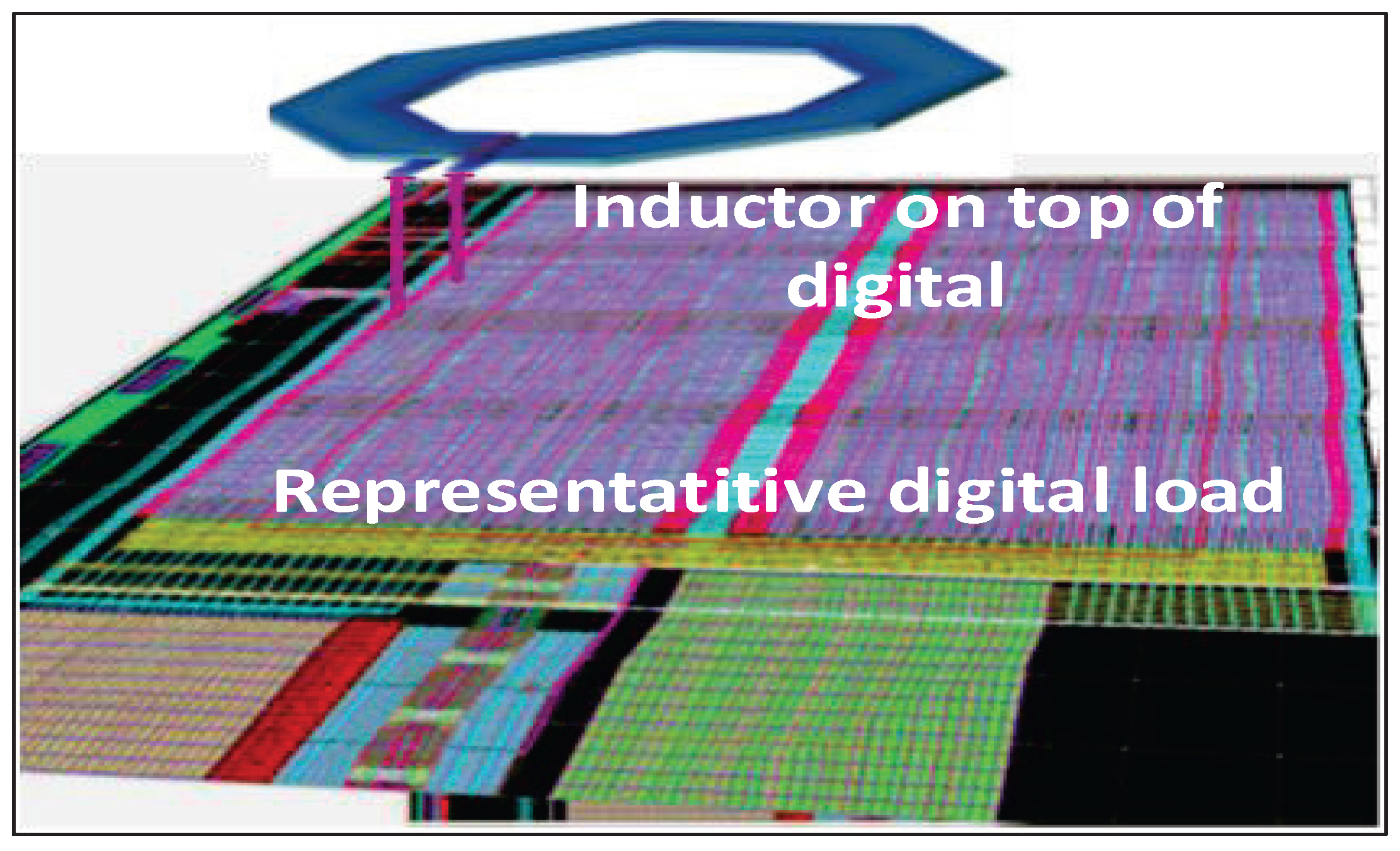
2.1. Digital under Inductor—Proof of Concept

One of the key features of this work is to reuse the area under the inductor for placing representative digital loads thereby making the DC-DC conversion solution achieve a higher power density. For achieving this, we propose to reuse the area under the inductor for digital loads as only the top two metal layers are used for the inductor. To check the feasibility of area reuse, a separate test chip as a part of the internal research, fabricated in 130 nm bulk, with ring oscillators as representative digital circuits underneath the inductor was compared to an inductor only design on a high resistivity substrate to study the impact of digital circuits on the inductor and vice versa. The coupling from the digital to inductor is lower than −50 dB (Figure 5a). The coupling from the inductor to digital circuits is less than −40 dB at 300 MHz (Figure 5b) which is less than other active circuits on the same substrate. The presence of digital circuits under the inductor decreases the inductance value slightly [24]. However, for power converters this degradation is not significant. Hence we make a design trade-off where we take a slight hit on efficiency which we observed in the measurement results for a considerable increase in area efficiency.

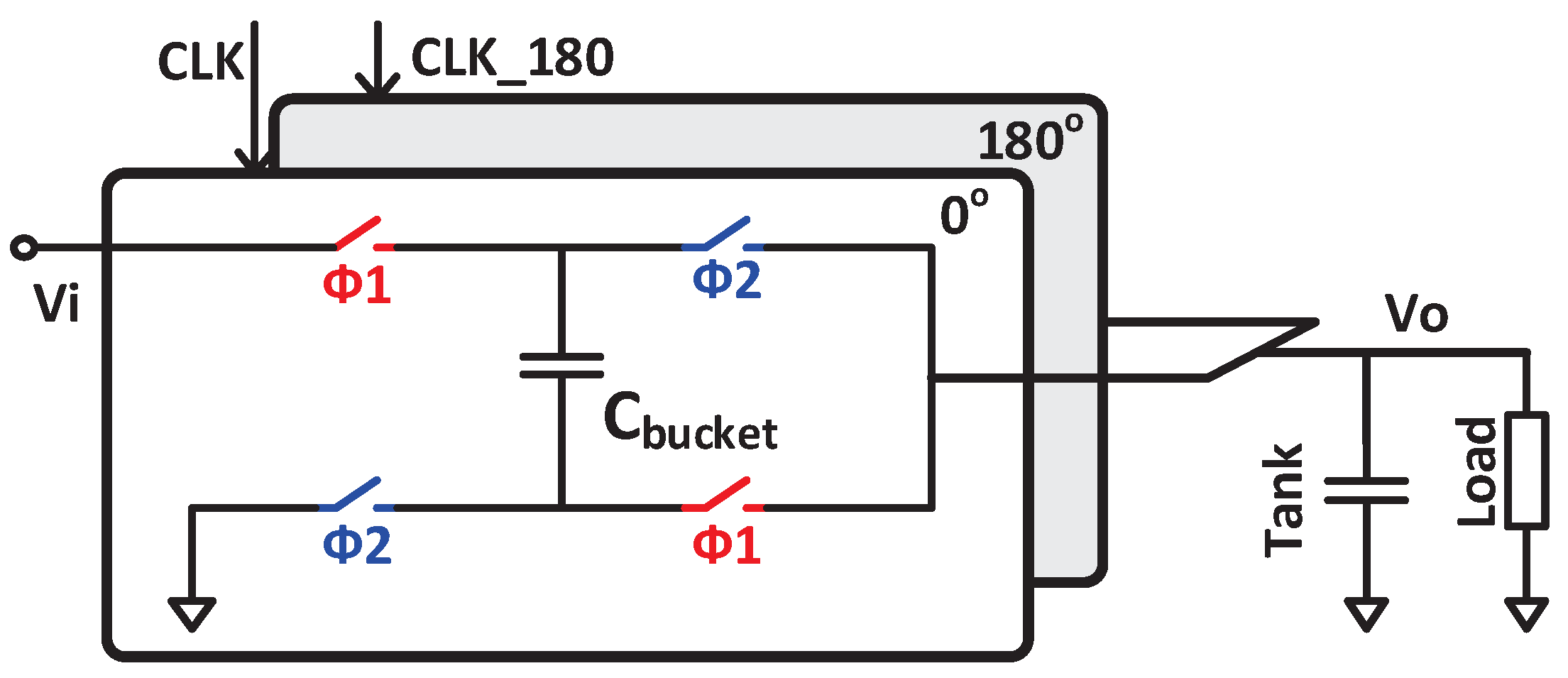
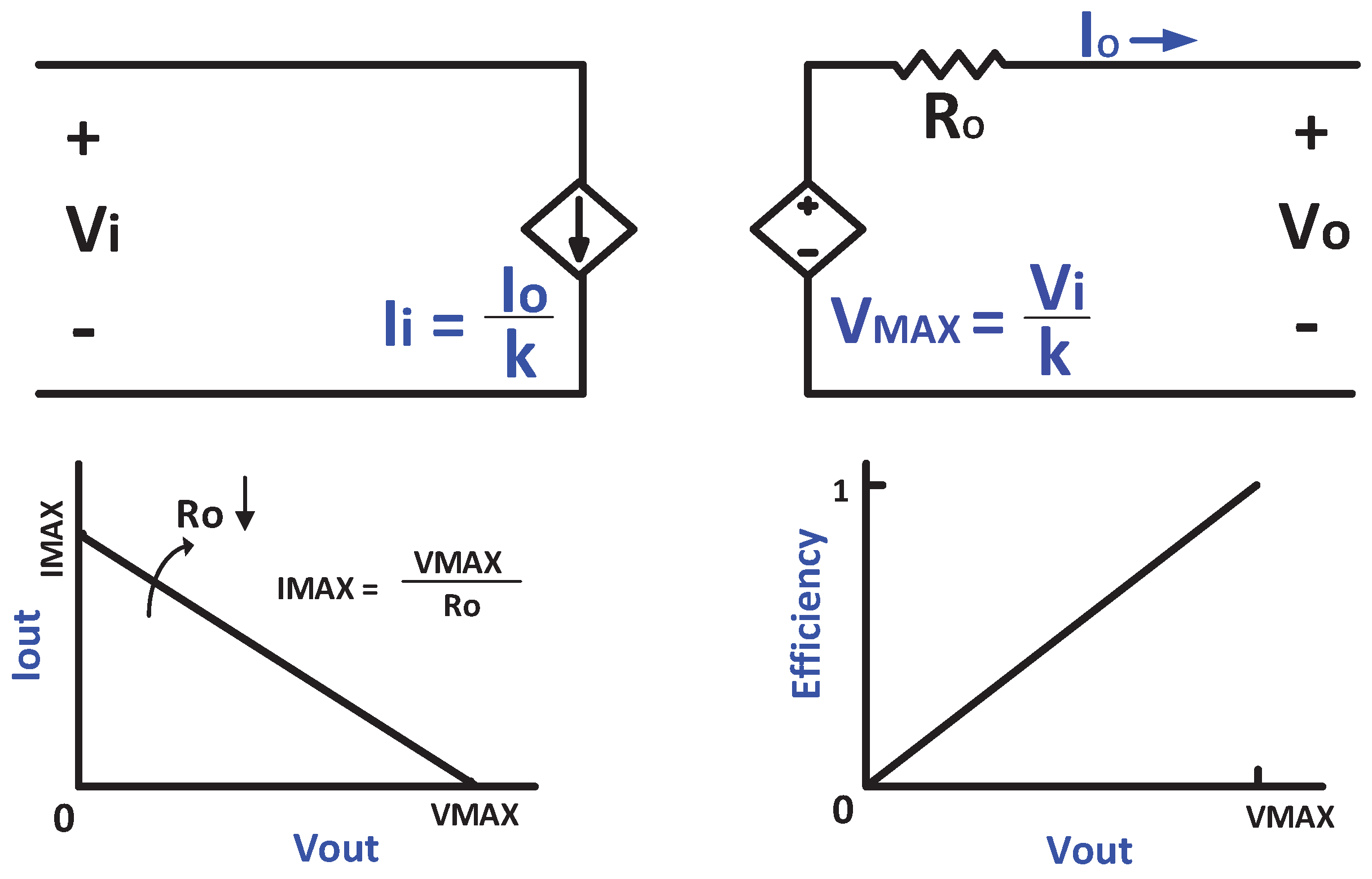
2.2. Capacitive Converter

Switched capacitor (SC) or capacitive DC-DC converters have gained popularity in recent years due to ease of implementation and fairly high efficiencies. These capacitive converters use only capacitance to achieve the desired voltage conversion. The capacitive converter consists of bucket capacitors which transfer the charge from the input supply to the tank capacitor by a periodic switching action. The tank capacitor filter the current to the load. In a typical closed loop scenario whenever the output voltage drops below the reference voltage (desired output voltage), transfer of charge from the input to output is initiated by a hysteresis based controller. Figure 6 shows functional description of a pair of 2:1 converters (in IPO-OPG topology) [25] connected in parallel where the no-load output voltage of each copy is equal to $V_{in}$/2. The efficiency of capacitive converter is given by $V_{out}$/$V_{max}$ where $V_{max}$ is the maximum output voltage that can be achieved by the converter under no-load condition i.e., $V_{in}$/2. The maximum load current supplied by the above mode is given by $I_{out}$ = 4n$C_{bucket}$f($V_{in}/2-V_{out}$) where f is the frequency of switching, $C_{bucket}$ is the size of each bucket capacitor and n is the number of bucket capacitors connected in parallel. Figure 7 shows the transformer model for the capacitive converter as discussed in detail in [25]. Through Figure 7 it can be inferred that the converter achieves maximum efficiency at no-load voltage($V_{max}$) but losses the capability to deliver any power to the output. So, there his a tradeoff between the maximum current transferred and efficiency achieved for a given capacitive converter.

Figure 6 shows a two phase interleaved converter where there are exactly two copies of similar converters switching with a phase shift of 180 degrees. This implementation reduces the output voltage ripple by effectively doubling the operating frequency. Figure 8 shows the actual circuit level implementation of capacitive converter part of the hybrid converter. PMOS and NMOS devices are used as switches and deep trench capacitors are used as bucket capacitors. This implementation is designed to operate when the output voltage ranges from 0.4–0.55 V at an input of 1.2 V.

For our DVS load the switched capacitive converter is enabled by a state machine when the reference voltage is lower than 0.55 V which is based on the calculations of Equation (5). In this prototype a single mode (IPO-OPG) [23] capacitive converter which is 2-phase interleaved has been implemented. The IPO-OPG configuration achieves a maximum conversion ratio of 2:1 (Vout = Vin/2). The complete capacitive converter configuration that was implemented is shown in Figure 8. A single bound hysteretic controller achieves the regulation. In this type of control the output voltage is compared with the reference voltage and when the output voltage dips below the reference voltage a switching action is initiated to transfer a quanta of charge from the supply to the output. In this implementation, single capacitive converter mode has been implemented but multiple modes can be easily implemented and the appropriate mode selected by the state machine based on the reference voltage.

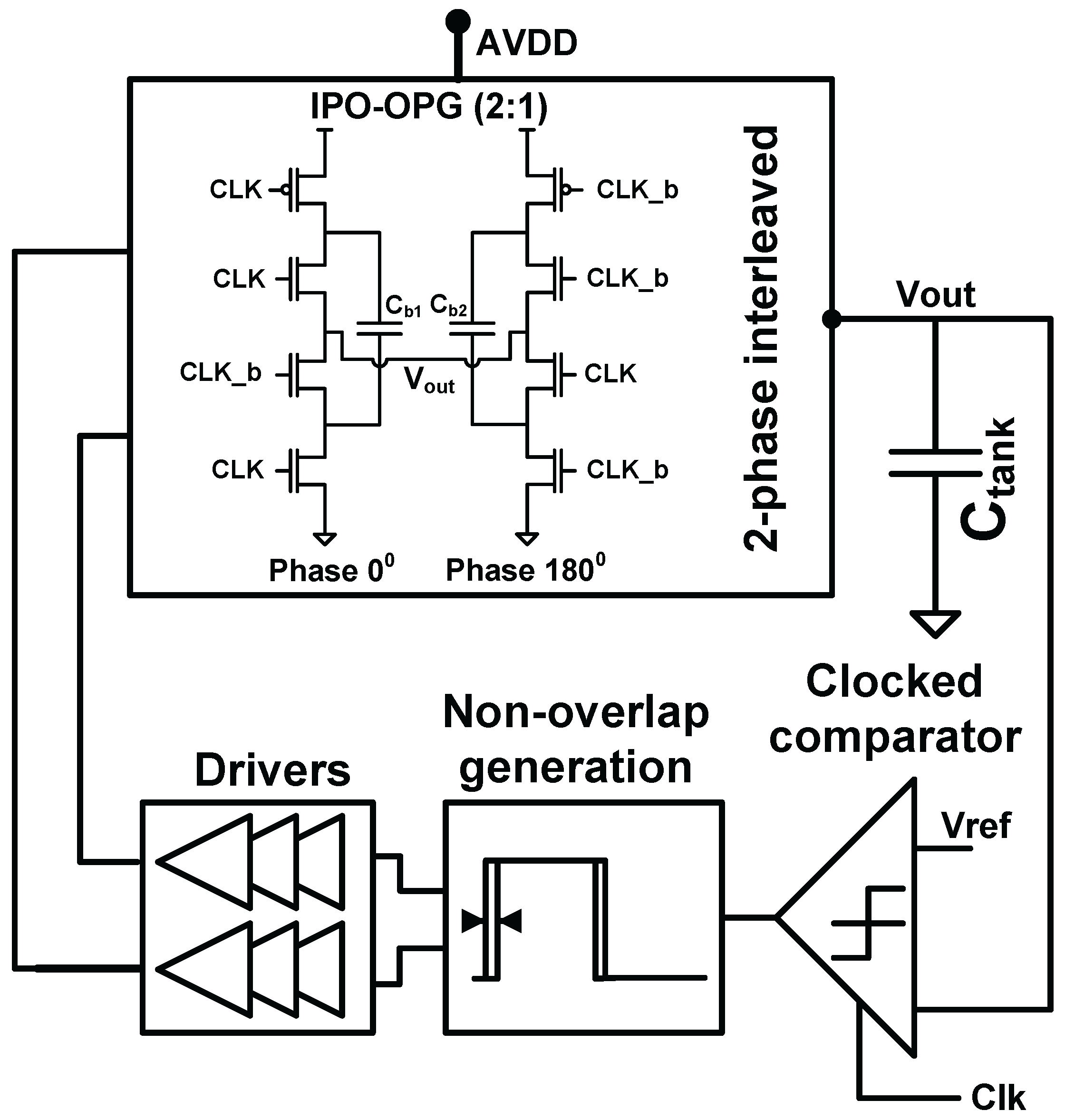
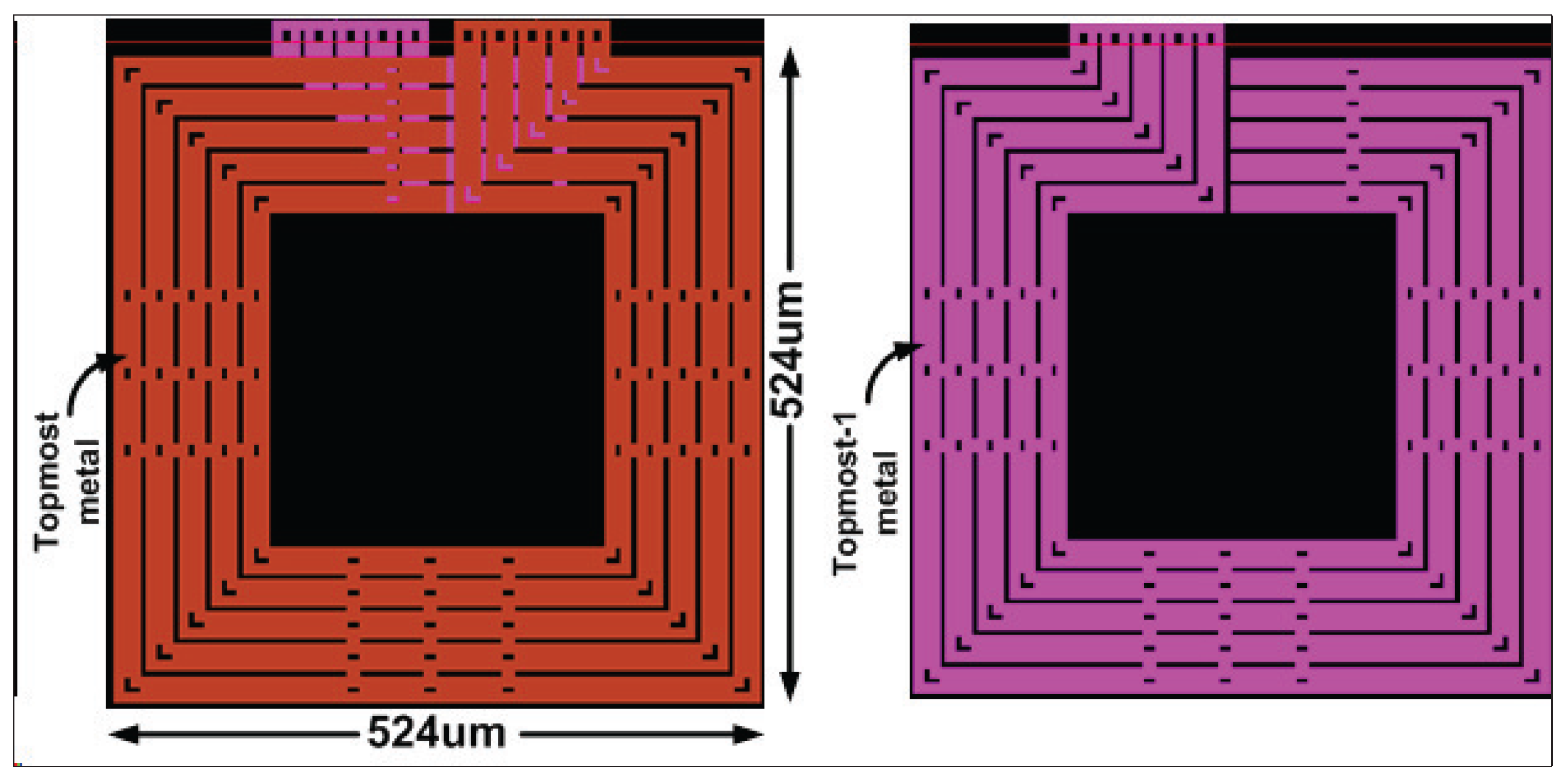
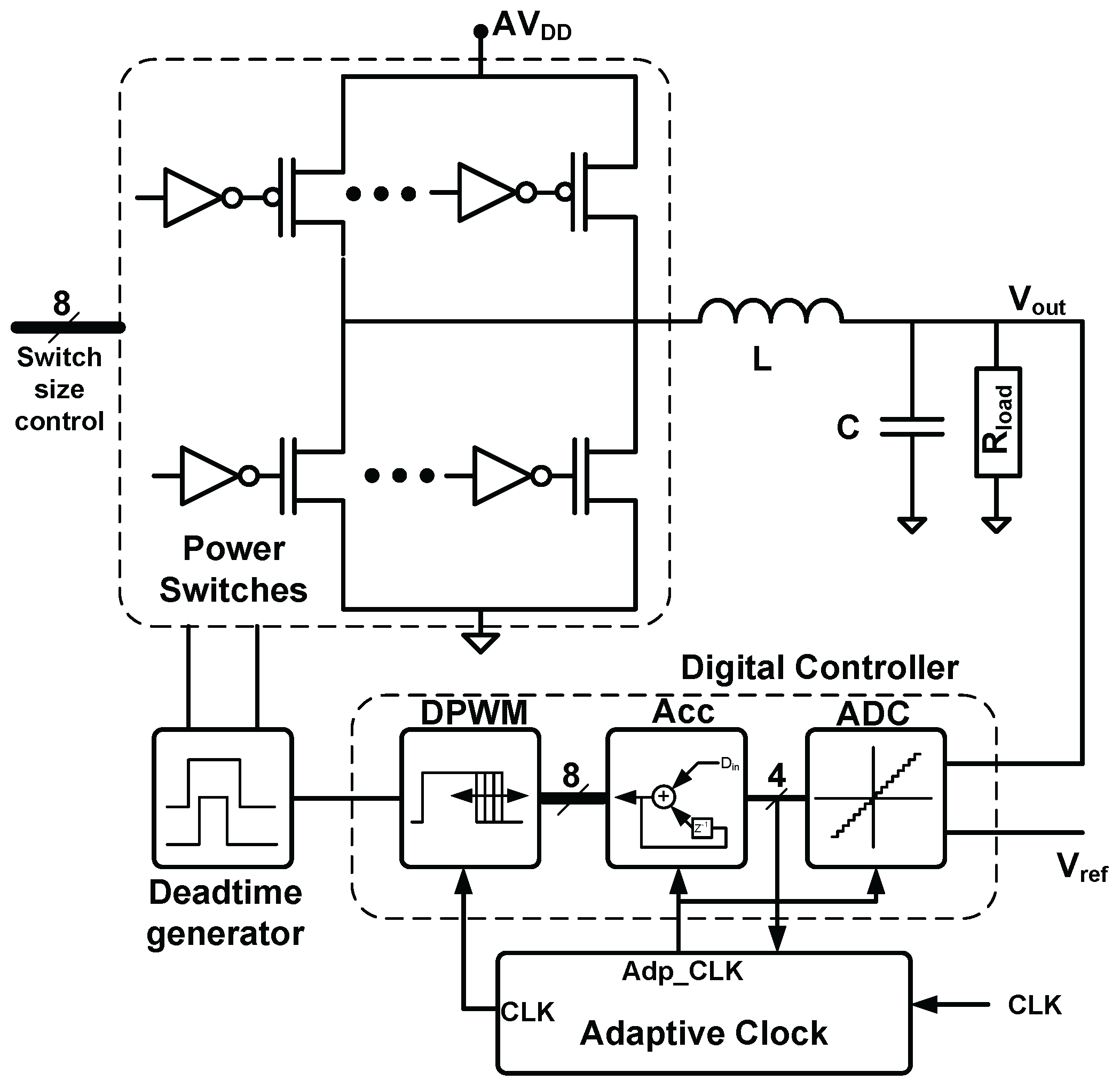
2.3. Inductive Converter

As discussed earlier, the capacitive converter transitions to the inductive converter when the output voltage is higher than 0.55 V up to 0.9 V. In the reverse direction the inductive converter transitions to the capacitive converter when the output voltage falls below 0.5 V. The clocks to the digital controller are enabled and the switching action resumes. The inductive converter consists of the core converter unit and the controller which regulates the output voltage to the desired value as shown in Figure 14. The digital PWM controller utilizes a time-to-digital based analog-to-digital converter to digitize the error between the reference voltage and the output voltage. The error is then digitally integrated in an accumulator, the output of which forms the code for generation of the appropriate duty-cycle pulses in the digital PWM generator.

Figure 9 shows the layout details for the 2 nH inductor that is realized with the top two metallic layers so that the digital circuits can be realized underneath. The inductor is roughly 524 $\mathsf{\mu }\mathrm{m}\times 524\mathsf{\mu }$m in size.

For a fully-integrated implementation of a buck converter, like the one shown in Figure 10, the physical size of the passives dominate the area occupied. On the other hand, the output ripple voltage is given by Equation (4) [3] where L and C are the inductance and filter capacitance, D is the duty cycle for generating the required output voltage and $f_{sw}$ is the switching frequency of the buck converter.

$$\Delta V=\frac{D(1-D)V_{DD}}{8LC{f}_{sw}^2}$$

(4)

Reducing the size of the passive filter components forces us to increase the switching frequency $f_{sw}$ so as to meet the output ripple voltage specifications. To understand this tradeoff carefully, let us consider the different components of input power $P_{in}$ are given by Equation (5), where $P_{out}$ is the power supplied to the load, $P_{sw}$ (given by Equation (6)) is the power consumed by switching the power device and its respective buffers, $P_{cond,PMOS}$ is the conduction loss in the PMOS device and $P_{otherloss}$ is the power loss in the rest of the circuit. The conduction loss for the NMOS device is treated separately as it does not carry the load current [3].

$$P_{in}=P_{out}+P_{sw}+P_{cond,PMOS}+P_{otherloss}$$

(5)

$$P_{sw}=C_{gate}{V}_{DD}^2{f}_{sw}$$

(6)

Here, $C_{gate}$ is the total capacitance switched.

The conductive loss in the PMOS device can be approximated by Equation (7), where ${\mu }_p$ is the PMOS hole mobility, $W_p$ is the width of the PMOS power device, $V_{Tp}$ is the threshold voltage of the PMOS device and $I_{PMOS}$ is the RMS current in the PMOS power device. The mean square value, $I_{PMOS}^2$, is given by $I_{PMOS}^2=D^2{I_{load}}^2+I_{PMOS,rms}^2$ where $I_{PMOS,rms}$ is the RMS value of $I_{PMOS,ripple}$. $I_{PMOS,ripple}$, in turn is given by Equation (8).

$$P_{cond,PMOS}=\frac{I_{PMOS}^2}{{\mu }_p{C}_{ox}\frac{W_p}{L}(V_{DD}-V_{Tp})}$$

(7)

$$I_{PMOS,ripple}=-\frac{D(1-D)V_{DD}}{2L{f}_{sw}}+(t-nT)\frac{(1-D)V_{DD}}{L}$$

(8)

The $P_{otherloss}$ (shown in Equation (9)) includes the conductive loss in the NMOS power device (Equation (10)), the power lost in the inductor series resistance (Equation (11)) and the short circuit current (Equation (12)).

$$P_{otherloss}=P_{cond,NMOS}+P_{cond,L}+P_{sc}$$

(9)

where

$$P_{cond,NMOS}=\frac{I_{NMOS}^2}{{\mu }_n{C}_{ox}\frac{W_n}{L}(V_{DD}-V_{Tn})}$$

(10)

is the conductive loss in the NMOS power device, with an electron mobility of ${\mu }_n$, width $W_n$ and $I_{NMOS}$, the RMS current through the NMOS power device which is the sum of $(1-D)I_{load}$ and $I_{NMOS,ripple}$ given by

$$P_{cond,L}=R_s{I}_{ind}^2$$

(11)

is the loss in the inductor series resistance $R_s$, where $I_{ind}$ is the RMS value of current through the inductor and

$$P_{sc}=V_{DD}{I}_{sc}$$

(12)

is the loss due to the direct current flowing when the PMOS and NMOS devices are simultaneously on.

Using the above analysis we try to investigate the efficiency profile of the inductive converter. The power efficiency is higher at larger load currents but it deteriorates at lower power ranges due to switching power losses. Figure 11 shows the simulated efficiency for a wide output power range.

Different techniques have been followed in this design to reduce each of these wasteful components but, special attention is paid to reducing the switching power losses, as it forms a significant portion of this wasteful power. At low output powers, more than 50% of the total input power is dissipated in switching the power devices and their associated buffers. The switching power losses of the inductive converter can be reduced by either reducing the switch capacitance being switched or by reducing the frequency of operation. Both techniques will be applied to our converter.

The details of the control loop implementation is discussed in the next subsections.

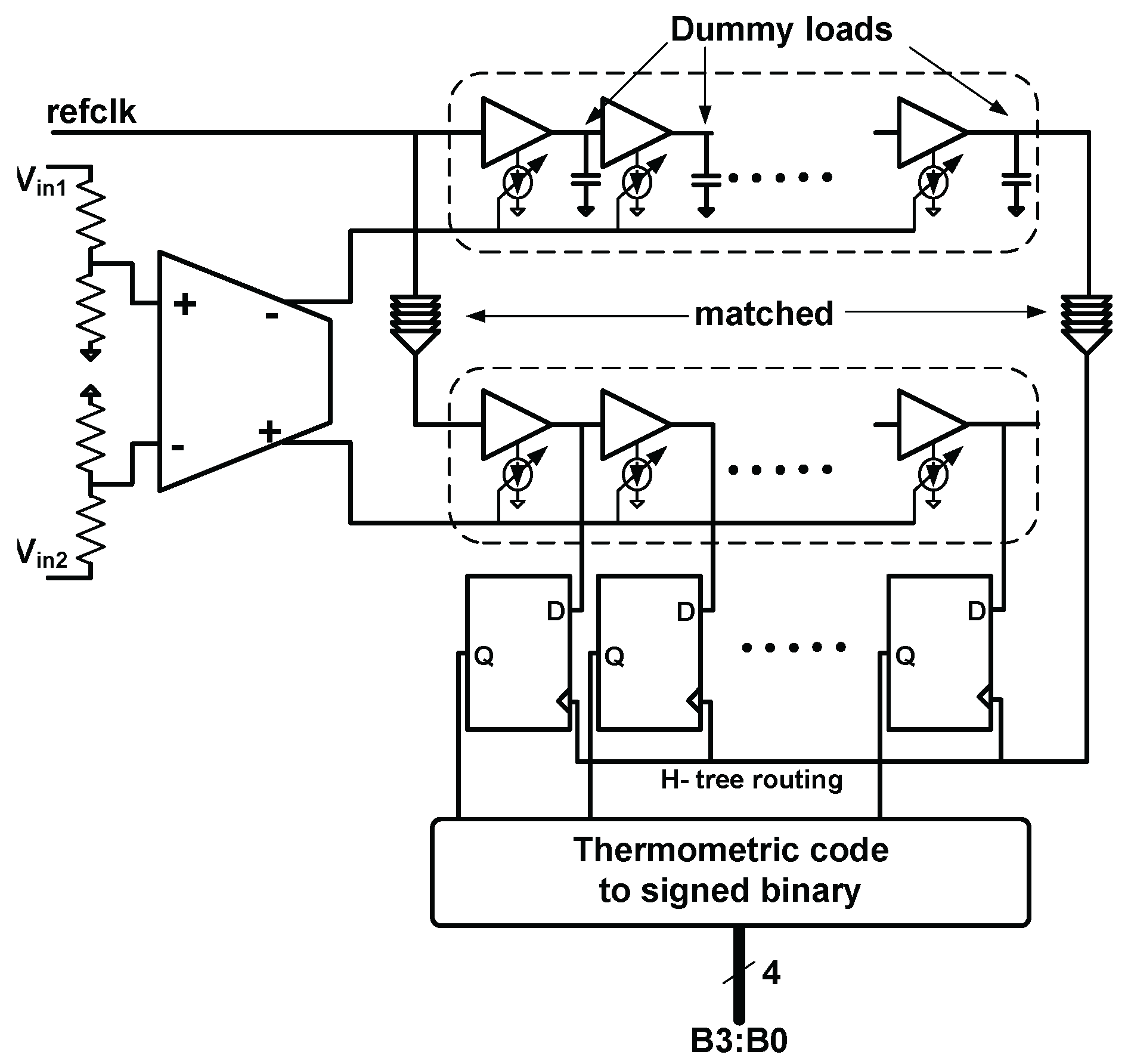
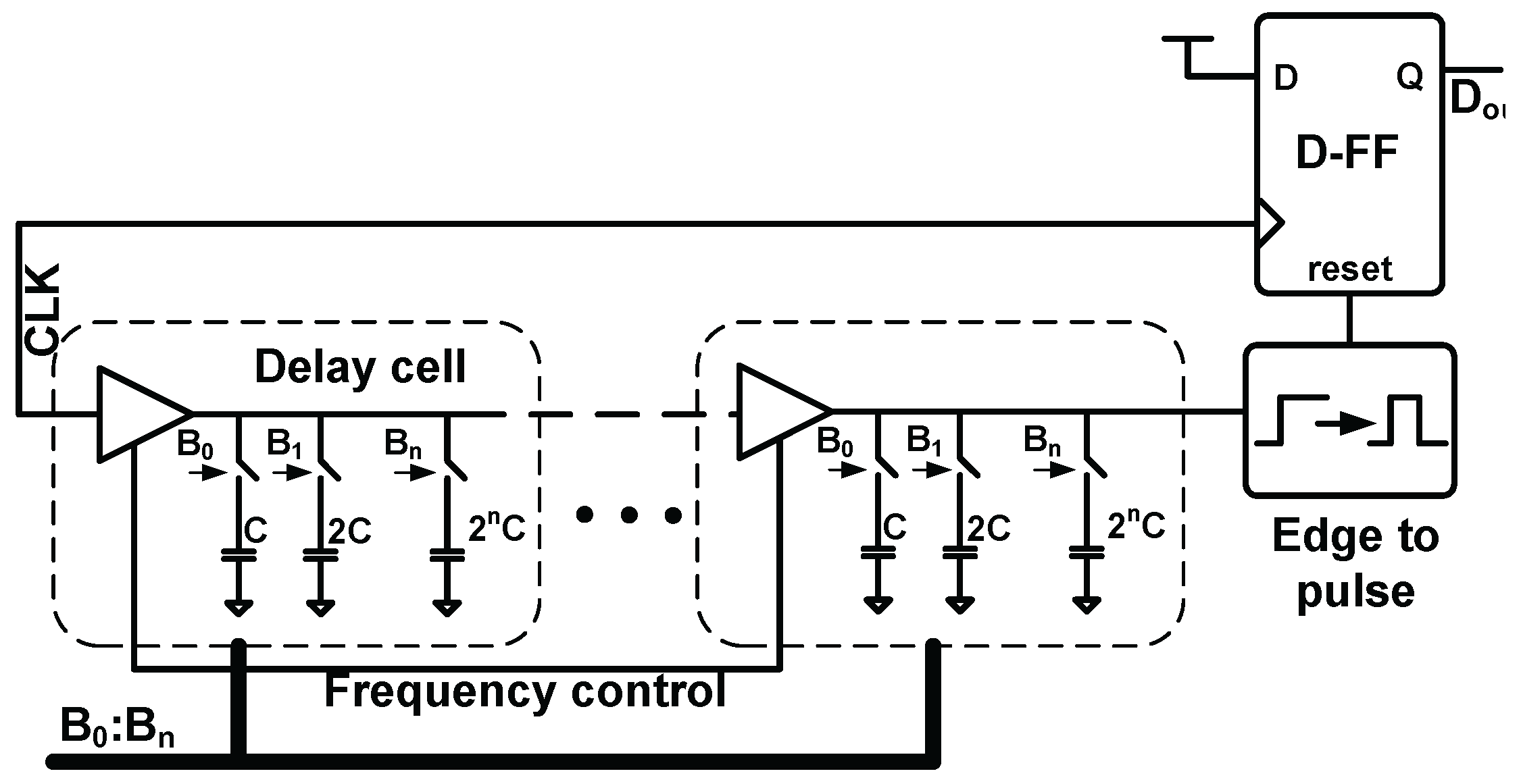
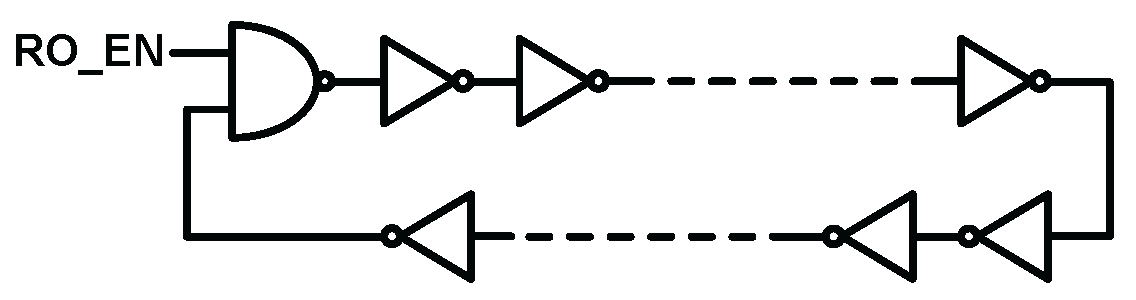
2.3.1. Time Based Analog to Digital Converter (TDC)

The ADC is required to digitize the difference between the reference voltage and the output voltage. The reference voltage is variable and the output voltage is expected to be close to the reference voltage. Hence, a low resolution ADC is sufficient for our purposes. For low power and high speed requirement we use time based ADC architecture [26,27]. In this design, the ADC output is a 4-bit signed binary number as shown in Figure 12. The difference between the output voltage and the reference voltage is amplified and used to control the delay of two variable delay lines whose input is the reference clock signal. The delay lines are composed of a chain of current starved inverters whose delay is controlled by the changing the current in these inverters. The output of one of the delay line is used as a clock signal for D-flip-flops to take the snapshot of the other delay line. The other delay line is tapped at 16-equidistant nodes to form the data input to the D-flip-flops. Based on the delay difference between the two delay lines a thermometric code is captured in the D-flip-flops which is proportional to the difference in the voltage. This thermometric code is then converted to a 4-bit signed binary number. This technique requires a delay matching between the clock line and the data line when the voltage difference is zero. The data line nodes have some extra capacitive loading due to the D-flip-flops which are not present on the clock delay line nodes. Hence dummy loads are added on this line to match the delay in the two lines when the zero control input difference.

2.3.2. Accumulator

The ADC output is integrated in a digital integrator built using a accumulator shown in Figure 14 with overflow prevention logic. The 4-bit output of the ADC is sign extended to a 10-bit signed binary number and added to the previous data using a ripple carry summer.

2.3.3. Digital Pulse Width Modulator

The digital PWM (DPWM) generation block receives the most significant 8-bits of the 10-bit accumulator output. The DPWM circuits consist of a D-flip flop and a chain of delay cells to generate the appropriate delay as shown in Figure 13. The D-flip flop is positive edge triggered. Here, the D-flip flop data input is connected to Vdd. The same edge is propagated through a delay chain whose delay is controlled by the DPWM control word from the accumulator. The delayed edge from the delay line is then converted to a pulse and used to reset the D-flip flop to zero thereby changing the duty-cycle of the clock signal according to the DPWM control word. The delay cell consists of an inverter loaded with binary weighted capacitors connected to a switch to set the appropriate loading on the delay line.

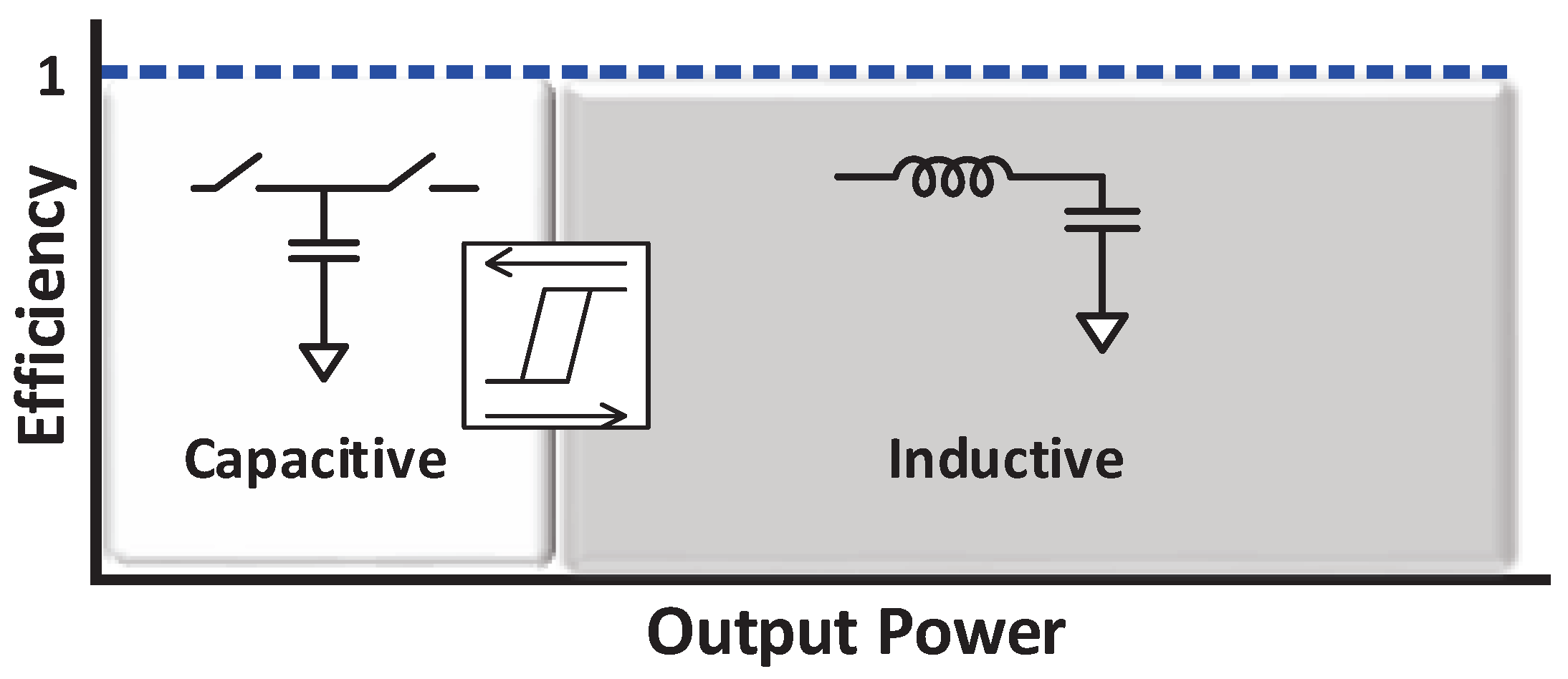
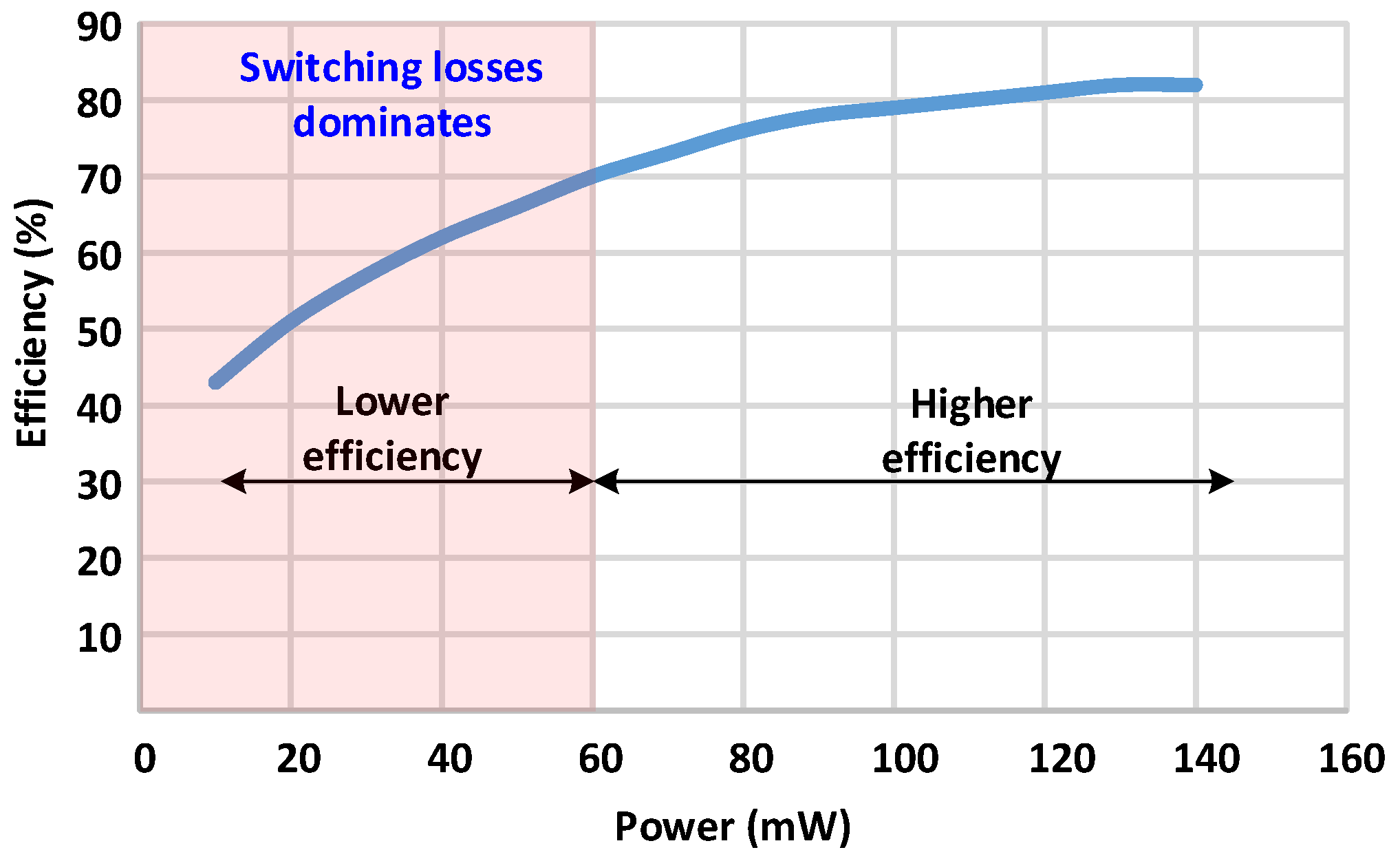
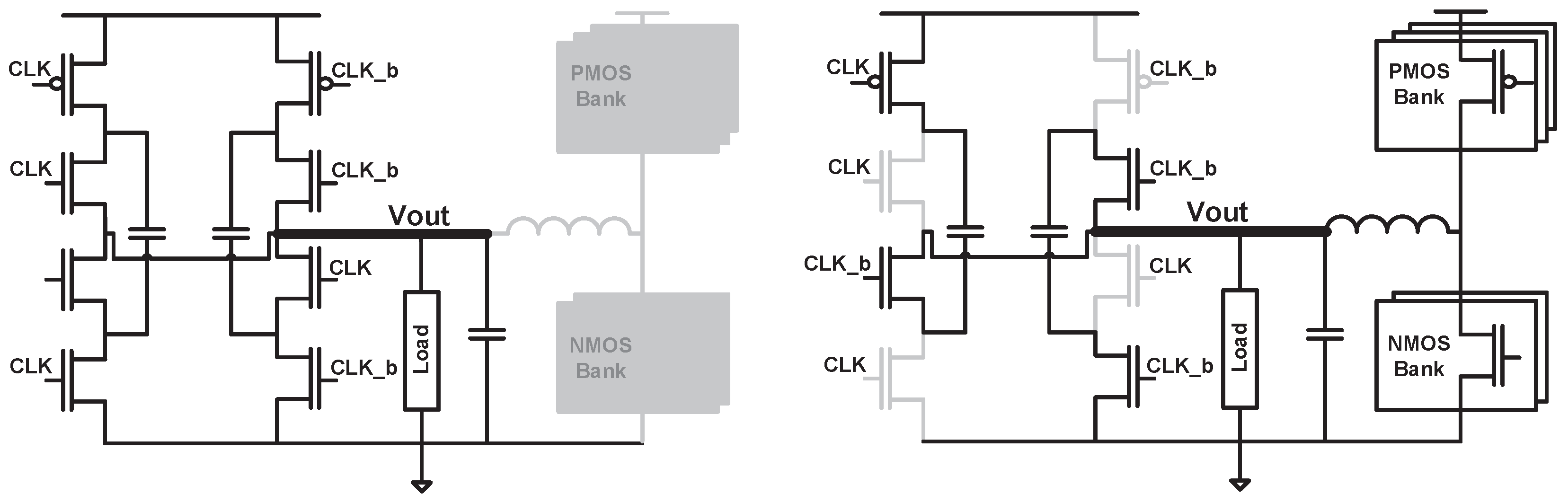
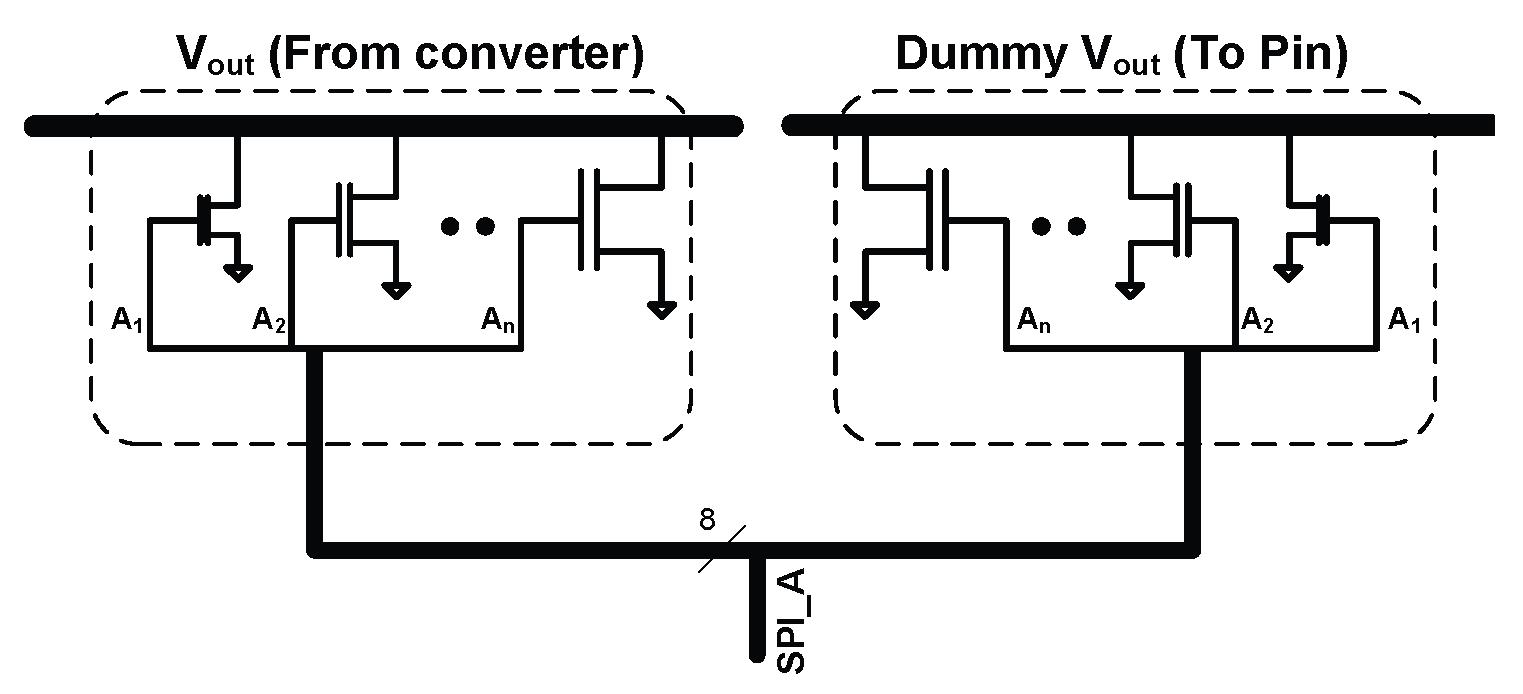
2.3.4. Efficiency Improvement Techniques

Two important techniques have been used for efficiency improvement, i.e., switch size scaling and adaptive clock frequency.

Switch size scaling: In order to reduce the switching losses the size of the power switches are scaled according to the load conditions. The PMOS switch consists of 6 equal sized cells each of width 2 mm and the corresponding drivers preceded by the MUX. Hence the switch size of the PMOS switches are varied from 2 mm to 12 mm in steps of 2 mm. Similarly, the NMOS switch is divided into 2 parallel cells of size 2 mm each, i.e, the size of the NMOS switches are varied from 2 mm to 4 mm in steps of 2 mm.

Adaptive clock frequency: The clock frequency of the ADC and the accumulator is reduced in steady state with the DPWM switching frequency remaining unaltered. This is possible because in steady state the reference voltage and the output voltage are not expected to change significantly. The steady state condition is detected by checking the ADC output which is the difference between the reference voltage and the output voltage. When the error is less than a certain value a clock whose frequency is 1/4th the frequency of the reference clock is selected with the normal clock frequency being selected when there are larger transients.

2.4. Combined Converter Design

A state machine selects between the inductive and capacitive converter based on the reference voltage with the inductive converter being selected when the reference voltage is greater than 0.55 V and capacitive converter otherwise. As discussed earlier, there is hysteresis in the loop. The switch from inductive to capacitive only occurs when output voltage drops below 0.5 V. The state machine also turns off the converter that is not in use by gating off the clock to that particular converter. The overall converter is shown in Figure 14 with the inductive on top and the capacitive on the bottom. The combined hybrid converter occupies a total area of 0.4 mm² that includes the area occupied by the decoupling capacitors on the input supply as shown in Figure 15. The filter capacitor is shared between the two converters. The input supply voltage of the converter is 1.2 V and the converter supplies a maximum power of 140 mW.

Transition Circuits: The transition between the inductive and capacitive converters is decided digitally (as explained in more details later), but the effective circuit during the transition is shown in Figure 16. In capacitive mode the filter capacitor of inductive part acts as tank capacitor, and in the inductive mode the bucket capacitors of capacitive converter acts as additional filter capacitors.

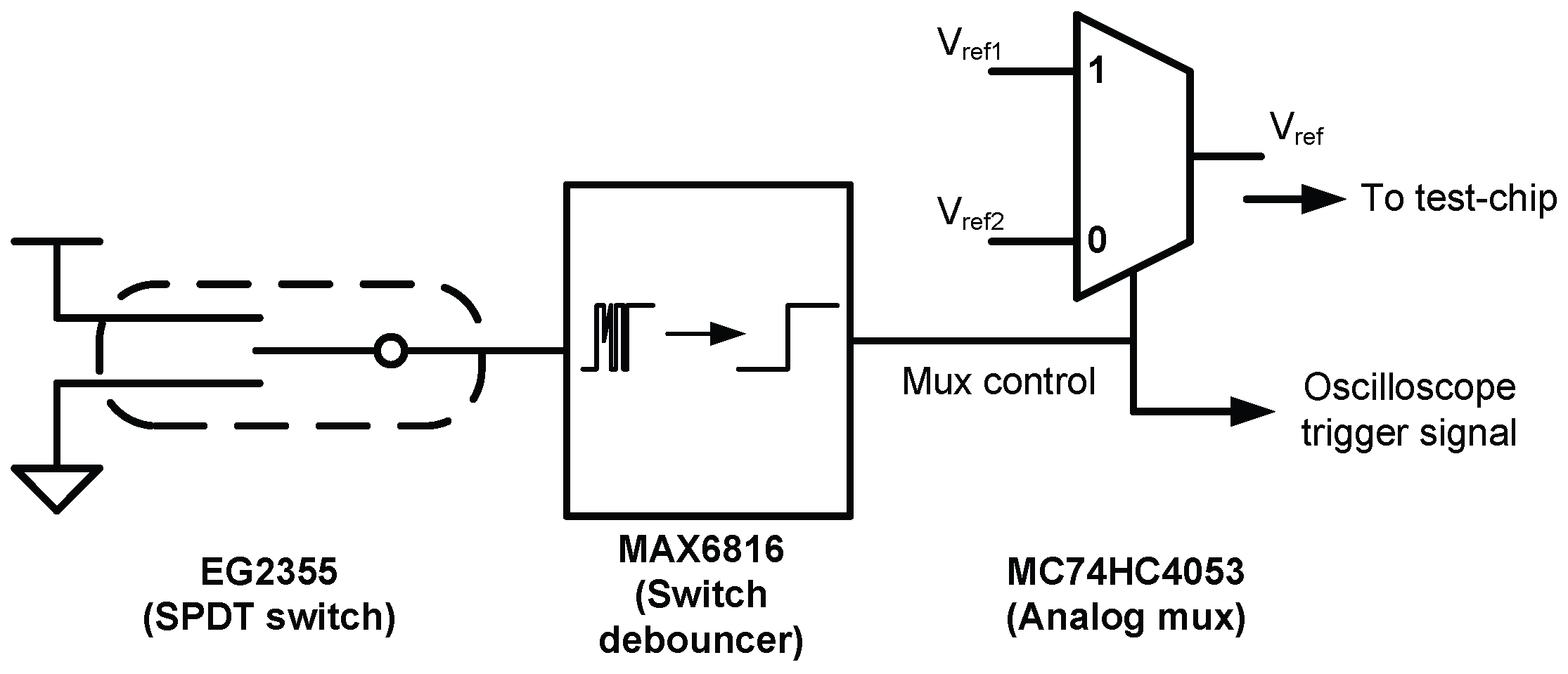
3. Measurement Test Setup

To aid in the testing process, a number of different test structures that are implemented on-chip. These structures and the corresponding test methodology are explained below.

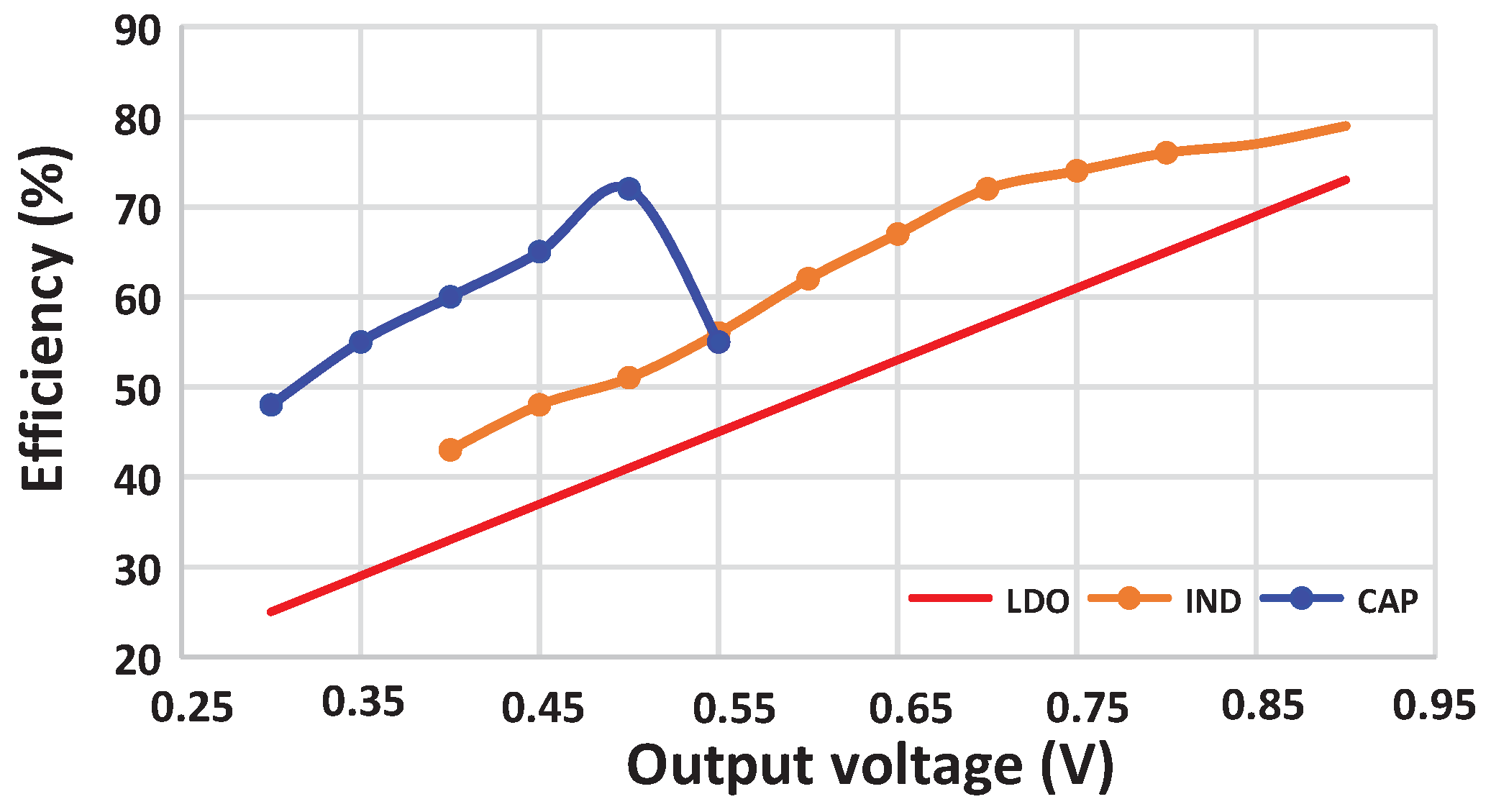
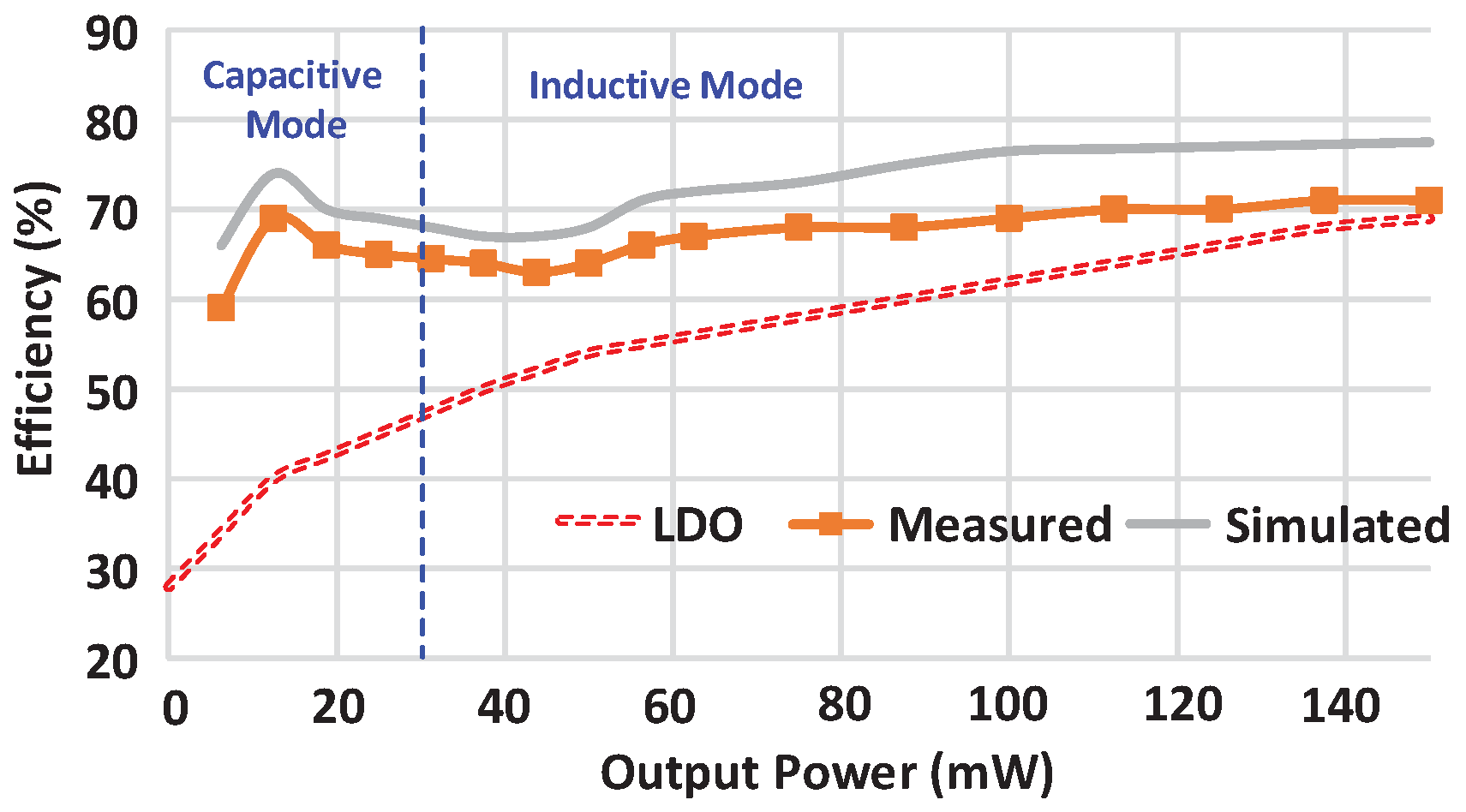
3.1. Steady State Efficiency

The converter can be stressed by setting the load current to appropriate values using the binary weighted NMOS transistors connected between the output node and the ground as shown in Figure 17. The current can be varied from 1.25 mA to 390 mA. The control signals generated from the serial programmable registers is used. In order to exactly measure the current being drawn an identical bank of NMOS transistors controlled by the same set of signals from SPI registers. The drain node of the of these transistor is connected to an output pin (dummy Vout). The voltage at the dummy $V_{out}$ node is set to the same value as the Vout and the current is measured. This experiment was repeated for different reference voltages and load currents. For digital load we used the gated ring oscillators as shown in Figure 18.

3.2. Load Transient Measurement

In order to observe the effect of a load transient on the converter, the setup shown in Figure 17 is used. Here, two banks of NMOS current loads are connected to the output voltage. The current drawn by these banks are set to appropriate values using the SPI register control signals. An external signal is used to switch between the bank of NMOS transistors. The same external signal was used as a trigger signal to capture the effect of the load transient on the output voltage.

3.3. Transient Measurement

The effect of a change of the reference voltage is studied by abruptly switching the reference voltage from one value to other. This is achieved by using the setup shown in Figure 19. The SPDT switch is used to switch between the two reference voltages through an analog multiplexer. The mux control signal is used to trigger the oscilloscope to capture the output voltage. Both reference voltage and the load current can be simultaneously switched by using the mux control signal as the external signal to switch the banks of load current.

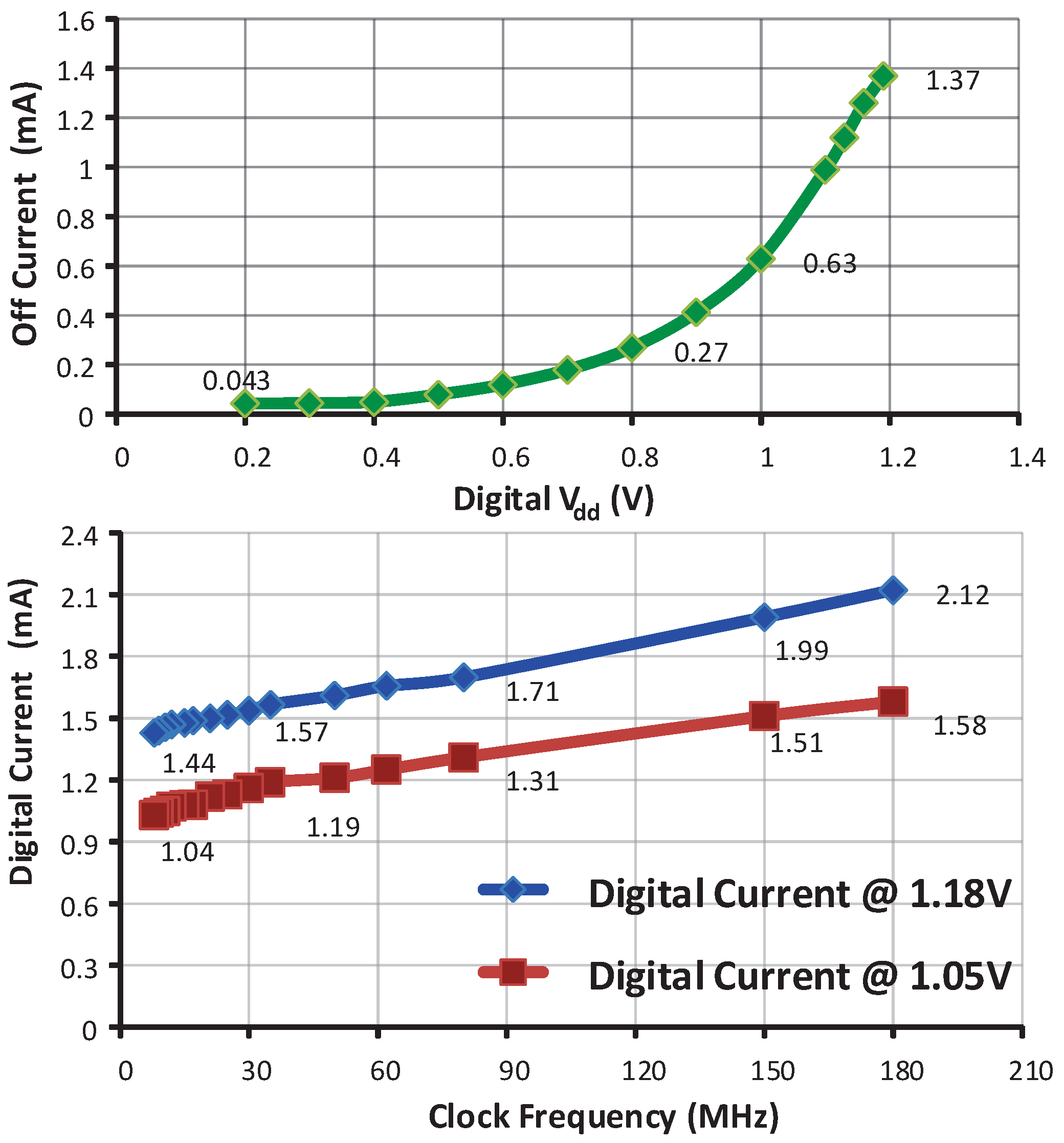
4. Measurement Results

For steady state efficiency measurements the hybrid converter was stressed with two kinds of loads, resistive and digital, in both open and closed loop mode. On chip MOS transistor banks were used as resistive loads and a group of eight ring oscillators under inductor acted as the representative digital load. Figure 20 shows the efficiency for resistive loads for both the converters. The capacitive converter achieves 71% closed loop peak efficiency at 0.52 V while the inductive converter shows 76.4% peak efficiency at 0.9 V for a resistive load of 20 Ω. Vdd was 1.2 V. An ideal LDO is also included in this figure for comparison purposes.

Figure 21 shows the simulated (gray) and measured efficiencies (orange) vs. power from 2 mW to 140 mW for digital load. Two separate designs were included onchip, one with digital under inductor and one without. The measured peak efficiency for the inductive converter that was 74.3% peak without digital under inductor and 70.3% for digital under inductor. The measured plot in Figure 21 shows the values for the digital under inductor design. The slight decrease in efficiency can be attributed to the coupling losses between digital circuits and the inductor. An ideal LDO is included in this figure as well for comparison purposes. We note that we see a maximum efficiency increase at lower powers. This is particularly important as time spent in sleep modes (i.e., lower power) tend to dominate for portable devices.

Figure 22 shows the die photograph. The converter achieves a power density of 0.387 W/mm². Re-using the area occupied by the inductor by placing digital circuits underneath the inductor increases the power density of the converter to 4.1 W/mm² as shown in

Table 1. Design summary.

Parameter	Value
Technology	IBM 32 nm SOI
Converter type	Hybrid (Capacitive + Inductive)
Area with decaps	0.4 mm2
Peak efficiency(Inductive)	74.5% (@300 MHz and room temp)
Max O/P power	140 mW
Min O/P power	2 mW
Input voltage	1.2 V
Max output voltage	0.9 V
Min output voltage	0.4 V
O/P ripple @ 750 mV	28 mV
O/P current range	70×
Filter capacitor	2 nF
Inductor	2 nH

. The power density using this technique is among the highest achieved to date.

Figure 23 shows the leakage profile for the converter. Since leakage current causes the majority of discrepancy between simulated and measured results, it is important to study the leakage results of the converter. The top graph in Figure 23 shows the leakage current verses digital voltage of the control loop of the chip when the clock is disabled. The two graphs below shows the dynamic digital power consumption of the chip vs. clock frequency. The y-intercept of the two graphs on the bottom chart corresponds to the peak leakage current of the top chart. This leakage is direct result of the gate leakage of the MOS capacitor and the subthreshold leakage of the switches involved. This is particularly true for switches involved with the inductive converter as they are especially large. Another reason for the measured efficiency offset (as compared to simulated results) in inductive converter is due to the systematic mismatch in the routing of the measurement circuitry. As shown in Figure 22, the digital under inductor prototype is placed to the far left to the output (filter capacitor) which results in IR routing drops. Better floor planning would have avoided this problem.

Table 1 presents a technical summary of this design. The hybrid converter achieves 74.5% measured peak efficiency in the inductive mode of operation at 300 MHz clock frequency. The design uses a 2 nF on-chip MOS decoupling capacitor and 2 nH on-chip spiral inductor as passives. The output power ranges from 2 mW to 140 mW and the output ripple at 0.75 V output is 28 mV.

Table 2. Summary comparison with other related work.

	[28]	[29]	[30]	[31]	[3]	[32]	[33]	[8]	[34]	This Work
Technology(nm)	1500	500	250	180	130 bulk	32 bulk	600	32 SOI	130	32 SOI
Ind(L)/Cap(SC)	L	L	L	L	L	SC	SC	SC	SC	Hybrid
Power Eff %	40–60	75–93.7	70–92	35–64	77.9	60	87	79.76	82	74
In/Out Voltage (V)	5/2.5	3.3/2.5	5.5–2.8/1.8	2.8/1.5–2.0	1.2/0.3–0.88	1/2	1.8–3.2/3.3	2/0.88	1–1.2/2–2.1	1.2/0.4–0.9
Pwr Den(W/mm2)	-	-	-	-	0.21	1.123	2.185	0.86	0.67	0.38–4.1
Ripple(mV)	-	-	-	-	40	-	20	-	8.9	30
Passive Size	0.1 μH/30 nF	Offchip	10 μH/47 μF	22 nH/6 nF	2 nH/5 nF	2 pF	1 μF	-	1 nF	2 nH/2 nF
Pwr Range(mW)	50–200	10–450	0.15–600	95–400	0.6–266	1–16	66–530	-	-	2–130
Area (mm2)	-	-	-	5.12	1.59	0.000714	5.4752	0.378	2.25	0.431

presents a performance comparison of the current design with some of the prior designs. Refs [3,28,29,30,31] are inductive converters while [8,32,33,34] are capacitive converters. The design presented here is the only hybrid converter design having both capacitive and inductive converters connected in parallel. As can be seen from the table, [3,31] have comparable output power performance. This work achieves a 70× output load range which is comparable to the design in [31] but this design is fully integrated whereas [31] uses off-chip passives. The design in [3] performs better in terms of the maximum output range but this design has a much higher power density.

5. Conclusions

Using capacitive converters to improve the efficiency at lower voltages enables a 70× output power range (Table 1) while maintaining the efficiency above 61% even at loads as low as 2 mW. The efficiency at extremely small loads could easily be further improved by implementing multiple modes for the capacitive converter [23]. Reuse of area under the inductor boosts power density from 0.387 W/mm² to 4.1 W/mm² at the cost of some degradation in efficiency(<5%). In this design we ended up using the top two metal layers for inductor due finite metal thickness in this process. Addition of a single thick metal layer optimized for inductors (as is often found in RF and mixed-signal processes) eliminates any potential power/ground bus congestion and is cheaper than off-chip magnetics.