Assessment of Global Variability in UTBB MOSFETs in Subthreshold Regime ^†

Abstract

The global variability of ultra-thin body and buried oxide (UTBB) MOSFETs in subthreshold and off regimes of operation is analyzed. The variability of the off-state drain current, subthreshold slope, drain-induced barrier lowering (DIBL), gate leakage current, threshold voltage and their correlations are considered. Two threshold voltage extraction techniques were used. It is shown that the transconductance over drain current (g_m/I_d) method is preferable for variability studies. It is demonstrated that the subthreshold drain current variability in short channel devices cannot be described by threshold voltage variability. It is suggested to include the effective body factor incorporating short channel effects in order to properly model the subthreshold drain current variability.

1. Introduction

Ultra-thin body and buried oxide (UTBB) technology is promising for future MOSFET nodes due to its short channel effects immunity [1] and low variability [2]. The quantification of global variability improves fabrication process optimization and MOSFET model extraction. Whereas threshold voltage variability has been widely studied [3,4,5], subthreshold variability has received little attention. Characterization of subthreshold variability has become essential nowadays. Design is shifting towards the subthreshold regime for low power applications. Furthermore, the off-state drain current variability is important for stand-by power considerations.

The variability of MOSFET parameters is due to geometry fluctuations, the granularity of materials and doping randomness [6]. Doping randomness affects MOSFET variability through random dopant fluctuations (RDF) in the channel, the source and drain extensions and in the ground plane. Fabrication imperfections cause the variability of device dimensions, such as line edge roughness (LER), as well as Si channel and buried oxide (BOX) thicknesses. The granularity of gate material also contributes to the parameter variability of a device. Typically, the channel of an FD SOI device (including UTBB) is left undoped, thus eradicating RDF in the channel. In general, well-controlled process, small, short channel effects [3] and low series resistance [7] contribute to the low variability of FD SOI [1,2,5,7].

The aim of the study is to perform a qualitative analysis of global subthreshold parameter variability. Such an analysis can be carried out even on devices that are not yet fully optimized from the short channel effects perspective. The parameters of interest for the subthreshold regime are the off-state drain current (I_d-off) and gate current (I_g-off), threshold voltage (V_th), subthreshold slope (S) and drain-induced barrier lowering (DIBL). The off-state currents were extracted at gate voltage V_g = 0 V. Absolute values of the correlation coefficients are presented in this work. This paper is an extended version of our previous work [8]. It also incorporates some results from [9]. The data from [9] were improved by doubling the number of characterized devices, thus enhancing statistics.

2. Experimental Details

The devices studied in this work are fully-depleted (FD) silicon-on-insulator (SOI) n-channel MOSFETs fabricated on 25 nm-thick BOX. The top Si layer is 7.5 nm-thick. The channel is left undoped allowing the avoidance of RDF. The n-type ground plane was incorporated below BOX. The equivalent oxide thickness of the gate dielectric is 1.2 nm. Devices with gate lengths L_g from 28 to 88 nm and a gate width W_g of 10 µm are characterized. 106 transistors of each gate length are measured across the wafer. A 3-sigma normality test was carried out to exclude outliers.

Two threshold voltage extraction techniques are used in this work: using the constant current method, V_th is obtained as V_g, where I_d/(W_g/L_g)) = 10⁻⁷ A; the transconductance over drain current (g_m/I_d) method is described in [10,11,12]. Both extraction methods are widely used in the linear and saturation regimes of operation.

3. Results and Discussion

Figure 1 shows the ratios of standard deviations (σ) to mean values (μ) of I_d-off, S, DIBL and V_th extracted using the g_m/I_d technique at drain voltages V_d of 1 V and 20 mV. As expected, shorter devices exhibit stronger variation in both regimes of operation. It can be seen that I_d-off variability is rather strong and presumably impacted by the variability of other parameters (e.g., V_th, S and DIBL).

Figure 1. The ratio of standard deviation over the mean value of the off-state drain current (I_d-off), subthreshold slope (S), drain-induced barrier lowering (DIBL) and threshold voltage (V_th) extracted using the g_m/I_d method in devices with gate lengths of 28 and 88 nm.

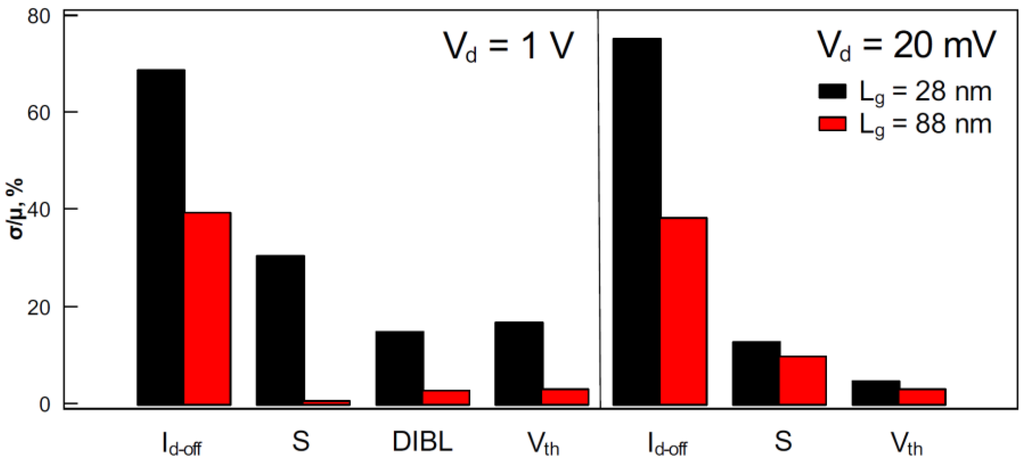
Figure 1. The ratio of standard deviation over the mean value of the off-state drain current (I_d-off), subthreshold slope (S), drain-induced barrier lowering (DIBL) and threshold voltage (V_th) extracted using the g_m/I_d method in devices with gate lengths of 28 and 88 nm.

3.1. Off-State Gate Current

Figure 2 shows σI_d-off in devices with gate lengths from 28 nm to 88 nm in linear and saturation regimes. The higher variability of I_d-off is observed in shorter devices. Different parameters, such as short channel effects, I_g and V_th, have an impact on I_d in the off-state.

First, I_g-off is considered. The standard deviation of I_g-off is shown in Figure 2. An increase of σI_g-off with V_d can be related to the amplified generation current, which is a function of V_d [13]. There is no pronounced dependence of I_g-off variability on the gate length. Furthermore, σI_g-off remains small compared with σI_d-off, except for the longest devices at V_d of 1 V. Absolute values of I_g-off are also negligibly small compared with I_d-off (except for devices with a gate length of 88 nm at V_d of 1 V). Therefore, the effect of I_g-off variability on I_d-off is expected to be negligible. In order to confirm this, Figure 3 plots coefficients of correlation between I_g-off and I_d-off for devices with various gate lengths at V_d of 1 V and 20 mV and at temperatures of 25 and 125 °C. Only in the case of V_d of 1 V and a temperature of 25 °C does the correlation become stronger with a gate length increase as the I_g-off component of I_d-off increases. I_g-off is small at low V_d, as the gate-induced drain leakage (GIDL) is alleviated. This is confirmed by weak I_g-off and I_d-off correlation at V_d of 20 mV for all gate lengths. With a temperature rise, due to V_th shift and S degradation, I_d increases stronger than I_g. Thus, the effect of I_g on I_d decreases, and the correlation between I_d-off and I_g-off reduces (Figure 3). The above discussion suggests that the effect of I_g-off variability on I_d-off variability should be accounted for only in relatively long devices at high V_d and room temperature, whereas in other cases, it can be neglected.

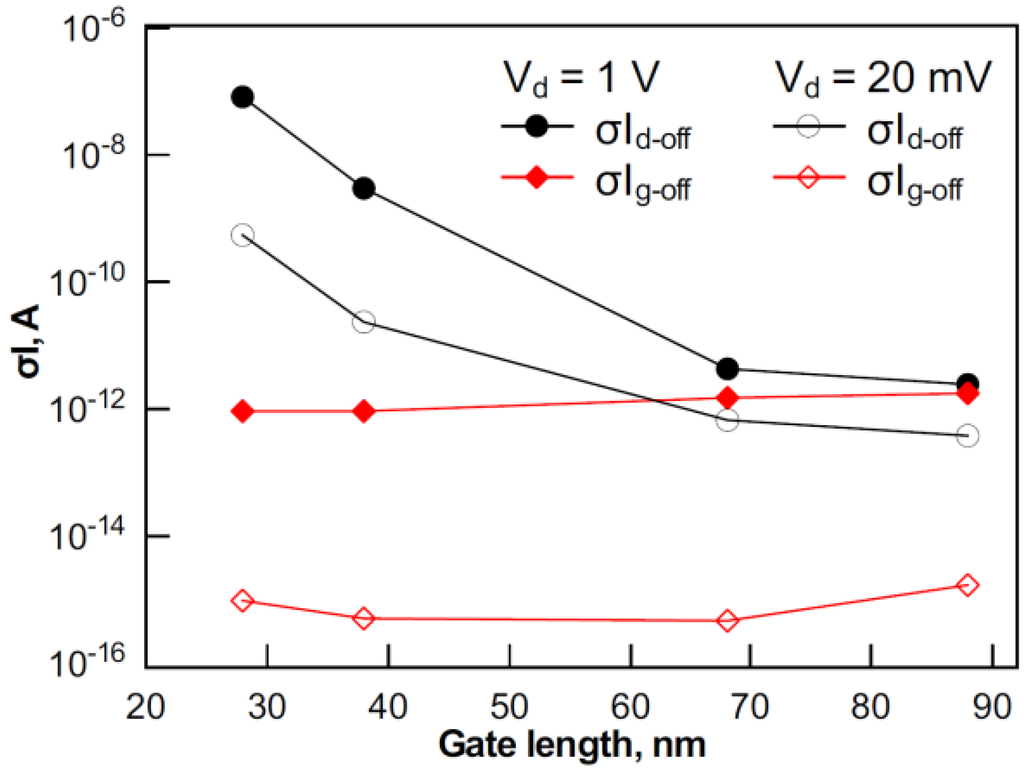
Figure 2. σI_d-off and σI_g-off variations with gate length at drain voltages (V_d) of 20 mV and 1 V.

Figure 2. σI_d-off and σI_g-off variations with gate length at drain voltages (V_d) of 20 mV and 1 V.

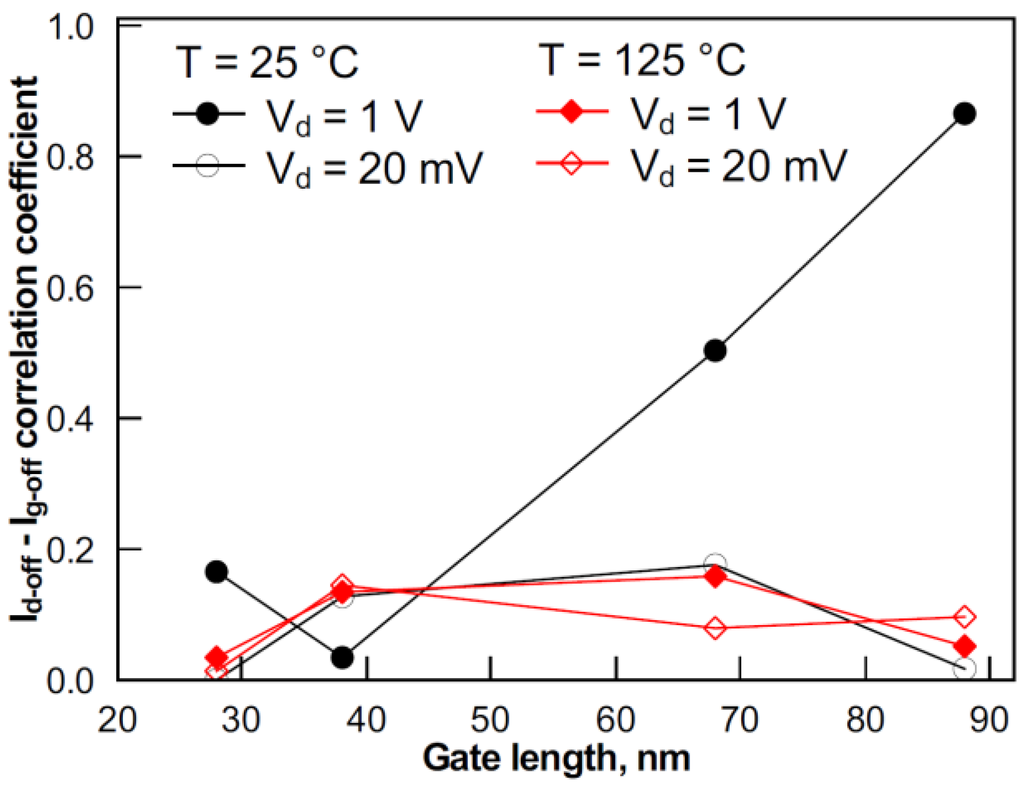
Figure 3. The I_d-off-I_g-off correlation in devices with various gate lengths at V_d of 20 mV and 1 V and temperatures of 25 °C and 125 °C.

Figure 3. The I_d-off-I_g-off correlation in devices with various gate lengths at V_d of 20 mV and 1 V and temperatures of 25 °C and 125 °C.

3.2. Threshold Voltage

Secondly, the effect of V_th variability on σI_d-off is considered. Figure 4 shows σV_th for devices with gate lengths from 28 to 88 nm at V_d of 20 mV and 1 V. The variability in shorter devices is obviously stronger than in long devices. At V_d of 1 V, σV_th is larger than at V_d of 20 mV in short devices. However, in long devices, values of σV_th are similar in both regimes of operation. At V_d of 1 V in the shortest devices, σV_th is considerably different for two V_th extraction methods. The g_m/I_d method results in a lower V_th variability than the constant current method. This is due to V_th extraction from different parts of current-voltage characteristics and the smaller sensitivity of the g_m/I_d method to short channel effects (S, DIBL), as discussed in [9]. This difference vanishes in long devices.

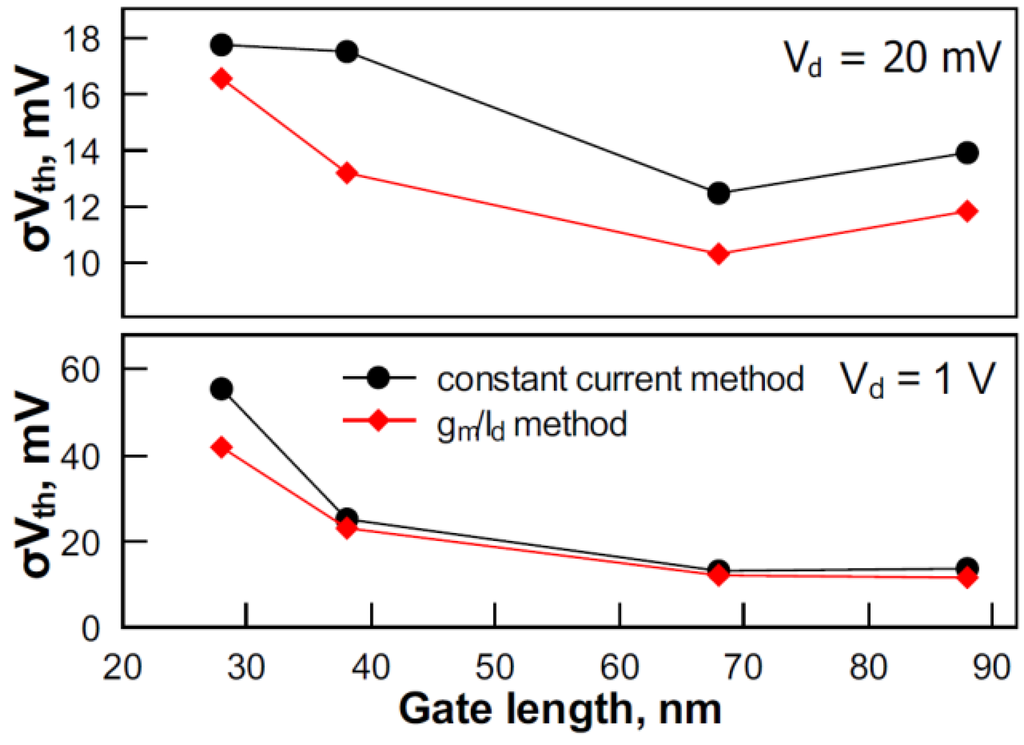
Figure 4. σV_th obtained using the constant current and g_m/I_d methods at V_d of 20 mV (top); and V_d of 1 V (bottom).

Figure 4. σV_th obtained using the constant current and g_m/I_d methods at V_d of 20 mV (top); and V_d of 1 V (bottom).

Since in the subthreshold regime, I_d exponentially depends on V_th, it is generally assumed that σI_d in this region is dominated by σV_th. This holds true for the relatively long devices studied in this work. Correlation between I_d-off and V_th at V_d of 1 V is plotted in Figure 5 for 28 nm- and 100 nm-long devices. V_th was extracted using the constant current and g_m/I_d methods. To quantify the correlation, Figure 6 plots the coefficients of correlation between I_d and V_th (extracted using the constant current method) as a function of V_g in devices with various gate lengths. In the subthreshold region, correlation is strong for 68 and 88 nm-long devices. In strong inversion, the correlation reduces due to the dominance of mobility and series resistance variability [13]. However, in shorter devices, the I_d and V_th correlation significantly decreases, not only in strong inversion, but also in the subthreshold regime. This effect is also seen in Figure 7, where variation of the I_d-off and V_th correlation coefficients with the gate length is plotted. Therefore, the variability of other parameters apart from I_g-off and V_th has to be taken into account.

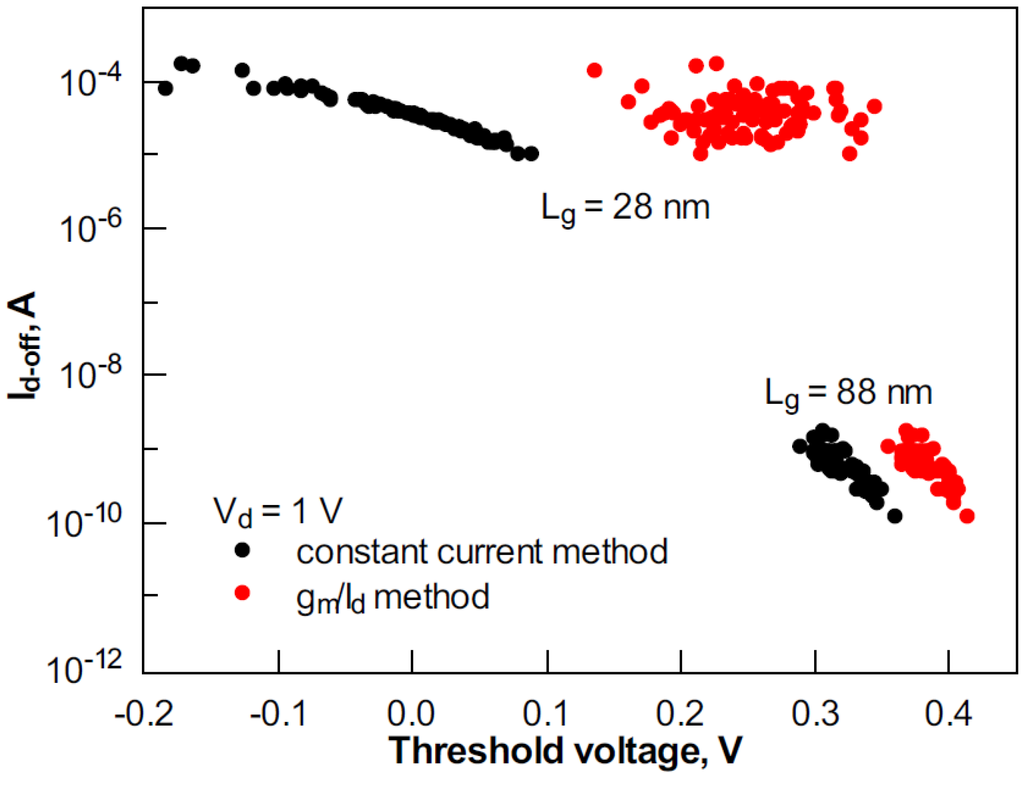
Figure 5. The variation of I_d-off at V_d = 1.0 V with V_th extracted using the constant current and g_m/I_d methods at V_d = 1 V in devices with gate lengths of 28 nm and 88 nm.

Figure 5. The variation of I_d-off at V_d = 1.0 V with V_th extracted using the constant current and g_m/I_d methods at V_d = 1 V in devices with gate lengths of 28 nm and 88 nm.

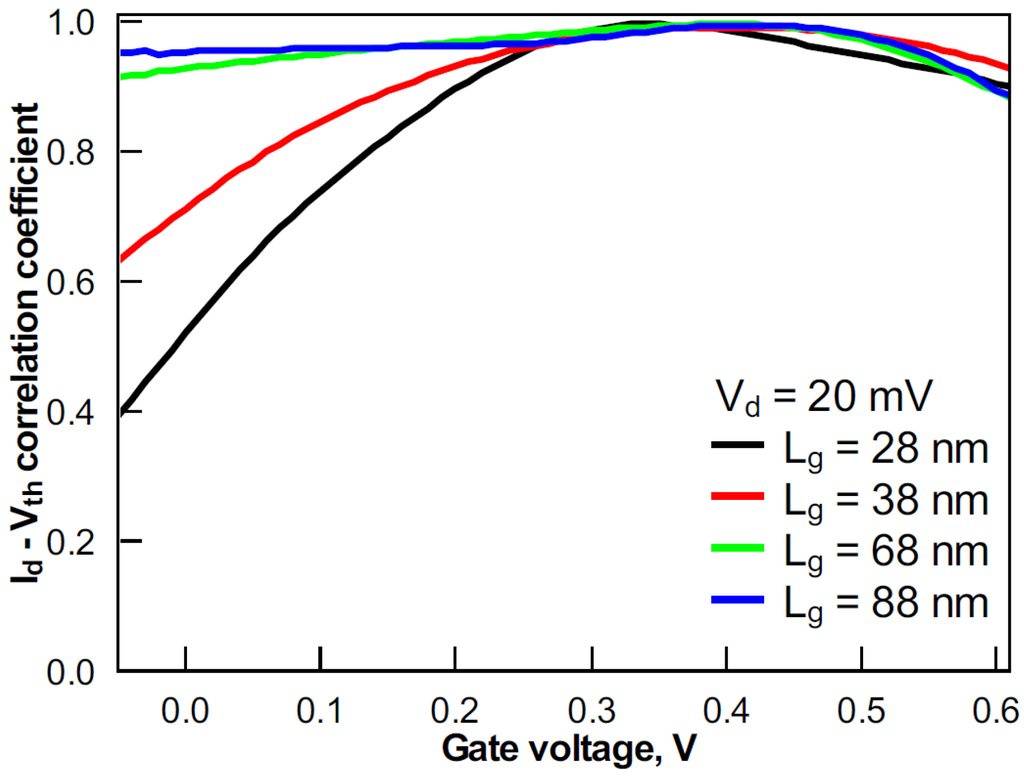
Figure 6. The variation of the I_d-V_th correlation coefficient with V_g in devices with various gate lengths. V_th was obtained using the constant current method.

Figure 6. The variation of the I_d-V_th correlation coefficient with V_g in devices with various gate lengths. V_th was obtained using the constant current method.

It is important to note the importance of the V_th extraction method in variability studies. In [9], it was shown that the g_m/I_d V_th extraction method is beneficial over other techniques from the short channel effects perspective. A similar property can be observed in Figure 7. The low correlation of V_th‑gm/Id and I_d-off in short devices suggests the parasitic effect immunity of V_th extraction using the g_m/I_d technique [11,12] compared with the constant current method, as the latter is obviously sensitive to DIBL [9].

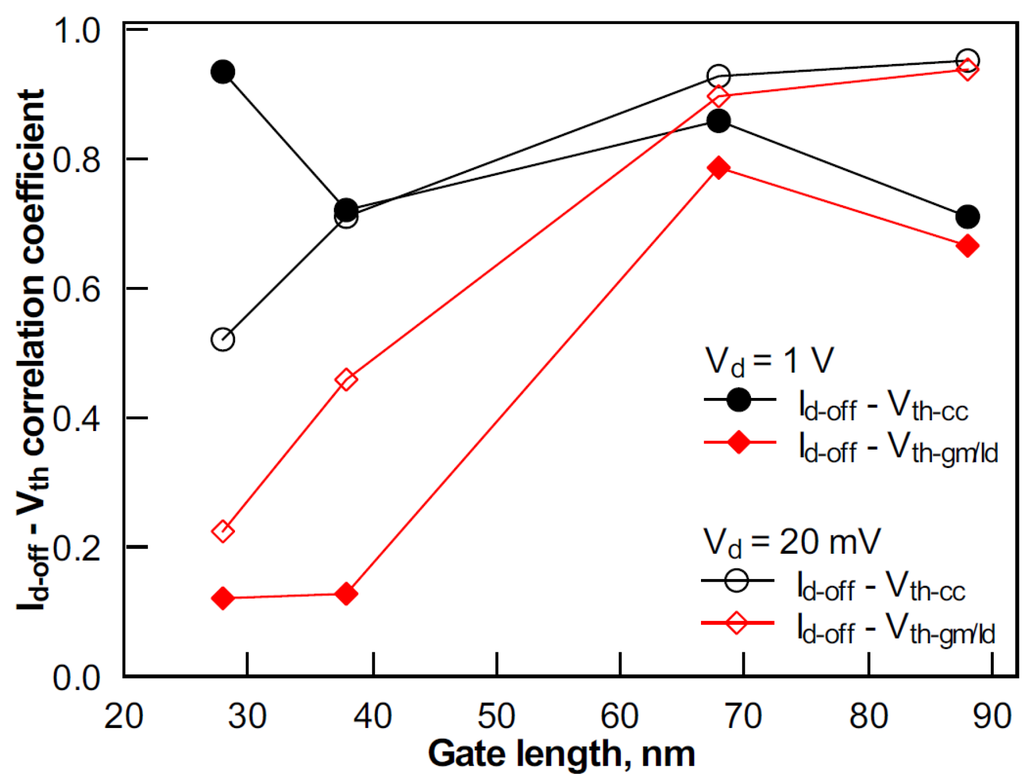
Figure 7. The V_th-I_d-off correlation coefficients in devices with various gate lengths. V_th was obtained using the constant current (cc) and g_m/I_d methods.

Figure 7. The V_th-I_d-off correlation coefficients in devices with various gate lengths. V_th was obtained using the constant current (cc) and g_m/I_d methods.

3.3. Short Channel Effects

Thirdly, an impact of short channel effect variability on subthreshold I_d is considered. The data in Figure 8 show strong correlation between I_d-off and DIBL in shorter devices. The correlation coefficient decreases to ~0.2 and even more for devices with gate lengths of 68 nm and 88 nm, where the average DIBL is below 60 mV/V. Correlation between I_d-off and V_th (extracted at V_d of 20 mV) featured an opposite trend increasing with the gate length, as seen from Figure 7. Therefore, in devices with gate lengths of 68 and 88 nm, I_d-off and V_th variability is caused by the same mechanisms, while the variability of DIBL and subthreshold slope dominates in short devices.

Figure 8. The DIBL-I_d-off correlation coefficients in devices with various gate lengths.

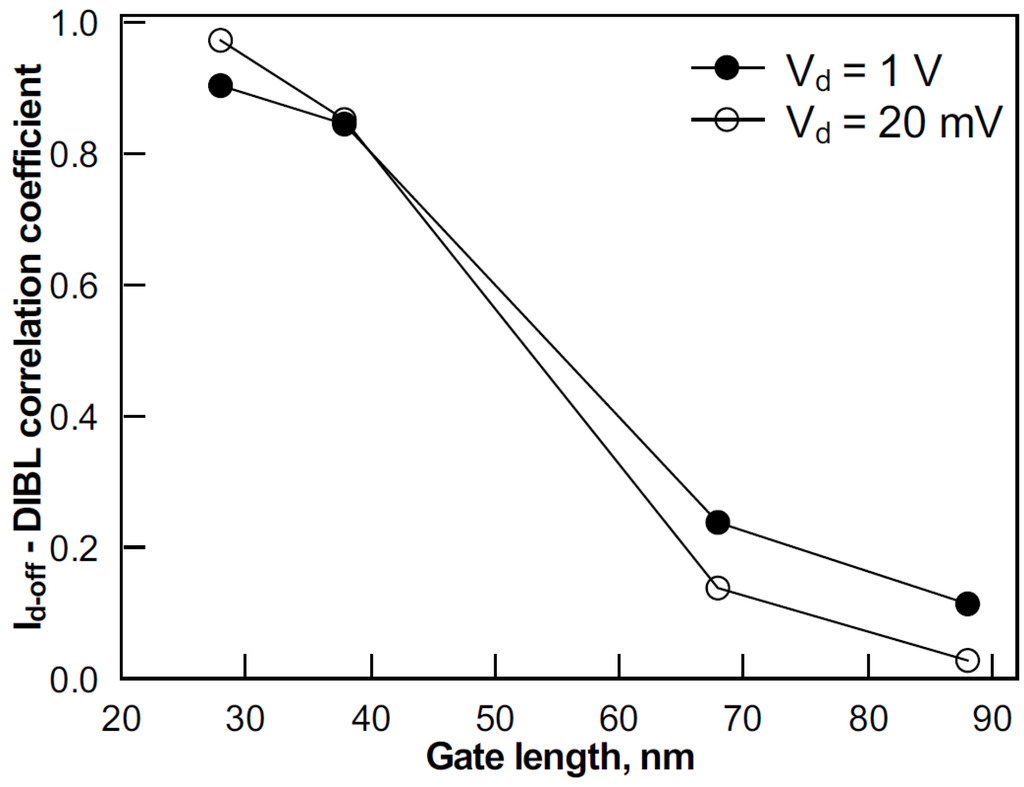
Figure 8. The DIBL-I_d-off correlation coefficients in devices with various gate lengths.

Figure 9 presents the variation of the subthreshold slope and V_th extracted using the constant current and the g_m/I_d methods, at high V_d in saturation. Scatter is much stronger in short devices than in longer ones, as expected. Furthermore, in short devices, the correlation of the subthreshold slope with V_th-cc is stronger than the correlation with V_th-gm/Id. This correlation is quantified in Figure 10. Figure 10 shows DIBL and V_th, as well as the S and V_th correlation in 28 nm- and 88 nm-long devices at 25 °C and 125 °C. V_th was extracted with the g_m/I_d and constant current methods. V_th extracted using the g_m/I_d technique shows little dependence on short channel effects, even at high temperatures. V_th obtained with the constant current method shows very strong correlation with DIBL at room and elevated temperatures. This comparison confirms that the g_m/I_d technique enables an evaluation of intrinsic V_th, only slightly affected by short channel effects. Evaluation of V_th free of short channel effects is of interest for device models that incorporate variability. If variability is imposed on each of the correlating parameters in a model, the total performance variability might be overestimated [9]. This can be avoided either by including correlation factors in the models or using independent (zero correlation) parameters.

Figure 9. Variations of V_th obtained using the g_m/I_d and constant current methods as a function of the subthreshold slope.

Figure 9. Variations of V_th obtained using the g_m/I_d and constant current methods as a function of the subthreshold slope.

Figure 10. The V_th-DIBL and V_th-S correlation coefficients in devices with gate lengths of 28 nm and 88 nm at 25 °C and 125 °C temperatures. V_th was obtained using the constant current and g_m/I_d methods.

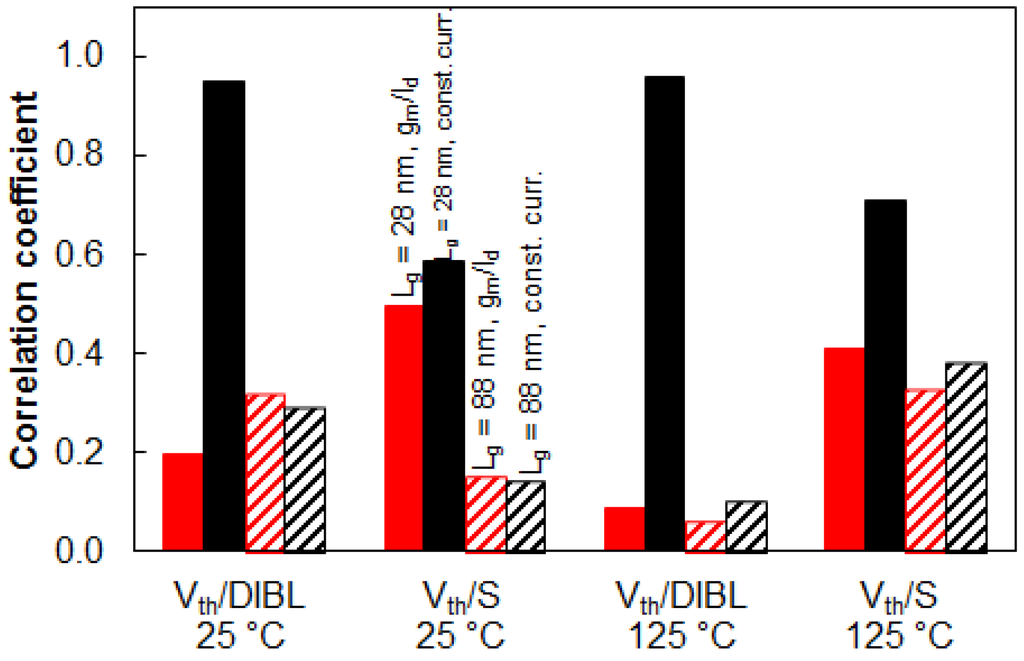
Figure 10. The V_th-DIBL and V_th-S correlation coefficients in devices with gate lengths of 28 nm and 88 nm at 25 °C and 125 °C temperatures. V_th was obtained using the constant current and g_m/I_d methods.

The temperature dependence of the I_d-off and DIBL correlation is shown in Figure 11. In the case of short devices (gate lengths of 28 nm and 38 nm), the correlation factor being very strong shows nearly no dependence on temperature. However, in long devices (gate lengths of 68 nm and 88 nm), the correlation between I_d-off and DIBL rises with temperature. This can be explained by the DIBL increase with temperature, as the inset in Figure 11 shows.

Figure 11. The I_d-off–DIBL correlation in devices with various gate lengths in the 25–125 °C temperature range at V_d of 1 V. The inset shows the DIBL temperature dependence.

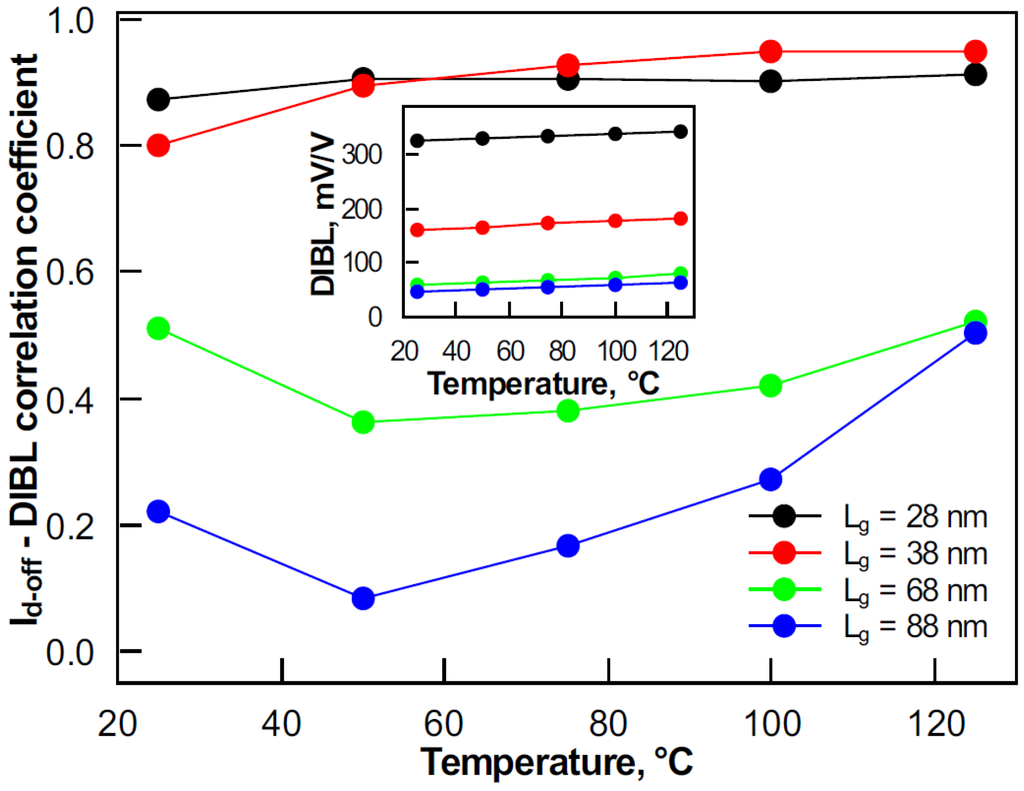
Figure 11. The I_d-off–DIBL correlation in devices with various gate lengths in the 25–125 °C temperature range at V_d of 1 V. The inset shows the DIBL temperature dependence.

3.4. Drain Current Variability Modelling

Following the above discussion, Figure 12 compares σI_d and g_m·σV_th dependences on V_g in devices with a gate length of 88 nm at V_d of 1 V and 20 mV. σI_d agrees well with g_m·σV_th in around-threshold and subthreshold regions, i.e., moderate and weak inversion. In order to ease the comparison of devices with different gate lengths and at various temperatures, the results are plotted as a function of the gate overdrive V_g–V_th.

Figure 12. Variation of σI_d and its components with gate overdrive at V_d of 20 mV and 1 V at 25 °C in devices with a gate length of 88 nm. V_th was extracted using the g_m/I_d method.

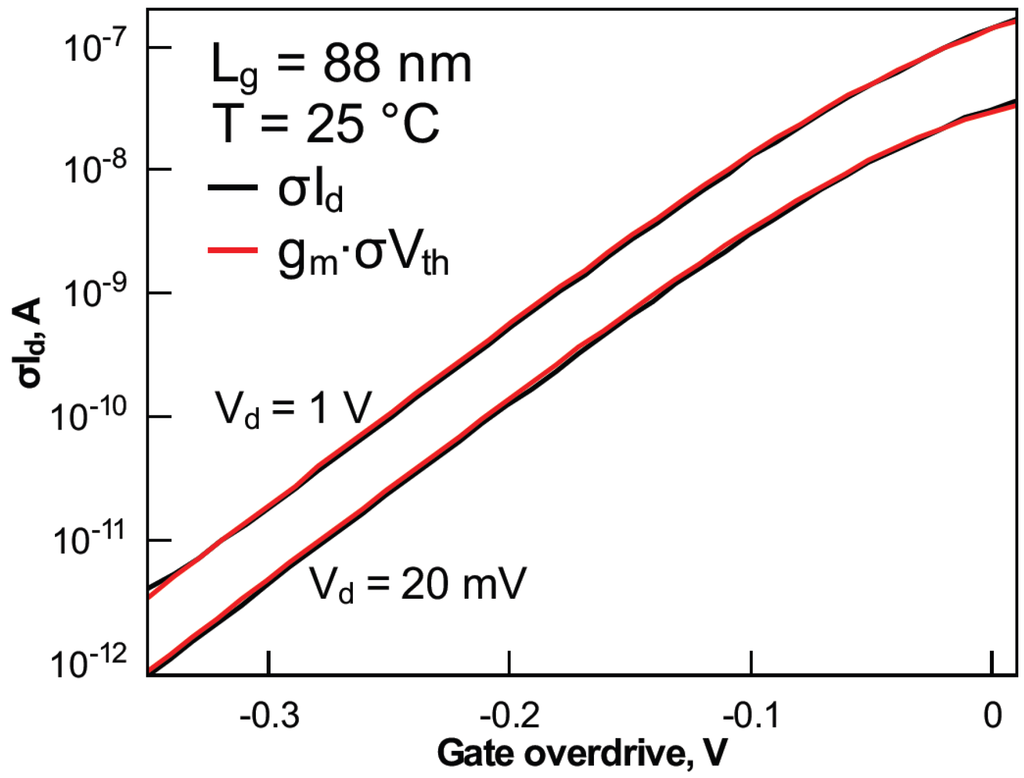
Figure 12. Variation of σI_d and its components with gate overdrive at V_d of 20 mV and 1 V at 25 °C in devices with a gate length of 88 nm. V_th was extracted using the g_m/I_d method.

The situation is different in short channel devices. As seen from Figure 13, σ_Id can be described by g_m·σV_th only in a very narrow V_g range around V_th. In the subthreshold, the curves strongly deviate. In [14], it was suggested to consider the variability of the body factor in weak inversion in addition to V_th. The impact of the body factor dependences on V_g and temperature was emphasized and related to depletion width variation [14]. The UTBB devices studied here remain fully-depleted in the whole weak-to-moderate inversion range at any temperature. Furthermore, Si and oxide thickness fluctuations are not significant, due to the well-controlled fabrication process [2,9]. In [2], reflectometry was used to evaluate top silicon layer thickness variability and correlate it with electrically obtained data. Furthermore, in [9], it was found that global variability does not degrade with temperature through Si layer thickness variation, confirming that the process matches σI_d sufficiently well (Figure 12). As this is not the case in the shortest device (Figure 13), we consider the effective body factor n, which includes short channel effects. Thus, in our case, n dependence on V_g originates from the gate and the drain counteraction on electrostatics. In this work, n (V_g) is derived in the first approximation from S(V_g) according to $S=nkT/q·\text{ln}(10)$ , where q is the elementary charge, k is the Boltzmann constant and T is the temperature. At V_d of 20 mV, the combined effect of σV_th and σn can fit σI_d sufficiently well:

$$\text{σ}{I}_d=\sqrt{{\left(g_m\text{σ}{V}_{th}\right)}^2+{\left(I_d\text{σ}n\right)}^2}$$

(1)

However at V_d of 1 V, Equation (1) does not allow one to fit σI_d. This is due to amplification of short channel effects at V_d of 1 V and, thus, their stronger impact on V_th. In order to fit σI_d, V_th and n, correlation coefficient ρ has to be accounted for:

$$\text{σ}{I}_d=\sqrt{{\left(g_m\text{σ}{V}_{th}\right)}^2+{\left(I_d\text{σ}n\right)}^2-2\text{ρ}{g}_m\text{σ}{V}_{th}{I}_d\text{σ}n}$$

(2)

This approach is shown to work sufficiently well at elevated temperature. In Figure 14, it is shown that σI_d at 125 °C is fitted well when the V_g-dependent effective body factor and its correlation with the V_th are considered (Equation (2)).

Figure 13. Variation of σI_d and its components with gate overdrive at V_d of 20 mV and 1 V at 25 °C in devices with a gate length of 28 nm. V_th was extracted using the g_m/I_d method.

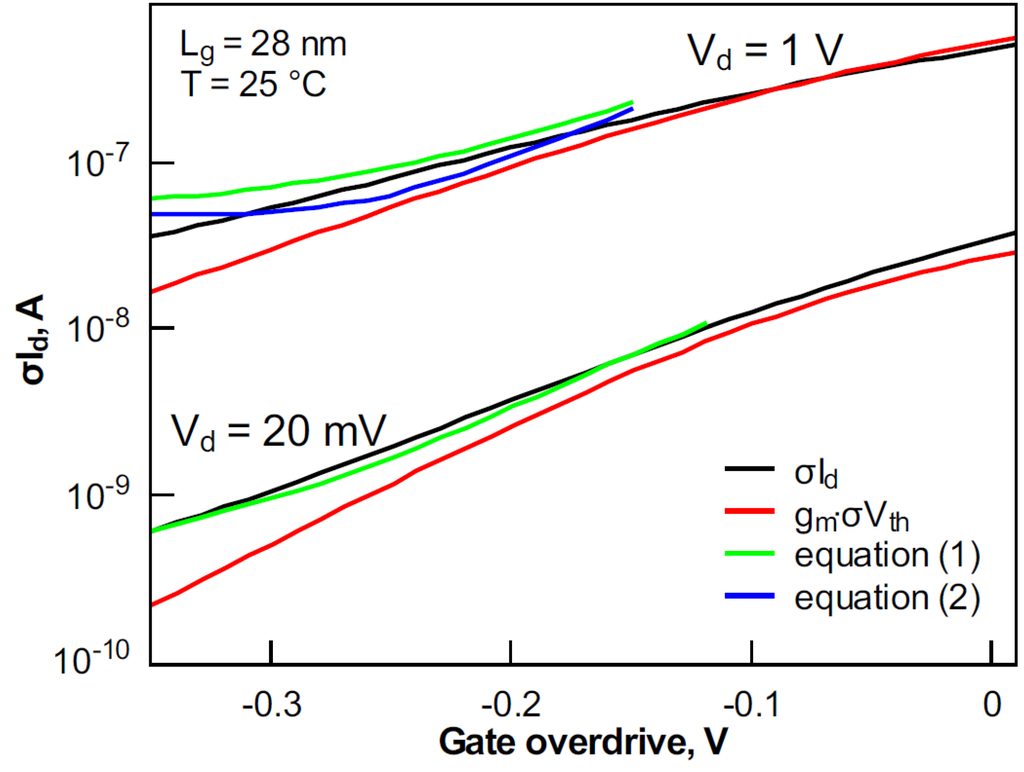
Figure 13. Variation of σI_d and its components with gate overdrive at V_d of 20 mV and 1 V at 25 °C in devices with a gate length of 28 nm. V_th was extracted using the g_m/I_d method.

The results presented in Figure 12, Figure 13 and Figure 14 were obtained using the g_m/I_d V_th extraction technique. Figure 15 shows σI_d fitting in 28 nm-long devices at 25 °C with V_th obtained using the constant current method. The fitting is acceptable at V_d of 20 mV, as short channel effects are not strongly pronounced. However, at V_d of 1 V, the fitting works only in a very narrow V_g region close to V_th. This can be explained by the strong impact of short channel effects on the constant current extraction of V_th. This again confirms the advantages of the g_m/I_d V_th extraction method for variability assessment.

Further σI_d modelling improvement can be done by accounting for GIDL in the very low V_g region. In strong inversion, mobility and series resistance should be considered [13].

Figure 14. Variation of σI_d and its components with gate overdrive at V_d of 20 mV and 1 V at 125 °C in devices with a gate length of 28 nm. V_th was extracted using the g_m/I_d method.

Figure 14. Variation of σI_d and its components with gate overdrive at V_d of 20 mV and 1 V at 125 °C in devices with a gate length of 28 nm. V_th was extracted using the g_m/I_d method.

Figure 15. Variation of σI_d and its components with gate overdrive at V_d of 20 mV and 1 V at 25 °C in devices with a gate length of 28 nm. V_th was extracted using the constant current method.

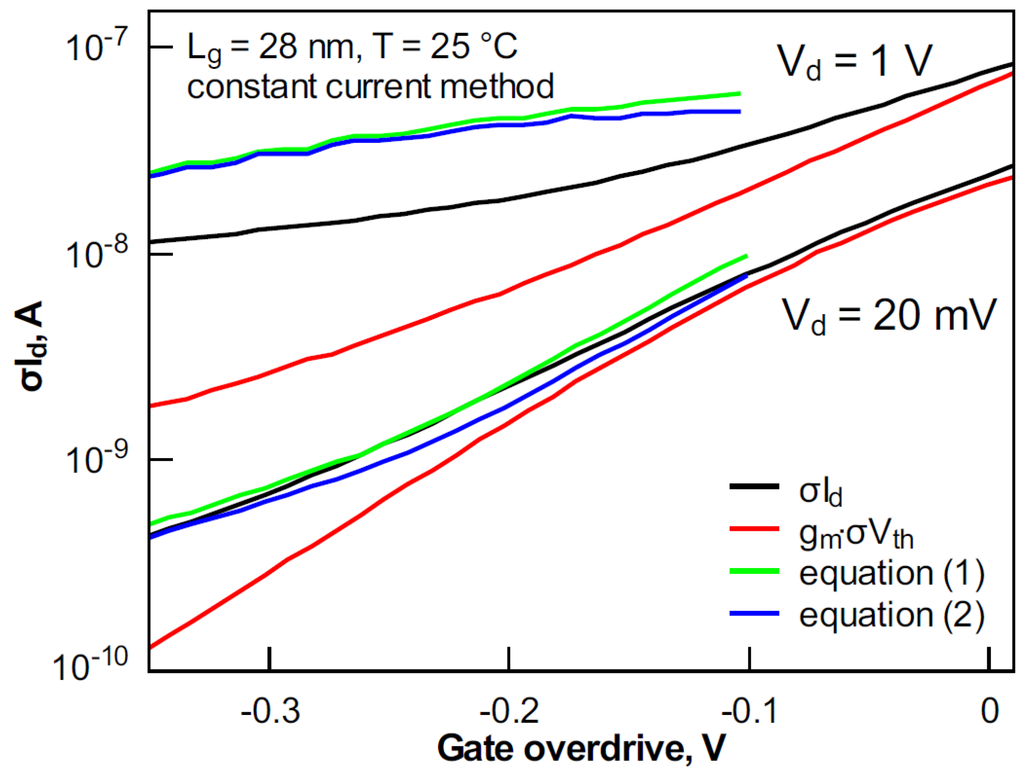
Figure 15. Variation of σI_d and its components with gate overdrive at V_d of 20 mV and 1 V at 25 °C in devices with a gate length of 28 nm. V_th was extracted using the constant current method.

4. Conclusions

The global variability of UTBB devices in the subthreshold has been analyzed through I_d-off, I_g-off, S, V_th, DIBL and their correlations. A generally used approach to model σI_d using σV_th is shown to work well for long devices. For short channel devices, an improved procedure that accounts for the V_g-dependent effective body factor (incorporating short channel effects) was proposed and validated in the temperature range from 25 °C to 125 °C. This is important for power consumption considerations and compact model parameter extraction in the off-regime. It was shown that the g_m/I_d V_th extraction technique is beneficial for accurate variability assessment and modeling.