Design and Analysis of an Ultra-Wideband High-Precision Active Phase Shifter in 0.18 μm SiGe BiCMOS Technology
Abstract
1. Introduction
2. Analysis and Design of the Active Phase Shifter Circuit
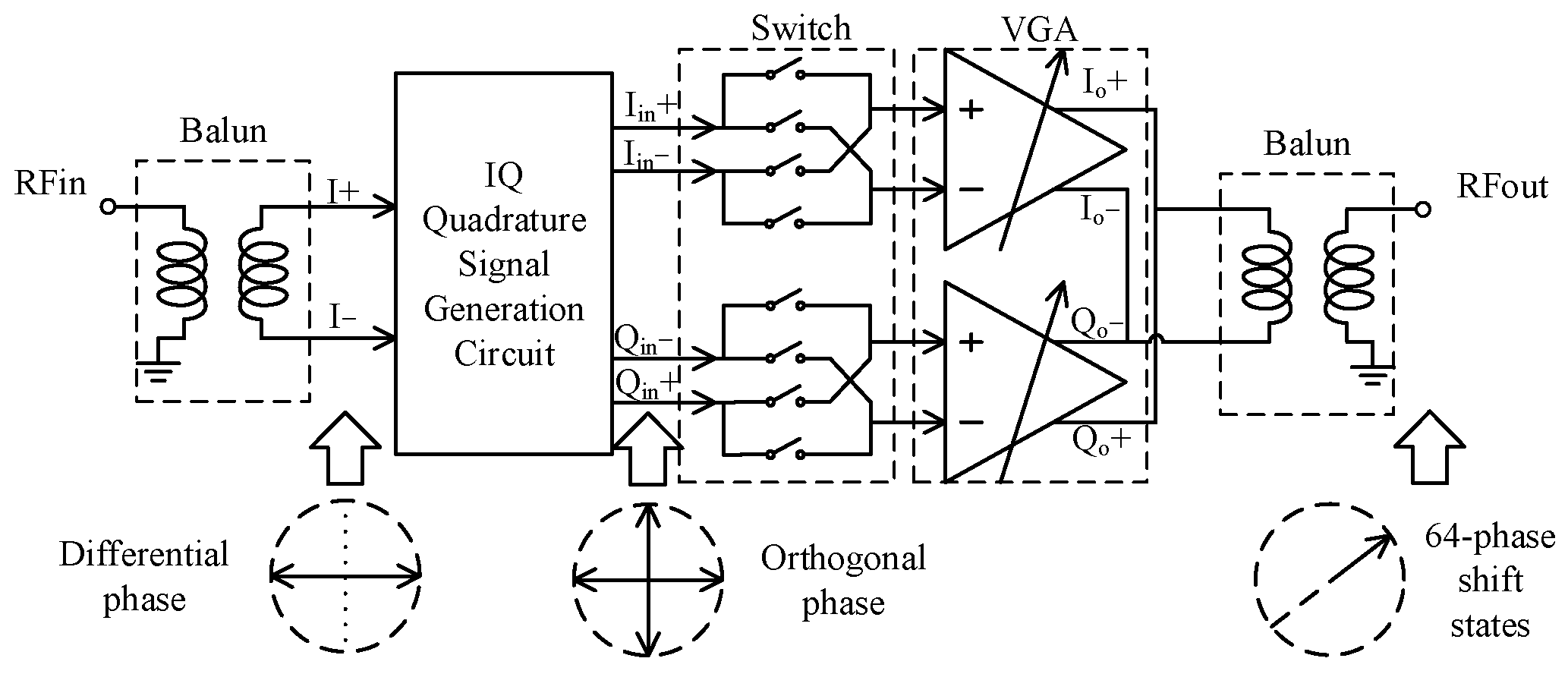
2.1. Circuit Architecture
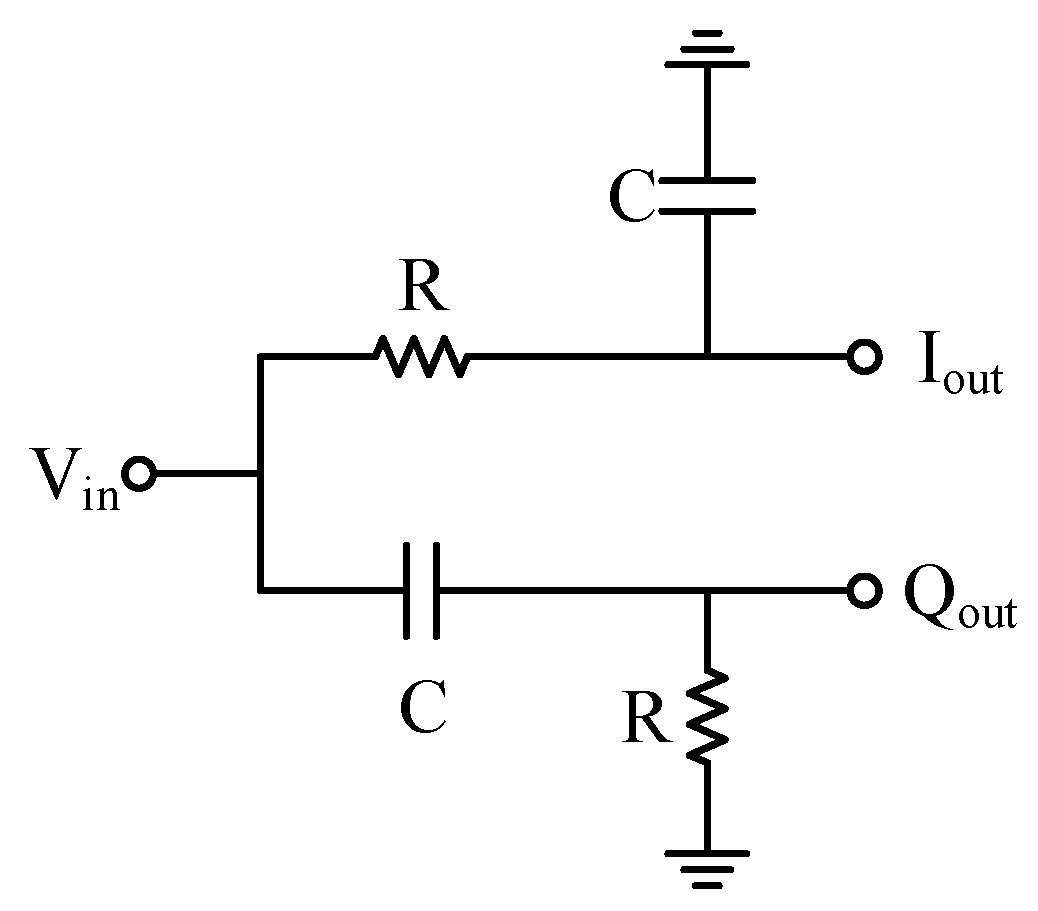
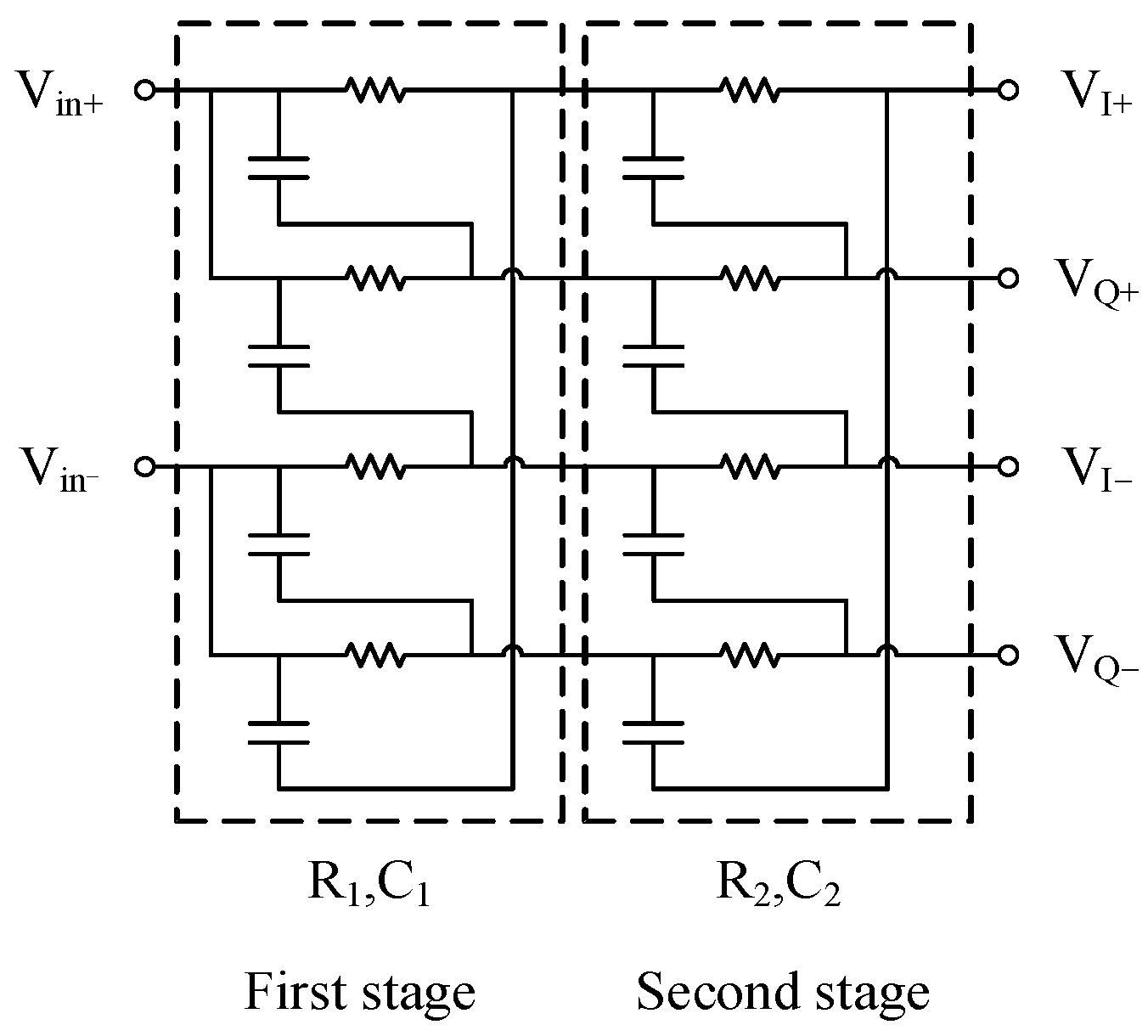
2.2. Quadrature Signal Generation Circuit Design
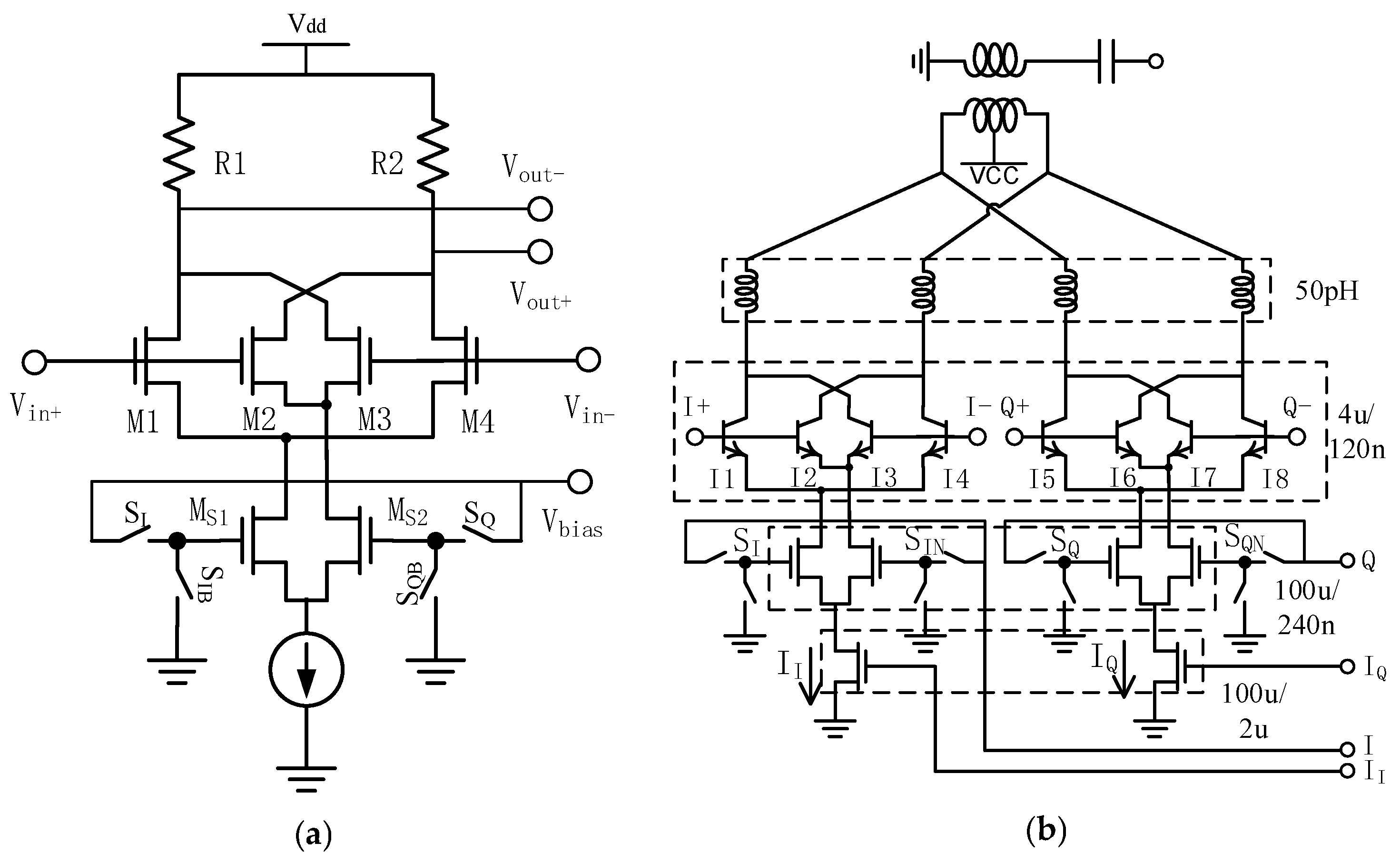
2.3. Vector Modulator Design
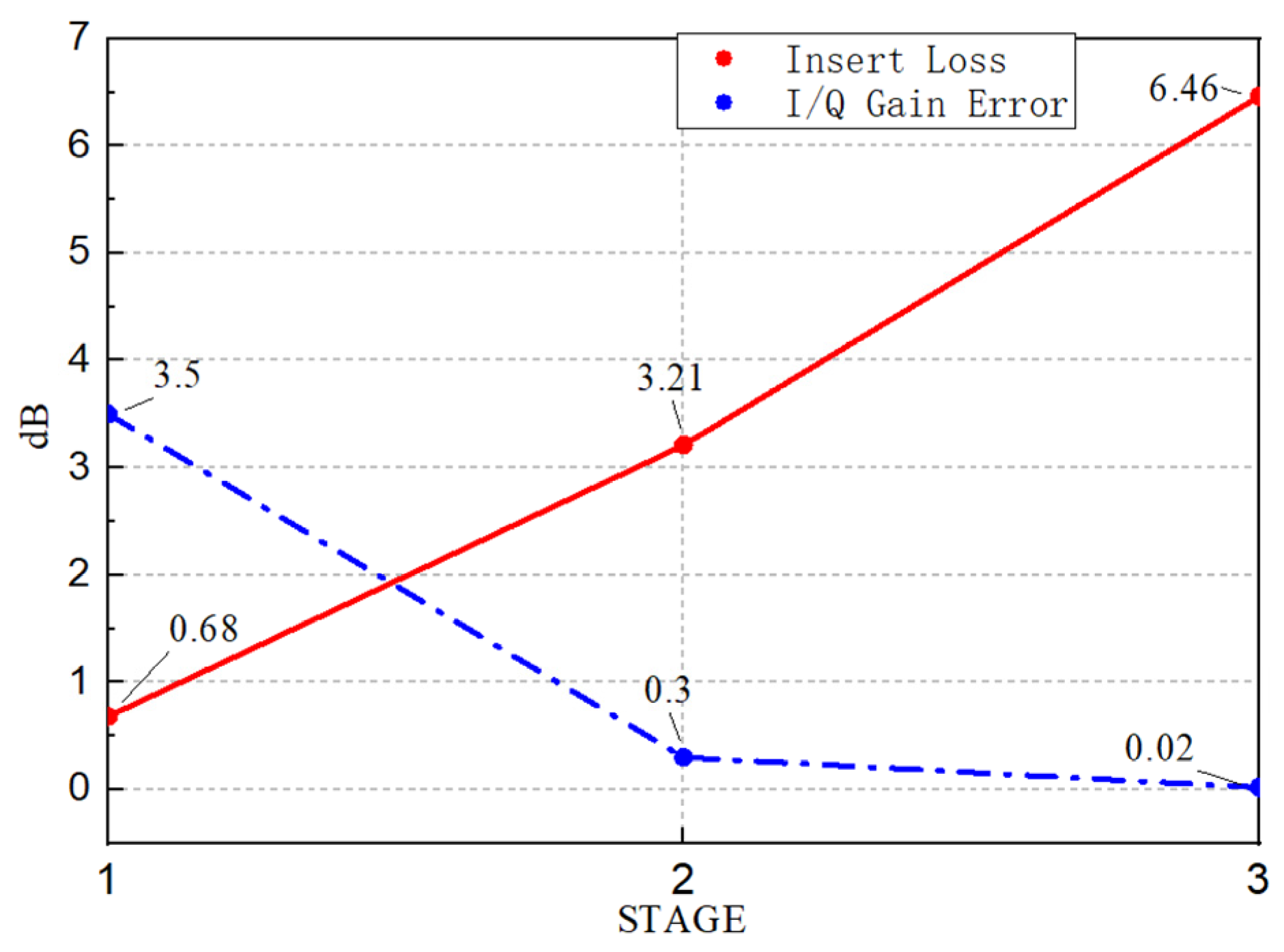
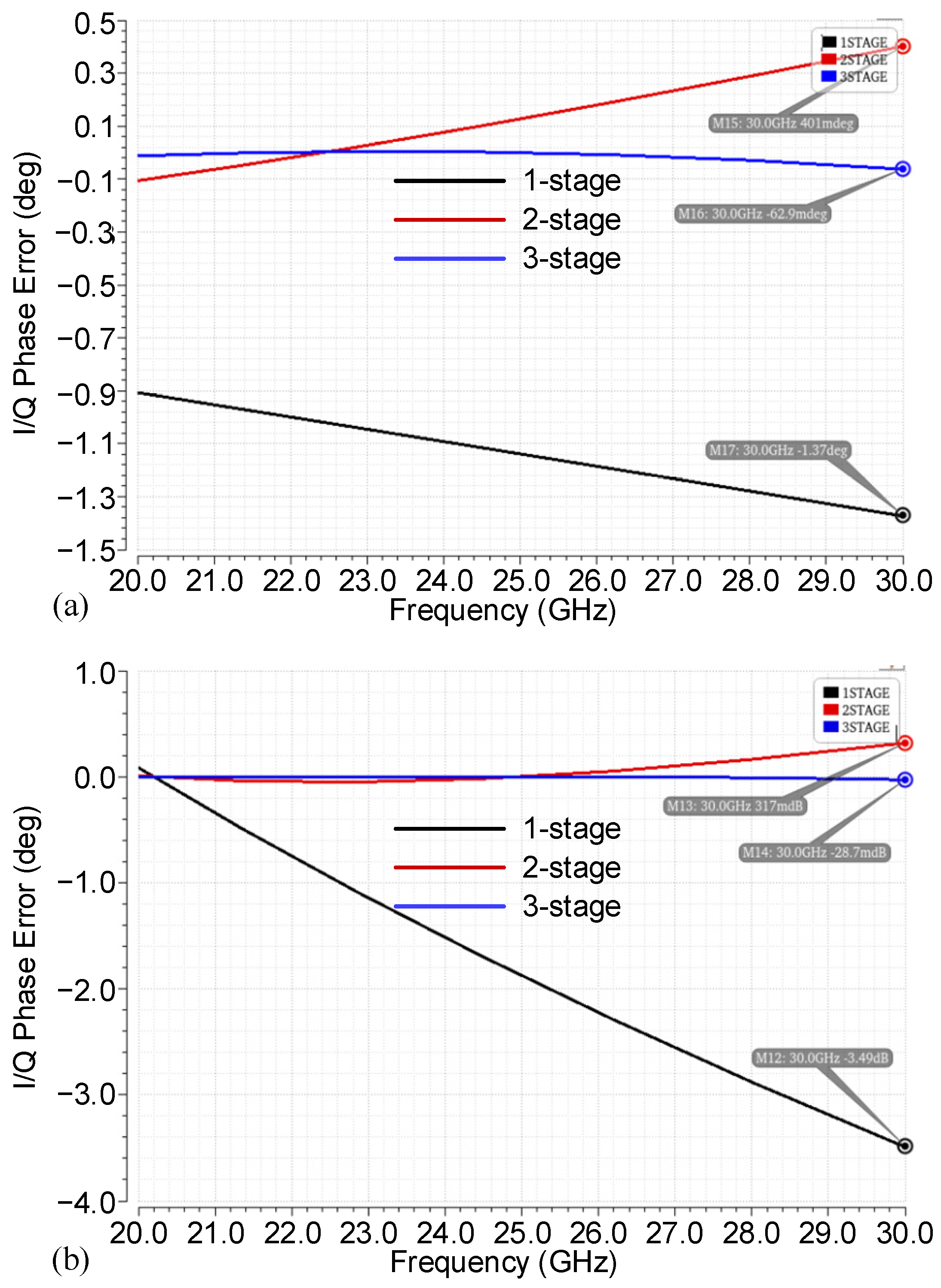
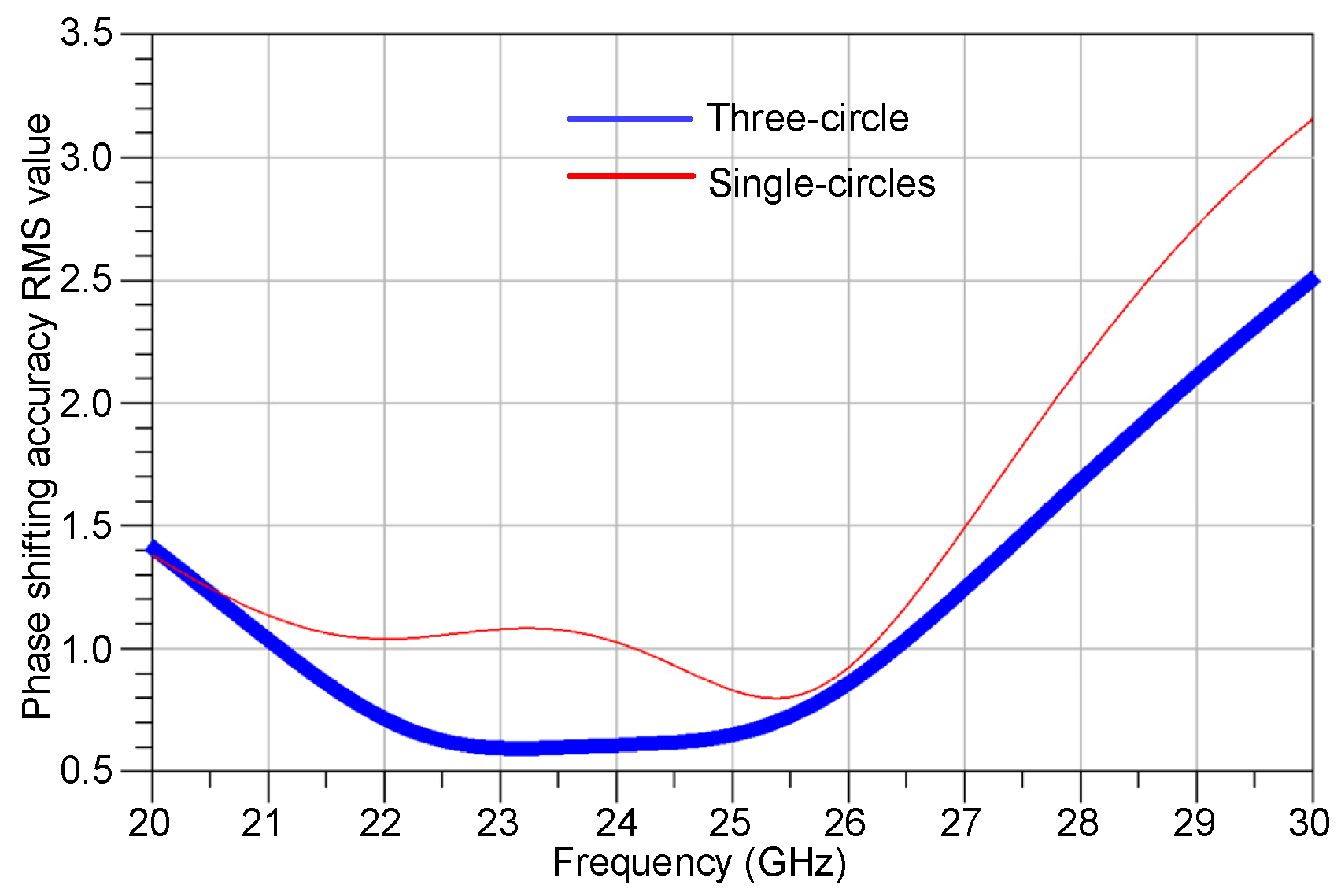
2.4. Amplitude Fluctuation Mitigation Technique
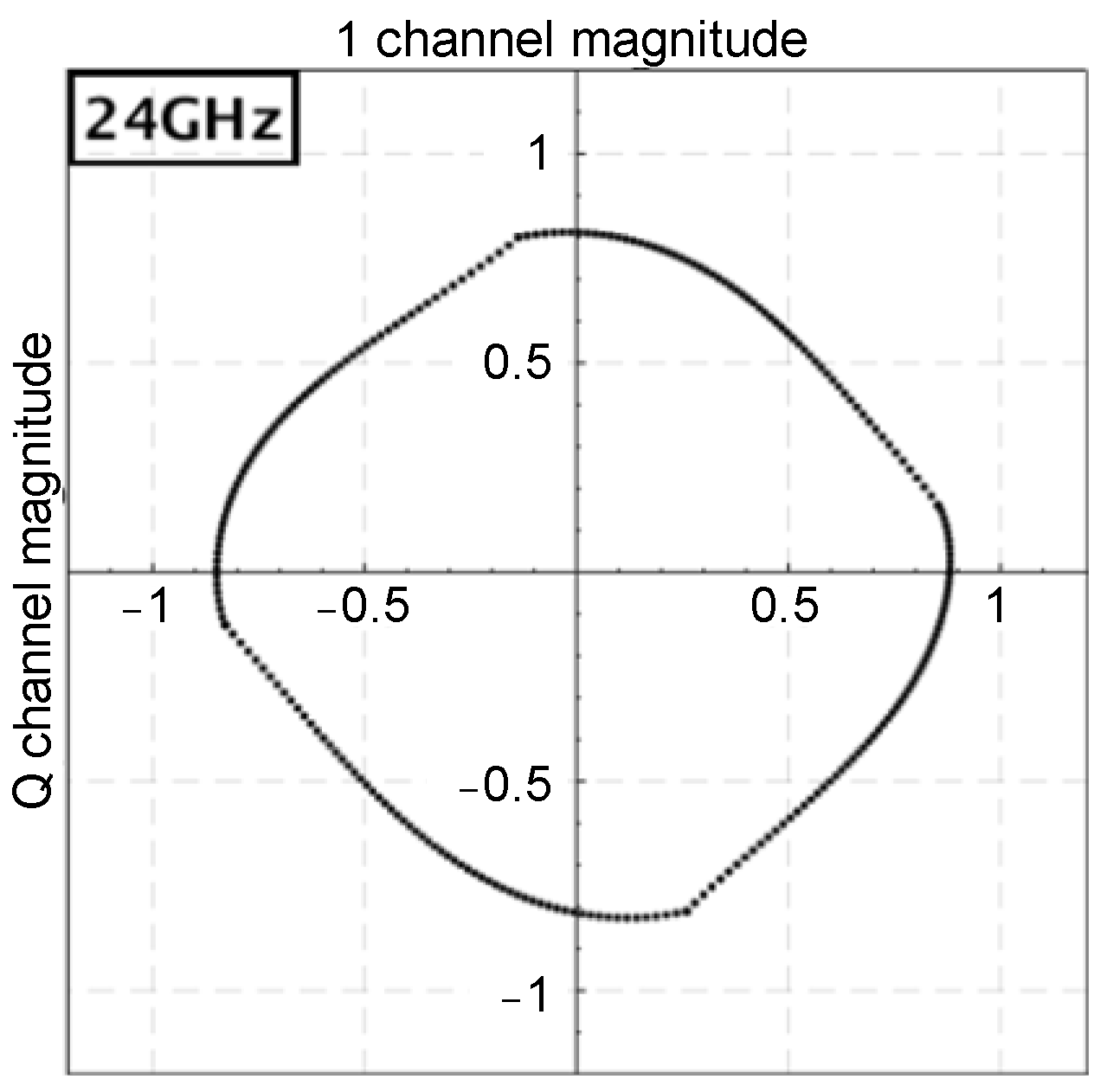
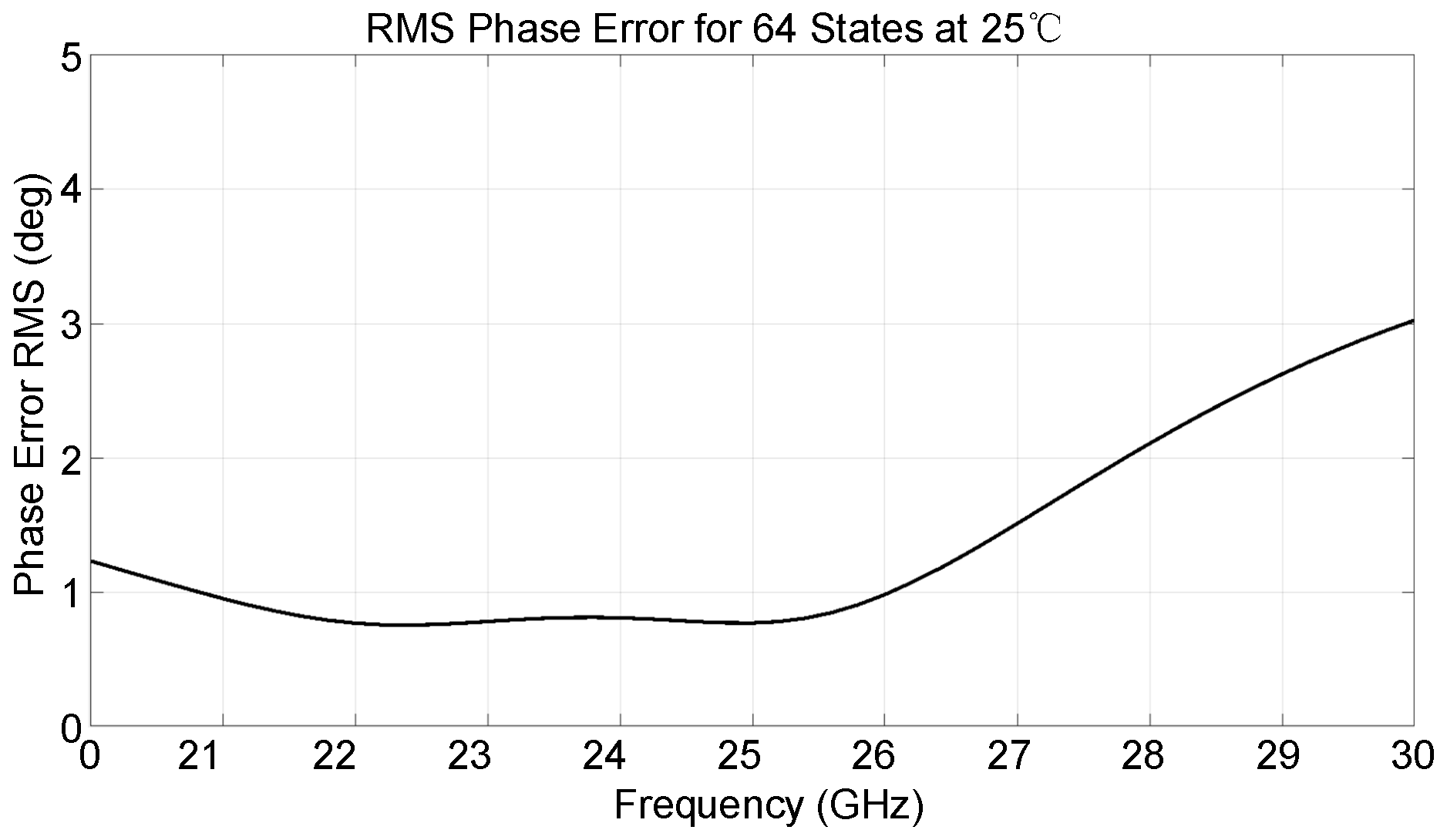
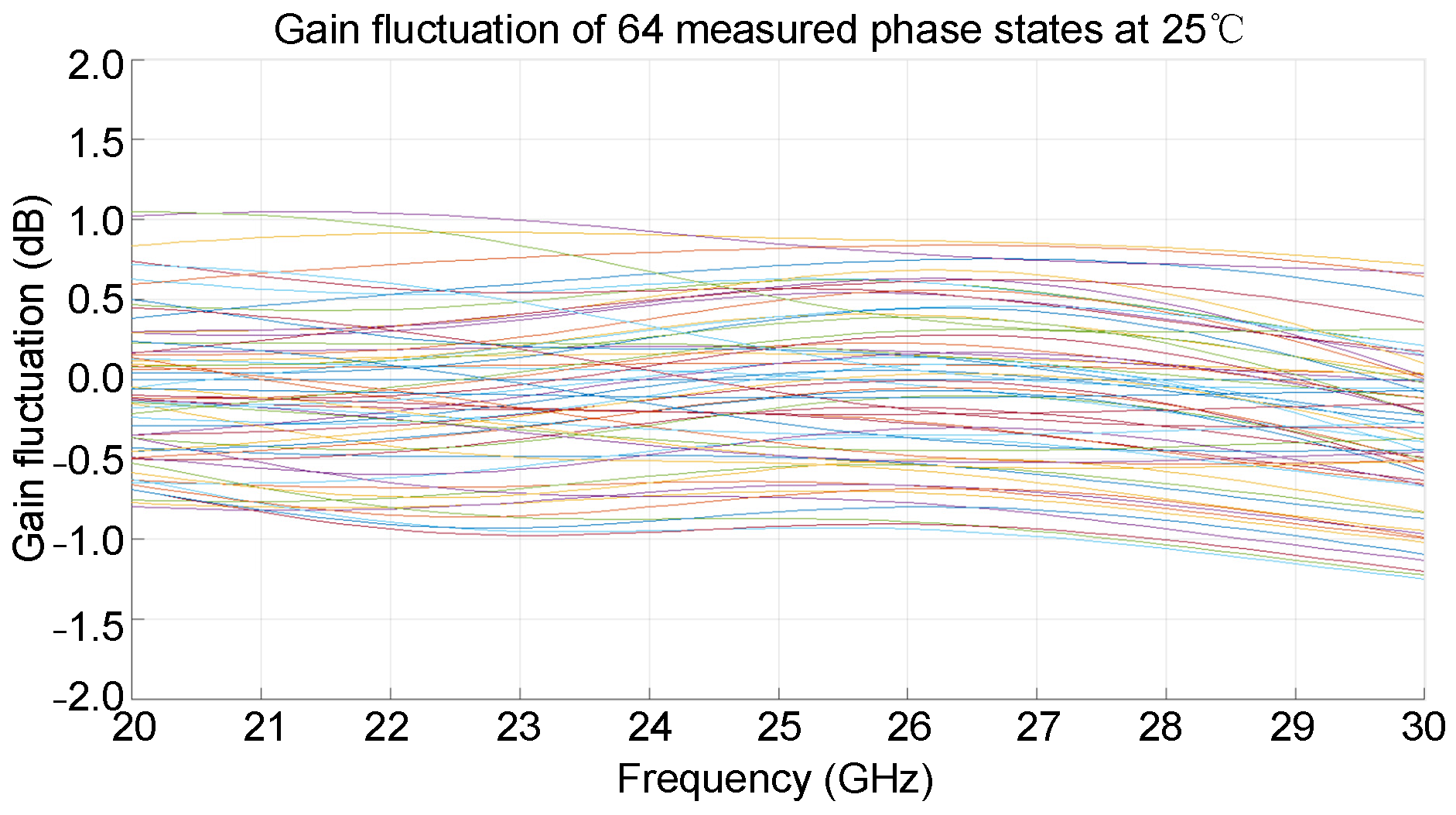
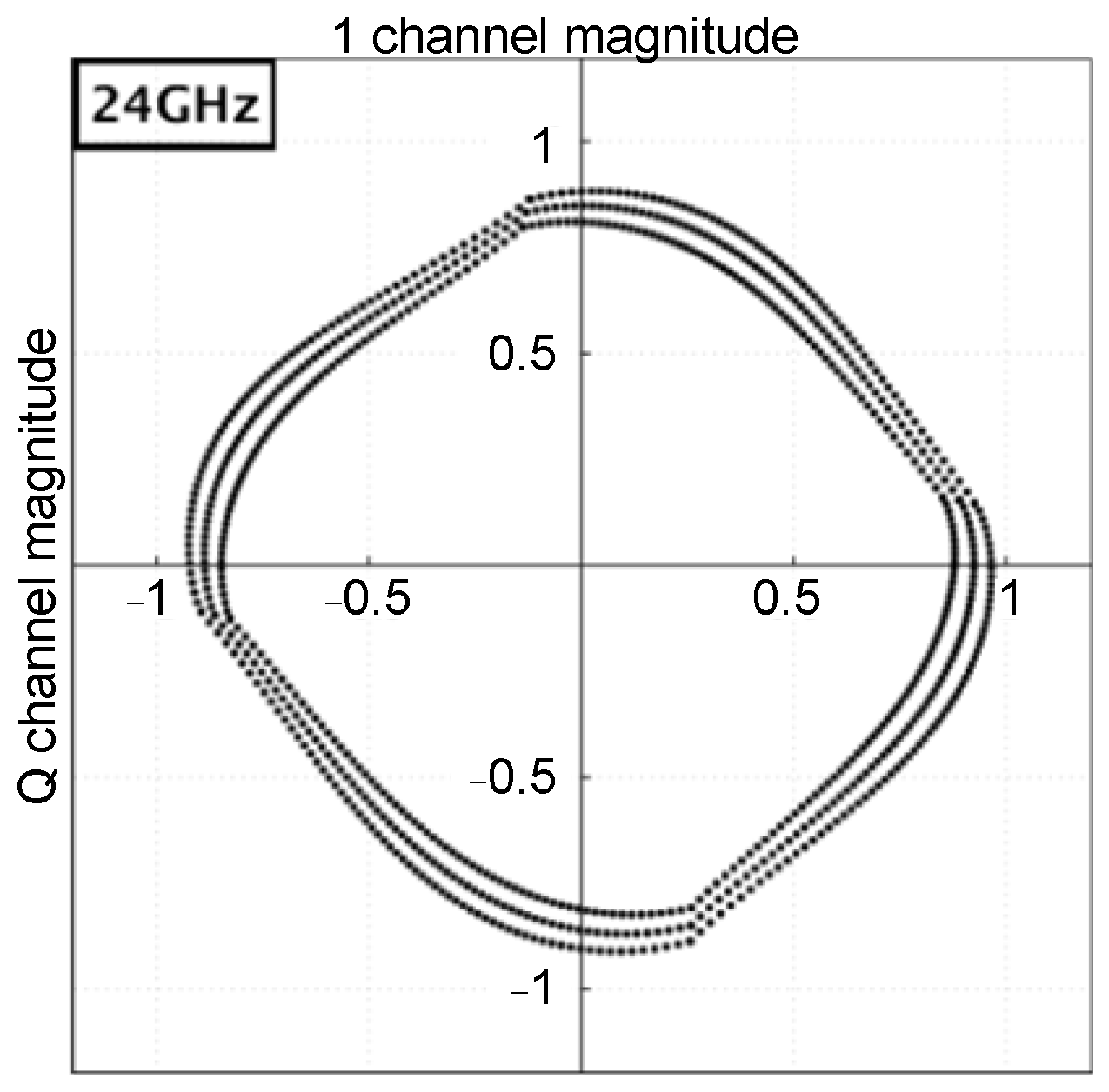
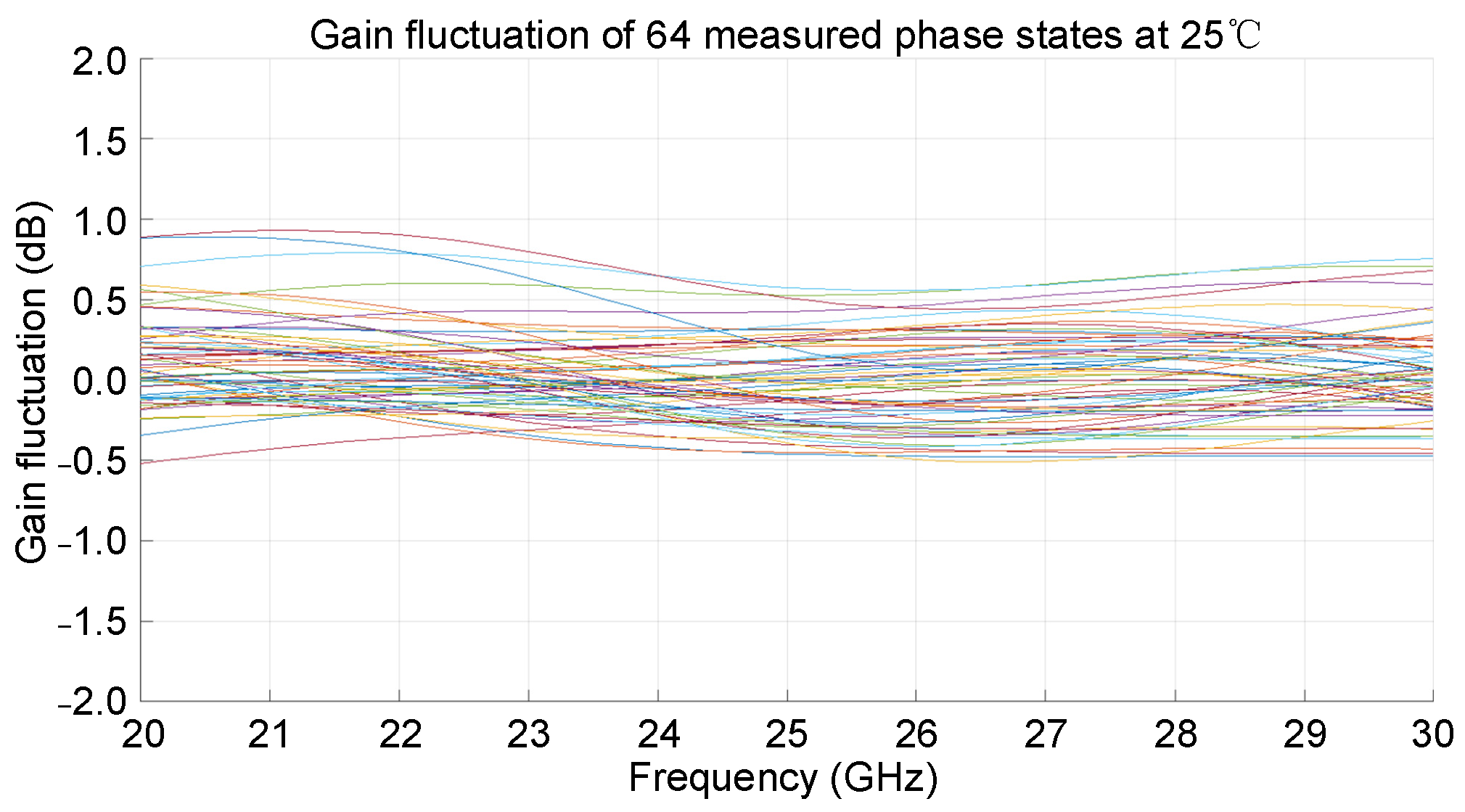
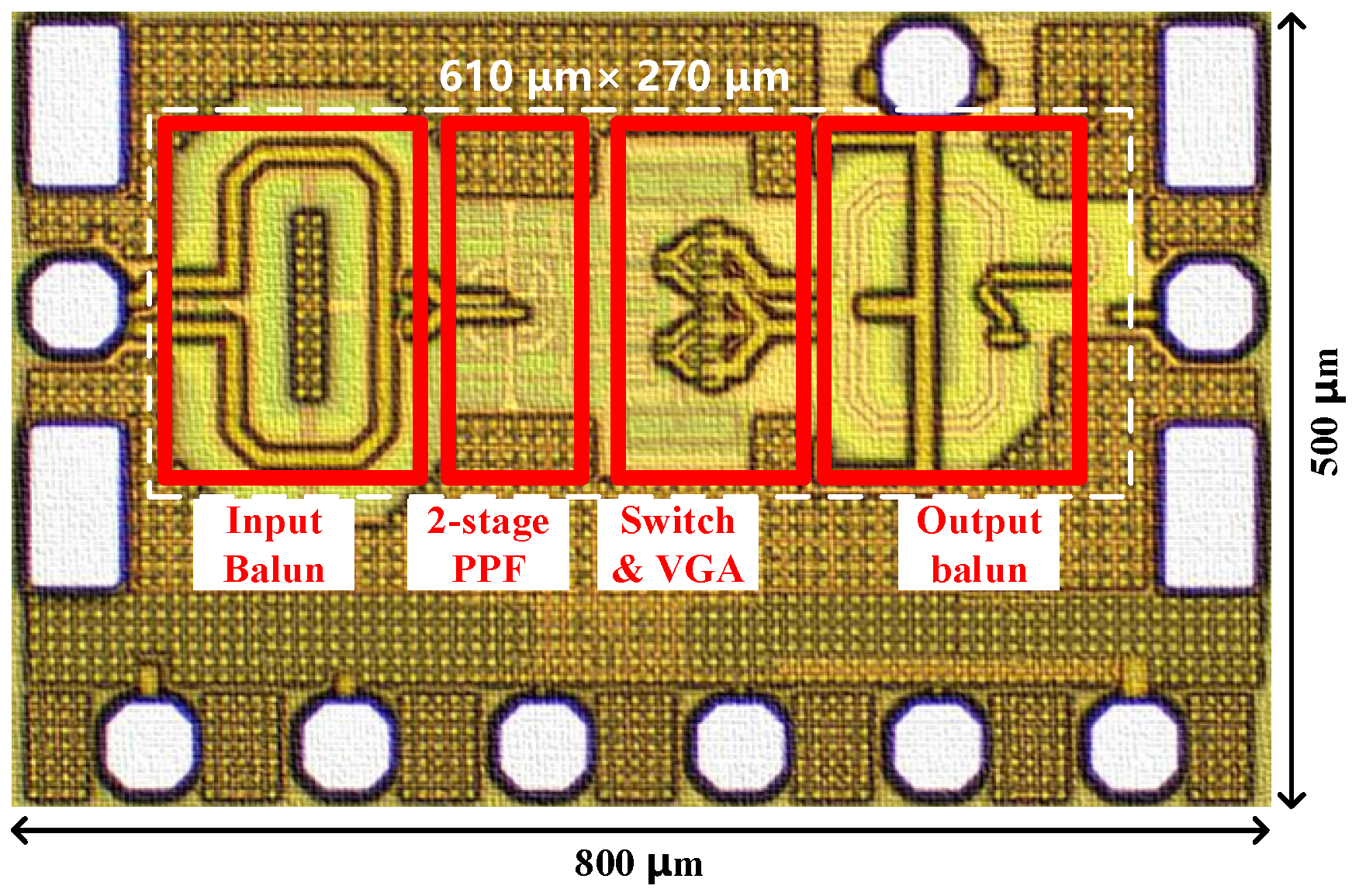
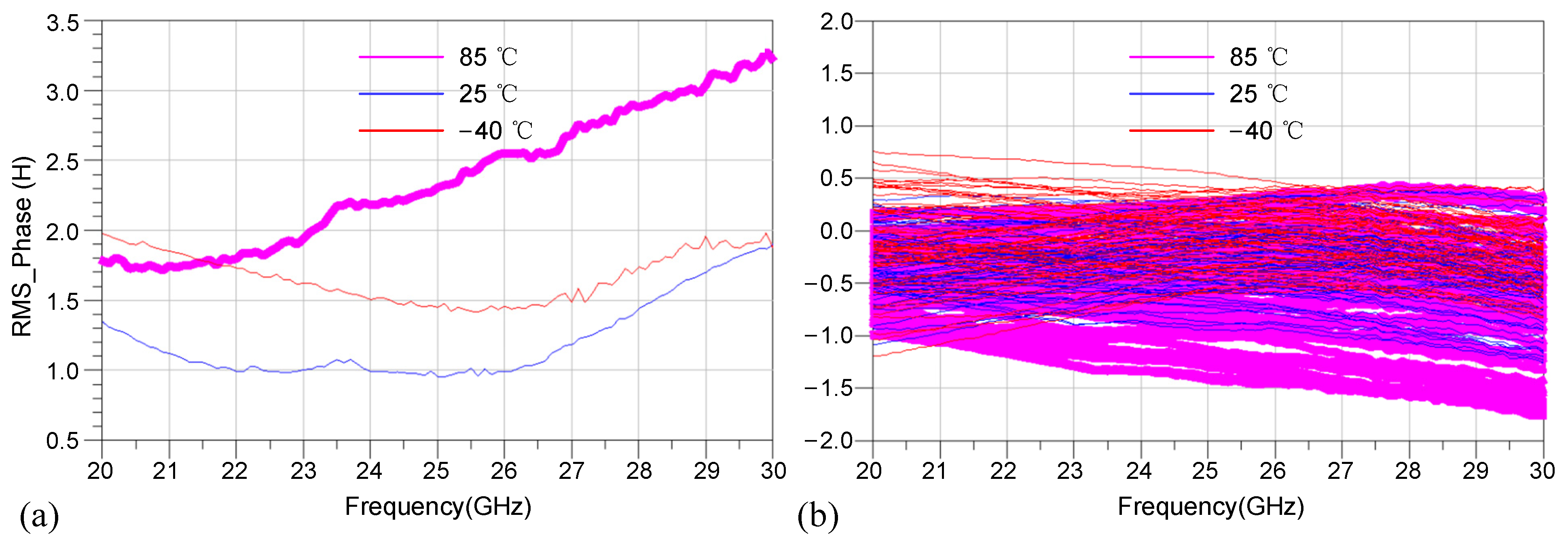
3. Measurement Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zaiden, D.M.; Grandfield, J.E.; Weller, T.M.; Mumcu, G. Compact and Wideband MMIC Phase Shifters Using Tunable Active Inductor-Loaded All-Pass Networks. IEEE Trans. Microw. Theory Tech. 2018, 66, 1047–1057. [Google Scholar] [CrossRef]
- Al-Saedi, H.; Gigoyan, S.; Abdel-Wahab, W.M.; Palizban, A.; Taeb, A.; Ehsandar, A.; Nenasheva, E.; Safavi-Naeini, S. A Low-cost Ka-band Circularly Polarized Passive Phased-Array Antenna for Mobile Satellite Applications. IEEE Trans. Antennas Propag. 2019, 67, 221–231. [Google Scholar] [CrossRef]
- Townley, A.; Swirhun, P.; Titz, D.; Bisognin, A.; Gianesello, F.; Pilard, R.; Luxey, C.; Niknejad, A.M. A 94-GHz 4TX–4RX Phased-Array FMCW Radar Transceiver With Antenna-in-Package. IEEE J. Solid-State Circuits 2017, 52, 1245–1259. [Google Scholar] [CrossRef]
- Tsai, J.-H.; He, T.-T.; Lin, W.-H. A K/Ka-Band Low RMS Phase Error 5-Bit CMOS Phase Shifter. In Proceedings of the 2021 IEEE International Symposium on Radio-Frequency Integration Technology (RFIT), Hualien, Taiwan, 25–27 August 2021; pp. 1–3. [Google Scholar] [CrossRef]
- Tsai, J.-H.; Tung, Y.-L.; Lin, Y.-H. A 27–42-GHz Low Phase Error 5-Bit Passive Phase Shifter in 65-nm CMOS Technology. IEEE Microw. Wirel. Components Lett. 2020, 30, 900–903. [Google Scholar] [CrossRef]
- Jung, M.; Min, B.-W. A Compact Ka-Band 4-bit Phase Shifter With Low Group Delay Deviation. IEEE Microw. Wirel. Components Lett. 2020, 30, 414–416. [Google Scholar] [CrossRef]
- Trinh, K.T.; Yang, Y.; Karmakar, N.C. Design of Ka-Band Reflection-Type Phase Shifter Using Offset Broadside-Coupled Line Coupler in 0.13 µm SiGe BiCMOS Technology. In Proceedings of the 2020 IEEE Eighth International Conference on Communications and Electronics (ICCE), Phu Quoc Island, Vietnam, 13–15 January 2021; pp. 203–208. [Google Scholar] [CrossRef]
- Basaligheh, A.; Saffari, P.; Boroujeni, S.R.; Filanovsky, I.; Moez, K. A 28–30 GHz CMOS Reflection-Type Phase Shifter With Full 360° Phase Shift Range. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 2452–2456. [Google Scholar] [CrossRef]
- Lim, J.-T.; Choi, S.; Lee, E.-G.; Choi, H.-W.; Song, J.-H.; Kim, S.-H.; Kim, C.-Y. 25–40 GHz 180° Reflective-Type Phase Shifter using 65-nm CMOS Technology. In Proceedings of the 2019 49th European Microwave Conference (EuMC), Paris, France, 1–3 October 2019; pp. 480–483. [Google Scholar] [CrossRef]
- Kim, S.; Choi, K.W.; Yoon, B.; Kim, J.; Ju, I. Compact, Low Loss 4-Bit Ku-Band Hybrid Passive Phase Shifter Realized in 0.13-μm SiGe HBT BiCMOS for LEO SATCOM. In Proceedings of the 2024 IEEE/MTT-S International Microwave Symposium—IMS 2024, Washington, DC, USA, 16–21 June 2024; pp. 760–763. [Google Scholar] [CrossRef]
- Li, X.; Liu, B.; Fu, H.; Ma, K. A 30–36 GHz Passive Hybrid Phase Shifter With a Transformer-Based High-Resolution Reflect-Type Phase Shifting Technique. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2419–2423. [Google Scholar] [CrossRef]
- Meng, F.; Ma, K.; Yeo, K.S.; Xu, S. A 57-to-64-GHz 0.094-mm2 5-bit Passive Phase Shifter in 65-nm CMOS. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2015, 24, 1917–1925. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, H.; Lu, W.; Lu, Q.; Yin, X.; An, X.; Liu, B.; Zhu, Z. A Wideband Compact Digitally-Assisted Variable Gain Phase Shifter for Ka-Band Applications. IEEE Trans. Circuits Syst. II Express Briefs 2024, 72, 404–408. [Google Scholar] [CrossRef]
- Wang, S.; Park, J.; Hong, S. A K-Band Variable-Gain Phase Shifter Based on Gilbert-Cell Vector Synthesizer With RC–RL Poly-Phase Filter. IEEE Microw. Wirel. Components Lett. 2021, 31, 393–396. [Google Scholar] [CrossRef]
- Yuan, Y.; Li, N.; Zhou, J.; Gao, H.; Wang, S.; Lu, H.; Gu, Q.J.; Song, C.; Xu, Z. A Compact Ka-Band Eight-Element Four-Beam Receiver for Low-Earth-Orbit Satellite Communications in 65-nm CMOS. IEEE Microw. Wirel. Technol. Lett. 2023, 33, 883–886. [Google Scholar] [CrossRef]
- He, H.; Wang, F.; Zhang, H.; Zhang, L.; Li, J.; Luo, J. A Digitally Controlled CMOS Vector-sum Phase Shifter with Low RMS Phase Error for Ka-band Phased-arrays. In Proceedings of the 2024 Photonics & Electromagnetics Research Symposium (PIERS), Chengdu, China, 21–25 April 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Fu, X.; You, D.; Wang, Y.; Wang, X.; Fadila, A.A.; Liu, C.; Kato, S.; Wang, C.; Li, Z.; Pang, J.; et al. A Low-Power Radiation-Hardened Ka-Band CMOS Phased-Array Receiver for Small Satellite Constellation. IEEE J. Solid-State Circuits 2024, 59, 349–363. [Google Scholar] [CrossRef]
- Zihir, S.; Gurbuz, O.D.; Kar-Roy, A.; Raman, S.; Rebeiz, G.M. 60-GHz 64- and 256-Elements Wafer-Scale Phased-Array Transmitters Using Full-Reticle and Subreticle Stitching Techniques. IEEE Trans. Microw. Theory Tech. 2016, 64, 4701–4719. [Google Scholar] [CrossRef]
- Akbar, F.; Mortazawi, A. A Frequency Tunable 360° Analog CMOS Phase Shifter With an Adjustable Amplitude. IEEE Trans. Circuits Syst. II Express Briefs 2017, 64, 1427–1431. [Google Scholar] [CrossRef]
- Quan, X.; Yi, X.; Boon, C.C.; Yang, K.; Li, C.; Liu, B.; Liang, Z.; Zhuang, Y. A 52–57 GHz 6-Bit Phase Shifter With Hybrid of Passive and Active Structures. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 236–238. [Google Scholar] [CrossRef]
- Balashov, E.V.; Rumyancev, I.A. A fully integrated 6-bit vector-sum phase shifter in 0.18 μm CMOS. In Proceedings of the 2015 International Siberian Conference on Control and Communications (SIBCON), Omsk, Russia, 21–23 May 2015; pp. 1–5. [Google Scholar]
- Cetindogan, B.; Ustundag, B.; Burak, A.; Wietstruck, M.; Kaynak, M.; Gurbuz, Y. A 5–13 GHz 6-Bit Vector-Sum Phase Shifter with +3.5 dBm IP1 dB in 0.25-μm SiGe BiCMOS. In Proceedings of the 2017 IEEE Asia Pacific Microwave Conference (APMC), Kuala Lumpur, Malaysia, 13–16 November 2017; pp. 1111–1114. [Google Scholar]
- Qiu, F.; Zhu, H.; Wu, L.; Che, W.; Xue, Q. A 15–38 GHz Vector-Summing Phase-Shifter With 360° Phase-Shifting Range Using Improved I/Q Generator. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 3199–3203. [Google Scholar] [CrossRef]
- Lee, J.; Lee, J.; Jang, S.; Park, C. A Ka-band CMOS Active Phase Shifter Using Active Balun for Phase optimization. In Proceedings of the 2023 18th European Microwave Integrated Circuits Conference (EuMIC), Berlin, Germany, 18–19 September 2023; pp. 253–256. [Google Scholar] [CrossRef]
- Park, J.; Jeong, G.; Hong, S. A Ka-Band Variable-Gain Phase Shifter With Multiple Vector Generators. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 1798–1802. [Google Scholar] [CrossRef]
- Liu, Y.; Cheng, J.; Wu, Y.; Wang, J.; Chen, Z.; Lu, M.; Hu, J. A 22~30 GHz Active Phase Shifter for Radio Beamforming Systems In 65 nm SOI CMOS. In Proceedings of the 2024 IEEE MTT-S International Wireless Symposium (IWS), Beijing, China, 16–19 May 2024; pp. 1–3. [Google Scholar] [CrossRef]
- Sah, S.P.; Yu, X.; Heo, D. Design and Analysis of a Wideband 15–35-GHz Quadrature Phase Shifter With Inductive Loading. IEEE Trans. Microw. Theory Tech. 2013, 61, 3024–3033. [Google Scholar] [CrossRef]
- Kalyoncu, I.; Burak, A.; Kaynak, M.; Gurbuz, Y. A 26-GHz Vector Modulator in 130-nm SiGe BiCMOS Achieving Monotonic 10-b Phase Resolution Without Calibration. In Proceedings of the 2019 IEEE Radio Frequency Integrated Circuits Symposium (RFIC), Boston, MA, USA, 2–4 June 2019; pp. 75–78. [Google Scholar] [CrossRef]





| SI | 1 | 0 | 0 | 1 |
| SIN | 0 | 1 | 1 | 0 |
| SQ | 1 | 1 | 0 | 0 |
| SQN | 0 | 0 | 1 | 1 |
| quadrant | first | second | third | fourth |
| Ref. | Process | Frequency (GHz) | Resolution (bits) | RMS Phase Error (deg) | DC Power (mW) | Core Area (mm2) |
|---|---|---|---|---|---|---|
| [13] | 65 nm CMOS | 25.4–34 | 4 | 0.5–3 | 40 | 0.19 |
| [14] | 65 nm CMOS | 20.8–25 | 7 | 1.4 c | 6.6 | 0.134 |
| [15] | 65 nm CMOS | 27.5–32 | 6 | 0.87–2.43 | 1115.8 ^ | 21.2 ^ |
| [23] | 65 nm CMOS | 15–38 | 6 | 2–3.5 | 19.2 | 0.16 |
| [24] | 65 nm CMOS | 25–30 | 6 | <3.55 | 38 | 0.13 |
| [25] | 65 nm CMOS | 30–32.5 | 4 | 2.2–3.5 | 18 | 0.32 |
| [26] | 65 nm CMOS | 22–30 | 6 | 0.68–3 | 32 | 0.15 |
| [22] | 0.25 µm SiGe BiCMOS | 5–13 | 6 | <7.9 | 90 | 0.71 * |
| [27] | 0.18 µm SiGe BiCMOS | 15–35 | 4 | 4.2–13 | 25.2 d | 0.19 |
| [28] | 0.13 µm SiGe BiCMOS | 26–28 | 8 | <0.65 | 23 | 0.45 * |
| This work | 0.18 µm SiGe BiCMOS | 20–30 | 6 | <2 | 19.5 | 0.165 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; Zhao, Z.; Zhu, N.; Meng, F. Design and Analysis of an Ultra-Wideband High-Precision Active Phase Shifter in 0.18 μm SiGe BiCMOS Technology. J. Low Power Electron. Appl. 2025, 15, 30. https://doi.org/10.3390/jlpea15020030
Jiang H, Zhao Z, Zhu N, Meng F. Design and Analysis of an Ultra-Wideband High-Precision Active Phase Shifter in 0.18 μm SiGe BiCMOS Technology. Journal of Low Power Electronics and Applications. 2025; 15(2):30. https://doi.org/10.3390/jlpea15020030
Chicago/Turabian StyleJiang, Hao, Zenglong Zhao, Nengxu Zhu, and Fanyi Meng. 2025. "Design and Analysis of an Ultra-Wideband High-Precision Active Phase Shifter in 0.18 μm SiGe BiCMOS Technology" Journal of Low Power Electronics and Applications 15, no. 2: 30. https://doi.org/10.3390/jlpea15020030
APA StyleJiang, H., Zhao, Z., Zhu, N., & Meng, F. (2025). Design and Analysis of an Ultra-Wideband High-Precision Active Phase Shifter in 0.18 μm SiGe BiCMOS Technology. Journal of Low Power Electronics and Applications, 15(2), 30. https://doi.org/10.3390/jlpea15020030







