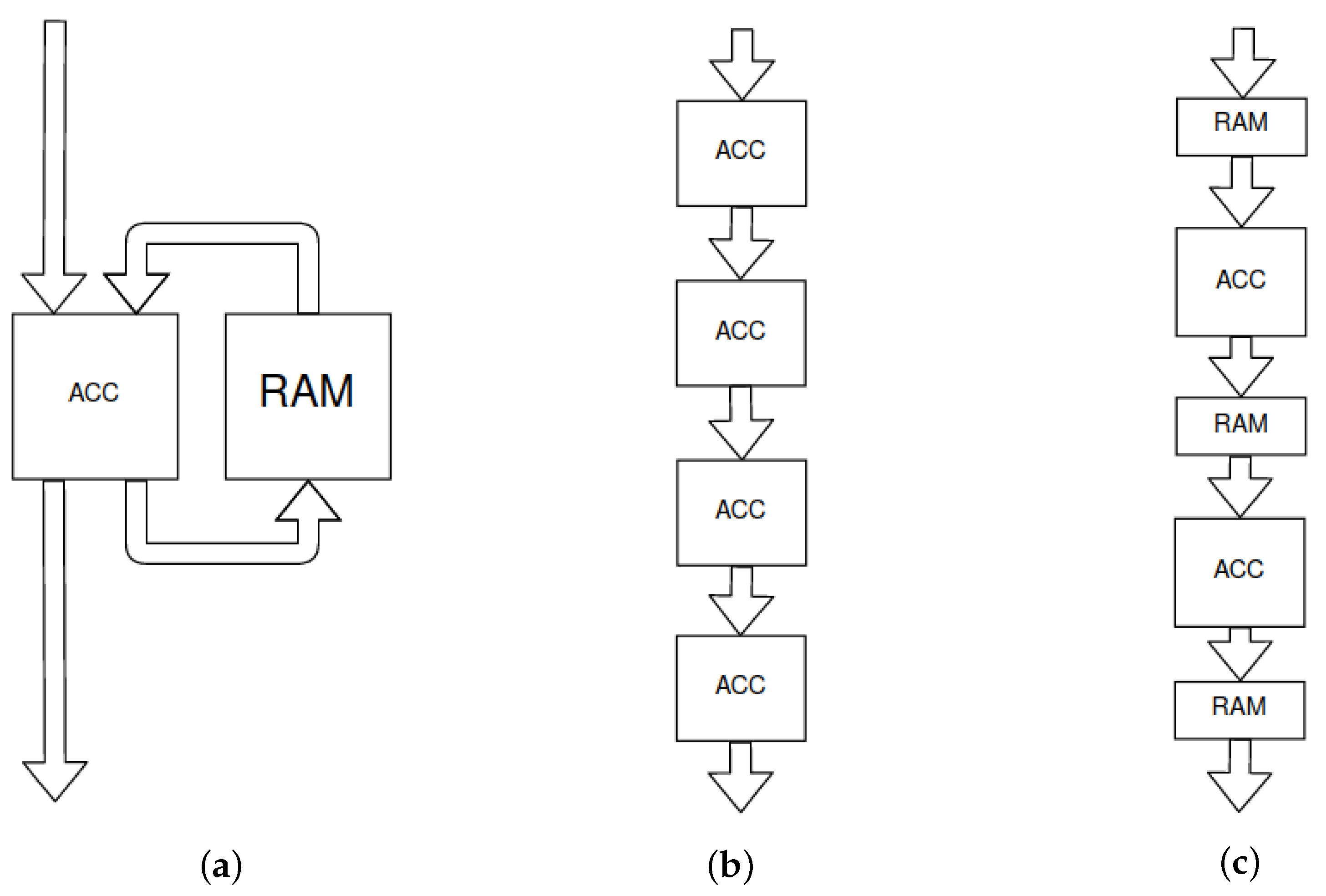
Figure 1.
Schemes of DNNs accelerators: (a) sequential, (b) fine-grained and (c) coarse-grained.
Figure 1.
Schemes of DNNs accelerators: (a) sequential, (b) fine-grained and (c) coarse-grained.
Figure 2.
Merged VOT and VTB datasets. In (a), correctly marked bounding boxes are presented. (b) shows improper annotations: a fully covered object, wrong object, wrong object part, object not fully marked or inaccurately marked. Also visible are different images’ sizes.
Figure 2.
Merged VOT and VTB datasets. In (a), correctly marked bounding boxes are presented. (b) shows improper annotations: a fully covered object, wrong object, wrong object part, object not fully marked or inaccurately marked. Also visible are different images’ sizes.
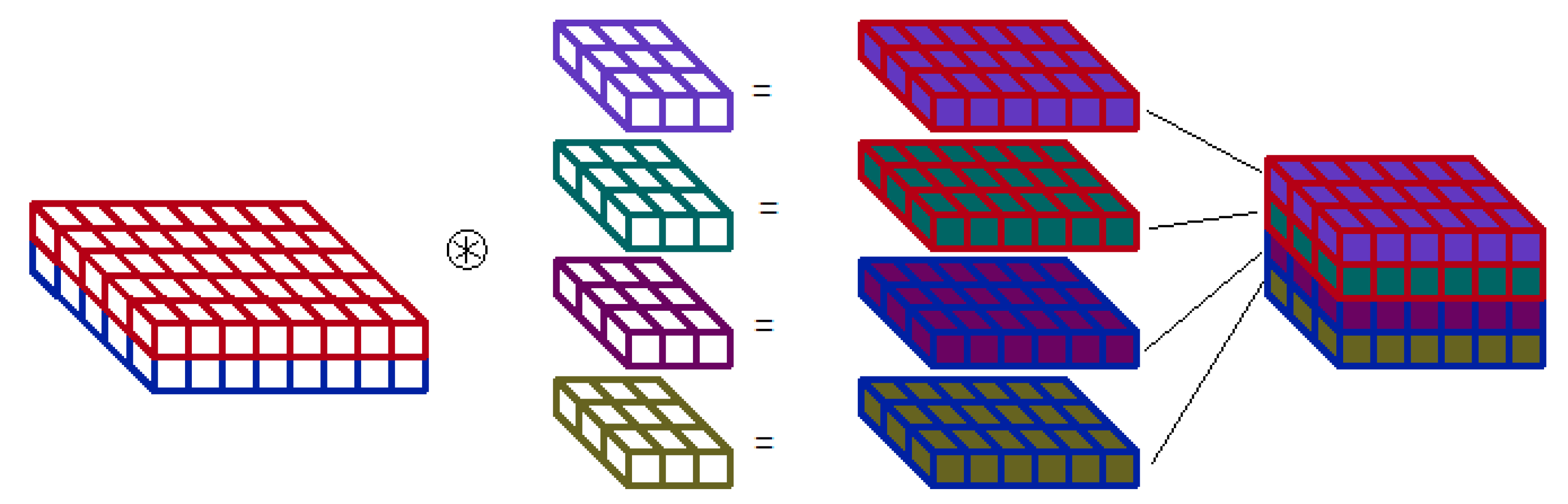
Figure 3.
Multi-depthwise convolution scheme. Two input features maps are convolved with 4 filters— 2 different filters for each map. The output map contains results of all 4 convolutions—edge colour points to the input map, colour of filling is related to filter. The output features order depends on implementation strategy.
Figure 3.
Multi-depthwise convolution scheme. Two input features maps are convolved with 4 filters— 2 different filters for each map. The output map contains results of all 4 convolutions—edge colour points to the input map, colour of filling is related to filter. The output features order depends on implementation strategy.
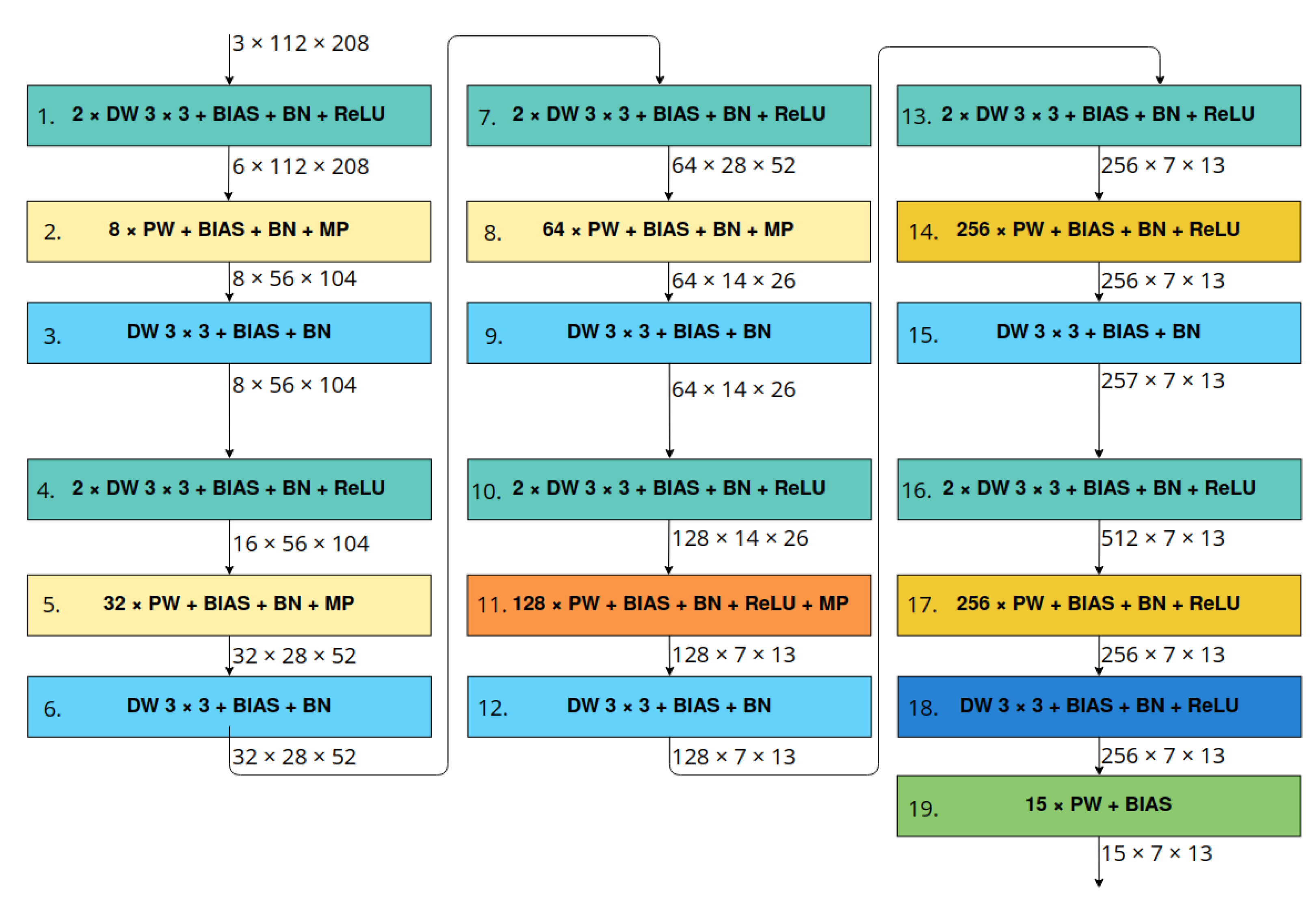
Figure 4.
LittleNet architecture’s scheme. Denotations: M × DW —depthwise convolution with kernel of size and M sets of filters, F × PW—pointwise convolution with F filters, BIAS—using bias in convolution, BN—using batch normalisation, ReLU—applying ReLU activation function, MP—max pooling 2D layer. Blocks with the same colours have similar structure.
Figure 4.
LittleNet architecture’s scheme. Denotations: M × DW —depthwise convolution with kernel of size and M sets of filters, F × PW—pointwise convolution with F filters, BIAS—using bias in convolution, BN—using batch normalisation, ReLU—applying ReLU activation function, MP—max pooling 2D layer. Blocks with the same colours have similar structure.
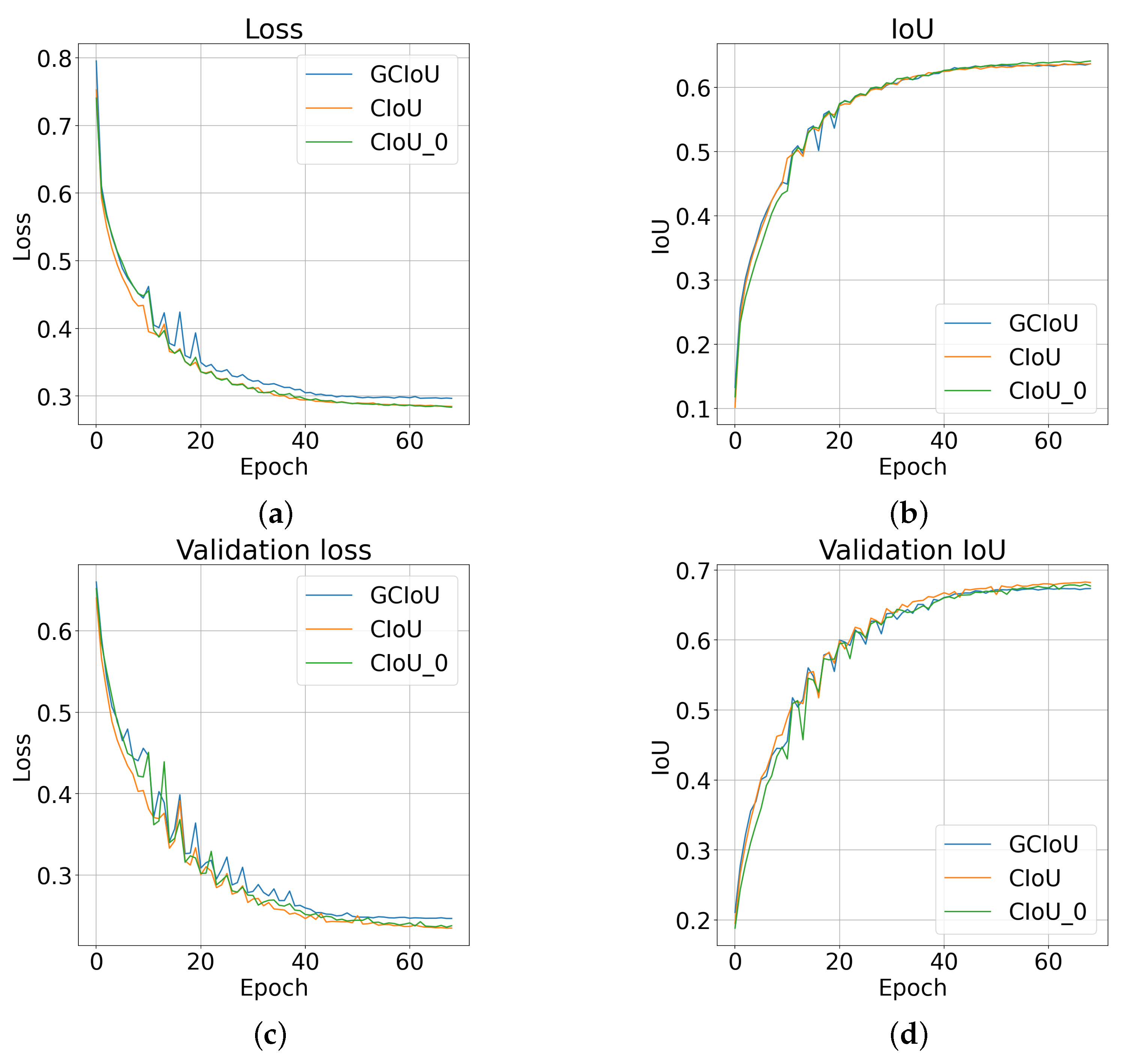
Figure 5.
Networks’s training results with the selected loss functions. The following graphs show: (a)—loss and (b)—IoU for training data, (c)—loss and (d)—IoU for validation data. By , we have denoted the version with zero coefficient for a small value of . The obtained waveforms achieve relatively similar values of the metric. For , there is noticeably higher loss value in comparison to .
Figure 5.
Networks’s training results with the selected loss functions. The following graphs show: (a)—loss and (b)—IoU for training data, (c)—loss and (d)—IoU for validation data. By , we have denoted the version with zero coefficient for a small value of . The obtained waveforms achieve relatively similar values of the metric. For , there is noticeably higher loss value in comparison to .
Figure 6.
The quantisation process waveforms: (a)—loss and (b)—. The red lines indicate the epochs starting the quantisation of the normalisation layers and the change in the integer approximation method from to . The introduction of quantisation for the normalisation layers does not introduce significant changes in the error value and accuracy. Changing the approximation method causes a significant increase in the error value as well as a decrease in the accuracy.
Figure 6.
The quantisation process waveforms: (a)—loss and (b)—. The red lines indicate the epochs starting the quantisation of the normalisation layers and the change in the integer approximation method from to . The introduction of quantisation for the normalisation layers does not introduce significant changes in the error value and accuracy. Changing the approximation method causes a significant increase in the error value as well as a decrease in the accuracy.
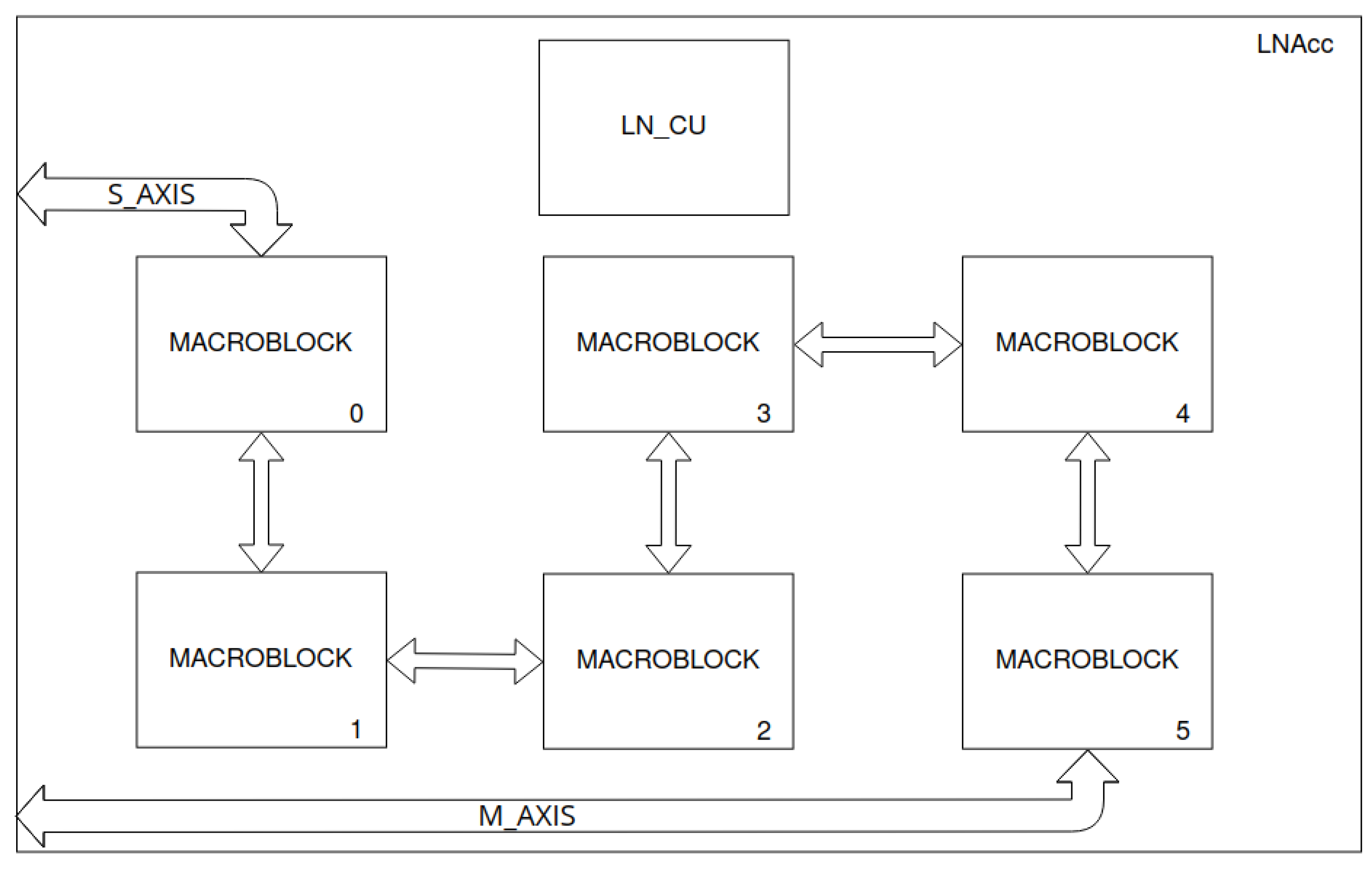
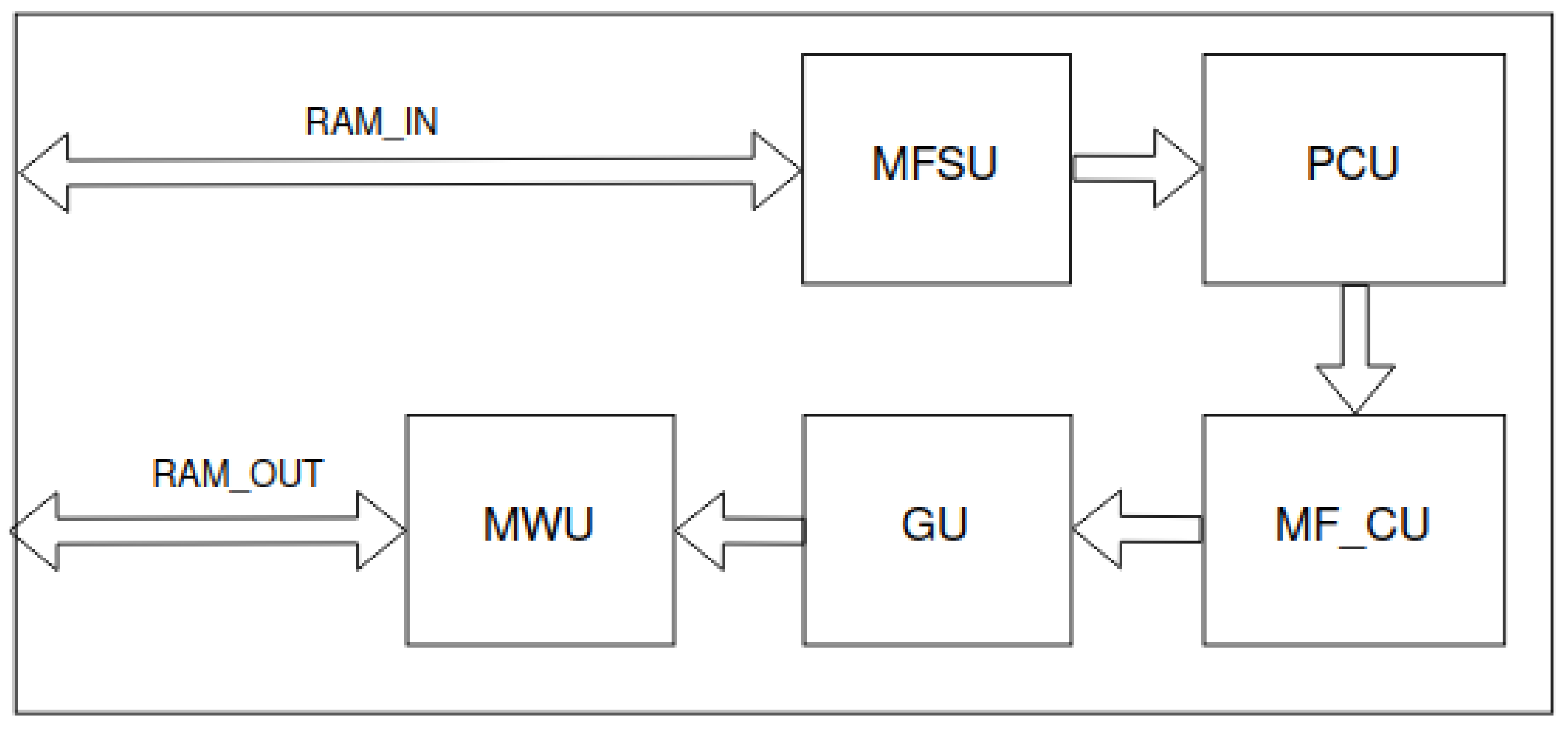
Figure 7.
LittleNet accelerator’s scheme. Connections between macroblocks are buses for reading data from previous macroblocks.
Figure 7.
LittleNet accelerator’s scheme. Connections between macroblocks are buses for reading data from previous macroblocks.
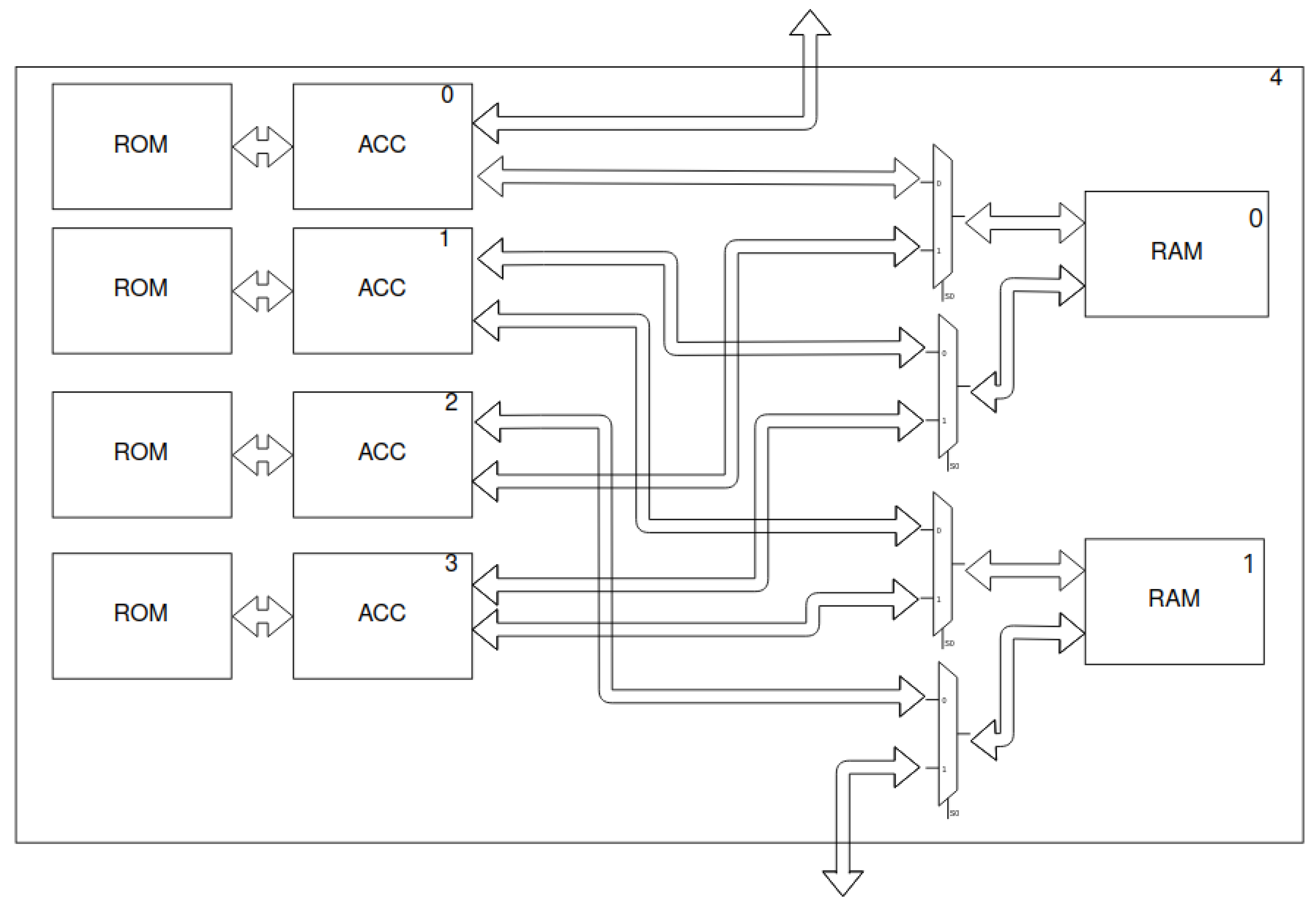
Figure 8.
Macroblock’s scheme—two shared memories (RAM and ROM) and four layer accelerators (ACC). The last macroblock in
Figure 7 is not complete—only 2 accelerators are present. In addition, the output bus is connected directly to the last accelerator—the output layer. Moreover, the presence of ROM depends on the type of the accelerator.
Figure 8.
Macroblock’s scheme—two shared memories (RAM and ROM) and four layer accelerators (ACC). The last macroblock in
Figure 7 is not complete—only 2 accelerators are present. In addition, the output bus is connected directly to the last accelerator—the output layer. Moreover, the presence of ROM depends on the type of the accelerator.
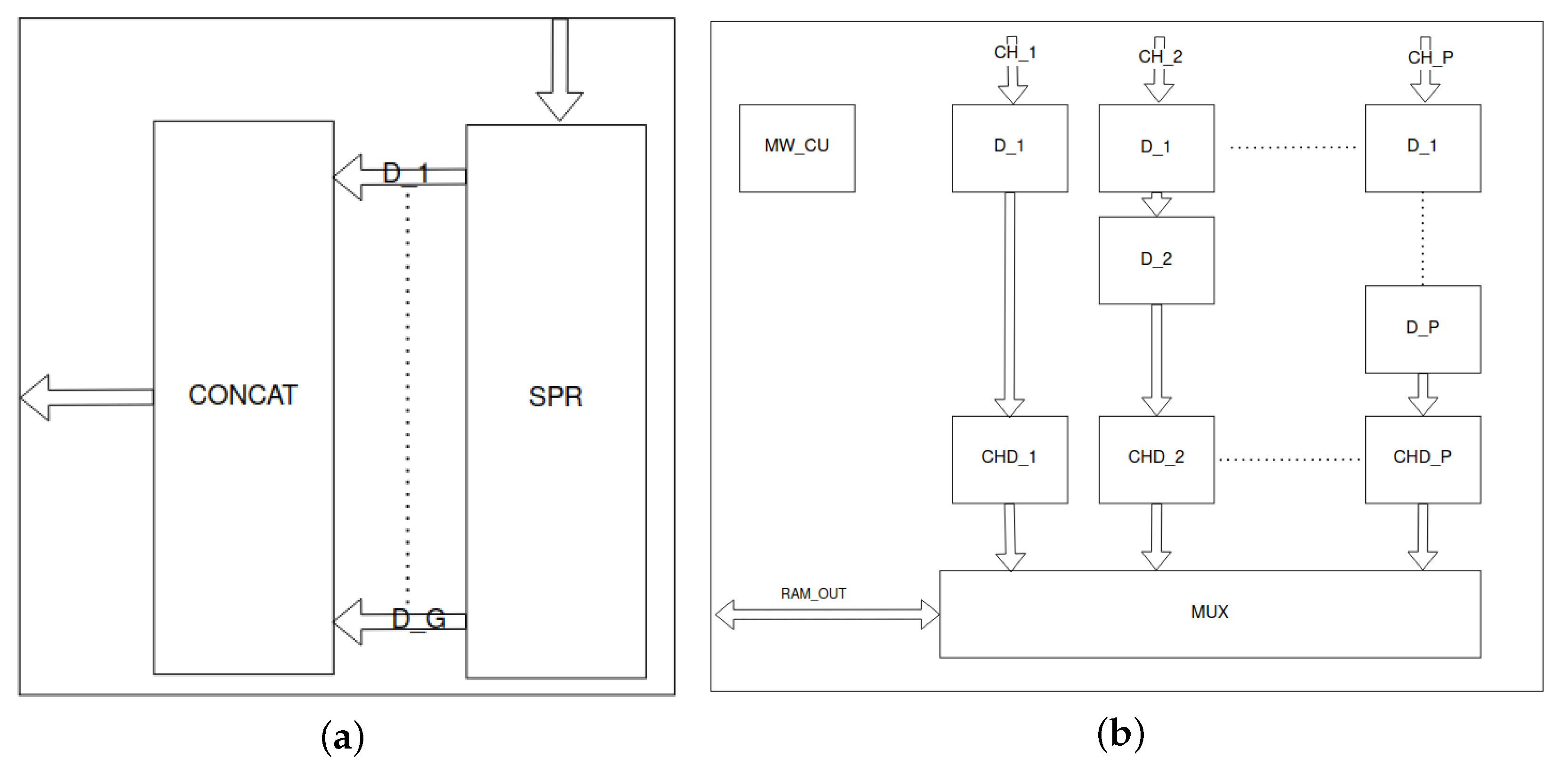
Figure 9.
Grouper unit is presented in (a). Input signals are stored in the serial-parallel register (SPR). Next they are concatenated (CONCAT) into a wider package. (b) presents the memory writer unit. Parallel input channels () are delayed by blocks. The blocks determine the addresses for the valid data from each channel. Next, the multiplexer (MUX) iterates over channels and selects channel’s data, address and validity as output signals. The memory writer control unit (MW_CU) controls the entire module.
Figure 9.
Grouper unit is presented in (a). Input signals are stored in the serial-parallel register (SPR). Next they are concatenated (CONCAT) into a wider package. (b) presents the memory writer unit. Parallel input channels () are delayed by blocks. The blocks determine the addresses for the valid data from each channel. Next, the multiplexer (MUX) iterates over channels and selects channel’s data, address and validity as output signals. The memory writer control unit (MW_CU) controls the entire module.
Figure 10.
Schematic of the input layer (IL) accelerator—receiving data from the AXI4-Stream stream, changing the “channel last” representation to “channel first”, and writing to RAM. Denotations: GU—grouper unit, SU—splitter unit (byte reordering is represented by coloured arrows), MWU—memory writer unit, IL_CU—input layer control unit.
Figure 10.
Schematic of the input layer (IL) accelerator—receiving data from the AXI4-Stream stream, changing the “channel last” representation to “channel first”, and writing to RAM. Denotations: GU—grouper unit, SU—splitter unit (byte reordering is represented by coloured arrows), MWU—memory writer unit, IL_CU—input layer control unit.
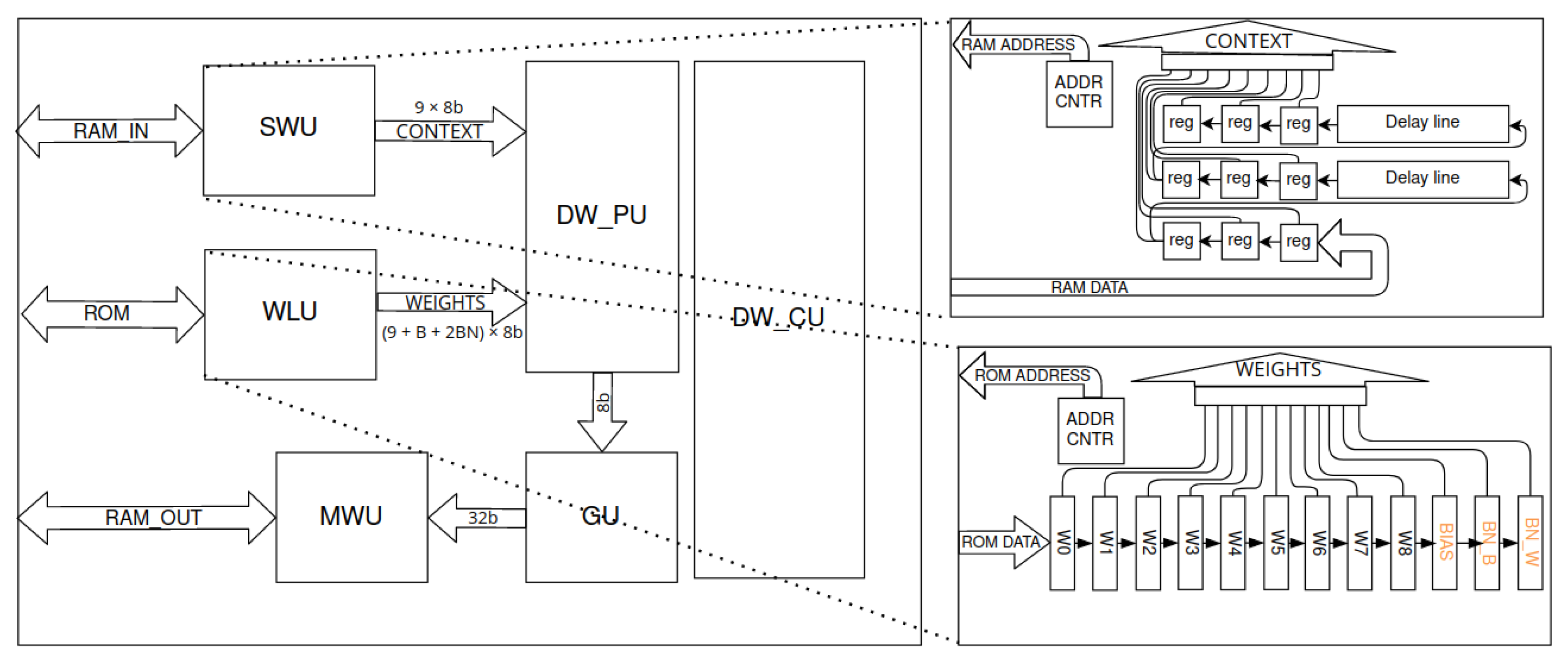
Figure 11.
Depthwise layer accelerator scheme. The entire block depending on configuration consumes up to 10 DSP48 modules. Denotations: SWU—sliding window unit, WLU—weights loading unit, DW_PU—depthwise processing unit, DW_CU—depthwise control unit. SWU is implemented with a basic fine-grained stream method for context generation. WLU stores weights in serial-parallel register.
Figure 11.
Depthwise layer accelerator scheme. The entire block depending on configuration consumes up to 10 DSP48 modules. Denotations: SWU—sliding window unit, WLU—weights loading unit, DW_PU—depthwise processing unit, DW_CU—depthwise control unit. SWU is implemented with a basic fine-grained stream method for context generation. WLU stores weights in serial-parallel register.
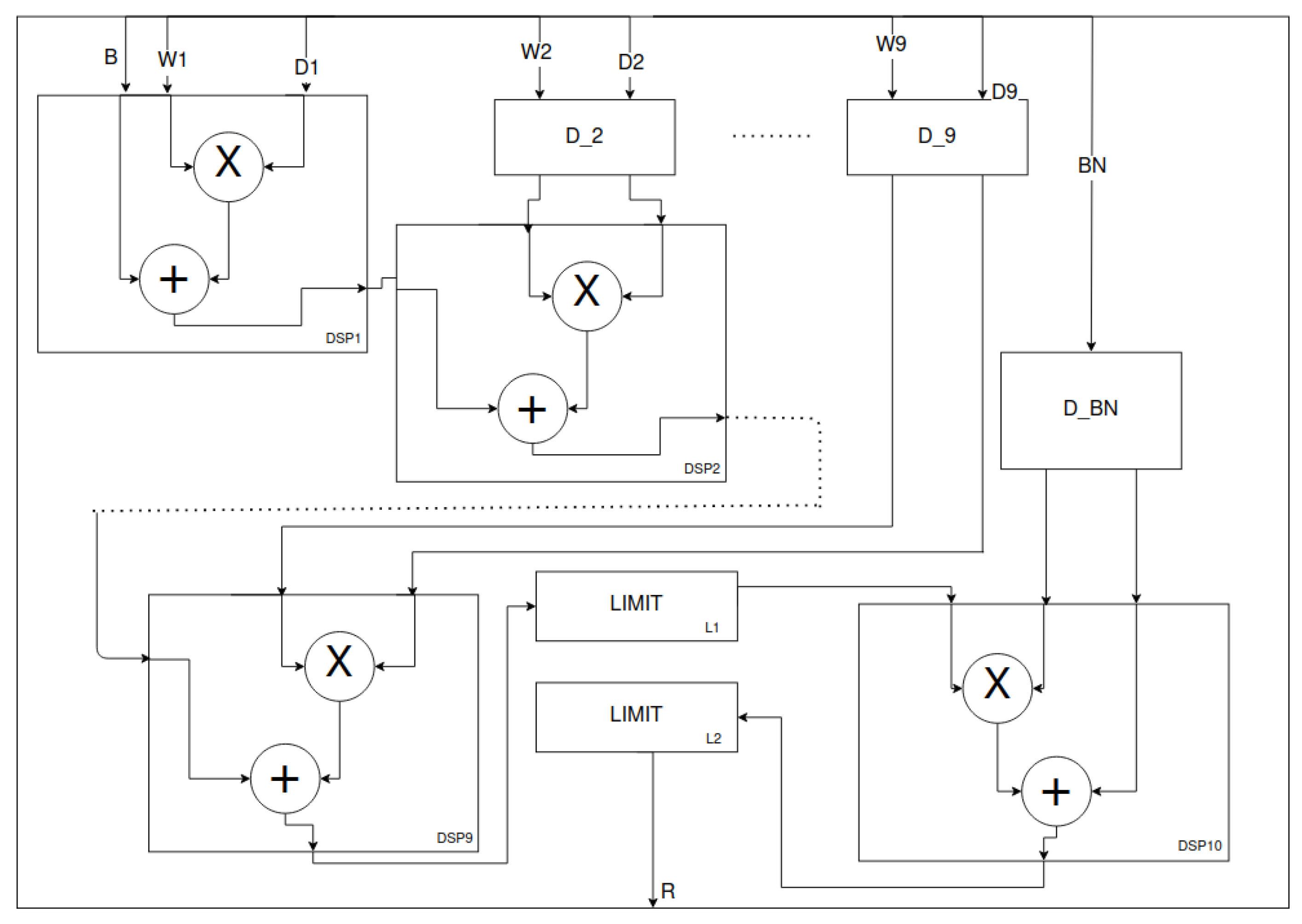
Figure 12.
Depthwise processing unit—cascaded connected DSPs. The design is based on [
29]. The L2 and DSP10 blocks are optional depending on the configuration. The LIMIT blocks limit the input data to a range given by the fixed-point notation parameters or the applied
activation. The mentioned DSP10 block implements the normalisation operation as an affine transformation. In addition, the corresponding delays of the
signals are present.
Figure 12.
Depthwise processing unit—cascaded connected DSPs. The design is based on [
29]. The L2 and DSP10 blocks are optional depending on the configuration. The LIMIT blocks limit the input data to a range given by the fixed-point notation parameters or the applied
activation. The mentioned DSP10 block implements the normalisation operation as an affine transformation. In addition, the corresponding delays of the
signals are present.
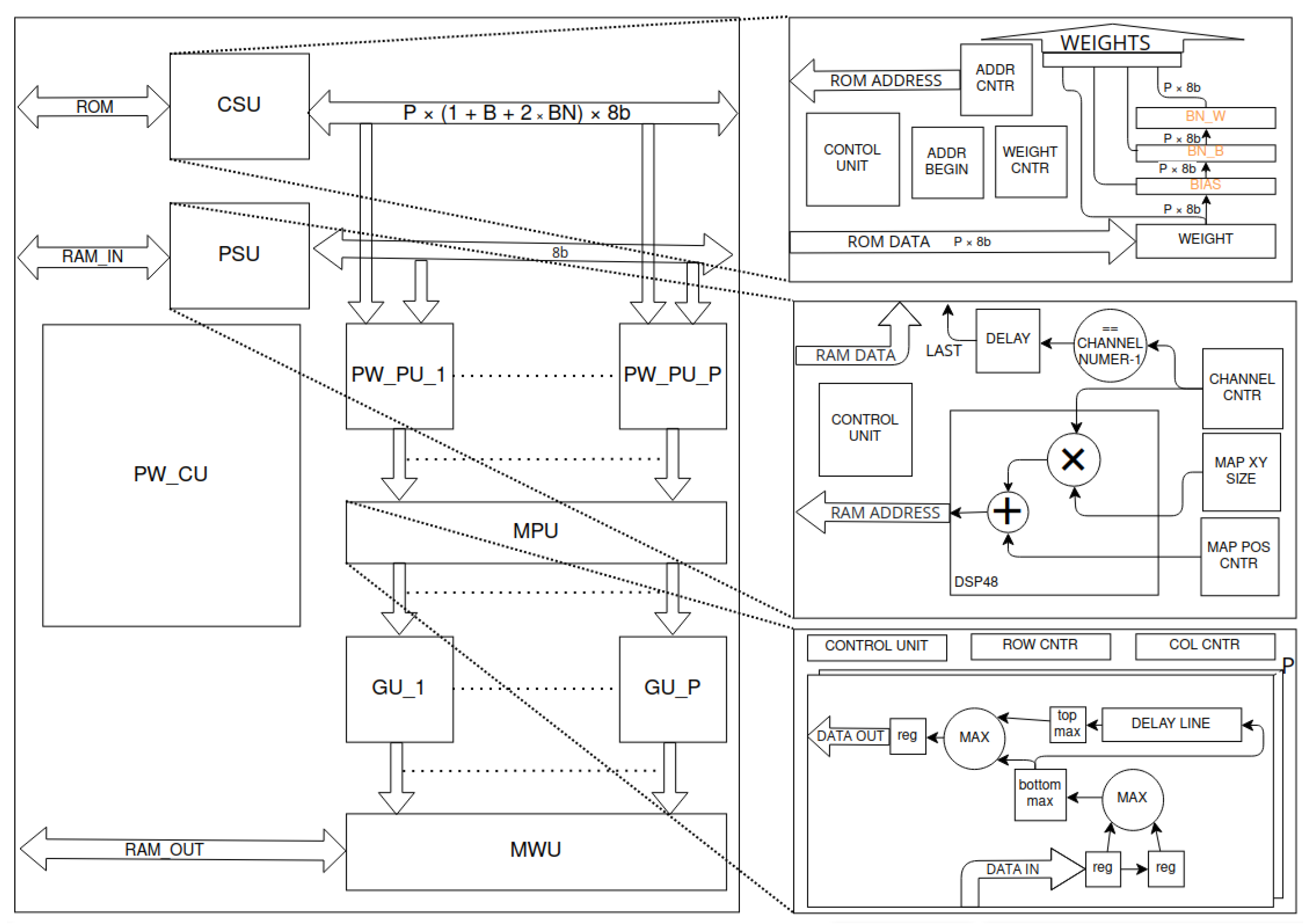
Figure 13.
Pointwise convolution layer accelerator’s scheme. The input data stream is generated by the point stream unit (PSU)—the module uses proper counters to iterate over channels and determines signal of last channel of each point. Appropriate weights are streamed by the cyclic streamer unit (CSU)—incremented ADDR_CNTR (counter) is reset to ADDR_BEGIN when WEIGHT_CNTR (counter) achieves size of filter. Based on both streams, the pointwise processing units (PW_PU_x) calculate dot products. Next, the max pool unit (MPU) performs a max pool 2D operation on each channel. For each channel, for the next two elements, max function is applied. The result is properly delayed. Next, the results of subsequent lines are compared and the higher value is selected. The validity of the results and delay lines clock are dependent on the row and column of the pixel. The results are grouped in the grouper units (GU_x). For each group, the memory writer unit (MWU) assigns the memory address. The whole process is controlled by the pointwise control unit (PW_CU).
Figure 13.
Pointwise convolution layer accelerator’s scheme. The input data stream is generated by the point stream unit (PSU)—the module uses proper counters to iterate over channels and determines signal of last channel of each point. Appropriate weights are streamed by the cyclic streamer unit (CSU)—incremented ADDR_CNTR (counter) is reset to ADDR_BEGIN when WEIGHT_CNTR (counter) achieves size of filter. Based on both streams, the pointwise processing units (PW_PU_x) calculate dot products. Next, the max pool unit (MPU) performs a max pool 2D operation on each channel. For each channel, for the next two elements, max function is applied. The result is properly delayed. Next, the results of subsequent lines are compared and the higher value is selected. The validity of the results and delay lines clock are dependent on the row and column of the pixel. The results are grouped in the grouper units (GU_x). For each group, the memory writer unit (MWU) assigns the memory address. The whole process is controlled by the pointwise control unit (PW_CU).
![Jlpea 12 00030 g013]()
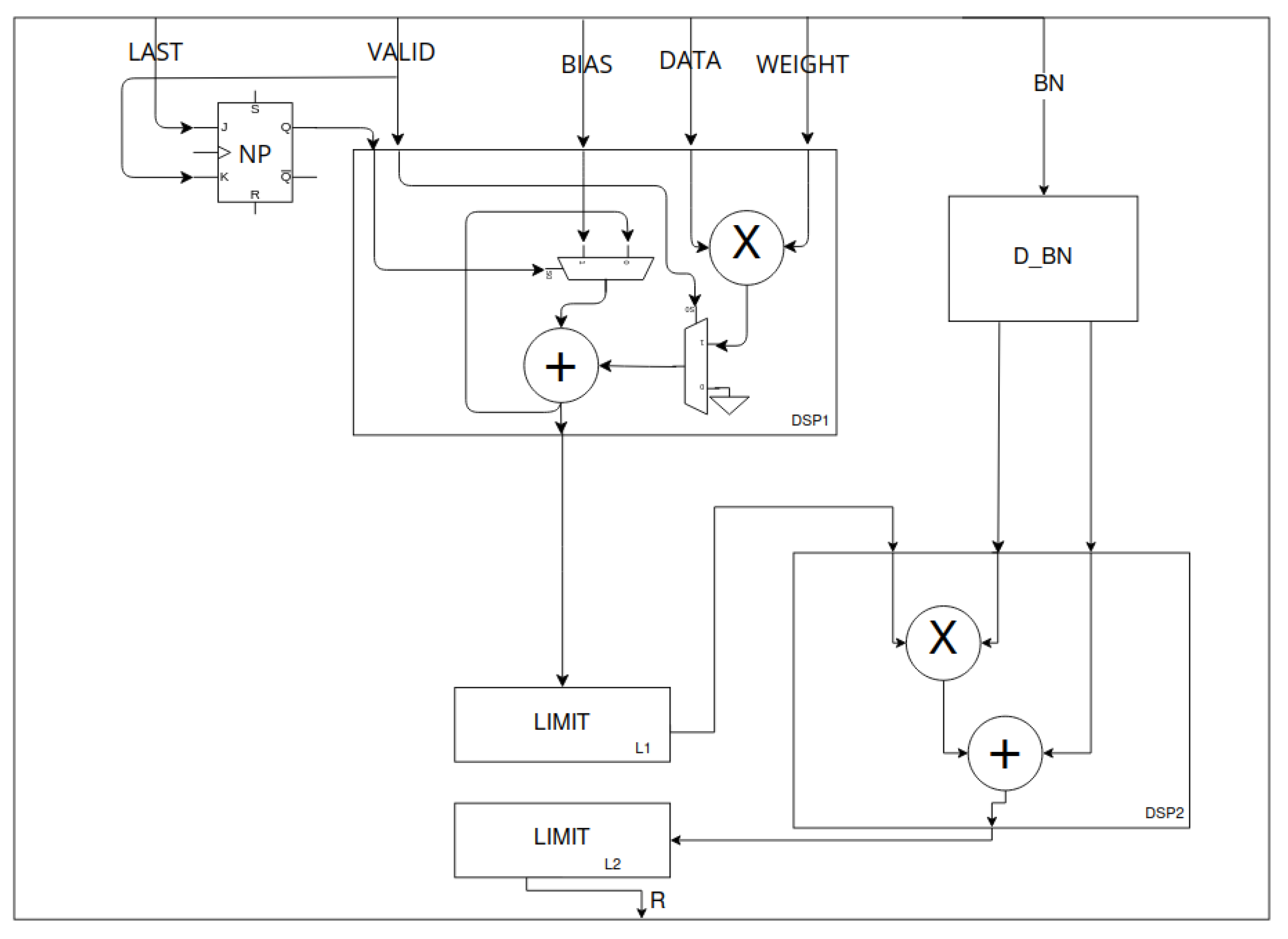
Figure 14.
Pointwise processing unit—multiplication and accumulation (MAC). The design is based on [
30]. DATA, WEIGHT and BIAS are 8-bit signals that represent input feature and filter weight and bias. BN is a pair of 8-bit signals—weights ofnormalisation. LAST is a one-bit signal that is high if DATA comes from the last channel of input data. DSP1 implements the MAC operation. The new point (NP) flip-flop allows the accumulator to be initialised with a bias value. DSP1 uses internal multiplexing based on NP state and data validation signal (VALID). The L2 and DSP2 blocks are optional depending on the configuration. The LIMIT blocks limit the input data to a range given by the fixed-point notation parameters or the applied
activation. The mentioned DSP2 block implements the normalisation operation as an affine transformation with delayed BN weighs by D_BN block.
Figure 14.
Pointwise processing unit—multiplication and accumulation (MAC). The design is based on [
30]. DATA, WEIGHT and BIAS are 8-bit signals that represent input feature and filter weight and bias. BN is a pair of 8-bit signals—weights ofnormalisation. LAST is a one-bit signal that is high if DATA comes from the last channel of input data. DSP1 implements the MAC operation. The new point (NP) flip-flop allows the accumulator to be initialised with a bias value. DSP1 uses internal multiplexing based on NP state and data validation signal (VALID). The L2 and DSP2 blocks are optional depending on the configuration. The LIMIT blocks limit the input data to a range given by the fixed-point notation parameters or the applied
activation. The mentioned DSP2 block implements the normalisation operation as an affine transformation with delayed BN weighs by D_BN block.
Figure 15.
Max finder unit (MFU)—finding parameters of the object for the highest validity. The max finder streamer unit (MFSU) generates a data stream. For each element of the stream, the position counter unit (PCU) assigns coordinates of map and anchor positions. The max finder control unit (MF_CU) implements the main functionality—it finds coordinates of the most probable object and its parameters. The resulting single bytes of object description are grouped in the grouper unit (GU). The aforementioned description are values of the anchor channels (
and
in Equations (
4)–(
8)), location of the object on the grid and anchor index. Next, the memory writer unit assigns the address for each group.
Figure 15.
Max finder unit (MFU)—finding parameters of the object for the highest validity. The max finder streamer unit (MFSU) generates a data stream. For each element of the stream, the position counter unit (PCU) assigns coordinates of map and anchor positions. The max finder control unit (MF_CU) implements the main functionality—it finds coordinates of the most probable object and its parameters. The resulting single bytes of object description are grouped in the grouper unit (GU). The aforementioned description are values of the anchor channels (
and
in Equations (
4)–(
8)), location of the object on the grid and anchor index. Next, the memory writer unit assigns the address for each group.
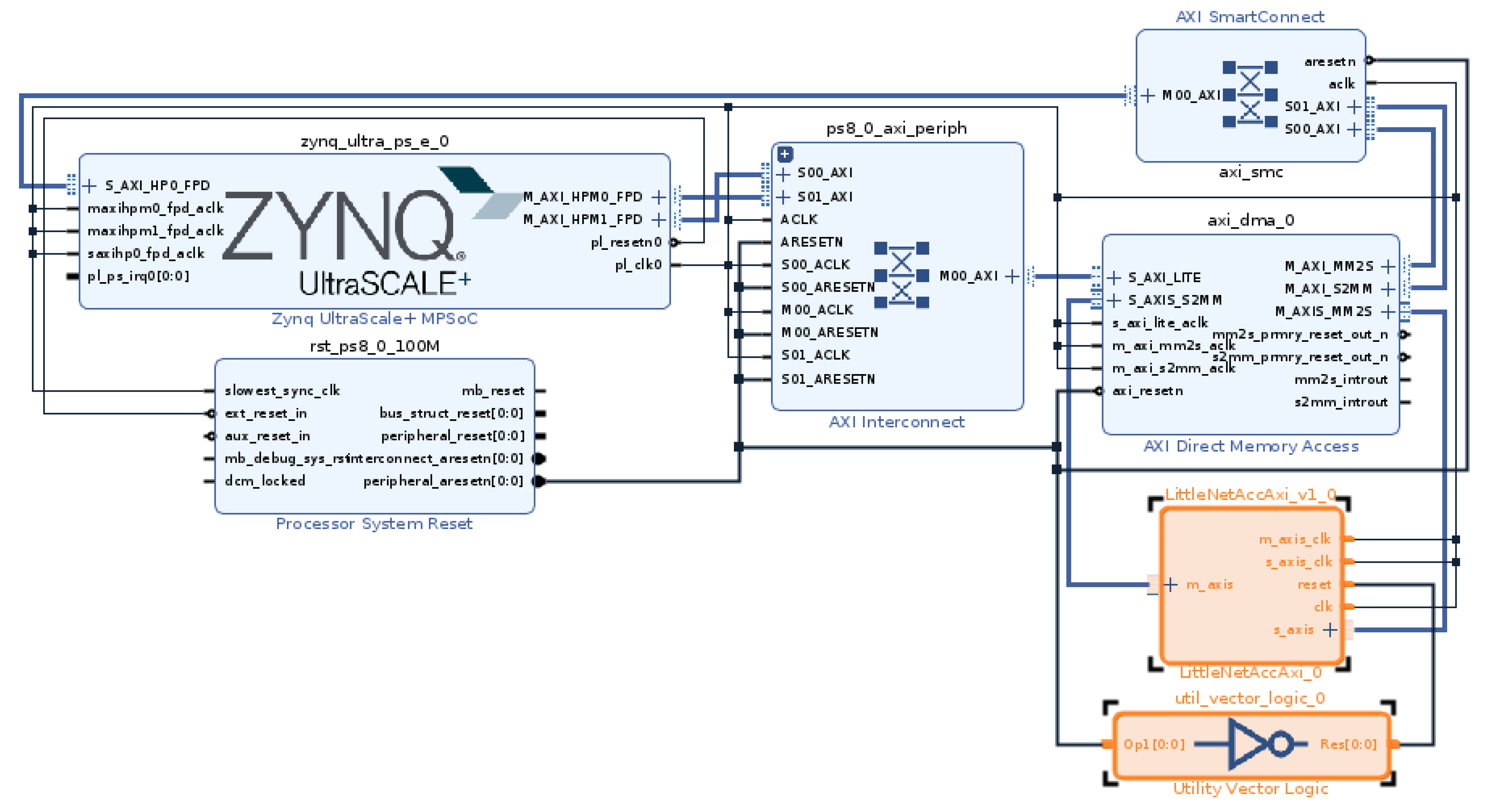
Figure 16.
Block design with our accelerator and inverter of reset signal highlighted—our accelerator is reset with logical 1.
Figure 16.
Block design with our accelerator and inverter of reset signal highlighted—our accelerator is reset with logical 1.
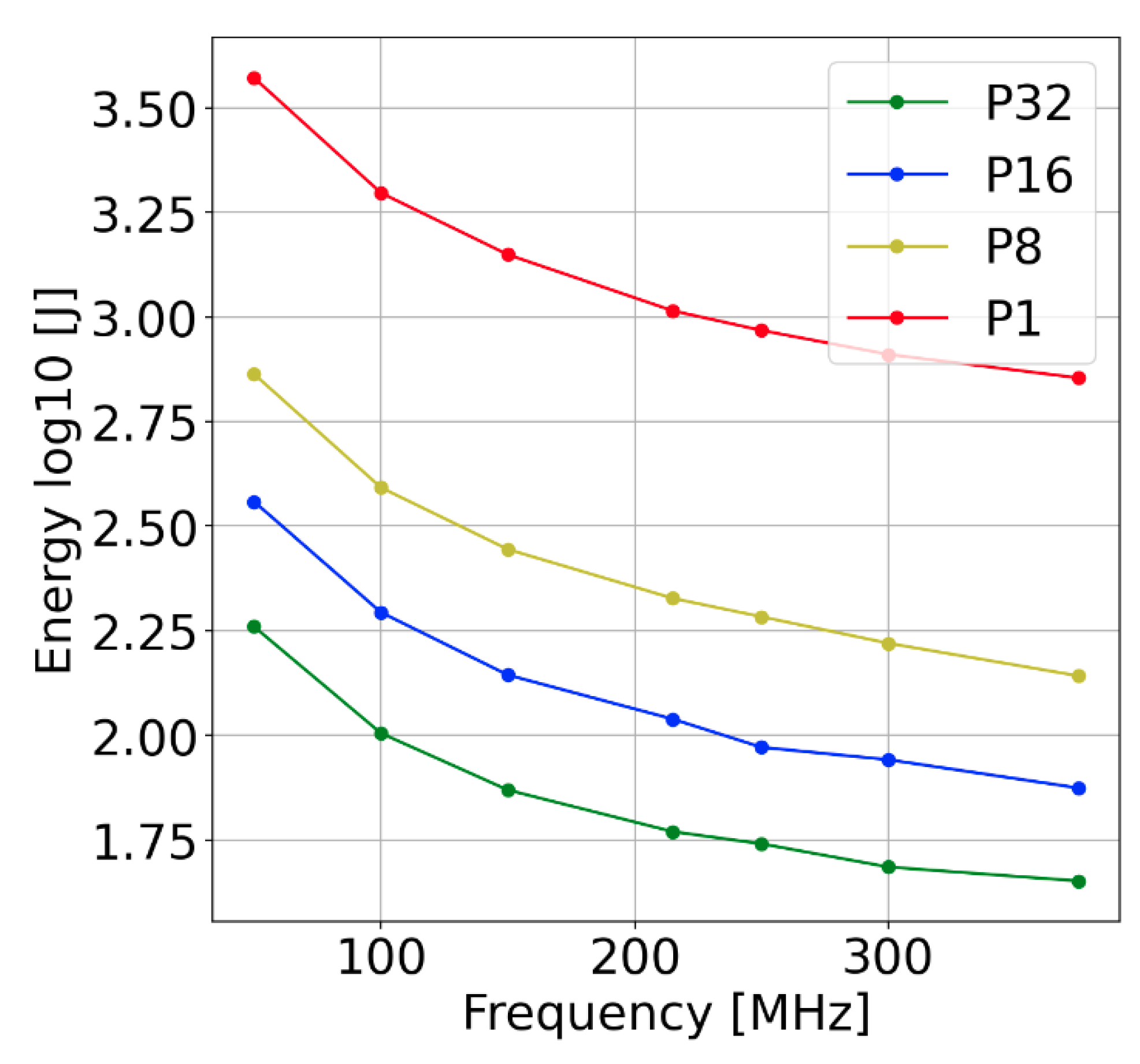
Figure 17.
Result of the experiments. Energy dependency on frequency and parallelisation. Applying higher frequencies and higher parallelism allows us to decrease total energy consumption (CPU + FPGA) for the processing of a fixed size dataset. The parallelism is limited by the available resources. The frequency is limited by the value that allows for correct results. The energy consumption saturates slightly with the increase in the frequency.
Figure 17.
Result of the experiments. Energy dependency on frequency and parallelisation. Applying higher frequencies and higher parallelism allows us to decrease total energy consumption (CPU + FPGA) for the processing of a fixed size dataset. The parallelism is limited by the available resources. The frequency is limited by the value that allows for correct results. The energy consumption saturates slightly with the increase in the frequency.
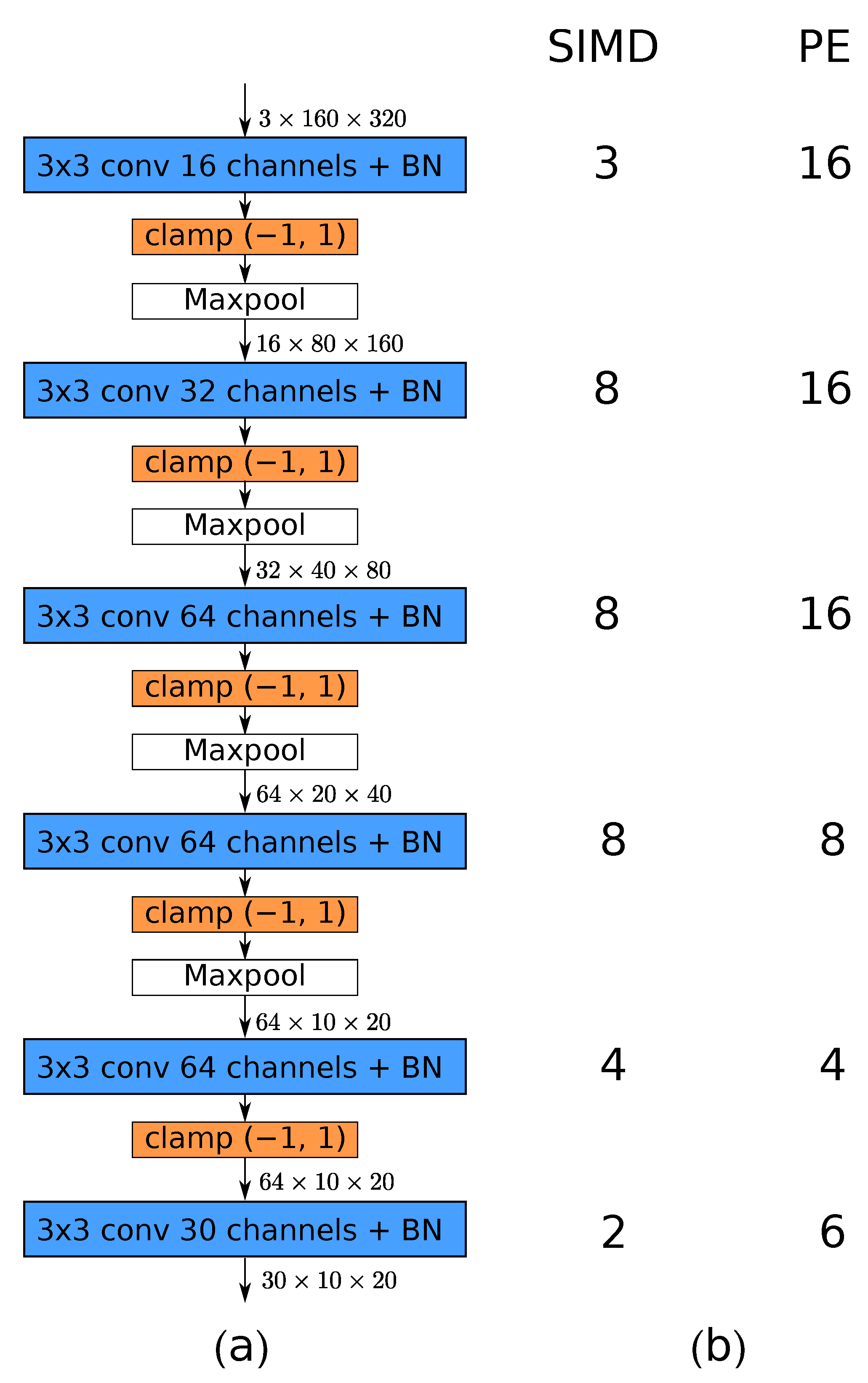
Figure 18.
(
a) Convolutional architecture used in the FINN accelerator and (
b) folding parameters for each layer. The number of processing elements (PE) and SIMD lanes used for each layer determines the level of parallelism. Note that the use of maxpool layers results in the reduction in spatial dimensions of the processed tensor. Therefore, fewer FPGA resources are needed for later layers of the network. For details, refer to
Section 7.2.
Figure 18.
(
a) Convolutional architecture used in the FINN accelerator and (
b) folding parameters for each layer. The number of processing elements (PE) and SIMD lanes used for each layer determines the level of parallelism. Note that the use of maxpool layers results in the reduction in spatial dimensions of the processed tensor. Therefore, fewer FPGA resources are needed for later layers of the network. For details, refer to
Section 7.2.
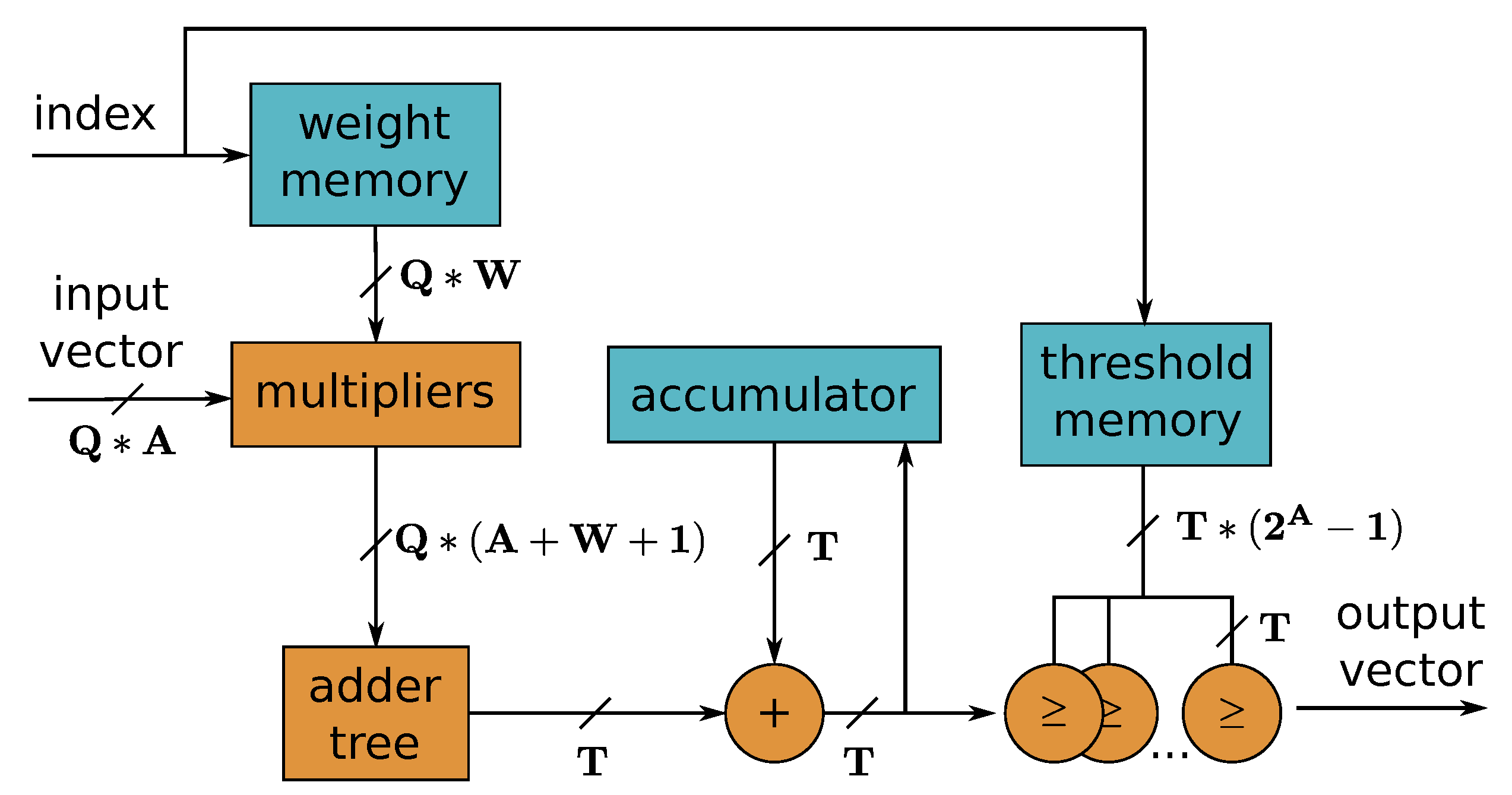
Figure 19.
Single processing element (PE) used for dot product computation in FINN framework. Q input channels with A-bit precision are processed in parallel. The W-bit weights are stored in on-chip memory to avoid memory bandwidth bottlenecks. As a result of the fine-grained architecture of the system, the processed input pixels are accumulated sequentially before an output channel is computed. The values from the threshold memory are used for comparisons with the accumulated result to implement the required activation function.
Figure 19.
Single processing element (PE) used for dot product computation in FINN framework. Q input channels with A-bit precision are processed in parallel. The W-bit weights are stored in on-chip memory to avoid memory bandwidth bottlenecks. As a result of the fine-grained architecture of the system, the processed input pixels are accumulated sequentially before an output channel is computed. The values from the threshold memory are used for comparisons with the accumulated result to implement the required activation function.
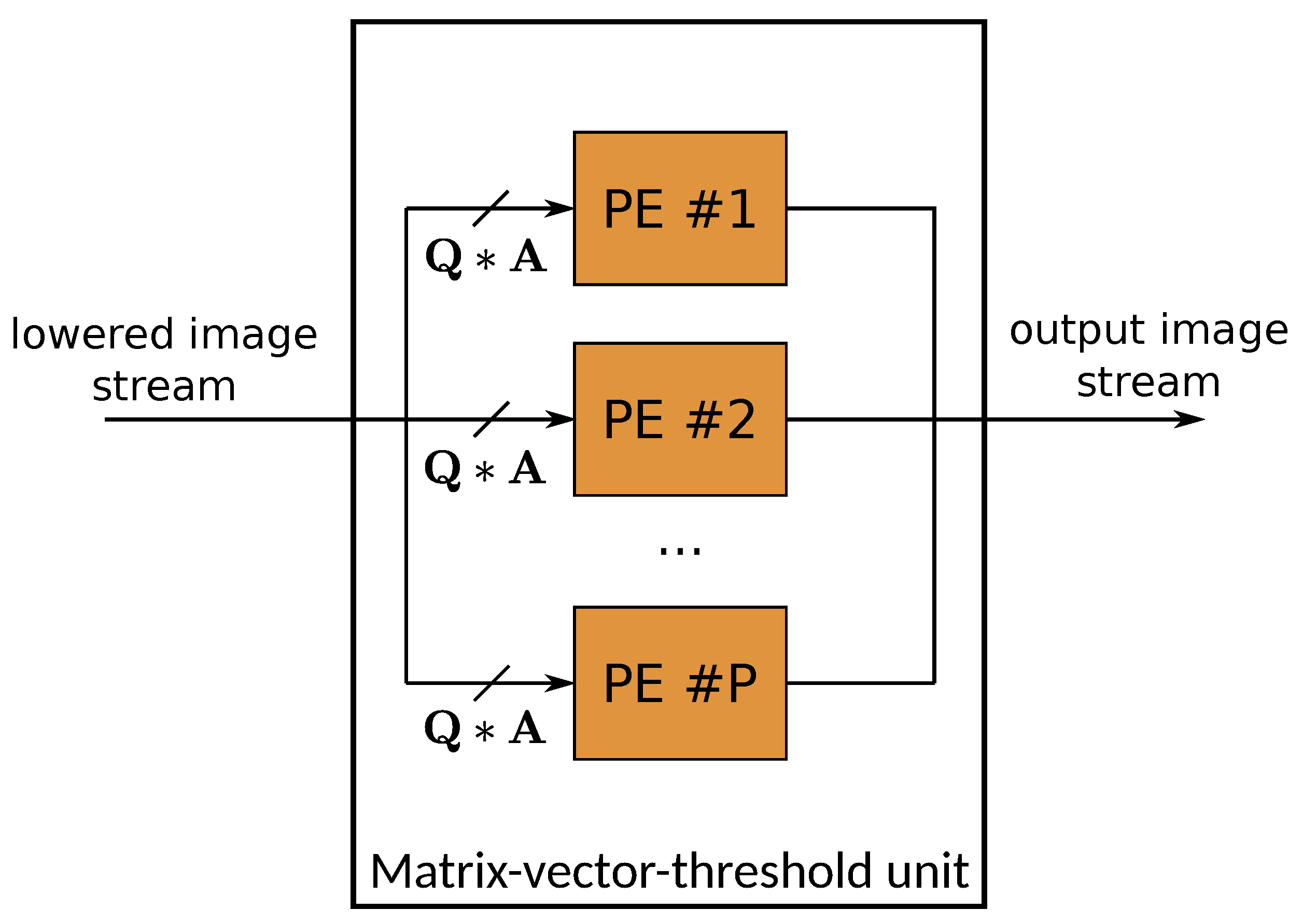
Figure 20.
Matrix-vector-threshold unit used for fully connected and convolutional layers in FINN. The module processes the data stream generated by the sliding window unit (SWU), which reduces convolution operation to a multiplication between filter and image matrices. The columns of the filter matrix are split between SIMD lanes and each row is mapped to a different PE.
Figure 20.
Matrix-vector-threshold unit used for fully connected and convolutional layers in FINN. The module processes the data stream generated by the sliding window unit (SWU), which reduces convolution operation to a multiplication between filter and image matrices. The columns of the filter matrix are split between SIMD lanes and each row is mapped to a different PE.
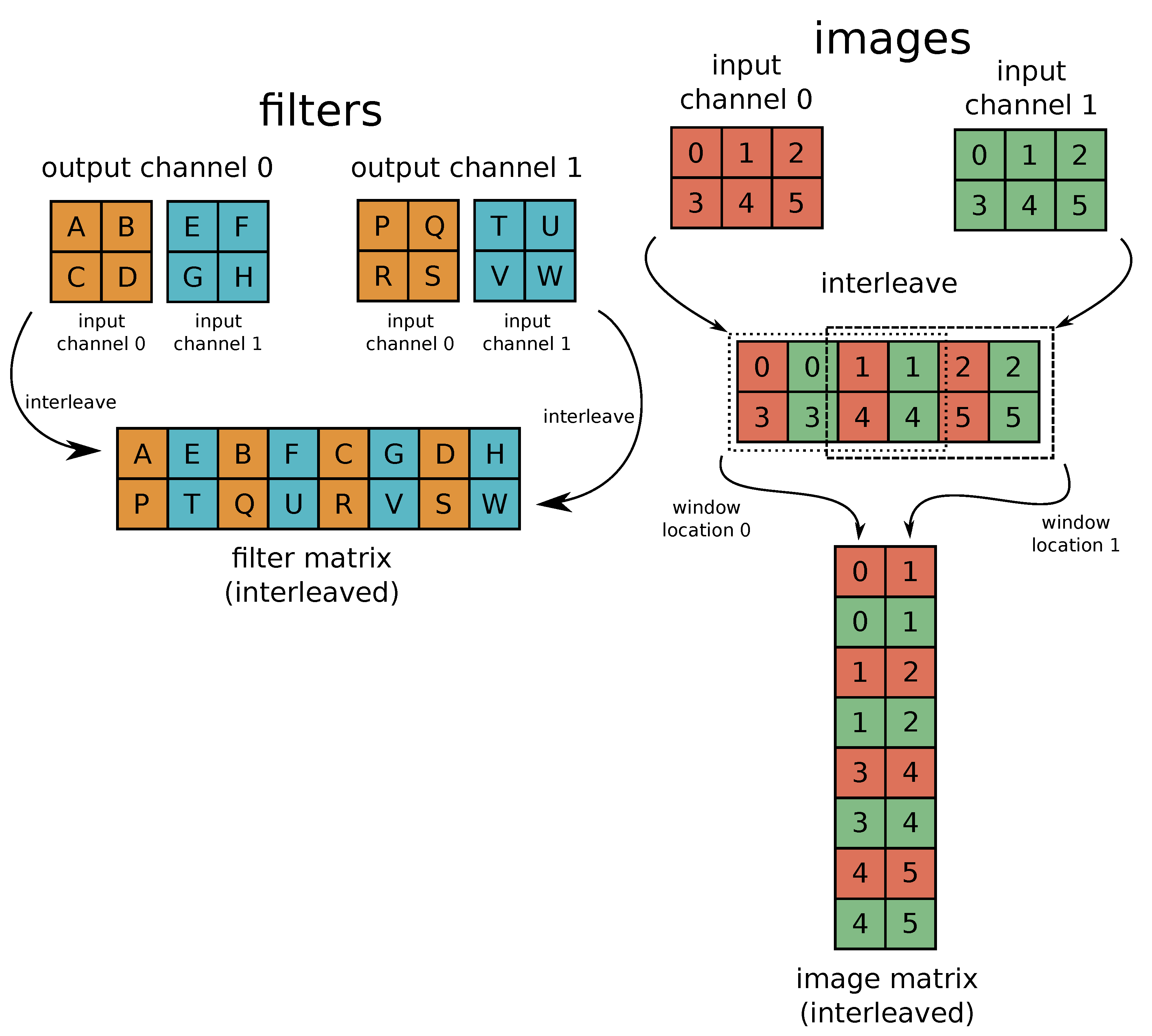
Figure 21.
The figure shows the process of reducing the convolution operation to a matrix–matrix multiplication. In this example, two-channel input is processed by four convolutional filters to produce two-channel output. The proper filter matrix is kept inside weight memory of every PE and the image matrix is constructed by the SWU during inference. The result of the convolution is a product of the filter matrix and the image matrix. Every column of the image matrix contains image context for a single filter location and each row of the filter matrix contains weights corresponding to a single output channel.
Figure 21.
The figure shows the process of reducing the convolution operation to a matrix–matrix multiplication. In this example, two-channel input is processed by four convolutional filters to produce two-channel output. The proper filter matrix is kept inside weight memory of every PE and the image matrix is constructed by the SWU during inference. The result of the convolution is a product of the filter matrix and the image matrix. Every column of the image matrix contains image context for a single filter location and each row of the filter matrix contains weights corresponding to a single output channel.
Figure 22.
The training procedure of the YoloFINN architecture. The dashed red line denotes the moment of changing the precision from 8 to 4 bits. Such level of quantisation was necessary to meet the constraints of the embedded platform.
Figure 22.
The training procedure of the YoloFINN architecture. The dashed red line denotes the moment of changing the precision from 8 to 4 bits. Such level of quantisation was necessary to meet the constraints of the embedded platform.
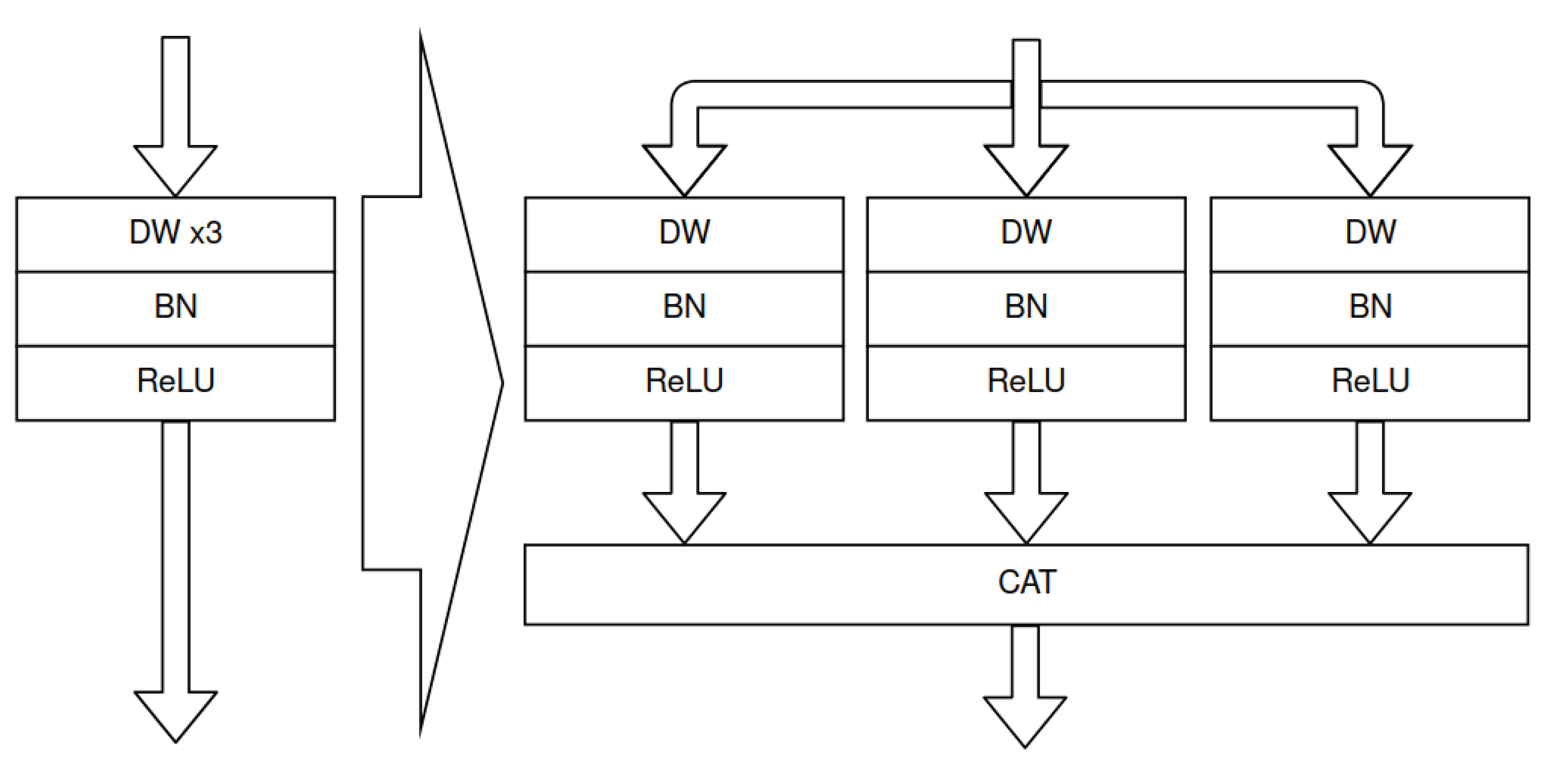
Figure 23.
Multi-depthwise convolution replaced by concatenated 3 single depthwise convolutions. The presented transformation allows for multi-depthwise convolution acceleration with Vitis AI DPU.
Figure 23.
Multi-depthwise convolution replaced by concatenated 3 single depthwise convolutions. The presented transformation allows for multi-depthwise convolution acceleration with Vitis AI DPU.
Table 1.
Applied parallelisation of pointwise accelerators.
Table 1.
Applied parallelisation of pointwise accelerators.
| Layer | 2. PW | 5. PW | 8. PW | 11. PW | 14. PW | 17. PW | 19. PW |
| Parallelisation | 8 | 16 | 18 | 18 | 22 | 32 | 2 |
Table 2.
Normalised approximated times of execution. They were determined based on the multiplication of the input features maps’ sizes and the number of readings of the whole map. The weights reloading or initialisation times were ignored. The normalisation was performed by dividing all results by their largest value. The processing of PW layers takes much longer than DW layers.
Table 2.
Normalised approximated times of execution. They were determined based on the multiplication of the input features maps’ sizes and the number of readings of the whole map. The weights reloading or initialisation times were ignored. The normalisation was performed by dividing all results by their largest value. The processing of PW layers takes much longer than DW layers.
| | State | 0 | 1 | 2 | 3 |
|---|
| Macroblock | |
|---|
|
0 | IL 0.0015 | DW 0.0117 | PW 0.0938 | DW 0.0039 |
| 1 | DW 0.0078 | PW 0.2500 | DW 0.0039 | DW 0.0078 |
| 2 | PW 0.5000 | DW 0.0020 | DW 0.0039 | PW 0.5000 |
| 3 | DW 0.0010 | DW 0.0020 | PW 0.5000 | DW 0.0020 |
| 4 | DW 0.0039 | PW 1.0000 | DW 0.0020 | PW 0.0312 |
| 5 | MF 0.0001 | OL 0.0000 | | |
Table 3.
Maximal times of processing for each state for selected layer types. The duration of each state depends on the processing times of the PW layers.
Table 3.
Maximal times of processing for each state for selected layer types. The duration of each state depends on the processing times of the PW layers.
| | State | 0 | 1 | 2 | 3 | Sum |
|---|
| Layer Type | |
|---|
|
PW | 0.5000 | 1.0000 | 0.5000 | 0.5000 | 2.500 |
| non-PW | 0.0078 | 0.0117 | 0.0039 | 0.0078 | 0.0312 |
| all | 0.5000 | 1.0000 | 0.5000 | 0.5000 | 2.500 |
Table 4.
Sets of parallelisation with labels. Configuration P32 allows for maximal performance. The next two have two and four times smaller parallelisms. The last one is the minimal configuration.
Table 4.
Sets of parallelisation with labels. Configuration P32 allows for maximal performance. The next two have two and four times smaller parallelisms. The last one is the minimal configuration.
| | Layer | 2. PW | 5. PW | 8. PW | 11. PW | 14. PW | 17. PW | 19. PW |
|---|
| Label | |
|---|
| P32 | 8 | 16 | 18 | 18 | 22 | 32 | 2 |
| P16 | 4 | 8 | 9 | 9 | 11 | 16 | 1 |
| P8 | 2 | 4 | 4 | 4 | 5 | 8 | 1 |
| P1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Table 5.
Evaluation results—energy consumptions and fps for different parallelisations and frequencies. There is a noticeable decrease in energy consumption for higher parallelisations and higher frequencies—for higher throughput in general.
Table 5.
Evaluation results—energy consumptions and fps for different parallelisations and frequencies. There is a noticeable decrease in energy consumption for higher parallelisations and higher frequencies—for higher throughput in general.
| Label | Frequency 1 [MHz] | Throughput [fps] | Energy [J] | Power [W] |
|---|
| P32 | 375 | 236 | 44.845 | 3.528 |
| 300 | 195 | 48.414 | 3.147 |
| 250 | 167 | 55.032 | 3.063 |
| 215 | 145 | 58.829 | 2.843 |
| 150 | 105 | 73.990 | 2.590 |
| 100 | 71 | 101.134 | 2.394 |
| 50 | 35 | 181.750 | 2.120 |
| P16 | 375 | 130 | 74.805 | 3.242 |
| 300 | 105 | 87.393 | 3.059 |
| 250 | 88 | 93.597 | 2.746 |
| 215 | 76 | 109.306 | 2.769 |
| 150 | 53 | 139.347 | 2.462 |
| 100 | 35 | 196.697 | 2.295 |
| 50 | 17 | 361.815 | 2.050 |
| P8 | 375 | 65 | 138.635 | 3.004 |
| 300 | 52 | 165.928 | 2.876 |
| 250 | 43 | 191.968 | 2.752 |
| 215 | 37 | 212.532 | 2.621 |
| 150 | 26 | 278.281 | 2.412 |
| 100 | 17 | 390.941 | 2.215 |
| 50 | 8 | 729.939 | 2.115 |
| P1 | 375 | 12 | 714.737 | 2.859 |
| 300 | 10 | 813.676 | 2.712 |
| 250 | 8 | 928.440 | 2.476 |
| 215 | 7 | 1034.701 | 2.414 |
| 150 | 5 | 1409.458 | 2.349 |
| 100 | 3.3 | 1979.160 | 2.177 |
| 50 | 1.7 | 3727.046 | 2.112 |
Table 6.
Comparison of detection quality and resource utilisation for different degrees of quantisation.
Table 6.
Comparison of detection quality and resource utilisation for different degrees of quantisation.
| Precision | LUT Utilisation (% of Available) | IoU on Hardware Test Set |
|---|
| 8-bit | 301,968 (428%) | 0.7153 |
| 5-bit | 85,932 (122%) | 0.6970 |
| 4-bit | 54,079 (77%) | 0.6513 |
Table 7.
Evaluation results of acceleration with Vitis AI. Both models achieves similar accuracy, but with different throughputs and energy consumptions. The YoloFINN network has higher computational complexity, especially due to the applied activation approximation.
Table 7.
Evaluation results of acceleration with Vitis AI. Both models achieves similar accuracy, but with different throughputs and energy consumptions. The YoloFINN network has higher computational complexity, especially due to the applied activation approximation.
| Model | IoU | fps | Energy [J] | Power [W] |
|---|
| LittleNet | 0.6625 | 123.3 | 68.332 | 2.808 |
| YoloFINN | 0.6746 | 53.2 | 175.818 | 3.118 |
Table 8.
Results of acceleration with different methods. Abbreviations: C-G—coarse-grained, F-G— fine-grained, Seq.—sequential. The highest throughput is achieved by our C-G solution. YoloFINN architecture gives better accuracy results, but with higher computational complexity than LittleNet.
Table 8.
Results of acceleration with different methods. Abbreviations: C-G—coarse-grained, F-G— fine-grained, Seq.—sequential. The highest throughput is achieved by our C-G solution. YoloFINN architecture gives better accuracy results, but with higher computational complexity than LittleNet.
| Model | | Method | Quantisation | | fps | E [J] | P [W] |
|---|
| LittleNet | 0.6682 | C-G | 8-bit | 0.6616 | 196 | 49.88 | 3.259 |
| Seq. | 8-bit | 0.6625 | 123.3 | 68.33 | 2.808 |
| YoloFINN | 0.7209 | F-G | 4-bit | 0.6608 | 111 | 79.83 | 2.954 |
| Seq. | 8-bit | 0.6746 | 53.2 | 175.82 | 3.118 |
Table 9.
Resource usage for each architecture. Our coarse-grained solution can be considered as memory-hungry. On the other hand, the implementation with FINN uses more LUTs than other resources. Vitis AI DPU consumes less resources than our solution, but more than FINN.
Table 9.
Resource usage for each architecture. Our coarse-grained solution can be considered as memory-hungry. On the other hand, the implementation with FINN uses more LUTs than other resources. Vitis AI DPU consumes less resources than our solution, but more than FINN.
| HW Architecture | LUT | LUT RAM | FF | BRAM | DSP |
|---|
| LN P32 | 33,029 | 7077 | 64,918 | 198.5 | 349 |
| LN P16 | 25,321 | 4724 | 47,339 | 198.5 | 238 |
| LN P8 | 21,025 | 3772 | 39,328 | 202.5 | 187 |
| LN P1 | 17,120 | 3044 | 30,023 | 205.0 | 140 |
| Vitis AI DPU 1 | 45,051 | 0 | 63,033 | 168.0 | 262 |
| Vitis AI DPU 2 | 34,924 | 2875 | 57,094 | 163.0 | 312 |
| YoloFINN 4-bit | 54,079 | 8002 | 57,118 | 26.5 | 10 |
Table 10.
Parameter numbers and characteristics of selected networks architectures.
Table 10.
Parameter numbers and characteristics of selected networks architectures.
| Network Architecture | Dataset | Parameters | Features |
|---|
| YOLOv3-tiny [39] | COCO | 8.818 M | multi-scale detection, standard convolutions, upsampling |
| MobileNetV2 [40] | COCO | 4.3 M | separable convolution, inverted residual blocks |
| SkyNet [20] | DAC SDC | 0.309 M | separable convolution, PSO algorithm used for structure optimisation |
| UltraNet [35] | DAC SDC | 0.256 M | , standard convolution with quantisation |
| LittleNet (our) | VOT+VTB | 0.244 M | multi-depthwise convolution, linear activation for some layers, anchors multipliers |
| YoloFINN (our) | VOT+VTB | 0.115 M | activation function |