CORDIC Hardware Acceleration Using DMA-Based ISA Extension
Abstract
:1. Introduction
2. Background
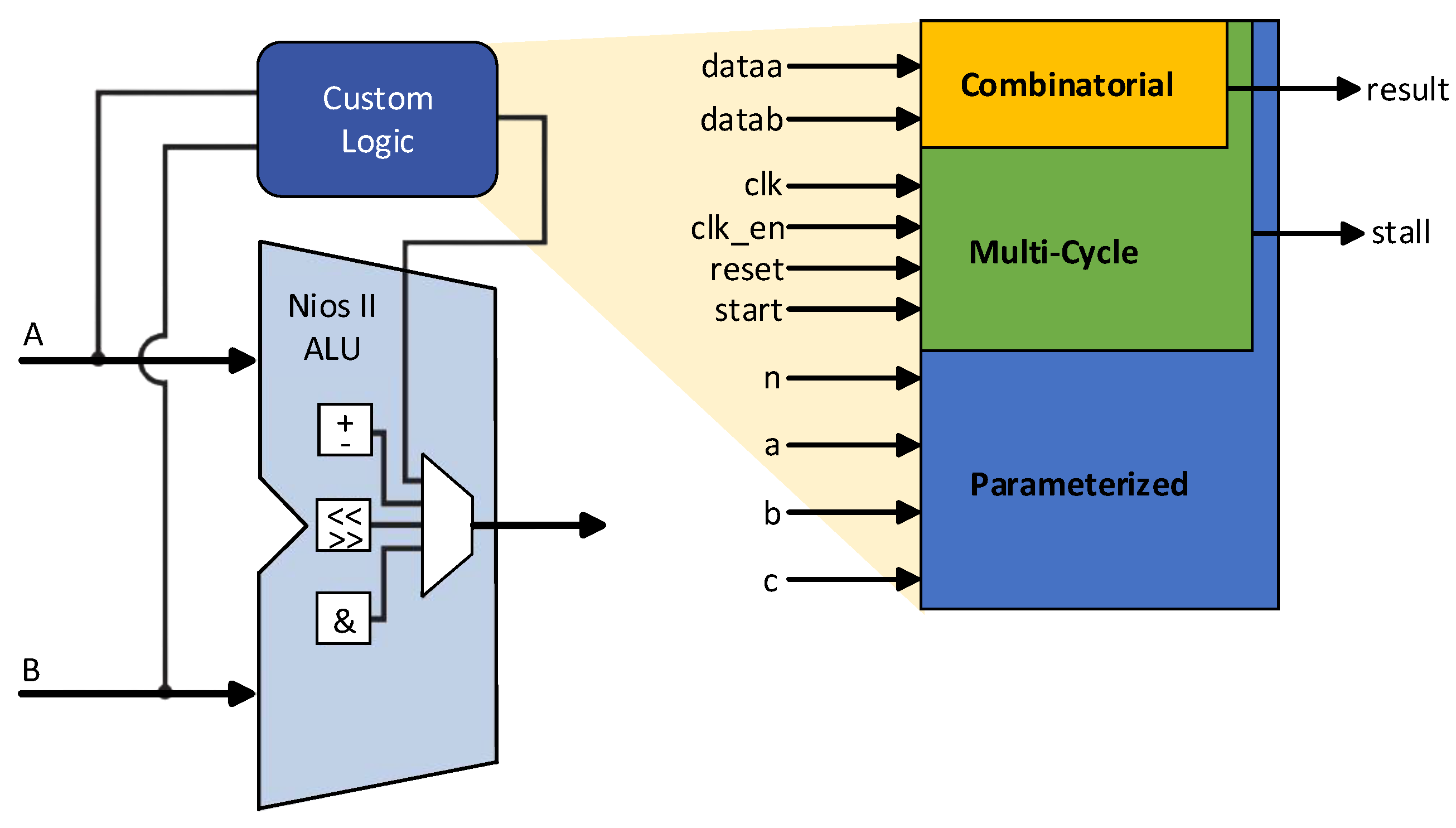
2.1. Nios-II Custom Instruction
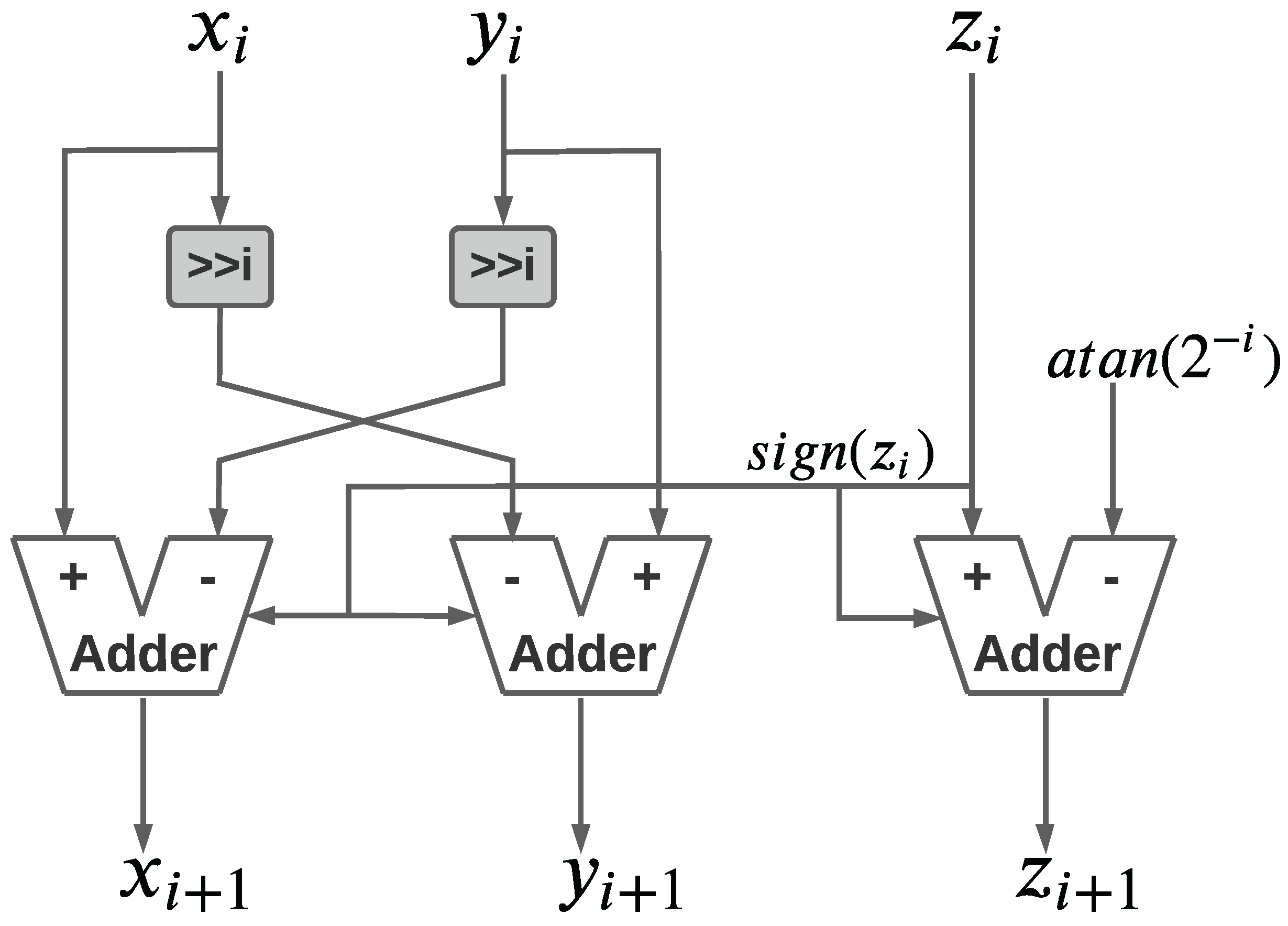
2.2. Altera Hardware CORDIC Unit
3. Related Work
4. Methodology
4.1. ISA Extension Basic Implementation
4.2. ISA Extension Using Pipelined Approach
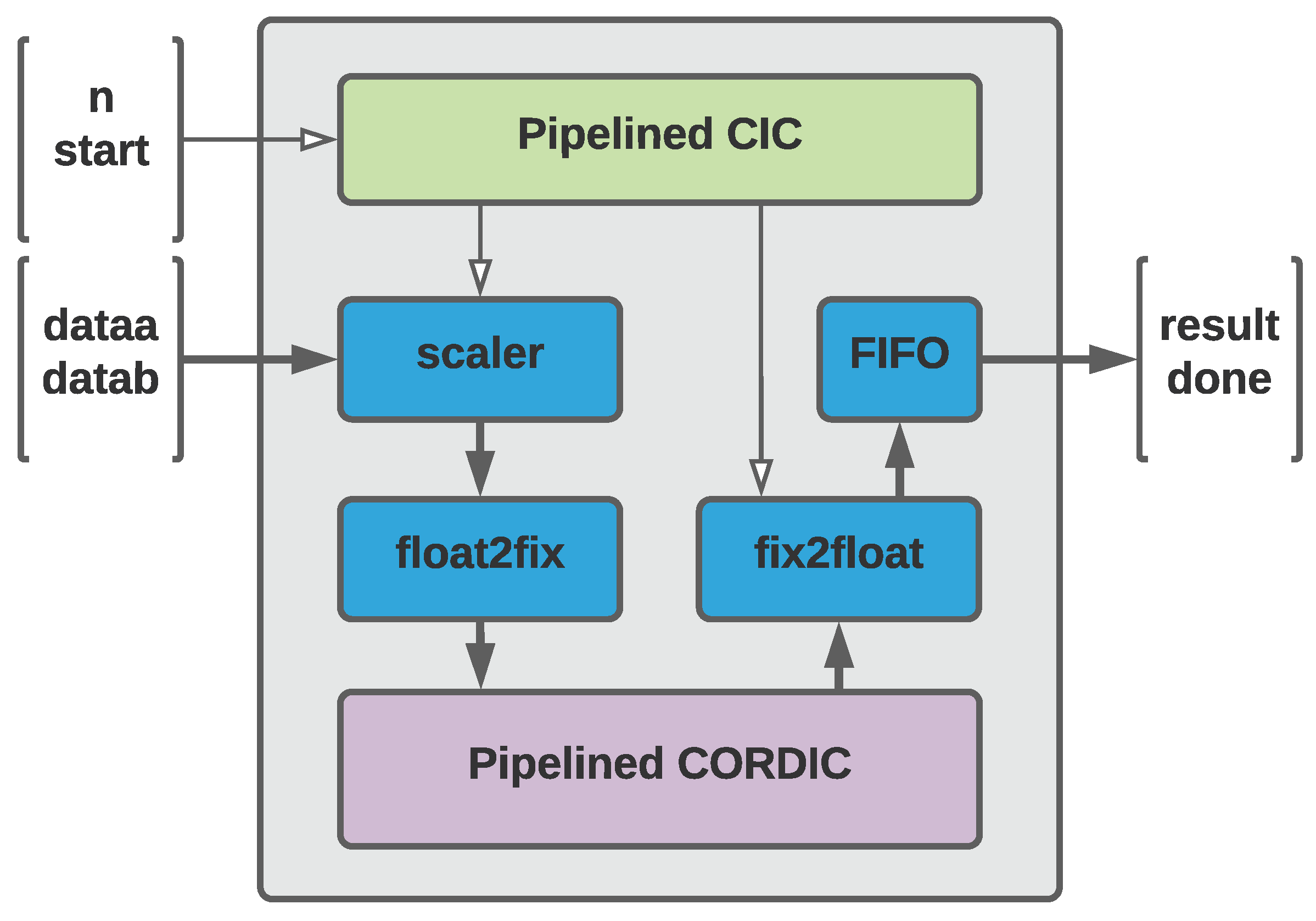
4.3. ISA Extension Using DMA Approach
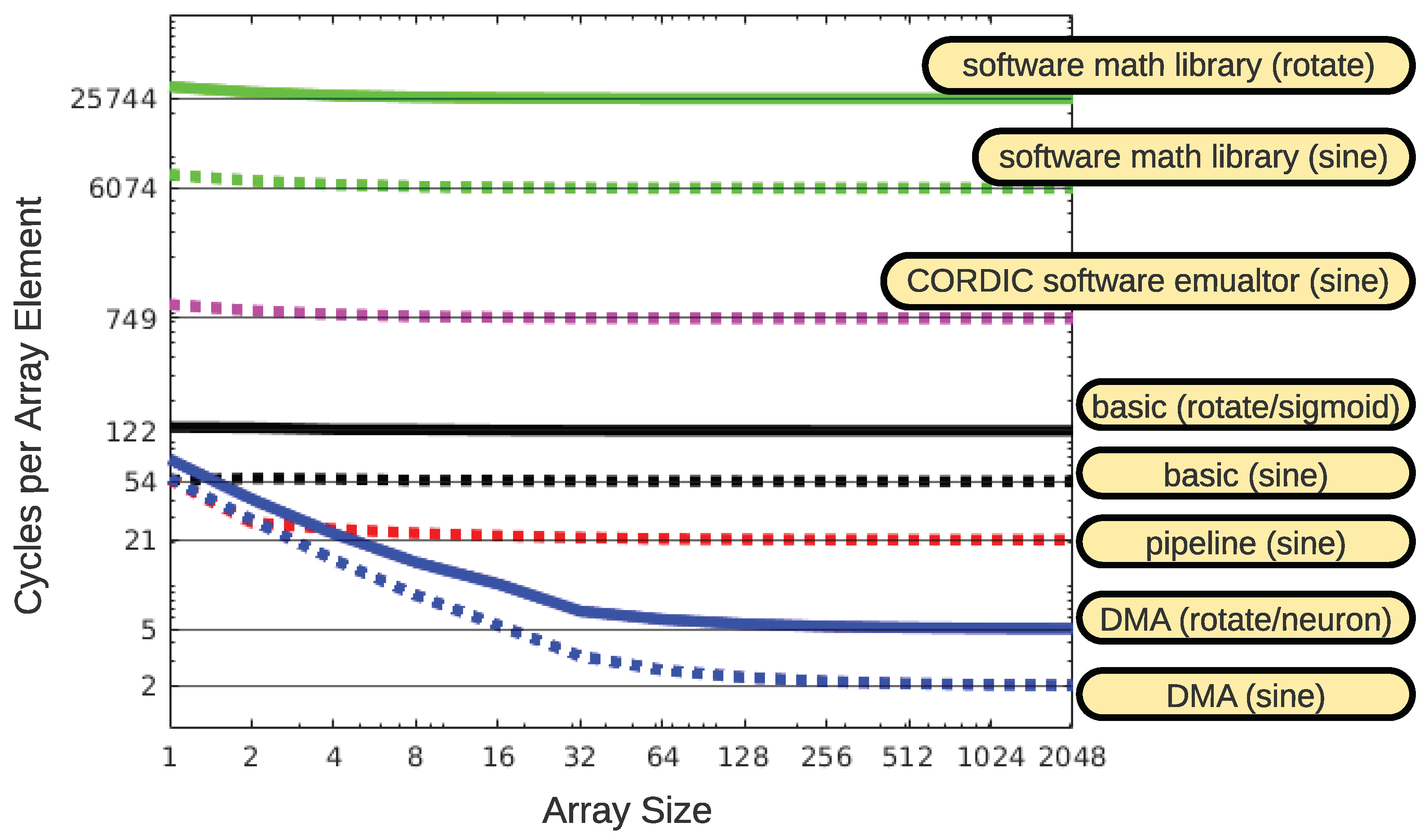
5. Results
6. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cadence. Tensilica Customizable Processors. Available online: https://ip.cadence.com (accessed on 9 November 2021).
- Intel. Nios II Processors. Available online: https://www.intel.com (accessed on 9 November 2021).
- Davide Schiavone, P.; Conti, F.; Rossi, D.; Gautschi, M.; Pullini, A.; Flamand, E.; Benini, L. Slow and steady wins the race? A comparison of ultra-low-power RISC-V cores for Internet-of-Things applications. In Proceedings of the 2017 27th International Symposium on Power and Timing Modeling, Optimization and Simulation (PATMOS), Thessaloniki, Greece, 25–27 September 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Joseph Yiu, A. Innovate by Customized Instructions, but without Fragmenting the Ecosystem. Available online: https://armkeil.blob.core.windows.net/developer/Files/pdf/white-paper/arm-custom-instructions-without-fragmentation-whitepaper.pdf (accessed on 9 November 2021).
- Wang, X.; Magno, M.; Cavigelli, L.; Benini, L. FANN-on-MCU: An Open-Source Toolkit for Energy-Efficient Neural Network Inference at the Edge of the Internet of Things. arXiv 2019, arXiv:1911.03314. [Google Scholar] [CrossRef]
- Sharma, N.K.; Rathore, S.; Khan, M.R. A Comparative Analysis on Coordinate Rotation Digital Computer (CORDIC) Algorithm and Its use on Computer Vision Technology. In Proceedings of the 2020 First International Conference on Power, Control and Computing Technologies (ICPC2T), Raipur, India, 3–5 January 2020; pp. 106–110. [Google Scholar] [CrossRef]
- Raut, G.; Rai, S.; Vishvakarma, S.K.; Kumar, A. A CORDIC Based Configurable Activation Function for ANN Applications. In Proceedings of the 2020 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Limassol, Cyprus, 6–8 July 2020; pp. 78–83. [Google Scholar] [CrossRef]
- Raut, G.; Rai, S.; Vishvakarma, S.K.; Kumar, A. RECON: Resource-Efficient CORDIC-Based Neuron Architecture. IEEE Open J. Circuits Syst. 2021, 2, 170–181. [Google Scholar] [CrossRef]
- Heidarpur, M.; Ahmadi, A.; Ahmadi, M.; Rahimi Azghadi, M. CORDIC-SNN: On-FPGA STDP Learning with Izhikevich Neurons. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 2651–2661. [Google Scholar] [CrossRef]
- Hao, X.; Yang, S.; Wang, J.; Deng, B.; Wei, X.; Yi, G. Efficient Implementation of Cerebellar Purkinje Cell With the CORDIC Algorithm on LaCSNN. Front. Neurosci. 2019, 13, 1078. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Manor, E.; Greenberg, S. Efficient Hardware/Software partitioning for Heterogeneous Embedded Systems. In Proceedings of the 2018 IEEE International Conference on the Science of Electrical Engineering in Israel (ICSEE), Eilat, Israel, 12–14 December 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Volder, J.E. The Birth of Cordic. J. VLSI Signal Process. Syst. 2000, 25, 101–105. [Google Scholar] [CrossRef]
- Lin, K.J.; Hou, C.C. Implementation of trigonometric custom functions hardware on embedded processor. In Proceedings of the 2013 IEEE 2nd Global Conference on Consumer Electronics (GCCE), Tokyo, Japan, 14 November 2013; pp. 155–157. [Google Scholar]
- Walther, J.S. A Unified Algorithm for Elementary Functions. In Proceedings of the Spring Joint Computer Conference—AFIPS ’71 (Spring), Atlantic City, NJ, USA, 18–20 May 1971; Association for Computing Machinery: New York, NY, USA, 1971; pp. 379–385. [Google Scholar] [CrossRef]
- Walther, J.S. A Unified Algorithm for Elementary Functions; AFIPS ’71; Spring: Berlin/Heidelberg, Germany, 1971. [Google Scholar]
- Nguyen, H.; Nguyen, X.; Pham, C.; Hoang, T.; Le, D. A parallel pipeline CORDIC based on adaptive angle selection. In Proceedings of the 2016 International Conference on Electronics, Information, and Communications (ICEIC), Danang, Vietnam, 27–30 January 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Detrey, J.; de Dinechin, F. Floating-Point Trigonometric Functions for FPGAs. In Proceedings of the 2007 International Conference on Field Programmable Logic and Applications, Amsterdam, The Netherlands, 27–29 August 2007; pp. 29–34. [Google Scholar]
- Liventsev, E.; Silantiev, A.; Primakov, E.; Telminov, O. Extending MIPSfpga instruction set for navigation data processing. In Proceedings of the 2017 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), St. Petersburg and Moscow, Russia, 1–3 February 2017; pp. 480–484. [Google Scholar] [CrossRef]
- Andraka, R. A Survey of CORDIC Algorithms for FPGA Based Computers. In Proceedings of the 1998 ACM/SIGDA Sixth International Symposium on Field Programmable Gate Arrays—FPGA ’98, Monterey, CA, USA, 22–24 February 1998; Association for Computing Machinery: New York, NY, USA, 1998; pp. 191–200. [Google Scholar] [CrossRef]
- Nolting, S.; Payá-Vayá, G.; Schmeadecke, I.; Blume, H. Evaluation of a Generic Radix-4 CORDIC Coprocessor Tightly Coupled with a Generic VLIW-SIMD ASIP Architecture. 2012. Available online: https://www.researchgate.net/profile/Guillermo-Paya-Vaya/publication/260614052_Evaluation_of_a_Generic_Radix-4_CORDIC_Coprocessor_Tightly_Coupled_with_a_Generic_VLIW-SIMD_ASIP_Architecture/links/570121bb08aea6b7746a78b1/Evaluation-of-a-Generic-Radix-4-CORDIC-Coprocessor-Tightly-Coupled-with-a-Generic-VLIW-SIMD-ASIP-Architecture.pdf (accessed on 9 November 2021).
- Ibrahim, M.; Chen, K.T.; Idroas, M.; Yahya, Z. The implementation of a pipelined floating-point CORDIC coprocessor on NIOS II soft processor. Int. J. Electr. Electron. Data Commun. 2015, 3, 15–20. [Google Scholar]
- Zhou, J.; Dong, Y.; Dou, Y.; Lei, Y. Dynamic Configurable Floating-Point FFT Pipelines and Hybrid-Mode CORDIC on FPGA. In Proceedings of the 2008 International Conference on Embedded Software and Systems, Chengdu, China, 29–31 July 2008; pp. 616–620. [Google Scholar]
- Li, B.; Fang, L.; Xie, Y.; Chen, H.; Chen, L. A unified reconfigurable floating-point arithmetic architecture based on CORDIC algorithm. In Proceedings of the 2017 International Conference on Field Programmable Technology (ICFPT), Melbourne, VIC, Australia, 11–13 December 2017; pp. 301–302. [Google Scholar] [CrossRef]
- Nguyen, K.D.; Kiet, D.T.; Hoang, T.T.; Quynh, N.Q.N.; Tran, X.T.; Pham, C.K. A trigonometric hardware acceleration in 32-bit RISC-V microcontroller with custom instruction. IEICE Electron. Express 2021, 18, 20210266. [Google Scholar] [CrossRef]
- Buzdar, A.; Sun, L.; Khan, S.; Buzdar, A. Area and Energy efficient CORDIC Accelerator for Embedded Processor Datapaths. Inf. Midem Ljubl. 2016, 46, 197–208. [Google Scholar]
- Sun, F.; Ravi, S.; Raghunathan, A.; Jha, N.K. A Synthesis Methodology for Hybrid Custom Instruction and Coprocessor Generation for Extensible Processors. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2007, 26, 2035–2045. [Google Scholar] [CrossRef]
- Wolf, M. Chapter 2 -Instruction Sets. In Computers as Components, 3rd ed.; Wolf, M., Ed.; The Morgan Kaufmann Series in Computer Architecture and Design; Morgan Kaufmann: Boston, MA, USA, 2012; pp. 51–93. [Google Scholar] [CrossRef]
- Kavvadias, N.; Masselos, K. Efficient Hardware Looping Units for FPGAs. In Proceedings of the 2010 IEEE Computer Society Annual Symposium on VLSI, Lixouri, Greece, 5–7 July 2010; pp. 35–40. [Google Scholar] [CrossRef]
- STMicroelectronics. AN5325 Getting Started with the CORDIC Accelerator Using STM32CubeG4 MCU Package. Available online: https://www.st.com/en/embedded-software/stm32cubeg4.html#documentation (accessed on 9 November 2021).



| Function | Mode | x_in | y_in | z_in | Result | Phase Type |
|---|---|---|---|---|---|---|
| A*cos(B) | 1 | A | 0 | B | x_out | Circular |
| A*sin(B) | 1 | A | 0 | B | y_out | Circular |
| asin(A) | 1 | Unit | 0 | A | z_out | Circular |
| atan(B/A) | 0 | A | B | 0 | z_out | Circular |
| Mag(A,B) | 0 | A | B | 0 | x_out | Linear |
| C-B/A | 0 | A | B | C | z_out | Hyperbolic |
| A*cosh(B) | 1 | A | 0 | B | x_out | Hyperbolic |
| A*sinh(B) | 1 | 0 | A | B | x_out | Hyperbolic |
| A*exp(B) | 1 | A | A | B | y_out | Hyperbolic |
| atanh(B/A) | 0 | A | B | 0 | z_out | Hyperbolic |
| 0.5*ln(A) | 0 | A + 1 | A − 1 | 0 | z_out | Hyperbolic |
| sqrt(A) | 0 | A + | A − | 0 | x_out | Hyperbolic |
| Macro | C Equivalent Function |
|---|---|
| CORDIC_COS(phase) | cos(phase) |
| CORDIC_SIN(phase) | sin(phase) |
| CORDIC_AMPCOS(amp,phase) | amp*cos(phase) |
| CORDIC_AMPSIN(amp,phase) | amp*sin(phase) |
| CORDIC_ROTATEX(x,y,phase) | x*cos(phase) − y*sin(phase) |
| CORDIC_ROTATEY(x,y,phase) | y*cos(phase) + x*sin(phase) |
| CORDIC_SIGMOID(x) | sigmoid(x) |
| Macro | Functionality |
|---|---|
| DMA_CORDIC_COS(z_in*,x_out*,size) | x_out = cos(z_in) |
| DMA_CORDIC_SIN(z_in*,y_out*,size) | y_out = sin(z_in) |
| DMA_CORDIC_AMPCOS (z_in*,x_in*,x_out*,size) | x_out = x_in*cos(z_in) |
| DMA_CORDIC_AMPSIN (z_in*,x_in*,y_out*,size) | y_out = x_in*sin(z_in) |
| DMA_CORDIC_ROTATEXY (z_in*,x_in*,y_in*,x_out*,y_out*,size) | x_out = x_in*cos(z_in) − y_in*sin(z_in) y_out = y_in*cos(z_in) + x_in*sin(z_in) |
| DMA_CORDIC_NEURON (x_in*,y_in*,y_out*,size) | y_out = sigmoid() |
| LUTs | Registers | Memory | DSP | Speed (MHz) | |
|---|---|---|---|---|---|
| Component | |||||
| Nios-II/f Core | 1290 | 376 | 10,240 | 6 | - |
| FPU Accelerator | 415 | 198 | 144 | 7 | - |
| CORDIC | 1099 | 170 | 0 | 0 | - |
| scaler | 126 | 148 | 0 | 0 | - |
| float2fix | 261 | 257 | 0 | 0 | - |
| fix2float | 192 | 238 | 0 | 0 | - |
| Basic CIC | 634 | 1039 | 768 | 4 | - |
| Pipelined CIC | 658 | 1071 | 1280 | 6 | - |
| DMA CIC (+Avalon I/F) | 1790 | 2382 | 4096 | 6 | - |
| System | |||||
| Nios with FPU | 1819 | 717 | 10,453 | 13 | 114 |
| Basic Implementation | 4933 | 2463 | 12,032 | 10 | 145 |
| Pipelined Approach | 4955 | 2495 | 12,544 | 12 | 143 |
| DMA Approach | 6089 | 3796 | 15,360 | 12 | 146 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manor, E.; Ben-David, A.; Greenberg, S. CORDIC Hardware Acceleration Using DMA-Based ISA Extension. J. Low Power Electron. Appl. 2022, 12, 4. https://doi.org/10.3390/jlpea12010004
Manor E, Ben-David A, Greenberg S. CORDIC Hardware Acceleration Using DMA-Based ISA Extension. Journal of Low Power Electronics and Applications. 2022; 12(1):4. https://doi.org/10.3390/jlpea12010004
Chicago/Turabian StyleManor, Erez, Avrech Ben-David, and Shlomo Greenberg. 2022. "CORDIC Hardware Acceleration Using DMA-Based ISA Extension" Journal of Low Power Electronics and Applications 12, no. 1: 4. https://doi.org/10.3390/jlpea12010004
APA StyleManor, E., Ben-David, A., & Greenberg, S. (2022). CORDIC Hardware Acceleration Using DMA-Based ISA Extension. Journal of Low Power Electronics and Applications, 12(1), 4. https://doi.org/10.3390/jlpea12010004






