Using Early Data to Estimate the Actual Infection Fatality Ratio from COVID-19 in France
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.2. Mechanistic-Statistical Model
2.3. Statistical Inference
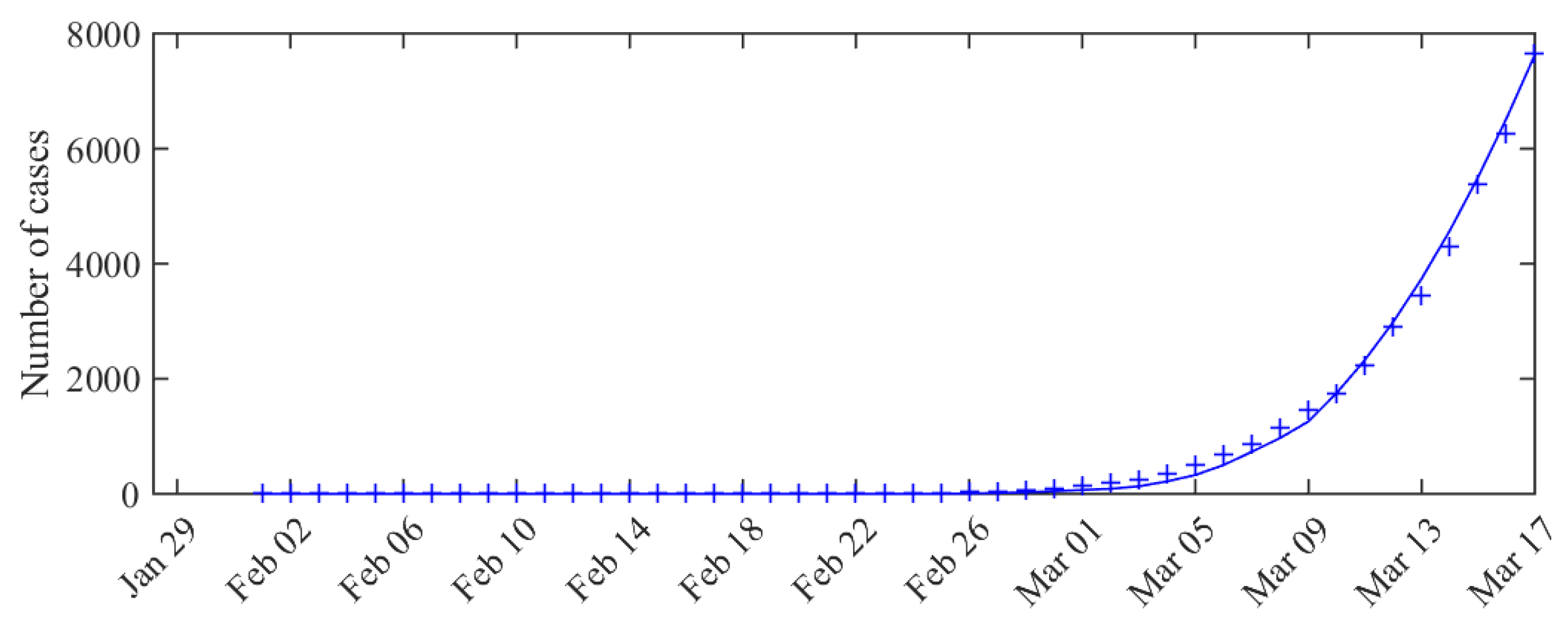
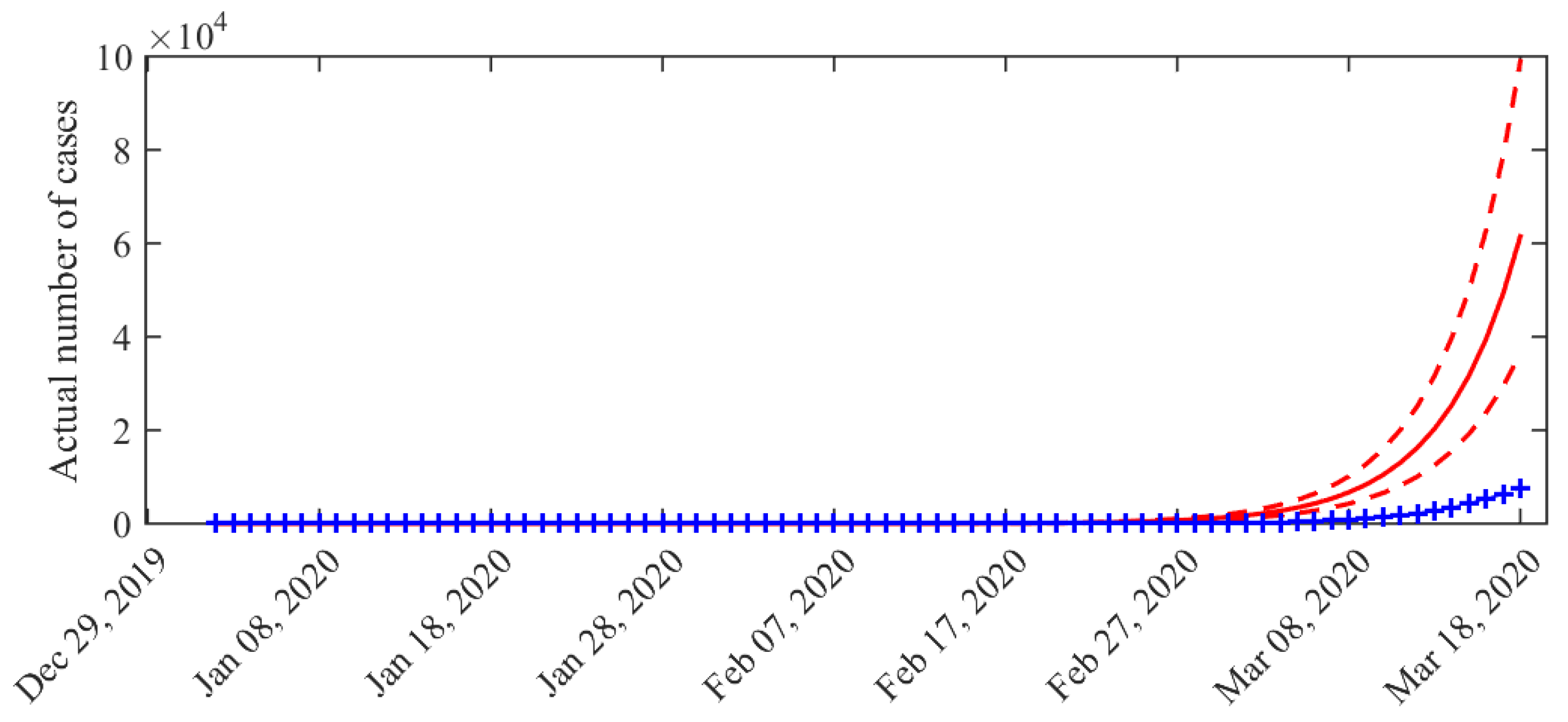
3. Results
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| IFR | Infection fatality ratio |
| CFR | Case fatality rate |
| ODE | Ordinary differential equation |
| ARS | Agence Régionale de Santé |
| WHO | World Health Organization |
| MLE | Maximum likelihood estimator |
| DREES | Direction de la recherche, des études, de l’évaluation et des statistiques |
Appendix A
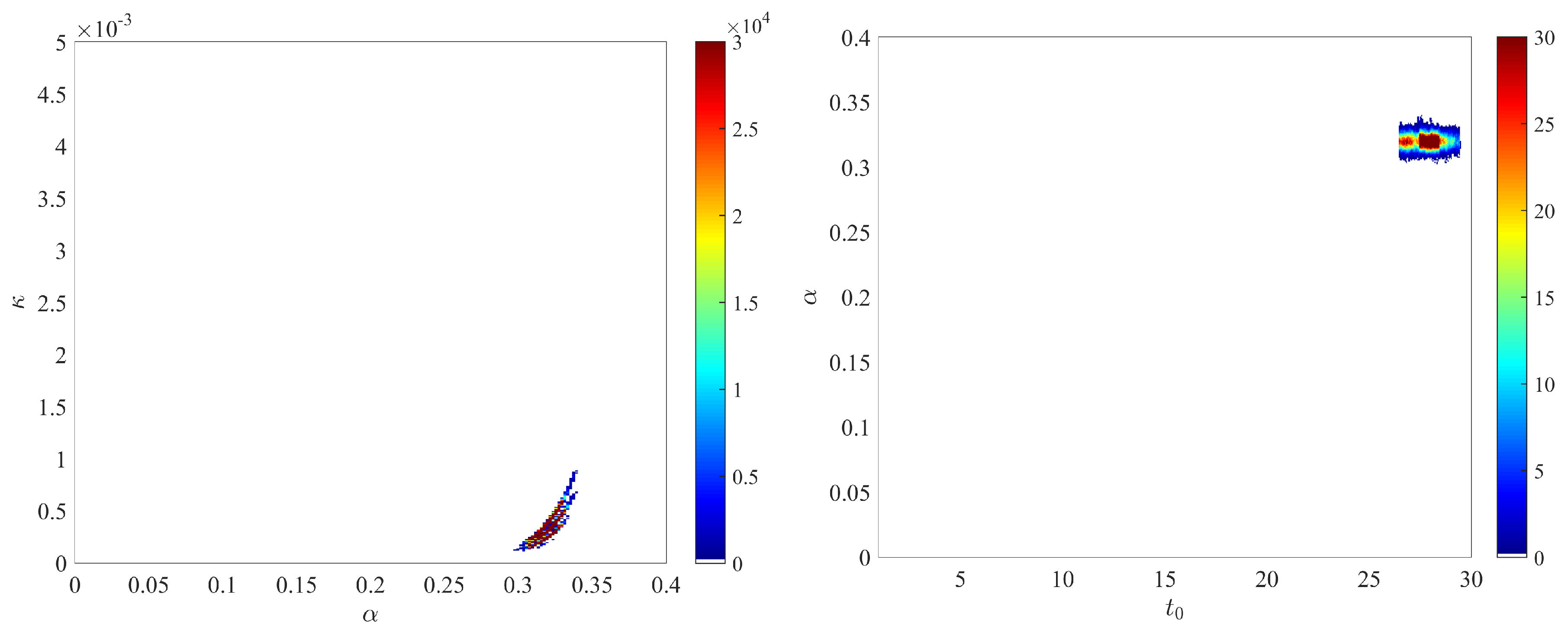
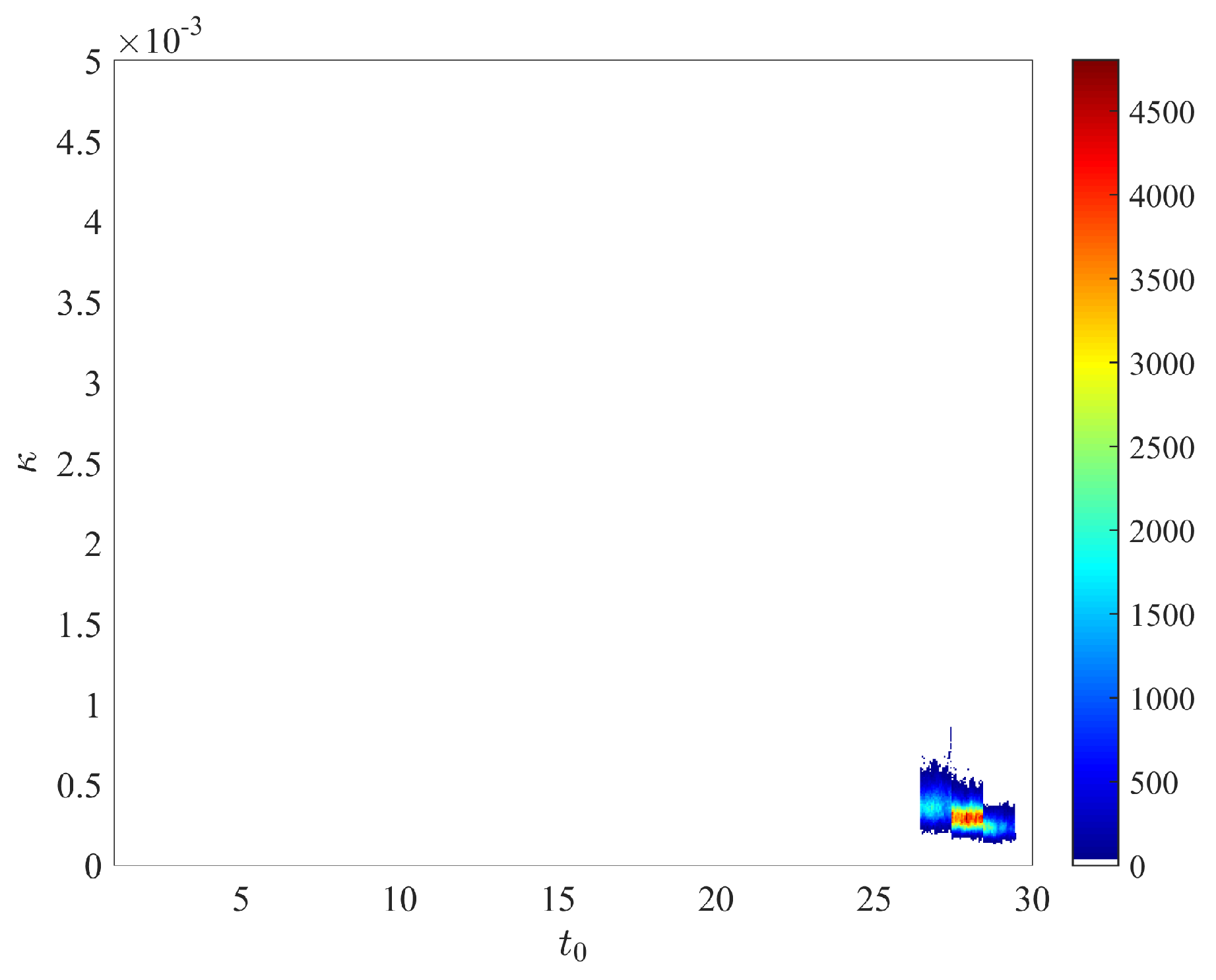
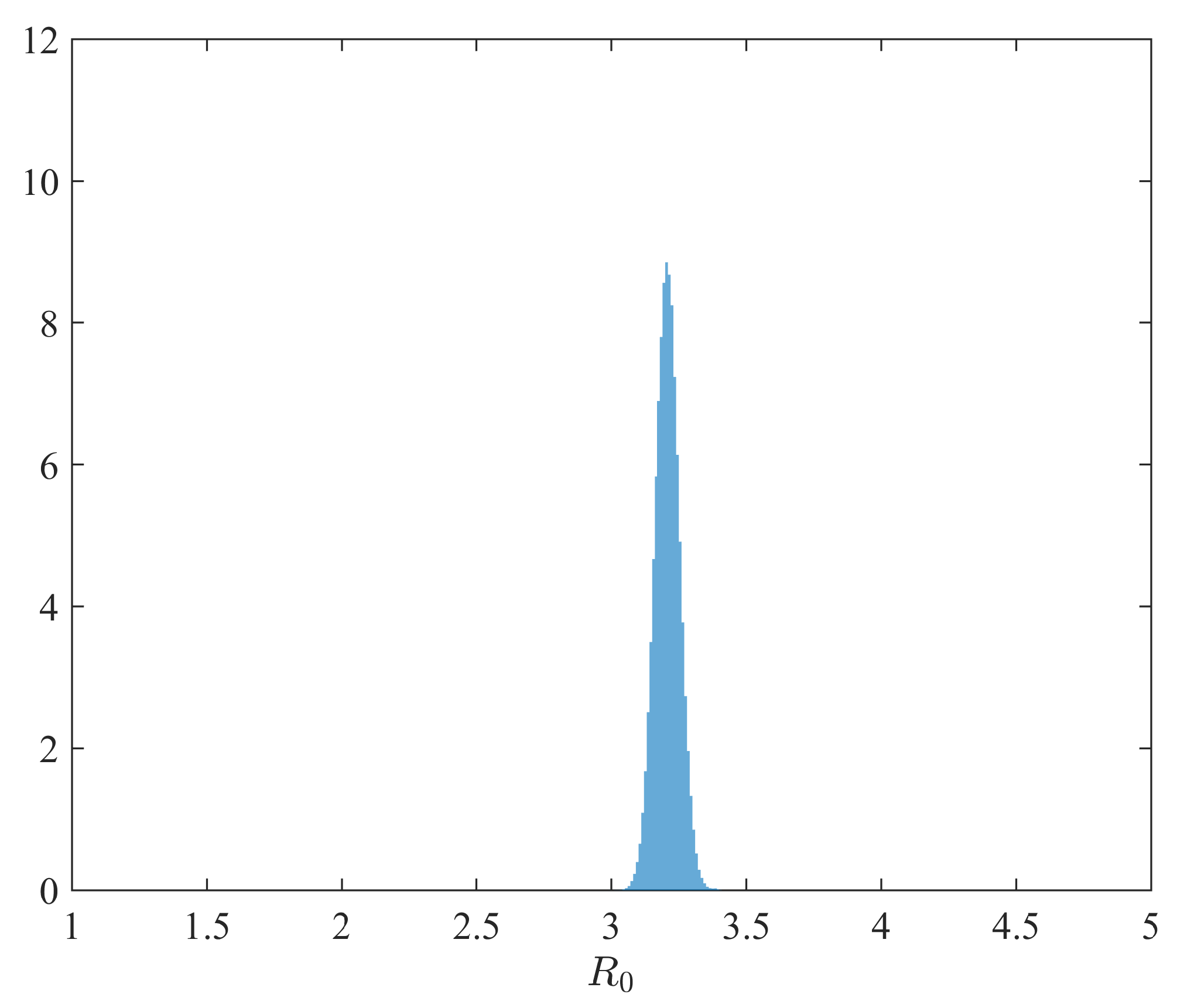
- The joint posterior distributions of the three pairs of parameters , and are depicted in Figure A1.
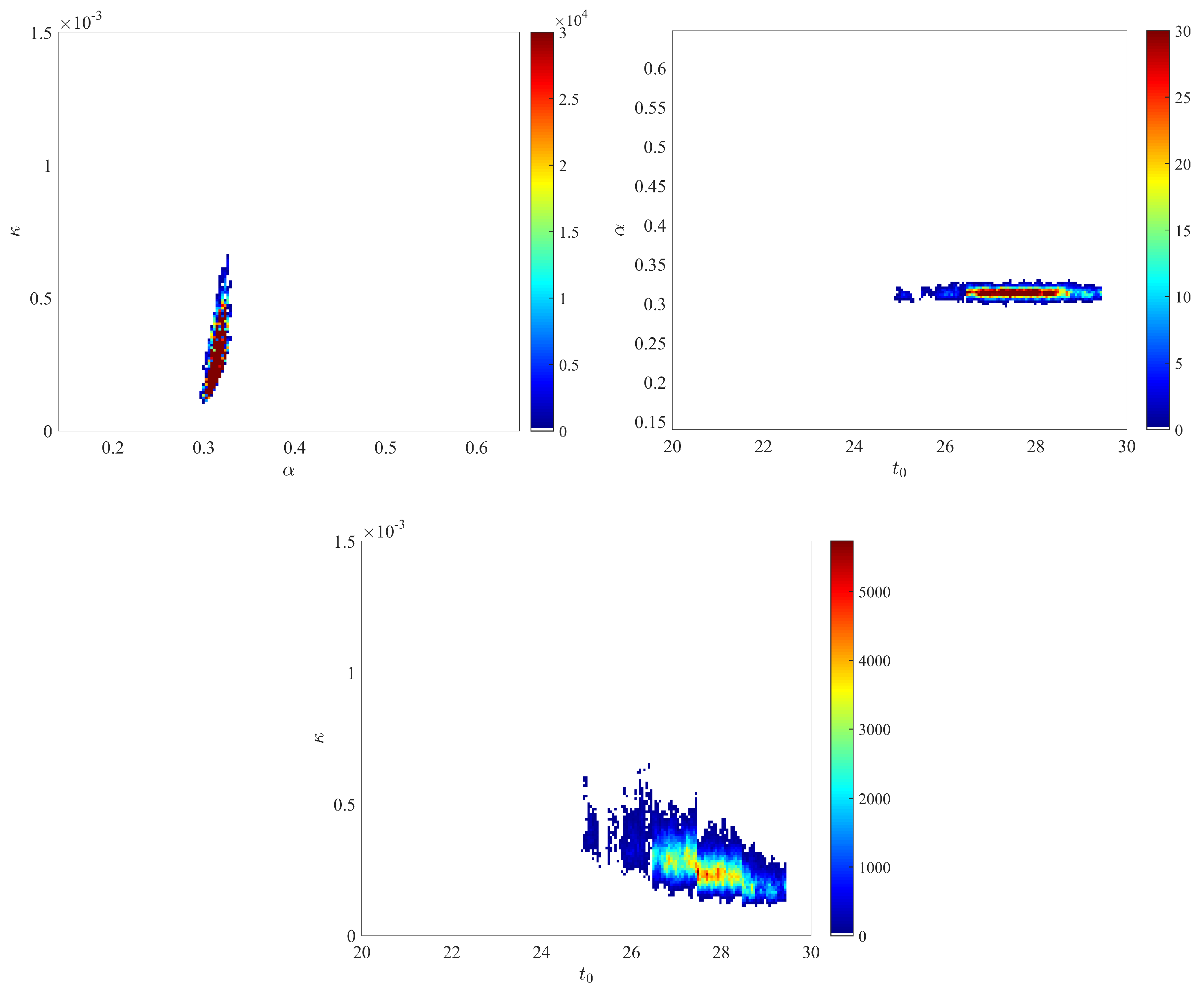
- To check the robustness of our results with respect to the choice of the prior distribution, we also considered the case of a more informative prior. Namely, we assumed the following uniform prior distributions:
- ∘
- , corresponding to with and values ranging between 1.4 and 6.49 (the range described in [18]);
- ∘
- corresponding to an introduction during late January;
- ∘
- , corresponding to a small probability of being tested for the susceptible cases, compared to the infected cases.
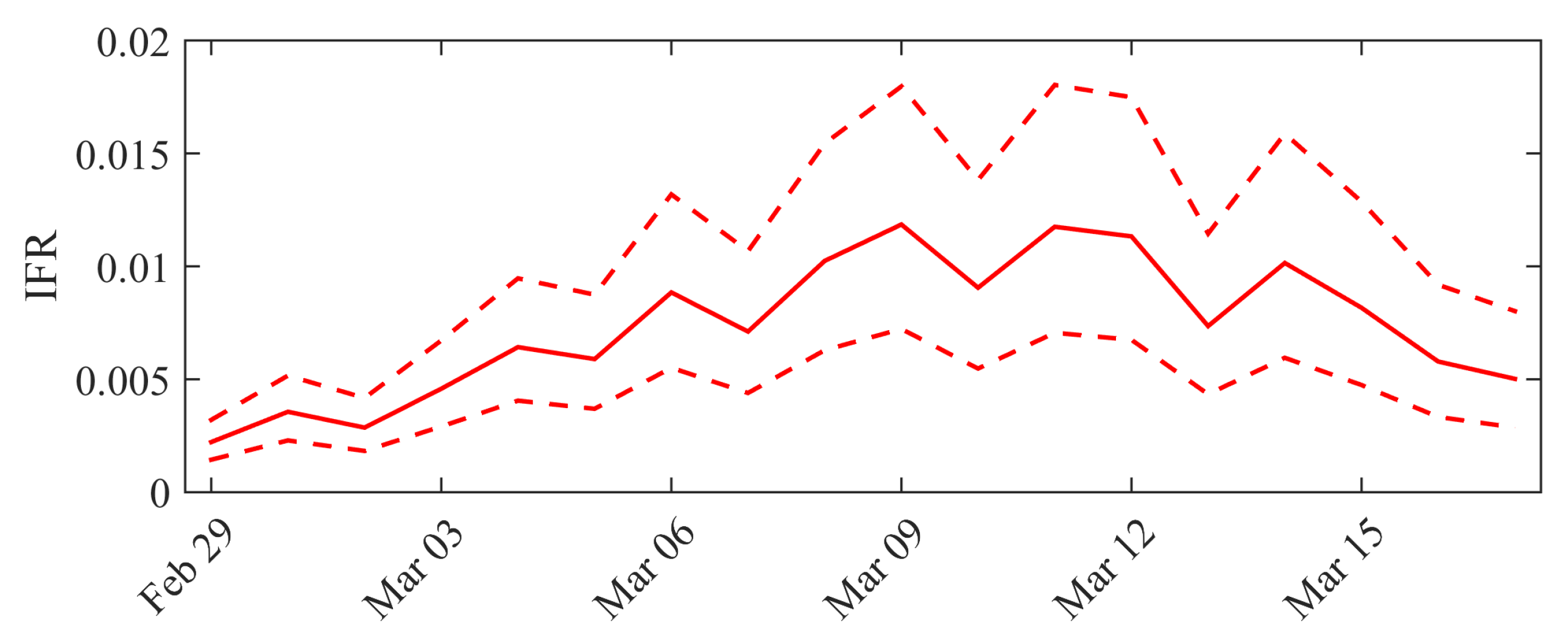
We obtained the posterior distributions shown in Figure A2, based on two independent chains with iterations (only the second half of the iterations are used to generate the posterior). Overall, these distributions are relatively similar to those displayed on Figure A1 and obtained with the prior distributions defined in the main text. - The dynamics of the estimated distribution of the IFR are depicted in Figure A3.
- The marginal posterior distribution of is depicted in Figure A4.
References
- World Health Organization. WHO Director-General’s Opening Remarks at the Media Briefing on COVID-19—11 March 2020; WHO: Geneva, Switzerland, 2020. [Google Scholar]
- Verity, R.; Okell, L.C.; Dorigatti, I.; Winskill, P.; Whittaker, C.; Imai, N.; Cuomo-Dannenburg, G.; Thompson, H.; Walker, P.; Fu, H.; et al. Estimates of the severity of COVID-19 disease. medRxiv 2020. [Google Scholar] [CrossRef]
- Ferguson, N.M.; Laydon, D.; Nedjati-Gilani, G.; Imai, N.; Ainslie, K.; Baguelin, M.; Bhatia, S.; Boonyasiri, A.; Cucunubá, Z.; Cuomo-Dannenburg, G.; et al. Impact of Non-Pharmaceutical Interventions (NPIs) to Reduce COVID-19 Mortality and Healthcare Demand; Imperial College: London, UK, 2020. [Google Scholar] [CrossRef]
- Russell, T.W.; Hellewell, J.; Jarvis, C.I.; van Zandvoort, K.; Abbott, S.; Ratnayake, R.; Flasche, S.; Eggo, R.M.; Edmunds, W.J.; Kucharski, A.J.; et al. Estimating the infection and case fatality ratio for coronavirus disease (COVID-19) using age-adjusted data from the outbreak on the Diamond Princess cruise ship, February 2020. Eurosurveillance 2020, 25. [Google Scholar] [CrossRef] [PubMed]
- Dong, E.; Du, H.; Gardner, L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect. Dis. 2020. [Google Scholar] [CrossRef]
- Santé Pulique France. COVID-19: Points Épidémiologiques du 17 et 24 Mars 2020. Available online: https://www.santepubliquefrance.fr/recherche/#search=COVID-19%20:%20point%20epidemiologique&sort=dat (accessed on 8 May 2020).
- DREES. 728,000 Résidents en Établissements d’Hébergement pour Personnes Agées en 2015. Available online: https://drees.solidarites-sante.gouv.fr/IMG/pdf/er1015.pdf (accessed on 8 May 2020).
- Agence Régionale de Santé Grand Est. Dossier de Presse—COVID-19: Point de Situation Dans le Grand Est; Agence Régionale de Santé Grand Est: Nancy, France, 2020; Available online: https://www.grand-est.ars.sante.fr/system/files/2020-04/DP_point%20de%20situation%20COVID%2019%20en%20Grand%20Est_010420.pdf (accessed on 8 May 2020).
- Roques, L.; Soubeyrand, S.; Rousselet, J. A statistical-reaction-diffusion approach for analyzing expansion processes. J. Theor. Biol. 2011, 274, 43–51. [Google Scholar] [CrossRef] [PubMed]
- Roques, L.; Bonnefon, O. Modelling population dynamics in realistic landscapes with linear elements: A mechanistic-statistical reaction-diffusion approach. PLoS ONE 2016, 11, e0151217. [Google Scholar] [CrossRef] [PubMed]
- Abboud, C.; Bonnefon, O.; Parent, E.; Soubeyrand, S. Dating and localizing an invasion from post-introduction data and a coupled reaction–diffusion–absorption model. J. Math. Biol. 2019, 79, 765–789. [Google Scholar] [CrossRef] [PubMed]
- Zhou, F.; Yu, T.; Du, R.; Fan, G.; Liu, Y.; Liu, Z.; Xiang, J.; Wang, Y.; Song, B.; Gu, X.; et al. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: a retrospective cohort study. Lancet 2020. [Google Scholar] [CrossRef]
- He, X.; Lau, E.H.; Wu, P.; Deng, X.; Wang, J.; Hao, X.; Lau, Y.; Wong, J.Y.; Guan, Y.; Tan, X.; et al. Temporal dynamics in viral shedding and transmissibility of COVID-19. medRxiv 2020. [Google Scholar] [CrossRef]
- Wang, W.; Xu, Y.; Gao, R.; Lu, R.; Han, K.; Wu, G.; Tan, W. Detection of SARS-CoV-2 in different types of clinical specimens. JAMA 2020. [Google Scholar] [CrossRef]
- Murray, J.D. Mathematical Biology, 3rd ed.; Interdisciplinary Applied Mathematics 17; Springer: New York, NY, USA, 2002. [Google Scholar]
- Salje, H.; Tran Kiem, C.; Lefrancq, N.; Courtejoie, N.; Bosetti, P.; Paireau, J.; Andronico, A.; Hoze, N.; Richet, J.; Dubost, C.L.; et al. Estimating the burden of SARS-CoV-2 in France. medRxiv 2020. [Google Scholar] [CrossRef]
- Zhao, S.; Lin, Q.; Ran, J.; Musa, S.S.; Yang, G.; Wang, W.; Lou, Y.; Gao, D.; Yang, L.; He, D.; et al. Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, from 2019 to 2020: A data-driven analysis in the early phase of the outbreak. Int. J. Infect. Dis. 2020, 92, 214–217. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Gayle, A.A.; Wilder-Smith, A.; Rocklöv, J. The reproductive number of COVID-19 is higher compared to SARS coronavirus. J. Travel Med. 2020. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Magal, P.; Seydi, O.; Webb, G. Understanding unreported cases in the 2019-nCov epidemic outbreak in Wuhan, China, and the importance of major public health interventions. Biology 2020, 9, 50. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Magal, P.; Seydi, O.; Webb, G. Predicting the cumulative number of cases for the COVID-19 epidemic in China from early data. Math. Biosci. Eng. 2020, 17, 3040–3051. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roques, L.; Klein, E.K.; Papaïx, J.; Sar, A.; Soubeyrand, S. Using Early Data to Estimate the Actual Infection Fatality Ratio from COVID-19 in France. Biology 2020, 9, 97. https://doi.org/10.3390/biology9050097
Roques L, Klein EK, Papaïx J, Sar A, Soubeyrand S. Using Early Data to Estimate the Actual Infection Fatality Ratio from COVID-19 in France. Biology. 2020; 9(5):97. https://doi.org/10.3390/biology9050097
Chicago/Turabian StyleRoques, Lionel, Etienne K Klein, Julien Papaïx, Antoine Sar, and Samuel Soubeyrand. 2020. "Using Early Data to Estimate the Actual Infection Fatality Ratio from COVID-19 in France" Biology 9, no. 5: 97. https://doi.org/10.3390/biology9050097
APA StyleRoques, L., Klein, E. K., Papaïx, J., Sar, A., & Soubeyrand, S. (2020). Using Early Data to Estimate the Actual Infection Fatality Ratio from COVID-19 in France. Biology, 9(5), 97. https://doi.org/10.3390/biology9050097




