De-Escalation by Reversing the Escalation with a Stronger Synergistic Package of Contact Tracing, Quarantine, Isolation and Personal Protection: Feasibility of Preventing a COVID-19 Rebound in Ontario, Canada, as a Case Study
Abstract
1. Introduction
- Escalation-Phase 0:
- Monitoring and international travel advisories;
- Escalation-Phase 1:
- School closure;
- Escalation-Phase 2:
- Emergency declaration, with closure of public events and recreational venues;
- Escalation-Phase 3:
- Closure of all non-essential workplaces.
2. Materials and Methods
2.1. The Transmission Dynamics Model
2.2. Data
2.3. The Parameter Identification and Estimation of Intervention Effectiveness in Different Escalation Phases
3. De-Escalation Considerations
- De-escalation-Phase 1:
- Opening of workplaces;
- De-escalation-Phase 2:
- Resumption of public events and activities;
- De-escalation-Phase 3:
- School opening.
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hu, Y.; Sun, J.; Dai, Z.; Deng, H.; Li, X.; Huang, Q.; Wu, Y.; Sun, L.; Xu, Y. Prevalence and severity of corona virus disease 2019 (COVID-19): A systematic review and meta-analysis. J. Clin. Virol. 2020, 127, 104371. [Google Scholar] [CrossRef] [PubMed]
- Lovato, A.; de Filippis, C. Clinical Presentation of COVID-19: A Systematic Review Focusing on Upper Airway Symptoms. Ear Nose Throat J. 2020, 145561320920762. [Google Scholar] [CrossRef]
- Park, M.; Cook, A.R.; Lim, J.T.; Sun, Y.; Dickens, B.L. A Systematic Review of COVID-19 Epidemiology Based on Current Evidence. J. Clin. Med. 2020, 9, 967. [Google Scholar] [CrossRef] [PubMed]
- Scarabel, F.; Pellis, L.; Bragazzi, N.L.; Wu, J. Canada Needs to Rapidly Escalate Public Health Interventions for Its COVID-19 Mitigation Strategies. Infect. Dis. Model. 2020. [Google Scholar] [CrossRef]
- CMAJ News. COVID-19: Recent Updates on the Coronavirus Pandemic. 2020. Available online: https://cmajnews.com/2020/04/20/coronavirus-1095847/ (accessed on 27 April 2020).
- Government of Ontario. List of Essential Workplaces. 2020. Available online: https://www.ontario.ca/page/list-essential-workplaces (accessed on 27 April 2020).
- Tang, B.; Wang, X.; Li, Q.; Bragazzi, N.L.; Tang, S.; Xiao, Y.; Wu, J. Estimation of the transmission risk of 2019-nCov and its implication for public health interventions. J. Clin. Med. 2020, 9, 462. [Google Scholar] [CrossRef] [PubMed]
- Tang, B.; Xia, F.; Tang, S.; Bragazzi, N.L.; Li, Q.; Sun, X.; Liang, J.; Xiao, Y.; Wu, J. The effectiveness of quarantine and isolation determine the trend of the COVID-19 epidemics in the final phase of the current outbreak in China. Int. J. Infect. Dis. 2020, 95, 288–293. [Google Scholar] [CrossRef] [PubMed]
- Special Expert Group for Control of the Epidemic of Novel Coronavirus Pneumonia of the Chinese Preventive Medicine Association, The Chinese Preventive Medicine Association. An update on the epidemiological characteristics of novel coronavirus pneumonia (COVID-19). Chin. J. Epidemiol. 2020, 41, 139–144. [Google Scholar]
- Prem, K.; Liu, Y.; Russell, T.W.; Kucharski, A.J.; Eggo, R.M.; Davies, N.; Abbott, S. The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China: A modelling study. Lancet Public Health 2020, 5, e261–e270. [Google Scholar] [CrossRef]
- Fumanelli, L.; Ajelli, M.; Manfredi, P.; Vespignani, A.; Merler, S. Inferring the structure of social contacts from demographic data in the analysis of infectious diseases spread. PLoS Comput. Biol. 2012, 8. [Google Scholar] [CrossRef] [PubMed]
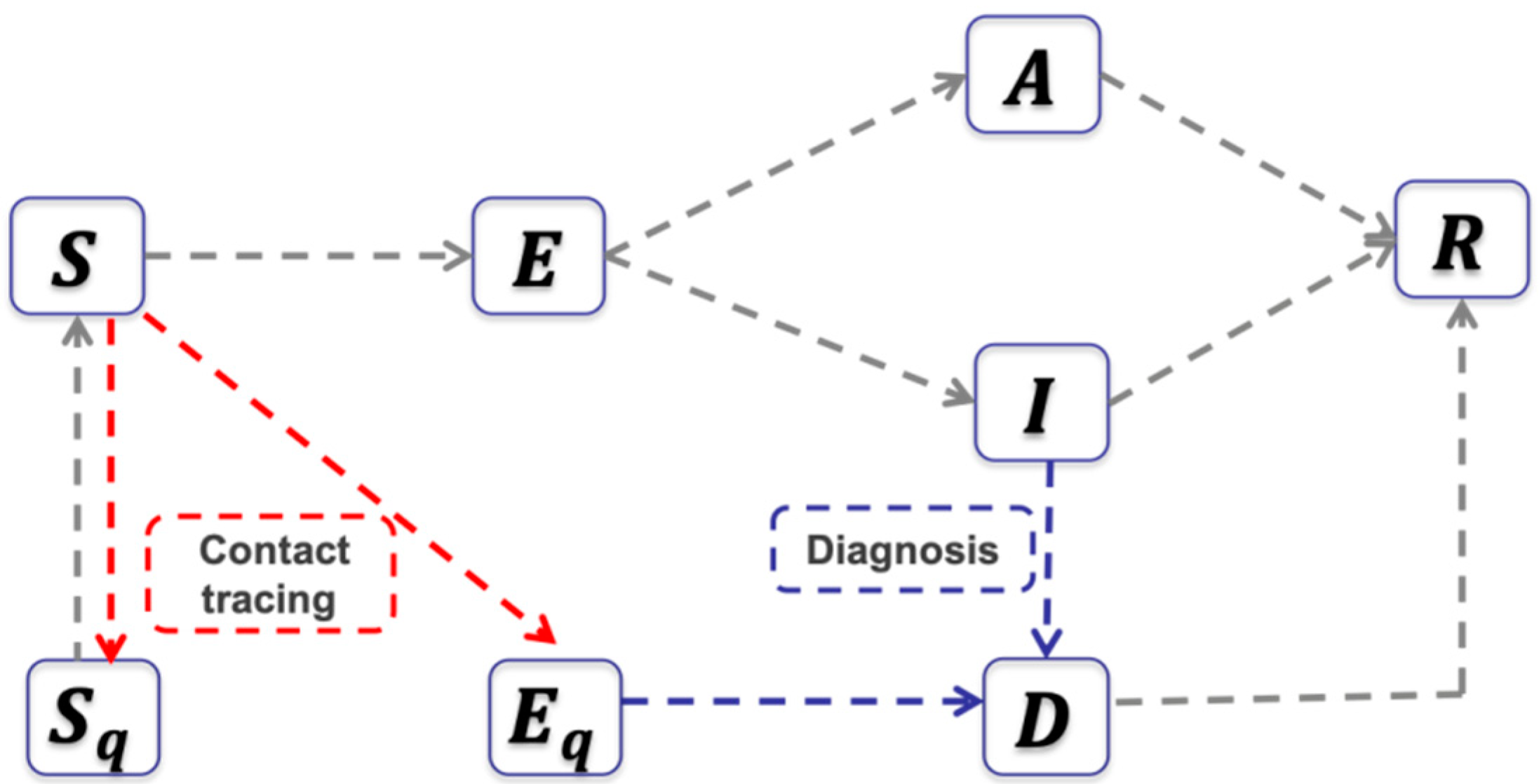
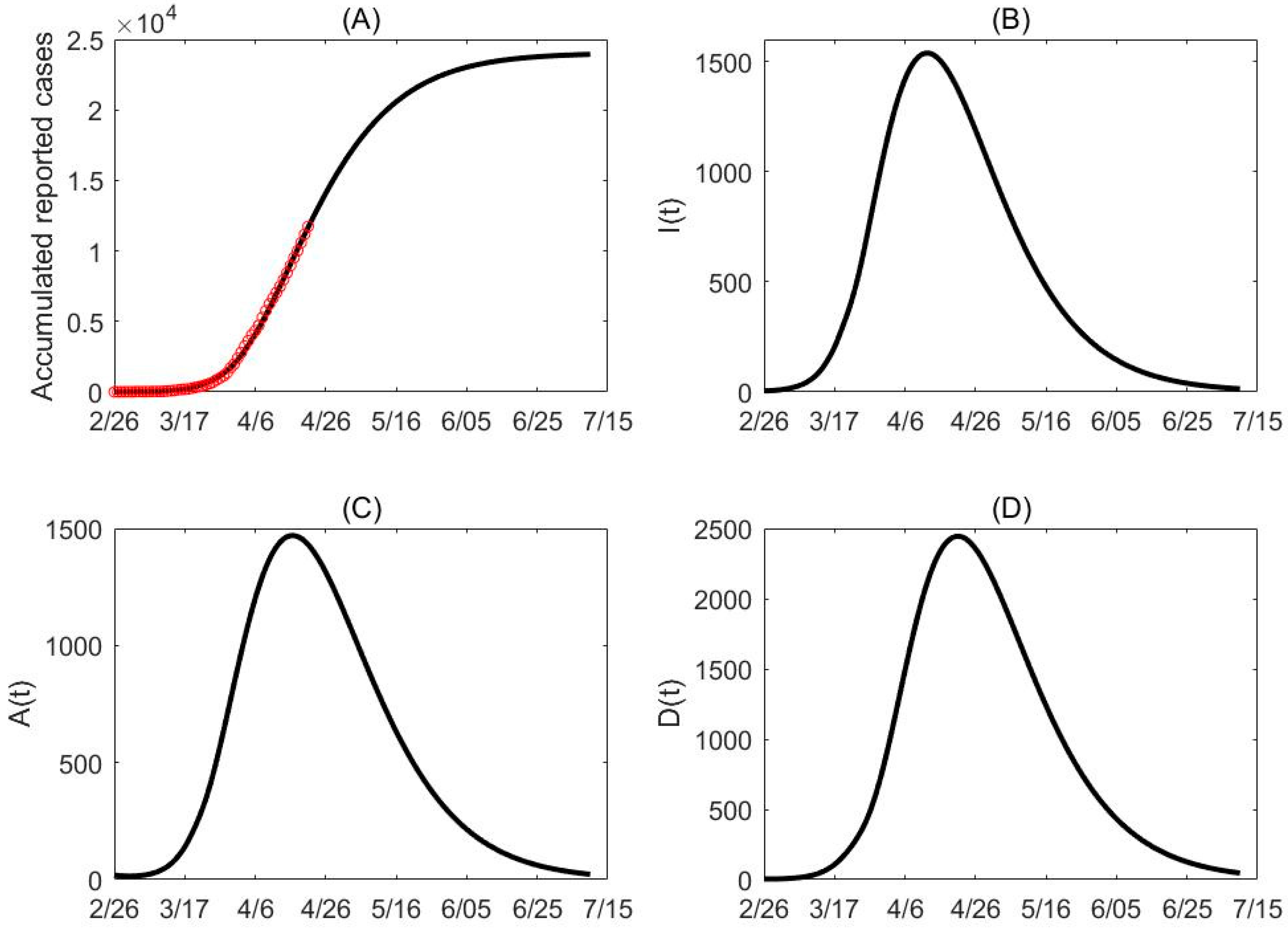
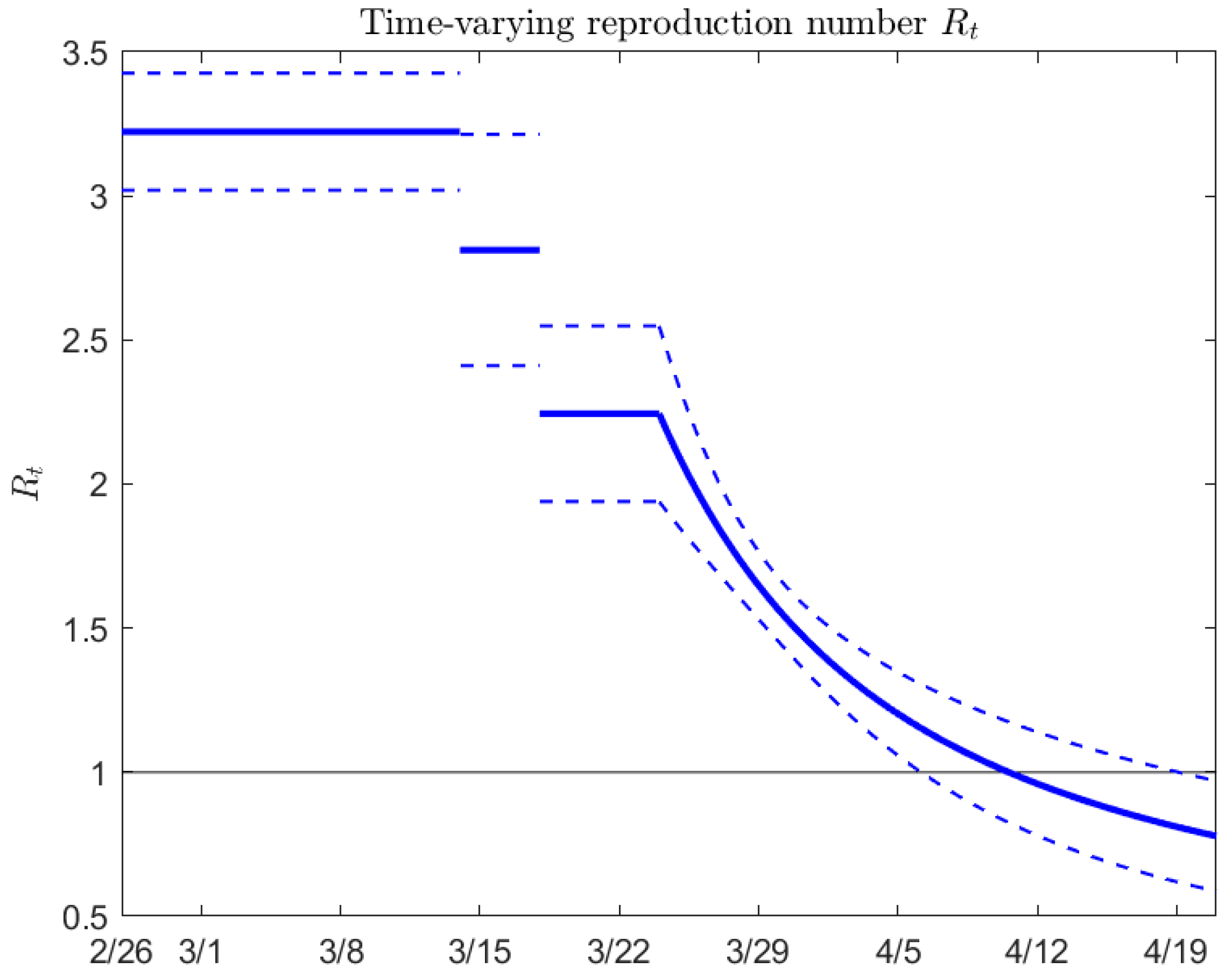
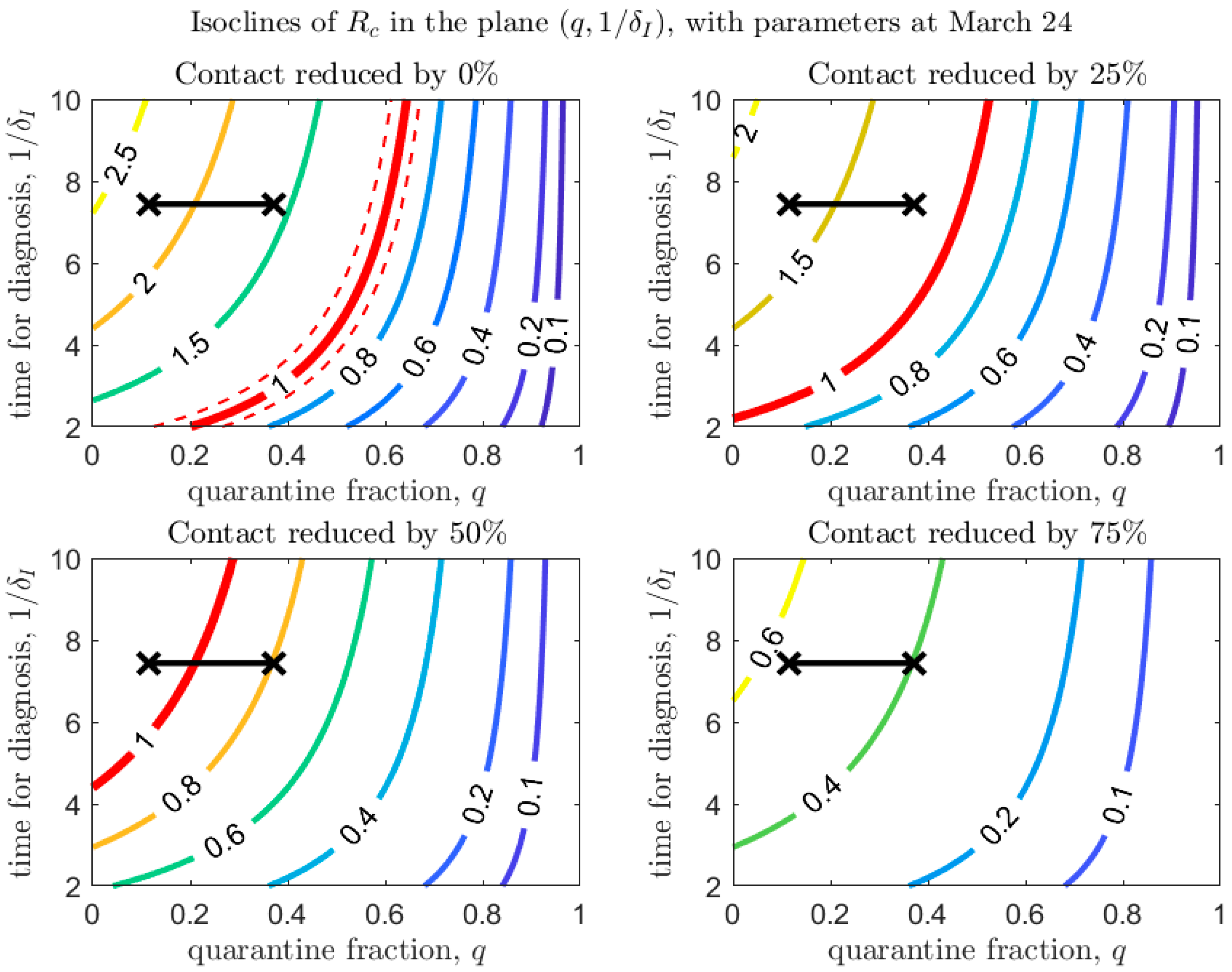
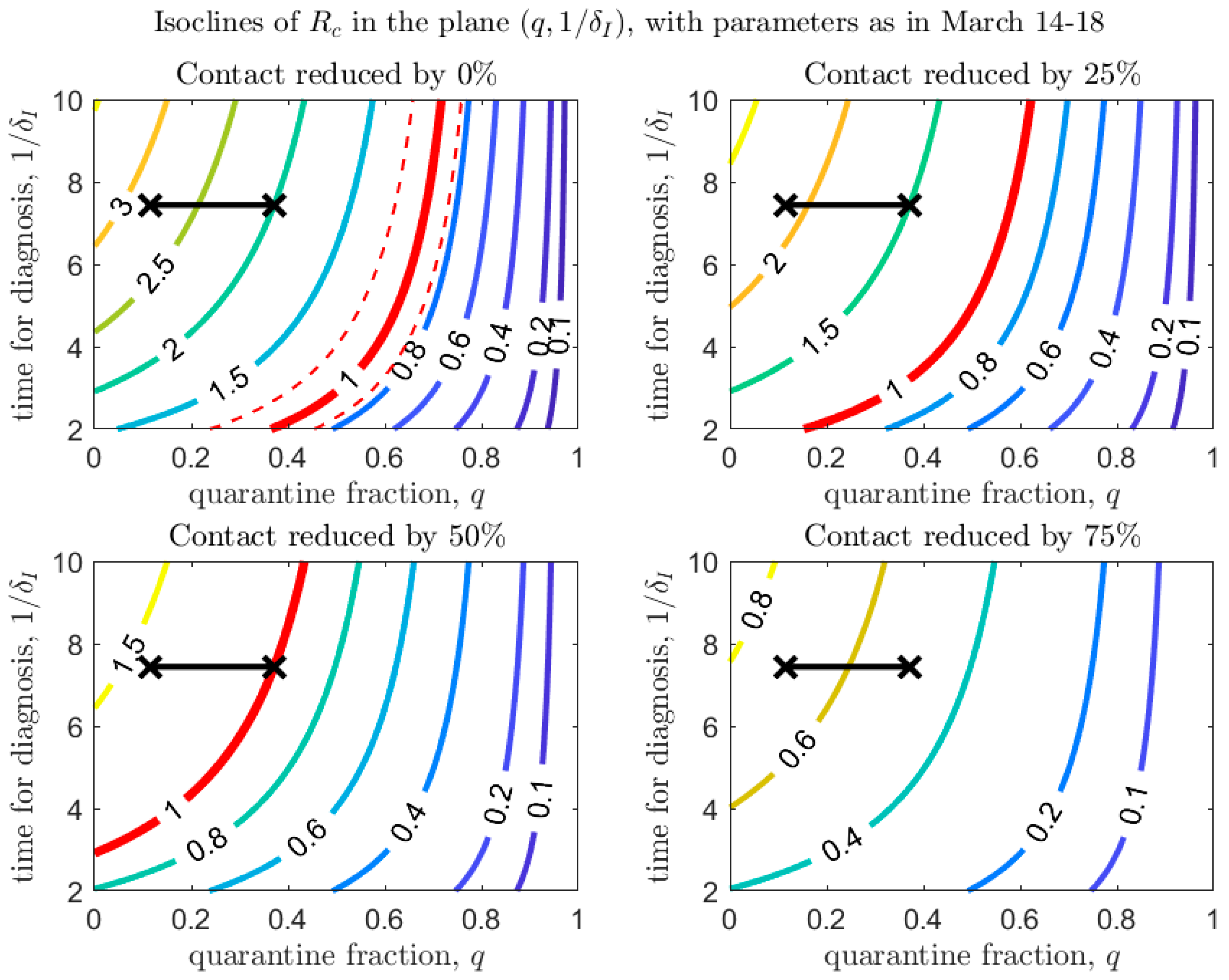
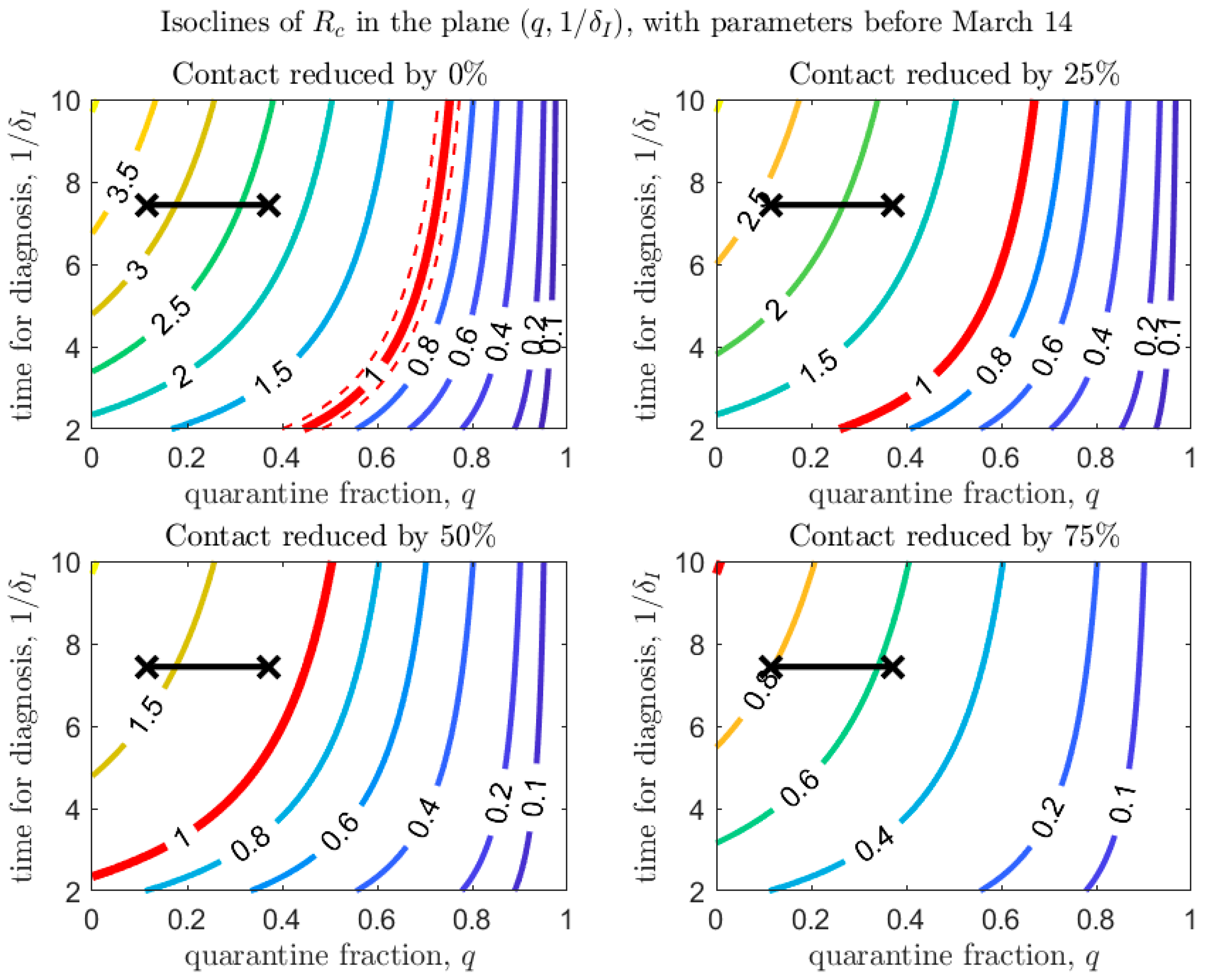
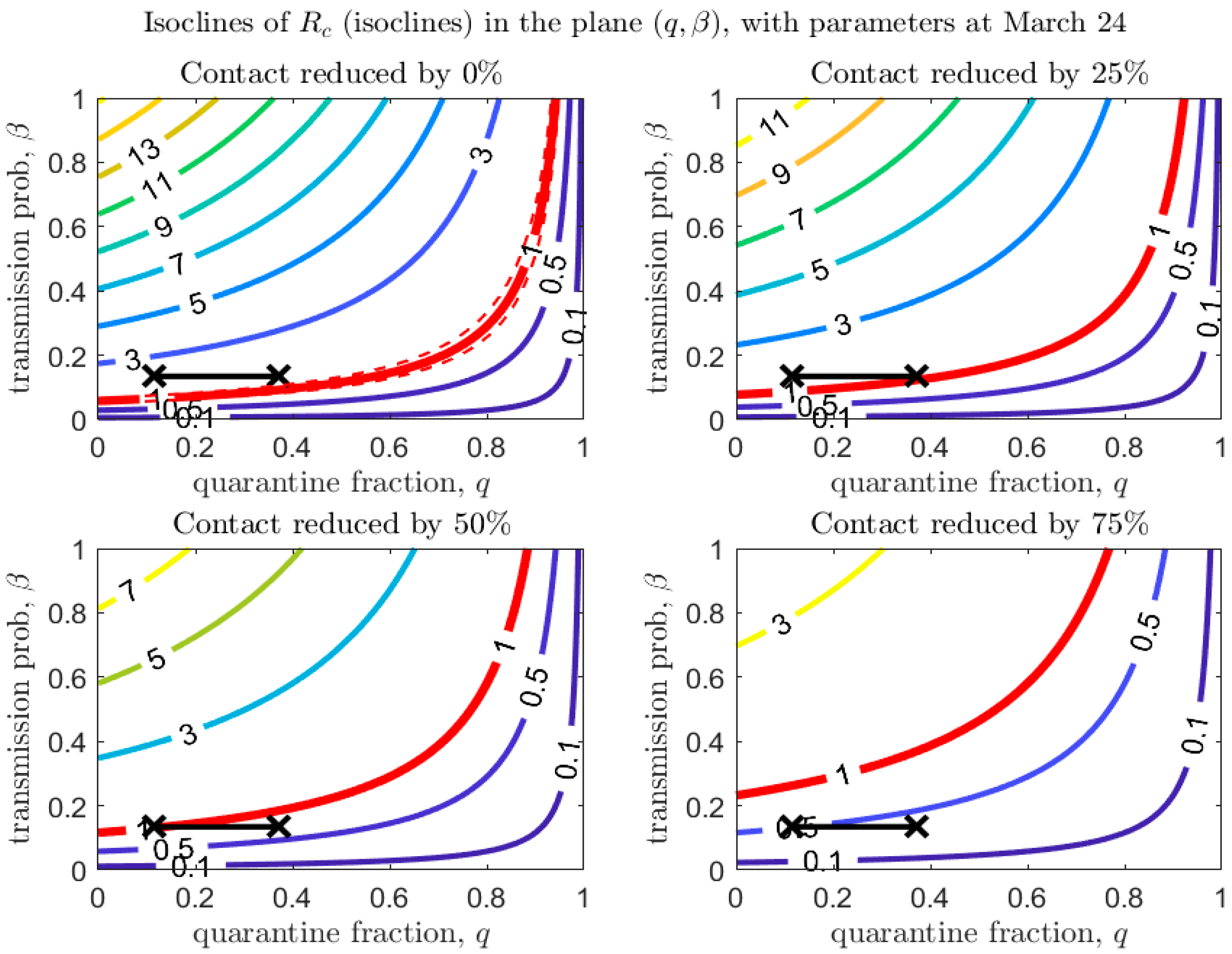
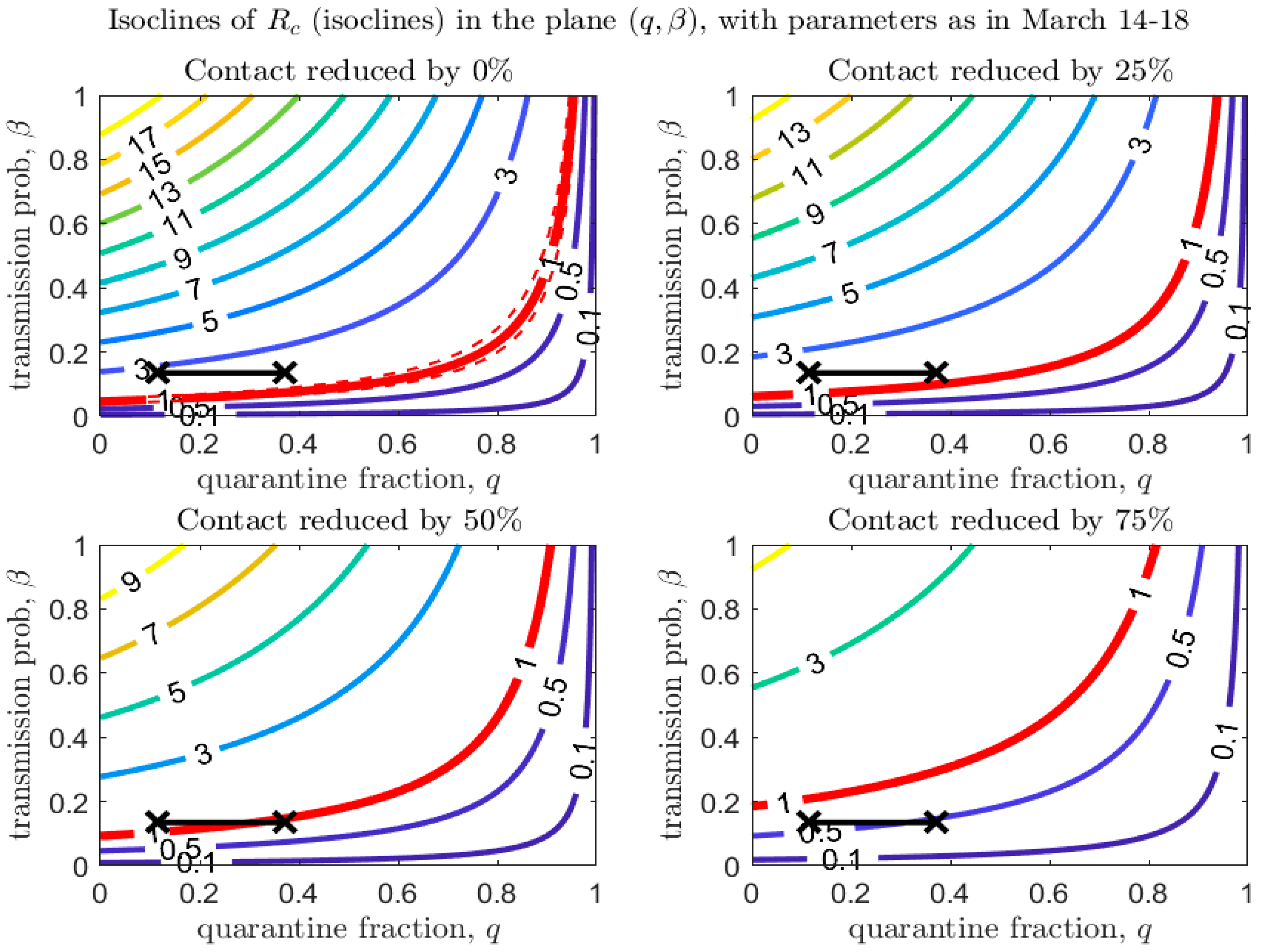
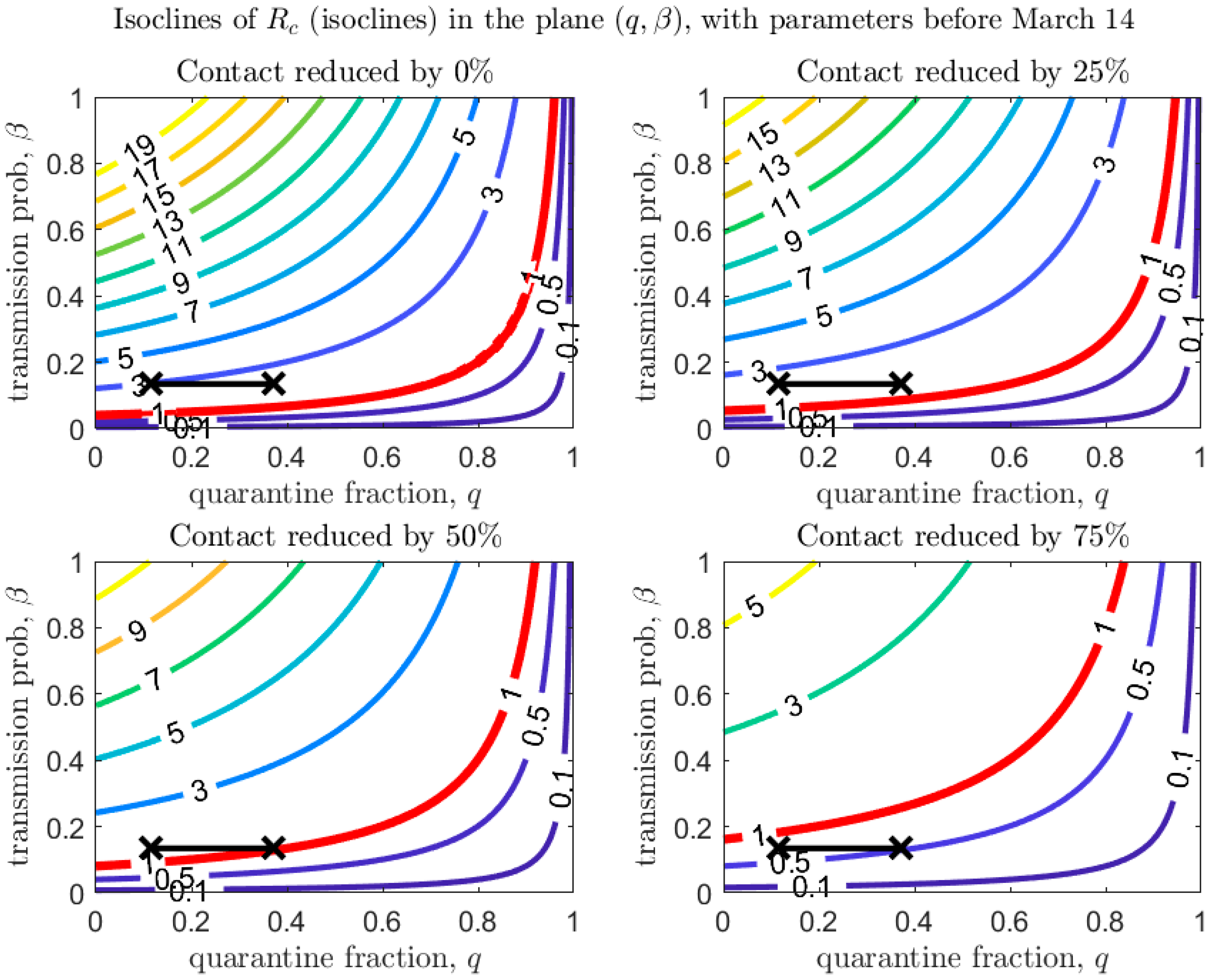
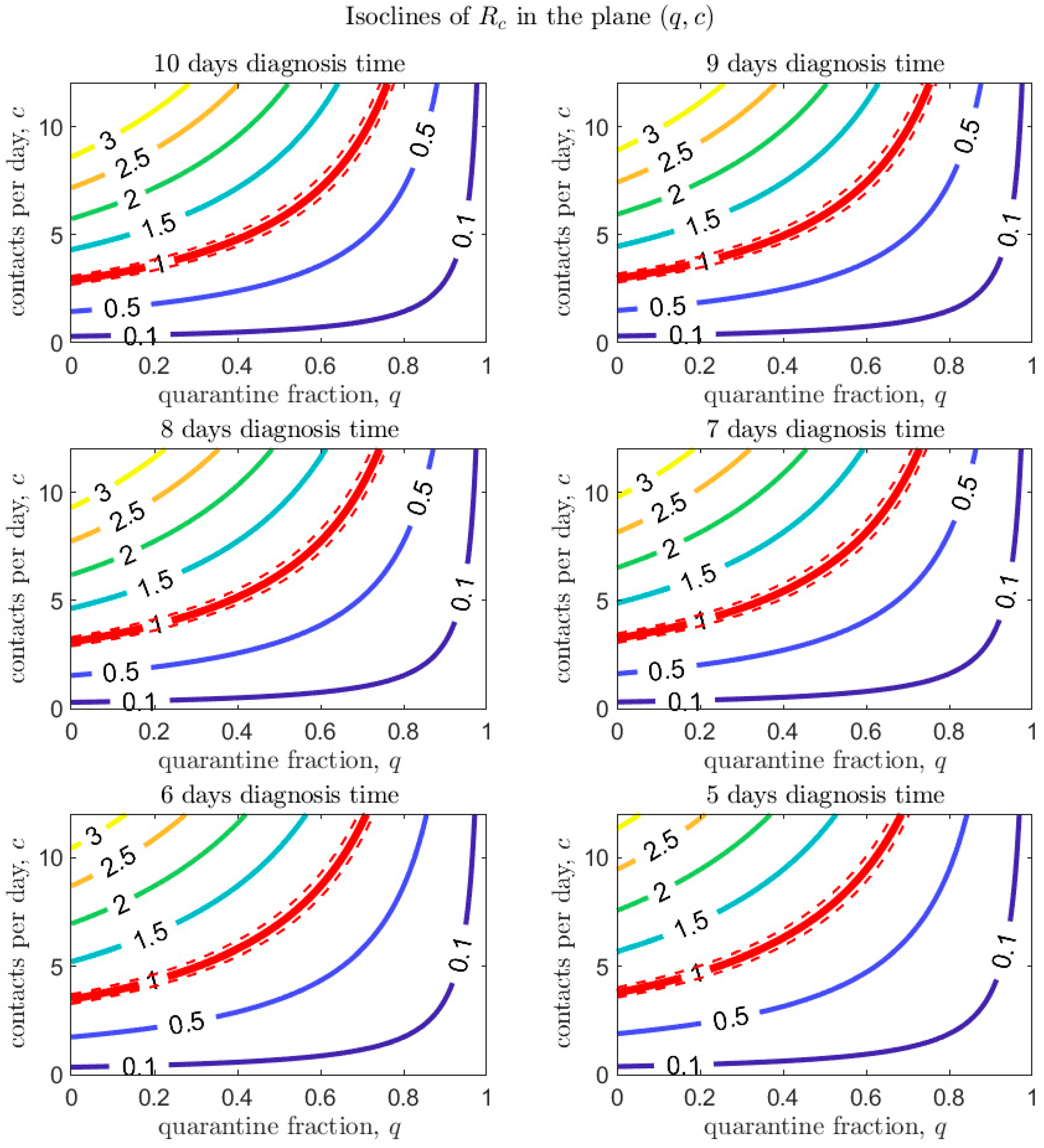
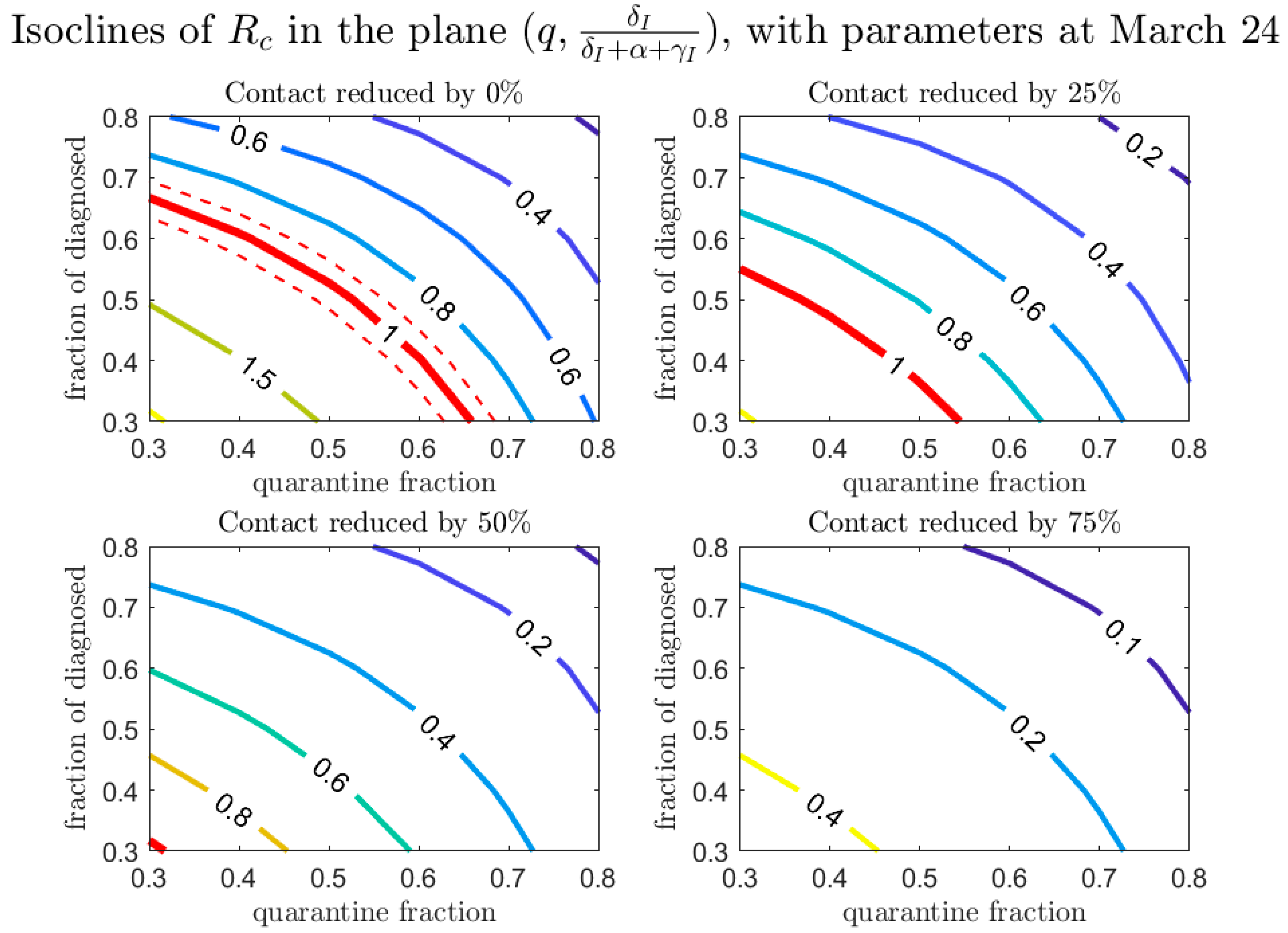
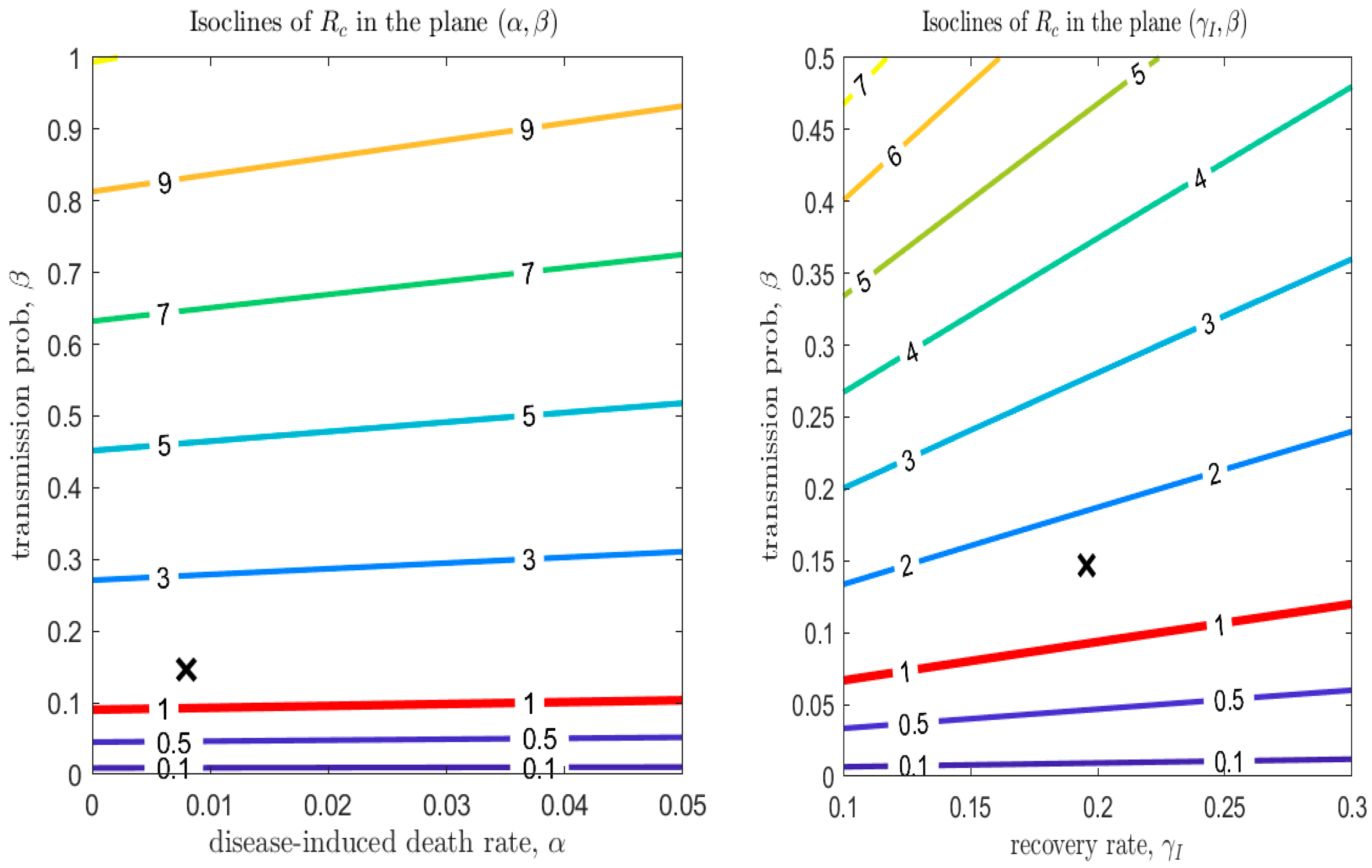
| Province | School Closure | Date of Emergency Declaration and Type | Date of Closure of Non-Essential Establishments |
|---|---|---|---|
| British Columbia | 14-March-2020 | 18-March-2020 (public health emergency) | 21-March-2020 |
| Alberta | 14-March-2020 | 17-March-2020 (provincial public health emergency) | 27-March-2020 |
| Saskatchewan | 21-March-2020 | 18-March-2020 (provincial state of emergency) | 20-March-2020; Expanded 23-March-2020 |
| Manitoba | 14-March-2020 | 20-March-2020 (provincial state of emergency) | 20-March-2020 |
| Ontario | 14-March-2020 | 17-March-2020 (provincial state of emergency) | 23-March-2020; Expanded 25-Mar-2020 |
| Quebec | 14-March-2020 | 13-March-2020 (provincial public health emergency) | 15-March-2020; Expanded 23-March-2020; Expanded further 28-March-2020 |
| Newfoundland & Labrador | 14-March-2020 | 18-March-2020 (public health emergency) | 18-March-2020; Expanded 23-March-2020: |
| New Brunswick | 14-March-2020 | 19-March-2020 (provincial state of emergency) | 19-March-2020 |
| Nova Scotia | 14-March-2020 | 22-March-2020 (provincial state of emergency) | 24-March-2020 |
| Prince Edward Island | 14-March-2020 | 16-March-2020 (public health emergency) | 18-March-2020 |
| Yukon | 14-March-2020 | 18-March-2020 (public health emergency) | |
| Northwest Territories | 14-March-2020 | 19-March-2020 (public health emergency) | |
| Nunavut | 14-March-2020 | 19-March-2020 (public health emergency) |
| Parameter | Definitions | Mean (Std) | Source | |
| Contact rate before March 14 | 11.5801 (0.3456) | Estimated | ||
| Contact rate between March 14 to March 18 | 10.1202 (0.9185) | Estimated | ||
| Contact rate between March 18 to March 24 | 8.0495 (0.2787) | Estimated | ||
| Constant contact rate at March 24 | 8.0495 (0.2787) | Estimated | ||
| Exponential decrease in contact rate | 0.0466 (0.0152) | Estimated | ||
| Minimum contact rate after March 24 | 2.1987 (0.2400) | Estimated | ||
| Probability of transmission per contact | 0.1469 (0.0023) | Estimated | ||
| Fraction of quarantined exposed individuals before March 24 | 0.1145 (0.0114) | Estimated | ||
| Quarantine fraction at March 24 | 0.1145 (0.0114) | Estimated | ||
| Exponential increase in quarantine fraction | 0.1230 (0.0123) | Estimated | ||
| The maximum quarantine fraction | 0.3721 (0.0371) | Estimated | ||
| Transition rate of exposed individuals to the infected class | 1/5 | [9] | ||
| Rate at which the quarantined uninfected contacts were released into the wider community | 1/14 | [7] | ||
| Probability of having symptoms among infected individuals | 0.7036 (0.0261) | Estimated | ||
| Transition rate of symptomatic infected individuals to the quarantined infected class | 0.1344 (0.0134) | Estimated | ||
| Transition rate of quarantined exposed individuals to the quarantined infected class | 0.1237 (0.0086) | Estimated | ||
| Recovery rate of symptomatic infected individuals | 0.1957 (0.0111) | Estimated | ||
| Recovery rate of asymptomatic infected individuals | 0.139 | [7] | ||
| Recovery rate of quarantined diagnosed individuals | 0.2 | [8] | ||
| Disease-induced death rate | 0.008 | [8] | ||
| Modification factor of asymptomatic infectiousness | 0.0275 (0.0128) | Estimated | ||
| Initial values | Definitions | Mean (Std) | Source | |
| Initial susceptible population | Data | |||
| Initial exposed population | 8.9743 (0.6558) | Estimated | ||
| Initial symptomatic infected population | 5.3887 (0.9442) | Estimated | ||
| Initial asymptomatic infected population | 19.4186 (3.9406) | Estimated | ||
| Initial quarantined susceptible population | 0 | Data | ||
| Initial quarantined exposed population | 0 | Data | ||
| Initial quarantined diagnosed population | 5 | Data | ||
| Initial recovered population | 0 | Data | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, B.; Scarabel, F.; Bragazzi, N.L.; McCarthy, Z.; Glazer, M.; Xiao, Y.; Heffernan, J.M.; Asgary, A.; Ogden, N.H.; Wu, J. De-Escalation by Reversing the Escalation with a Stronger Synergistic Package of Contact Tracing, Quarantine, Isolation and Personal Protection: Feasibility of Preventing a COVID-19 Rebound in Ontario, Canada, as a Case Study. Biology 2020, 9, 100. https://doi.org/10.3390/biology9050100
Tang B, Scarabel F, Bragazzi NL, McCarthy Z, Glazer M, Xiao Y, Heffernan JM, Asgary A, Ogden NH, Wu J. De-Escalation by Reversing the Escalation with a Stronger Synergistic Package of Contact Tracing, Quarantine, Isolation and Personal Protection: Feasibility of Preventing a COVID-19 Rebound in Ontario, Canada, as a Case Study. Biology. 2020; 9(5):100. https://doi.org/10.3390/biology9050100
Chicago/Turabian StyleTang, Biao, Francesca Scarabel, Nicola Luigi Bragazzi, Zachary McCarthy, Michael Glazer, Yanyu Xiao, Jane M. Heffernan, Ali Asgary, Nicholas Hume Ogden, and Jianhong Wu. 2020. "De-Escalation by Reversing the Escalation with a Stronger Synergistic Package of Contact Tracing, Quarantine, Isolation and Personal Protection: Feasibility of Preventing a COVID-19 Rebound in Ontario, Canada, as a Case Study" Biology 9, no. 5: 100. https://doi.org/10.3390/biology9050100
APA StyleTang, B., Scarabel, F., Bragazzi, N. L., McCarthy, Z., Glazer, M., Xiao, Y., Heffernan, J. M., Asgary, A., Ogden, N. H., & Wu, J. (2020). De-Escalation by Reversing the Escalation with a Stronger Synergistic Package of Contact Tracing, Quarantine, Isolation and Personal Protection: Feasibility of Preventing a COVID-19 Rebound in Ontario, Canada, as a Case Study. Biology, 9(5), 100. https://doi.org/10.3390/biology9050100







