Integrative Phylogenetics: Tools for Palaeontologists to Explore the Tree of Life
Abstract
:Simple Summary
Abstract
1. Introduction
2. Advances in Integrated Phylogenetics
2.1. Taxonomy
2.2. Morphological Datasets
2.3. Calibrating the Tree of Life
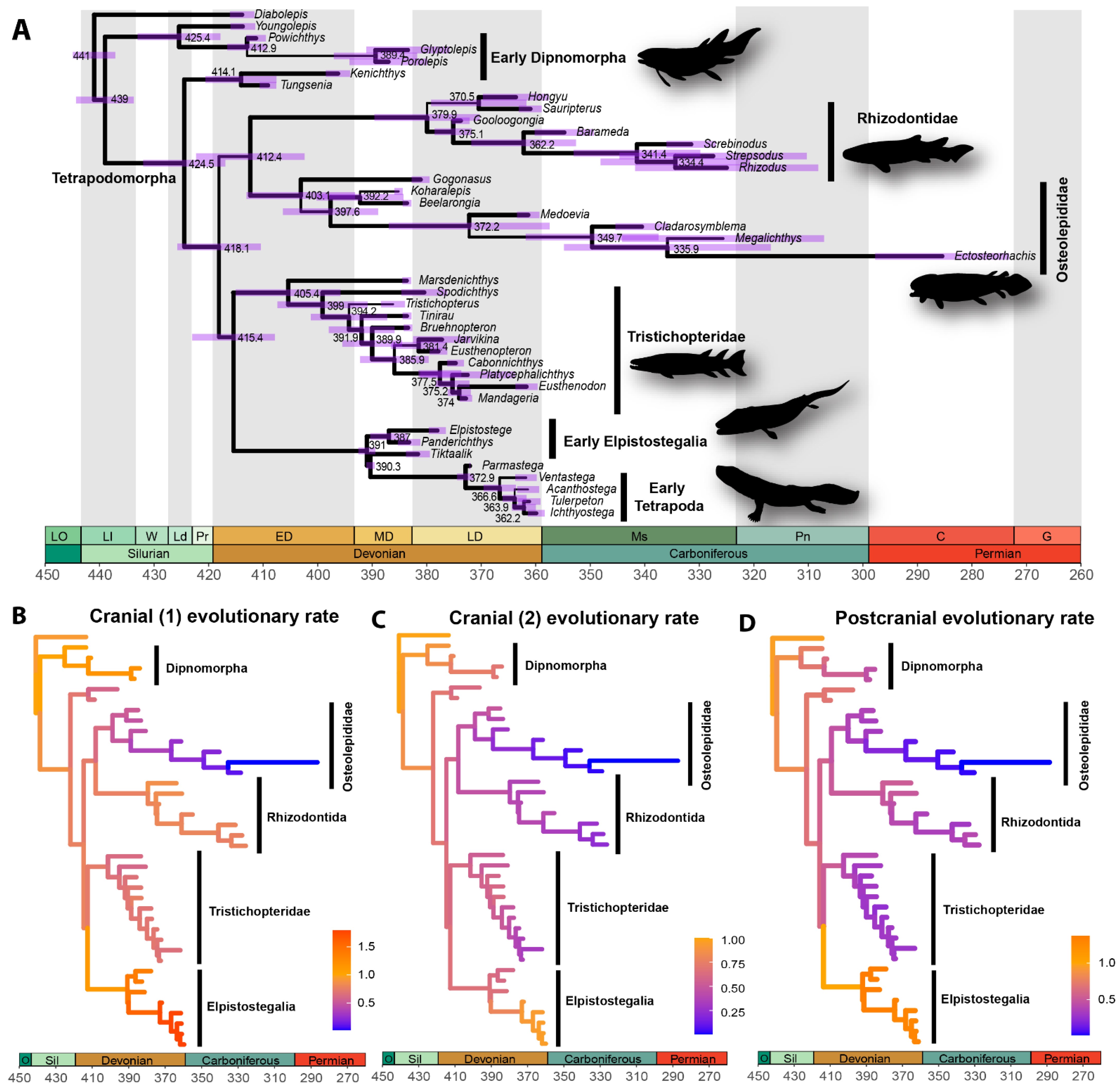
2.4. Exploring Macroevolution
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kumar, S. Molecular clocks: Four decades of evolution. Nat. Rev. Genet. 2005, 6, 654–662. [Google Scholar] [CrossRef]
- Kluge, A.G. A concern for evidence and a phylogenetic hypothesis of relationships among Epicrates (Boidae, Serpentes). Syst. Zool. 1989, 38, 7–25. [Google Scholar] [CrossRef]
- Nixon, K.C.; Carpenter, J.M. On simultaneous analysis. Cladistics 1996, 12, 221–241. [Google Scholar] [CrossRef]
- Reisz, R.R.; Müller, J. Molecular timescales and the fossil record: A paleontological perspective. Trends Genet. 2004, 20, 237–241. [Google Scholar] [CrossRef]
- Benton, M.J.; Donoghue, P.C.J. Paleontological Evidence to Date the Tree of Life. Mol. Biol. Evol. 2007, 24, 26–53. [Google Scholar] [CrossRef]
- Donoghue, P.C.J.; Benton, M. Rocks and clocks: Calibrating the Tree of Life using fossils and molecules. Trends Ecol. Evol. 2007, 22, 424–431. [Google Scholar] [CrossRef]
- Lee, M.S.; Palci, A. Morphological Phylogenetics in the Genomic Age. Curr. Biol. 2015, 25, R922–R929. [Google Scholar] [CrossRef] [Green Version]
- Parham, J.F.; Donoghue, P.C.J.; Bell, C.J.; Calway, T.D.; Head, J.J.; Holroyd, P.A.; Inoue, J.G.; Irmis, R.B.; Joyce, W.G.; Ksepka, D.T.; et al. Best Practices for Justifying Fossil Calibrations. Syst. Biol. 2011, 61, 346–359. [Google Scholar] [CrossRef]
- Pyron, R.A. Divergence time estimation using fossils as terminal taxa and the origins of Lissamphibia. Syst. Biol. 2011, 60, 466–481. [Google Scholar] [CrossRef] [Green Version]
- Ronquist, F.; Teslenko, M.; van der Mark, P.; Ayres, D.L.; Darling, A.; Höhna, S.; Larget, B.; Liu, L.; Suchard, M.A.; Huelsenbeck, J.P. MrBayes 3.2, efficient Bayesian phylogenetic inference and model choice across a large model space. Syst. Biol. 2012, 61, 539–542. [Google Scholar] [CrossRef] [Green Version]
- Turner, A.H.; Pritchard, A.C.; Matzke, N.J. Empirical and Bayesian approaches to fossil-only divergence times: A study across three reptile clades. PLoS ONE 2017, 12, e0169885. [Google Scholar] [CrossRef]
- Hunt, G.; Slater, G. Integrating Paleontological and Phylogenetic Approaches to Macroevolution. Annu. Rev. Ecol. Evol. Syst. 2016, 47, 189–213. [Google Scholar] [CrossRef]
- Gavryushkina, A.; Welch, D.; Stadler, T.; Drummond, A.J. Bayesian inference of sampled ancestor trees for epidemiology and fossil calibration. PLOS Comput. Biol. 2014, 10, e1003919. [Google Scholar] [CrossRef] [Green Version]
- Warnock, R.; Wright, A. Understanding the Tripartite Approach to Bayesian Divergence Time Estimation (Elements of Paleontology); Cambridge University Press: Cambridge, UK, 2021; pp. 1–46. [Google Scholar]
- Wright, A.; Wagner, P.; Wright, D. Testing Character Evolution Models in Phylogenetic Paleobiology: A Case Study with Cambrian Echinoderms (Elements of Paleontology); Cambridge University Press: Cambridge, UK, 2021; pp. 1–52. [Google Scholar]
- Simões, T.R.; Vernygora, O.; Caldwell, M.W.; Pierce, S.E. Megaevolutionary dynamics and the timing of evolutionary innovation in reptiles. Nat. Commun. 2020, 11, 3322. [Google Scholar] [CrossRef]
- Simões, T.R.; Caldwell, M.W.; Pierce, S.E. Sphenodontian phylogeny and the impact of model choice in Bayesian morphological clock estimates of divergence times and evolutionary rates. BMC Biol. 2020, 18, 191. [Google Scholar] [CrossRef]
- Zhang, C. Selecting and averaging relaxed clock models in Bayesian tip dating of Mesozoic birds. Paleobiology 2021, 48, 340–352. [Google Scholar] [CrossRef]
- Zhang, C.; Stadler, T.; Klopfstein, S.; Heath, T.A.; Ronquist, F. Total-evidence dating under the fossilized birth-death process. Syst. Biol. 2016, 65, 228–249. [Google Scholar] [CrossRef] [Green Version]
- Benton, M.J. Forth, J.; Langer, M.C. Models for the rise of the dinosaurs. Curr. Biol. 2014, 24, R87–R95. [Google Scholar] [CrossRef] [Green Version]
- Benton, M.J. Exploring macroevolution using modern and fossil data. Proc. R. Soc. B 2015, 282, 20150569. [Google Scholar] [CrossRef] [Green Version]
- Condamine, F.; Rolland, J.; Höhna, S.; Sperling, F.; Sanmartin, I. Testing the Role of the Red Queen and Court Jester as Drivers of the Macroevolution of Apollo Butterflies. Syst. Biol. 2018, 67, 940–964. [Google Scholar] [CrossRef]
- Cantalapiedra, J.L.; FitzJohn, R.G.; Kuhn, T.S.; Hernández-Fernández, M.; DeMiguel, D.; Azanza, B.; Morales, J.; Mooers, A.Ø. Dietary innovations spurred the diversification of ruminants during the Caenozoic. Proc. R. Soc. B 2014, 281, 20132746. [Google Scholar] [CrossRef]
- Clavel, J.; Morlon, H. Accelerated body size evolution during cold climatic periods in the Cenozoic. Proc. Natl. Acad. Sci. USA 2017, 114, 4183–4188. [Google Scholar] [CrossRef] [Green Version]
- Lawing, A.M.; Polly, P.D.; Hews, D.K.; Martins, E.P. Including Fossils in Phylogenetic Climate Reconstructions, A Deep Time Perspective on the Climatic Niche Evolution and Diversification of Spiny Lizards (Sceloporus). Am. Nat. 2016, 188, 133–148. [Google Scholar] [CrossRef] [Green Version]
- Louca, S.; Pennell, M.W. Extant timetrees are consistent with a myriad of diversification histories. Nature 2020, 580, 502–505. [Google Scholar] [CrossRef]
- Louca, S.; Pennell, M.W. Why extinction estimates from extant phylogenies are so often zero. Curr. Biol. 2021, 31, 3168–3173. [Google Scholar] [CrossRef]
- Agnarsson, I.; Kuntner, M. Taxonomy in a changing world, seeking solutions for a science in crisis. Syst. Biol. 2007, 56, 531–559. [Google Scholar] [CrossRef] [Green Version]
- López-Antoñanzas, R.; Knoll, F.; Maksoud, S.; Azar, D. Miocene rodent from Lebanon provides the “missing link” between Asian and African gundis (Rodentia, Ctenodactylidae). Sci. Rep. 2015, 5, 12871. [Google Scholar] [CrossRef] [Green Version]
- López-Antoñanzas, R.; Renaud, S.; Peláez-Campomanes, P.; Azar, D.; Kachacha, G.; Knoll, F. First levantine fossil murines shed new light on the first dispersal of mice. Sci. Rep. 2019, 9, 11874. [Google Scholar] [CrossRef] [Green Version]
- Wiens, J.J. Speciation and ecology revisited, phylogenetic niche conservatism and the origin of species. Evolution 2004, 58, 193–197. [Google Scholar] [CrossRef]
- Asher, R.J.; Geisler, J.H.; Sánchez-Villagra, M.R. Morphology, paleontology, and placental mammal phylogeny. Syst. Biol. 2008, 57, 311–317. [Google Scholar] [CrossRef] [Green Version]
- Springer, M.; Meredith, R.; Eizirik, E.; Teeling, E.; William, M. Morphology and Placental Mammal Phylogeny. Syst. Biol. 2008, 57, 499–503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guillerme, T.; Cooper, N. Assessment of available anatomical characters for linking living mammals to fossil taxa in phylogenetic analyses. Biol Lett. 2016, 12, 20151003. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Revell, L.J. Phytools, an R package for phylogenetic comparative biology (and other things). Methods Ecol. Evol. 2012, 3, 217–223. [Google Scholar] [CrossRef]
- May, M.R.; Moore, B.R. A Bayesian Approach for Inferring the Impact of a Discrete Character on Rates of Continuous-Character Evolution in the Presence of Background-Rate Variation. Syst. Biol. 2020, 69, 530–544. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Klingenberg, C.P.; Gidaszewski, N.A. Testing and Quantifying Phylogenetic Signals and Homoplasy in Morphometric Data. Syst. Biol. 2010, 59, 245–261. [Google Scholar]
- Adams, D.C.; Cardini, A.; Monteiro, L.R.; O’Higgins, P.; Rohlf, F.J. Morphometrics and phylogenetics: Principal components of shape from cranial modules are neither appropriate nor effective cladistic characters. J. Hum. Evol. 2011, 60, 240–243. [Google Scholar] [CrossRef]
- Renaud, S.; Michaux, J.; Jaeger, J.; Auffray, J. Fourier analysis applied to Stephanomys (Rodentia, Muridae) molars: Nonprogressive evolutionary pattern in a gradual lineage. Paleobiology 1996, 22, 255–265. [Google Scholar] [CrossRef]
- Skinner, M.M.; Gunz, P. The presence of accessory cusps in chimpanzee lower molars is consistent with a patterning cascade model of development. J. Anat. 2010, 217, 245–253. [Google Scholar] [CrossRef]
- Alhajeri, B.H.; Steppan, S.J. A phylogenetic test of adaptation to deserts and aridity in skull and dental morphology across rodents. J. Mammal. 2018, 99, 1197–1216. [Google Scholar] [CrossRef]
- Smith, U.E.; Hendricks, J.R. Geometric Morphometric Character Suites as Phylogenetic Data: Extracting Phylogenetic Signal from Gastropod Shells. Syst. Biol. 2013, 62, 366–385. [Google Scholar] [CrossRef] [Green Version]
- Clavel, J.; Escarguel, G.; Merceron, G. mvMORPH, an R package for fitting multivariate evolutionary models to morphometric data. Methods Ecol. Evol. 2015, 6, 1311–1319. [Google Scholar] [CrossRef]
- Alvarez-Carretero, S.; Goswami, A.; Yang, Z.; Dos Reis, M. Bayesian estimation of species divergence times using correlated quantitative characters. Syst. Biol. 2019, 68, 967–986. [Google Scholar] [CrossRef] [PubMed]
- Billet, G.; Bardin, J. Serial homology and correlated characters in morphological phylogenetics: Modeling the evolution of dental crests in Placentals. Syst. Biol. 2019, 68, 267–280. [Google Scholar] [CrossRef]
- Brocklehurst, N.; Romano, M.; Fröbisch, J. Principal component analysis as an alternative treatment for morphometric characters: Phylogeny of caseids as a case study. Palaeontology 2016, 59, 877–886. [Google Scholar] [CrossRef]
- Parins-Fukuchi, C. Bayesian placement of fossils on phylogenies using quantitative morphometric data. Evolution 2018, 72, 1801–1814. [Google Scholar] [CrossRef] [PubMed]
- Ascarrunz, E.; Claude, J.; Joyce, W.G. The phylogenetic relationships of geoemydid turtles from the Eocene Messel Pit Quarry: A first assessment using methods for continuous and discrete characters. PeerJ 2021, 9, e11805. [Google Scholar] [CrossRef] [PubMed]
- Gavryushkina, A.; Heath, T.A.; Ksepka, D.T.; Stadler, T.; Welch, D.; Drummond, A.J. Bayesian total-evidence dating reveals the recent crown radiation of penguins. Syst. Biol. 2017, 66, 57–73. [Google Scholar] [CrossRef] [Green Version]
- Parry, L.A.; Edgecombe, G.D.; Eibye-Jacobsen, D.; Vinther, J. The impact of fossil data on annelid phylogeny inferred from discrete morphological characters. Proc. R. Soc. B 2016, 283, 20161378. [Google Scholar] [CrossRef] [Green Version]
- Simões, T.R.; Caldwell, M.W.; Tałanda, M.; Bernardi, M.; Palci, A.; Vernygora, O.; Bernardini, F.; Mancini, L.; Nydam, R.L. The origin of squamates revealed by a Middle Triassic lizard from the Italian Alps. Nature 2018, 557, 706–709. [Google Scholar] [CrossRef]
- López-Antoñanzas, R.; Peláez-Campomanes, P. Bayesian morphological clock versus Parsimony: An insight into the relationships and dispersal events of postvacuum Cricetidae (Rodentia, Mammalia). Syst. Biol. 2022, 71, 512–525. [Google Scholar] [CrossRef]
- Miyashita, T.; Gess, R.W.; Tietjen, K. Non-ammocoete larvae of Palaeozoic stem lampreys. Nature 2021, 591, 408–412. [Google Scholar] [CrossRef] [PubMed]
- Fisher, D.C. Stratocladistics, morphological and temporal patterns and their relation to phylogenetic process. In Interpreting the Hierarchy of Nature—From Systematic Patterns to Evolutionary Theories; Grande, L., Rieppel, O., Eds.; Academic Press: New York, NY, USA, 1994; pp. 133–171. [Google Scholar]
- Wagner, P.J. Stratigraphic tests of cladistic hypotheses. Paleobiology 1995, 21, 153–178. [Google Scholar] [CrossRef]
- Bapst, D.W. Paleotree, an R package for paleontological and phylogenetic analyses of evolution. Methods Ecol. Evol. 2012, 3, 803–807. [Google Scholar] [CrossRef]
- Bapst, D.W. Assessing the effect of time-scaling methods on phylogeny-based analyses in the fossil record. Paleobiology 2014, 40, 331–351. [Google Scholar] [CrossRef]
- Bell, M.A.; Lloyd, G.T. Strap: An R package for plotting phylogenies against stratigraphy and assessing their stratigraphic congruence. Palaeontology 2014, 58, 379–389. [Google Scholar] [CrossRef]
- O’Connor, A.; Wills, M.A. Measuring stratigraphic congruence across Trees, higher taxa, and time. Syst Biol. 2016, 65, 792–811. [Google Scholar] [CrossRef] [Green Version]
- King, B.; Beck, R. Bayesian Tip-dated Phylogenetics, Topological Effects, Stratigraphic Fit and the Early Evolution of Mammals. bioRxiv 2019. [Google Scholar] [CrossRef] [Green Version]
- King, B. Bayesian tip-dated phylogenetics in paleontology: Topological effects and stratigraphic fit. Syst. Biol. 2021, 70, 283–294. [Google Scholar] [CrossRef]
- Sansom, R.S.; Choate, P.G.; Keating, J.N.; Randle, E. Parsimony, not Bayesian analysis, recovers more stratigraphically congruent phylogenetic trees. Biol. Lett. 2018, 14, 20180263. [Google Scholar] [CrossRef]
- King, B.; Qiao, T.; Lee, M.S.; Zhu, M.; Long, J.A. Bayesian morphological clock methods resurrect placoderm monophyly and reveal rapid early evolution in Jawed vertebrates. Syst. Biol. 2017, 66, 499–516. [Google Scholar] [CrossRef]
- King, B.; Rücklin, M. Tip dating with fossil sites and stratigraphic sequences. PeerJ 2020, 8, e9368. [Google Scholar] [CrossRef] [PubMed]
- Stadler, T. Sampling-through-time in birth–death trees. J. Theor. Biol. 2010, 267, 396–404. [Google Scholar] [CrossRef] [PubMed]
- Heath, T.A.; Huelsenbeck, J.P.; Stadler, T. Fossilized birth–death process. Proc. Natl. Acad. Sci. USA 2014, 111, E2957–E2966. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Simões, T.R.; Pierce, S.E. Sustained high rates of morphological evolution during the rise of tetrapods. Nat. Ecol. Evol. 2021, 5, 1403–1414. [Google Scholar] [CrossRef]
- Paterson, J.R.; Edgecombe, G.D.; Lee, M.S.Y. Trilobite evolutionary rates constrain the duration of the Cambrian explosion. Proc. Natl. Acad. Sci. USA 2019, 116, 4394–4399. [Google Scholar] [CrossRef] [Green Version]
- Jouault, C.; Maréchal, A.; Condamine, F.L.; Wang, B.; Nel, A.; Legendre, F.; Perrichot, V. Including fossils in phylogeny: A glimpse into the evolution of the superfamily Evanioidea (Hymenoptera, Apocrita) under tip-dating and the fossilized birth–death process. Zool. J. Linn. Soc. 2022, 194, 1396–1423. [Google Scholar] [CrossRef]
- Lee, M.S.Y.; Cau, A.; Naish, D.; Dyke, G.J. Morphological clocks in paleontology, and a mid-Cretaceous origin of crown Aves. Syst. Biol. 2014, 63, 442–449. [Google Scholar] [CrossRef]
- Giles, S.; Xu, G.-H.; Near, T.J.; Friedman, M. Early members of ‘living fossil’ lineage imply later origin of modern ray-finned fishes. Nature 2017, 549, 265. [Google Scholar] [CrossRef] [Green Version]
- Halliday, T.J.D.; dos Reis, M.; Tamuri, A.U.; Ferguson-Gow, H.; Yang, Z.; Goswami, A. Rapid morphological evolution in placental mammals post-dates the origin of the crown group. Proc. R. Soc. B 2019, 286, 20182418. [Google Scholar] [CrossRef] [Green Version]
- Pyron, R.A. Novel Approaches for Phylogenetic Inference from Morphological Data and Total-Evidence Dating in Squamate Reptiles (Lizards, Snakes, and Amphisbaenians). Syst. Biol. 2017, 66, 38–56. [Google Scholar] [CrossRef]
- Luo, A.; Duchêne, D.A.; Chao-Dong Zhu, C.Z.; Ho, S.Y.W.A. Simulation-Based Evaluation of Tip-Dating Under the Fossilized Birth–Death Process. Syst. Biol. 2020, 69, 325–344. [Google Scholar] [CrossRef] [PubMed]
- Mongiardino Koch, N.; Thompson, J.R.; Hiley, A.S.; McCowin, M.F.; Armstrong, A.F.; Coppard, S.E.; Aguilera, F.; Bronstein, O.; Kroh, A.; Mooi, R.; et al. Phylogenomic analyses of echinoid diversification prompt a re-evaluation of their fossil record. eLife 2022, 11, e72460. [Google Scholar] [CrossRef] [PubMed]
- O’Reilly, J.E.; Dos Reis, M.; Donoghue, P.C.J. Dating tips for divergence-time estimation. Trends Genet. 2015, 31, 637–650. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ronquist, F.; Lartillot, N.; Phillips, M.J. Closing the gap between rocks and clocks using total-evidence dating. Phil. Trans. R. Soc. B 2016, 371, 20150136. [Google Scholar] [CrossRef] [Green Version]
- Donoghue, P.C.; Yang, Z. The evolution of methods for establishing evolutionary timescales. Philos. Trans. R. Soc. Lond. B 2016, 371, 20160020. [Google Scholar] [CrossRef] [Green Version]
- O’Reilly, J.E.; Donoghue, P.C.J. Tips and nodes are complementary not competing approaches to the calibration of molecular clocks. Biol. Lett. 2016, 12, 20150975. [Google Scholar] [CrossRef]
- Cole, T.L.; Zhou, C.; Fang, M.; Pan, H.; Ksepka, D.; Fiddaman, S.; Emerling, C.; Thomas, D.; Bi, X.; Fang, Q.; et al. Genomic insights into the secondary aquatic transition of penguins. Nat. Commun. 2022, 13, 3912. [Google Scholar] [CrossRef]
- Neumann, J.S.; Desalle, R.; Narechania, A.; Schierwater, B.; Tessler, M. Morphological Characters Can Strongly Influence Early Animal Relationships Inferred from Phylogenomic Data Sets. Syst Biol. 2021, 70, 360–375. [Google Scholar] [CrossRef]
- Lipps, J.H. The future of paleontology—The next 10 years. Palaeontol. Electr. 2017, 10, 1A. [Google Scholar]
- Rabosky, D.L. Extinction rates should not be estimated from molecular phylogenies. Evolution 2010, 64, 1816–1824. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, M. Bayesian tip dating reveals heterogeneous morphological clocks in Mesozoic birds. R. Soc. Open Sci. 2019, 6, 182062. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ree, R.H.; Smith, S.A. Maximum Likelihood Inference of Geographic Range Evolution by Dispersal, Local Extinction, and Cladogenesis. Syst Biol. 2008, 57, 4–14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Landis, M.J.; Eaton, D.A.R.; Clement, W.L.; Park, B.; Spriggs, E.L.; Sweeney, P.W.; Edwards, E.J.; Donoghue, M.J. Joint phylogenetic estimation of geographic movements and biome shifts during the global diversification of Viburnum. Syst. Biol. 2021, 70, 67–85. [Google Scholar] [CrossRef] [PubMed]
- Schluter, D.; Price, T.; Mooers, A.Ø.; Ludwig, D. Likelihood of Ancestor States in Adaptive Radiation. Evolution 1997, 51, 1699–1711. [Google Scholar] [CrossRef]
- Ackerly, D.D.; Schwilk, D.W.; Webb, C.O. Niche evolution and adaptive radiation, testing the order of trait divergence. Ecology 2006, 87, S50–S61. [Google Scholar] [CrossRef]
- Beeravolu, C.R.; Condamine, F.L. An extended Maximum Likelihood inference of geographic range evolution by dispersal, local extinction and cladogenesis. bioRxiv 2016. [Google Scholar] [CrossRef] [Green Version]
- Matzke, N.J. Model selection in historical biogeography reveals that founder-event speciation is a crucial process in island clades. Syst. Biol. 2014, 63, 951–970. [Google Scholar] [CrossRef]
- Matzke, N.J. Statistical Comparison of DEC and DEC+J Is Identical to Comparison of Two Classe Submodels, and Is Therefore Valid. OSF Prepr. 2021. [Google Scholar] [CrossRef]
- Ree, R.H. Detecting the historical signature of key innovations using stochastic models of character evolution and cladogenesis. Evolution 2005, 59, 257–265. [Google Scholar] [CrossRef]
- Goldberg, E.E.; Lancaster, L.T.; Ree, R.H. Phylogenetic Inference of Reciprocal Effects between Geographic Range Evolution and Diversification. Syst. Biol. 2011, 60, 451–465. [Google Scholar] [CrossRef] [Green Version]
- Wood, H.M.; Matzke, N.J.; Gillespie, R.G.; Griswold, C.E. Treating Fossils as Terminal Taxa in Divergence Time Estimation Reveals Ancient Vicariance Patterns in the Palpimanoid Spiders. Syst Biol. 2013, 62, 264–284. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tejero-Cicuéndez, H.; Simó-Riudalbas, M.; Menéndez, I.; Carranza, S. Ecological specialization, rather than the island effect, explains morphological diversification in an ancient radiation of geckos. Proc. R. Soc. B 2021, 288, 20211821. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Zhang, Z.; Guo, Z.; Scotese, C.R.; Deng, C. Middle Miocene (∼14 Ma) and late Miocene (∼6 Ma) paleogeographic boundary conditions. Paleoceanogr. Paleoclimatol. 2021, 36, e2021PA004298. [Google Scholar] [CrossRef]
- Klaus, K.V.; Matzke, N.J. Statistical Comparison of Trait-Dependent Biogeographical Models Indicates That Podocarpaceae Dispersal Is Influenced by Both Seed Cone Traits and Geographical Distance. Syst. Biol. 2020, 69, 61–75. [Google Scholar] [CrossRef]
- Condamine, F.L.; Rolland, J.; Morlon, H. Macroevolutionary perspectives to environmental change. Ecol. Lett. 2013, 16, 72–85. [Google Scholar] [CrossRef]
- Condamine, F.L.; Silvestro, D.; Koppelhus, E.B.; Antonelli, A. The rise of angiosperms pushed conifers to decline during global cooling. Proc. Natl. Acad. Sci. USA 2020, 117, 28867–28875. [Google Scholar] [CrossRef] [PubMed]
- Condamine, F.L.; Romieu, J.; Guinot, G. Climate cooling and clade competition likely drove the decline of lamniform sharks. Proc. Natl. Acad. Sci. USA 2019, 116, 20584–20590. [Google Scholar] [CrossRef] [Green Version]
- Quental, T.; Marshall, C.R. Diversity dynamics: Molecular phylogenies need the fossil record. Trends Ecol. Evol. 2010, 25, 434–441. [Google Scholar] [CrossRef]
- O’Meara, B.C.; Beaulieu, J.M. Potential survival of some, but not all, diversification 661 methods. 2021. Available online: https://ecoevorxiv.org/w5nvd/ (accessed on 6 November 2021).
- Morlon, H.; Parsons, T.L.; Plotkin, J.B. Reconciling molecular phylogenies with the fossil record. Proc. Natl. Acad. Sci. USA 2011, 108, 16327–16332. [Google Scholar] [CrossRef] [Green Version]
- Mitchell, J.; Etienne, R.S.; Rabosky, D.L. Inferring diversification rate variation from phylogenies with fossils. Syst. Biol. 2019, 68, 1–18. [Google Scholar] [CrossRef]
- Silvestro, D.; Salamin, N.; Schnitzler, J. PyRate, a new program to estimate speciation and extinction rates from incomplete fossil data. Methods Ecol. Evol. 2014, 5, 1126–1131. [Google Scholar] [CrossRef]
- Currie, T.; Meade, A. Keeping yourself updated, Bayesian approaches in phylogenetic comparative methods with a focus on Markov Chain Models of discrete character evolution. In Modern Phylogenetic Comparative Methods; Garamszegi, L.Z., Ed.; Springer: Sevilla, Spain, 2014; pp. 263–287. [Google Scholar]
- Bürkner, P.-C. Advanced Bayesian Multilevel Modeling with the R Package brms. R J. 2018, 10, 395–411. [Google Scholar] [CrossRef]
- Smits, P.D. Expected time-invariant effects of biological traits on mammal species duration. Proc. Natl. Acad. Sci. USA 2015, 112, 13015–13020. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Smits, P.D. How macroecology affects macroevolution, The interplay between extinction intensity and trait-dependent extinction in brachiopods. bioRxiv 2019. [Google Scholar] [CrossRef] [Green Version]
- Drummond, C.S.; Eastwood, R.J.; Miotto, S.T.S.; Hughes, C.E. Multiple continental radiations and correlates of diversification in Lupinus (Leguminosae), testing for key innovation with incomplete taxon sampling. Syst. Biol. 2012, 61, 443–460. [Google Scholar] [CrossRef] [Green Version]
- Maddison, W.P.; FitzJohn, R.G. The Unsolved Challenge to Phylogenetic Correlation Tests for Categorical Characters. Syst. Biol. 2015, 64, 127–136. [Google Scholar] [CrossRef]
- Rabosky, D.L. Goldberg, E.E. FiSSE, A simple nonparametric test for the effects of a binary character on lineage diversification rates. Evolution 2017, 71, 1432–1442. [Google Scholar] [CrossRef]
- Silvestro, D.; Salamin, N.; Antonelli, A.; Meyer, X. Improved estimation of macroevolutionary rates from fossil data using a Bayesian framework. Paleobiology 2019, 45, 546–570. [Google Scholar] [CrossRef] [Green Version]
- Fuentes-G., J.A.; Polly, P.D.; Martins, E.P. A Bayesian extension of phylogenetic generalized least squares: Incorporating uncertainty in the comparative study of trait relationships and evolutionary rates. Evolution 2020, 74, 311–325. [Google Scholar] [CrossRef]
- Cole, S.R. Hierarchical controls on extinction selectivity across the diplobathrid crinoid phylogeny. Paleobiology 2021, 47, 251–270. [Google Scholar] [CrossRef]
- Hagen, O.; Andermann, T.; Quental, T.B.; Antonelli, A.; Silvestro, D. Estimating Age-Dependent Extinction: Contrasting Evidence from Fossils and Phylogenies. Syst. Biol. 2018, 67, 458–474. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Januario, M.; Quental, T.B. Re-evaluation of the “law of constant extinction” for ruminants at different taxonomical scales. Evolution 2021, 75, 656–671. [Google Scholar] [CrossRef] [PubMed]
- Kostikova, A.; Silvestro, D.; Pearman, P.B.; Salamin, N. Bridging Inter- and Intraspecific Trait Evolution with a Hierarchical Bayesian Approach. Syst. Biol. 2016, 65, 417–431. [Google Scholar] [CrossRef] [PubMed] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-Antoñanzas, R.; Mitchell, J.; Simões, T.R.; Condamine, F.L.; Aguilée, R.; Peláez-Campomanes, P.; Renaud, S.; Rolland, J.; Donoghue, P.C.J. Integrative Phylogenetics: Tools for Palaeontologists to Explore the Tree of Life. Biology 2022, 11, 1185. https://doi.org/10.3390/biology11081185
López-Antoñanzas R, Mitchell J, Simões TR, Condamine FL, Aguilée R, Peláez-Campomanes P, Renaud S, Rolland J, Donoghue PCJ. Integrative Phylogenetics: Tools for Palaeontologists to Explore the Tree of Life. Biology. 2022; 11(8):1185. https://doi.org/10.3390/biology11081185
Chicago/Turabian StyleLópez-Antoñanzas, Raquel, Jonathan Mitchell, Tiago R. Simões, Fabien L. Condamine, Robin Aguilée, Pablo Peláez-Campomanes, Sabrina Renaud, Jonathan Rolland, and Philip C. J. Donoghue. 2022. "Integrative Phylogenetics: Tools for Palaeontologists to Explore the Tree of Life" Biology 11, no. 8: 1185. https://doi.org/10.3390/biology11081185
APA StyleLópez-Antoñanzas, R., Mitchell, J., Simões, T. R., Condamine, F. L., Aguilée, R., Peláez-Campomanes, P., Renaud, S., Rolland, J., & Donoghue, P. C. J. (2022). Integrative Phylogenetics: Tools for Palaeontologists to Explore the Tree of Life. Biology, 11(8), 1185. https://doi.org/10.3390/biology11081185





