Volumetric Properties of Four-Stranded DNA Structures
Abstract
:Simple Summary
Abstract
1. Introduction
2. Definitions and Experimental Methods
2.1. Observables
2.2. Experimental Techniques
3. Differential Volume of Four-Stranded and Single-Stranded Conformations
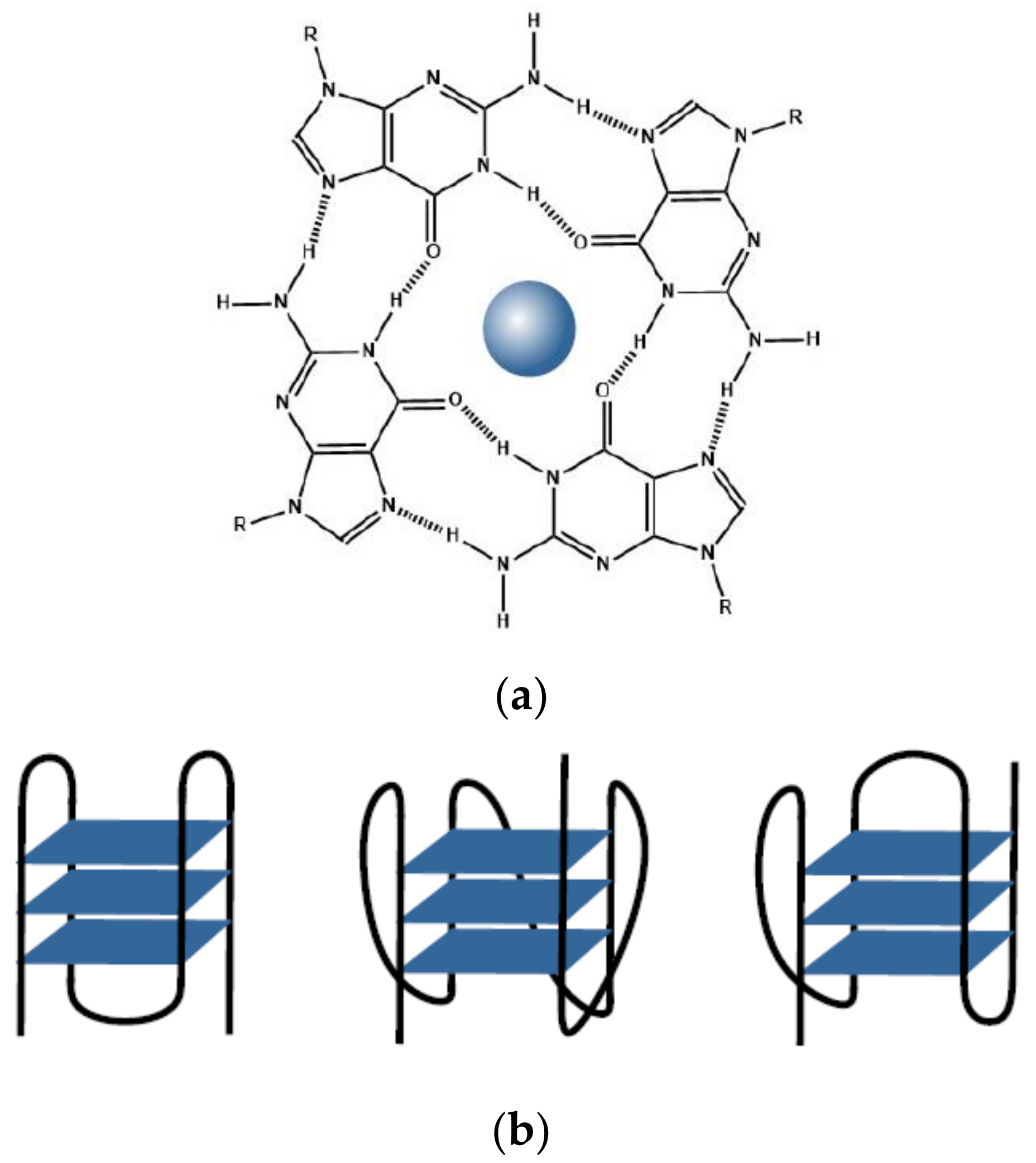
3.1. G-quadruplexes
3.2. Influence of the Bases in the Loops
3.3. i-Motifs
4. Differential Expansibility
5. Differential Compressibility
5.1. G-quadruplexes
5.2. i-Motifs
6. Pressure-Temperature Phase Diagram
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shafer, R.H.; Smirnov, I. Biological aspects of DNA/RNA quadruplexes. Biopolymers 2000, 56, 209–227. [Google Scholar] [CrossRef]
- Huppert, J.L. Four-stranded nucleic acids: Structure, function and targeting of G-quadruplexes. Chem. Soc. Rev. 2008, 37, 1375–1384. [Google Scholar] [CrossRef] [PubMed]
- Huppert, J.L. Structure, location and interactions of G-quadruplexes. FEBS J. 2010, 277, 3452–3458. [Google Scholar] [CrossRef]
- Day, H.A.; Pavlou, P.; Waller, Z.A. i-Motif DNA: Structure, stability and targeting with ligands. Bioorg. Med. Chem. 2014, 22, 4407–4418. [Google Scholar] [CrossRef] [PubMed]
- Benabou, S.; Avino, A.; Eritja, R.; Gonzalez, C.; Gargallo, R. Fundamental aspects of the nucleic acid i-motif structures. RSC Adv. 2014, 4, 26956–26980. [Google Scholar] [CrossRef] [Green Version]
- Alba, J.J.; Sadurni, A.; Gargallo, R. Nucleic acid i-motif structures in analytical chemistry. Crit. Rev. Anal. Chem. 2016, 46, 443–454. [Google Scholar] [CrossRef] [Green Version]
- Lane, A.N.; Chaires, J.B.; Gray, R.D.; Trent, J.O. Stability and kinetics of G-quadruplex structures. Nucleic Acids Res. 2008, 36, 5482–5515. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Balasubramanian, S.; Hurley, L.H.; Neidle, S. Targeting G-quadruplexes in gene promoters: A novel anticancer strategy? Nat. Rev. Drug Discov. 2011, 10, 261–275. [Google Scholar] [CrossRef] [Green Version]
- Dolinnaya, N.G.; Ogloblina, A.M.; Yakubovskaya, M.G. Structure, properties, and biological relevance of the DNA and RNA G-quadruplexes: Overview 50 Years after their discovery. Biochemistry 2016, 81, 1602–1649. [Google Scholar] [CrossRef]
- Hansel-Hertsch, R.; Di Antonio, M.; Balasubramanian, S. DNA G-quadruplexes in the human genome: Detection, functions and therapeutic potential. Nat. Rev. Mol. Cell Biol. 2017, 18, 279–284. [Google Scholar] [CrossRef]
- Qin, Y.; Hurley, L.H. Structures, folding patterns, and functions of intramolecular DNA G-quadruplexes found in eukaryotic promoter regions. Biochimie 2008, 90, 1149–1171. [Google Scholar] [CrossRef] [Green Version]
- Sen, D.; Gilbert, W. Formation of parallel four-stranded complexes by guanine-rich motifs in DNA and its implications for meiosis. Nature 1988, 334, 364–366. [Google Scholar] [CrossRef]
- Burge, S.; Parkinson, G.N.; Hazel, P.; Todd, A.K.; Neidle, S. Quadruplex DNA: Sequence, topology and structure. Nucleic Acids Res. 2006, 34, 5402–5415. [Google Scholar] [CrossRef] [Green Version]
- Brooks, T.A.; Kendrick, S.; Hurley, L. Making sense of G-quadruplex and i-motif functions in oncogene promoters. FEBS J. 2010, 277, 3459–3469. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Collie, G.W.; Parkinson, G.N. The application of DNA and RNA G-quadruplexes to therapeutic medicines. Chem. Soc. Rev. 2011, 40, 5867–5892. [Google Scholar] [CrossRef] [PubMed]
- Gehring, K.; Leroy, J.L.; Gueron, M. A Tetrameric DNA structure with protonated cytosine·cytosine base pairs. Nature 1993, 363, 561–565. [Google Scholar] [CrossRef]
- Sun, D.; Hurley, L.H. The importance of negative superhelicity in inducing the formation of G-quadruplex and i-motif structures in the c-Myc promoter: Implications for drug targeting and control of gene expression. J. Med. Chem. 2009, 52, 2863–2874. [Google Scholar] [CrossRef] [Green Version]
- Kang, H.J.; Kendrick, S.; Hecht, S.M.; Hurley, L.H. The transcriptional complex between the BCL2 i-motif and hnRNP LL is a molecular switch for control of gene expression that can be modulated by small molecules. J. Am. Chem. Soc. 2014, 136, 4172–4185. [Google Scholar] [CrossRef] [PubMed]
- Kendrick, S.; Kang, H.J.; Alam, M.P.; Madathil, M.M.; Agrawal, P.; Gokhale, V.; Yang, D.; Hecht, S.M.; Hurley, L.H. The dynamic character of the BCL2 promoter i-motif provides a mechanism for modulation of gene expression by compounds that bind selectively to the alternative DNA hairpin structure. J. Am. Chem. Soc. 2014, 136, 4161–4171. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Wei, C.; Jia, G.; Wang, X.; Feng, Z.; Li, C. Formation of i-motif structure at neutral and slightly alkaline pH. Mol. Biosyst. 2010, 6, 580–586. [Google Scholar] [CrossRef]
- Tateishi-Karimata, H.; Sugimoto, N. Chemical biology of non-canonical structures of nucleic acids for therapeutic applications. Chem. Commun. 2020, 56, 2379–2390. [Google Scholar] [CrossRef]
- Spiegel, J.; Adhikari, S.; Balasubramanian, S. The structure and function of DNA G-quadruplexes. Trends Chem. 2020, 2, 123–136. [Google Scholar] [CrossRef] [Green Version]
- Varshney, D.; Spiegel, J.; Zyner, K.; Tannahill, D.; Balasubramanian, S. The regulation and functions of DNA and RNA G-quadruplexes. Nat. Rev. Mol. Cell Biol. 2020, 21, 459–474. [Google Scholar] [CrossRef]
- Bryan, T.M. Mechanisms of DNA replication and repair: Insights from the study of G-quadruplexes. Molecules 2019, 24, 3439. [Google Scholar] [CrossRef] [Green Version]
- Armas, P.; David, A.; Calcaterra, N.B. Transcriptional control by G-quadruplexes: In vivo roles and perspectives for specific intervention. Transcription 2017, 8, 21–25. [Google Scholar] [CrossRef] [Green Version]
- Biffi, G.; Tannahill, D.; McCafferty, J.; Balasubramanian, S. Quantitative visualization of DNA G-quadruplex structures in human cells. Nat. Chem. 2013, 5, 182–186. [Google Scholar] [CrossRef] [PubMed]
- Lam, E.Y.; Beraldi, D.; Tannahill, D.; Balasubramanian, S. G-quadruplex structures are stable detectable in human genomic DNA. Nat. Commun. 2013, 4, 1796. [Google Scholar] [CrossRef] [Green Version]
- Biffi, G.; Di, A.M.; Tannahill, D.; Balasubramanian, S. Visualization and selective chemical targeting of RNA G-quadruplex structures in the cytoplasm of human cells. Nat. Chem. 2014, 6, 75–80. [Google Scholar] [CrossRef] [PubMed]
- Zeraati, M.; Langley, D.B.; Schofield, P.; Moye, A.L.; Rouet, R.; Hughes, W.E.; Bryan, T.M.; Dinger, M.E.; Christ, D. i-motif DNA structures are formed in the nuclei of human cells. Nat. Chem. 2018, 10, 631–637. [Google Scholar] [CrossRef]
- Abou Assi, H.; Garavis, M.; Gonzalez, C.; Damha, M.J. i-Motif DNA: Structural features and significance to cell biology. Nucleic Acids Res. 2018, 46, 8038–8056. [Google Scholar] [CrossRef] [Green Version]
- Kim, B.G.; Chalikian, T.V. Thermodynamic linkage analysis of pH-induced folding and unfolding transitions of i-motifs. Biophys. Chem. 2016, 216, 19–22. [Google Scholar] [CrossRef] [PubMed]
- Chalikian, T.V.; Liu, L.; Macgregor, R.B., Jr. Duplex-tetraplex equilibria in guanine- and cytosine-rich DNA. Biophys. Chem. 2020, 267, 106473. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, S.; Sugimoto, N. Stability prediction of canonical and non-canonical structures of nucleic acids in various molecular environments and cells. Chem. Soc. Rev. 2020, 49, 8439–8468. [Google Scholar] [CrossRef] [PubMed]
- Kim, B.G.; Evans, H.M.; Dubins, D.N.; Chalikian, T.V. Effects of salt on the stability of a G-quadruplex from the human c-MYC promoter. Biochemistry 2015, 54, 3420–3430. [Google Scholar] [CrossRef] [PubMed]
- Kim, B.G.; Long, J.; Dubins, D.N.; Chalikian, T.V. Ionic effects on VEGF G-quadruplex stability. J. Phys. Chem. B 2016, 120, 4963–4971. [Google Scholar] [CrossRef] [PubMed]
- Aslanyan, L.; Ko, J.; Kim, B.G.; Vardanyan, I.; Dalyan, Y.B.; Chalikian, T.V. Effect of urea on G-quadruplex stability. J. Phys. Chem. B 2017, 121, 6511–6519. [Google Scholar] [CrossRef]
- Sugimoto, N. Noncanonical structures and their thermodynamics of DNA and RNA under molecular crowding: Beyond the Watson-Crick double helix. Int. Rev. Cell Mol. Biol. 2014, 307, 205–273. [Google Scholar]
- Nakano, S.; Miyoshi, D.; Sugimoto, N. Effects of molecular crowding on the structures, interactions, and functions of nucleic acids. Chem. Rev. 2014, 114, 2733–2758. [Google Scholar] [CrossRef]
- Boncina, M.; Lah, J.; Prislan, I.; Vesnaver, G. Energetic basis of human telomeric DNA folding into G-quadruplex structures. J. Am. Chem. Soc. 2012, 134, 9657–9663. [Google Scholar] [CrossRef]
- Boncina, M.; Vesnaver, G.; Chaires, J.B.; Lah, J. Unraveling the thermodynamics of the folding and interconversion of human telomere G-quadruplexes. Angew. Chem. Int. Ed. Engl. 2016, 55, 10340–10344. [Google Scholar] [CrossRef] [Green Version]
- Olsen, C.M.; Gmeiner, W.H.; Marky, L.A. Unfolding of G-quadruplexes: Energetic, and ion and water contributions of G-quartet stacking. J. Phys. Chem. B 2006, 110, 6962–6969. [Google Scholar] [CrossRef]
- Kaushik, M.; Suehl, N.; Marky, L.A. Calorimetric unfolding of the bimolecular and i-motif complexes of the human telomere complementary strand, d(C3TA2)4. Biophys. Chem. 2007, 126, 154–164. [Google Scholar] [CrossRef] [PubMed]
- Macgregor, R.B., Jr. Effect of hydrostatic pressure on nucleic acids. Biopolymers 1998, 48, 253–263. [Google Scholar] [CrossRef]
- Chalikian, T.V.; Macgregor, R.B. Nucleic acid hydration: A volumetric perspective. Phys. Life Rev. 2007, 4, 91–115. [Google Scholar] [CrossRef]
- Chalikian, T.V.; Sarvazyan, A.P.; Breslauer, K.J. Hydration and partial compressibility of biological compounds. Biophys. Chem. 1994, 51, 89–107. [Google Scholar] [CrossRef]
- Chalikian, T.V.; Breslauer, K.J. Thermodynamic analysis of biomolecules: A volumetric approach. Curr. Opin. Struct. Biol. 1998, 8, 657–664. [Google Scholar] [CrossRef]
- Chalikian, T.V.; Breslauer, K.J. Volumetric properties of nucleic acids. Biopolymers 1998, 48, 264–280. [Google Scholar] [CrossRef]
- Takahashi, S.; Sugimoto, N. Pressure-dependent formation of i-motif and G-quadruplex DNA structures. Phys. Chem. Chem. Phys. 2015, 17, 31004–31010. [Google Scholar] [CrossRef] [PubMed]
- Winter, R. Interrogating the structural dynamics and energetics of biomolecular systems with pressure modulation. Annu. Rev. Biophys. 2019, 48, 441–463. [Google Scholar] [CrossRef] [PubMed]
- Chalikian, T.V. Volumetric properties of proteins. Annu. Rev. Biophys. Biomol. Struct. 2003, 32, 207–235. [Google Scholar] [CrossRef] [PubMed]
- Chalikian, T.V. Volumetric measurements in binary solvents: Theory to experiment. Biophys. Chem. 2011, 156, 3–12. [Google Scholar] [CrossRef]
- Cooper, A. Protein fluctuations and the thermodynamic uncertainty principle. Prog. Biophys. Mol. Biol. 1984, 44, 181–214. [Google Scholar] [CrossRef]
- Chen, C.R.; Makhatadze, G.I. Molecular determinants of temperature dependence of protein volume change upon unfolding. J. Phys. Chem. B 2017, 121, 8300–8310. [Google Scholar] [CrossRef]
- Chen, C.R.; Makhatadze, G.I. Molecular determinant of the effects of hydrostatic pressure on protein folding stability. Nat. Commun. 2017, 8, 14561. [Google Scholar] [CrossRef] [PubMed]
- Krobath, H.; Chen, T.; Chan, H.S. Volumetric physics of polypeptide coil-helix transitions. Biochemistry 2016, 55, 6269–6281. [Google Scholar] [CrossRef] [PubMed]
- Kim, B.G.; Shek, Y.L.; Chalikian, T.V. Polyelectrolyte effects in G-quadruplexes. Biophys.Chem. 2013, 184, 95–100. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Kim, B.G.; Feroze, U.; Macgregor, R.B., Jr.; Chalikian, T.V. Probing the ionic atmosphere and hydration of the c-MYC i-motif. J. Am. Chem. Soc. 2018, 140, 2229–2238. [Google Scholar] [CrossRef]
- Blandamer, M.J.; Davis, M.I.; Douheret, G.; Reis, J.C.R. Apparent molar isentropic compressions and expansions of solutions. Chem. Soc. Rev. 2001, 30, 8–15. [Google Scholar] [CrossRef]
- Desnoyers, J.E.; Philip, P.R. Isothermal compressibilities of aqueous solutions of tetraalkylammonium bromides. Can. J. Chem. 1972, 50, 1094–1096. [Google Scholar] [CrossRef] [Green Version]
- Kharakoz, D.P. Partial molar volumes of molecules of arbitrary shape and the effect of hydrogen bonding with water. J. Solut. Chem. 1992, 21, 569–595. [Google Scholar] [CrossRef]
- Pierotti, R.A. Scaled particle theory of aqueous and non-aqueous solutions. Chem. Rev. 1976, 76, 717–726. [Google Scholar] [CrossRef]
- Chalikian, T.V. On the molecular origins of volumetric data. J. Phys. Chem. B 2008, 112, 911–917. [Google Scholar] [CrossRef]
- Patel, N.; Dubins, D.N.; Pomes, R.; Chalikian, T.V. Parsing partial molar volumes of small molecules: A molecular dynamics study. J. Phys. Chem. B 2011, 115, 4856–4862. [Google Scholar] [CrossRef] [PubMed]
- Chalikian, T.V. Structural thermodynamics of hydration. J. Phys. Chem. B 2001, 105, 12566–12578. [Google Scholar] [CrossRef]
- Lee, S.Y.; Chalikian, T.V. Volumetric properties of solvation in binary solvents. J. Phys. Chem. B 2009, 113, 2443–2450. [Google Scholar] [CrossRef]
- Han, F.; Chalikian, T.V. Hydration changes accompanying nucleic acid intercalation reactions:volumetric characterizations. J. Am. Chem. Soc. 2003, 125, 7219–7229. [Google Scholar] [CrossRef] [PubMed]
- Han, F.; Taulier, N.; Chalikian, T.V. Association of the minor groove binding drug Hoechst 33258 with d(CGCGAATTCGCG)2: Volumetric, calorimetric, and spectroscopic characterizations. Biochemistry 2005, 44, 9785–9794. [Google Scholar] [CrossRef] [PubMed]
- Filfil, R.; Chalikian, T.V. The thermodynamics of protein-protein recognition as characterized by a combination of volumetric and calorimetric techniques: The binding of turkey ovomucoid third domain to α-chymotrypsin. J. Mol. Biol. 2003, 326, 1271–1288. [Google Scholar] [CrossRef]
- Filfil, R.; Chalikian, T.V. Volumetric and spectroscopic characterizations of glucose-hexokinase association. FEBS Lett. 2003, 554, 351–356. [Google Scholar] [CrossRef] [Green Version]
- Son, I.; Shek, Y.L.; Dubins, D.N.; Chalikian, T.V. Volumetric characterization of tri-N-acetylglucosamine binding to lysozyme. Biochemistry 2012, 51, 5784–5790. [Google Scholar] [CrossRef]
- Son, I.; Selvaratnam, R.; Dubins, D.N.; Melacini, G.; Chalikian, T.V. Ultrasonic and densimetric characterization of the association of cyclic AMP with the cAMP-binding domain of the exchange protein EPAC1. J. Phys. Chem. B 2013, 117, 10779–10784. [Google Scholar] [CrossRef]
- Liu, L.; Stepanian, L.; Dubins, D.N.; Chalikian, T.V. Binding of L-argininamide to a DNA aptamer: A volumetric study. J. Phys. Chem. B 2018, 122, 7647–7653. [Google Scholar] [CrossRef] [PubMed]
- Filfil, R.; Chalikian, T.V. Volumetric and spectroscopic characterizations of the native and acid-induced denatured states of staphylococcal nuclease. J. Mol. Biol. 2000, 299, 827–842. [Google Scholar] [CrossRef]
- Taulier, N.; Chalikian, T.V. Characterization of pH-induced transitions of β-lactoglobulin: Ultrasonic, densimetric, and spectroscopic studies. J. Mol. Biol. 2001, 314, 873–889. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taulier, N.; Beletskaya, I.V.; Chalikian, T.V. Compressibility changes accompanying conformational transitions of apomyoglobin. Biopolymers 2005, 79, 218–229. [Google Scholar] [CrossRef] [PubMed]
- Taulier, N.; Chalikian, T.V. Hydrophobic hydration in cyclodextrin complexation. J. Phys. Chem. B 2006, 110, 12222–12224. [Google Scholar] [CrossRef] [PubMed]
- Taulier, N.; Chalikian, T.V. γ-Cyclodextrin forms a highly compressible complex with 1-adamantanecarboxylic acid. J. Phys. Chem. B 2008, 112, 9546–9549. [Google Scholar] [CrossRef]
- Chalikian, T.V.; Volker, J.; Anafi, D.; Breslauer, K.J. The native and the heat-induced denatured states of α-chymotrypsinogen A: Thermodynamic and spectroscopic studies. J. Mol. Biol. 1997, 274, 237–252. [Google Scholar] [CrossRef] [PubMed]
- Lin, L.N.; Brandts, J.F.; Brandts, J.M.; Plotnikov, V. Determination of the volumetric properties of proteins and other solutes using pressure perturbation calorimetry. Anal. Biochem. 2002, 302, 144–160. [Google Scholar] [CrossRef]
- Suladze, S.; Kahse, M.; Erwin, N.; Tomazic, D.; Winter, R. Probing volumetric properties of biomolecular systems by pressure perturbation calorimetry (PPC)—The effects of hydration, cosolvents and crowding. Methods 2015, 76, 67–77. [Google Scholar]
- Heerklotz, H. Pressure Perturbation Calorimetry. In Methods in Molecular Biology; Dopica, A.M., Ed.; Humana Press, Inc.: Totowa, NJ, USA, 2007; pp. 197–206. [Google Scholar]
- Mitra, L.; Smolin, N.; Ravindra, R.; Royer, C.; Winter, R. Pressure perturbation calorimetric studies of the solvation properties and the thermal unfolding of proteins in solution—Experiments and theoretical interpretation. Phys. Chem. Chem. Phys. 2006, 8, 1249–1265. [Google Scholar] [CrossRef]
- Schweiker, K.L.; Makhatadze, G.I. Use of pressure perturbation calorimetry to characterize the volumetric properties of proteins. Methods Enzymol. 2009, 466, 527–547. [Google Scholar]
- Sarvazyan, A.P. Ultrasonic velocimetry of biological compounds. Annu. Rev. Biophys. Biophys. Chem. 1991, 20, 321–342. [Google Scholar] [CrossRef]
- Sarvazian, A.P. Ultrasonic velocimetry of biological compounds. Mol. Biol. 1983, 17, 916–927. [Google Scholar] [CrossRef]
- Owen, B.B.; Simons, H.L. Standard partial molal compressibilities by ultrasonics. 1. Sodium chloride and potassium chloride at 25 °C. J. Phys. Chem. 1957, 61, 479–482. [Google Scholar] [CrossRef]
- Barnartt, S. The velocity of sound in electrolytic solutions. J. Chem. Phys. 1952, 20, 278–279. [Google Scholar] [CrossRef]
- Lerch, M.T.; Horwitz, J.; McCoy, J.; Hubbell, W.L. Circular dichroism and site-directed spin labeling reveal structural and dynamical features of high-pressure states of myoglobin. Proc. Natl. Acad. Sci. USA 2013, 110, E4714–E4722. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dellarole, M.; Royer, C.A. High-pressure fluorescence applications. Methods Mol. Biol. 2014, 1076, 53–74. [Google Scholar] [PubMed]
- Akasaka, K. Probing conformational fluctuation of proteins by pressure perturbation. Chem. Rev. 2006, 106, 1814–1835. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.Q.; Macgregor, R.B., Jr. Pressure dependence of the melting temperature of dA·dT polymers. Biochemistry 1993, 32, 12531–12537. [Google Scholar] [CrossRef] [PubMed]
- Fan, H.Y.; Shek, Y.L.; Amiri, A.; Dubins, D.N.; Heerklotz, H.; Macgregor, R.B., Jr.; Chalikian, T.V. Volumetric characterization of sodium-induced G-quadruplex formation. J. Am. Chem. Soc. 2011, 133, 4518–4526. [Google Scholar] [CrossRef]
- Shek, Y.L.; Noudeh, G.D.; Nazari, M.; Heerklotz, H.; Abu-Ghazalah, R.M.; Dubins, D.N.; Chalikian, T.V. Folding thermodynamics of the hybrid-1 type intramolecular human telomeric G-quadruplex. Biopolymers 2014, 101, 216–227. [Google Scholar] [CrossRef]
- Takahashi, S.; Sugimoto, N. Effect of pressure on the stability of G-quadruplex DNA: Thermodynamics under crowding conditions. Angew. Chem.-Int. Ed. 2013, 52, 13774–13778. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, S.; Sugimoto, N. Effect of pressure on thermal stability of G-quadruplex DNA and double-stranded DNA structures. Molecules 2013, 18, 13297–13319. [Google Scholar] [CrossRef] [Green Version]
- Molnar, O.R.; Somkuti, J.; Smeller, L. Negative volume changes of human G-quadruplexes at unfolding. Heliyon 2020, 6, 6. [Google Scholar] [CrossRef]
- Li, Y.Y.; Dubins, D.N.; Le, D.; Leung, K.; Macgregor, R.B., Jr. The role of loops and cation on the volume of unfolding of G-quadruplexes related to HTel. Biophys. Chem. 2017, 231, 55–63. [Google Scholar] [CrossRef]
- Chalikian, T.V.; Macgregor, R.B., Jr. On empirical decomposition of volumetric data. Biophys. Chem. 2019, 246, 8–15. [Google Scholar] [CrossRef]
- Liu, L.; Scott, L.; Tariq, N.; Kume, T.; Dubins, D.N.; Macgregor, R.B., Jr.; Chalikian, T.V. Volumetric interplay between the conformational states adopted by guanine-rich DNA from the c-MYC promoter. J. Phys. Chem. B 2021, 125, 7406–7416. [Google Scholar] [CrossRef]
- Li, K.; Yatsunyk, L.; Neidle, S. Water spines and networks in G-quadruplex structures. Nucleic Acids Res. 2021, 49, 519–528. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, S.; Sugimoto, N. Volumetric contributions of loop regions of G-quadruplex DNA to the formation of the tertiary structure. Biophys. Chem. 2017, 231, 146–154. [Google Scholar] [CrossRef] [PubMed]
- Lepper, C.P.; Williams, M.A.K.; Edwards, P.J.B.; Filichev, V.V.; Jameson, G.B. Effects of pressure and pH on the physical stability of an i-motif DNA structure. Chem. Phys. Chem. 2019, 20, 1567–1571. [Google Scholar] [CrossRef]
- Somkuti, J.; Molnar, O.R.; Smeller, L. Revealing unfolding steps and volume changes of human telomeric i-motif DNA. Phys. Chem. Chem. Phys. 2020, 22, 23816–23823. [Google Scholar] [CrossRef]
- Rashin, A.A.; Iofin, M.; Honig, B. Internal cavities and buried waters in globular proteins. Biochemistry 1986, 25, 3619–3625. [Google Scholar] [CrossRef]
- Liang, J.; Dill, K.A. Are proteins well-packed? Biophys. J. 2001, 81, 751–766. [Google Scholar] [CrossRef] [Green Version]
- Chalikian, T.V.; Sarvazyan, A.P.; Breslauer, K.J. Partial molar volumes, expansibilities, and compressibilities of α,ω-aminocarboxylic acids in aqueous solutions between 18 and 55 °C. J. Phys. Chem. 1993, 97, 13017–13026. [Google Scholar] [CrossRef]
- Chalikian, T.V.; Sarvazyan, A.P.; Funck, T.; Breslauer, K.J. Partial molar volumes, expansibilities, and compressibilities of oligoglycines in aqueous solutions at 18–55 °C. Biopolymers 1994, 34, 541–553. [Google Scholar] [CrossRef]
- Lee, A.; Chalikian, T.V. Volumetric characterization of the hydration properties of heterocyclic bases and nucleosides. Biophys. Chem. 2001, 92, 209–227. [Google Scholar] [CrossRef]
- Kharakoz, D.P. Volumetric properties of proteins and their analogs in diluted water solutions. 1. Partial volumes of amino acids at 15–55 °C. Biophys. Chem. 1989, 34, 115–125. [Google Scholar] [CrossRef]
- Hedwig, G.R.; Hastie, J.D.; Høiland, H. Thermodynamic properties of peptide solutions. 14. Partial molar expansibilities and isothermal compressibilities of some glycyl dipeptides in aqueous solution. J. Solut. Chem. 1996, 25, 615–633. [Google Scholar] [CrossRef]
- Hedwig, G.R.; Jameson, G.B.; Høiland, H. The partial molar heat capacity, expansion, isentropic, and isothermal compressions of thymidine in aqueous solution at T=298.15 K. J. Chem. Thermodyn. 2011, 43, 1936–1941. [Google Scholar] [CrossRef]
- Chalikian, T.V. Ultrasonic and densimetric characterizations of the hydration properties of polar groups in monosaccharides. J. Phys. Chem. B 1998, 102, 6921–6926. [Google Scholar] [CrossRef]
- Lee, S.; Tikhomirova, A.; Shalvardjian, N.; Chalikian, T.V. Partial molar volumes and adiabatic compressibilities of unfolded protein states. Biophys. Chem. 2008, 134, 185–199. [Google Scholar] [CrossRef]
- Chalikian, T.V.; Totrov, M.; Abagyan, R.; Breslauer, K.J. The hydration of globular proteins as derived from volume and compressibility measurements: Cross correlating thermodynamic and structural data. J. Mol. Biol. 1996, 260, 588–603. [Google Scholar] [CrossRef] [Green Version]
- Kharakoz, D.P. Protein compressibility, dynamics, and pressure. Biophys. J. 2000, 79, 511–525. [Google Scholar] [CrossRef] [Green Version]
- Taulier, N.; Chalikian, T.V. Compressibility of protein transitions. Biochim. Biophys. Acta 2002, 1595, 48–70. [Google Scholar] [CrossRef]
- Chalikian, T.V.; Sarvazyan, A.P.; Plum, G.E.; Breslauer, K.J. Influence of base composition, base sequence, and duplex structure on DNA hydration: Apparent molar volumes and apparent molar adiabatic compressibilities of synthetic and natural DNA duplexes at 25 °C. Biochemistry 1994, 33, 2394–2401. [Google Scholar] [CrossRef]
- Tikhomirova, A.; Chalikian, T.V. Probing hydration of monovalent cations condensed around polymeric nucleic acids. J. Mol. Biol. 2004, 341, 551–563. [Google Scholar] [CrossRef]
- Chalikian, T.V.; Volker, J.; Srinivasan, A.R.; Olson, W.K.; Breslauer, K.J. The hydration of nucleic acid duplexes as assessed by a combination of volumetric and structural techniques. Biopolymers 1999, 50, 459–471. [Google Scholar] [CrossRef]
- Kharakoz, D.P. Volumetric properties of proteins and their analogs in diluted water solutions. 2. Partial adiabatic compressibilities of amino acids at 15–70 °C. J. Phys. Chem. 1991, 95, 5634–5642. [Google Scholar] [CrossRef]
- Doster, W.; Friedrich, J. Pressure-temperature phase diagrams of proteinsC. In Protein Folding Handbook; Buchner, J., Kiefhaber, T., Eds.; Wiley-V C H Verlag Gmbh: Weinheim, Germany, 2005; pp. 99–126. [Google Scholar]
- Hawley, S.A. Reversible pressure-temperature denaturation of chymotrypsinogen. Biochemistry 1971, 10, 2436–2442. [Google Scholar] [CrossRef]
- Ravindra, R.; Winter, R. On the temperature-pressure free-energy landscape of proteins. Chem. Phys. Chem. 2003, 4, 359–365. [Google Scholar] [CrossRef] [PubMed]
- Winter, R.; Lopes, D.; Grudzielanek, S.; Vogtt, K. Towards an understanding of the temperature/pressure configurational and free-energy landscape of biomolecules. J. Non-Equilib. Thermodyn. 2007, 32, 41–97. [Google Scholar] [CrossRef]
- Daniel, I.; Oger, P.; Winter, R. Origins of life and biochemistry under high-pressure conditions. Chem. Soc. Rev. 2006, 35, 858–875. [Google Scholar] [CrossRef]
- Luong, T.Q.; Kapoor, S.; Winter, R. Pressure-a gateway to fundamental insights into protein solvation, dynamics, and function. Chem. Phys. Chem. 2015, 16, 3555–3571. [Google Scholar] [CrossRef]
- Majhi, P.R.; Qi, J.Y.; Tang, C.F.; Shafer, R.H. Heat capacity changes associated with guanine quadruplex formation: An isothermal titration calorimetry study. Biopolymers 2008, 89, 302–309. [Google Scholar] [CrossRef]
- Scharnagl, C.; Reif, M.; Friedrich, J. Stability of proteins: Temperature, pressure and the role of the solvent. Biochim. Biophys. Acta 2005, 1749, 187–213. [Google Scholar] [CrossRef]
- Dubins, D.N.; Lee, A.; Macgregor, R.B., Jr.; Chalikian, T.V. On the stability of double stranded nucleic acids. J. Am. Chem. Soc. 2001, 123, 9254–9259. [Google Scholar] [CrossRef]


| Sequence (DNA) | Topology | Cation | T, °C | ΔV, cm3 mol−1 |
|---|---|---|---|---|
| d(G2T2G2TGT-G2T2G2) (TBA) a | Antiparallel | K+ | 58.1 ± 1.4 | −54.6 ± 4.2 |
| d[A(G3T2A)3G3](Tel22) b | Antiparallel | Na+ | 54.6 ± 0.9 | −38.4 ± 10.1 |
| d[A(G3T2A)3G3](Tel22) c | Antiparallel | Na+ | 40.0 ± 0.6 | −66 ± 3 |
| d[A(G3T2A)3G3](Tel22) b | Hybrid | K+ | 64.6 ± 2.2 | −42.7 ± 6.7 |
| d[TGA(G3TG3TA)2A](c-MYC) d | Parallel | K+ | 83.4 ± 1.1 | −16.9 ± 1.8 |
| d(AG3AG3CGCTG3-AG2AG3) (KIT) d | Parallel | K+ | 58.5 ± 0.4 | −6.2 ± 0.9 |
| d(T2G4CG3C2G5C-G4T2) (VEGF) d | Parallel | K+ | 78.8 ± 1.1 | −18.1 ± 4.6 |
| d[A3(G3T2A)3G3A2](Tel26) e | Hybrid | K+ | 25.0 | −69 ± 7 |
| d[TGA(G3TG3TA)2A](c-MYC) f | Parallel | K+ | 25.0 | −34 ± 15 |
| G-Quadruplex | ΔV | ΔVM | ΔSA | ΔVT = δΔSA | ΔVI a |
|---|---|---|---|---|---|
| Tel22 | −67 | −233 b | 1230 b | 370 | −186 |
| Tel26 | −69 | −4 c | 2348 c | 707 | −779 |
| c-MYC | −34 | 2 d | 879 d | 265 | −306 |
| DNA | Sequence | TM, °C e | ΔV, cm3 mol−1 |
|---|---|---|---|
| TBA a,c | d(G2T2G2TGTG2T2G2) | 52.6 ± 3.4 | −54.6 ± 4.2 |
| TBA T3A b,c | d(G2ATG2TGTG2T2G2) | 45.1 ± 0.1 | −75.5 ± 2.2 |
| TBA G8T b,c | d(G2T2G2TTTG2T2G2) | 47.1 ± 6.6 | −41.1 ± 2.4 |
| TBA 1LC12 b,c | d[G2-(CH2)12-G2TGTG2T2G2] | 49.0 ± 3.9 | −57.8 ± 8.4 |
| TBA 2LC12 b,c | d[G2T2G2-(CH2)12-G2T2G2] | 36.5 ± 0.6 | −103.4 ± 8.0 |
| TBA a,d | d(G2T2G2TGTG2T2G2) | 59.3 ± 2.3 | −12.9 ± 0.9 |
| TBA T3A b,d | d(G2ATG2TGTG2T2G2) | 56.7 ± 2.2 | −14.7 ± 4.9 |
| TBA G8T b,d | d(G2T2G2TTTG2T2G2) | 54.5 ± 0.7 | −13.2 ± 2.1 |
| TBA 1LC12 b,d | d[G2-(CH2)12-G2TGTG2T2G2] | 56.6 ± 6.0 | −9.7 ± 5.2 |
| TBA 2LC12 b,d | d[G2T2G2-(CH2)12-G2T2G2] | 62.4 ± 0.3 | −5.6 ± 1.7 |
| DNA | Sequence | (ΔV, cm3 mol−1) | |
|---|---|---|---|
| Na+ | K+ | ||
| Tel22 | d(AG3T2AG3T2AG3T2AG3) | −38.4 ± 10.1 | −42.7 ± 6.7 |
| L1AAT | d(AG3AATG3T2AG3T2AG3) | −29.4 ± 5.6 | −38.0 ± 7.3 |
| L2AAT | d(AG3T2AG3AATG2T2AG3) | −29.8 ± 10.1 | −35.6 ± 8.0 |
| L3AAT | d(AG3T2AG3T2AG3AATG3) | −34.5 ± 1.1 | −27.2 ± 6.4 |
| L1TTT | d(AG3TTTG3T2AG3T2AG3) | −35.2 ± 3.0 | −35.2 ± 3.9 |
| L2TTT | d(AG3T2AG3TTTG3T2AG3) | −26.2 ± 8.0 | −30.5 ± 11.1 |
| L3TTT | d(AG3T2AG2T2AG3TTTG3) | −38.6 ± 4.0 | −21.9 ± 7.9 |
| L1AAA | d(AG3AAAG3T2AG3T2AG3) | −37.7 ± 9.0 | −37.7 ± 4.8 |
| L2AAA | d(AG3T2AG3AAAG3T2AG3) | −30.2 ± 13.1 | −37.8 ± 1.0 |
| L3AAA | d(AG3T2AG3T2AG3AAAG3) | −41.4 ± 6.8 | −31.7 ± 1.0 |
| Sequence (DNA) | pH | T, °C | ΔV, cm3 mol−1 | ΔKS, 10−4 cm3 mol−1bar−1 |
|---|---|---|---|---|
| d(C3TA2)3C3 (Tel22-iM) a | 4.6 | 36 | ~0 | |
| d(C3TA2)3C3 (Tel22-iM) b | 5.15 | 45.5 | −11 ± 2 | |
| d(T2AC3AC3TAC3A-C3TCA) (c-MYC-iM) c | 5.0 | 25.0 | ~0 | ~0 |
| Sequence (DNA) | Topology | Cation | ΔKS, 10−4 cm3 mol−1bar−1 | ΔE, cm3 mol−1K−1 |
|---|---|---|---|---|
| d[A(G3T2A)3G3](Tel22) a | Antiparallel | Na+ | −236 ± 20 | 0.87 ± 0.16 |
| d[A3(G3T2A)3G3A2](Tel26) b | Hybrid | K+ | −332 ± 18 | 0.92 ± 0.07 |
| d[TGA(G3TG3TA)2A](c-MYC) c | Parallel | K+ | −304 ± 26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chalikian, T.V.; Macgregor, R.B., Jr. Volumetric Properties of Four-Stranded DNA Structures. Biology 2021, 10, 813. https://doi.org/10.3390/biology10080813
Chalikian TV, Macgregor RB Jr. Volumetric Properties of Four-Stranded DNA Structures. Biology. 2021; 10(8):813. https://doi.org/10.3390/biology10080813
Chicago/Turabian StyleChalikian, Tigran V., and Robert B. Macgregor, Jr. 2021. "Volumetric Properties of Four-Stranded DNA Structures" Biology 10, no. 8: 813. https://doi.org/10.3390/biology10080813
APA StyleChalikian, T. V., & Macgregor, R. B., Jr. (2021). Volumetric Properties of Four-Stranded DNA Structures. Biology, 10(8), 813. https://doi.org/10.3390/biology10080813






