Optimal Input Representation in Neural Systems at the Edge of Chaos
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
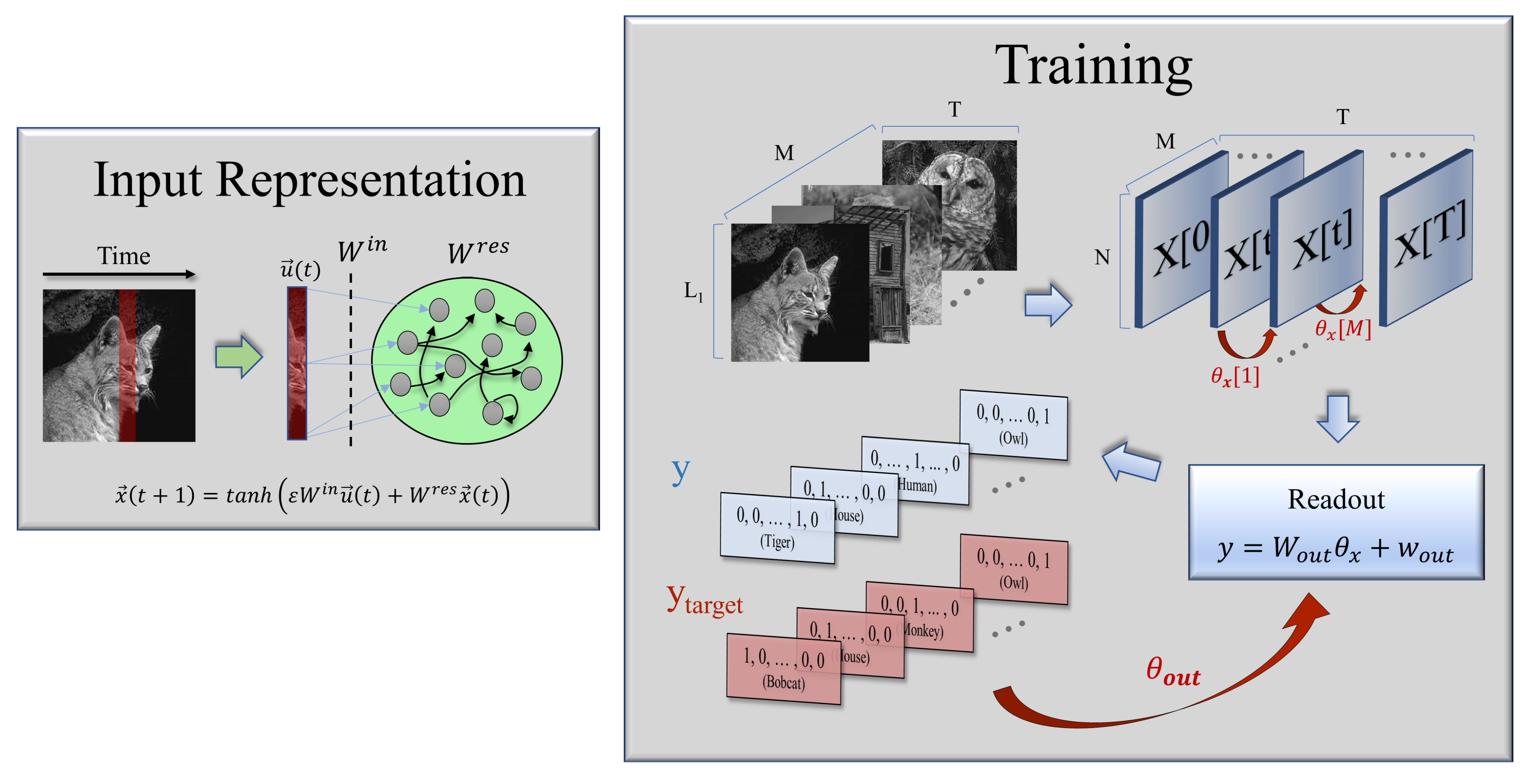
2.1. Model Formulation
- An input layer, which scales a number of inputs at each time step before they arrive in the reservoir, according to some random weights .
- A reservoir consisting of N internal units connected with random weights , whose corresponding states evolve according to a non-linear, time-discrete dynamical equation under the influence of a time-dependent input. In this way, the reservoir maps the external input into a high-dimensional space.
- An output layer, with trainable weights that converts the information contained in the high-dimensional states of the neurons (the internal representation of the inputs) to generate the final output.
2.2. Image Datasets and Parameter Selection
2.3. PCA and cvPCA
3. Results
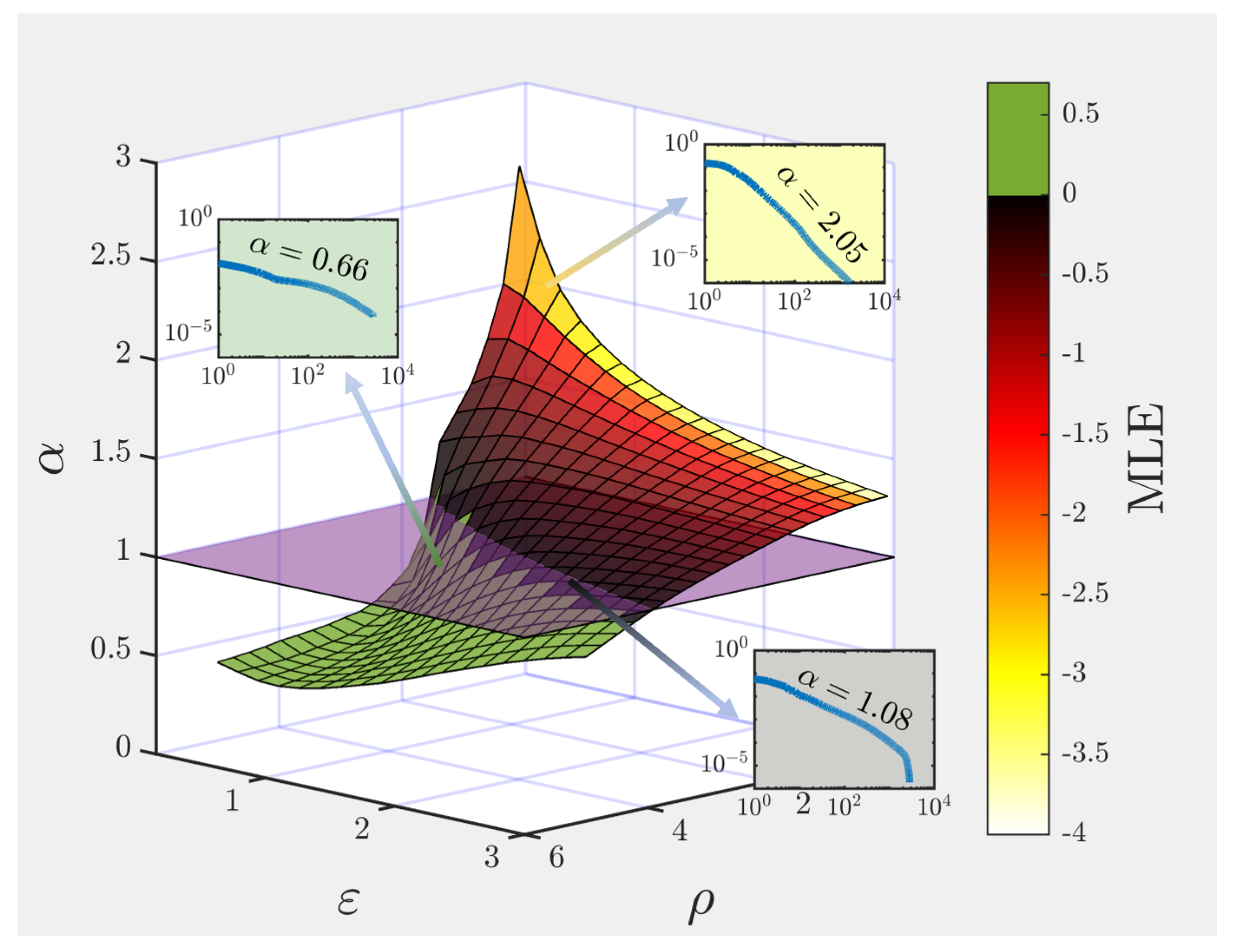
3.1. Non-Trivial Scaling and Robust Input Representation at the Edge of Chaos
- (i)
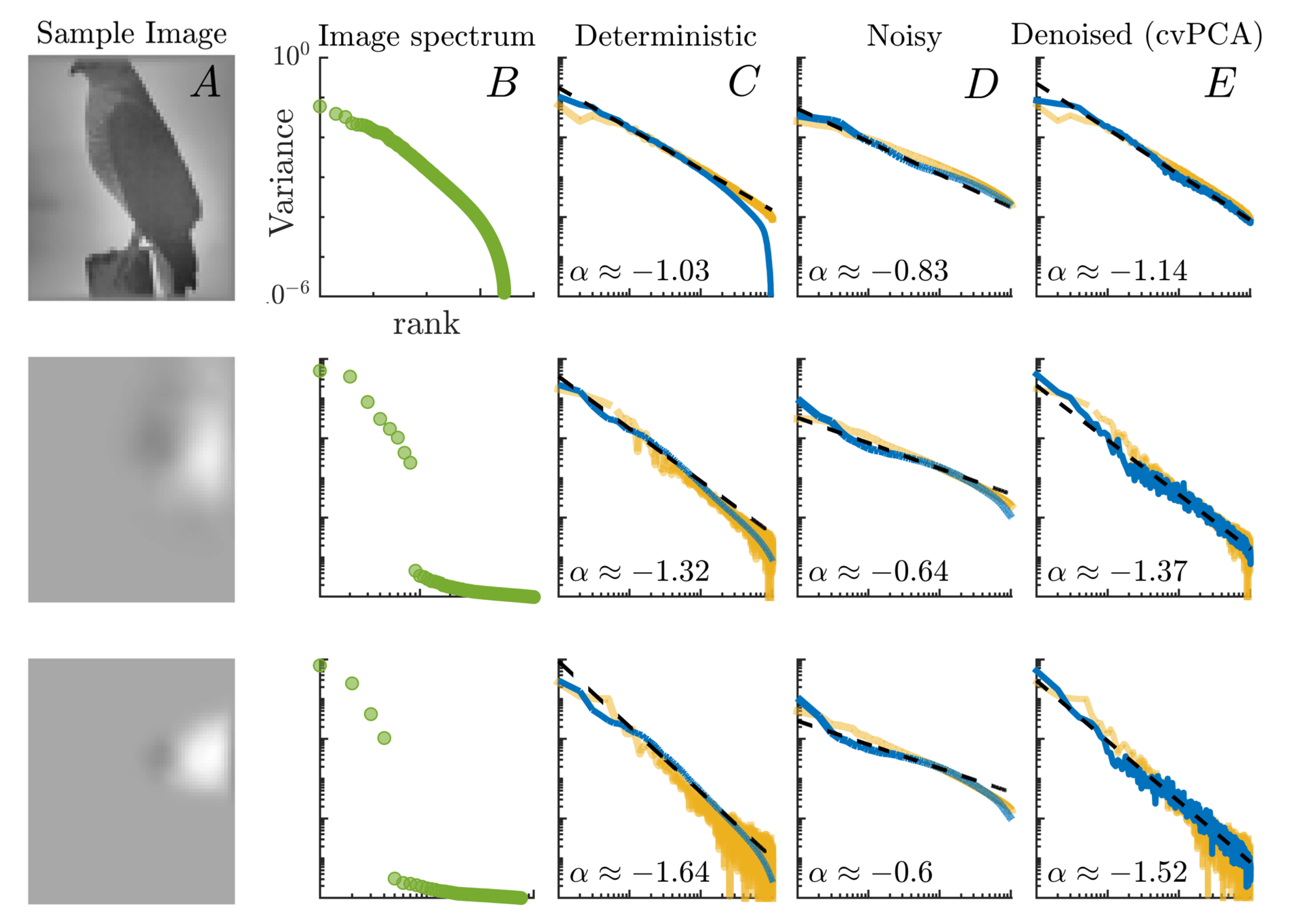
- First of all, as in the case of real neurons, the observed correlations between the internal units are not just a byproduct emerging from scale-free features of natural images (see the second column in Figure 3). In particular, one can see that the power-law decay of the covariance matrix eigenspectrum persists even in response to low-dimensional inputs whose embedding vector space can be spanned with just a few principal components (i.e., lacking a power-law decaying intrinsic spectrum).
- (ii)
- In our model, images are processed sequentially in time along their horizontal dimension so that for each image one can measure the activity of the N internal units over time steps. In contrast, the activity of V1 neurons [20] is scanned at a relatively low rate, so that for each image the neural representation is characterized by just one amplitude value in each neuron.
- (iii)
- To avoid confusion, let us remark that the covariance matrix observed by Stringer et al. is not directly measured over the raw activity of the neurons. Instead, the author’s first project out the network spontaneous activity from the data, and then perform a cross-validated PCA (see Materials and Methods) that allows them to filter out the trial-to-trial variability or “noise”. However, as our model is completely deterministic for a given initialization of an ESN, the stimulus-related variance computed through cvPCA trivially matches that of a standard PCA.
3.2. Solving a Benchmark Classification Task
4. Conclusions and Discussions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Ridge Regression
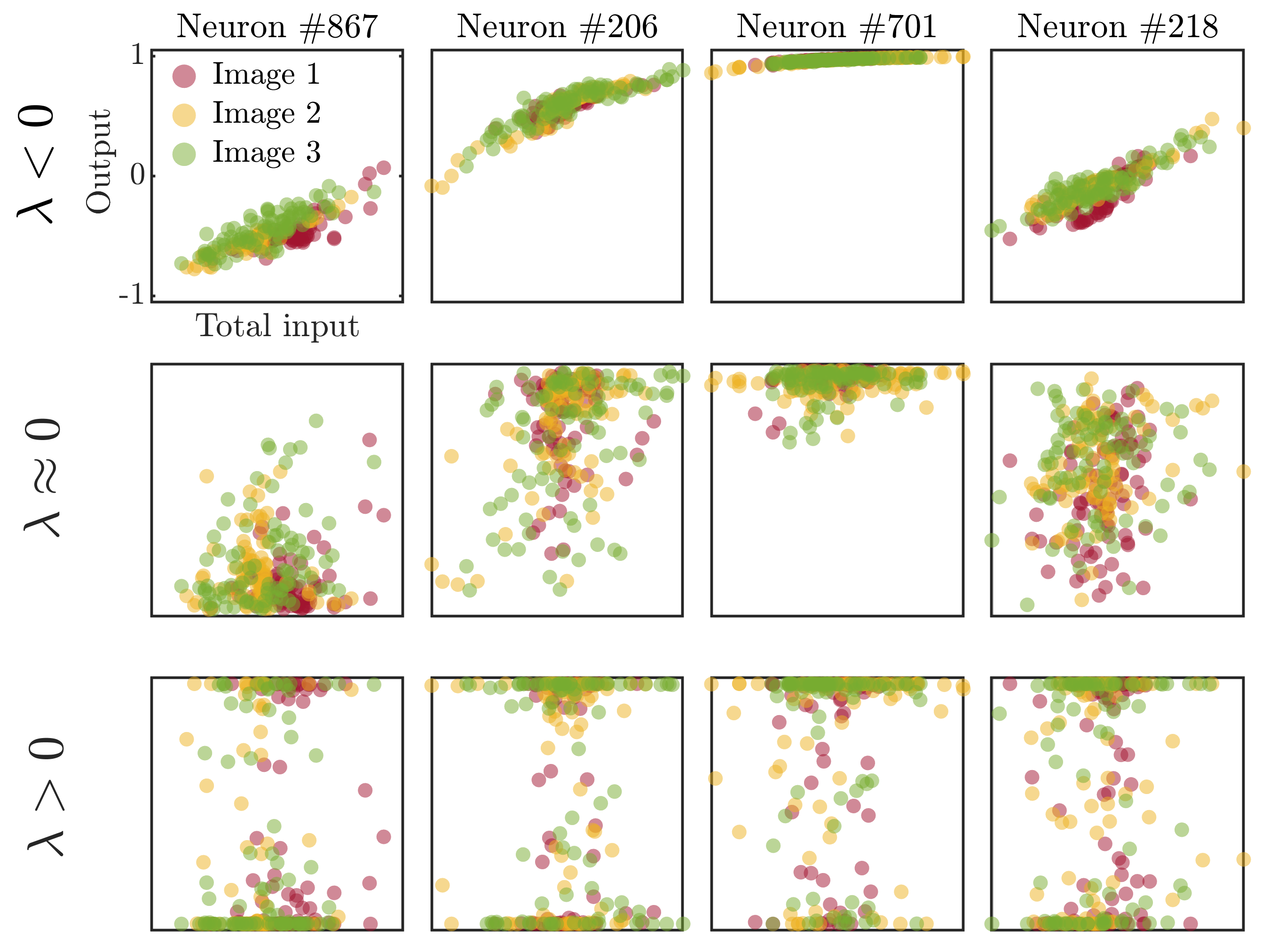
Appendix B. Phase Space of Reservoir Units
References
- Langton, C.G. Computation at the edge of chaos: Phase transitions and emergent computation. Phys. D Nonlinear Phenom. 1990, 42, 12–37. [Google Scholar] [CrossRef] [Green Version]
- Melanie, M. Dynamics, computation, and the “edge of chaos”: A reexamination. Complex. Metaphor. Model. Real. 1993, 19, 497–513. [Google Scholar]
- Muñoz, M.A. Colloquium: Criticality and Dynamical Scaling in Living Systems. Rev. Mod. Phys. 2018, 90, 031001. [Google Scholar] [CrossRef] [Green Version]
- Mora, T.; Bialek, W. Are biological systems poised at criticality? J. Stat. Phys. 2011, 144, 268–302. [Google Scholar] [CrossRef] [Green Version]
- Shew, W.L.; Plenz, D. The Functional Benefits of Criticality in the Cortex. Neuroscientist 2013, 19, 88–100. [Google Scholar] [CrossRef]
- Chialvo, D.R. Emergent complex neural dynamics. Nat. Phys. 2010, 6, 744–750. [Google Scholar] [CrossRef] [Green Version]
- Kinouchi, O.; Copelli, M. Optimal dynamical range of excitable networks at criticality. Nat. Phys. 2006, 2, 348–351. [Google Scholar] [CrossRef] [Green Version]
- Shriki, O.; Yellin, D. Optimal Information Representation and Criticality in an Adaptive Sensory Recurrent Neuronal Network. PLoS Comput. Biol. 2016, 12, e1004698. [Google Scholar] [CrossRef] [PubMed]
- Cocchi, L.; Gollo, L.L.; Zalesky, A.; Breakspear, M. Criticality in the brain: A synthesis of neurobiology, models and cognition. Prog. Neurobiol. 2017, 158, 132–152. [Google Scholar] [CrossRef] [Green Version]
- Shew, W.L.; Clawson, W.P.; Pobst, J.; Karimipanah, Y.; Wright, N.C.; Wessel, R. Adaptation to sensory input tunes visual cortex to criticality. Nat. Phys. 2015, 11, 659–663. [Google Scholar] [CrossRef] [Green Version]
- di Santo, S.; Villegas, P.; Burioni, R.; Muñoz, M.A. Landau–Ginzburg theory of cortex dynamics: Scale-free avalanches emerge at the edge of synchronization. Proc. Natl. Acad. Sci. USA 2018, 115, E1356–E1365. [Google Scholar] [CrossRef] [Green Version]
- Martinello, M.; Hidalgo, J.; Maritan, A.; di Santo, S.; Plenz, D.; Muñoz, M.A. Neutral theory and scale-free neural dynamics. Phys. Rev. X 2017, 7, 041071. [Google Scholar] [CrossRef] [Green Version]
- Dahmen, D.; Grün, S.; Diesmann, M.; Helias, M. Second type of criticality in the brain uncovers rich multiple-neuron dynamics. Proc. Natl. Acad. Sci. USA 2019, 116, 13051–13060. [Google Scholar] [CrossRef] [Green Version]
- Beggs, J.M.; Plenz, D. Neuronal Avalanches in Neocortical Circuits. J. Neurosci. 2003, 23, 11167–11177. [Google Scholar] [CrossRef] [Green Version]
- Petermann, T.; Thiagarajan, T.C.; Lebedev, M.A.; Nicolelis, M.A.; Chialvo, D.R.; Plenz, D. Spontaneous cortical activity in awake monkeys composed of neuronal avalanches. Proc. Natl. Acad. Sci. USA 2009, 106, 15921–15926. [Google Scholar] [CrossRef] [Green Version]
- Tagliazucchi, E.; Balenzuela, P.; Fraiman, D.; Chialvo, D.R. Criticality in large-scale brain fMRI dynamics unveiled by a novel point process analysis. Front. Physiol. 2012, 3, 15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, H.; Shew, W.L.; Roy, R.; Plenz, D. Maximal Variability of Phase Synchrony in Cortical Networks with Neuronal Avalanches. J. Neurosci. 2012, 32, 1061–1072. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Plenz, D.; Niebur, E. Criticality in Neural Systems; John Wiley & Sons: New York, NY, USA, 2014. [Google Scholar]
- Touboul, J.; Destexhe, A. Power-Law Statistics and Universal Scaling in the Absence of Criticality. Phys. Rev. E 2017, 95, 012413. [Google Scholar] [CrossRef] [Green Version]
- Stringer, C.; Pachitariu, M.; Steinmetz, N.; Carandini, M.; Harris, K.D. High-dimensional geometry of population responses in visual cortex. Nature 2019, 571, 361–365. [Google Scholar] [CrossRef]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards deep learning models resistant to adversarial attacks. arXiv 2017, arXiv:1706.06083. [Google Scholar]
- Nassar, J.; Sokol, P.A.; Chung, S.; Harris, K.D.; Park, I.M. On 1/n neural representation and robustness. arXiv 2020, arXiv:2012.04729. [Google Scholar]
- Jaeger, H. The “Echo State” Approach to Analysing and Training Recurrent Neural Networks-with an Erratum Note’; GMD Technical Report; German National Research Center for Information Technology: Bonn, Germany, 2001; Volume 148. [Google Scholar]
- Maass, W. Liquid state machines: Motivation, theory, and applications. In Computability in Context: Computation and Logic in the Real World; Imperial College Press: London, UK, 2011; pp. 275–296. [Google Scholar]
- Maass, W.; Natschläger, T.; Markram, H. Real-Time Computing without Stable States: A New Framework for Neural Computation Based on Perturbations. Neural Comput. 2002, 14. [Google Scholar] [CrossRef] [PubMed]
- Lukoševičius, M.; Jaeger, H. Reservoir computing approaches to recurrent neural network training. Comput. Sci. Rev. 2009, 3, 127–149. [Google Scholar] [CrossRef]
- Jaeger, H.; Haas, H. Harnessing Nonlinearity: Predicting Chaotic Systems and Saving Energy in Wireless Communication. Science 2004, 304, 78–80. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reinhart, R.F.; Steil, J.J. A Constrained Regularization Approach for Input-Driven Recurrent Neural Networks. Differ. Equ. Dyn. Syst. 2010, 19, 27–46. [Google Scholar] [CrossRef]
- Reinhart, R.F.; Steil, J.J. Reservoir Regularization Stabilizes Learning of Echo State Networks with Output Feedback. In Proceedings of the ESANN 2011 Proceedings, European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning, Bruges, Belgium, 27–29 April 2011. [Google Scholar]
- Babinec, S.; Pospíchal, J. Merging Echo State and Feedforward Neural Networks for Time Series Forecasting. In Artificial Neural Networks—ICANN 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 367–375. [Google Scholar] [CrossRef]
- Bianchi, F.M.; Scardapane, S.; Løkse, S.; Jenssen, R. Reservoir Computing Approaches for Representation and Classification of Multivariate Time Series. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 2169–2179. [Google Scholar] [CrossRef]
- Lukoševičius, M. A Practical Guide to Applying Echo State Networks. In Neural Networks: Tricks of the Trade: Second Edition; Montavon, G., Orr, G.B., Müller, K.R., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; pp. 659–686. [Google Scholar] [CrossRef]
- Morales, G.B.; Mirasso, C.R.; Soriano, M.C. Unveiling the role of plasticity rules in reservoir computing. arXiv 2021, arXiv:2101.05848. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Li, F.-F. ImageNet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar] [CrossRef] [Green Version]
- Stringer, C.; Pachitariu, M.; Carandini, M.; Harris, K. Recordings of 10,000 neurons in visual cortex in response to 2800 natural images. Figshare Repos. 2018. [Google Scholar] [CrossRef]
- Shlens, J. A Tutorial on Principal Component Analysis. arXiv 2014, arXiv:1404.1100. [Google Scholar]
- Clauset, A.; Shalizi, C.R.; Newman, M.E. Power-law distributions in empirical data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef] [Green Version]
- Jaeger, H. Short Term Memory in Echo State Networks; GMD-Report 152; German National Research Center for Information Techonology: Bremen, Germany, 2001. [Google Scholar]
- Yildiz, I.B.; Jaeger, H.; Kiebel, S.J. Re-visiting the echo state property. Neural Netw. 2012, 35, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Buehner, M.; Young, P. A tighter bound for the echo state property. IEEE Trans. Neural Netw. 2006, 17, 820–824. [Google Scholar] [CrossRef] [PubMed]
- Gallicchio, C. Chasing the Echo State Property. arXiv 2018, arXiv:1811.10892. [Google Scholar]
- Manjunath, G.; Jaeger, H. Echo State Property Linked to an Input: Exploring a Fundamental Characteristic of Recurrent Neural Networks. Neural Comput. 2013, 25, 671–696. [Google Scholar] [CrossRef] [PubMed]
- Boedecker, J.; Obst, O.; Lizier, J.T.; Mayer, N.M.; Asada, M. Information Processing in Echo State Networks at the Edge of Chaos. Theory Biosci. 2011, 131. [Google Scholar] [CrossRef]
- Sprott, J.C. Chaos and Time-Series Analysis; Oxford University Press: Oxford, UK, 2003; Google-Books-ID: SEDjdjPZ158C. [Google Scholar]
- Crutchfield, J.P.; Young, K. Computation at the Onset of Chaos; The Santa Fe Institute, Westview Press: Boulder, CO, USA, 1988; pp. 223–269. [Google Scholar]
- Bertschinger, N.; Natschläger, T. Real-Time Computation at the Edge of Chaos in Recurrent Neural Networks. Neural Comput. 2004, 16, 1413–1436. [Google Scholar] [CrossRef]
- Legenstein, R.; Maass, W. Edge of chaos and prediction of computational performance for neural circuit models. Neural Netw. 2007, 20, 323–334. [Google Scholar] [CrossRef]
- Büsing, L.; Schrauwen, B.; Legenstein, R. Connectivity, dynamics, and memory in reservoir computing with binary and analog neurons. Neural Comput. 2010, 22, 1272–1311. [Google Scholar] [CrossRef]
- Schaetti, N.; Salomon, M.; Couturier, R. Echo State Networks-Based Reservoir Computing for MNIST Handwritten Digits Recognition. In Proceedings of the 2016 IEEE Intl Conference on Computational Science and Engineering (CSE) and IEEE Intl Conference on Embedded and Ubiquitous Computing (EUC) and 15th Intl Symposium on Distributed Computing and Applications for Business Engineering (DCABES), Paris, France, 24–26 August 2016; pp. 484–491. [Google Scholar] [CrossRef] [Green Version]
- Skowronski, M.D.; Harris, J.G. Automatic Speech Recognition Using a Predictive Echo State Network Classifier. Neural Netw. 2007, 20. [Google Scholar] [CrossRef]
- Aswolinskiy, W.; Reinhart, R.F.; Steil, J. Time Series Classification in Reservoir- and Model-Space: A Comparison. In Artificial Neural Networks in Pattern Recognition; Schwenker, F., Abbas, H.M., El Gayar, N., Trentin, E., Eds.; Springer International Publishing: Cham, Switzerland, 2016; Lecture Notes in Computer Science; pp. 197–208. [Google Scholar] [CrossRef]
- Ma, Q.; Shen, L.; Chen, W.; Wang, J.; Wei, J.; Yu, Z. Functional echo state network for time series classification. Inf. Sci. 2016, 373, 1–20. [Google Scholar] [CrossRef]
- Yusoff, M.H.; Chrol-Cannon, J.; Jin, Y. Modeling Neural Plasticity in Echo State Networks for Classification and Regression. Inf. Sci. 2016, 364–365. [Google Scholar] [CrossRef]
- Jalalvand, A.; Demuynck, K.; Neve, W.D.; Walle, R.; Martens, J. Design of reservoir computing systems for noise-robust speech and handwriting recognition. In Proceedings of the 28th Conference on Graphics, Patterns and Images (accepted in the Workshop of Theses and Dissertations (WTD)), Sociedade Brasileira de Computaçao, Salvador, Brazil, 26–29 August 2015. [Google Scholar]
- Clemson, P.T.; Stefanovska, A. Discerning non-autonomous dynamics. Phys. Rep. 2014, 542, 297–368. [Google Scholar] [CrossRef] [Green Version]
- Gandhi, M.; Tiño, P.; Jaeger, H. Theory of Input Driven Dynamical Systems. In Proceedings of the ESANN 2012: 20th European Symposium on Artificial Neural Networks, Bruges, Belgium, 25–27 April 2012. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morales, G.B.; Muñoz, M.A. Optimal Input Representation in Neural Systems at the Edge of Chaos. Biology 2021, 10, 702. https://doi.org/10.3390/biology10080702
Morales GB, Muñoz MA. Optimal Input Representation in Neural Systems at the Edge of Chaos. Biology. 2021; 10(8):702. https://doi.org/10.3390/biology10080702
Chicago/Turabian StyleMorales, Guillermo B., and Miguel A. Muñoz. 2021. "Optimal Input Representation in Neural Systems at the Edge of Chaos" Biology 10, no. 8: 702. https://doi.org/10.3390/biology10080702
APA StyleMorales, G. B., & Muñoz, M. A. (2021). Optimal Input Representation in Neural Systems at the Edge of Chaos. Biology, 10(8), 702. https://doi.org/10.3390/biology10080702





