Numerical Method for Coupled Nonlinear Schrödinger Equations in Few-Mode Fiber
Abstract
:1. Introduction
2. Computing Method for Complex Envelopes of Optical Wave Calculation
2.1. CNSES for Few Modes in Dimensionless Form
2.2. The Finite-Difference Scheme and Computing Scheme
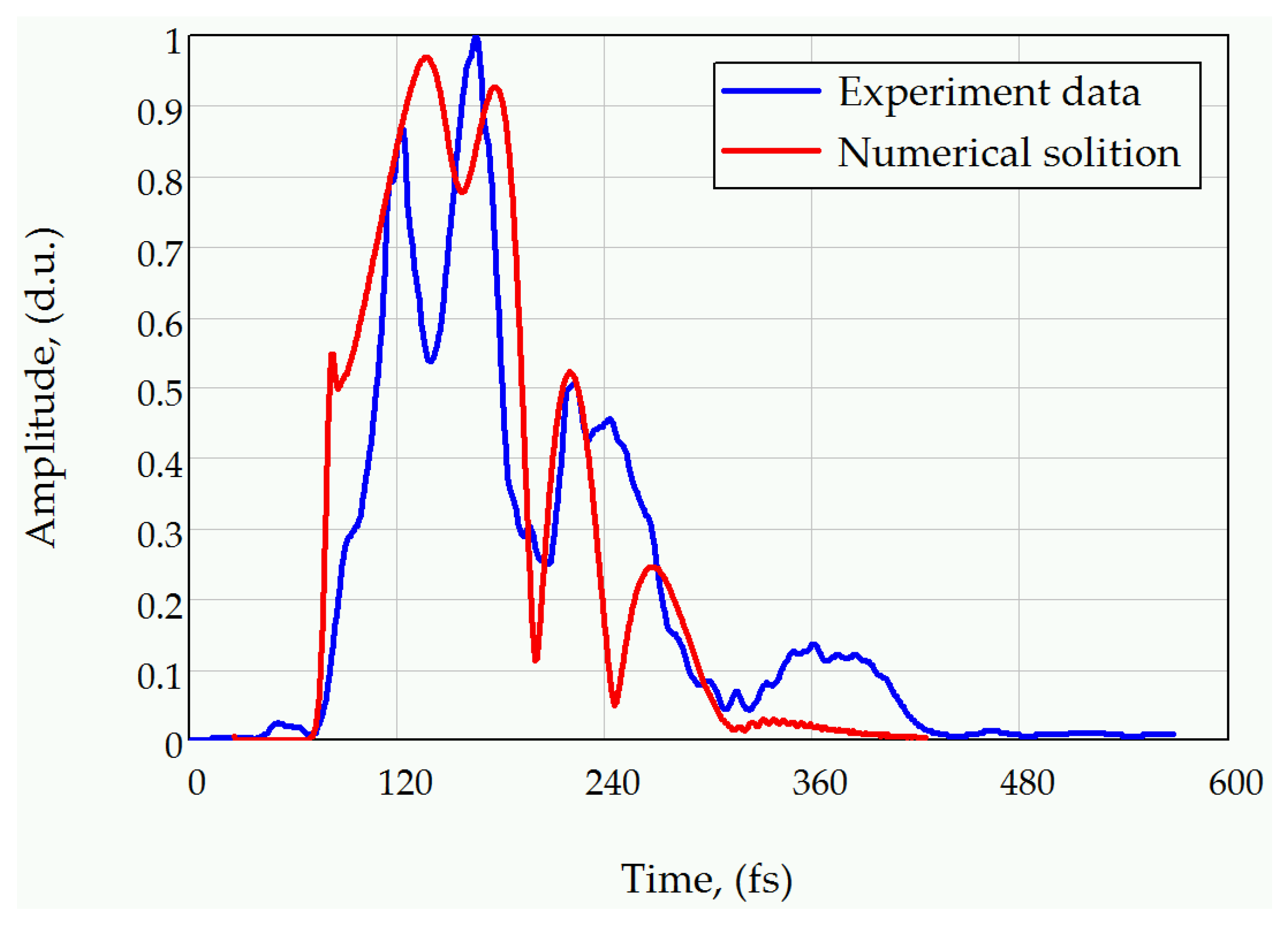
2.3. The Ultra-Short Pulse Evolution in Fiber
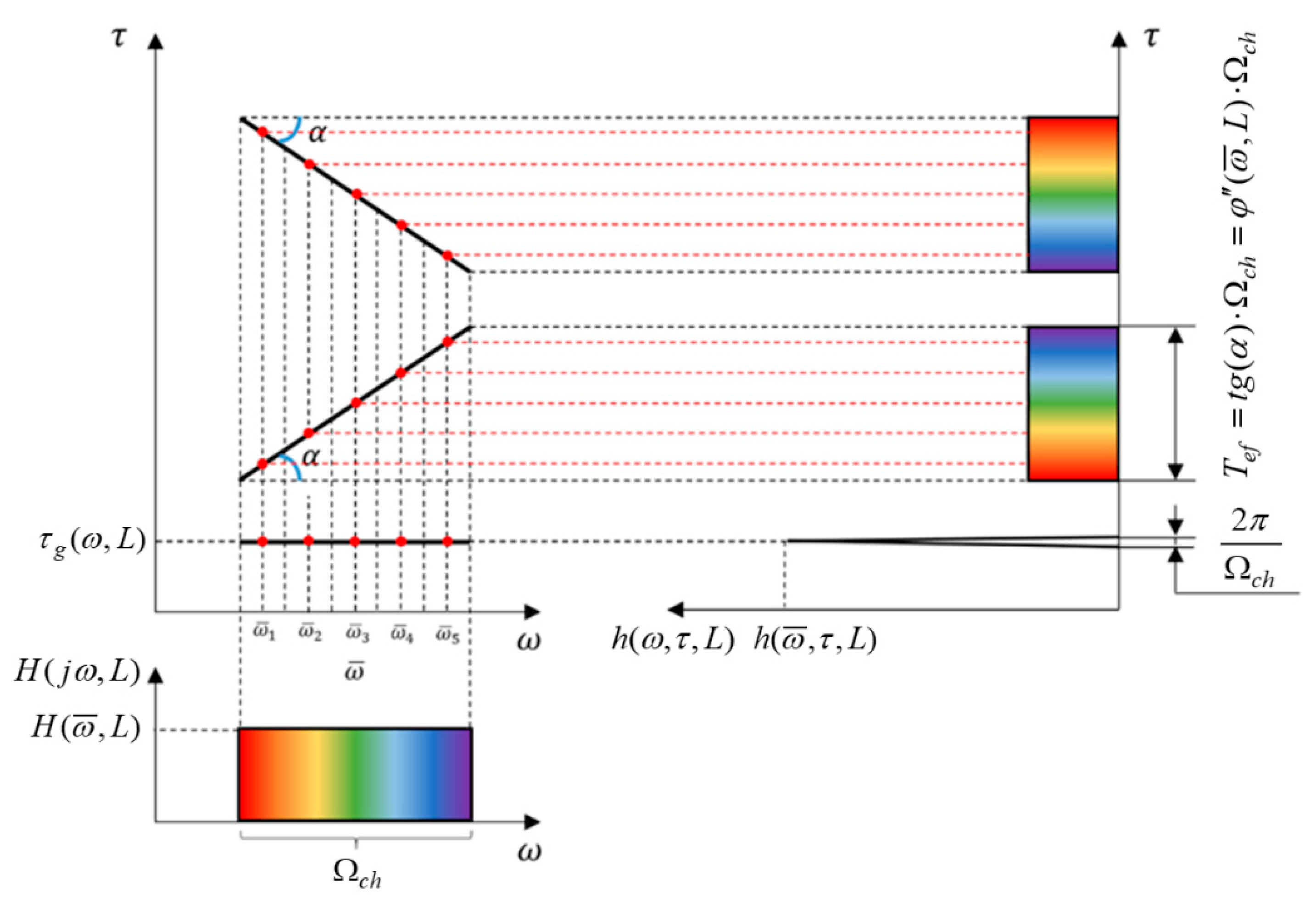
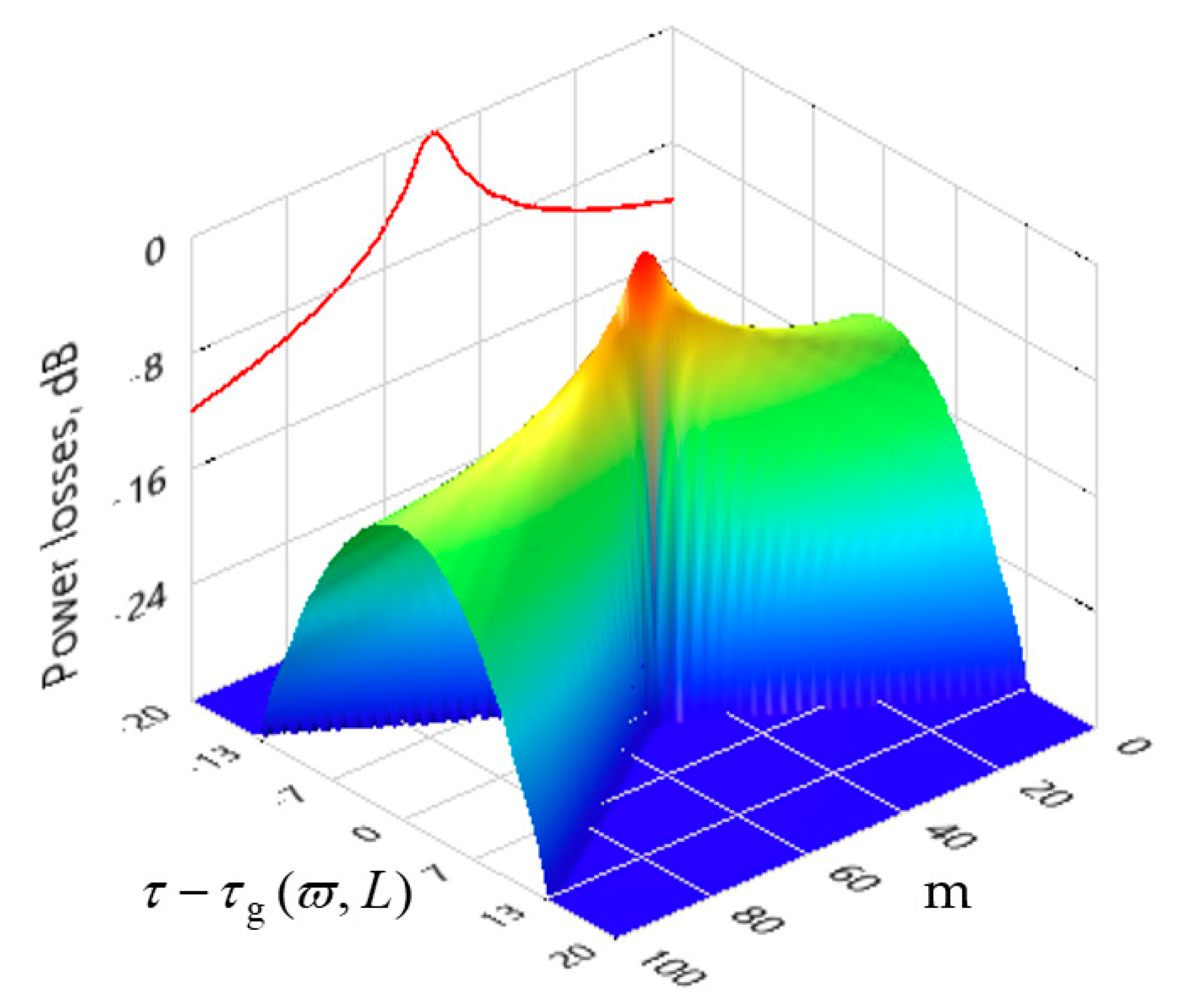
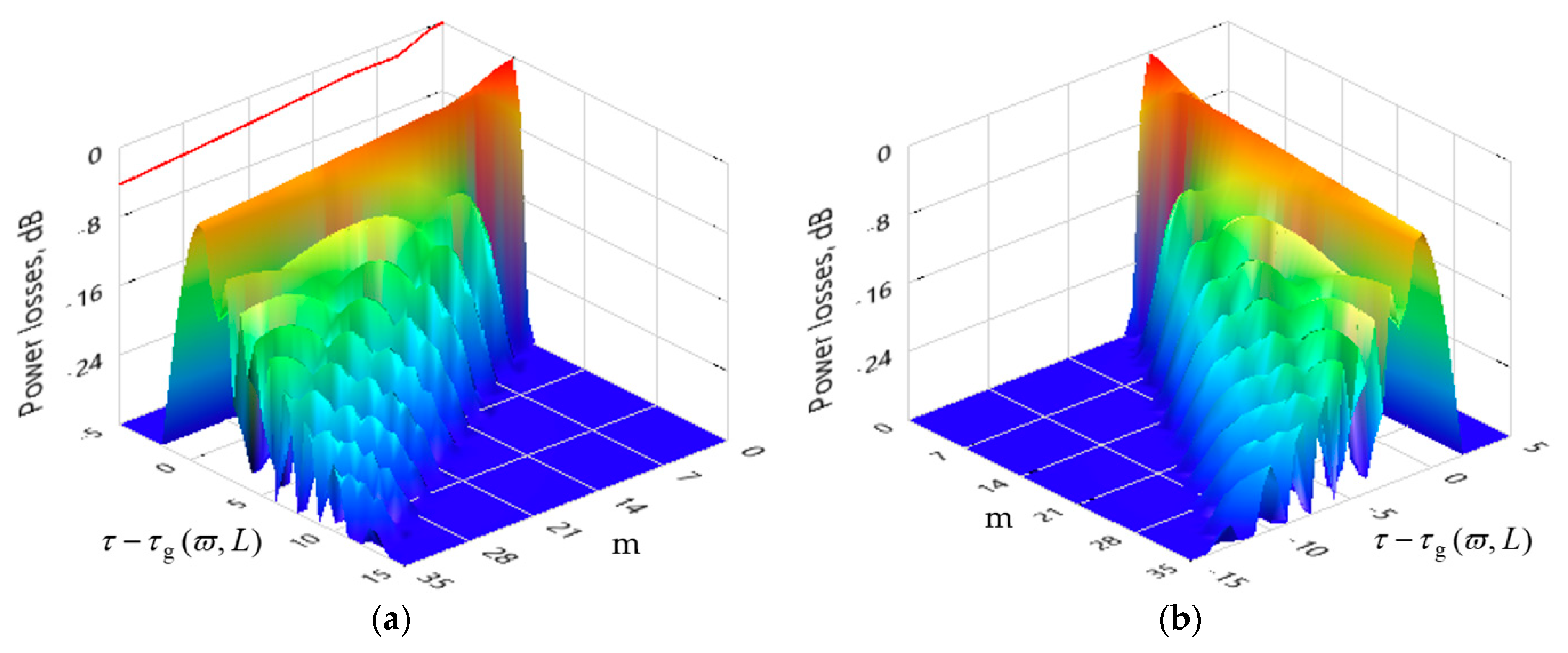
3. The Phase Velocity or Phase Delay Calculation during the Wave Propagation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sakhabutdinov, A.Z.; Anfinogentov, V.I.; Morozov, O.G.; Burdin, V.A.; Bourdine, A.V.; Gabdulkhakov, I.M.; Kuznetsov, A.A. Original Solution of Coupled Non-linear Schrödinger Equations for Simulation of Ultrashort Optical Pulse Propagation in a Birefringent Fiber. Fibers 2020, 8, 34. [Google Scholar] [CrossRef]
- Samad, R.; Courrol, L.; Baldochi, S.; Vieira, N. Ultrashort Laser Pulses Applications, Coherence and Ultrashort Pulse Laser Emission; Duarte, F.J., Ed.; IntechOpen: London, UK, 2010; pp. 663–688. [Google Scholar] [CrossRef] [Green Version]
- Sugioka, K.; Cheng, Y. Ultrafast lasers—Reliable tools for advanced materials processing. Light Sci. Appl. 2014, 3, e149. [Google Scholar] [CrossRef]
- Sugioka, K. Progress in ultrafast laser processing and future prospects. Nanophotonics 2017, 6, 393–413. [Google Scholar] [CrossRef] [Green Version]
- Hodgson, N.; Laha, M. Industrial Femtosecond Lasers and Material Processing; Industrial Laser Solutions, PennWell Publishing: Tulsa, OK, USA, 2019. [Google Scholar]
- Göbel, W.; Nimmerjahn, A.; Helmchen, F. Distortion-free delivery of nanojoule femtosecond pulses from a Ti:sapphire laser through a hollow-core photonic crystal fiber. Opt. Lett. 2004, 29, 1285–1287. [Google Scholar] [CrossRef] [PubMed]
- Michieletto, M.; Lyngsø, J.K.; Jakobsen, C.; Lægsgaard, J.; Bang, O.; Alkeskjold, T.T. Hollow-core fibers for high power pulse delivery. Opt. Express 2016, 24, 7103–7119. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sakhabutdinov, A.Z.; Anfinogentov, V.I.; Morozov, O.G.; Gubaidullin, R.R. Numerical approaches to solving a nonlinear system of Schrödinger equations for wave propagation in an optical fiber. Comput. Technol. 2020, 25, 42–54. [Google Scholar] [CrossRef]
- Karasawa, N.; Nakamura, S.; Morita, R.; Shigekawa, H.; Yamashita, M. Comparison between theory and experiment of non-linear propagation for 4.5-cycle optical pulses in a fused-silica fiber. Nonlinear Opt. 2000, 24, 133–138. [Google Scholar]
- Nakamura, S.; Li, L.; Karasawa, N.; Morita, R.; Shigekawa, H.; Yamashita, M. Measurements of Third-Order Dispersion Effects for Generation of High-Repetition-Rate, Sub-Three-Cycle Transform-Limited Pulses from a Glass Fiber. Jpn. J. Appl. Phys. 2002, 41, 1369–1373. [Google Scholar] [CrossRef] [Green Version]
- Nakamura, S.; Koyamada, Y.; Yoshida, N.; Karasawa, N.; Sone, H.; Ohtani, M.; Mizuta, Y.; Morita, R.; Shigekawa, H.; Yamashita, M. Finite-difference time-domain calculation with all parameters of Sellmeier’s fitting equation for 12-fs laser pulse propagation in a silica fiber. IEEE Photonics Technol. Lett. 2002, 14, 480–482. [Google Scholar] [CrossRef] [Green Version]
- Nakamura, S.; Takasawa, N.; Koyamada, Y. Comparison between finite-difference time-domain calculation with all parameters of Sellmeier’s fitting equation and experimental results for slightly chirped 12-fs laser pulse propagation in a silica fiber. J. Light. Technol. 2005, 23, 855–863. [Google Scholar] [CrossRef]
- Nakamura, S.; Takasawa, N.; Koyamada, Y.; Sone, H.; Xu, L.; Morita, R.; Yamashita, M. Extended Finite Difference Time Domain Analysis of Induced Phase Modulation and Four-Wave Mixing between Two-Color Femtosecond Laser Pulses in a Silica Fiber with Different Initial Delays. Jpn. J. Appl. Phys. 2005, 44, 7453–7459. [Google Scholar] [CrossRef]
- Nakamura, S. Comparison between Finite-Difference Time-Domain Method and Experimental Results for Femtosecond Laser Pulse Propagation. Coherence Ultrashort Pulse Laser Emiss. 2010, 442–449. [Google Scholar] [CrossRef] [Green Version]
- Burdin, V.A.; Bourdine, A.V. Simulation results of optical pulse non-linear few-mode propagation over optical fiber. Appl. Photonics 2016, 3, 309–320. (In Russian) [Google Scholar] [CrossRef]
- Burdin, V.A.; Bourdine, A.V. Model for a few-mode nonlinear propagation of optical pulse in multimode optical fiber. In Proceedings of the OWTNM, Warsaw, Poland, 20–21 May 2016. [Google Scholar]
- Ivanov, V.A.; Ivanov, D.V.; Ryabova, N.V.; Ryabova, M.I.; Chernov, A.A.; Ovchinnikov, V.V. Studying the Parameters of Frequency Dispersion for Radio Links of Different Length Using Software-Defined Radio Based Sounding System. Radio Sci. 2019, 54, 34–43. [Google Scholar] [CrossRef] [Green Version]
- Agrawal, G.P. Nonlinear Fiber Optics, 4th ed.; Academic Press: San Diego, CA, USA, 2006. [Google Scholar]
- Xiao, Y.; Maywar, D.N.; Agrawal, G.P. New approach to pulse propagation in nonlinear dispersive optical media. J. Opt. Soc. Am. B 2012, 29, 2958–2963. [Google Scholar] [CrossRef]
- Ivanov, D.V. Methods and Mathematical Models for Studying Propagation of Spread Spectrum Signals in the Ionosphere and Correction for Their Dispersion Distortions: Monograph; MarSTU: Yoshkar-Ola, Russia, 2006; 268p. (In Russian) [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakhabutdinov, A.Z.; Anfinogentov, V.I.; Morozov, O.G.; Burdin, V.A.; Bourdine, A.V.; Kuznetsov, A.A.; Ivanov, D.V.; Ivanov, V.A.; Ryabova, M.I.; Ovchinnikov, V.V.; et al. Numerical Method for Coupled Nonlinear Schrödinger Equations in Few-Mode Fiber. Fibers 2021, 9, 1. https://doi.org/10.3390/fib9010001
Sakhabutdinov AZ, Anfinogentov VI, Morozov OG, Burdin VA, Bourdine AV, Kuznetsov AA, Ivanov DV, Ivanov VA, Ryabova MI, Ovchinnikov VV, et al. Numerical Method for Coupled Nonlinear Schrödinger Equations in Few-Mode Fiber. Fibers. 2021; 9(1):1. https://doi.org/10.3390/fib9010001
Chicago/Turabian StyleSakhabutdinov, Airat Zh., Vladimir I. Anfinogentov, Oleg G. Morozov, Vladimir A. Burdin, Anton V. Bourdine, Artem A. Kuznetsov, Dmitry V. Ivanov, Vladimir A. Ivanov, Maria I. Ryabova, Vladimir V. Ovchinnikov, and et al. 2021. "Numerical Method for Coupled Nonlinear Schrödinger Equations in Few-Mode Fiber" Fibers 9, no. 1: 1. https://doi.org/10.3390/fib9010001
APA StyleSakhabutdinov, A. Z., Anfinogentov, V. I., Morozov, O. G., Burdin, V. A., Bourdine, A. V., Kuznetsov, A. A., Ivanov, D. V., Ivanov, V. A., Ryabova, M. I., Ovchinnikov, V. V., & Gabdulkhakov, I. M. (2021). Numerical Method for Coupled Nonlinear Schrödinger Equations in Few-Mode Fiber. Fibers, 9(1), 1. https://doi.org/10.3390/fib9010001







