Estimation of the Effects of the Cross-Head Speed and Temperature on the Mechanical Strength of Kenaf Bast Fibers Using Weibull and Monte-Carlo Statistics
Abstract
1. Introduction
2. Experimental Methods
2.1. Cultivation and Extraction of Kenaf
2.2. Materials
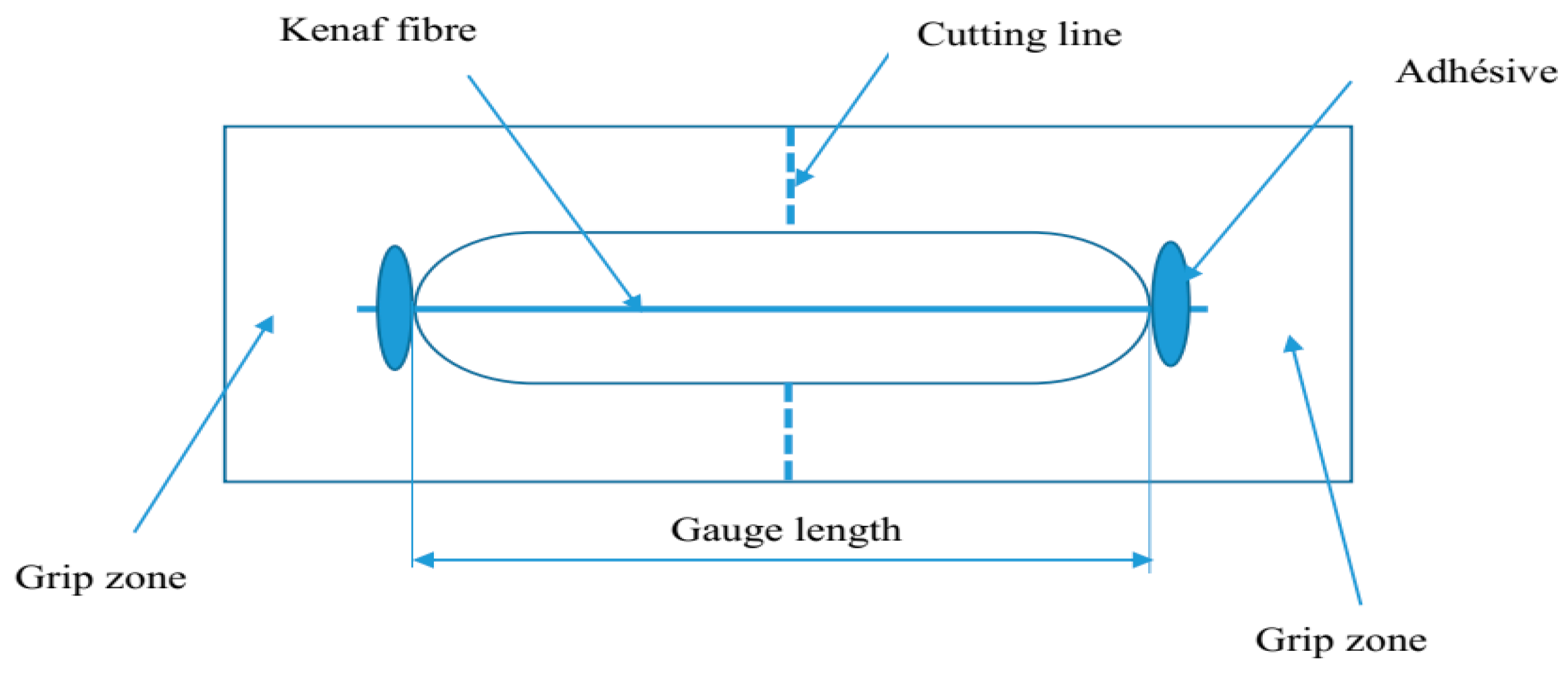
2.3. Tensile Strength of Kenaf Fibers and Heat Treatment
3. Statistical Analysis
3.1. Two-Parameters Weibull Distribution Model
3.2. Monte-Carlo Simulation
4. Results and Discussion
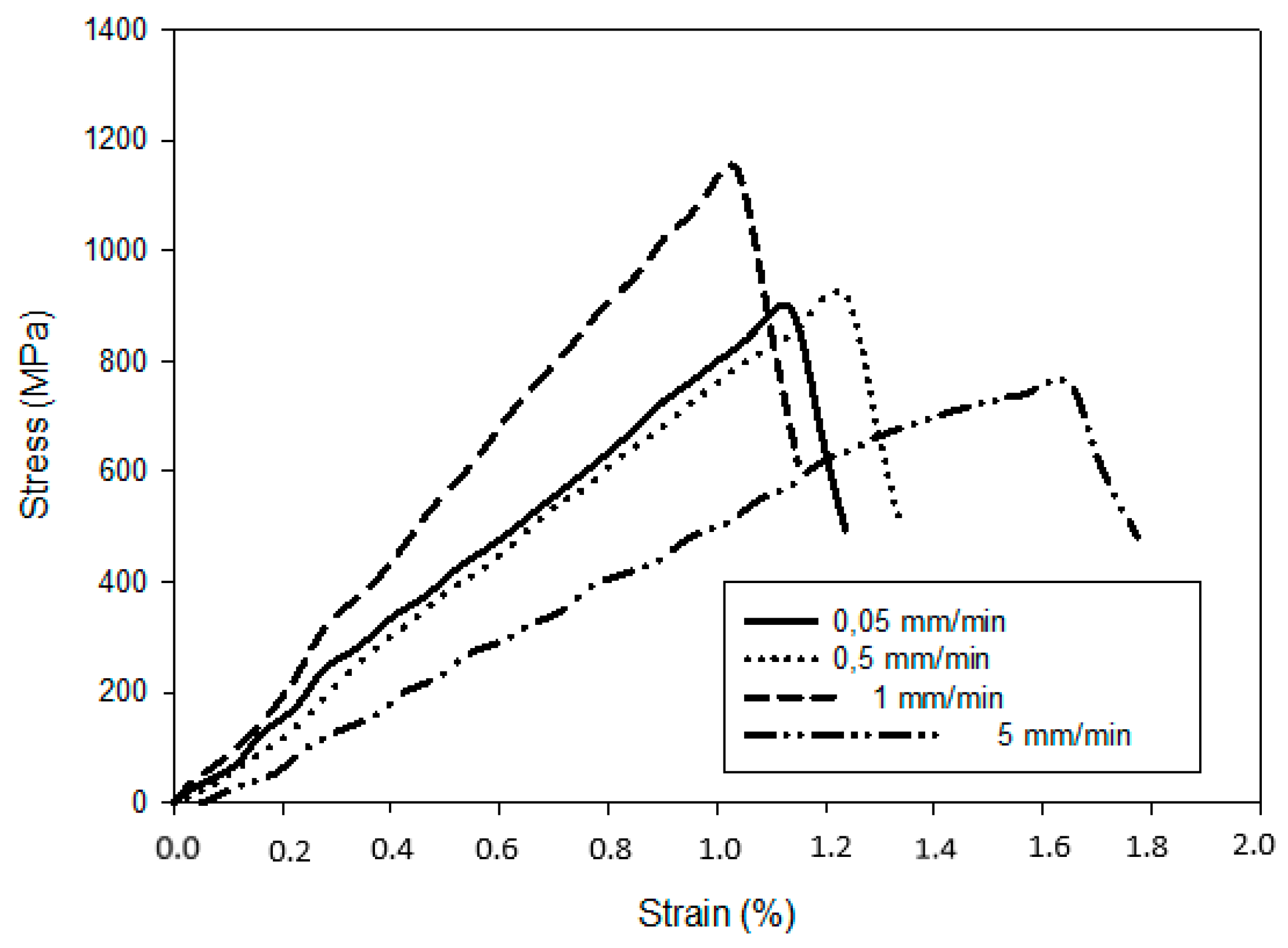
4.1. Influence of the Cross-Head Speed
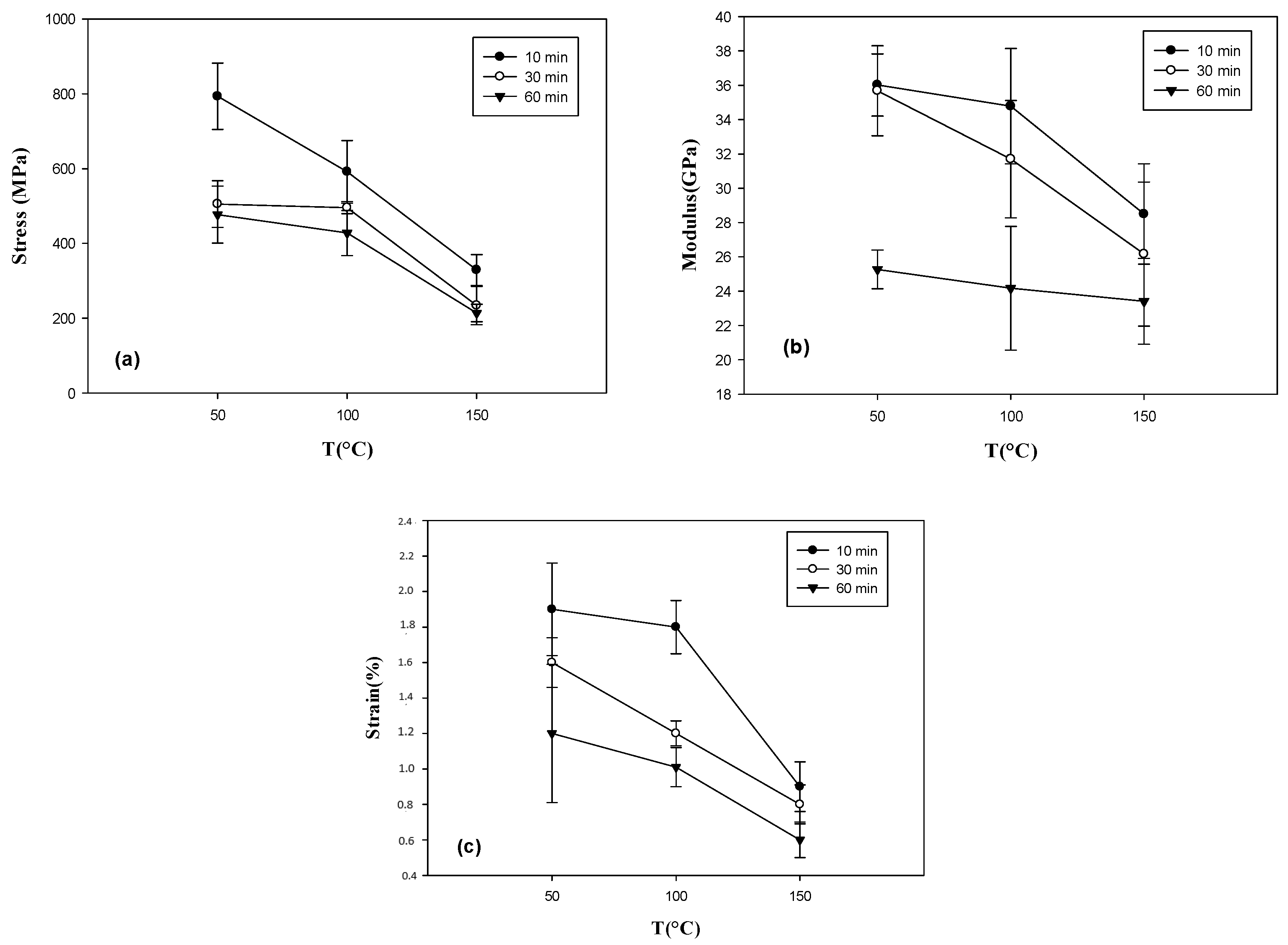
4.2. Temperature Dependence
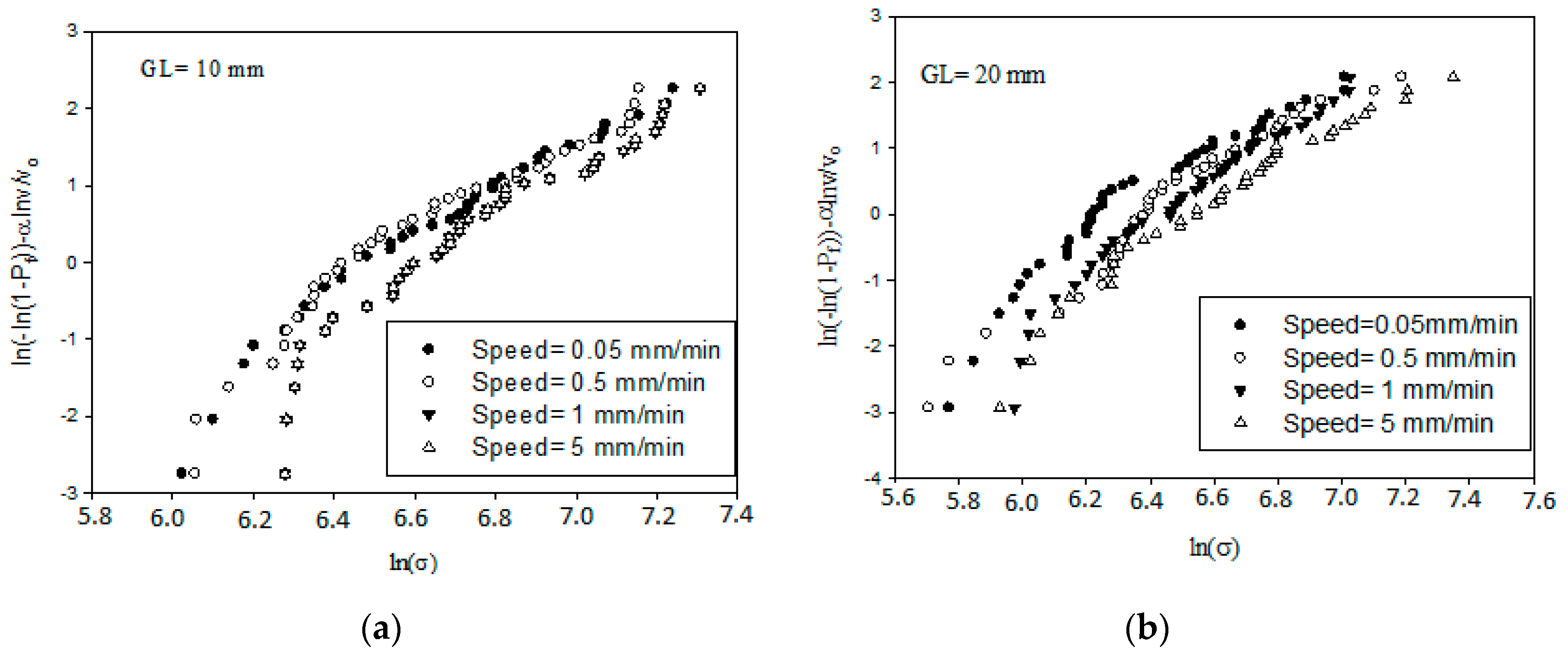
4.3. Two-Parameter Weibull Distribution Model
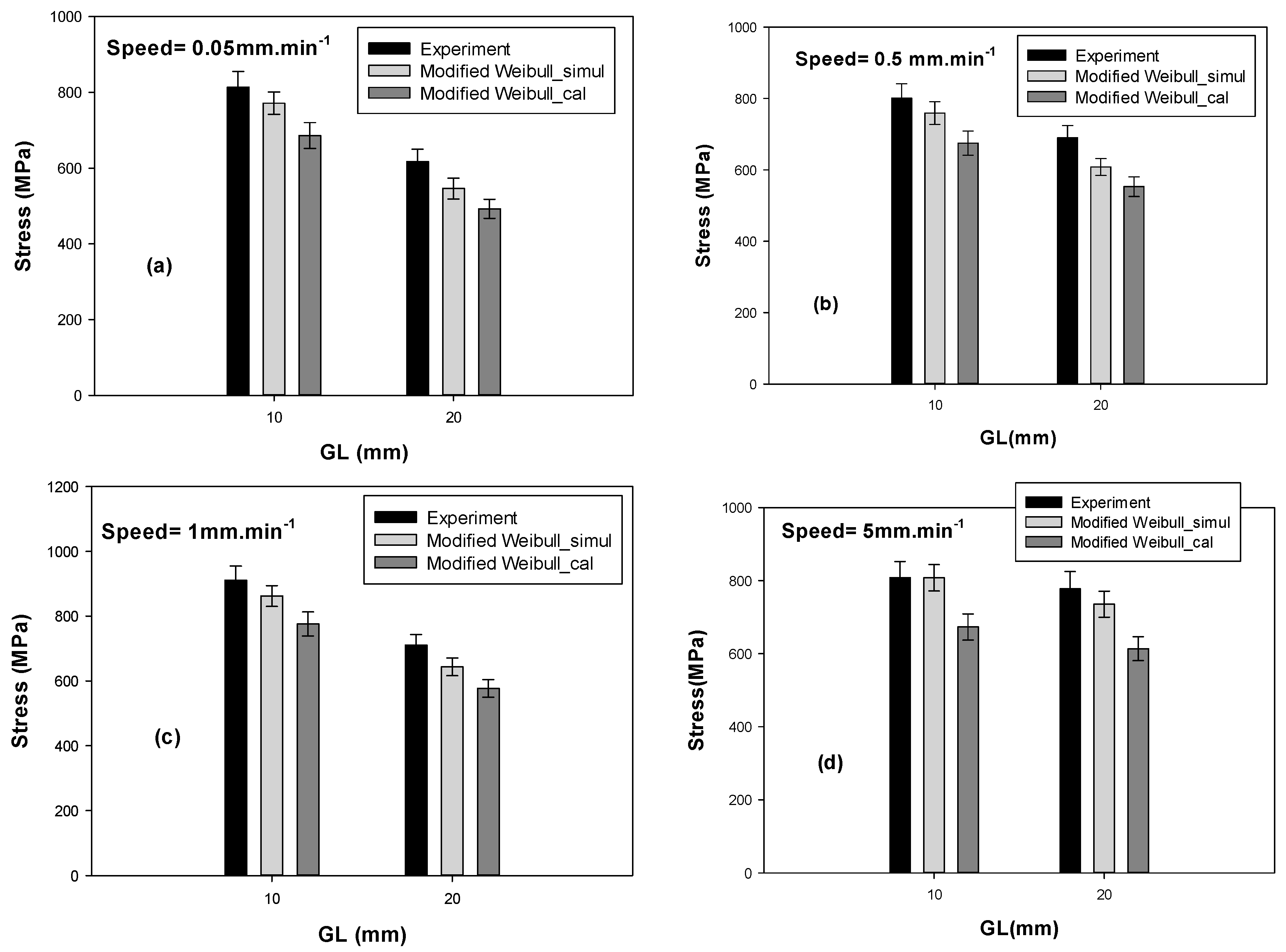
4.4. Monte-Carlo Simulation Results of the Tensile Strength
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Oksman, K.; Aitomäki, Y.; Mathew, A.P.; Siqueira, G.; Zhou, Q.; Butylina, S.; Tanpichai, S.; Zhou, X.; Hooshmand, S. Review of the recent developments in cellulose nanocomposite processing. Compos. Part A Appl. Sci. Manuf. 2016, 83, 2–18. [Google Scholar] [CrossRef]
- Pickering, K.L.; Efendy, M.G.A.; Le, T.M. A review of recent developments in natural fiber composites and their mechanical performance. Compos. Part A Appl. Sci. Manuf. 2016, 83, 98–112. [Google Scholar] [CrossRef]
- Madhu, P.; Sanjay, M.R.; Senthamaraikannan, P.; Pradeep, S.; Saravanakumar, S.S.; Yogesha, B. A review on synthesis and characterization of commercially available natural fibers: Part-I. J. Nat. Fibers 2018, 1–13. [Google Scholar] [CrossRef]
- Anuar, H.; Zuraida, A. Improvement in mechanical properties of reinforced thermoplastic elastomer composite with kenaf bast fiber. Compos. Part B 2011, 42, 462–465. [Google Scholar] [CrossRef]
- Akil, H.M.; Omar, M.F.; Mazuki, A.A.M.; Safiee, S.; Ishak, Z.A.M.; Bakar, A.A. Kenaf fiber reinforced composites: A review. Mater. Des. 2011, 32, 4107–4121. [Google Scholar] [CrossRef]
- Nishino, T.; Hirao, K.; Kotera, M.; Nakamae, K.; Inagaki, H. Kenaf reinforced biodegradable composite. Compos. Sci. Technol. 2003, 63, 1281–1286. [Google Scholar] [CrossRef]
- Shibata, S.; Cao, Y.; Fukumoto, I. Lightweight laminate composites made from kenaf and polypropylene fibers. Polym. Test. 2006, 25, 142–148. [Google Scholar] [CrossRef]
- Saaidia, A.; Bezazi, A.; Belbeh, A.; Zanache, N.; Scarpa, F. Characterization of Jute/Polyester Bio-Composites by the Use of Weibull’s Statistical Method and Anova Analysis of Variance. In French Congress of Mechanics, 22nd ed.; AFM, Association Française de Mécanique: Besancon, France, 2015; pp. 1–8. Available online: http://hdl.handle.net/2042/57504 (accessed on 20 September 2019).
- Elsaid, A.; Dawood, M.; Seracino, R.; Bobko, C. Mechanical properties of kenaf fiber reinforced concrete. Constr. Build. Mater. 2011, 25, 1991–2001. [Google Scholar] [CrossRef]
- Bharath, V.R.R.; Ramnath, B.V.; Manoharan, N. Kenaf Fibre Reinforced Composites: A Review. ARPN J. Eng. Applies Sci. 2015, 10, 5483–5485. [Google Scholar] [CrossRef]
- Ochi, S. Mechanical properties of kenaf fibers and kenaf/PLA composites. Mech. Mater. 2008, 40, 446–452. [Google Scholar] [CrossRef]
- Salleh, F.M.; Hassan, A.; Yahya, R.; Azzahari, A.D. Effects of extrusion temperature on the rheological, dynamic mechanical and tensile properties of kenaf fiber/HDPE composites. Compos. Part B Eng. 2014, 58, 259–266. [Google Scholar] [CrossRef]
- Baley, C. Analysis of the flax fibers tensile behavior and analysis of the tensile stiffness increase. Compos. Part A Appl. Sci. Manuf. 2002, 33, 939–948. [Google Scholar] [CrossRef]
- Fan, M. Characterization and Performance of Elementary Hemp Fiber: Factors influencing Tensile Strength. BioRessources 2010, 5, 2307–2322. [Google Scholar]
- Wang, F.; Shao, J. Modified Weibull distribution for analyzing the tensile strength of bamboo fibers. Polymers 2014, 6, 3005–3018. [Google Scholar] [CrossRef]
- Shahzad, A. A Study in Physical and Mechanical Properties of Hemp Fibers. Adv. Mater. Sci. Eng. 2013, 2013, 325085. [Google Scholar] [CrossRef]
- Cisse, O. Characterization of the Hygro-Mechanical Behavior of Elementary Bast Fibers from Hemp. Ph.D. Thesis, University of Franche-Comté, Besancon, France, 2014. [Google Scholar]
- Ntenga, R. Multi-Scale Modeling and Characterization of the Elastic Anisotropy of Plant Fibers Used in Reinforcing Composite Materials. Ph.D. Thesis, Blaise Pascal University, Auvergne, France, 2007. [Google Scholar]
- Negoudi, A.; Sayah, K. Mechanical Behavior Study of Biosourced Composites. Master’s Thesis, University Kasdi Merbah, Ouargla, Algeria, 2015. [Google Scholar]
- Andersons, J.; Sparniņš, E.; Joffe, R.; Wallström, L. Strength distribution of elementary flax fibers. Compos. Sci. Technol. 2005, 65, 693–702. [Google Scholar] [CrossRef]
- Xue, Y.; Du, Y.; Elder, S.; Wang, K.; Zhang, J. Temperature and loading rate effects on tensile properties of kenaf bast fiber bundles and composites. Compos. Part B Eng. 2009, 40, 189–196. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Pan, N.; Postle, R. Weibull analysis of the tensile behavior of fibers with geometrical irregularities. J. Mater. Sci. 2002, 37, 1401–1406. [Google Scholar] [CrossRef][Green Version]
- Thomason, J.L. On the application of Weibull analysis to experimentally determined single fiber strength distributions. Compos. Sci. Technol. 2013, 77, 74–80. [Google Scholar] [CrossRef]
- ASTM International. Standard Test Method for Tensile Strength and Young’s Modulus for High-Modulus Single-Filament Materials; ASTM D3379-75 (1989) e1; ASTM International: West Conshohocken, PA, USA, 1975; pp. 1–5. Available online: WWW.astm.org (accessed on 20 September 2019). [CrossRef]
- Béakou, A.; Ntenga, R. Structure, morphology and mechanical properties of Rhectophyllum camerunense (RC) plant fiber. Part II: Computational homogenization of the anisotropic elastic properties. Comput. Mater. Sci. 2011, 50, 1550–1558. [Google Scholar] [CrossRef]
- Gourier, C.; Le Duigou, A.; Bourmaud, A.; Baley, C. Mechanical analysis of elementary flax fiber tensile properties after different thermal cycles. Compos. Part A Appl. Sci. Manuf. 2014, 64, 159–166. [Google Scholar] [CrossRef]
- Sia, C.V.; Nakai, Y.; Shiozawa, D.; Ohtani, H. Statistical Analysis of the Tensile Strength of Treated Oil Palm Fiber by Utilisation of Weibull Distribution Model. Open J. Compos. Mater. 2014, 4, 72–77. [Google Scholar] [CrossRef]
- Joffe, R.; Andersons, J. Modeling the Tensile Strength of Hemp Fibers and Short-Hemp-Fiber Reinforced Composites. In Natural Filler and Fibre Composites: Development and Characterisation. WIT Transactions on State of the Art in Science and Engineering; WIT Press: Southampton, UK, 2014; Volume 87, pp. 13–26. ISBN 9781784661472. [Google Scholar] [CrossRef]
- Engelbrecht-wiggans, A.; Phoenix, S.L. Comparison of maximum likelihood approaches for analysis of composite stress rupture data. J. Mater. Sci. 2016, 51, 6639–6661. [Google Scholar] [CrossRef]
- Andersons, J.; Joffe, R.; Sparnins, E.; Weichert, D. Modeling the effect of reinforcement discontinuity on the tensile strength of UD flax fiber composites. J. Mater. Sci. 2011, 46, 5104–5110. [Google Scholar] [CrossRef]
- Ochiai, S.; Osamura, K. Monte-Carlo Simulation On Notched Strength of unidirectional boron/aluminium composites. J. Mater. Sci. 1992, 27, 4061–4062. [Google Scholar] [CrossRef]
- Xu, J.; Xing, W.; Wang, H.; Xu, W.; Ding, Q. Monte-Carlo simulation study of the halogenated MIL-47 (V) frameworks: Influence of functionalization on H 2 S adsorption and separation properties. J. Mater. Sci. 2016, 51, 2307–2319. [Google Scholar] [CrossRef]
- Ilankeeran, P.K.; Mohite, P.M.; Kamle, S. Axial Tensile Testing of Single Fibers. Mod. Mech. Eng. 2012, 2012, 151–156. [Google Scholar] [CrossRef]
- Chin, C.W.; Yousif, B.F. Potential of kenaf fibers as reinforcement for tribological applications. Wear 2009, 267, 1550–1557. [Google Scholar] [CrossRef]
- Li, X.; Wang, F. Effect of the statistical nature of fiber strength on the predictability of tensile properties of polymer composites reinforced with bamboo fibers: Comparison of linear and power law Weibull models. Polymers 2016, 8, 24. [Google Scholar] [CrossRef]
- Singh, A.; Hall, W.; Summerscales, J. Composites: Part A Multiple Data Set (MDS) weak-link scaling analysis of jute fibers. Compos. Part A 2009, 40, 1764–1771. [Google Scholar] [CrossRef]
- Placet, V.; Bouali, A.; Garcin, C.; Cote, J.; Perre, P. Suivi Par Drx Des Réarrangements Microstructuraux Induits Par Sollicitations Mécaniques Dans Les Fibers végétales Tirées DU Chanvre. In French Congress of Mechanics, 20th ed.; AFM: Besancon, France, 2011; pp. 1–6. Available online: http://hdl.handle.net/2042/46471 (accessed on 20 September 2019).
- Charlet, K.; Eve, S.; Jernot, J.P.; Gomina, M.; Breard, J. Procedia Engineering Tensile deformation of a flax fiber. Procedia Eng. 2009, 1, 233–236. [Google Scholar] [CrossRef]
- Nilsson, T.; Gustafsson, P.J. Influence of dislocations and plasticity on the tensile behavior of flax and hemp fibers. Compos. Part A 2007, 38, 1722–1728. [Google Scholar] [CrossRef]
- Ilczyszyn, F. Caractérisation Expérimentale ET Numérique DU Comportement Mécanique Des Agro-Composites Renforcés Par Des Fibers DE Chanvre. Ph.D. Thesis, Université de Troyes, Troyes, France, 2013. [Google Scholar]
- Saba, N.; Paridah, M.T.; Jawaid, M. Mechanical properties of kenaf fiber reinforced polymer composite: A review. Constr. Build. Mater. 2015, 76, 87–96. [Google Scholar] [CrossRef]
- Nyström, B. Natural Fiber Composites: A Review. Engineering 2007, 15, 281–285. [Google Scholar]
- Gassan, J.; Bledzki, A.K. Thermal Degradation of Flax and Jute Fibers. J. Appl. Polym. Sci. 2001, 82, 1417–1422. [Google Scholar] [CrossRef]
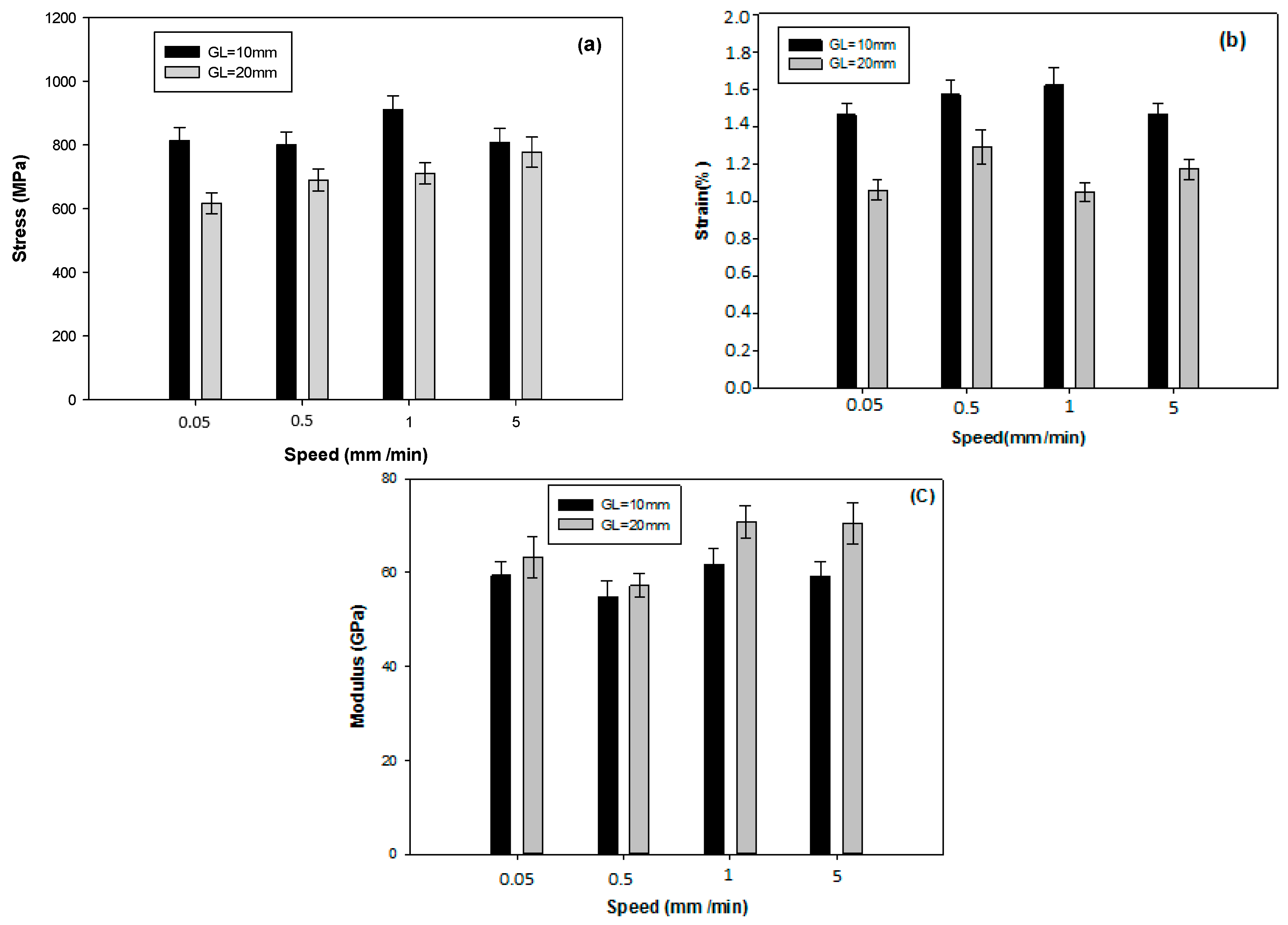
| GL (mm) | σU (MPa) | εU (%) | E (GPa) | Speed (mm·min−1) | |||
|---|---|---|---|---|---|---|---|
| 10 | 813.47 | ±41.57 | 1.46 | ±0.065 | 59.44 | ±2.94 | 0.05 |
| 20 | 617.18 | ±32.73 | 1.06 | ±0.054 | 63.32 | ±4.37 | |
| 10 | 800.53 | ±40.75 | 1.57 | ±0.079 | 54.81 | ±3.45 | 0.5 |
| 20 | 689.66 | ±34.78 | 1.29 | ±0.089 | 57.23 | ±2.54 | |
| 10 | 911.22 | ±43.29 | 1.62 | ±0.096 | 61.78 | ±3.33 | 1 |
| 20 | 710.83 | ±33.1 | 1.05 | ±0.05 | 70.87 | ±3.41 | |
| 10 | 808.16 | ±44.41 | 1.46 | ±0.063 | 59.33 | ±3.09 | 5 |
| 20 | 777.52 | ±47.44 | 1.17 | ±0.056 | 70.40 | ±4.42 | |
| HTs (min) | σ (MPa) | ε (%) | E (GPa) | T (°C) |
|---|---|---|---|---|
| 10 | 793.2 ± 88.78 | 1.9 ± 0.26 | 36.02 ± 1.81 | 50 |
| 591.7 ± 83.71 | 1.8 ± 0.15 | 34.78 ± 3.36 | 100 | |
| 329.1 ± 41.03 | 0.9 ± 0.14 | 28.5 ± 2.92 | 150 | |
| 30 | 505.5 ± 62.54 | 1.6 ± 0.14 | 35.68 ± 2.62 | 50 |
| 495.7 ± 16.12 | 1.2 ± 0.07 | 31.70 ± 3.42 | 100 | |
| 234.8 ± 51.20 | 0.8 ± 0.11 | 26.16 ± 4.226 | 150 | |
| 60 | 477.2 ± 76.38 | 1.2 ± 0.39 | 25.27 ± 1.13 | 50 |
| 427.9 ± 60.39 | 1.01 ± 0.11 | 24.17 ± 3.69 | 100 | |
| 214 ± 23.26 | 0.6 ± 0.10 | 23.41 ± 2.59 | 150 | |
| 911.22 ± 43.29 | 1.62 ± 0.096 | 61.78 ± 3.33 | 24 |
| GL (mm) | Mean Diameter (μm) | CVD (%) | Weibull Module m | Scale Parameter σ0 | Speed (mm·min−1) |
|---|---|---|---|---|---|
| 10 | 60 ± 1.8 | 7.2 | 3.49 | 904.46 | 0.05 |
| 20 | 59 ± 2.1 | 8.6 | 3.40 | 689.04 | |
| 10 | 60 ± 1.8 | 7.2 | 3.47 | 891.46 | 0.5 |
| 20 | 59 ± 2.1 | 8.6 | 3.51 | 765.74 | |
| 10 | 60 ± 1.8 | 7.2 | 3.69 | 1010 | 1 |
| 20 | 59 ± 2.1 | 8.6 | 3.74 | 786.32 | |
| 10 | 60 ± 1.8 | 7.2 | 3.23 | 902.7 | 5 |
| 20 | 59 ± 2.1 | 8.6 | 3.23 | 870.21 |
| GL (mm) | σexp (MPa) | σcal (MPa) | σrand–σsimul (MPa) | Speed (mm·min−1) |
|---|---|---|---|---|
| 10 | 813.47 ± 41.57 | 686.16 ± 34.23 | 771.54 ± 29.49 | 0.05 |
| 20 | 617.18 ± 32.73 | 492.93 ± 25.13 | 546.22 ± 27.53 | |
| 10 | 800.53 ± 40.75 | 674.9 ± 33.86 | 759.07 ± 31.81 | 0.5 |
| 20 | 689.66 ± 34.78 | 553.03 ± 27.38 | 608.10 ± 23.67 | |
| 10 | 911.22 ± 43.29 | 776.16 ± 36.86 | 862.45 ± 32.02 | 1 |
| 20 | 710.83 ± 33.1 | 577.44 ± 27.02 | 643.80 ± 27.29 | |
| 10 | 808.16 ± 44.41 | 673.25 ± 35.96 | 807.93 ± 36.22 | 5 |
| 20 | 777.52 ± 47.44 | 613.84 ± 32.74 | 735.48 ± 35.48 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ntenga, R.; SAÏDJO, S.; Beda, T.; Béakou, A. Estimation of the Effects of the Cross-Head Speed and Temperature on the Mechanical Strength of Kenaf Bast Fibers Using Weibull and Monte-Carlo Statistics. Fibers 2019, 7, 89. https://doi.org/10.3390/fib7100089
Ntenga R, SAÏDJO S, Beda T, Béakou A. Estimation of the Effects of the Cross-Head Speed and Temperature on the Mechanical Strength of Kenaf Bast Fibers Using Weibull and Monte-Carlo Statistics. Fibers. 2019; 7(10):89. https://doi.org/10.3390/fib7100089
Chicago/Turabian StyleNtenga, Richard, Saïdjo SAÏDJO, Tibi Beda, and Alexis Béakou. 2019. "Estimation of the Effects of the Cross-Head Speed and Temperature on the Mechanical Strength of Kenaf Bast Fibers Using Weibull and Monte-Carlo Statistics" Fibers 7, no. 10: 89. https://doi.org/10.3390/fib7100089
APA StyleNtenga, R., SAÏDJO, S., Beda, T., & Béakou, A. (2019). Estimation of the Effects of the Cross-Head Speed and Temperature on the Mechanical Strength of Kenaf Bast Fibers Using Weibull and Monte-Carlo Statistics. Fibers, 7(10), 89. https://doi.org/10.3390/fib7100089





