ANN-Based Shear Capacity of Steel Fiber-Reinforced Concrete Beams without Stirrups
Abstract
1. Introduction
2. Materials and Methods
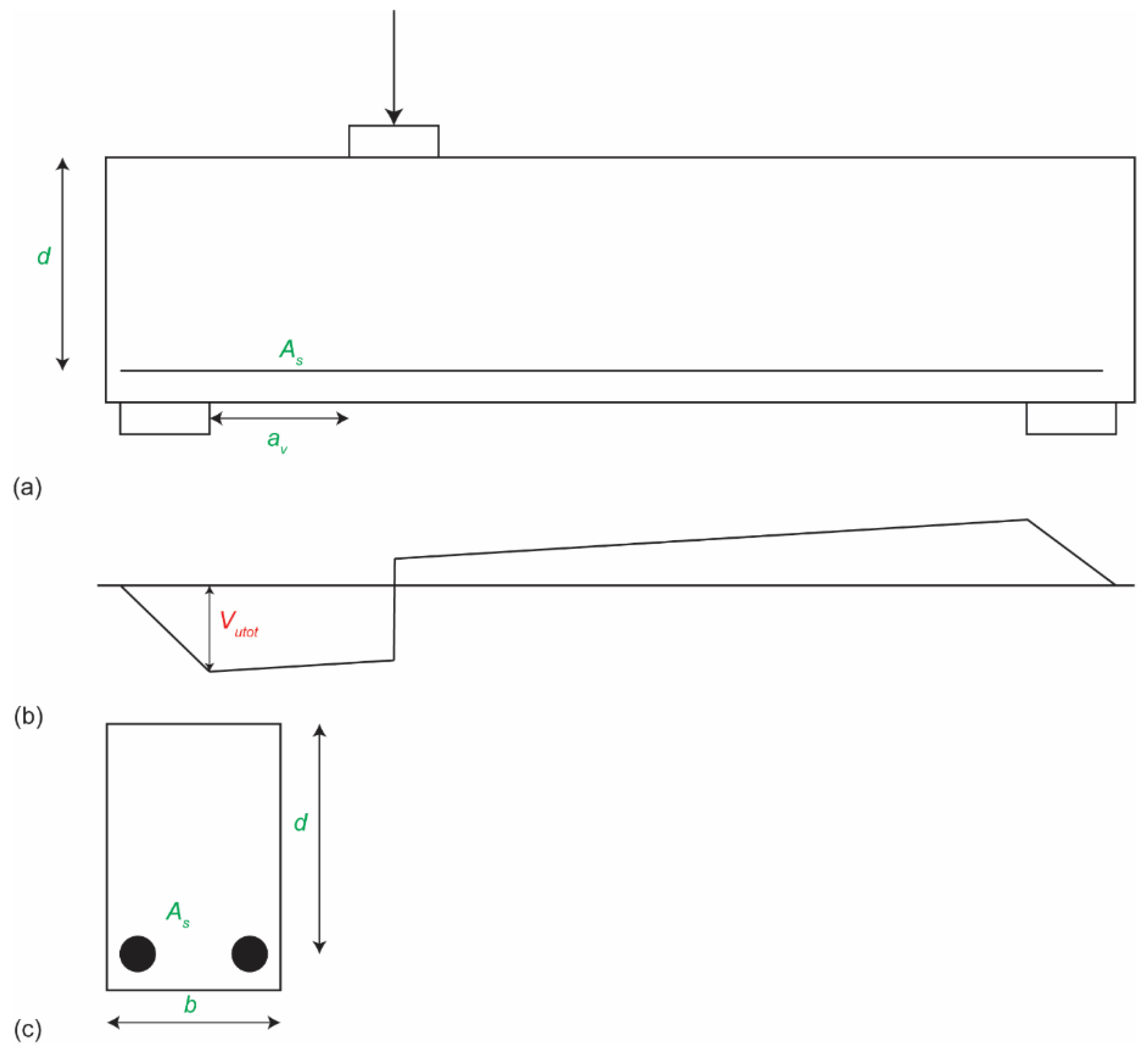
2.1. Data Gathering
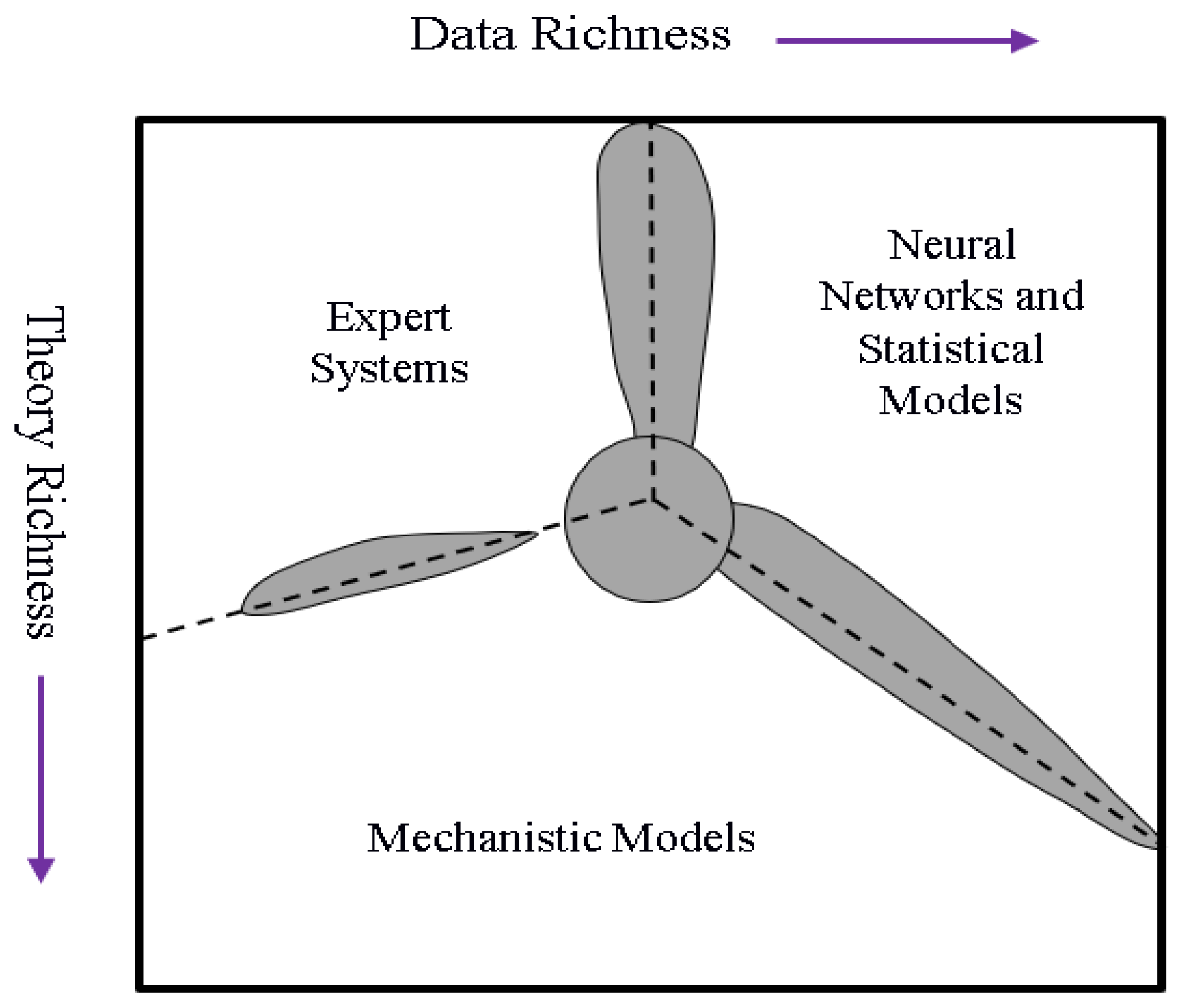
2.2. Artificial Neural Networks
2.2.1. Introduction
2.2.2. Implemented ANN Features
- Reduce pt-pv-ptt values by 10 units each.
- Compute minimum and maximum values for each variable q (row) of the full input dataset.
- Define patterns where each variable takes its minimum or maximum value from the full input dataset. These patterns ought to be included in the training dataset. If the number of patterns is lower than pt * P/100 (rounded off), more patterns should be added to the training set in the following way:
- (a)
- Compute the number of patterns (Lpt) that need to be added to the initially selected training patterns to equal round (pt * P/100).
- (b)
- Randomly select 10.000 combinations of Lpt patterns from all those not included in the training set defined prior to (a).
- (c)
- For each combination/scenario in (b), add those Lpt patterns to the set of training patterns defined prior to (a), and label all remaining learning patterns as “validation + testing”.
- (d)
- For each scenario in (c), and for each pattern labeled as “validation + testing”, check if that pattern has at least one input variable that equals a value not included in any pattern in the training set. If it hasn’t, then that pattern should be moved to the training set.
- (e)
- Among all 10,000 scenarios of training and “validation + testing” subsets addressed in (b) till (d), the selected scenario should be the one guaranteeing the amount of training data (Pt*) closest to round (pt * P/100).
- If the training set selected in (e) guarantees |Pt*/P − pt| ≤ 0.2, then that becomes the training data to be taken for simulation. Otherwise, the training data should be selected according to [112].
- Increase pt-pv-ptt values by 10 units each (to re-obtain the original input values—See step 1).
- Randomly select pv/(pv + ptt) of those patterns not belonging to the training dataset for the validation patterns. The remaining data then forms the testing dataset.
2.2.3. Parametric Analysis Results
3. Results
3.1. Proposed ANN-Based Model
3.1.1. Preprocessing of Input Data
3.1.2. ANN-Based Analytical Model
3.1.3. Output Data Post-Processing
3.2. Performance Indicators of Results
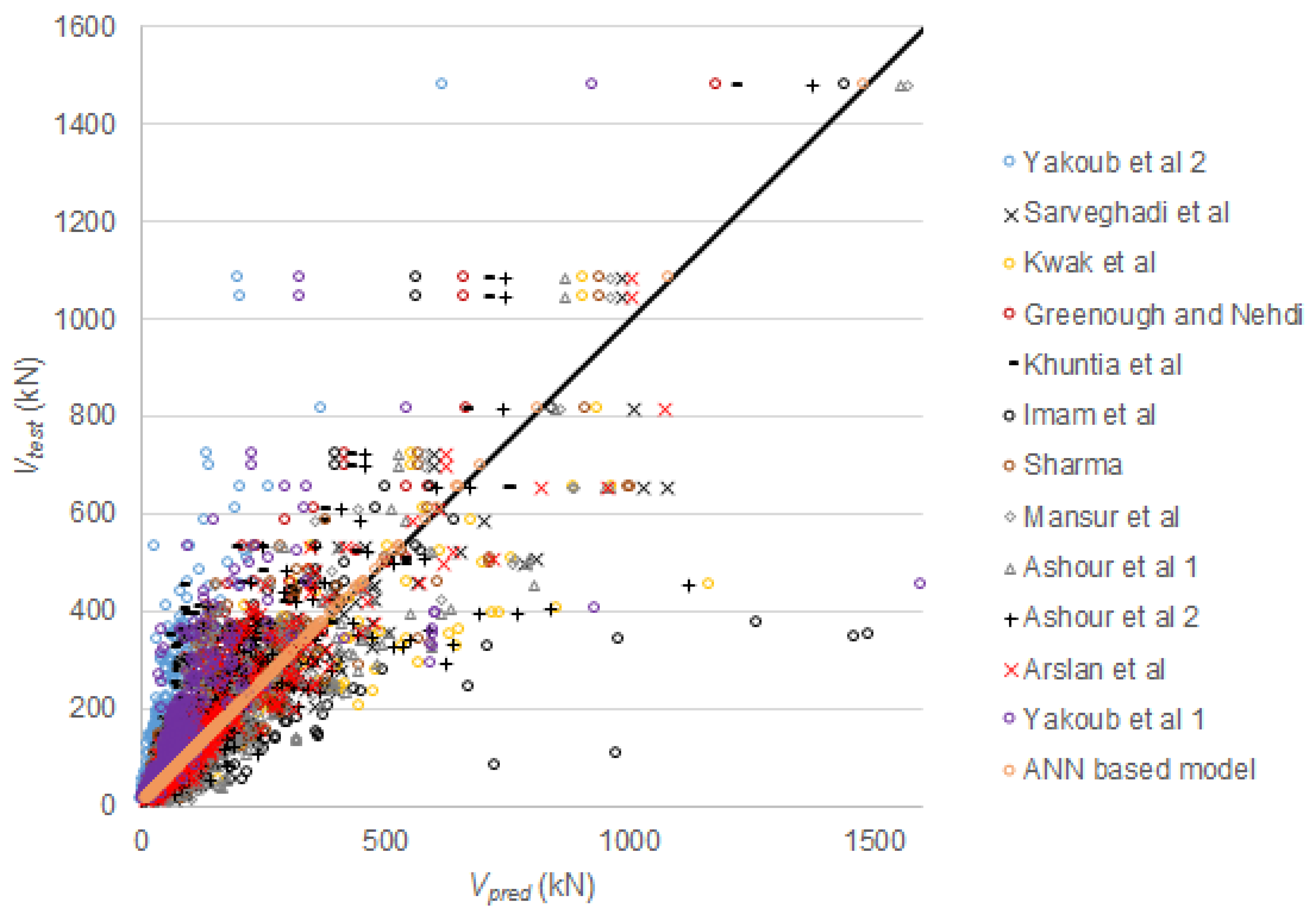
3.3. Comparison between ANN-Based and Existing Methods
4. Discussion
5. Conclusions
- We used a database with 430 datapoints from the literature.
- For the analysis, we selected nine input parameters related to the geometry, properties of the concrete, the flexural steel reinforcement, and the fibers, and one output parameter, the maximum sectional shear force caused by the applied load in the experiment and self-weight of the beam.
- To find the optimal ANN-based model, different combinations of 15 features of ANN models were analyzed.
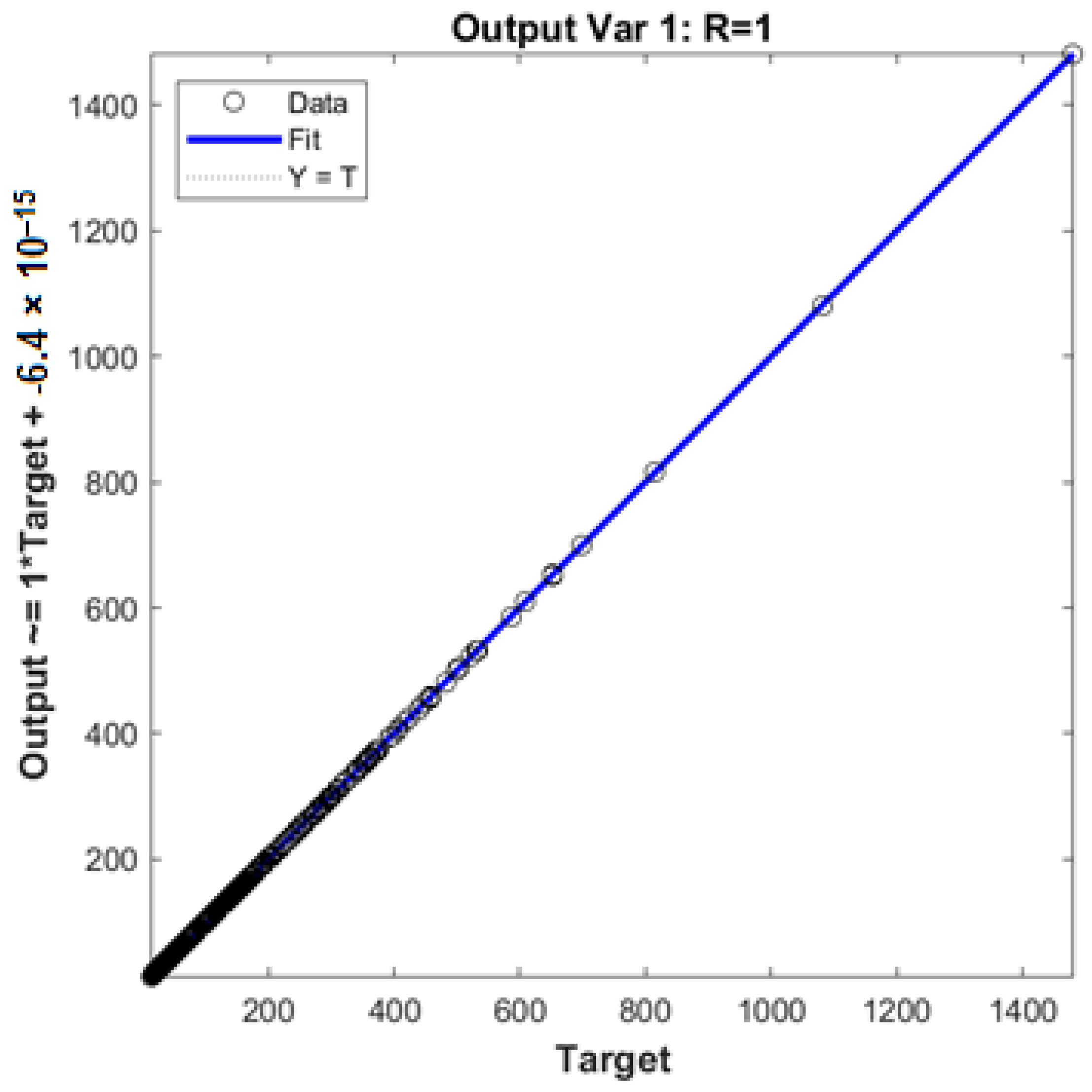
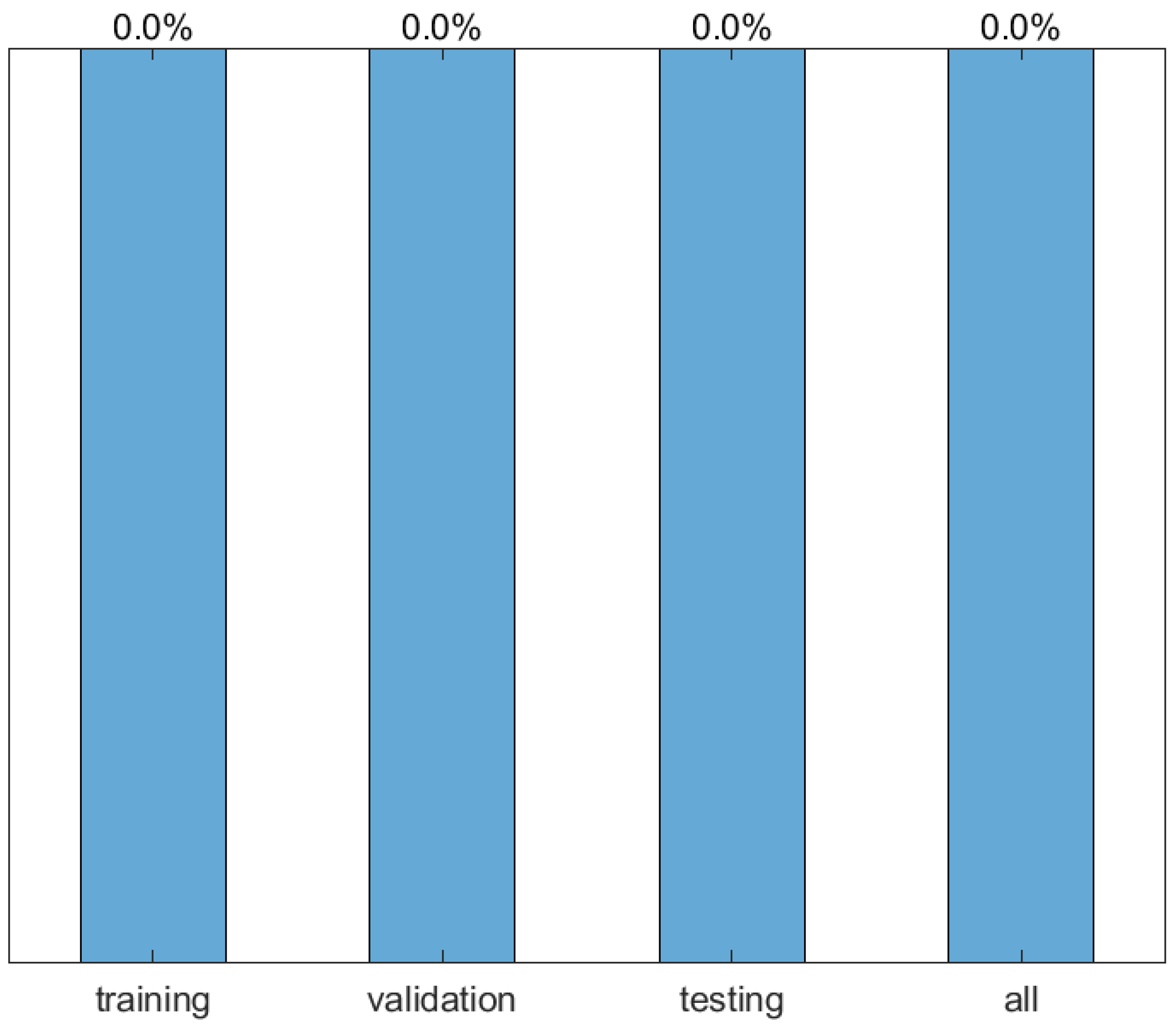
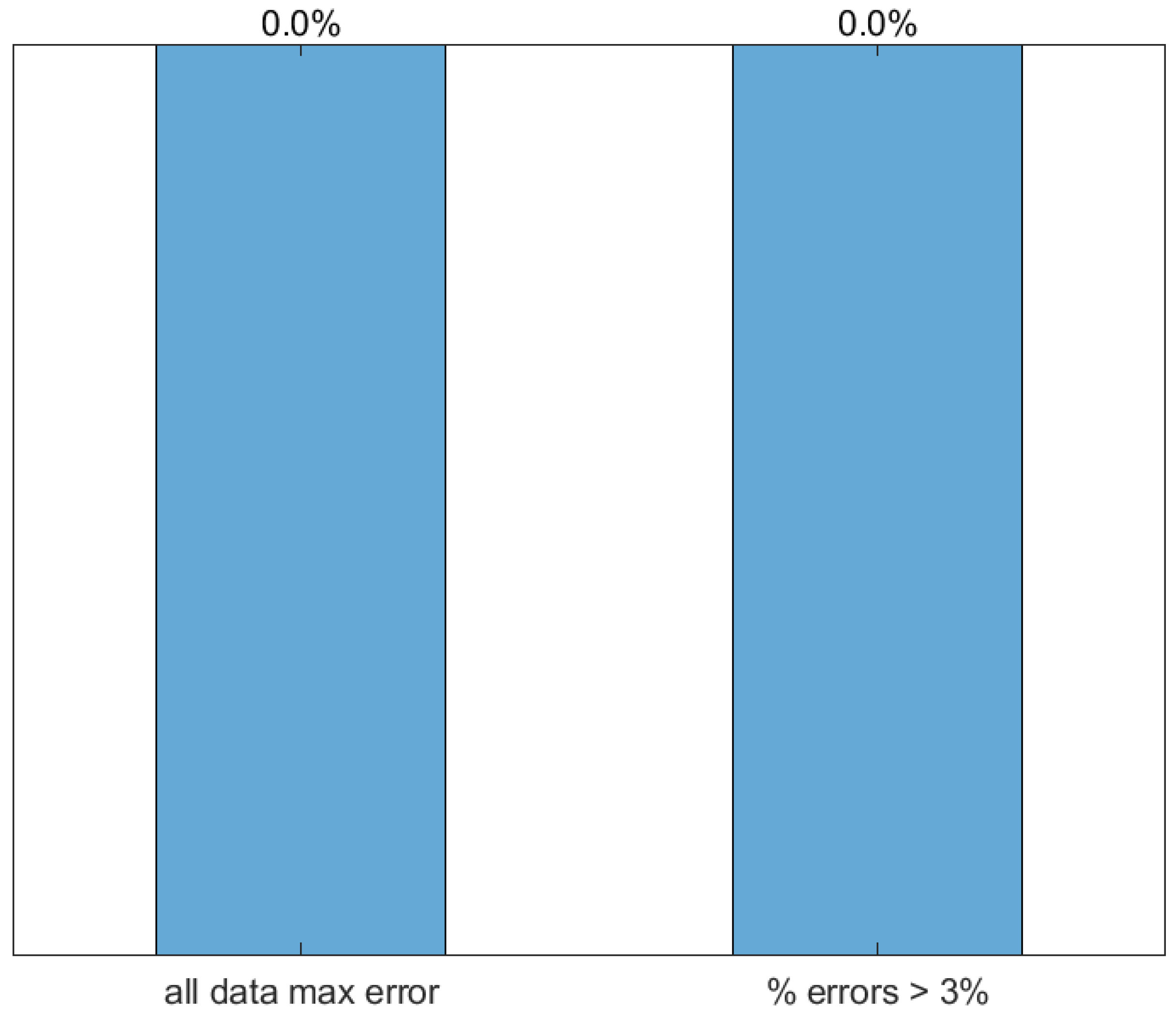
- The optimal model resulted in a maximum error of 0% and a mean relative error of 0.0% for the 430 datapoints, respectively.
- Our proposed model outperforms the available models and expressions for the shear capacity of SFRC.
- Our model can be used to prepare experiments, for design (within the input parameter ranges), and to support further development of mechanical models through robust parameter studies.
- The computational time of a datapoint with our model is less than 0.1 millisecond.
- The proposed model can only be used for the ranges of the variables available in the dataset.
- The model does not cover large-sized beams as a result of a lack of data on such specimens. As such, we recommend further experiments on large SFRC beams failing in shear and further studies on the size effect in SFRC.
- This study does not answer the question about the mechanics underlying the problem of shear in SFRC, but we can explore various influences with parametric studies using our proposed ANN-based model. Our model also facilitates the evaluation and improvement of existing and future mechanical models, based on the currently available experimental results.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| a | shear span |
| av | clear shear span |
| b | bias |
| bw | web width |
| c | height of compression zone |
| d | effective depth |
| da | maximum aggregate size |
| df | fiber diameter |
| dv | shear depth |
| e | factor to take effect of shear span to depth ratio into account |
| fc’ | specified concrete compressive strength |
| fc,cube | average measured concrete cube compressive strength |
| fc,cyl | average measured concrete cylinder compressive strength |
| characteristic value of post-cracking flexural strength for a deflection of 3.5 mm | |
| fck | characteristic concrete cylinder compressive strength |
| fctk | characteristic tensile strength of concrete |
| uniaxial tensile strength of SFRC | |
| fcuf | cube compressive strength of fiber-reinforced concrete |
| fFtuk | characteristic value of post-cracking strength for ultimate crack opening |
| fRk,4 | characteristic residual flexural strength for the ultimate limit state at a CMOD (crack mouth opening displacement) of 3.5 mm |
| fspfc | splitting tensile strength of fiber-reinforced concrete |
| ft’ | specified tensile strength of concrete mix |
| ftenf | tensile strength of the fibers |
| fy | yield strength of the reinforcement steel |
| h | height of cross-section |
| hf | height of flange |
| k | size effect factor |
| kf | factor that considers the contribution of flanges in T-sections (= 1 for rectangular sections) |
| factor that considers the orientation of the fibers | |
| size factor, which accounts for the fact that fibers are better distributed in larger elements | |
| lf | fiber length |
| lspan | span length |
| ltot | total specimen length |
| n | parameter for effect of geometry of flanged sections |
| pt | amount of training examples |
| ptt | amount of testing examples |
| pv | amount of validation examples |
| q | value of row |
| rf | fiber radius |
| sx | crack spacing |
| sxe | equivalent crack spacing factor |
| vmax | shear stress at maximum sectional shear Vmax |
| wlim | limiting crack width |
| wmax | maximum crack width permitted by the code |
| wu | ultimate crack width, i.e., the value attained at the Ultimate Limit State for resistance to combined stresses on the outer fiber under the moment exerted in this section |
| vb | shear strength attributed to fibers |
| z | internal lever arm |
| effective area bw × d, with d limited to 1.5 m | |
| Af | cross-sectional area of the fiber |
| As | area of longitudinal tension reinforcement |
| Avf | shear area over which fibers contribute |
| CRd,c | calibration factor for the design shear capacity |
| Ef | modulus of elasticity of the fibers |
| Es | modulus of elasticity of reinforcement steel |
| F | fiber factor |
| Gm | matrix shear modulus |
| K | orientation coefficient |
| M | sectional moment |
| P | sum of all datapoints |
| Pmax | maximum load in experiment |
| R | Pearson Correlation Coefficient |
| Rg | geometry factor from Yakoub [31]: 0.83 for crimped fibers, 1.00 for hooked fibers, and 0.91 for round fibers |
| S | fiber spacing |
| V | sectional shear force |
| Vc | concrete contribution to shear capacity |
| Vcd | design value of concrete contribution to shear capacity |
| Vf | fiber volume fraction |
| Vfd | design value of fiber contribution to shear capacity |
| Vmax | maximum sectional shear in experiment caused by applied load only (without self-weight) |
| Vmin | lower bound to the shear capacity |
| Vpred | predicted shear capacity |
| VRd | design shear capacity |
| VRd,c | design shear capacity of the concrete contribution |
| design shear capacity of fiber-reinforced concrete | |
| VRd,cf | design shear capacity of the fiber contribution, notation used in German guideline |
| VRd,c,min | lower bound to the design shear capacity of the concrete contribution |
| VRd,f | design shear capacity of the steel fiber contribution |
| Vu | ultimate shear capacity |
| Vutot | experimental shear capacity, including contribution from self-weight |
| W | synaptic weight |
| factor that accounts for the long-term effects | |
| β | fiber and matrix property factor developed by Cox [146] |
| γc | concrete material factor |
| γcf | concrete material factor, notation used in French guideline |
| partial factor for tensile strength of fiber-reinforced concrete | |
| γE | additional safety factor |
| εel | elastic strain |
| εlim | limiting strain |
| εmax | maximum strain |
| εu | ultimate strain at the ULS for bending combined with axial forces on the outer fiber under the moment exerted in the section |
| εx | strain at mid-depth of the cross-section |
| ηo | fiber orientation factor = 0.41 for fibers with a 3D random orientation, as derived by Romualdi and Mandel [147], but can be larger for members with thin webs |
| ηl | a length factor used to account for the variability in the fiber embedment length across the cracking plane |
| θ | angle of compression strut |
| ξ | size effect factor from Bažant and Kim [106] |
| ρ | reinforcement ratio |
| ρf | fiber bond factor: 0.5 for straight fibers, 0.75 for crimped fibers, 1 for hooked fibers |
| σRd,f | residual tensile strength of fiber-reinforced cross-section |
| σf(ε) | experimentally determined relation between stress in fiber concrete and strain |
| σf(w) | experimentally determined relation between post-cracking stress and crack width w |
| σtu | average stress at the ultimate limit state in the equivalent tensile stress block used for bending moment analysis of SFRC |
| τ | bond strength between fibers and matrix |
| τfd | design value of bond strength between fibers and matrix |
| ψ | size effect factor from Imam et al. [30] |
| ω | reinforcement ratio that includes the effect of fibers |
References
- Amin, A.; Foster, S.J.; Watts, M. Modelling the tension stiffening effect in SFR-RC. Mag. Concr. Res. 2016, 68, 339–352. [Google Scholar] [CrossRef]
- Lantsoght, E.O.L. How do steel fibers improve the shear capacity of reinforced concrete beams without stirrups? Compos. Part B Eng. 2019, 175, 107079. [Google Scholar] [CrossRef]
- Singh, B.; Jain, K. An appraisal of steel fibers as minimum shear reinforcement in concrete beams (with Appendix). ACI Struct. J. 2014, 111. [Google Scholar] [CrossRef]
- Kim, K.S.; Lee, D.H.; Hwang, J.-H.; Kuchma, D.A. Shear behavior model for steel fiber-reinforced concrete members without transverse reinforcements. Compos. Part B Eng. 2012, 43, 2324–2334. [Google Scholar] [CrossRef]
- Stevens, D.J.; Liu, D. Constitutive Modeling of Fiber Reinforced Concrete. ACI Spec. Publ. 1994, 142. [Google Scholar] [CrossRef]
- Lee, S.-C.; Cho, J.-Y.; Vecchio, F.J. Analysis of Steel Fiber-Reinforced Concrete Elements Subjected to Shear. ACI Struct. J. 2016, 113. [Google Scholar] [CrossRef]
- Minelli, F.; Vecchio, F.J. Compression Field Modeling of Fiber-Reinforced Concrete Members Under Shear Loading. ACI Struct. J. 2006, 103. [Google Scholar] [CrossRef]
- Vecchio, F.J. Disturbed stress field model for reinforced concrete: Formulation. J. Struct. Eng. ASCE 2000, 126, 1070–1077. [Google Scholar] [CrossRef]
- Susetyo, J.; Gauvreau, P.; Vecchio, F.J. Steel Fiber-Reinforced Concrete Panels in Shear: Analysis and Modeling. ACI Struct. J. 2013, 110. [Google Scholar] [CrossRef]
- Matthys, S.; Soetens, T. Engineering Model for SFRC Shear Strength Based on MC2010 MCFT Approach. In Proceedings of the Fib Symposium 2017, Maastricht, The Netherlands, 12–24 June 2017. [Google Scholar]
- Barros, J.A.O.; Foster, S.J. An integrated approach for predicting the shear capacity of fibre reinforced concrete beams. Eng. Struct. 2018, 174, 346–357. [Google Scholar] [CrossRef]
- Foster, S.J.; Agarwal, A.; Amin, A. Design of steel fiber reinforced concrete beams for shear using inverse analysis for determination of residual tensile strength. Struct. Concr. 2018, 19, 129–140. [Google Scholar] [CrossRef]
- Lee, D.H.; Kim, K.S.; Han, S.J.; Zhang, D.; Kim, J. Dual potential capacity model for reinforced concrete short and deep beams subjected to shear. Struct. Concr. 2018, 19, 76–85. [Google Scholar] [CrossRef]
- Lee, D.H.; Han, S.-J.; Kim, K.S.; LaFave, J.M. Shear capacity of steel fiber-reinforced concrete beams. Struct. Concr. 2017, 18, 278–291. [Google Scholar] [CrossRef]
- Batson, G.B.; Youssef, A.G. Shear Capacity of Fiber Reinforced Concrete Based on Plasticity of Concrete: A Review. ACI Spec. Publ. 1994, 142. [Google Scholar] [CrossRef]
- Spinella, N. Shear strength of full-scale steel fibre-reinforced concrete beams without stirrups. Comput. Concr. 2013, 11, 365–382. [Google Scholar] [CrossRef]
- Lim, T.Y.; Paramasivam, P.; Lee, S.L. Shear and moment capacity of reinforced steel-fibre-concrete beams. Mag. Concr. Res. 1987, 39, 148–160. [Google Scholar] [CrossRef]
- Lim, T.Y.; Paramasivam, P.; Lee, S.L. Analytical Model for Tensile Behavior of Steel-Fiber Concrete. ACI Mater. J. 1987, 84. [Google Scholar] [CrossRef]
- Narayanan, R.; Kareem-Palanjian, A.S. Effect of Fibre Addition on Concrete Strengths. Indian Concr. J. 1984, 58, 100–103. [Google Scholar]
- Lantsoght, E.O.L. Database of Shear Experiments on Steel Fiber Reinforced Concrete Beams without Stirrups. Materials 2019, 12, 917. [Google Scholar] [CrossRef]
- Conforti, A.; Minelli, F. Compression field modelling of fibre reinforced concrete shear critical deep beams: A numerical study. Mater. Struct. 2016, 49, 3369–3383. [Google Scholar] [CrossRef]
- Sarveghadi, M.; Gandomi, A.H.; Bolandi, H.; Alavi, A.H. Development of prediction models for shear strength of SFRCB using a machine learning approach. Neural Comput. Appl. 2015. [Google Scholar] [CrossRef]
- Kwak, Y.-K.; Eberhard, M.O.; Kim, W.-S.; Kim, J. Shear Strength of Steel Fiber-Reinforced Concrete Beams without Stirrups. ACI Struct. J. 2002, 99. [Google Scholar] [CrossRef]
- Greenough, T.; Nehdi, M. Shear Behavior of Fiber-Reinforced Self-Consolidating Concrete Slender Beams. ACI Mater. J. 2008, 105. [Google Scholar] [CrossRef]
- Khuntia, M.; Stojadinovic, B.; Goel, S.C. Shear Strength of Normal and High-Strength Fiber Reinforced Concrete Beams without Stirrups. ACI Struct. J. 1999, 96. [Google Scholar] [CrossRef]
- Sharma, A.K. Shear Strength of Steel Fiber Reinforced Concrete Beams. ACI J. Proc. 1986, 83. [Google Scholar] [CrossRef]
- Mansur, M.A.; Ong, K.C.G.; Paramasivam, P. Shear Strength of Fibrous Concrete Beams Without Stirrups. J. Struct. Eng. 1986, 112, 2066–2079. [Google Scholar] [CrossRef]
- Ashour, S.A.; Hasanain, G.S.; Wafa, F.F. Shear Behavior of High-Strength Fiber Reinforced Concrete Beams. ACI Struct. J. 1992, 89. [Google Scholar] [CrossRef]
- Arslan, G. Shear strength of Steel Fiber Reinforced Concrete (SFRC) slender beams. KSCE J. Civ. Eng. 2014, 18, 587–594. [Google Scholar] [CrossRef]
- Imam, M.; Vandewalle, L.; Mortelmans, F.; Van Gemert, D. Shear domain of fibre-reinforced high-strength concrete beams. Eng. Struct. 1997, 19, 738–747. [Google Scholar] [CrossRef]
- Yakoub, H.E. Shear Stress Prediction: Steel Fiber-Reinforced Concrete Beams without Stirrups. ACI Struct. J. 2011, 108. [Google Scholar] [CrossRef]
- Association Française de Génie Civil. Bétons Fibrés à Ultra-Hautes Performances: Recommandations; Association Française de Génie Civil: Paris, France, 2013; p. 359. [Google Scholar]
- DAfStB. DAfStB-Richtlinie Stahlfaserbeton; DIN: Berlin, Germany, 2012; p. 47.
- RILEM TC 162-TDF. σ-ε-Design Method. Mater. Struct. 2003, 36, 560–567. [CrossRef]
- FIB. Model Code 2010: Final Draft; International Federation for Structural Concrete: Lausanne, Switzerland, 2012; p. 676. [Google Scholar]
- CNR—Advisory Committee on Technical Recommendations for Construction. Guide for the Design and Construction of Fiber-Reinforced Concrete Structures: CNR-DT 204/2006; CNR: Rome, Italy, 2007; p. 57.
- Hertzmann, A.; Fleet, D. Machine LearningData Mining, Lecture Notes CSC 411/D11; Computer Science Department, University of Toronto: Toronto, ON, Canada, 2012. [Google Scholar]
- Basheer, I.A.; Hajmeer, M. Artificial neural networks: Fundamentals, computing, design, and application. J. Microbiol. Methods 2000, 43, 3–31. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Hern, A. Google Says Machine Learning Is the Future. So I Tried it Myself. Available online: https://www.theguardian.com/technology/2016/jun/28/google-says-machine-learning-is-the-future-so-i-tried-it-myself (accessed on 2 November 2016).
- Flood, I. Towards the next generation of artificial neural networks for civil engineering. Adv. Eng. Inform. 2008, 22, 4–14. [Google Scholar] [CrossRef]
- Hossain, K.M.A.; Gladson, L.R.; Anwar, M.S. Modeling shear strength of medium- to ultra-high-strength steel fiber-reinforced concrete beams using artificial neural network. Neural Comput. Appl. 2016. [Google Scholar] [CrossRef]
- Kara, I.F. Empirical modeling of shear strength of steel fiber reinforced concrete beams by gene expression programming. Neural Comput. Appl. 2013, 23, 823–834. [Google Scholar] [CrossRef]
- Cuenca, E.; Conforti, A.; Minelli, F.; Plizzari, G.A.; Navarro Gregori, J.; Serna, P. A material-performance-based database for FRC and RC elements under shear loading. Mater. Struct. 2018, 51, 11. [Google Scholar] [CrossRef]
- Sahoo, D.R.; Sharma, A. Effect of Steel Fiber Content on Behavior of Concrete Beams with and without Stirrups. ACI Struct. J. 2014, 111, 1157–1166. [Google Scholar] [CrossRef]
- Shoaib, A.; Lubell, A.S.; Bindiganavile, V.S. Shear response of lightweight steel fiber reinforced concrete members without stirrups. Mater. Struct. 2015, 48, 3141–3157. [Google Scholar] [CrossRef]
- Sathya, S.; Sylviya, B. Shear strength of high-strength steel fibre reinforced concrete rectangular beams. Int. J. Civ. Eng. Technol. 2017, 8, 1716–1729. [Google Scholar]
- Arslan, G.; Keskin, R.S.O.; Ulusoy, S. An experimental study on the shear strength of SFRC beams without stirrups. J. Theor. Appl. Mech. 2017, 55, 1205. [Google Scholar] [CrossRef]
- Parra-Montesinos, G.J.; Wight, J.K.; Dinh, H.H.; Libbrecht, A.; Padilla, C. Shear Strengthfiber Reinforced Concrete Beams Without Stirrups; University of Michigan: Ann Arbor, MI, USA, 2006; p. 39. [Google Scholar]
- Rosenbusch, J.; Teutsch, M. Trial Beams in Shear Brite/Euram Project 97-4163 Final Rep. Sub Task 4.2; Technical University of Braunschweig: Braunschweig, Germany, 2003; pp. 105–117. [Google Scholar]
- Sahoo, D.R.; Bhagat, S.; Reddy, T.C.V. Experimental study on shear-span to effective-depth ratio of steel fiber reinforced concrete T-beams. Mater. Struct. 2016, 49, 3815–3830. [Google Scholar] [CrossRef]
- Amin, A.; Foster, S.J. Shear strength of steel fibre reinforced concrete beams with stirrups. Eng. Struct. 2016, 111, 323–332. [Google Scholar] [CrossRef]
- Tahenni, T.; Chemrouk, M.; Lecompte, T. Effect of steel fibers on the shear behavior of high strength concrete beams. Constr. Build. Mater. 2016, 105, 14–28. [Google Scholar] [CrossRef]
- Narayanan, R.; Darwish, I.Y.S. Use of Steel Fibers as Shear Reinforcement. ACI Struct. J. 1987, 84. [Google Scholar] [CrossRef]
- Cucchiara, C.; La Mendola, L.; Papia, M. Effectiveness of stirrups and steel fibres as shear reinforcement. Cem. Concr. Compos. 2004, 26, 777–786. [Google Scholar] [CrossRef]
- Lim, D.H.; Oh, B.H. Experimental and theoretical investigation on the shear of steel fibre reinforced concrete beams. Eng. Struct. 1999, 21, 937–944. [Google Scholar] [CrossRef]
- Dinh, H.H.; Parra-Montesinos, G.J.; Wight, J.K. Shear Behavior of Steel Fiber-Reinforced Concrete Beams without Stirrup. Reinforcement. ACI Struct. J. 2010, 107. [Google Scholar] [CrossRef]
- Lima Araujo, D.; Tibúrcio Nunes, F.G.; Toledo Filho, R.D.; Souza de Andrade, M.A. Shear strength of steel fiber-reinforced concrete beams. Acta Sci. 2014, 36, 389–397. [Google Scholar] [CrossRef]
- Casanova, P.; Rossi, P.; Schaller, l. Can Steel Fibers Replace Transverse Reinforcements in Reinforced Concrete Beams? ACI Mater. J. 1997, 94. [Google Scholar] [CrossRef]
- Aoude, H.; Belghiti, M.; Cook, W.D.; Mitchell, D. Response of Steel Fiber-Reinforced Concrete Beams with and without Stirrups. ACI Struct. J. 2012, 109. [Google Scholar] [CrossRef]
- Minelli, F.; Plizzari, G.A. On the Effectiveness of Steel Fibers as Shear Reinforcement. ACI Struct. J. 2013, 110. [Google Scholar] [CrossRef]
- Kang, T.H.-K.; Kim, W.; Kwak, Y.-K.; Hong, S.-G. Shear Testing of Steel Fiber-Reinforced Lightweight Concrete Beams without Web Reinforcement. ACI Struct. J. 2011, 108. [Google Scholar] [CrossRef]
- Casanova, P.; Rossi, P. High-Strength Concrete Beams Submitted to Shear: Steel Fibers Versus Stirrups. ACI Spec. Publ. 1999, 182. [Google Scholar] [CrossRef]
- Zarrinpour, M.R.; Chao, S.-H. Shear Strength Enhancement Mechanisms of Steel Fiber-Reinforced Concrete Slender Beams. ACI Struct. J. 2017, 114. [Google Scholar] [CrossRef]
- Noghabai, K. Beams of Fibrous Concrete in Shear and Bending: Experiment and Model. J. Struct. Eng. 2000, 126, 243–251. [Google Scholar] [CrossRef]
- Randl, N.; Mészöly, T.; Harsányi, P. Shear Behaviour of UHPC Beams with Varying Degrees of Fibre and Shear Reinforcement. In Proceedings of the Fib Symposium 2017, Maastricht, The Netherlands, 12–14 June 2017. [Google Scholar]
- Tan, K.H.; Murugappan, K.; Paramasivam, P. Shear Behavior of Steel Fiber Reinforced Concrete Beams. ACI Struct. J. 1993, 90. [Google Scholar] [CrossRef]
- Pansuk, W.; Nguyen, T.N.; Sato, Y.; Den Uijl, J.A.; Walraven, J.C. Shear capacity of high performance fiber reinforced concrete I-beams. Constr. Build. Mater. 2017, 157, 182–193. [Google Scholar] [CrossRef]
- Kim, C.-G.; Lee, H.; Park, H.-G.; Hong, G.-H.; Kang, S.-M. Effect of Steel Fibers on Minimum Shear Reinforcement of High-Strength Concrete Beams. ACI Struct. J. 2017, 114. [Google Scholar] [CrossRef]
- Narayanan, R.; Darwish, I.Y.S. Fiber Concrete Deep. Beams in Shear. ACI Struct. J. 1988, 85. [Google Scholar] [CrossRef]
- Li, V.C.; Ward, R.; Hamza, A.M. Steel and Synthetic Fibers as Shear Reinforcement. ACI Mater. J. 1992, 89. [Google Scholar] [CrossRef]
- Swamy, R.N.; Jones, R.; Chiam, A.T.P. Influence of Steel fibers on the Shear Resistance of Lightweight Concrete I-Beams. ACI Struct. J. 1993, 90. [Google Scholar] [CrossRef]
- Cho, S.-H.; Kim, Y.I.L. Effects of Steel Fibers on Short Beams Loaded in Shear. ACI Struct. J. 2003, 100. [Google Scholar] [CrossRef]
- Kang, T.H.-K.; Kim, W.; Massone, L.M.; Galleguillos, T.A. Shear-Flexure Coupling Behavior of Steel Fiber-Reinforced Concrete Beams. ACI Struct. J. 2012, 109. [Google Scholar] [CrossRef]
- Dupont, D.; Vandewalle, L. Shear Capacity of Concrete Beams Containing Longitudinal Reinforcement and Steel Fibers. ACI Spec. Publ. 2003, 216. [Google Scholar] [CrossRef]
- Dupont, D. Modelling and Experimental Validation of the Constitutive Law (σ-ε) and Cracking Behaviour of Steel Fibre Reinforced Concrete; KU Leuven: Leuven, Belgium, 2003. [Google Scholar]
- Kal, K.W.; Lee, D.H.; Bang, Y.S.; Cho, H.C.; Kang, J.O.; Kim, K.S. The Effectiveness of Steel Fibers as Shear Reinforcement. Concr. Int. 1985, 7, 59–60. [Google Scholar]
- Batson, G.; Jenkins, E.; Spatney, R. Steel Fibers as Shear Reinforcement in Beams. ACI J. Proc. 1972, 69. [Google Scholar] [CrossRef]
- Zhao, J.; Liang, J.; Chu, L.; Shen, F. Experimental Study on Shear Behavior of Steel Fiber Reinforced Concrete Beams with High-Strength Reinforcement. Materials 2018, 11, 1682. [Google Scholar] [CrossRef]
- Jindal, R.L. Shear and Moment Capacities of Steel Fiber Reinforced Concrete Beams. ACI Spec. Publ. 1984, 81. [Google Scholar] [CrossRef]
- Shin, S.-W.; Oh, J.-G.; Ghosh, S.K. Shear Behavior of Laboratory-Sized High-Strength Concrete Beams Reinforced With Bars and Steel Fibers. ACI Spec. Publ. 1994, 142. [Google Scholar] [CrossRef]
- Imam, M.; Vandewalle, L.; Mortelmans, F. Shear Capacity of Steel Fiber High-Strength Concrete Beams. ACI Spec. Publ. High Perform. Concr. 1994, 149. [Google Scholar] [CrossRef]
- Imam, M.; Vandewalle, L. Role of Fibers in Controlling Failure Modes of High-Strength Concrete Beams. Spec. Publ. 2000, 193. [Google Scholar] [CrossRef]
- Huang, C.-K.; Zhang, H.Z.; Guan, Z.G. Experimental Study on Shear Resistance of Steel Fiber Reinforced High-Strength Concrete Beams. ACI Spec. Publ. 2005, 228. [Google Scholar] [CrossRef]
- Kwak, K.-H.; Suh, J.; Hsu, C.-T.T. Shear-Fatigue Behavior of Steel Fiber Reinforced Concrete Beams. ACI Struct. J. 1991, 88. [Google Scholar] [CrossRef]
- Roberts, T.M.; Ho, N.L. Shear failure of deep fibre reinforced concrete beams. Int. J. Cem. Compos. Lightweight Concr. 1982, 4, 145–152. [Google Scholar] [CrossRef]
- Hwang, J.-H.; Lee, D.H.; Kim, K.S.; Ju, H.; Seo, S.-Y. Evaluation of shear performance of steel fibre reinforced concrete beams using a modified smeared-truss model. Mag. Concr. Res. 2013, 65, 283–296. [Google Scholar] [CrossRef]
- Spinella, N.; Colajanni, P.; Mendola, L.L. Nonlinear Analysis of Beams Reinforced in Shear with Stirrups and Steel Fibers. ACI Struct. J. 2012, 109. [Google Scholar] [CrossRef]
- Chalioris, C.E.; Sfiri, E.F. Shear Performance of Steel Fibrous Concrete Beams. Procedia Eng. 2011, 14, 2064–2068. [Google Scholar] [CrossRef]
- Cohen, M.; Aoude, H. Shear behavior of SFRC and SCFRC beams. In Proceedings of the 3rd International Structural Specialty Conference, Edmonton, AB, Canada, 6–9 June 2012. [Google Scholar]
- Aoude, H.; Cohen, M. Shear response of SFRC beams constructed with SCC and Steel Fibers. Electron. J. Struct. Eng. 2014, 14, 71–83. [Google Scholar]
- Qissab, M.; Salman, M.M. Shear strength of non-prismatic steel fiber reinforced concrete beams without stirrups. Struct. Eng. Mech. 2018, 67, 347–358. [Google Scholar]
- Furlan, S.; de Hanai, J.B. Shear behaviour of fiber reinforced concrete beams. Cem. Concr. Compos. 1997, 19, 359–366. [Google Scholar] [CrossRef]
- Dancygier, A.N.; Savir, Z. Effects of Steel Fibers on Shear Behavior of High-Strength Reinforced Concrete Beams. Adv. Struct. Eng. 2011, 14, 745–761. [Google Scholar] [CrossRef]
- Krassowska, J.; Kosior-Kazberuk, M. Failure mode in shear of steel fiber reinforced concrete beams. MATEC Web Conf. 2018, 163, 02003. [Google Scholar] [CrossRef]
- Yoo, D.-Y.; Yang, J.-M. Effects of stirrup, steel fiber, and beam size on shear behavior of high-strength concrete beams. Cem. Concr. Compos. 2018, 87, 137–148. [Google Scholar] [CrossRef]
- Gali, S.; Subramaniam, K.V.L. Shear behavior of steel fiber reinforced concrete using full-field displacements from digital image correlation. MATEC Web Conf. 2017, 120, 04003. [Google Scholar] [CrossRef]
- Zamanzadeh, Z.; Lourenço, L.; Barros, J. Recycled Steel Fibre Reinforced Concrete failing in bending and in shear. Constr. Build. Mater. 2015, 85, 195–207. [Google Scholar] [CrossRef]
- Shoaib, A.; Lubell, A.S.; Bindiganavile, V.S. Size Effect in Shear for Steel Fiber-Reinforced Concrete Members without Stirrups. ACI Struct. J. 2014, 111, 1081–1089. [Google Scholar] [CrossRef]
- Shoaib, A. Shear in Steel Fiber Reinforced Concrete without Stirrups; University of Alberta: Edmonton, AB, Canada, 2012. [Google Scholar]
- Bae, B.I.; Choi, H.K.; Choi, C.S. Flexural and Shear Capacity Evaluation of Reinforced Ultra-High Strength Concrete Members with Steel Rebars. Key Eng. Mater. 2014, 577, 17–20. [Google Scholar] [CrossRef]
- Abdul-Zaher, A.S.; Abdul-Hafez, L.M.; Tawfic, Y.R.; Hammed, O. Shear behavior of fiber reinforced concrete beams. J. Eng. Sci. Assiut Univ. 2016, 44, 132–144. [Google Scholar]
- Ruiz, M.F.; Muttoni, A. Size effect in shear and punching shear failures of concrete members without transverse reinforcement: Differences between statically determinate members and redundant structures. Struct. Concr. 2018, 19, 65–75. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Kazemi, M.T. Size effect on Diagonal Shear Failure of Beams without Stirrups. ACI Struct. J. 1991, 88, 268–276. [Google Scholar]
- Shioya, T.; Iguro, M.; Nojiri, Y.; Akiyama, H.; Okada, T. Shear strength of large reinforced concrete beams. Fract. Mech. Appl. Concr. 1989, 118, 259–279. [Google Scholar]
- Bazant, Z.P.; Kim, J.K. Size Effect in Shear Failure of Longitudinally Reinforced Beams. J. Am. Concr. Inst. 1984, 81, 456–468. [Google Scholar]
- Developer. SFRC Dataset + Target vs. Output [Data Set]; Zenodo: Genève, Switzerland, 2019. [Google Scholar] [CrossRef]
- Haykin, S.S. Neural Networks Learning Machines, 3rd ed.; Prentice Hall/Pearson: New York, NY, USA, 2009; p. 906. [Google Scholar]
- Abambres, M.; Lantsoght, E.O.L. Neural network-based formula for shear capacity prediction of one-way slabs under concentrated loads. engrXiv 2018, 1–33. [Google Scholar] [CrossRef]
- The Mathworks, I. Matlab R2017a, User’s Guide; MathWorks: Natick, MA, USA, 2017. [Google Scholar]
- Abambres, M. ANN Software Validation Report. Figshare. Available online: https://figshare.com/articles/ANNSoftwareValidation-Report_pdf/6962873 (accessed on 12 December 2018). [CrossRef]
- Abambres, M.; Marcy, M.; Doz, G. Potential of Neural Networks for Structural Damage Localization. ACI Av. Cienc. Ing. 2019, 11. [Google Scholar] [CrossRef]
- Developer. W and b Arrays [Data Set]; Zenodo: Genève, Switzerland, 2019. [Google Scholar] [CrossRef]
- Lantsoght, E. Database of Experiments on SFRC Beams without Stirrups Failing in Shear, 1st ed.; Zenodo: Genève, Switzerland, 2019. [Google Scholar] [CrossRef]
- Reissen, K.; Classen, M.; Hegger, J. Shear in reinforced concrete slabs—Experimental investigations in the effective shear width of one-way slabs under concentrated loads and with different degrees of rotational restraint. Struct. Concr. 2018, 19, 36–48. [Google Scholar] [CrossRef]
- He, Z.-Q.; Liu, Z.; Ma, Z.J. Investigation of Load-Transfer Mechanisms in Deep. Beams and Corbels. ACI Struct. J. 2012, 109, 467–476. [Google Scholar]
- Shatarat, N.; Katkhuda, H.; Abdel-Jaber, M.; Alqam, M. Experimental investigation of reinforced concrete beams with spiral reinforcement in shear. Constr. Build. Mater. 2016, 125, 585–594. [Google Scholar] [CrossRef]
- Naik, U.; Kute, S. Span-to-depth ratio effect on shear strength of steel fiber-reinforced high-strength concrete deep beams using ANN model. Int. J. Adv. Struct. Eng. 2013, 5, 29. [Google Scholar] [CrossRef]
- Lantsoght, E.O.L.; van der Veen, C.; de Boer, A.; Walraven, J.C. Recommendations for the Shear Assessment of Reinforced Concrete Slab Bridges from Experiments. Struct. Eng. Int. 2013, 23, 418–426. [Google Scholar]
- Cladera, A.; Marí, A.; Bairán, J.M.; Ribas, C.; Oller, E.; Duarte, N. The compression chord capacity model for the shear design and assessment of reinforced and prestressed concrete beams. Struct. Concr. 2016, 17, 1017–1032. [Google Scholar] [CrossRef]
- Gastebled, O.J.; May, I.M. Fracture mechanics model applied to shear failure of reinforced concrete beams without stirrups. ACI Struct. J. 2001, 98, 184–190. [Google Scholar]
- Vintzileou, E. Shear transfer by dowel action and friction as related to size effects. CEB Bull. 1997, 237, 53–77. [Google Scholar]
- Millard, S.G.; Johnson, R.P. Shear transfer across cracks in reinforced concrete due to aggregate interlock and dowel action. Mag. Concr. Res. 1984, 36, 9–21. [Google Scholar] [CrossRef]
- Dulacska, H. Dowel Action of Reinforcement Crossing Cracks in Concrete. ACI J. Proc. 1972, 69, 754–757. [Google Scholar]
- Al-Musawi, A.A. Determination of shear strength of steel fiber RC beams: Application of data-intelligence models. Front. Struct. Civ. Eng. 2018. [Google Scholar] [CrossRef]
- Leone, M.; Centonze, G.; Colonna, D.; Micelli, F.; Aiello, M.A. Fiber-reinforced concrete with low content of recycled steel fiber: Shear behaviour. Constr. Build. Mater. 2018, 161, 141–155. [Google Scholar] [CrossRef]
- Yoo, D.-Y.; Yuan, T.; Yang, J.-M.; Yoon, Y.-S. Feasibility of replacing minimum shear reinforcement with steel fibers for sustainable high-strength concrete beams. Eng. Struct. 2017, 147, 207–222. [Google Scholar] [CrossRef]
- Lee, S.-C.; Oh, J.-H.; Cho, J.-Y. Fiber efficiency in SFRC members subjected to uniaxial tension. Constr. Build. Mater. 2016, 113, 479–487. [Google Scholar] [CrossRef]
- Marar, K.; Eren, Ö.; Roughani, H. The influence of amount and aspect ratio of fibers on shear behaviour of steel fiber reinforced concrete. KSCE J. Civ. Eng. 2017, 21, 1393–1399. [Google Scholar] [CrossRef]
- Torres, J.A.; Lantsoght, E.O.L. Influence of Fiber Content on Shear Capacity of Steel Fiber Reinforced Concrete Beams. Preprints 2019. [Google Scholar] [CrossRef]
- Valle, M.; Buyukozturk, O. Behavior of Fiber Reinforced High Strength Concrete Under Direct Shear. ACI Spec. Publ. 1994, 142. [Google Scholar] [CrossRef]
- Khaloo, A.R.; Kim, N. Influence of Concrete and Fiber Characteristics on Behavior of Steel Fiber Reinforced Concrete under Direct Shear. ACI Mater. J. 1997, 94. [Google Scholar] [CrossRef]
- Swamy, R.N.; Mangat, P.S. The interfacial bond stress in steel fiber cement composites. Cem. Concr. Res. 1976, 6, 641–649. [Google Scholar] [CrossRef]
- Zheng, H.; Fang, Z.; Chen, B. Experimental study on shear behavior of prestressed reactive powder concrete I-girders. Front. Struct. Civ. Eng. 2019, 13, 618–627. [Google Scholar] [CrossRef]
- Abbas, Y.M.; Iqbal Khan, M. Influence of Fiber Properties on Shear Failure of Steel Fiber Reinforced Beams Without Web Reinforcement: ANN Modeling. Lat. Am. J. Solids Struct. 2016, 13, 1483–1498. [Google Scholar] [CrossRef]
- Morita, S.; Fuji, S.; Kondo, G. Experimental Study on Size Effect in Concrete Structures. In Proceedings of the JCI International Workshop on Size Effect in Concrete Structures, Sendai, Japan, 31 October–2 November 1993; pp. 21–40. [Google Scholar]
- Ghazavy-Khorasgany, M.; Gopalaratnam, V. Shear Strength of Concrete—Size and other influences. In Proceedings of the JCI International Workshop on Size Effect in Concrete Structures, Sendai, Japan, 31 October–2 November 1993; pp. 51–62. [Google Scholar]
- Minelli, F.; Conforti, A.; Cuenca, E.; Plizzari, G. Are steel fibres able to mitigate or eliminate size effect in shear? Mater. Struct. 2014, 47, 459–473. [Google Scholar] [CrossRef]
- Chalioris, C.E.; Kosmidou, P.-M.K.; Karayannis, C.G. Cyclic Response of Steel Fiber Reinforced Concrete Slender Beams: An Experimental Study. Materials 2019, 12, 1398. [Google Scholar] [CrossRef]
- Soetens, T.; Matthys, S. Shear-stress transfer across a crack in steel fibre-reinforced concrete. Cem. Concr. Compos. 2017, 82, 1–13. [Google Scholar] [CrossRef]
- Reineck, K.H. Ultimate shear force of structural concrete members without transverse reinforcement derived from a mechanical model. ACI Struct. J. 1991, 88, 592–602. [Google Scholar]
- Sherwood, E.G. One-Way Shear Behaviour of Large, Lightly-Reinforced Concrete Beams and Slabs. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2008. [Google Scholar]
- Kaprielov, S.S.; Sheynfeld, A.V.; Chilin, I.A.; Bezgodov, I.M. Properties of Ultra-High-Strength Self-Compacting Fiber-Reinforced Concrete. ACI Spec. Publ. 2018, 326, 60–61. [Google Scholar]
- Stroeven, P. Stereological Principles of Spatial Modeling Applied to Steel Fiber-Reinforced Concrete in Tension. ACI Mater. J. 2009, 106. [Google Scholar] [CrossRef]
- Lakavath, C.; Joshi, S.S.; Prakash, S.S. Investigation of the effect of steel fibers on the shear crack-opening and crack-slip. behavior of prestressed concrete beams using digital image correlation. Eng. Struct. 2019, 193, 28–42. [Google Scholar] [CrossRef]
- Cox, H.L. The elasticity and strength of paper and other fibrous materials. Br. J. Appl. Phys. 1952, 3, 72. [Google Scholar] [CrossRef]
- Romualdi, J.P.; Mandel, J.A. Tensile Strength of Concrete Affected by Uniformly Distributed and Closely Spaced Short Lengths of Wire Reinforcement. ACI J. Proc. 1964, 61. [Google Scholar] [CrossRef]


| Authors | Ref | Expression | |
|---|---|---|---|
| Sarveghadi et al. | [22] | (2) | |
| (3) | |||
| with τ = 4.15 MPa | (4) | ||
| Kwak et al. | [23] | (5) | |
| in MPa | (6) | ||
| (7) | |||
| Greenough and Nehdi | [24] | (8) | |
| Kuntia et al. | [25] | (9) | |
| Sharma | [26] | (10) | |
| Mansur et al. | [27] | (11) | |
| (12) | |||
| (13) | |||
| (14) | |||
| (15) | |||
| (16) | |||
| Ashour et al. | [28] | (17) | |
| (18) | |||
| (19) | |||
| Arslan et al. | [29] | (20) | |
| (21) | |||
| Imam et al. | [30] | (22) | |
| (23) | |||
| (24) | |||
| Yakoub | [31] | (25) | |
| (26) | |||
| (27) | |||
| (28) | |||
| (29) | |||
| (30) | |||
| (31) | |||
| (32) | |||
| Association Française de Génie Civil | [32] | (33) | |
| with γcfγE = 1.5 | (34) | ||
| with θ ≥ 30o | (35) | ||
with K = 1.25 or based on tension tests on the SFRC mix | (36) | ||
| (37) | |||
| (38) | |||
| (39) | |||
| DAfStB | [33] | (40) | |
| with CRd,c = 0.15 and γc = 1.5, ρ ≤ 2% | (41) | ||
| with and | (42) | ||
| with | (43) | ||
| (44) | |||
| (45) | |||
| (46) | |||
| RILEM | [34] | (47) | |
| with ρ ≤ 2% | (48) | ||
| (49) | |||
| (50) | |||
| (51) | |||
| (52) | |||
| fib | [35] | with CRd,c = 0.18, γc = 1.5, and ρ ≤ 2% | (53) |
| (54) | |||
| CNR-DT | [36] | with VRd,f from Equation (53) | (55) |
| (56) | |||
| Input Parameters | Input Number | Min. | Max. | ||
|---|---|---|---|---|---|
| Geometry | b (mm) | width | 1 | 50 | 610 |
| d (mm) | effective depth | 2 | 85.3 | 1118 | |
| av/d (-) | clear shear span to depth ratio | 3 | 0.2 | 6.0 | |
| Properties of reinforcement | ρ (-) | reinforcement ratio | 4 | 0.004 | 0.057 |
| fy (MPa) | yield strength of steel | 5 | 257.9 | 900 | |
| Concrete properties | da (mm) | maximum aggregate size | 6 | 0.4 | 22 |
| fc,cyl (MPa) | average concrete compressive strength | 7 | 9.8 | 215 | |
| Fiber properties | F (-) | fiber factor | 8 | 0.1 | 2.9 |
| ftenf (MPa) | tensile strength of fiber | 9 | 260 | 4913 | |
| Output | Vutot (kN) | sectional shear capacity | 1 | 12.9 | 1480.9 |
| Feature Method | F1 | F2 | F3 | F4 | F5 |
|---|---|---|---|---|---|
| Qualitative Var Represent | Dimensional Analysis | Input Dimensionality Reduction | % Train-Valid-Test | Input Normalization | |
| 1 | Boolean Vectors | Yes | Linear Correlation | 80-10-10 | Linear Max Abs |
| 2 | Eq Spaced in [0, 1] | No | Auto-Encoder | 70-15-15 | Linear [0, 1] |
| 3 | - | - | - | 60-20-20 | Linear [−1, 1] |
| 4 | - | - | Ortho Rand Proj | 50-25-25 | Nonlinear |
| 5 | - | - | Sparse Rand Proj | - | Lin Mean Std |
| 6 | - | - | No | - | No |
| Feature Method | F6 | F7 | F8 | F9 | F10 |
|---|---|---|---|---|---|
| Output Transfer | Output Normalization | Net Architecture | Hidden Layers | Connectivity | |
| 1 | Logistic | Lin [a, b] = 0.7[φmin, φmax] | MLPN | 1 HL | Adjacent Layers |
| 2 | - | Lin [a, b] = 0.6[φmin, φmax] | RBFN | 2 HL | Adj Layers + In-Out |
| 3 | Hyperbolic Tang | Lin [a, b] = 0.5[φmin, φmax] | - | 3 HL | Fully Connected |
| 4 | - | Linear Mean Std | - | - | - |
| 5 | Bilinear | No | - | - | - |
| 6 | Compet | - | - | - | - |
| 7 | Identity | - | - | - | - |
| Feature Method | F11 | F12 | F13 | F14 | F15 |
|---|---|---|---|---|---|
| Hidden Transfer | Parameter Initialization | Learning Algorithm | Performance Improvement | Training Mode | |
| 1 | Logistic | Midpoint (W) + Rands (b) | BP | - | Batch |
| 2 | Identity-Logistic | Rands | BPA | - | Mini-Batch |
| 3 | Hyperbolic Tang | Randnc (W) + Rands (b) | LM | - | Online |
| 4 | Bipolar | Randnr (W) + Rands (b) | ELM | - | - |
| 5 | Bilinear | Randsmall | mb ELM | - | - |
| 6 | Positive Sat Linear | Rand [−Δ, Δ] | I ELM | - | - |
| 7 | Sinusoid | SVD | CI ELM | - | - |
| 8 | Thin-Plate Spline | MB SVD | - | - | - |
| 9 | Gaussian | - | - | - | - |
| 10 | Multiquadratic | - | - | - | - |
| 11 | Radbas | - | - | - | - |
| SA | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 | F15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 6 | 2 | 5 | 7 | 1 | 1 | 1 | 1 | 3 | 2 | 3 | 3 |
| 2 | 1 | 2 | 6 | 2 | 3 | 7 | 1 | 1 | 1 | 1 | 3 | 2 | 5 | 3 |
| 3 | 1 | 2 | 1 | 1 | 5 | 3 | 1 | 1 | 1 | 1 | 3 | 2 | 3 | 3 |
| 4 | 1 | 2 | 6 | 2 | 5 | 1 | 2 | 1 | 1 | 1 | 3 | 2 | 3 | 3 |
| 5 | 1 | 2 | 6 | 3 | 5 | 1 | 3 | 1 | 1 | 1 | 3 | 2 | 3 | 3 |
| 6 | 1 | 2 | 6 | 3 | 5 | 7 | 4 | 1 | 1 | 1 | 3 | 2 | 3 | 3 |
| 7 | 1 | 2 | 6 | 4 | 5 | 7 | 5 | 1 | 1 | 1 | 3 | 2 | 3 | 3 |
| 8 | 1 | 2 | 6 | 4 | 5 | 7 | 5 | 1 | 1 | 1 | 1 | 5 | 3 | 3 |
| 9 | 1 | 2 | 6 | 4 | 5 | 7 | 5 | 1 | 3 | 3 | 1 | 5 | 3 | 3 |
| SA | ANN | ||||
|---|---|---|---|---|---|
| Max Error (%) | Performance all Data (%) | Errors > 3% (%) | Total Hidden Nodes | Running Time/Data Point (s) | |
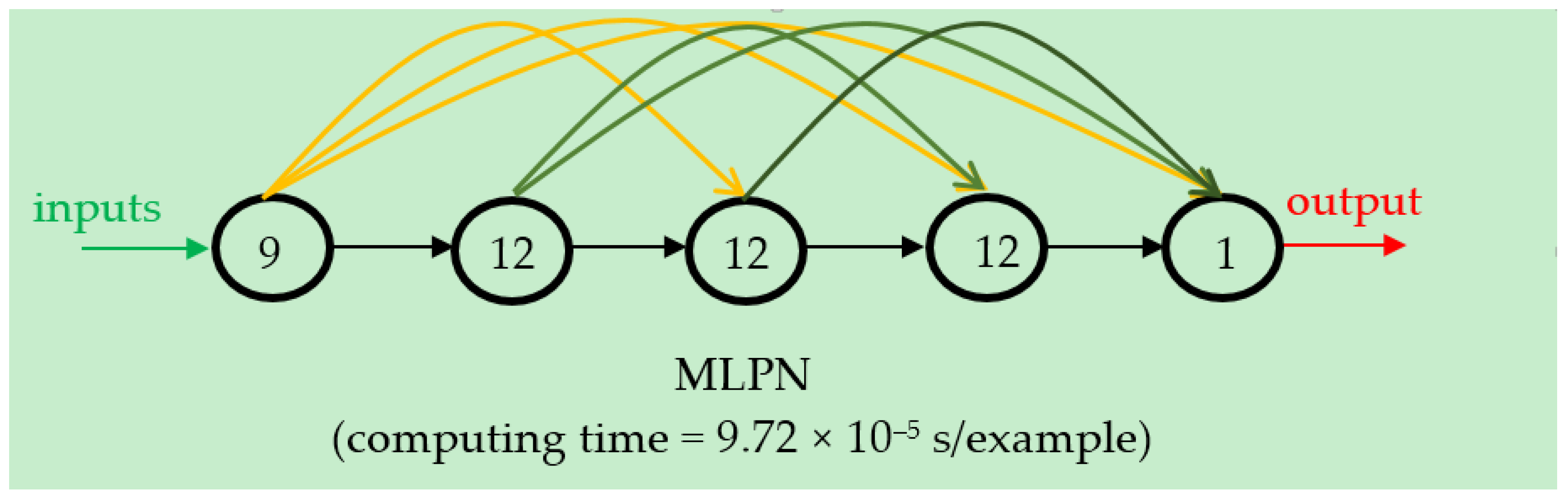
| 1 | 24.2 | 0.7 | 5.6 | 36 | 1.88 × 10−4 |
| 2 | 1375.2 | 21.6 | 83.7 | 120 | 9.96 × 10−5 |
| 3 | 15.4 | 0.5 | 4.0 | 36 | 1.31 × 10−4 |
| 4 | 11.7 | 0.5 | 4.0 | 36 | 1.14 × 10−4 |
| 5 | 15.9 | 0.7 | 7.0 | 36 | 1.06 × 10−4 |
| 6 | 12.7 | 0.5 | 3.0 | 36 | 9.58 × 10−5 |
| 7 | 67.0 | 5.3 | 40.0 | 36 | 1.07 × 10−4 |
| 8 | 90.0 | 4.0 | 24.0 | 36 | 1.10 × 10−4 |
| 9 | 0.0 | 0.0 | 0.0 | 36 | 9.72 × 10−5 |
| Model | AVG | STD | COV | Min | Max |
|---|---|---|---|---|---|
| Proposed model | 1.00 | 1.08 × 10−15 | 1.08 × 10−15 | 1.00 | 1.00 |
| Sarveghadi et al. [22] | 1.03 | 0.29 | 28% | 0.23 | 2.49 |
| Kwak et al. [23] | 1.01 | 0.28 | 27% | 0.27 | 2.39 |
| Greenough and Nehdi [24] | 1.34 | 0.48 | 36% | 0.31 | 3.11 |
| Khuntia et al. [25] | 1.81 | 0.85 | 47% | 0.18 | 6.53 |
| Imam et al. [30] | 0.97 | 0.36 | 37% | 0.06 | 2.51 |
| Sharma [26] | 1.24 | 0.49 | 39% | 0.18 | 3.59 |
| Mansur et al. [27] | 1.30 | 0.60 | 46% | 0.15 | 3.85 |
| Ashour et al. [28] 1 | 1.08 | 0.38 | 35% | 0.24 | 3.14 |
| Ashour et al. [28] 2 | 1.29 | 0.37 | 29% | 0.31 | 3.22 |
| Arslan et al. [29] | 1.17 | 0.37 | 31% | 0.43 | 3.24 |
| Yakoub [31] 1 | 1.90 | 0.76 | 40% | 0.28 | 7.50 |
| Yakoub [31] 2 | 2.97 | 1.37 | 46% | 0.51 | 17.48 |
| French code [32] | 1.85 | 0.88 | 48% | 0.22 | 5.95 |
| German code [33] | 1.12 | 0.31 | 27% | 0.21 | 2.13 |
| fib [35] | 1.24 | 0.36 | 29% | 0.30 | 2.33 |
| RILEM [34] | 1.16 | 0.33 | 29% | 0.23 | 2.28 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abambres, M.; Lantsoght, E.O.L. ANN-Based Shear Capacity of Steel Fiber-Reinforced Concrete Beams without Stirrups. Fibers 2019, 7, 88. https://doi.org/10.3390/fib7100088
Abambres M, Lantsoght EOL. ANN-Based Shear Capacity of Steel Fiber-Reinforced Concrete Beams without Stirrups. Fibers. 2019; 7(10):88. https://doi.org/10.3390/fib7100088
Chicago/Turabian StyleAbambres, Miguel, and Eva O.L. Lantsoght. 2019. "ANN-Based Shear Capacity of Steel Fiber-Reinforced Concrete Beams without Stirrups" Fibers 7, no. 10: 88. https://doi.org/10.3390/fib7100088
APA StyleAbambres, M., & Lantsoght, E. O. L. (2019). ANN-Based Shear Capacity of Steel Fiber-Reinforced Concrete Beams without Stirrups. Fibers, 7(10), 88. https://doi.org/10.3390/fib7100088






