Simulation of Convection–Diffusion Transport in a Laminar Flow Past a Row of Parallel Absorbing Fibers
Abstract
1. Introduction
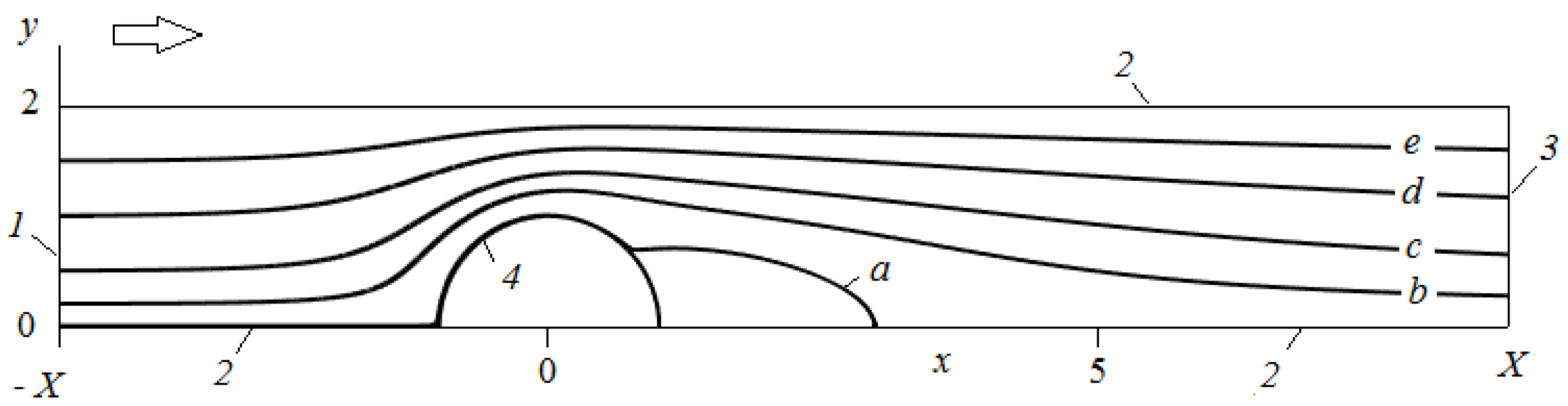
2. Flow Field in a System of Parallel Fibers at Re > 1
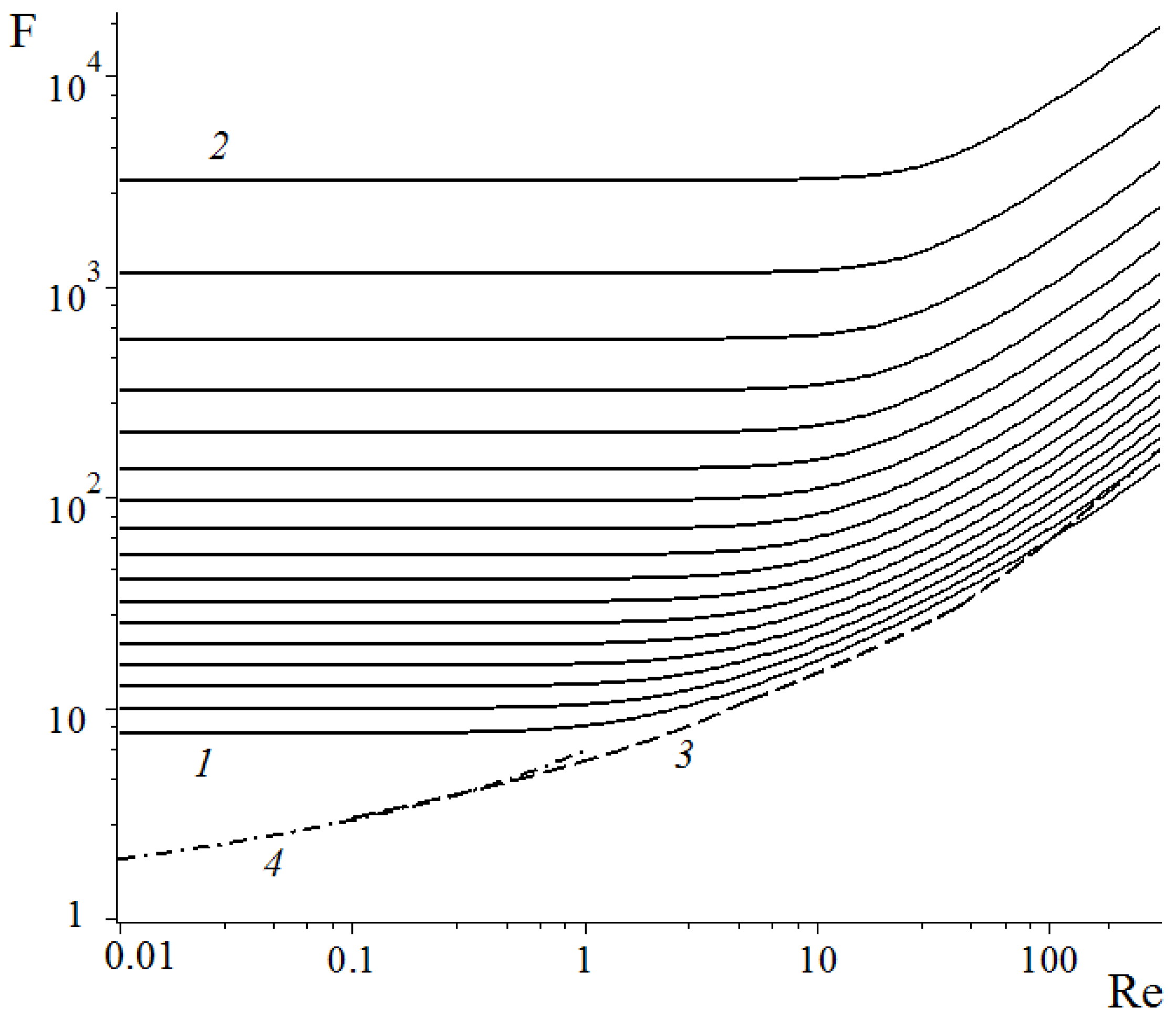
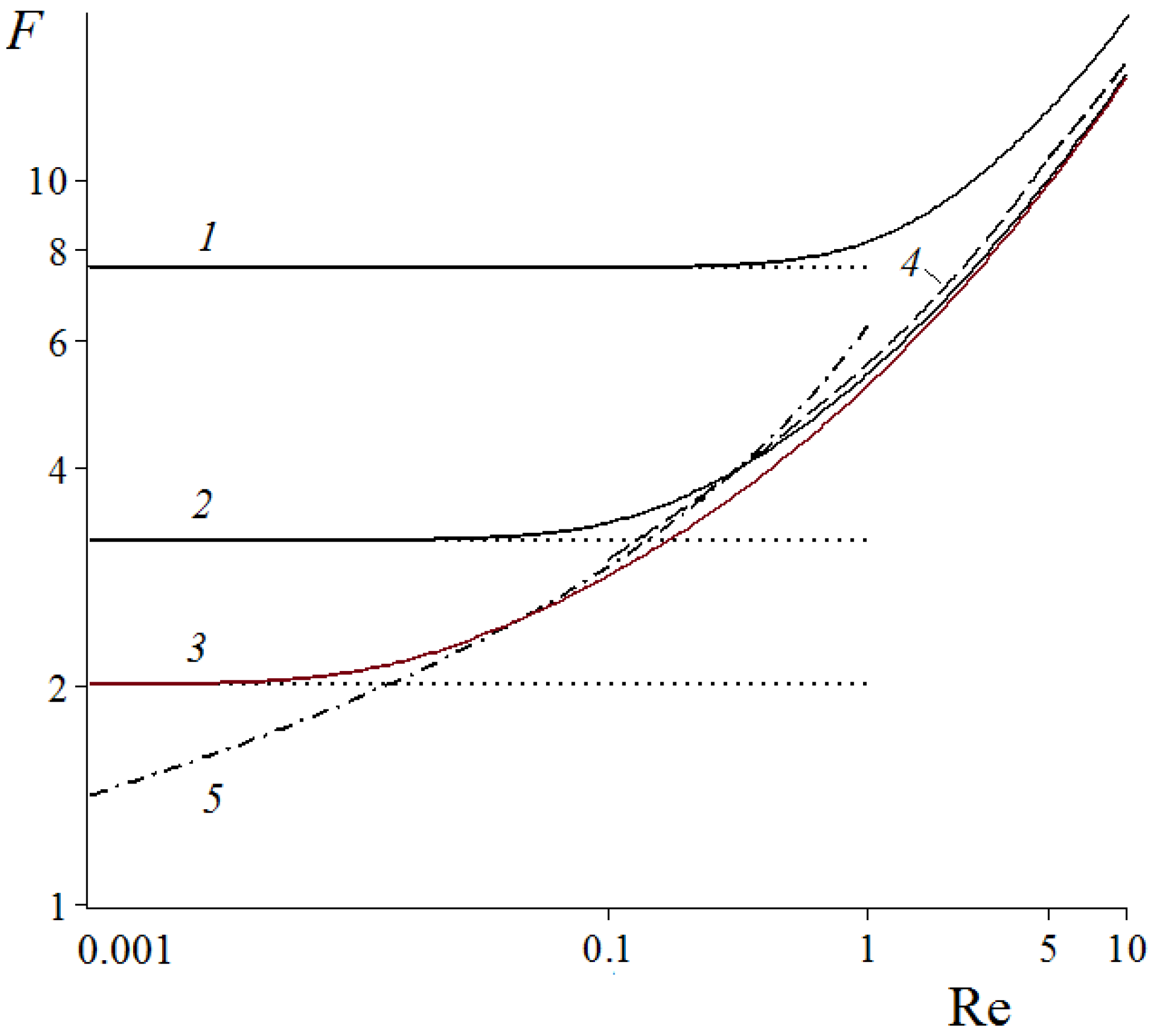
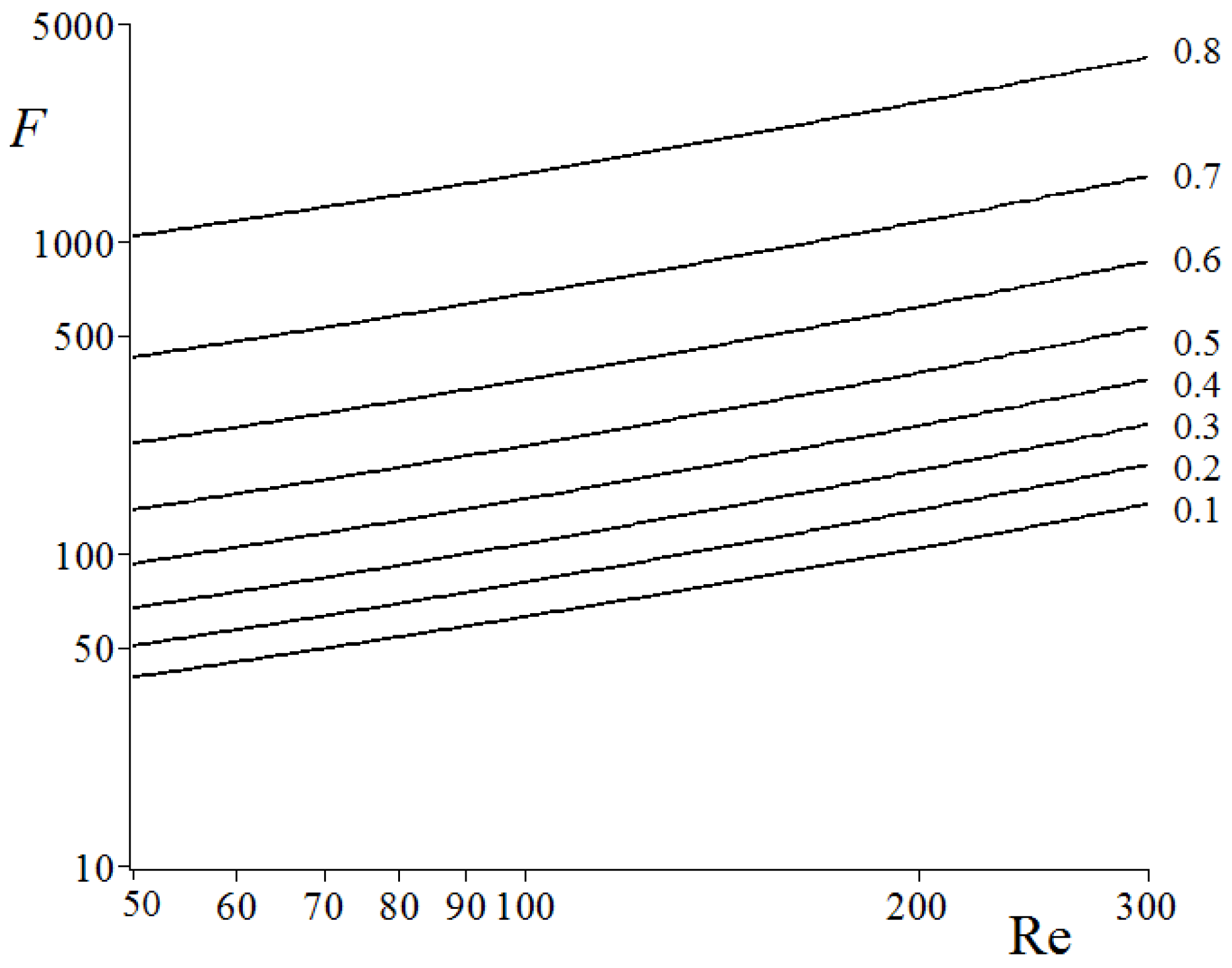
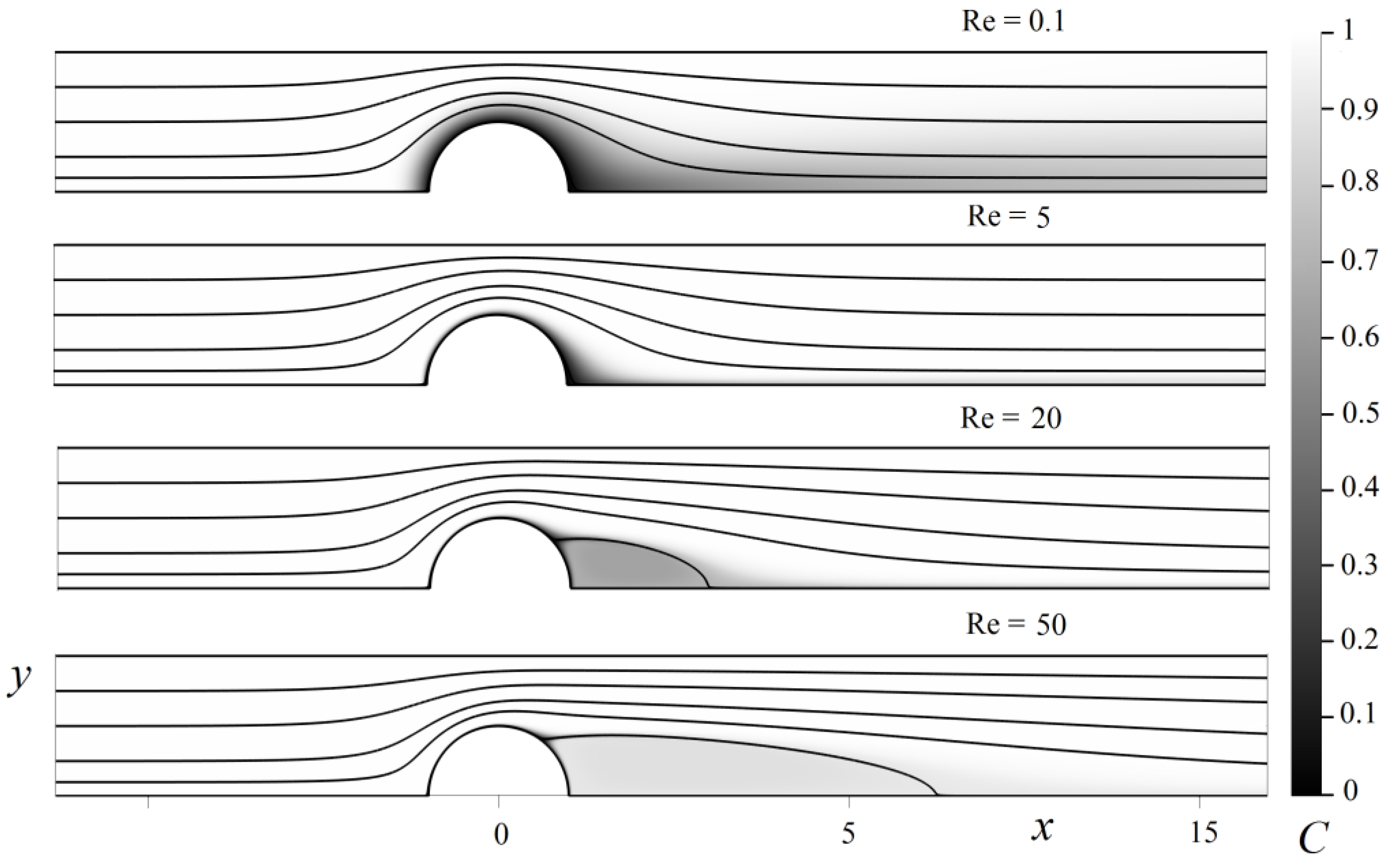
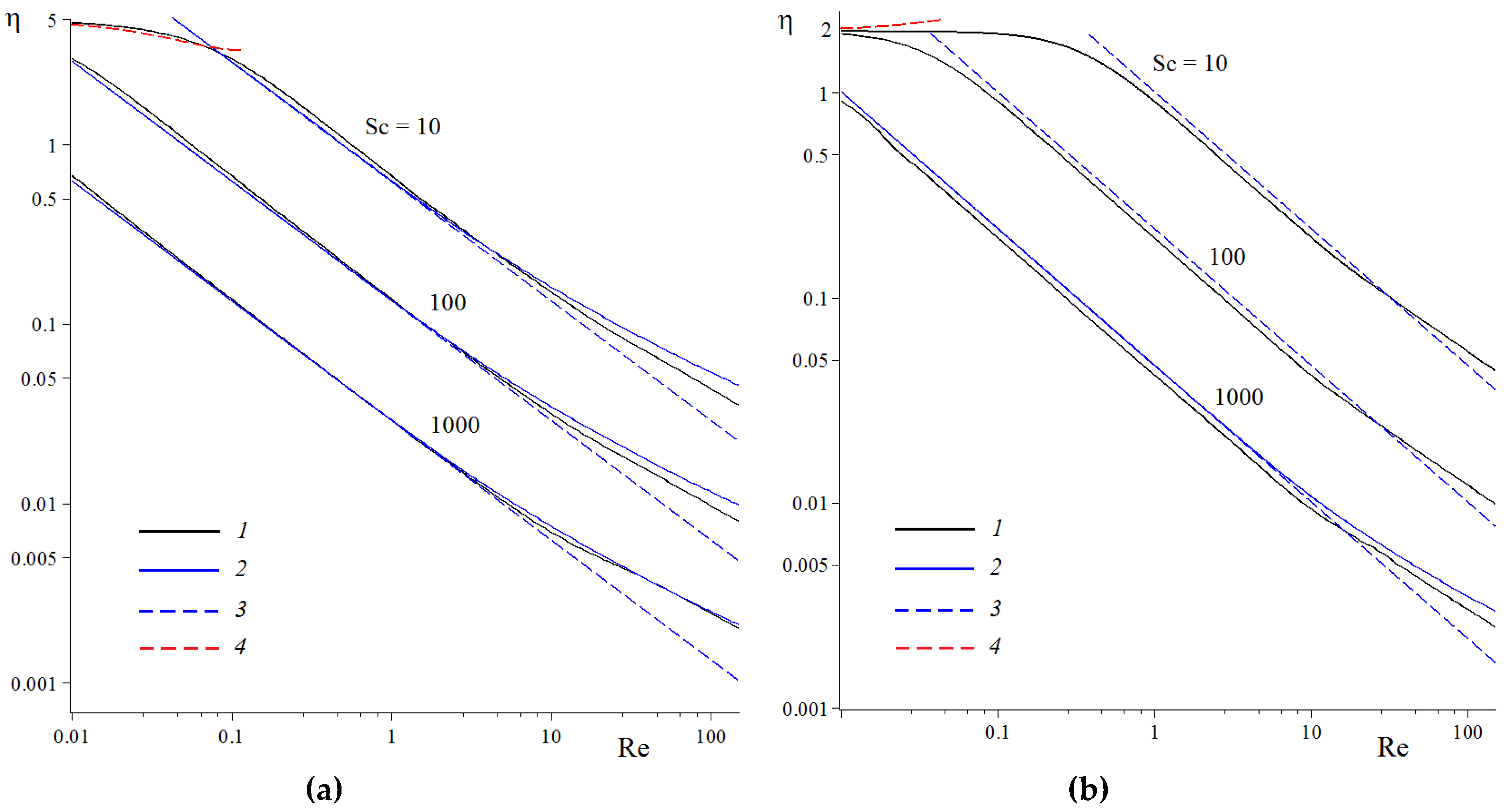
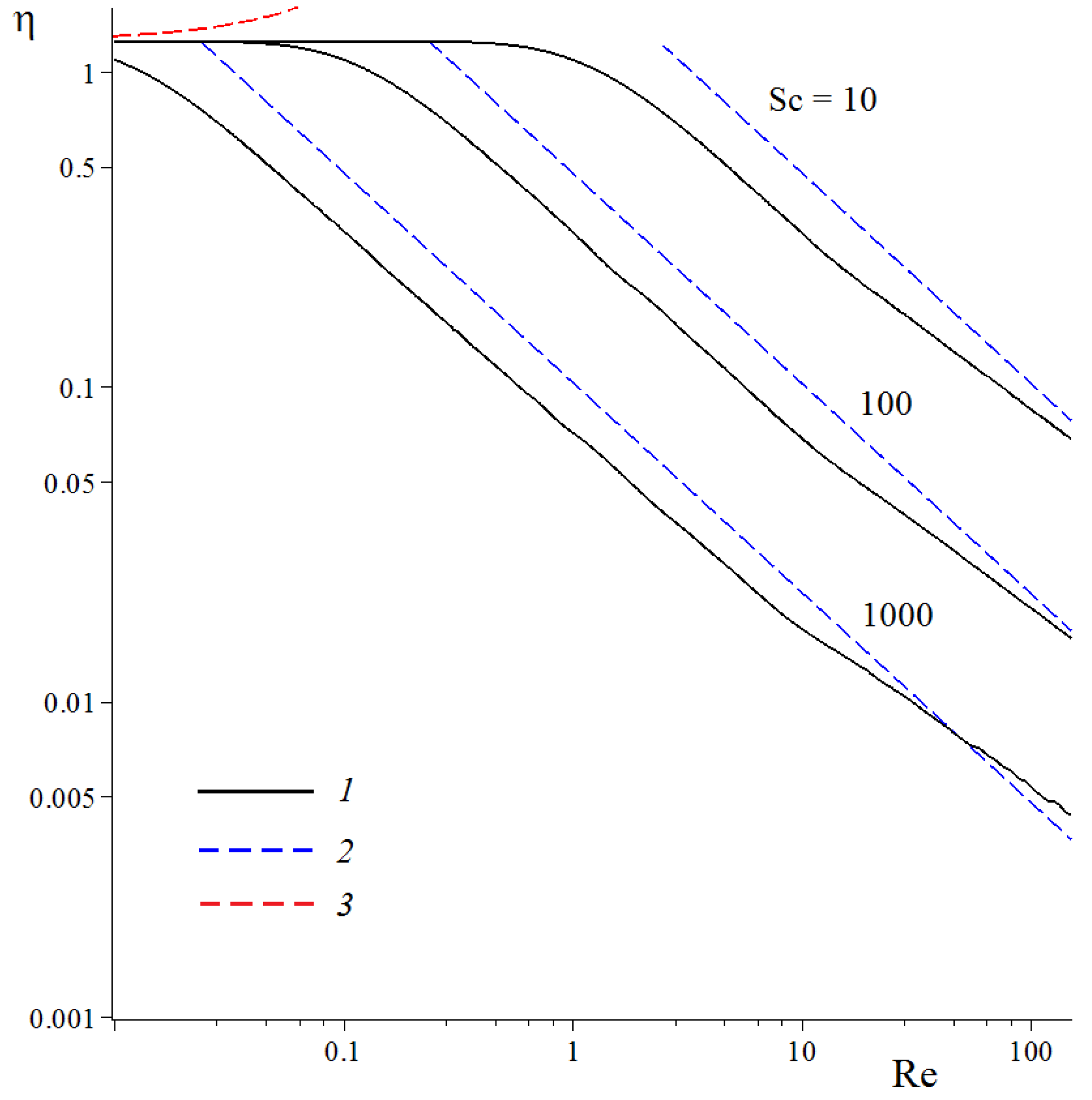
3. Convection–Diffusion Mass Transfer in a System of Absorbing Fibers
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix
| Coefficients in Equation (A1) | |||||
|---|---|---|---|---|---|
| A | 2.1217 | 289.9297 | 26.9531 | 39.913 | −300.7297 |
| B | −1.1934 | −215.0368 | −19.077 | −31.4594 | 222.6869 |
| C | 0.2835 | 61.5072 | 5.3081 | 9.5571 | − 63.5653 |
| D | −0.0312 | −7.4111 | −0.635 | −1.1996 | 7.654 |
| E | 0.0013 | 0.3224 | 0.0277 | 0.5381 | −0.3330 |
| Coefficientsin Equation (A1) | |||||||
|---|---|---|---|---|---|---|---|
| A | −16,813.6833 | −8371.0393 | −737.937 | 10.4997 | 1.348 | −24.9981 | 16,818.5536 |
| B | 5090.8957 | 2496.3936 | 264.9326 | −39.2739 | 5.7935 | 31.2227 | −5096.2083 |
| C | 176.1791 | 107.063 | −13.1498 | 18.2408 | −3.2293 | −11.6302 | −174.2677 |
| D | 42,356.9489 | 21,175.9228 | 1767.2858 | 57.3744 | 1.0235 | 1.5894 | −42,357.2119 |
| E | −406.1734 | −202.9051 | −17.1196 | −0.4041 | −0.0559 | −0.1074 | 406.1907 |
References
- Kirsch, A.A.; Stechkina, I.B. The theory of aerosol filtration with fibrous filters. In Fundamentals of Aerosol Science; Shaw, D.T., Ed.; John Wiley & Sons: Hoboken, NY, USA, 1978; pp. 165–256, ISBN-10: 0471029491. [Google Scholar]
- Kirsch, V.A.; Kirsch, A.A. Deposition of aerosol nanoparticles in model fibrous filters. In Aerosols–Science and Technology; Agranovski, I., Ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2010; pp. 283–314. [Google Scholar]
- Bazhenov, S.D.; Bildyukevich, A.V.; Volkov, A.V. Gas-liquid hollow fiber membrane contactors for different applications. Fibers 2018, 6, 76. [Google Scholar] [CrossRef]
- Ovcharova, A.; Vasilevsky, V.; Borisov, I.; Bazhenov, S.; Volkov, A.; Bildyukevich, A.; Volkov, V. Polysulfone porous hollow fiber membranes for ethylene-ethane separation in gas-liquid membrane contactor. Sep. Purif. Technol. 2017, 183, 162–172. [Google Scholar] [CrossRef]
- Scholes, C.A.; Kentish, S.E.; Stevens, G.W.; Jin, J.; deMontigny, D. Thin-film composite membrane contactors for desorption of CO2 from monoethanolamine at elevated temperatures. Sep. Purif. Technol. 2015, 156, 841–847. [Google Scholar] [CrossRef]
- Bildyukevich, A.V.; Plisko, T.V.; Liubimova, A.S.; Volkov, V.V.; Usosky, V.V. Hydrophilization of polysulfone hollow fiber membranes via addition of polyvinylpyrrolidone to the bore fluid. J. Membr. Sci. 2017, 524, 537–549. [Google Scholar] [CrossRef]
- Thong, Z.; Gao, J.; Lim, J.X.Z.; Wang, K.-Y.; Chung, T.-S. Fabrication of loose outer-selective nanofiltration (NF) polyethersulfone (PES) hollow fibers via single-step spinning process for dye removal. Sep. Purif. Technol. 2018, 192, 483–490. [Google Scholar] [CrossRef]
- Dibrov, G.; Ivanov, M.; Semyashkin, M.; Sudin, V.; Kagramanov, G. High-Pressure Aging of Asymmetric Torlon® Hollow Fibers for Helium Separation from Natural Gas. Fibers 2018, 6, 83. [Google Scholar] [CrossRef]
- Babu, V.P.; Kraftschik, B.E.; Koros, W.J. Crosslinkable TEGMC asymmetric hollow fiber membranes for aggressive sour gas separations. J. Membr. Sci. 2018, 558, 94–105. [Google Scholar] [CrossRef]
- Günther, J.; Schmitz, P.; Albasi, C.; Lafforgue, C. A numerical approach to study the impact of packing density on fluid flow distribution in hollow fiber module. J. Membr. Sci. 2010, 348, 277–286. [Google Scholar] [CrossRef]
- Li, G.-P.; Zhang, L.-Z. Conjugate heat and mass transfer in a cross-flow hollow fiber membrane bundle used for seawater desalination considering air side turbulence. J. Membr. Sci. 2017, 533, 321–335. [Google Scholar] [CrossRef]
- Usman, M.; Dai, Z.; Hillestad, M.; Deng, L. Mathematical modelling and validation of CO2 mass transfer in a membrane contactor using ionic liquids for pre-combustion CO2 Capture. Chem. Eng. Res. Des. 2017, 123, 377–387. [Google Scholar] [CrossRef]
- Razavi, S.M.R.; Rezakazemi, M.; Albadarin, A.B.; Shirazian, S. Simulation of CO2 absorption by solution of ammonium ionic liquid in hollow-fiber contactors. Chem. Eng. Process. Process. Intensif. 2016, 108, 27–34. [Google Scholar] [CrossRef]
- Tantikhajorngosol, P.; Laosiripojana, N.; Jiraratananon, R.; Assabumrungrat, S. Physical absorption of CO2 and H2S from synthetic biogas at elevated pressures using hollow fiber membrane contactors: The effects of Henry’s constants and gas diffusivities. Int. J. Heat Mass Transf. 2019, 128, 1136–1148. [Google Scholar] [CrossRef]
- Sabelfeld, M.; Geißen, S.-U. Effect of helical structure on ozone mass transfer in a hollow fiber membrane contactor. J. Membr. Sci. in press. Available online: https://doi.org/10.1016/j.memsci.2018.10.056 (accessed on 20 November 2018). [CrossRef]
- Kirsch, V.A.; Roldugin, V.I.; Bildyukevich, A.V.; Volkov, V.V. Simulation of convective-diffusional processes in hollow fiber membrane contactors. Sep. Purif. Technol. 2016, 167, 63–69. [Google Scholar] [CrossRef]
- Miyagi, T. Viscous flow at low Reynolds numbers past an infinite row of equal circular cylinders. J. Phys. Soc. Japan 1958, 13, 493–496. [Google Scholar] [CrossRef]
- Tamada, К.; Fujikawa, Н. The steady two-dimensional flow of viscous fluid at low Re numbers passing through an infinite row of equal parallel circular cylinders. Quart. J. Mech. Appl. Math. 1957, 10, 425–432. [Google Scholar] [CrossRef]
- Golovin, A.M.; Lopatin, V.A. The flow of a viscous fluid through a doubly periodic rows of cylinders (English transl.). J. Appl. Mech. Techn. Physics. 1968, 9, 198–201. [Google Scholar] [CrossRef]
- Sangani, A.; Acrivos, A. Slow flow past periodic arrays of cylinders with application to heat transfer. Int. J. Multiph. Flow 1982, 8, 193–206. [Google Scholar] [CrossRef]
- Wang, W.; Sangani, A.S. Nusselt number for flow perpendicular to arrays of cylinders in the limit of small Reynolds and large Peclet numbers. Phys. Fluids 1997, 9, 1529–1539. [Google Scholar] [CrossRef]
- Fornberg, B. Steady incompressible flow past a row of circular cylinders. J. Fluid Mech. 1991, 225, 655–671. [Google Scholar] [CrossRef]
- Gajjar, J.S.B.; Azzam, N.A. Numerical solution of the Navier–Stokes equations for the flow in a cylinder cascade. J. Fluid Mech. 2004, 520, 51–82. [Google Scholar] [CrossRef]
- Li, T.; Deen, N.G.; Kuipers, J.A.M. Numerical investigation of hydrodynamics and mass transfer for in-line fiber arrays in laminar cross-flow at low Reynolds numbers. Chem. Eng. Sci. 2005, 60, 1837–1847. [Google Scholar] [CrossRef]
- Kirsh, V.A.; Shabatin, A.V.; Vysotskii, V.V.; Roldughin, V.I. Simulation of aerosol fibrous filters at Reynolds numbers of the order of unity. Colloid J. 2015, 77, 160–164. [Google Scholar] [CrossRef]
- Launder, B.E.; Massey, T.H. The Numerical Prediction of Viscous Flow and Heat Transfer in Tube Banks. ASME J. Heat Transf. 1978, 100, 565–571. [Google Scholar] [CrossRef]
- Martin, A.; Saltiel, C.; Shyy, W. Frictional losses and convective heat transfer in sparse, periodic cylinder arrays in cross flow. Int. J. Heat Mass Transf. 1998, 41, 2383–2397. [Google Scholar] [CrossRef]
- Ram, R.P.; Bharti, R.P.; Dhiman, A.K. Forced convection flow and heat transfer across an in-line bank of circular cylinders. Can. J. Chem. Eng. 2016, 94, 1381–1395. [Google Scholar] [CrossRef]
- Keller, J.B. Viscous flow through a grating or lattice of cylinders. J. Fluid Mech. 1964, 18, 94–96. [Google Scholar] [CrossRef]
- Wang, C.Y. Stokes flow through a rectangular array of circular cylinders. Fluid Dyn. Res. 2001, 29, 65–80. [Google Scholar] [CrossRef]
- Koch, D.L.; Ladd, A.J.C. Moderate Reynolds number flows through periodic and random arrays of aligned cylinders. J. Fluid Mech. 1997, 349, 31–66. [Google Scholar] [CrossRef]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles; Academic Press: New York, NY USA, 1978; p. 154. ISBN 012176950X. [Google Scholar]
- Lamb, H. Hydrodynamics, 6th Revised ed.; Dover Publications: New York, NY, USA, 1954; ISBN-10: 0486602567. [Google Scholar]
- Berkovskii, B.M.; Polevikov, V.K. Effect of the Prandtl number on the convection field and the heat transfer during natural convection (English translation). J. Eng. Phys. 1973, 24, 598–603. [Google Scholar] [CrossRef]
- Kirsh, V.A. Deposition of aerosol nanoparticles in fibrous filters. Colloid J. 2003, 65, 726–732. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Kutepov, A.M.; Kazenin, D.A.; Vyazmin, A.V. Hydrodynamics, Mass and Heat Transfer in Chemical Engineering. Series: Topics in Chemical Engineering (Book 14), 1st ed.; CRC Press: Boca Raton, FL, USA, 2001; ISBN-10: 0415272378. [Google Scholar]
- Natanson, G.L. Diffusional precipitation of aerosols on a streamlined cylinder with a small capture coefficient (English translation, Dokl. Akad. Nauk SSSR). Proc. Acad. Sci. USSR Phys. Chem. Sec. 1957, 112, 21–25. [Google Scholar]
- Chernyakov, A.L.; Kirsh, A.A.; Roldugin, V.I.; Stechkina, I.B. Diffusion deposition of aerosol particles on fibrous filters at small Peclet numbers. Colloid J. 2000, 62, 490–494. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kirsch, V.A.; Bildyukevich, A.V.; Bazhenov, S.D. Simulation of Convection–Diffusion Transport in a Laminar Flow Past a Row of Parallel Absorbing Fibers. Fibers 2018, 6, 90. https://doi.org/10.3390/fib6040090
Kirsch VA, Bildyukevich AV, Bazhenov SD. Simulation of Convection–Diffusion Transport in a Laminar Flow Past a Row of Parallel Absorbing Fibers. Fibers. 2018; 6(4):90. https://doi.org/10.3390/fib6040090
Chicago/Turabian StyleKirsch, Vasily A., Alexandr V. Bildyukevich, and Stepan D. Bazhenov. 2018. "Simulation of Convection–Diffusion Transport in a Laminar Flow Past a Row of Parallel Absorbing Fibers" Fibers 6, no. 4: 90. https://doi.org/10.3390/fib6040090
APA StyleKirsch, V. A., Bildyukevich, A. V., & Bazhenov, S. D. (2018). Simulation of Convection–Diffusion Transport in a Laminar Flow Past a Row of Parallel Absorbing Fibers. Fibers, 6(4), 90. https://doi.org/10.3390/fib6040090






