Preparation and Behavior of Bamboo Fiber-Reinforced Polydimethylsiloxane Composite Foams during Compression
Abstract
1. Introduction
2. Materials and Methods
2.1. Fiber Preparation
2.2. Bamboo Fiber-Reinforced PDMS Foam
2.3. Mechanical, Thermal and Morphological Characterization
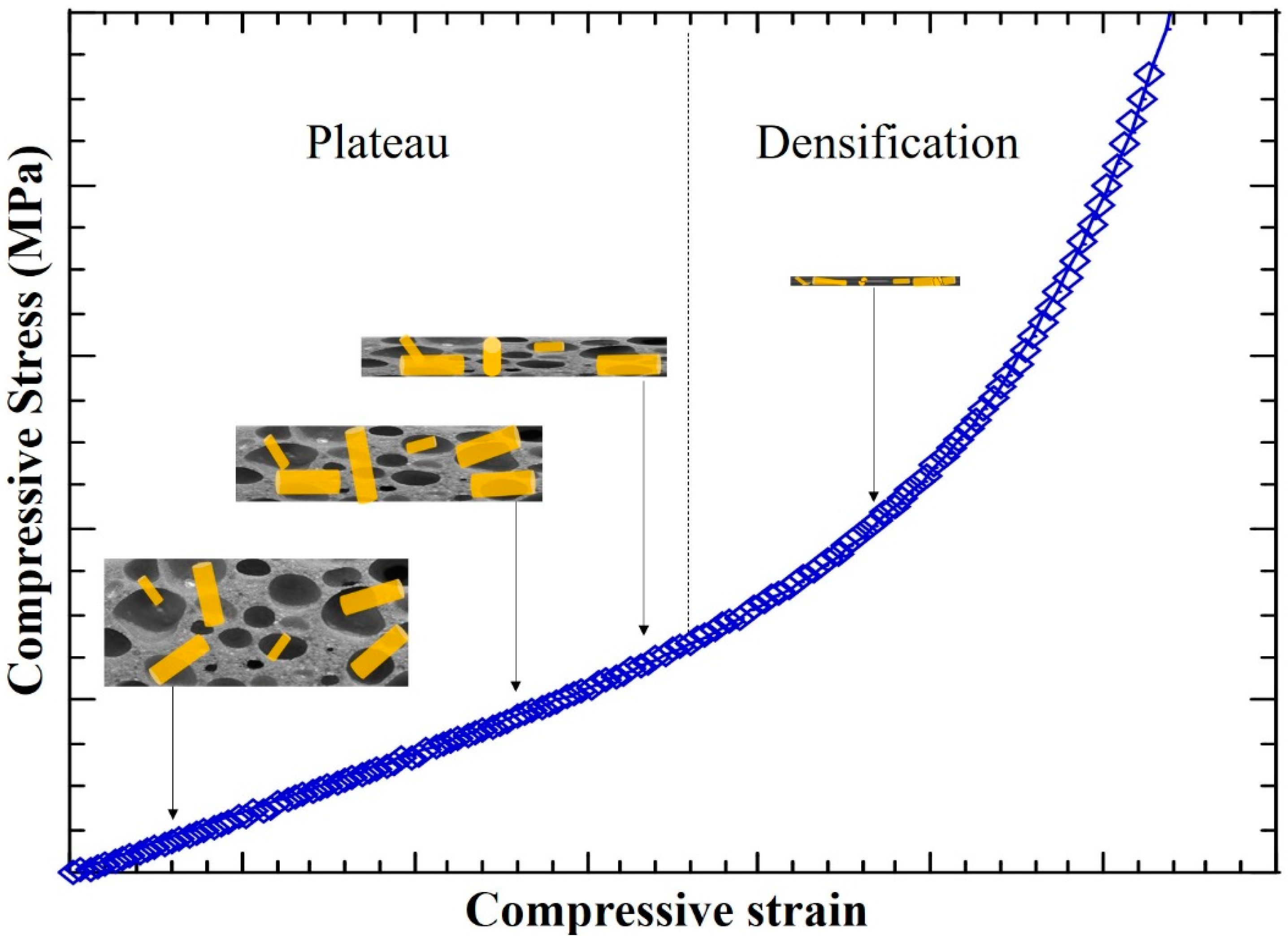
3. Mathematical Model
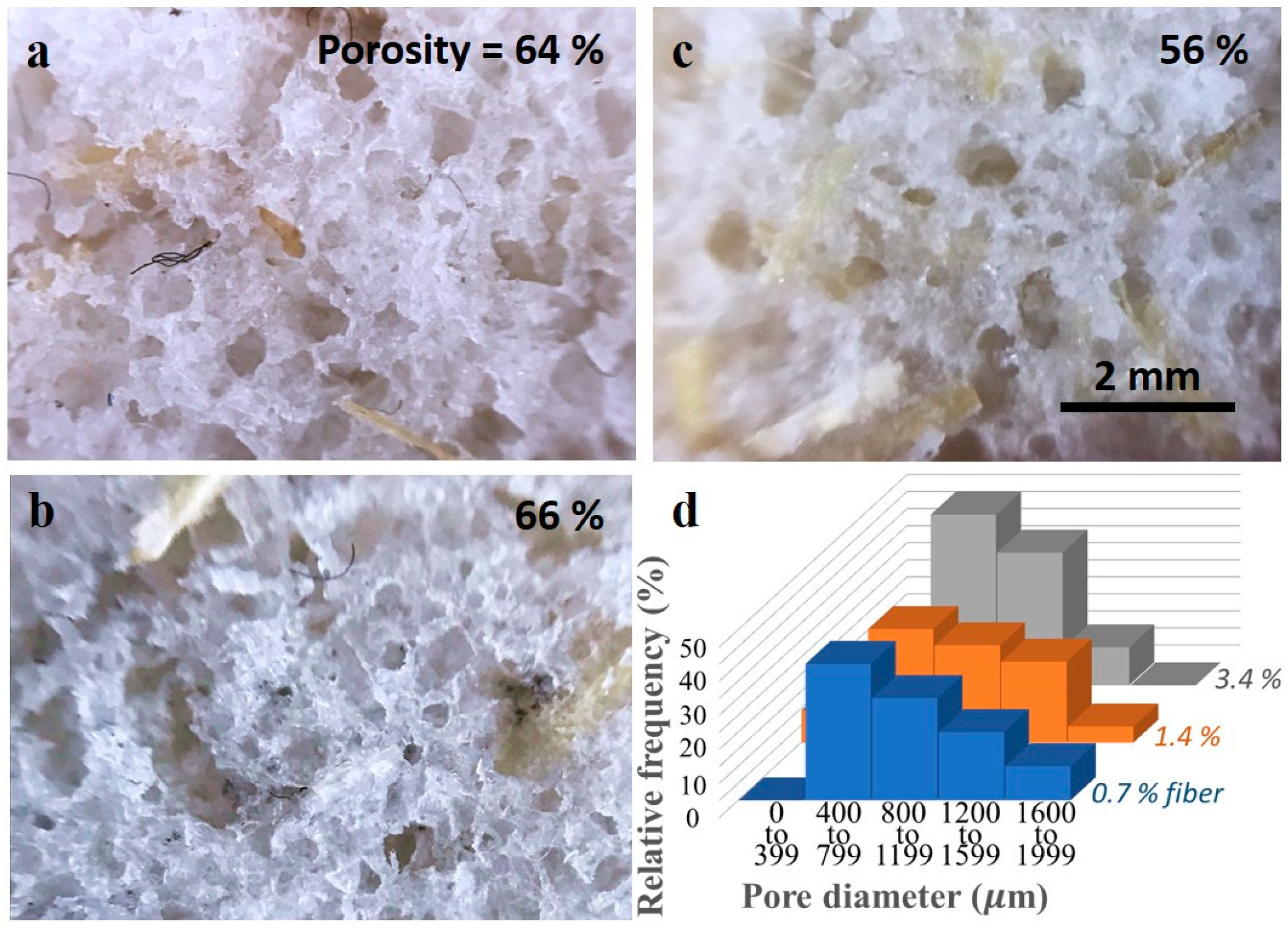
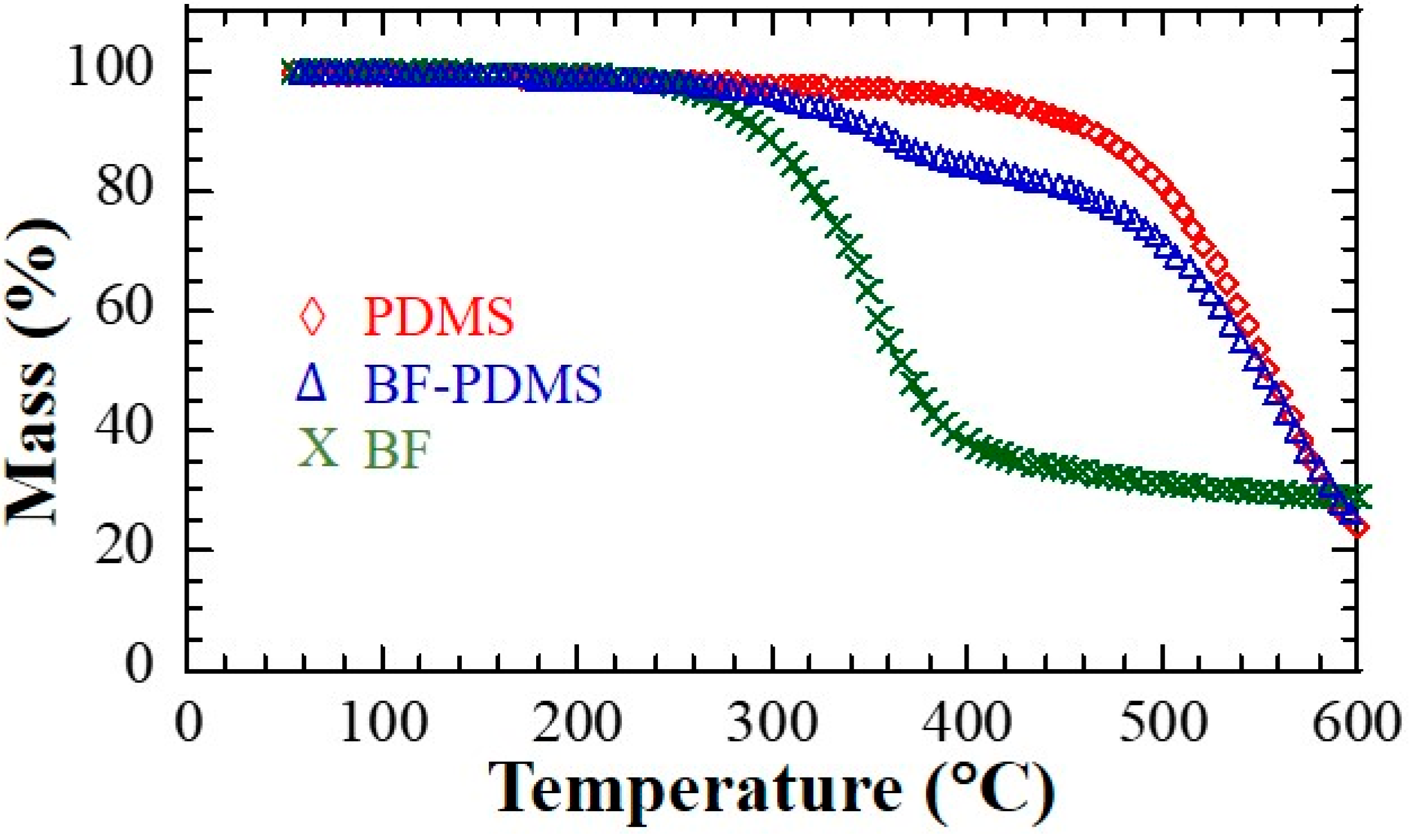
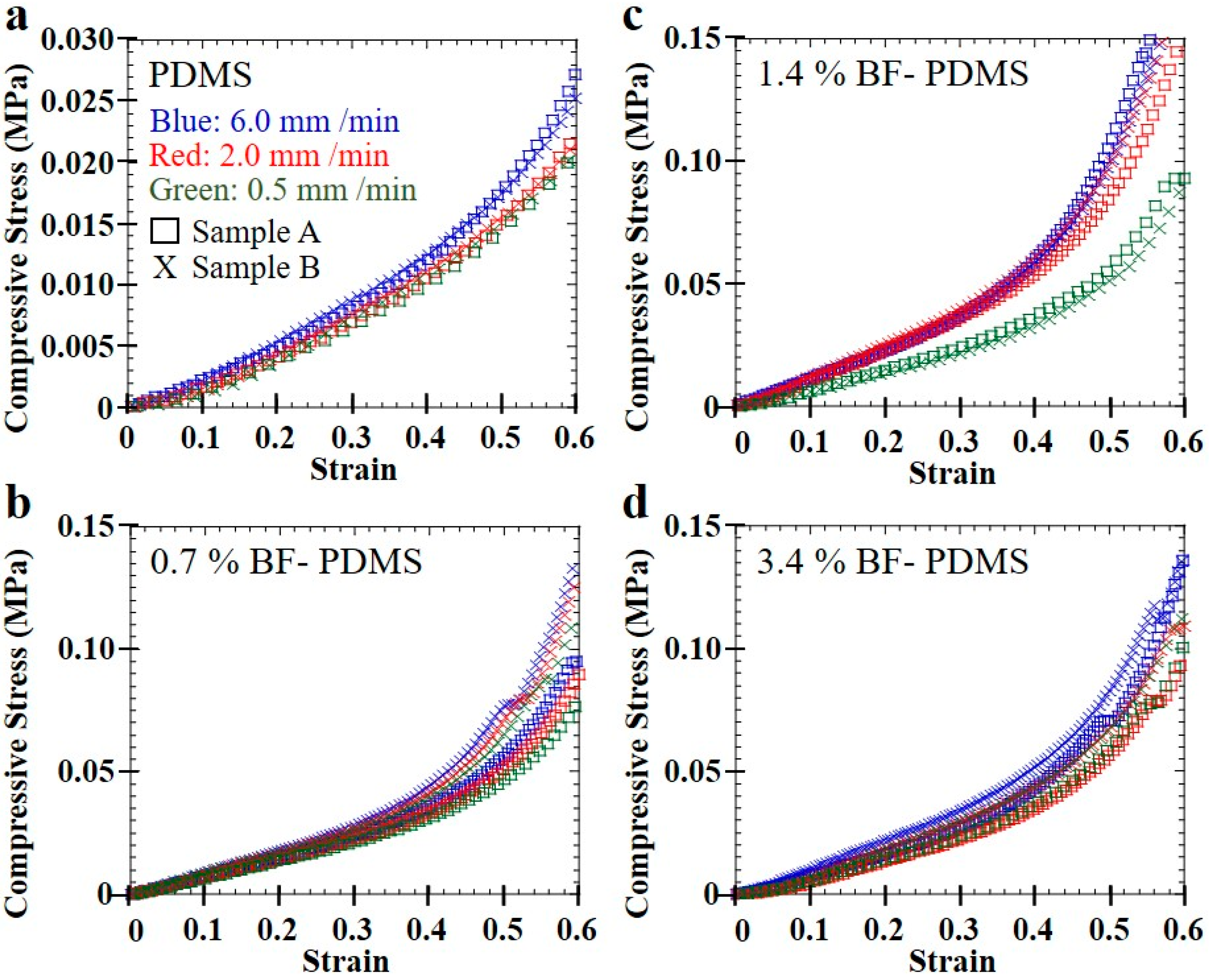
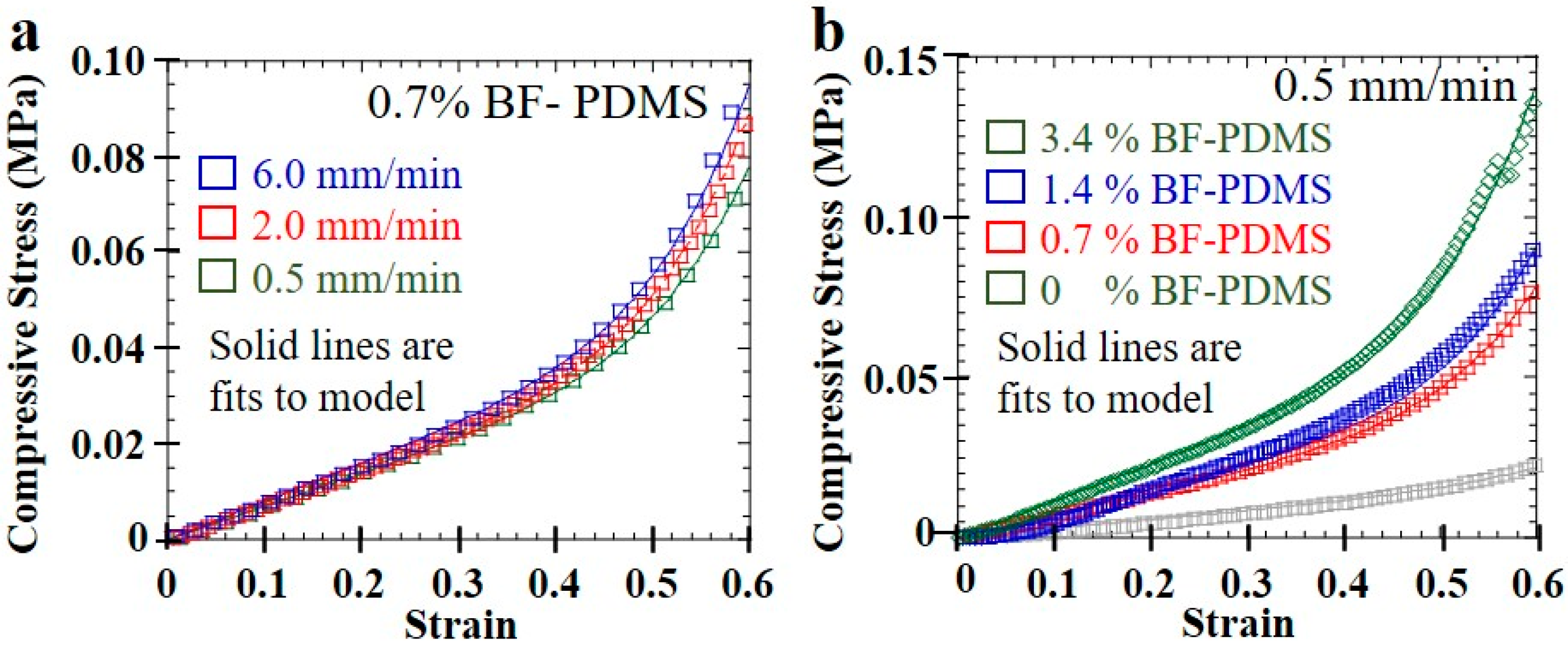
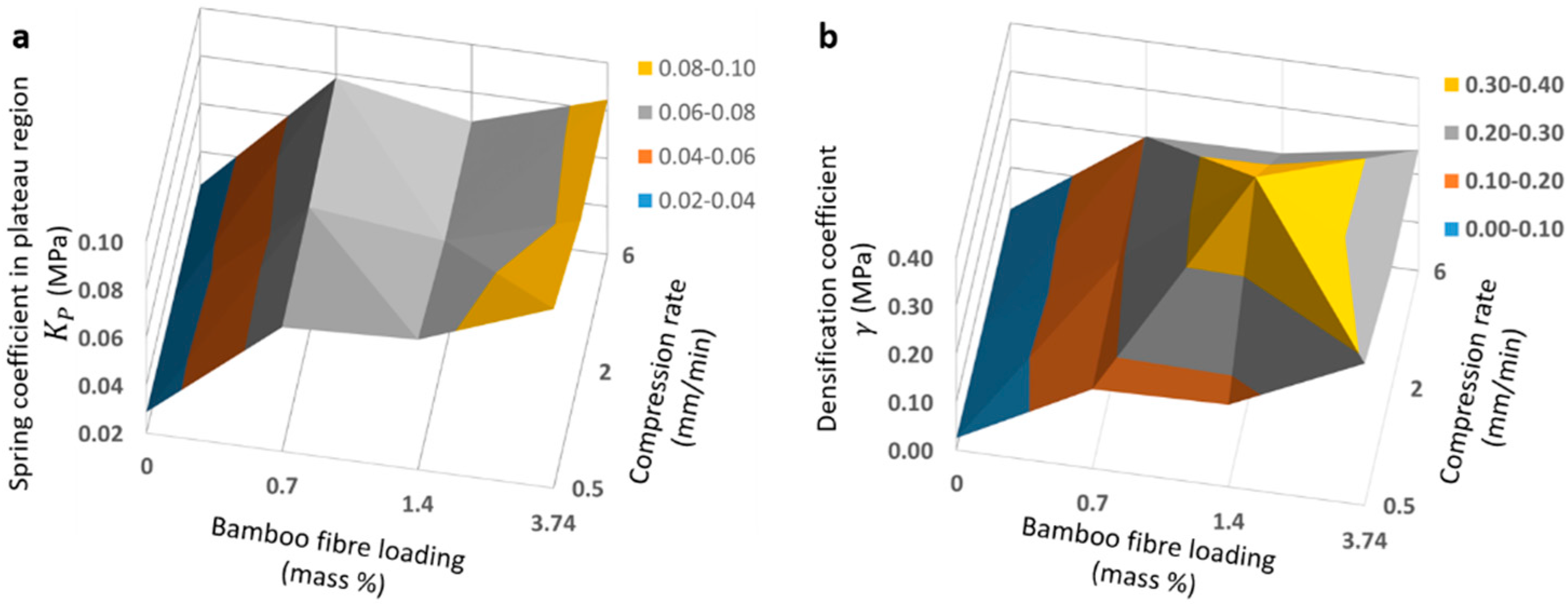
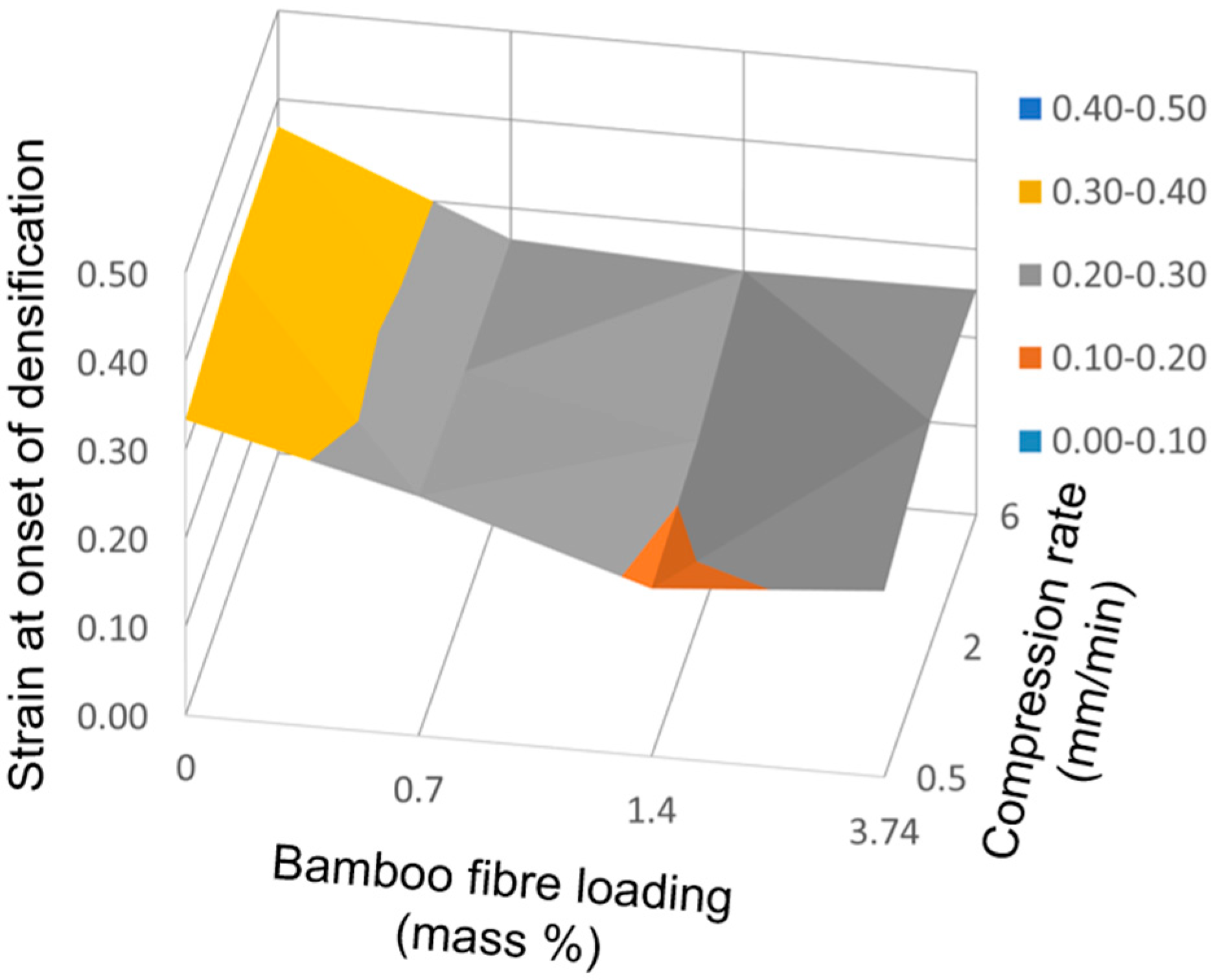
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ba, A.; Kovalenko, A.; Aristégui, C.; Mondain-Monval, O.; Brunet, T. Soft porous silicone rubbers with ultra-low sound speeds in acoustic metamaterials. Sci. Rep. 2017, 7, 40106. [Google Scholar] [CrossRef] [PubMed]
- Zuruzi, A.S.; Tuah, M.H.; Daruis, A.; Amirul, A.; Norfatriah, A.; Nurmawati, M.H. Towards wearable pressure sensors using multiwall carbon nanotube/polydimethylsiloxane nanocomposite foams. Mater. Des. 2017, 132, 449–458. [Google Scholar] [CrossRef]
- Zhu, D.; Handschuh-Wang, S.; Zhou, X. Recent progress in fabrication and application of polydimethylsiloxane sponges. J. Mater. Chem. A 2017, 5, 16467–16497. [Google Scholar] [CrossRef]
- Choi, S.-J.; Kwon, T.-H.; Im, H.; Moon, D.-I.; Baek, D.J.; Seol, M.-L.; Duarte, J.P.; Choi, Y.-K. A Polydimethylsiloxane (PDMS) Sponge for the Selective Absorption of Oil from Water. ACS Appl. Mater. Interfaces 2011, 3, 4552–4556. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Zhao, X.; Wu, P.; Zhang, S.; Geng, B. Facile preparation of superhydrophobic and superoleophilic porous polymer membranes for oil/water separation from a polyarylester polydimethylsiloxane block copolymer. J. Mater. Sci. 2016, 51, 3211–3218. [Google Scholar] [CrossRef]
- Yu, C.; Cui, L.; Song, Z.; Zhao, X.; Ma, Y.; Jiang, L. Facile Preparation of the Porous PDMS Oil-Absorbent for Oil/Water Separation. Adv. Mater. Interfaces 2017, 4, 1600862. [Google Scholar] [CrossRef]
- Chen, X.; Weibel, J.A.; Garimella, S.V. Continuous Oil–Water Separation Using Polydimethylsiloxane-Functionalized Melamine Sponge. Ind. Eng. Chem. Res. 2016, 55, 3596–3602. [Google Scholar] [CrossRef]
- Tran, D.N.H.; Kabiri, S.; Sim, T.R.; Losic, D. Selective adsorption of oil–water mixtures using polydimethylsiloxane (PDMS)–graphene sponges. Environ. Sci. Water Res. Technol. 2015, 1, 298–305. [Google Scholar] [CrossRef]
- González-Rivera, J.; Iglio, R.; Barillaro, G.; Duce, C.; Tinè, R.M. Structural and Thermoanalytical Characterization of 3D Porous PDMS Foam Materials: The Effect of Impurities Derived from a Sugar Templating Process. Polymers 2018, 10, 616. [Google Scholar] [CrossRef]
- Johnston, I.; McCluskey, D.; Tan, C.K.L.; Tracey, M. Mechanical characterization of bulk Sylgard 184 for microfluidics and microengineering. J. Micromech. Microeng. 2014, 24, 035017. [Google Scholar] [CrossRef]
- Lötters, J.C.; Olthuis, W.; Veltink, P.H.; Bergveld, P. The mechanical properties of the rubber elastic polymer polydimethylsiloxane for sensor applications. J. Micromech. Microeng. 1997, 7, 145–147. [Google Scholar] [CrossRef]
- Mata, A.; Fleischman, A.J.; Roy, S. Characterization of Polydimethylsiloxane (PDMS) Properties. Biomed. Microdevices 2005, 7, 281–293. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Bian, Z.; Fang, C.; Zhou, X.; Song, J. Experimental and Theoretical Study on Mechanical Properties of Porous PDMS. J. Appl. Mech. 2018, 85, 041009. [Google Scholar] [CrossRef]
- Rinaldi, A.; Tamburrano, A.; Fortunato, M.; Sarto, M.S. A Flexible and Highly Sensitive Pressure Sensor Based on a PDMS Foam Coated with Graphene Nanoplatelets. Sensors 2016, 16, 2148. [Google Scholar] [CrossRef] [PubMed]
- Ghavami, K. Bamboo as Reinforcement in Structural Concrete Elements. Cem. Concr. Compos. 2005, 27, 637–649. [Google Scholar] [CrossRef]
- Chen, X.; Guo, Q.; Mi, Y. Bamboo fiber-reinforced polypropylene composites: A study of the mechanical properties. J. Appl. Polym. Sci. 1998, 69, 1891–1899. [Google Scholar] [CrossRef]
- Md Shah, A.U.; Sultan, M.T.H.; Jawaid, M.; Cardona, F.; Abu Talib, A.R. A review of on the tensile properties of bamboo fiber reinforced polymer composites. BioResources 2016, 11, 10654–10676. [Google Scholar] [CrossRef]
- Ortiz-Acosta, D. Sylgard® Cure Inhibition Characterization; Project Report LA-UR-12-25325; Los Alomos National Laboratory: Los Alomos, NM, USA, 2012. [Google Scholar] [CrossRef]
- Alzoubi, M.F.; Al-Hallaj, S.; Abu-Ayyad, M. Modeling of Compression Curves of Flexible Polyurethane Foam with Variable Density Chemical Formulations and Strain Rates. J. Solid Mech. 2014, 6, 82–97. [Google Scholar]
- Planes, M.; Le Coz, C.; Soum, A.; Carlotti, S.; Rejsek-Riba, V.; Lewandowski, S.; Remaury, S.; Solé, S. Polydimethylsiloxane/Additive Systems for Thermal and Ultraviolet Stability in Geostationary Environment. J. Spacecr. Rockets 2017, 53, 1128–1133. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, F.; Liang, W.; Wang, Z.; Duan, Z.; Yang, B. Thermal and Mechanical Properties of Bamboo Fiber Reinforced Epoxy Composites. Polymers 2018, 10, 608. [Google Scholar] [CrossRef]
- Martin, A.; Martins, M.; da Silva, O.; Mattoso, L. Studies on the thermal properties of sisal fiber and its constituents. Thermochim. Acta 2010, 506, 14–19. [Google Scholar] [CrossRef]
- Yang, H.; Yan, R.; Chen, H.; Lee, D.H.; Zheng, C. Characteristics of hemicellulose, cellulose and lignin pyrolysis. Fuel 2007, 86, 1781–1788. [Google Scholar] [CrossRef]
- Mulliken, A.D.; Boyce, M.C. Mechanics of the rate-dependent elastic–plastic deformation of glassy polymers from low to high strain rates. Int. J. Solids Struct. 2006, 43, 1331–1356. [Google Scholar] [CrossRef]
- Bartolini, L.; Iannuzzi, D.; Mattei, G. Comparison of frequency and strain-rate domain mechanical characterization. Sci. Rep. 2018, 8, 13697. [Google Scholar] [CrossRef] [PubMed]




| Fibre Loading (%) | Mass (g) | |||
|---|---|---|---|---|
| PDMS Resin | PDMS Curing Agent | Sugar | Bamboo Fibre | |
| 0.7 | 70 | 7 | 170 | 0.54 |
| 1.4 | 1.09 | |||
| 3.4 | 2.71 | |||
| BF Loading Mass (%) | Spring Coefficient in Plateau Region (MPa) | Densification Coefficient (MPa) | ||||
|---|---|---|---|---|---|---|
| Average ± Standard Deviation | Average ± Standard Deviation | |||||
| 0.5 mm/min | 2.0 mm/min | 6.0 mm/min | 0.5 mm/min | 2.0 mm/min | 6.0 mm/min | |
| 0.00 | 0.029 ± 0.003 | 0.027 ± 0.002 | 0.026 ± 0.002 | 0.025 ± 0.008 | 0.015 ± 0.003 | 0.014 ± 0.003 |
| 0.70 | 0.072 ± 0.012 | 0.073 ± 0.012 | 0.078 ± 0.014 | 0.16 ± 0.065 | 0.192 ± 0.085 | 0.203 ± 0.097 |
| 1.40 | 0.074 ± 0.027 | 0.067 ± 0.011 | 0.068 ± 0.005 | 0.171 ± 0.398 | 0.410 ± 0.157 | 0.206 ± 0.034 |
| 3.74 | 0.095 ± 0.016 | 0.083 ± 0.010 | 0.085 ± 0.009 | 0.294 ± 0.159 | 0.248 ± 0.066 | 0.252 ± 0.067 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zubaidah, I.; Norfatriah, A.; Zatul Amali, S.N.; Zuruzi, A.S. Preparation and Behavior of Bamboo Fiber-Reinforced Polydimethylsiloxane Composite Foams during Compression. Fibers 2018, 6, 91. https://doi.org/10.3390/fib6040091
Zubaidah I, Norfatriah A, Zatul Amali SN, Zuruzi AS. Preparation and Behavior of Bamboo Fiber-Reinforced Polydimethylsiloxane Composite Foams during Compression. Fibers. 2018; 6(4):91. https://doi.org/10.3390/fib6040091
Chicago/Turabian StyleZubaidah, Isa, Abdullah Norfatriah, Serbini Noorul Zatul Amali, and Abu Samah Zuruzi. 2018. "Preparation and Behavior of Bamboo Fiber-Reinforced Polydimethylsiloxane Composite Foams during Compression" Fibers 6, no. 4: 91. https://doi.org/10.3390/fib6040091
APA StyleZubaidah, I., Norfatriah, A., Zatul Amali, S. N., & Zuruzi, A. S. (2018). Preparation and Behavior of Bamboo Fiber-Reinforced Polydimethylsiloxane Composite Foams during Compression. Fibers, 6(4), 91. https://doi.org/10.3390/fib6040091





