Abstract
A numerical simulation of the laminar flow field and convection–diffusion mass transfer in a regular system of parallel fully absorbing fibers for the range of Reynolds numbers up to Re = 300 is performed. An isolated row of equidistant circular fibers arranged normally to the external flow is considered as the simplest model for a hollow-fiber membrane contactor. The drag forces acting on the fibers with dependence on Re and on the ratio of the fiber diameter to the distance between the fiber axes, as well as the fiber Sherwood number versus Re and the Schmidt number, Sc, are calculated. A nonlinear regression formula is proposed for calculating the fiber drag force versus Re in a wide range of the interfiber distances. It is shown that the Natanson formula for the fiber Sherwood number as a function of the fiber drag force, Re, and Sc, which was originally derived in the limit of high Peclet numbers, is applicable for small and intermediate Reynolds numbers; intermediate and large Peclet numbers, where Pe = Re × Sc; and for sparse and moderately dense rows of fibers.
1. Introduction
Studies of convection–diffusion transfer in fibrous media are essential for the development of various technological processes. The results obtained are employed in solutions to the problems concerning the filtration of suspended particles [1,2], sorption, catalysis, electrochemistry, and especially, in membrane separation technology [3,4], where membranes in the form of hollow fibers are used for membrane gas absorption/desorption [5,6], ultra- [7] and nanofiltration [8], and gas separation [9,10]. Within the field of membrane technology, a great number of studies is devoted to the modelling of different mass-transfer processes in hollow-fiber membrane contactors [11,12,13,14,15,16]. When simulating the membrane separation of mixtures in gas-liquid hollow-fiber contactors, it is important to calculate the arrival of the solute at the streamlined fiber surface; that is, to determine the collected fraction of the solute (Sherwood number), which depends on the solute diffusion coefficient, the fiber diameter, and the flow conditions—the flow velocity, viscosity, and temperature. It should be noted that the solute transport towards the fiber surface is strongly influenced by the velocity distribution near the fiber. At low flow velocities, corresponding to low Reynolds numbers Re < 1, the flow field depends on the single parameter α—the fiber packing density, whereas at higher velocities, at Re ≥ 1, it is governed by the two parameters of α and Re. In studying transport processes in real porous media, the models with known flow fields are used in order to eliminate the influence of structural uncertainty. The ordered systems of parallel cylinders with circular cross sections, arranged normally to the laminar flow with square or hexagonal packing or a single row of parallel fibers are usually used as models [1]. The so-called cell models with axially symmetric flow past a fiber in a cell are commonly used at low Reynolds numbers. However, they are nonapplicable for the case of Re > 1. They also were shown to be not well-suited for dense systems of fibers, such as hollow-fiber membrane contactors, which are characterized by a high packing density with > 0.3 ( > 0.5, where is the fiber radius and is the distance between the axes of neighboring fibers). However, using the cell model, the role of the mutual hydrodynamic influence of fibers on the hydrodynamic resistance of the fiber system and on the diffusion mass transfer was clarified [1].
The mass and heat transfer have been studied in detail [1,16,17,18,19,20,21,22,23] on the basis of analytical and numerical solutions for the flow fields obtained for the fiber lattices [24,25,26,27,28]. As it turned out, a single row of fibers is a particularly convenient model when studying fluid flow and mass transfer at Re > 1 [16,20], when the flow symmetry is broken with increasing Re, and when vortices are formed behind the fibers, leading to an increase in the diffusion flux to the fibers. At Re > 1, the fiber drag force and the Sherwood number should increase. This increase is more noticeable when the system is more porous. Calculations for the fiber drag force and the fiber Sherwood number in a single row were performed in our previous work [16] for Re < 50 and for a single prescribed value of the Schmidt number, Sc. For this example, the fiber Sherwood number was found as a function of the inlet flow velocity . The case considered in [16] corresponds to typical operating conditions of a membrane contactor employed for the separation of gases and liquids. However, in a number of processes, for example in membrane distillation, the Reynolds numbers can be several times higher. In this paper, we consider the diffusion mass transfer in a wider range of Reynolds numbers up to Re = 300. Based on the obtained flow field, the fiber drag force and the fiber retention efficiency are obtained versus the process conditions and the interfiber distance.
2. Flow Field in a System of Parallel Fibers at Re > 1
Let us consider the viscous incompressible flow at low and intermediate Reynolds numbers in a single row of parallel equidistant fibers arranged normally to the flow direction. The corresponding simulation cell is shown in Figure 1.
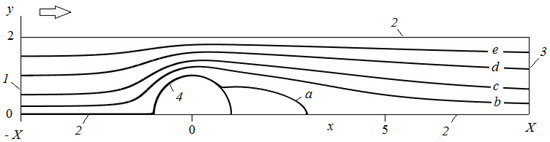
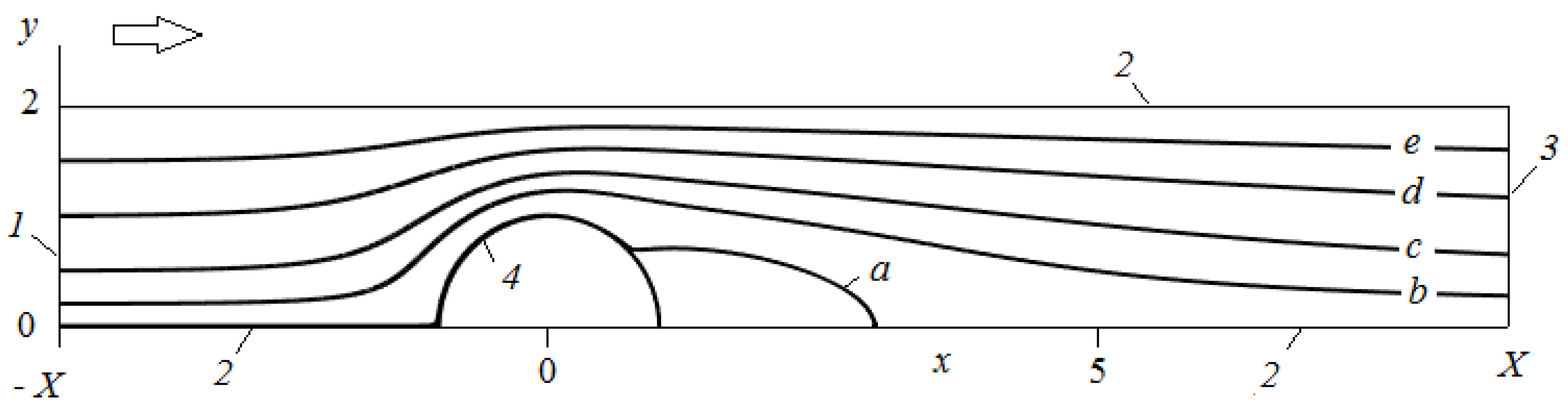
Figure 1.
A scheme of the computational cell: flow past a row of parallel fibers, where the Reynolds number (Re) = 20 and = 0.5; the flow direction is shown by the arrow. The streamline ordinates are: 10−4 (a), 0.2 (b), 0.5 (c), 1 (d), and 1.5 (e); 1—inlet, 2—symmetry boundaries, 3—outlet, 4—fiber surface.
To find the flow field, we will numerically solve the Navier–Stokes equations in the steady-state approximation:
where is the Reynolds number based on the fiber diameter, is the fluid density, is the dynamic viscosity, Δ is the Laplace operator, ∇ is the nabla operator, is the flow velocity vector, is the pressure, the symbol ∙ is the scalar product, and * denotes the dimensional variable. Hereinafter, all the values are reduced to dimensionless form by normalization to the fiber radius and to the inlet unperturbed velocity . The no-slip condition u = 0 is set at the fiber surface 4, while the condition of undisturbed flow u = {1,0} is set at the entrance of the simulation cell 1; the condition of vanishing viscous stresses (zero gradients) is applied at the outlet boundary 3; and at the boundaries labelled 2, the conditions of symmetry for the velocity components are used. The dimensionless fiber drag force per unit length was found as the surface integral of the projection of the local total stress on the flow direction:
where is the local total stress, is the viscous stress tensor, I is the unit tensor, n is the outer normal vector to the surface, is the surface element, and is the fiber surface area. The fiber drag force is related with the dimensionless pressure drop across the fiber row as shown by .
Figure 2, Figure 3 and Figure 4 show the results of simulations of the fiber drag force in a row of fibers dependent on Re. It is seen from Figure 2 and Figure 3 that at the limit of small Reynolds numbers, the curves tend asymptotically to straight lines, corresponding to the Stokes flow regime at small but nonzero Re numbers. The Stokes flow region at Re ≪ 1 is described at < 0.5 by the analytical formula of Miyagi [24]:
and at > 0.7, it is governed by the formula derived in the lubrication approximation by Keller [29]:
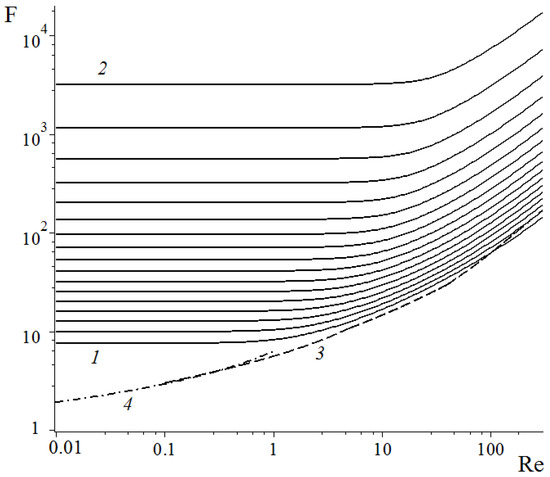
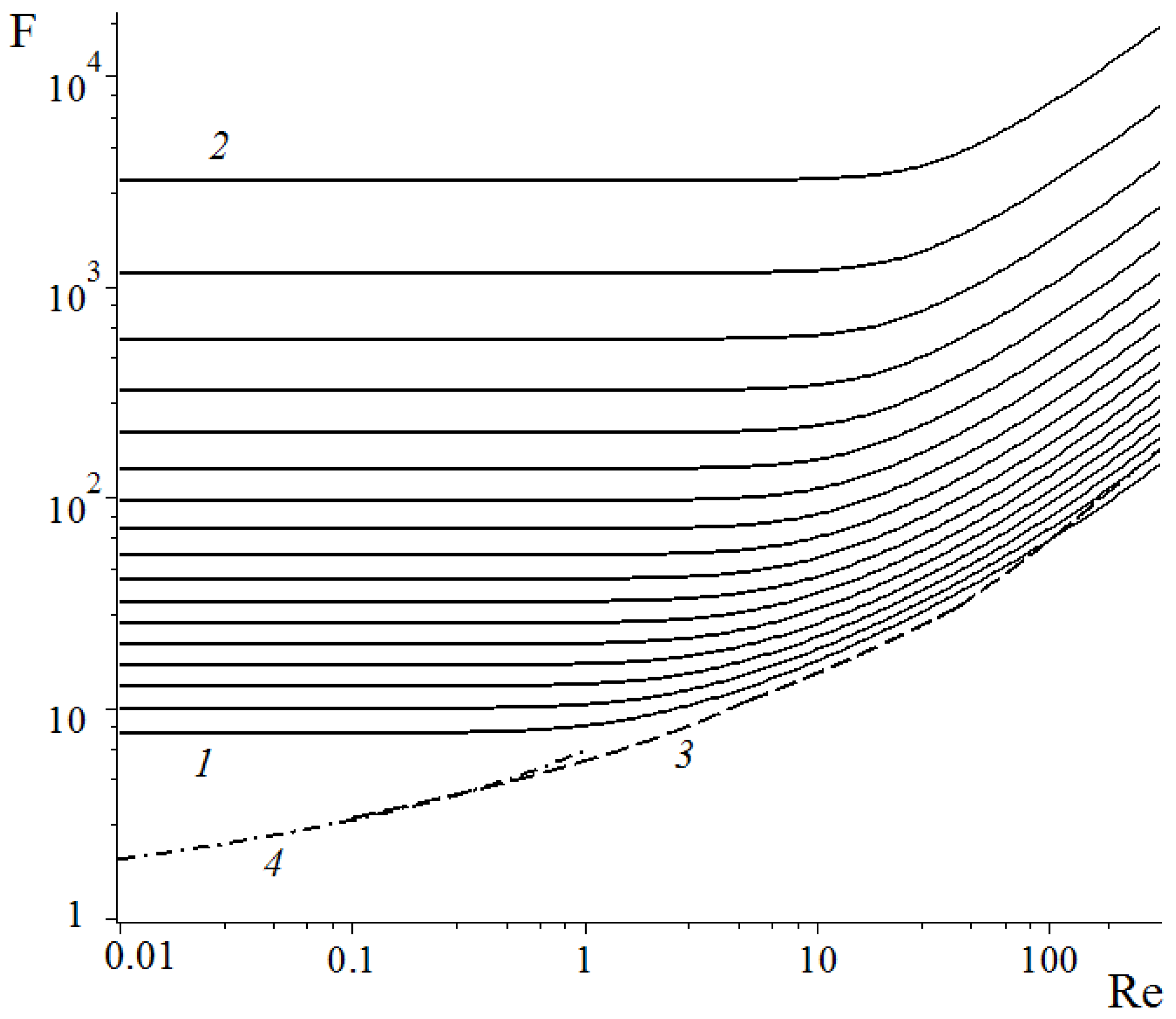
Figure 2.
The dimensionless fiber drag force (F) in a row of fibers vs. the Reynolds number for different distances between the fiber axes with computed with the step 0.05 starting from = 0.1 (curve 1) to 0.9 (curve 2); curve 3 is determined by the regression formula for an isolated fiber, Equation 7 [32]; and curve 4 is determined by the Lamb formula for an isolated fiber [33].
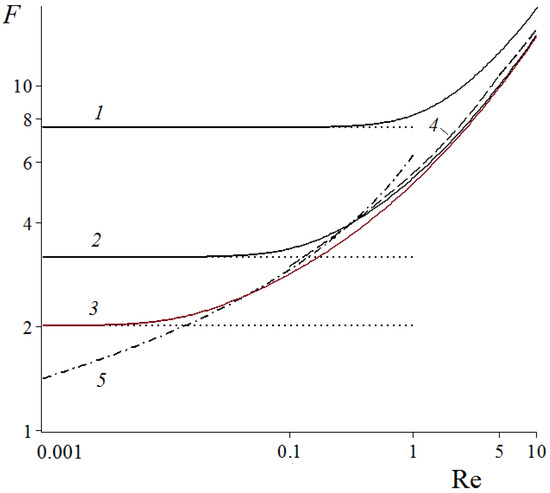
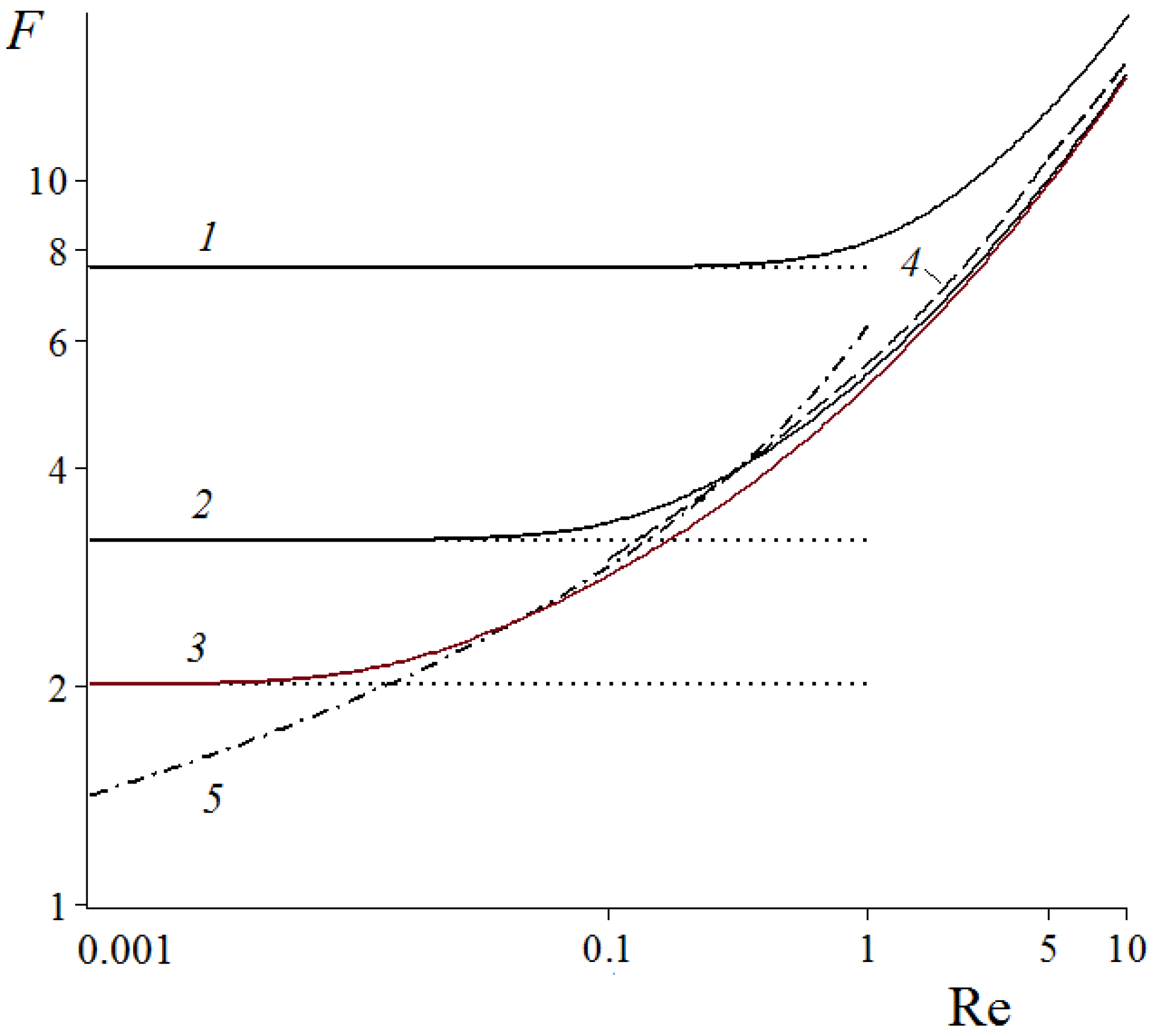
Figure 3.
The fiber drag force in a row of fibers vs. the Reynolds number; in the case of low Reynolds numbers and sparse rows: = 0.1 (1), 0.01 (2), 0.001 (3); 4 is given by the regression formula for an isolated cylinder, Equation (7) [32]; 5 is given by the Lamb formula for an isolated cylinder [33]; horizontal asymptotic lines (⋅⋅⋅⋅⋅)—values for the Stokes flow limit at Re ≪ 1.
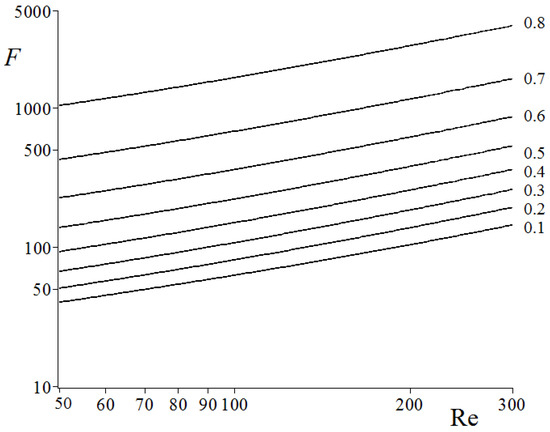
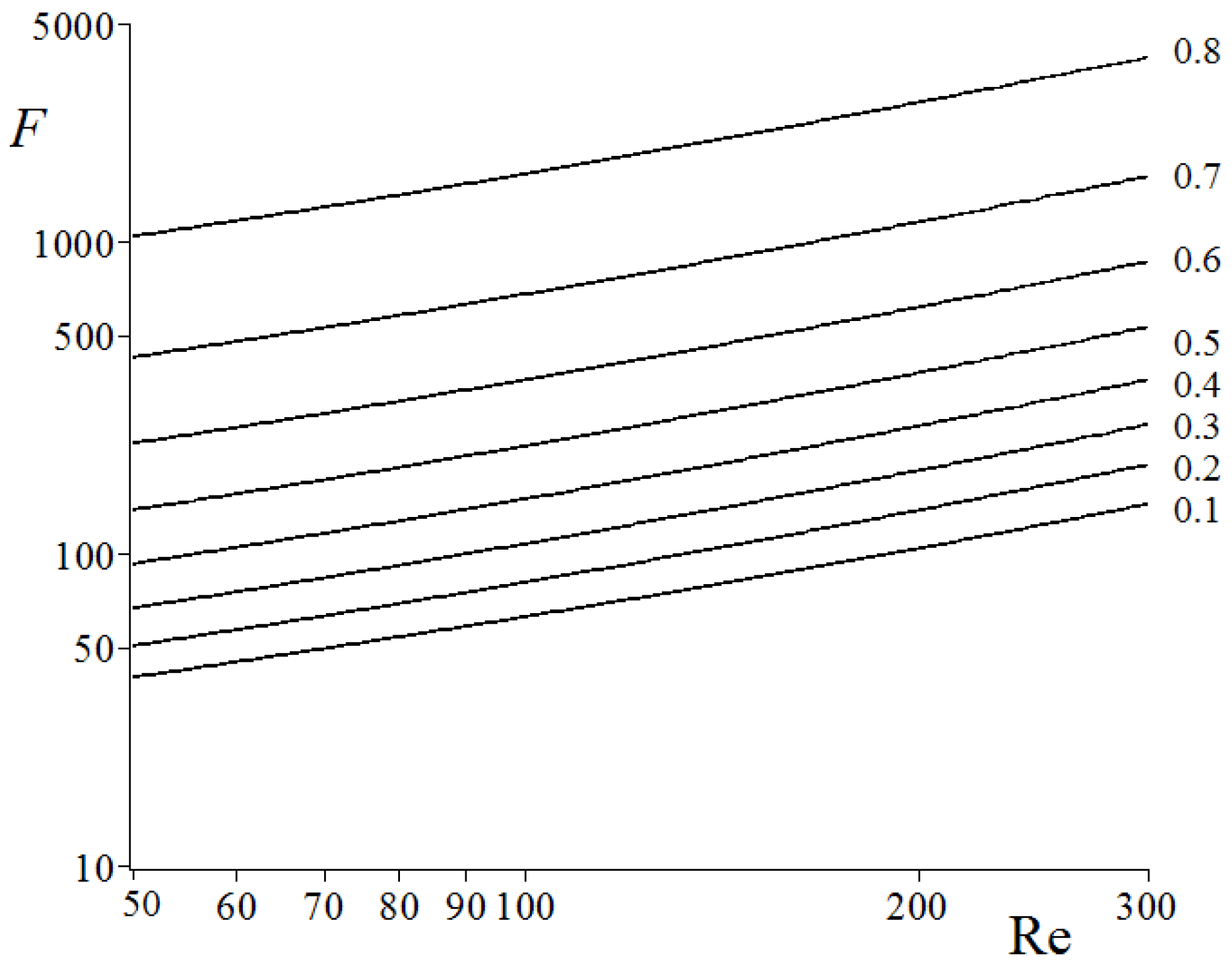
Figure 4.
The fiber drag force in a row of fibers vs. the Reynolds number: in the case of intermediate Reynolds numbers, the values are marked on the curves.
The regression formula for estimating in the whole range of was proposed in [16]. Our results of computations for the drag force on a fiber in a row and in lattices of fibers are in excellent agreement with the known experimental data, with the results of computations of other authors, and with other analytical formulas [1,24,25,26,30].
Figure 2 and Figure 3 show the onset of the flow inertia effect. It is seen that the denser the row, the later the onset of nonlinear inertial effects; that is, the higher the Re number is at which the drag force begins to increase. This effect was shown for the square array of cylinders in [31], where it was noted that the relative importance of inertia becomes smaller as the volume fraction approaches close packing, because the largest contribution to the dissipation in this limit comes from the viscous lubrication flow in the small gaps between the cylinders. Furthermore, in the region 100 ≤ Re ≤ 300, these curves, as can be seen from Figure 4, are linear and parallel, which allows us to fit them by a simple formula (with the mean average percentage error <> less than 0.6%):
where
Approximations for the fiber drag force in the whole considered Re range are given in the Appendix. Next, as expected, the decrease in results in the decrease in the lateral interaction of the neighboring fibers, and they begin to behave like an isolated cylinder. For comparison, we have also plotted (in Figure 2 and Figure 3) the curves for an isolated cylinder by the piecewise continuous approximation formula from [32]:
It should be noted that the (Re) curve for an isolated cylinder does not reach the plateau at Re ≪ 1. At the same time, the fiber drag force in the fiber row increases more slowly with Re, as compared with that of an isolated cylinder. This is explained by the mutual hydrodynamic influence of the fibers. In the next Section, the calculated flow field is used for modeling the diffusion transport in the row of fibers.
3. Convection–Diffusion Mass Transfer in a System of Absorbing Fibers
To determine the distribution of the solute concentration in the flow, the elliptic equation of convection–diffusion is solved:
where is the fiber diameter-based diffusion Peclet number, is the Schmidt number, D is the solute diffusion coefficient, and . Here, all the values are reduced to dimensionless form by normalizing to , , and the inlet concentration . The condition of full retention (absorption), , is set at the fiber surface 4. At the entrance of the cell 1, the condition of uniform concentration is set, and at the outlet boundary 3, the zero-gradient condition, . At the boundaries 2, the conditions of symmetry are used. The method of solving Equation (8) is based on the finite-difference scheme suggested in [34] and later used in [35].
The density of the integral diffusion flux of particles per fiber length is calculated as
where and θ are dimensionless polar coordinates and Sh is the fiber mean Sherwood number (per unit length) [36]. An example of the simulated profiles of concentration is shown in Figure 5 together with the streamlines. Here, the flow asymmetry and the diffusion wake evolution with Re are highly evident. The calculated curves for versus Re are plotted in Figure 6, where for comparison, the results of calculations by the formula of Natanson [37] (written in our notations)
are provided with and without allowance for flow inertia, i.e., with and .
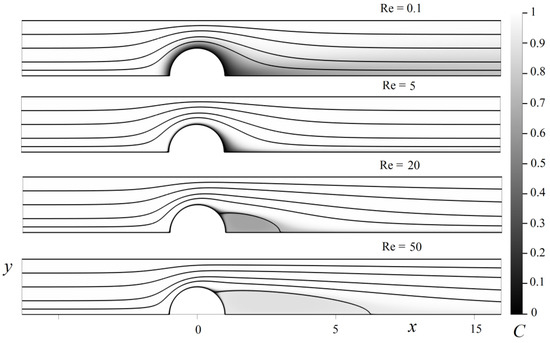
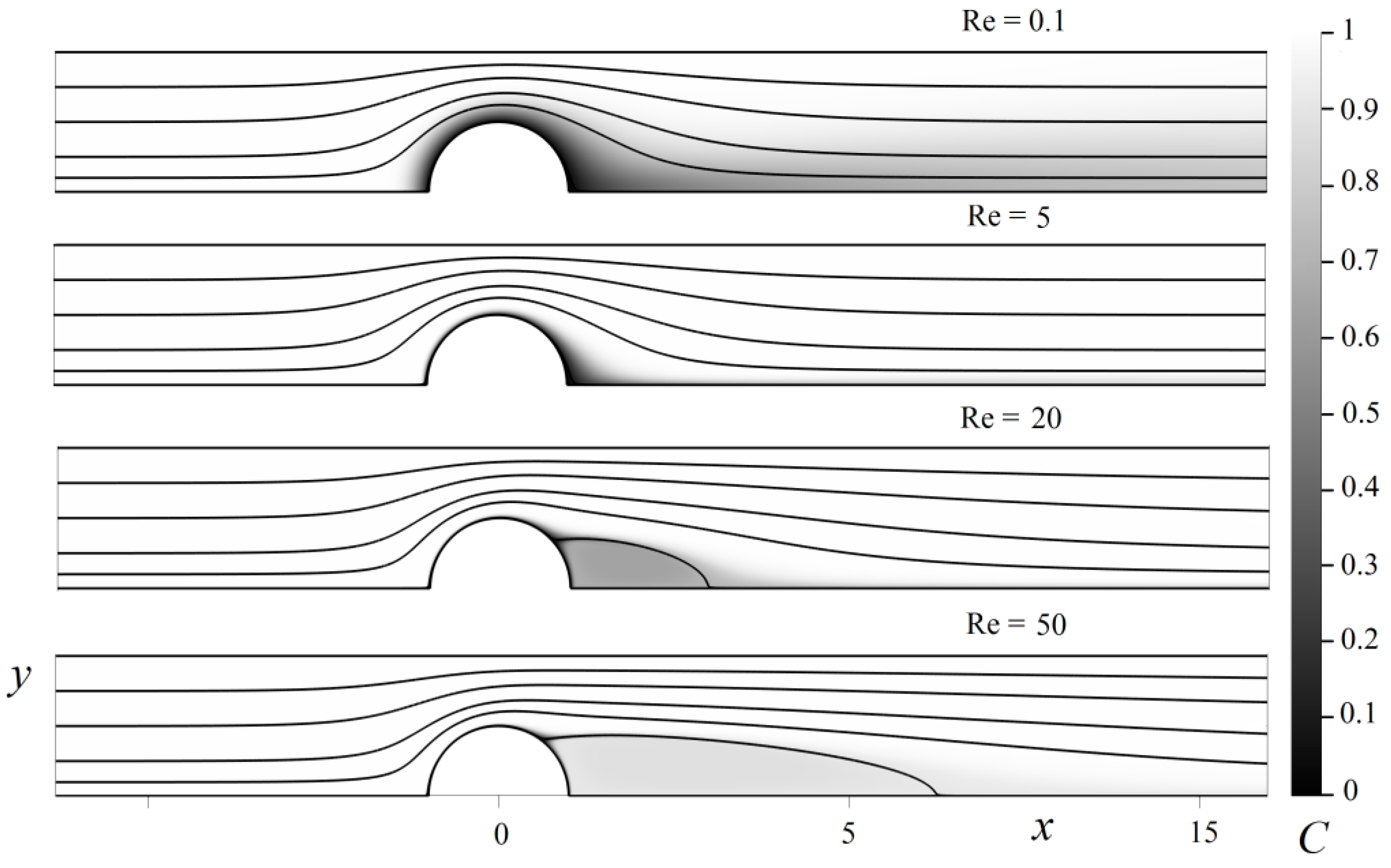
Figure 5.
The flow and concentration C fields past a row of fibers at different values of the Reynolds number, where Sc = 1000, = 0.5, and the streamline inlet ordinates are 10−4, 0.2, 0.5, 1, and 1.5.
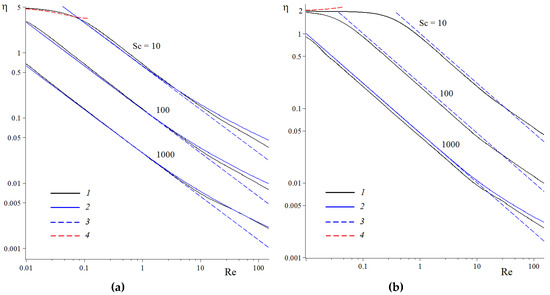
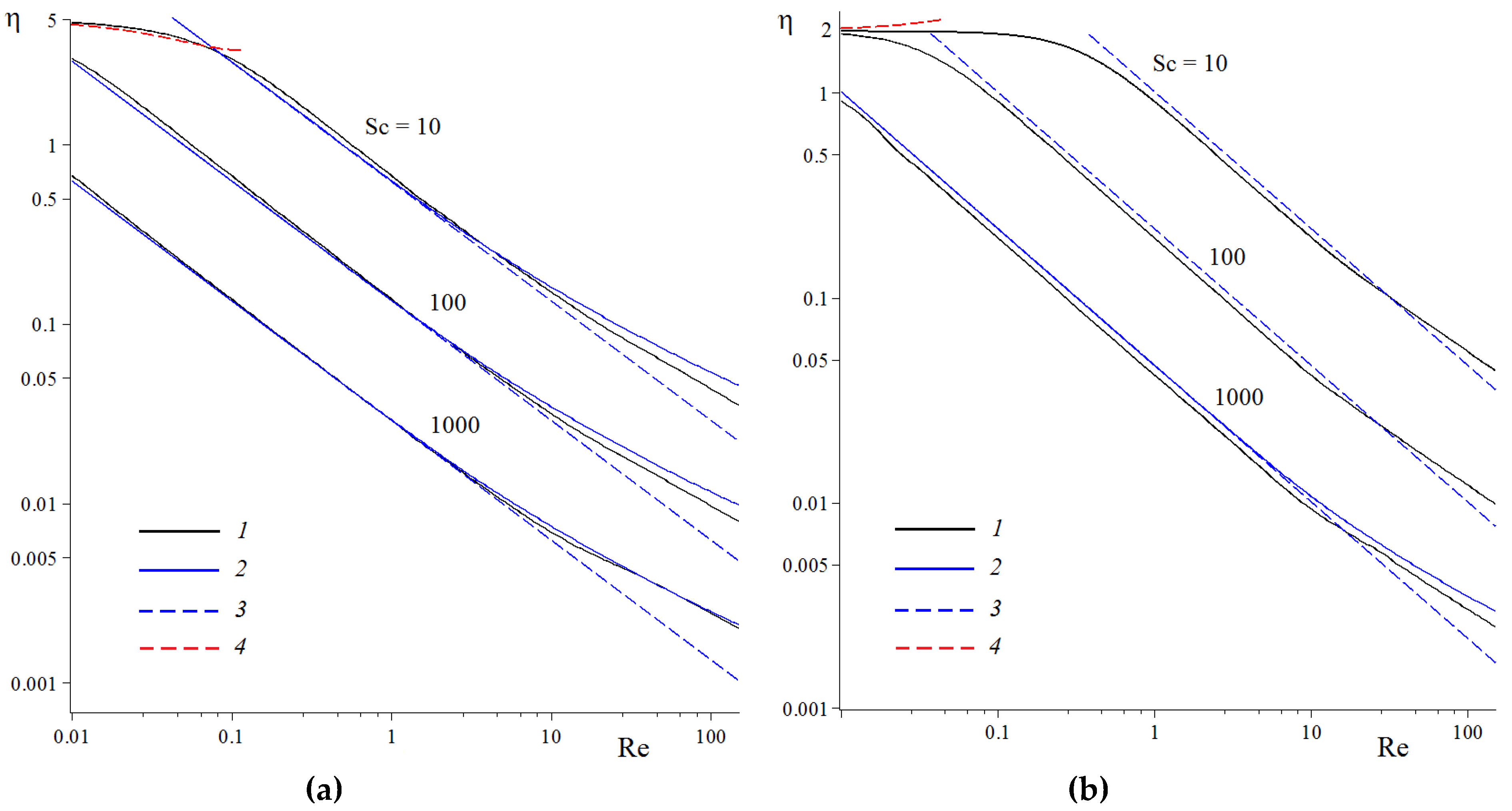
Figure 6.
Fiber retention efficiencies per unit length in a row of fibers with different interfiber distances: (a) = 0.2 and (b) 0.5, vs. Reynolds number, found from the combined numerical solution of the Navier–Stokes and convection–diffusion equations (curves 1): Schmidt numbers are marked on the curves. Curves 2 were plotted by Equation (10) with allowance for ; curves 3 were plotted by Equation (10) with = for the Stokes flow approximation at Re ≪ 1; curves 4 were plotted by the asymptotic formula (Equation (12)) for Pe ≪ 1.
The drag force as a function of Re is found from the solution of the Navier–Stokes equations or is estimated by the regression formulas given by Equations (A1) and (A4) (see Appendix, Table A1 and Table A2), while the value of for Re ≪ 1 is given in [16]. The case of a dense row is illustrated in Figure 7. The formula given by Equation (10) was originally derived in the limit of high Peclet numbers, , and for small values of . However, the simulations performed for a wide range of parameters reveal the wider range of validity of this formula. For estimations, it can be used at high Schmidt numbers, at high and intermediate Peclet numbers, and at < 0.5, i.e., for sparse and moderately dense rows of fibers. As follows from the figures, the formula of Natanson has better consistency with simulations for b = 0.2 and Sc = 1000. For this particular case, the following approximation can be used: . For the range 100 ≤ Re ≤ 300 and for non-dense rows, we suggest a simple formula, which is obtained using the corresponding regression formula for the drag force in Equation (5):
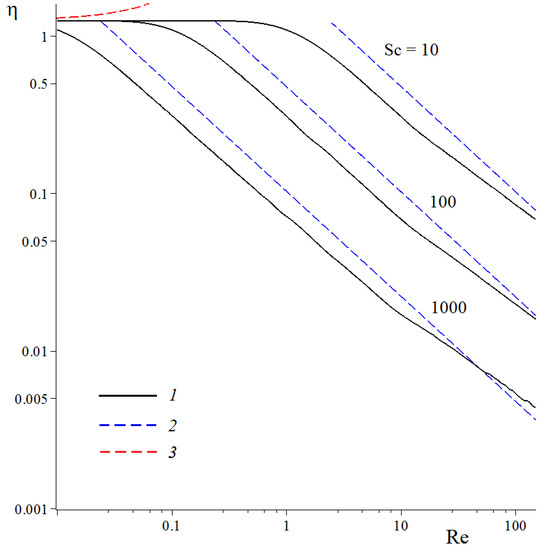
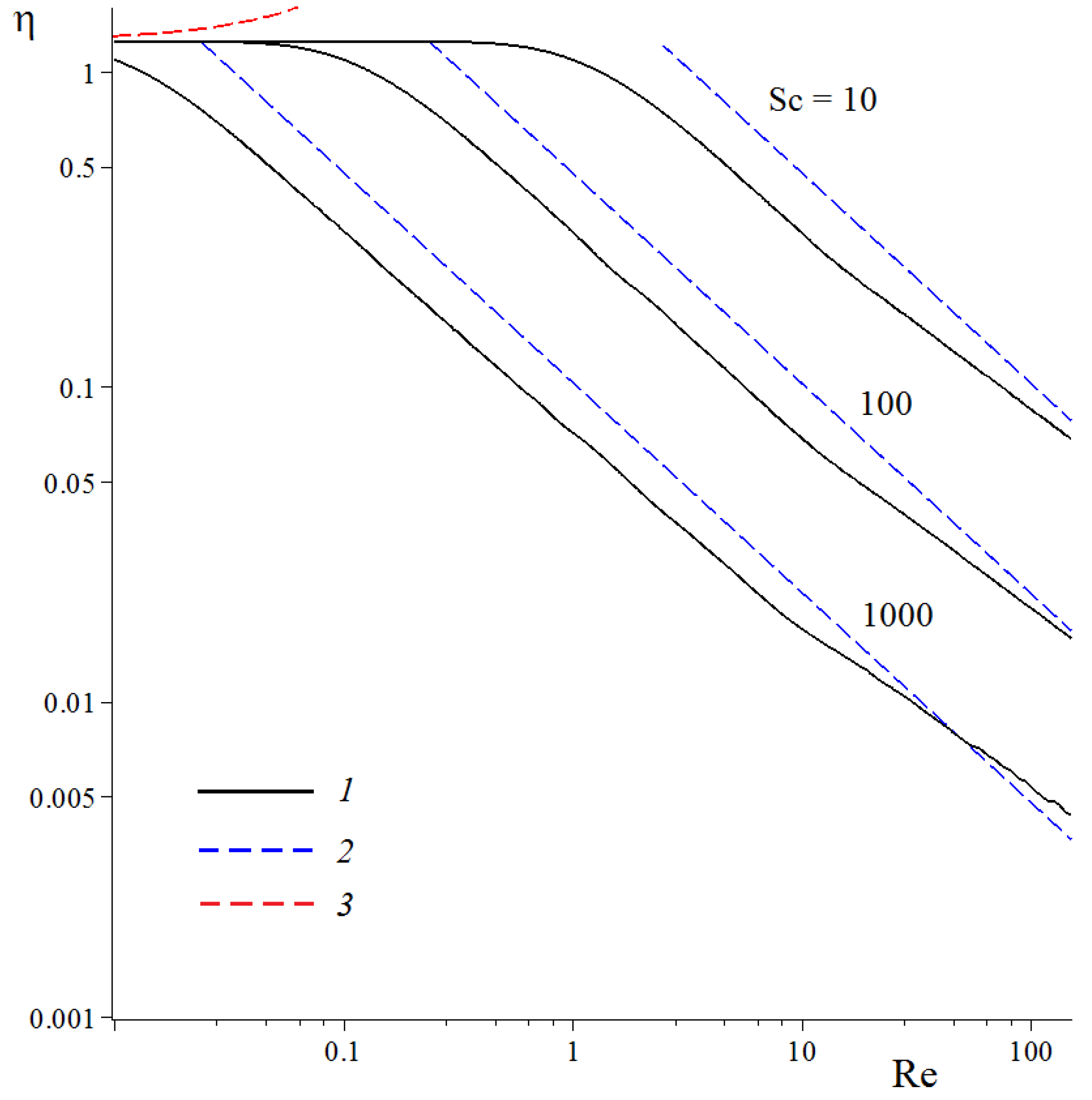
Figure 7.
Fiber retention efficiencies per unit length in a dense row of fibers with = 0.8 vs. Reynolds number, found from the combined numerical solution of the Navier–Stokes and convection–diffusion equations (curves 1): Schmidt numbers are marked on the curves; curves 2 were plotted by Equation (10) with = for the Stokes flow at Re ≪ 1; curves 3 were plotted by the asymptotic formula (Equation (12)) for Pe ≪ 1.
It is seen from the above figures that the slope of the curves varies with Re (the curves become nonlinear), which is explained by mixing in the wake region (Figure 5), which leads to the increase of the diffusion flux to the fiber. The slope varies also as Pe decreases at any Sc, which is associated with a transition from a convective–diffusion transport to a fully diffusion transport when the curves reach the plateau at Pe → 0 [38]. In this case, under the condition at the fiber surface, the fibers completely absorb the arriving solute and the fiber retention efficiency is equal to the inlet flux, which in dimensionless form, is equal to the distance between the axes of the neighbor fibers. This case is illustrated in Figure 6a, where the curve 4 was plotted by the asymptotic formula for the fiber retention efficiency, derived at Pe ≪ 1 in [38] for a uniform creeping flow with in a sparse row of fibers:
where is the modified Bessel function of the imaginary argument. It should be noted that small Peclet numbers are realized in gases at low Reynolds and low Schmidt numbers.
4. Discussion
In this work, the hydrodynamic resistance and convection–diffusion mass transfer in the isolated rows of parallel circular fibers arranged normally to the direction of the external laminar flow, which is used as the simplest model for a hollow-fiber membrane contactor with regions of constricted flow, were simulated. The computations were preformed for the Stokes flow and inertial flow regimes for the Reynolds numbers up to Re = 300. The dimensionless fiber drag force per unit length was calculated, which determines the dimensionless pressure drop in the fiber row system, and a correlation for the dependence was proposed. Also, the dimensionless solute retention efficiency of a fully absorbing fiber in a row of fibers was calculated, using , where Sh is the fiber Sherwood number, versus the Reynolds number for the prescribed Schmidt number values of Sc = 10, 100, and 1000. It was shown that the Natanson formula, which simultaneously relates the fiber retention efficiency with , Re, and Sc, and which was originally derived in the limit of high Peclet numbers for the case of small retention efficiency, is applicable for small and intermediate Reynolds numbers; intermediate and large Peclet numbers, where Pe = Re × Sc; and for sparse and moderately dense rows of fibers for < 0.5. The results obtained allow one to estimate the solute retention efficiency of a streamlined hollow fibers in a contactor with simultaneous consideration of contactor parameters, such as fiber packing density, and process conditions characterized by dimensionless criteria—the Reynolds, Peclet, and Schmidt numbers. The results can find application in the field of separation and purification with absorbing fibrous media.
Author Contributions
Statement of the problem, simulations, and writing—original draft preparation, V.A.K.; writing—review and editing, A.V.B. and S.D.B.
Funding
This work was carried out in the A.V. Topchiev Institute of Petrochemical Synthesis (Russian Academy of Sciences) and was funded by the Russian Science Foundation, grant number 14-49-00101.
Acknowledgments
The authors acknowledge the financial support of the Russian Science Foundation.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix
The calculated values of the fiber drag force in a row of fibers are approximated by the nonlinear regression formulae. In the range 0 ≤ Re ≤ 50 at = = 0.1–0.85, the two-parameter correlation is used:
where is the fiber drag force derived in [16] at Re ≪ 1. The coefficients , , , , and are fitted at 0.1 ≤ ≤ 0.5 by the function
while at 0.5 ≤ ≤ 0.85, they are approximated by
The coefficients are given in Table A1 and Table A2. In the range 50 ≤ Re ≤ 300 at = 0.1–0.9, the following approximation is proposed:
The maximum and mean average percentage errors of the derived correlations do not exceed max () = 2 and <> = 0.1 %, respectively.

Table A1.
Coefficients in Equation (А2).
Table A1.
Coefficients in Equation (А2).
| Coefficients in Equation (A1) | |||||
|---|---|---|---|---|---|
| A | 2.1217 | 289.9297 | 26.9531 | 39.913 | −300.7297 |
| B | −1.1934 | −215.0368 | −19.077 | −31.4594 | 222.6869 |
| C | 0.2835 | 61.5072 | 5.3081 | 9.5571 | − 63.5653 |
| D | −0.0312 | −7.4111 | −0.635 | −1.1996 | 7.654 |
| E | 0.0013 | 0.3224 | 0.0277 | 0.5381 | −0.3330 |

Table A2.
Coefficients in Equation (А3).
Table A2.
Coefficients in Equation (А3).
| Coefficientsin Equation (A1) | |||||||
|---|---|---|---|---|---|---|---|
| A | −16,813.6833 | −8371.0393 | −737.937 | 10.4997 | 1.348 | −24.9981 | 16,818.5536 |
| B | 5090.8957 | 2496.3936 | 264.9326 | −39.2739 | 5.7935 | 31.2227 | −5096.2083 |
| C | 176.1791 | 107.063 | −13.1498 | 18.2408 | −3.2293 | −11.6302 | −174.2677 |
| D | 42,356.9489 | 21,175.9228 | 1767.2858 | 57.3744 | 1.0235 | 1.5894 | −42,357.2119 |
| E | −406.1734 | −202.9051 | −17.1196 | −0.4041 | −0.0559 | −0.1074 | 406.1907 |
References
- Kirsch, A.A.; Stechkina, I.B. The theory of aerosol filtration with fibrous filters. In Fundamentals of Aerosol Science; Shaw, D.T., Ed.; John Wiley & Sons: Hoboken, NY, USA, 1978; pp. 165–256, ISBN-10: 0471029491. [Google Scholar]
- Kirsch, V.A.; Kirsch, A.A. Deposition of aerosol nanoparticles in model fibrous filters. In Aerosols–Science and Technology; Agranovski, I., Ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2010; pp. 283–314. [Google Scholar]
- Bazhenov, S.D.; Bildyukevich, A.V.; Volkov, A.V. Gas-liquid hollow fiber membrane contactors for different applications. Fibers 2018, 6, 76. [Google Scholar] [CrossRef]
- Ovcharova, A.; Vasilevsky, V.; Borisov, I.; Bazhenov, S.; Volkov, A.; Bildyukevich, A.; Volkov, V. Polysulfone porous hollow fiber membranes for ethylene-ethane separation in gas-liquid membrane contactor. Sep. Purif. Technol. 2017, 183, 162–172. [Google Scholar] [CrossRef]
- Scholes, C.A.; Kentish, S.E.; Stevens, G.W.; Jin, J.; deMontigny, D. Thin-film composite membrane contactors for desorption of CO2 from monoethanolamine at elevated temperatures. Sep. Purif. Technol. 2015, 156, 841–847. [Google Scholar] [CrossRef]
- Bildyukevich, A.V.; Plisko, T.V.; Liubimova, A.S.; Volkov, V.V.; Usosky, V.V. Hydrophilization of polysulfone hollow fiber membranes via addition of polyvinylpyrrolidone to the bore fluid. J. Membr. Sci. 2017, 524, 537–549. [Google Scholar] [CrossRef]
- Thong, Z.; Gao, J.; Lim, J.X.Z.; Wang, K.-Y.; Chung, T.-S. Fabrication of loose outer-selective nanofiltration (NF) polyethersulfone (PES) hollow fibers via single-step spinning process for dye removal. Sep. Purif. Technol. 2018, 192, 483–490. [Google Scholar] [CrossRef]
- Dibrov, G.; Ivanov, M.; Semyashkin, M.; Sudin, V.; Kagramanov, G. High-Pressure Aging of Asymmetric Torlon® Hollow Fibers for Helium Separation from Natural Gas. Fibers 2018, 6, 83. [Google Scholar] [CrossRef]
- Babu, V.P.; Kraftschik, B.E.; Koros, W.J. Crosslinkable TEGMC asymmetric hollow fiber membranes for aggressive sour gas separations. J. Membr. Sci. 2018, 558, 94–105. [Google Scholar] [CrossRef]
- Günther, J.; Schmitz, P.; Albasi, C.; Lafforgue, C. A numerical approach to study the impact of packing density on fluid flow distribution in hollow fiber module. J. Membr. Sci. 2010, 348, 277–286. [Google Scholar] [CrossRef]
- Li, G.-P.; Zhang, L.-Z. Conjugate heat and mass transfer in a cross-flow hollow fiber membrane bundle used for seawater desalination considering air side turbulence. J. Membr. Sci. 2017, 533, 321–335. [Google Scholar] [CrossRef]
- Usman, M.; Dai, Z.; Hillestad, M.; Deng, L. Mathematical modelling and validation of CO2 mass transfer in a membrane contactor using ionic liquids for pre-combustion CO2 Capture. Chem. Eng. Res. Des. 2017, 123, 377–387. [Google Scholar] [CrossRef]
- Razavi, S.M.R.; Rezakazemi, M.; Albadarin, A.B.; Shirazian, S. Simulation of CO2 absorption by solution of ammonium ionic liquid in hollow-fiber contactors. Chem. Eng. Process. Process. Intensif. 2016, 108, 27–34. [Google Scholar] [CrossRef]
- Tantikhajorngosol, P.; Laosiripojana, N.; Jiraratananon, R.; Assabumrungrat, S. Physical absorption of CO2 and H2S from synthetic biogas at elevated pressures using hollow fiber membrane contactors: The effects of Henry’s constants and gas diffusivities. Int. J. Heat Mass Transf. 2019, 128, 1136–1148. [Google Scholar] [CrossRef]
- Sabelfeld, M.; Geißen, S.-U. Effect of helical structure on ozone mass transfer in a hollow fiber membrane contactor. J. Membr. Sci. in press. Available online: https://doi.org/10.1016/j.memsci.2018.10.056 (accessed on 20 November 2018). [CrossRef]
- Kirsch, V.A.; Roldugin, V.I.; Bildyukevich, A.V.; Volkov, V.V. Simulation of convective-diffusional processes in hollow fiber membrane contactors. Sep. Purif. Technol. 2016, 167, 63–69. [Google Scholar] [CrossRef]
- Miyagi, T. Viscous flow at low Reynolds numbers past an infinite row of equal circular cylinders. J. Phys. Soc. Japan 1958, 13, 493–496. [Google Scholar] [CrossRef]
- Tamada, К.; Fujikawa, Н. The steady two-dimensional flow of viscous fluid at low Re numbers passing through an infinite row of equal parallel circular cylinders. Quart. J. Mech. Appl. Math. 1957, 10, 425–432. [Google Scholar] [CrossRef]
- Golovin, A.M.; Lopatin, V.A. The flow of a viscous fluid through a doubly periodic rows of cylinders (English transl.). J. Appl. Mech. Techn. Physics. 1968, 9, 198–201. [Google Scholar] [CrossRef]
- Sangani, A.; Acrivos, A. Slow flow past periodic arrays of cylinders with application to heat transfer. Int. J. Multiph. Flow 1982, 8, 193–206. [Google Scholar] [CrossRef]
- Wang, W.; Sangani, A.S. Nusselt number for flow perpendicular to arrays of cylinders in the limit of small Reynolds and large Peclet numbers. Phys. Fluids 1997, 9, 1529–1539. [Google Scholar] [CrossRef]
- Fornberg, B. Steady incompressible flow past a row of circular cylinders. J. Fluid Mech. 1991, 225, 655–671. [Google Scholar] [CrossRef]
- Gajjar, J.S.B.; Azzam, N.A. Numerical solution of the Navier–Stokes equations for the flow in a cylinder cascade. J. Fluid Mech. 2004, 520, 51–82. [Google Scholar] [CrossRef]
- Li, T.; Deen, N.G.; Kuipers, J.A.M. Numerical investigation of hydrodynamics and mass transfer for in-line fiber arrays in laminar cross-flow at low Reynolds numbers. Chem. Eng. Sci. 2005, 60, 1837–1847. [Google Scholar] [CrossRef]
- Kirsh, V.A.; Shabatin, A.V.; Vysotskii, V.V.; Roldughin, V.I. Simulation of aerosol fibrous filters at Reynolds numbers of the order of unity. Colloid J. 2015, 77, 160–164. [Google Scholar] [CrossRef]
- Launder, B.E.; Massey, T.H. The Numerical Prediction of Viscous Flow and Heat Transfer in Tube Banks. ASME J. Heat Transf. 1978, 100, 565–571. [Google Scholar] [CrossRef]
- Martin, A.; Saltiel, C.; Shyy, W. Frictional losses and convective heat transfer in sparse, periodic cylinder arrays in cross flow. Int. J. Heat Mass Transf. 1998, 41, 2383–2397. [Google Scholar] [CrossRef]
- Ram, R.P.; Bharti, R.P.; Dhiman, A.K. Forced convection flow and heat transfer across an in-line bank of circular cylinders. Can. J. Chem. Eng. 2016, 94, 1381–1395. [Google Scholar] [CrossRef]
- Keller, J.B. Viscous flow through a grating or lattice of cylinders. J. Fluid Mech. 1964, 18, 94–96. [Google Scholar] [CrossRef]
- Wang, C.Y. Stokes flow through a rectangular array of circular cylinders. Fluid Dyn. Res. 2001, 29, 65–80. [Google Scholar] [CrossRef]
- Koch, D.L.; Ladd, A.J.C. Moderate Reynolds number flows through periodic and random arrays of aligned cylinders. J. Fluid Mech. 1997, 349, 31–66. [Google Scholar] [CrossRef]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles; Academic Press: New York, NY USA, 1978; p. 154. ISBN 012176950X. [Google Scholar]
- Lamb, H. Hydrodynamics, 6th Revised ed.; Dover Publications: New York, NY, USA, 1954; ISBN-10: 0486602567. [Google Scholar]
- Berkovskii, B.M.; Polevikov, V.K. Effect of the Prandtl number on the convection field and the heat transfer during natural convection (English translation). J. Eng. Phys. 1973, 24, 598–603. [Google Scholar] [CrossRef]
- Kirsh, V.A. Deposition of aerosol nanoparticles in fibrous filters. Colloid J. 2003, 65, 726–732. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Kutepov, A.M.; Kazenin, D.A.; Vyazmin, A.V. Hydrodynamics, Mass and Heat Transfer in Chemical Engineering. Series: Topics in Chemical Engineering (Book 14), 1st ed.; CRC Press: Boca Raton, FL, USA, 2001; ISBN-10: 0415272378. [Google Scholar]
- Natanson, G.L. Diffusional precipitation of aerosols on a streamlined cylinder with a small capture coefficient (English translation, Dokl. Akad. Nauk SSSR). Proc. Acad. Sci. USSR Phys. Chem. Sec. 1957, 112, 21–25. [Google Scholar]
- Chernyakov, A.L.; Kirsh, A.A.; Roldugin, V.I.; Stechkina, I.B. Diffusion deposition of aerosol particles on fibrous filters at small Peclet numbers. Colloid J. 2000, 62, 490–494. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).