Photon-Pair Sources Based on Intermodal Four-Wave Mixing in Few-Mode Fibers
Abstract
:1. Introduction
2. Spontaneous Four-Wave Mixing for Photon-Pair Generation
Phase Matching
3. Single-Photon Quantum Purity
3.1. Coincidence-to-Accidental Ratio in Spontaneous FWM
3.2. Spectral Purity
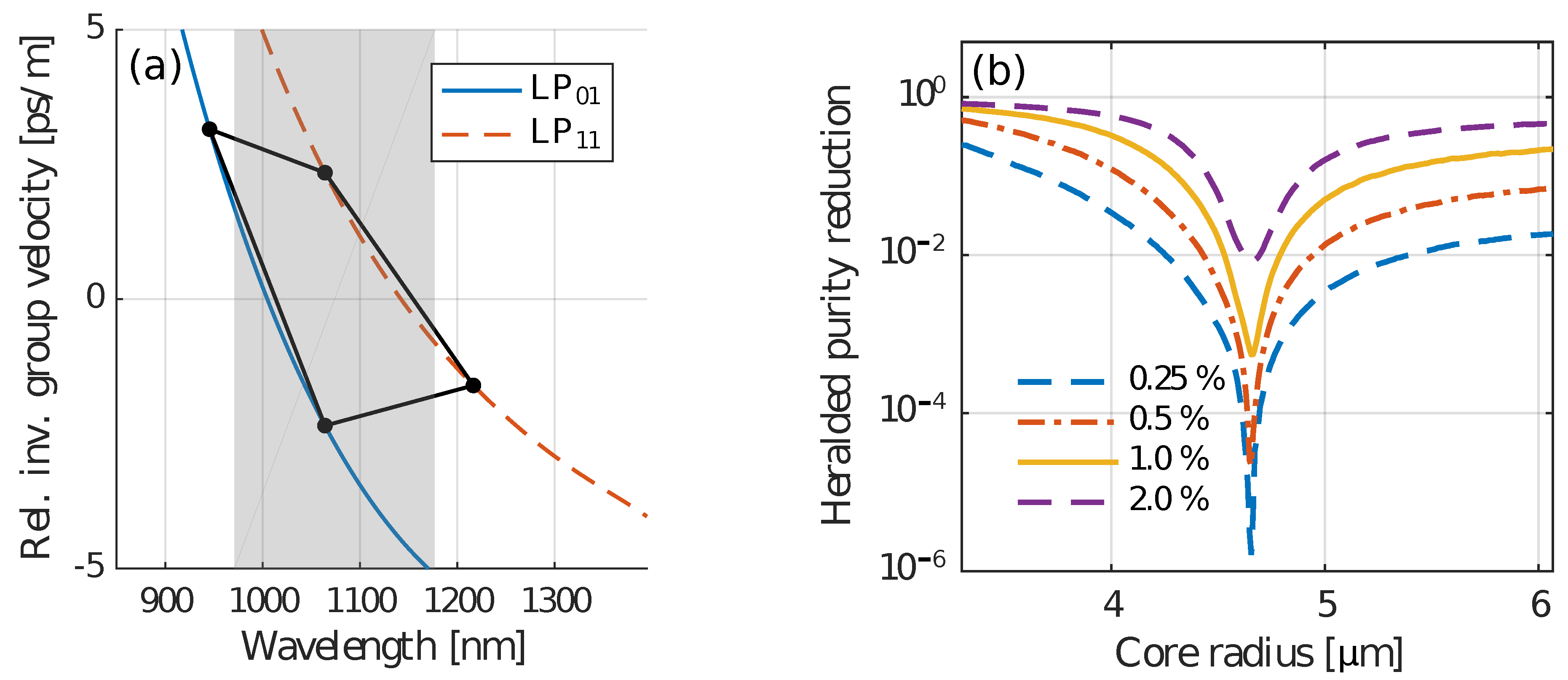
4. Few-Mode Fiber Design for Photon-Pair Sources
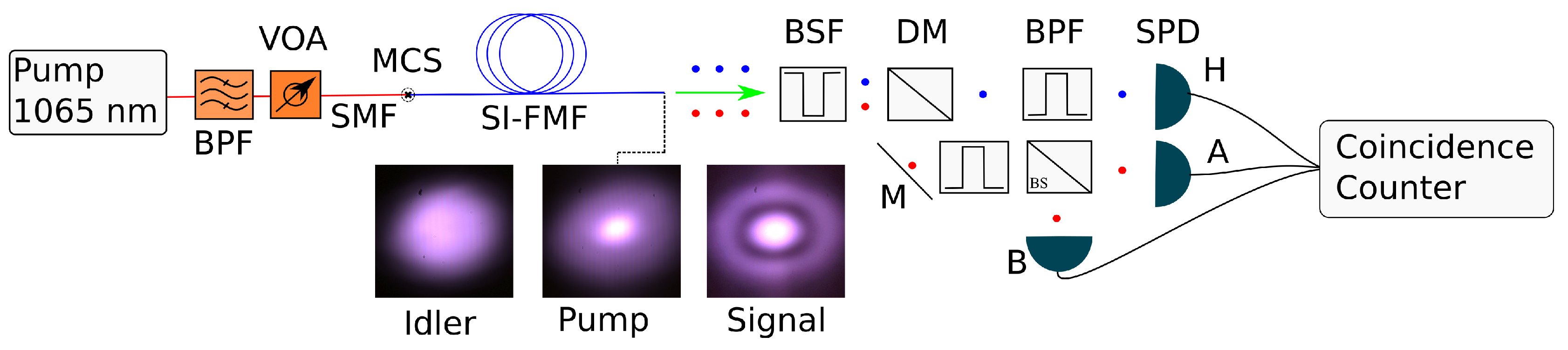
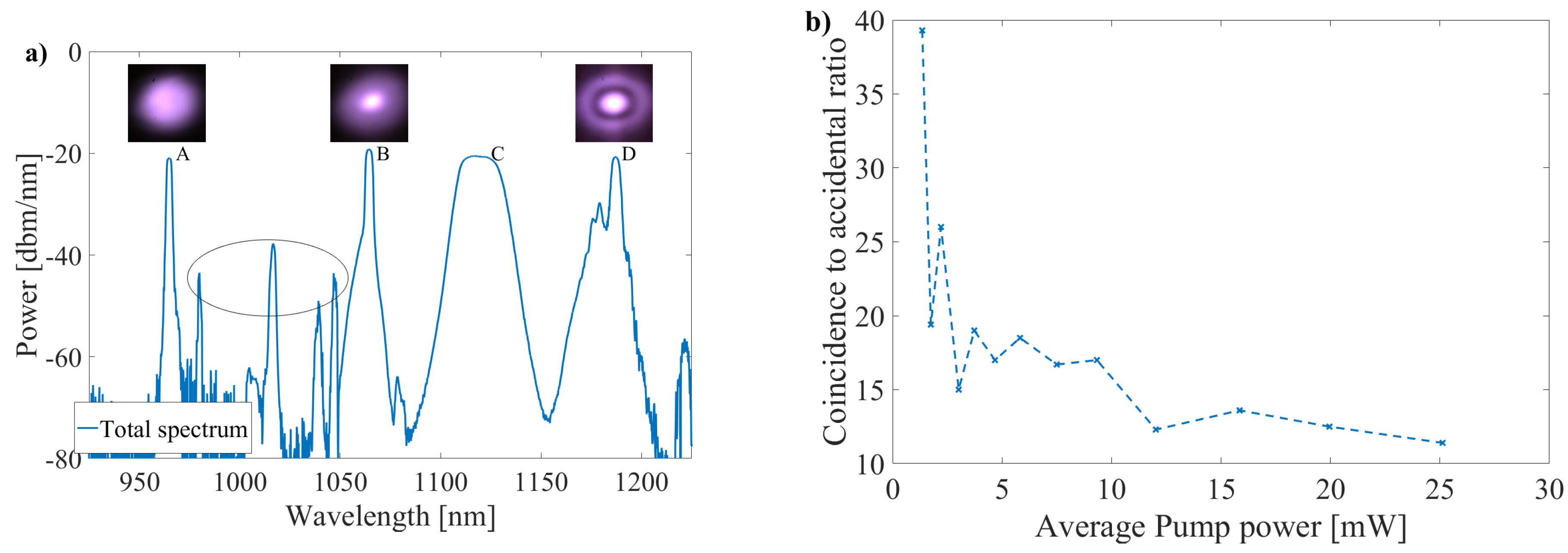
5. Experimental Intermodal Photon-Pair Generation
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| FWM | Four-wave mixing |
| LP | Linearly polarized |
| CAR | Coincidence-to-accidental ratio |
| APD | Avalanche photodiode |
References
- Inoue, K.; Toba, H. Wavelength Conversion Experiment Using Fiber Four-Wave Mixing. IEEE Photonics Technol. Lett. 1992, 4, 69–72. [Google Scholar] [CrossRef]
- Galili, M.; Huettl, B.; Schmidt-Langhorst, C.; Gaul i Coca, A.; Ludwig, R.; Schu-bert, C. 320 Gbit/s DQPSK all-optical wavelength conversion using four wave mixing. In Proceedings of the Conference on Optical Fiber Communication and the National Fiber Optic Engineers Conference, Anaheim, CA, USA, 25–29 March 2007. [Google Scholar]
- McKinstrie, C.J.; Radic, S.; Raymer, M.G.; Vasilyev, M.V. Phase-sensitive amplification produced by degenerate four-wave mixing in a fiber. In Proceedings of the Conference on Lasers and Electro-Optics, Baltimore, MD, USA, 22–27 May 2005. [Google Scholar]
- Tong, Z.; Lundström, C.; Andrekson, P.A.; McKinstrie, C.J.; Karlsson, M.; Blessing, D.J.; Tipsuwannakul, E.; Puttnam, B.J.; Toda, H.; Grüner-Nielsen, L. Towards ultrasensitive optical links enabled by low-noise phase-sensitive amplifiers. Nat. Photonics 2011, 5, 430436. [Google Scholar] [CrossRef]
- Andrekson, P.A.; Westlund, M. Nonlinear optical fiber based high resolution all-optical waveform sampling. Laser Photonics Rev. 2007, 1, 231–248. [Google Scholar] [CrossRef]
- Yaman, F.; Bai, N.; Zhu, B.; Wang, T.; Li, G. Long distance transmission in few-mode fibers. Opt. Express 2010, 18, 13250–13257. [Google Scholar] [CrossRef] [PubMed]
- Grüner-Nielsen, L.; Sun, Y.; Nicholson, J.W.; Jakobsen, D.; Jespersen, K.G.; Lingle, R.; Pálsdóttir, B. Few Mode Transmission Fiber with Low DGD, Low Mode Coupling, and Low Loss. J. Lightware Technol. 2012, 30, 3693–3698. [Google Scholar] [CrossRef]
- Julsgaard, B.; Sherson, J.; Cirac, J.I.; Fiurásek, J.; Polzik, E.S. Experimental demonstration of quantum memory for light. Nature 2004, 432, 482–486. [Google Scholar] [CrossRef] [PubMed]
- McKinstrie, C.J.; Mejling, L.M.; Raymer, M.G.; Rottwitt, K. Quantum-state-preserving optical frequency conversion and pulse reshaping by four-wave mixing. Phys. Rev. A 2012, 85, 053829. [Google Scholar] [CrossRef]
- Christensen, J.B.; Reddy, D.V.; McKinstrie, C.J.; Rottwitt, K.; Raymer, M.G. Temporal mode sorting using dual-stage quantum frequency conversion by asymmetric Bragg scattering. Opt. Express 2015, 23, 23287. [Google Scholar] [CrossRef] [PubMed]
- Christensen, J.B.; McKinstrie, C.J.; Rottwitt, K. Temporally uncorrelated photon-pair generation by dual-pump four-wave mixing. Phys. Rev. A 2016, 94, 013819. [Google Scholar] [CrossRef]
- McKinstrie, C.J.; Christensen, J.B.; Rottwitt, K.; Raymer, M.G. Generation of two-temporal-mode photon states by vector four-wave mixing. Opt. Express 2017, 25, 20877–20893. [Google Scholar] [CrossRef] [PubMed]
- Dyer, S.D.; Baek, B.; Nam, S.W. High Brightness, low noise, all fiber photon pair source. Opt. Exress 2009, 17, 10290–10297. [Google Scholar] [CrossRef]
- Lee, K.F.; Chen, J.; Liang, C.; Li, X.; Voss, P.; Kumar, P. Generation of high-purity telecom-band engtangled photon pairs in dispersion-shifted fiber. Opt. Lett. 2006, 31, 1905–1907. [Google Scholar] [CrossRef] [PubMed]
- Francis-Jones, R.J.; Hoggarth, R.A.; Mosley, P.J. All-fiber multiplexed source of high-purity single photons. Optica 2016, 3, 1270–1273. [Google Scholar] [CrossRef]
- Alibart, O.; Fulconus, J.; Wong, G.K.L.; Murdoch, S.G.; Wadsworth, W.J.; Rarity, J.G. Photon pair generation using four-wave mxing in a microstructured fire: theory versus experiment. New J. Phys. 2006, 8, 67. [Google Scholar] [CrossRef]
- Cui, L.; Li, X.; Zhao, N. Spectral properties of photon pairs generated by spontaneous four-wave mixing in inhomogeneous photonic crystal fibers. Phys. Rev. A 2012, 85, 023825. [Google Scholar] [CrossRef]
- Francis-Jones, R.J.; Mosley, P.J. Characterisation of longitudinal variation in photonic crystal fibre. Opt. Express 2016, 24, 24836–24845. [Google Scholar] [CrossRef] [PubMed]
- Christensen, E.N.; Friis, S.M.; Koefoed, J.G.; Castaneda, M.U.; Rottwitt, K. Near-infrared photon-pair generation by intermodal four-wave mixing in a few-mode fiber. In Proceedings of the Frontiers in Optics 2017, Washington, DC, USA, 18–21 September 2017. [Google Scholar]
- Demas, J.; Steinvurzel, P.; Tai, B.; Rishøj, L.; Chen, Y.; Ramachandran, S. Intermodal nonlinear mixing with Bessel bemas in optical fiber. Optica 2015, 2, 1. [Google Scholar] [CrossRef]
- Xiong, C.; Collins, M.J.; Steel, M.J.; Krauss, T.F.; Eggleton, B.J.; Clark, A.S. Photonic Crystal Waveguide Sources of Photons for Quantum Communication Applications. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 6967705. [Google Scholar]
- Garay-Palmett, K.; McGuinness, H.J.; Cohen, O.; Lundeen, J.S.; Rangel-Rojo, R.; Ren, A.B.U.; Raymer, M.G.; McKinstrie, C.J.; Radic, S.; Walmsley, I.A. Photon pair-state preparation with tailored spectral properties by spontaneous four-wave mixing in photonic-crystal fiber. Opt. Express 2007, 15, 14870–14886. [Google Scholar] [CrossRef] [PubMed]
- Buck, J.A. Fundamentals of Optical Fibers, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2004. [Google Scholar]
- Koefoed, J.G.; Friis, S.M.M.; Christensen, J.B.; Rottwitt, K. Spectrally pure heralded single photons by spontaneous four-wave mixing in a fiber: reducing impact of dispersion fluctuations. Opt. Express 2017, 25, 20835–20849. [Google Scholar] [CrossRef] [PubMed]
- Hong, C.K.; Ou, Z.Y.; Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 1987, 59, 2044. [Google Scholar] [CrossRef] [PubMed]
- Knill, E.; Laflamme, R.; Milburn, G.J. A scheme for efficient quantum computation with linear optics. Nature 2001, 409, 46–52. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Chen, J.; Voss, P.; Sharping, J.; Kumar, P. All-fiber photon-pair source for quantum communications: Improved generation of correlated photons. Opt. Express 2004, 12, 3737. [Google Scholar] [CrossRef] [PubMed]
- Lin, Q.; Yaman, F.; Agrawal, G.P. Photon-pair generation in optical fibers through four-wave mixing: Role of Raman scattering and pump polarization. Phys. Rev. A 2007, 75, 023803. [Google Scholar] [CrossRef]
- Rottwitt, K.; Tidemand-Lichtenberg, P. Nonlinear Optics-Principles and Applications; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Cordier, M.; Orieux, A.; Gabet, R.; Harlé, T.; Dubreuil, N.; Diamanti, E.; Delaye, P.; Zaquine, I. Raman-tailored photonic crystal fber for telecom band photon-pair generation. Opt. Lett. 2017, 42, 2583. [Google Scholar] [CrossRef] [PubMed]
- Koefoed, J.G.; Christensen, J.B.; Rottwitt, K. Effects of noninstantaneous nonlinear processes on photon-pair generation by spontaneous four-wave mixing. Phys. Rev. A 2017, 95, 043842. [Google Scholar] [CrossRef]
- Christensen, E.N.; Koefoed, J.G.; Friis, S.M.M.; Usuga Castaneda, M.A.; Rottwitt, K. Experimental characterization of Raman overlaps between mode-groups. Sci. Rep. 2016, 6, 34693. [Google Scholar] [CrossRef] [PubMed]
- U’Ren, A.B.; Silberhorn, C.; Erdmann, R.; Banaszek, K.; Grice, W.P.; Walmsley, I.A.; Raymer, M.G. Generation of pure-state single-photon wavepackets by conditional preparation based on spontaneous parametric downconversion. Laser Phys. 2005, 15, 146–161. [Google Scholar]
- Söller, C.; Cohen, O.; Smith, B.J.; Walmsley, I.A.; Silberhorn, C. High-performance single-photon generation with commercial-grade optical fiber. Phys. Rev. A 2011, 83, 031806. [Google Scholar] [CrossRef]
- Cohen, O.; Lundeen, J.S.; Smith, B.J.; Puentes, G.; Mosley, P.J.; Walmsley, I.A. Tailored Photon-Pair Generation in Optical Fibers. Phys. Rev. Lett. 2009, 102, 123603. [Google Scholar] [CrossRef] [PubMed]
- Fang, B.; Cohen, O.; Moreno, J.B.; Lorenz, V.O. State engineering of photon pairs produced through dual-pump spontaneous four-wave mixing. Opt. Express 2013, 21, 2707–2717. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Chen, X.; Wang, J.; Gray, S.; Liu, A.; Demeritt, J.A.; Ruffin, A.B.; Crowley, A.M.; Walton, D.T.; Zenteno, L.A. Al/Ge co-doped large mode area fiber with high SBS threshold. Opt. Express 2007, 15, 8290–8299. [Google Scholar] [CrossRef] [PubMed]
- Rishøj, L.S.; Svane, A.S.; Lund-Hansen, T.; Rottwitt, K. Quantitative evaluation of standard deviations of group velocity dispersion in optical fibre using parametric amplification. Electron. Lett. 2014, 50, 199–200. [Google Scholar] [CrossRef]
- Kuo, B.P.-P.; Fini, J.M.; Grüner-Nielsen, L.; Radic, S. Dispersion-stabilized highly-nonlinear fiber for wideband parametric mixer synthesis. Opt. Express 2012, 20, 18611. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rottwitt, K.; Koefoed, J.G.; Christensen, E.N. Photon-Pair Sources Based on Intermodal Four-Wave Mixing in Few-Mode Fibers. Fibers 2018, 6, 32. https://doi.org/10.3390/fib6020032
Rottwitt K, Koefoed JG, Christensen EN. Photon-Pair Sources Based on Intermodal Four-Wave Mixing in Few-Mode Fibers. Fibers. 2018; 6(2):32. https://doi.org/10.3390/fib6020032
Chicago/Turabian StyleRottwitt, Karsten, Jacob Gade Koefoed, and Erik Nicolai Christensen. 2018. "Photon-Pair Sources Based on Intermodal Four-Wave Mixing in Few-Mode Fibers" Fibers 6, no. 2: 32. https://doi.org/10.3390/fib6020032
APA StyleRottwitt, K., Koefoed, J. G., & Christensen, E. N. (2018). Photon-Pair Sources Based on Intermodal Four-Wave Mixing in Few-Mode Fibers. Fibers, 6(2), 32. https://doi.org/10.3390/fib6020032



