Ballistic Performance of Lightweight Armor Aramid Fabric with Different Bounding Technologies
Abstract
Highlights
- This study investigates the ballistic performance of Kevlar fabric laminated with epoxy and polyurethane binders using simulations and laboratory testing.
- Polyurethane-bonded composites demonstrated superior multi-hit resistance and energy absorption compared to epoxy and unbonded configurations.
- ANSYS Explicit Dynamics simulations correlated well with experimental results, validating the numerical model for high-strain-rate impact.
- The findings support polyurethane as the optimal binder for lightweight, flexible ballistic armor in military and civilian applications.
Abstract
1. Introduction
2. Numerical Analysis of the of the 9 mm Parabellum Bullet Projectile Penetration
2.1. Enhanced Description and Validation
2.1.1. Material Model Parameters and Source Justification
2.1.2. Model Validation with Experimental Data
- Mesh density in high-deformation zones (mesh sensitivity tested at 0.5 mm and 1 mm element size).
- Idealized contact definitions (frictionless penalty contacts were used).
- Homogeneous material assumption, neglecting micro-scale defects.
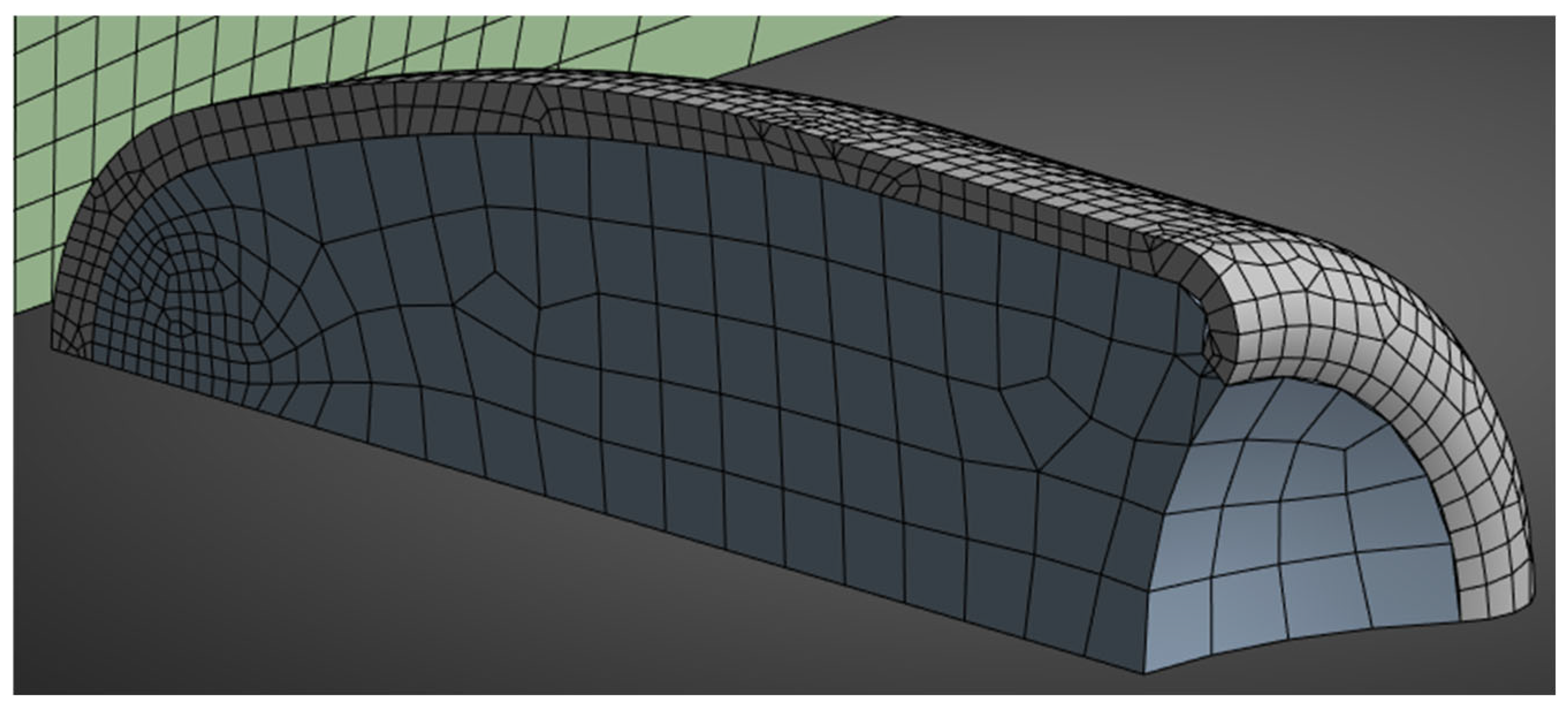
- Mesh Convergence Study: Local mesh refinement (0.25 mm) was applied in the impact zone. Coarser meshes (1.0 mm) were used elsewhere. The solution remained stable under CFL-limited time steps.
- Material Failure and Erosion: Johnson–Cook damage was combined with element deletion for materials exhibiting ductile fracture. For polymeric materials, an erosion strain threshold of 0.6 was applied.
- Multiple Impact Simulation: For polyurethane-bonded laminates, six consecutive impacts were modeled by updating the internal stress state and re-applying bullet boundary conditions sequentially.
- Binder Distribution: Although the simulations assumed uniform binder distribution, sensitivity tests were performed by applying graded elastic modulus regions to simulate non-uniformity (SEM-informed approximation).
- Autodyn and LS-DYNA solvers for explicit finite element analysis (FEA).
- Material models supporting metals, ceramics, composites, and layered armors.
- Failure criteria and erosion models, such as Johnson–Cook, Tsai–Wu, and Drucker–Prager.
- Contact algorithms for simulating projectile–target interaction.
- Adaptive meshing to optimize computational efficiency.
- Geometry and Meshing: Import CAD models of the bullet and target, applying fine meshing in critical regions.
- Material Assignment: Select appropriate material models with dynamic properties.
- Boundary Conditions and Loading: Apply velocity to the bullet and fixed constraints to the target.
- Solver Settings: Use an explicit solver with small time steps to capture high-speed interactions.
- Post-Processing: Analyze stress, strain, penetration depth, and failure zones.
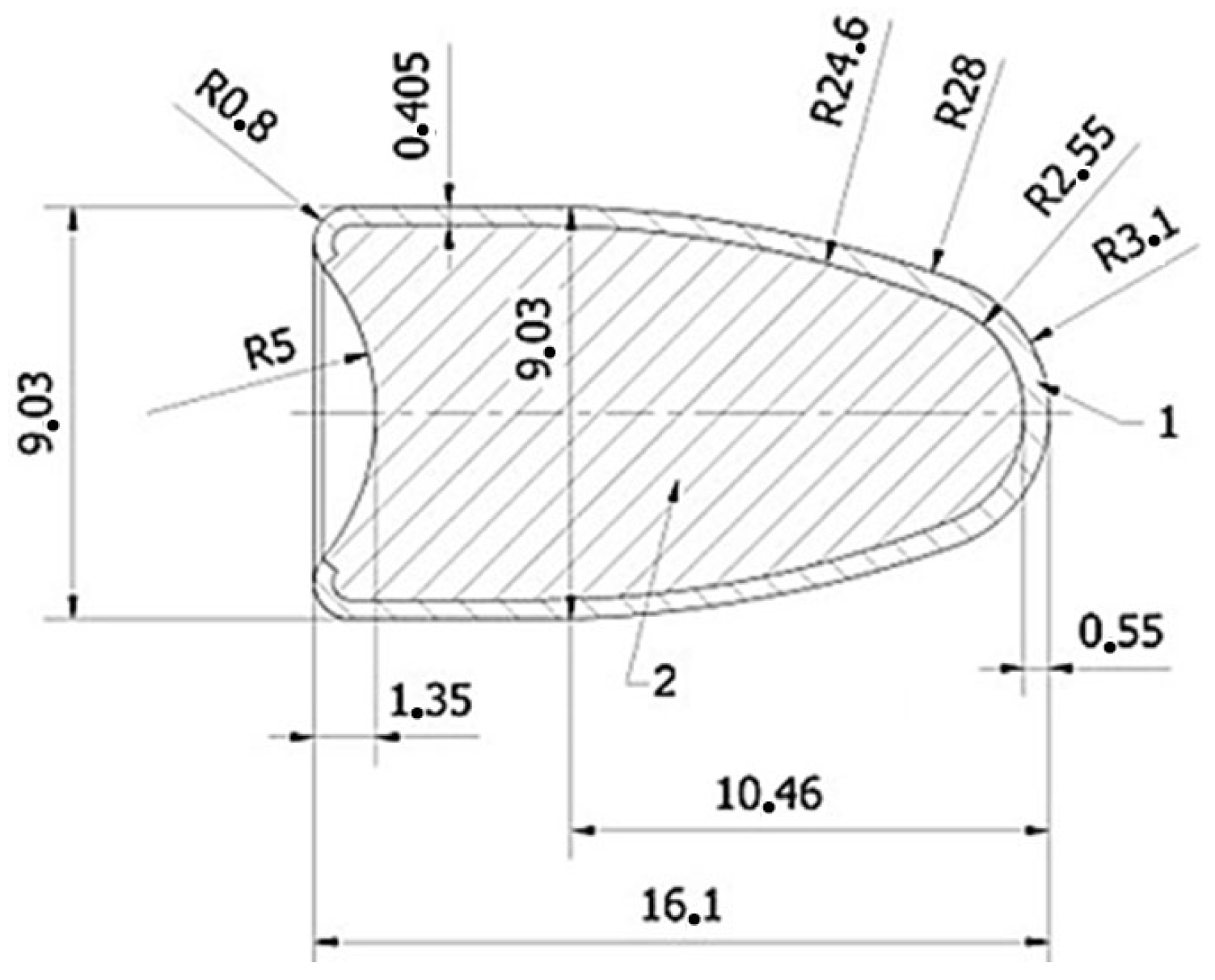
2.2. Development of Simulation Models
- Core—The lead core of the bullet.
- Jacket—The brass jacket of the bullet.
- Plate—The material to be tested, with a thickness of 5.5 mm (representing the average thickness of the selected materials) and a surface area of 300 × 300 mm.
- 34CrNiMo6 Steel (Steel 4340).
- Al 7075-T6.
- Rubber.
- Nylon.
- Polymethyl methacrylate (Plexiglass).
- a.
- Governing Equations
- b.
- Time Integration Using the Explicit Central Difference Method
- c.
- Material Modeling: Johnson–Cook Plasticity and Damage Criteria
2.3. Evaluation of Results
3. Experimental Section
3.1. Materials and Impact Specimen Configurations
3.2. Structural Properties of Aramid Composites
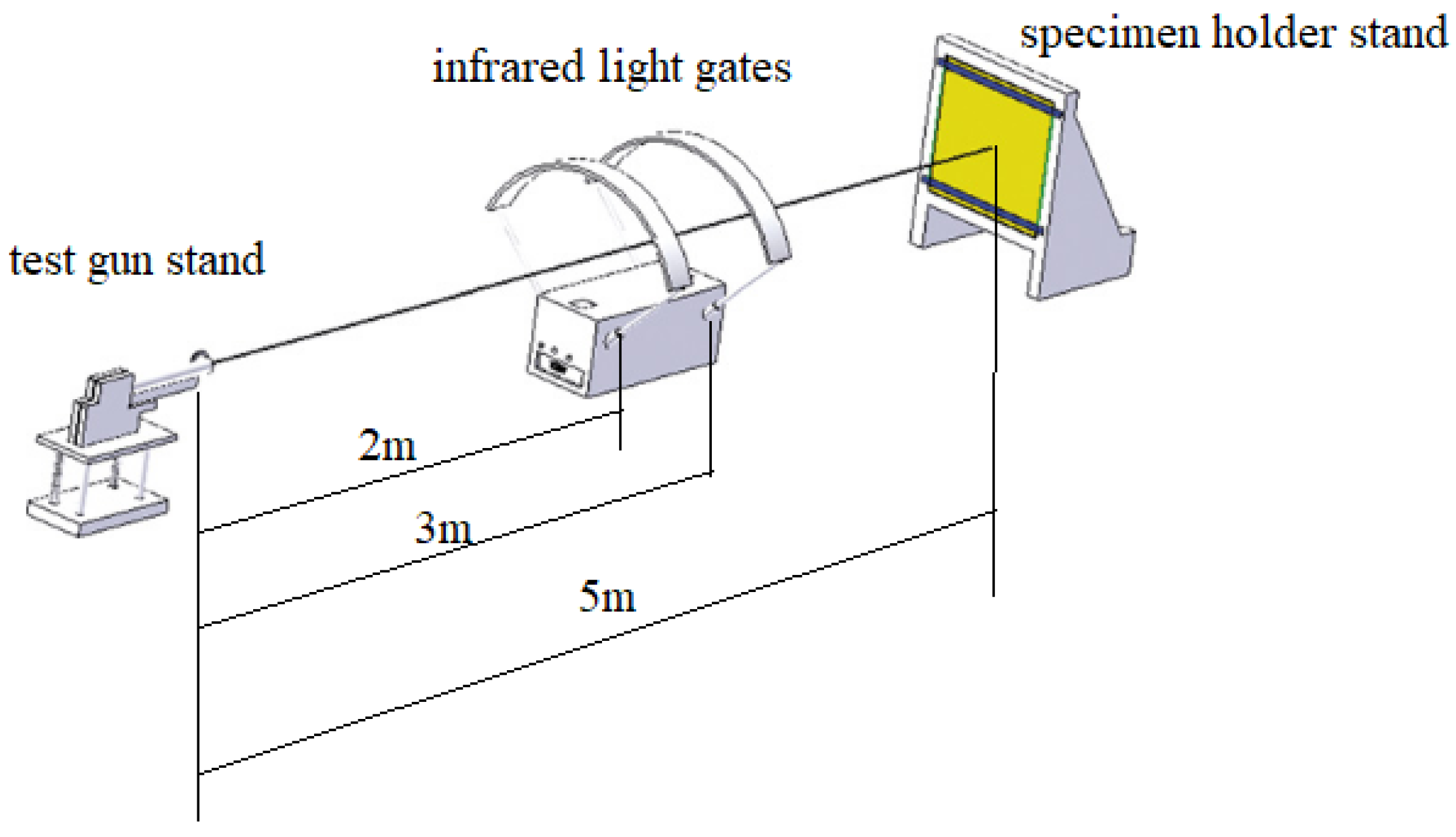
3.3. Ballistic Impact Testing
4. Results and Discussion
4.1. Projectile Impact Analysis
4.1.1. Neat Kevlar Projectile Analysis
4.1.2. Epoxy/Kevlar Projectile Analysis
4.1.3. Polyurethane/Kevlar Projectile Analysis
4.2. Comparison of Projectile Deformation and Material Energy Absorption
5. Conclusions
- The results highlight the effectiveness of ceramic composite armor in dissipating impact energy compared to conventional steel armor. Mesh refinement was applied to optimize computational efficiency in critical impact regions.
- The study demonstrates that numerical simulations in ANSYS Explicit Dynamics can effectively predict ballistic performance, aiding in the design of advanced protective materials.
- Due to the hardness of epoxy, it is also brittle, which is also shown by the cracks formed around the impact zone. With the second shot, the material was no longer able to adequately absorb the energy of the projectile, which penetrated thought the specimen. The specimen prepared with polyurethane binder met the L3 protection level.
- It was observed that the deformation of the bullet was greater than in the specimen without binder but less than in the specimen laminated with epoxy. The higher modulus of elasticity of the polyurethane resin proved to be suitable and performed adequately in the shooting test.
- During the tests, the polyurethane binder proved to be the most suitable, so the specimens for further tests will be laminated with this material.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PBO | Phenylene-benzobisoxazole |
| MSZ K | Hungarian Military Standard |
| FMJ | Full metal jacket |
| JSP | Jacketed soft-point bullet |
| RN | Round nose |
| FN | Flat nose |
| L | Lead |
| LR | Long rifle |
| HV | High velocity |
| SEM | Scanning electron microscope |
| SPC | Special purpose cartridge |
| STF | Shear thickening fluid |
| WR | Water repellent |
References
- Othman, A.R.; Hassan, M.H. Effect of different construction designs of aramid fabric on the ballistic performances. Mater. Des. 2013, 44, 407–413. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, X. A numerical investigation into the influence of fabric construction on ballistic performance. Compos. Part B Eng. 2015, 76, 209–217. [Google Scholar] [CrossRef]
- Zhou, Y.; Yao, W.; Zhang, Z.; Lin, Y.; Xiong, Z.; Zhao, Y.; Wang, M. Ballistic performance of the structure-modified plain weaves with the improved constraint on yarn mobility: Experimental investigation. Compos. Struct. 2022, 280, 114913. [Google Scholar] [CrossRef]
- Khodadadi, A.; Liaghat, G.; Vahid, S.; Sabet, A.R.; Hadavinia, H. Ballistic performance of Kevlar fabric impregnated with nanosilica/PEG shear thickening fluid. Compos. Part B Eng. 2019, 162, 643–652. [Google Scholar] [CrossRef]
- Bilisik, A.K.; Turhan, Y. Multidirectional stitched layered aramid woven fabric structures and their experimental characterization of ballistic performance. Text. Res. J. 2009, 79, 1331–1343. [Google Scholar] [CrossRef]
- Li, H.; Zhang, R.; Min, S.; Zhou, Y.; Sun, J. Parametric study on the ballistic performance of seamed woven fabrics. Def. Technol. 2023, 24, 173–189. [Google Scholar] [CrossRef]
- Zhang, Y.; Tan, Y.; Liu, Z.; Wang, Y.; Sun, G. Modeling ballistic impact on nylon-based composites. Compos. Struct. 2020, 234, 111713. [Google Scholar] [CrossRef]
- Vescovini, A.; Cruz, J.A.; Ma, D.; Colombo, C.; Salerno, A.; Bianchi, O.; Amico, S.C.; Manes, A. Experimental investigation on low-velocity impact behavior of glass, Kevlar, and hybrid composites with an elastomeric polyurethane matrix. Compos. Part C Open Access 2024, 13, 100426. [Google Scholar] [CrossRef]
- Ghosh, A.; Das, S.; Das, A.; Mandal, N. Modeling dynamic behavior of 4340 steel using Johnson-Cook parameters. J. Mater. Res. Technol. 2020, 9, 3435–3446. [Google Scholar] [CrossRef]
- Rahman, M.; Ahmed, I.; Hasan, M.; Mahmud, S. Dynamic response of PMMA under high-velocity impact. Polym. Test. 2021, 93, 106954. [Google Scholar] [CrossRef]
- Gloger, M.; Stempien, Z.; Pinkos, J. Numerical and experimental investigation of the ballistic performance of hybrid woven and embroidered-based soft armour under ballistic impact. Compos. Struct. 2023, 322, 117420. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. A Constitutive Model and Data for Metals Subjected to Large Strains, High Strain Rates, and High Temperatures. In Proceedings of the 7th International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983; pp. 541–547. [Google Scholar]
- Xu, H.; Zhang, Y.; Peng, R.; Zhu, L.; Lu, Y. Simulation and experimental study on the strength of Al7075-T6 clinched joint. Eng. Fail. Anal. 2021, 129, 105735. [Google Scholar] [CrossRef]
- ANSYS, Inc.: Ansys Fluent Theory Guide, Southpointe. 2021. Available online: https://dl.cfdexperts.net/cfd_resources/Ansys_Documentation/Fluent/Ansys_Fluent_Theory_Guide.pdf (accessed on 5 June 2025).
- Wiśniewski, A.; Gmitrzuk, M. Validation of Numerical Model of the Twaron® CT709 Ballistic Fabric. Probl. Mechatron. Armament Aviat. Saf. Eng. 2014, 5, 19–32. [Google Scholar]
- Wang, Z.; Zhang, H.; Dong, Y.; Zhou, H.; Huang, G. Ballistic performance and protection mechanism of aramid fabric modified with polyethylene and graphene. Int. J. Mech. Sci. 2022, 237, 107772. [Google Scholar] [CrossRef]
- Sockalingam, S.; Chowdhury, S.C.; Gillespie, J.W., Jr.; Keefe, M. Recent Advances in Modeling and Experiments of Kevlar Ballistic Fibrils, Fibers, Yarns and Flexible Woven Textile Fabrics—A Review. Text. Res. J. 2017, 87, 984–1010. [Google Scholar] [CrossRef]
- Min, S.; Chen, X.; Chai, Y.; Lowe, T. Effect of Reinforcement Continuity on the Ballistic Performance of Composites Reinforced with Multiply Plain Weave Fabric. Compos. B Eng. 2016, 90, 30–36. [Google Scholar] [CrossRef]
- Xu, Y.J.; Ma, Y.; Xie, Y.C.; Zhou, Y.; Zhang, H.; Huang, G.Y. Experimental and Numerical Study on the Ballistic Performance of a ZnO-Modified Aramid Fabric. Int. J. Impact Eng. 2023, 175, 104519. [Google Scholar] [CrossRef]
- Xu, F.; Fan, W.; Zhang, Y.; Gao, Y.; Jia, Z.; Qiu, Y.; Hui, D. Modification of Tensile, Wear and Interfacial Properties of Kevlar Fibers under Cryogenic Treatment. Compos. B Eng. 2017, 116, 398–405. [Google Scholar] [CrossRef]
- MSZ K 1114-1:1999; Ballistic Protection—Bulletproof Vests—Classification, Requirements and Test Methods. Hungarian Standards Institution: Budapest, Hungary, 1999.
- NIJ 0101.06; Ballistic Resistance of Body Armor. National Institute of Justice: Washington, DC, USA, 2008.
- NIJ 0101.07; Ballistic Resistance of Body Armor. National Institute of Justice: Washington, DC, USA, 2024.
- STANAG 2920; Ballistic Test Method for Personal Armour Materials and Combat Clothing. NATO Standardization Office (NSO): Brussels, Belgium, 2003.
- Karhankova, M.; Adamek, M.; Krstulovi’c-Opara, L.; Mach, V.; Bagavac, P.; Stoklasek, P.; Mizera, A. Composites in Ballistic Applications Focused on Ballistic Vests—A Review. J. Compos. Sci. 2024, 8, 415. [Google Scholar] [CrossRef]
- Tabiei, A.; Nilakantan, G. Ballistic Impact of Dry Woven Fabric Composites: A Review. Appl. Mech. Rev. 2008, 61, 010801. [Google Scholar] [CrossRef]
- Şenyilmaz, H.K.; Uslan, İ.; Demir, K. Investigation of the effect of a dilatant material on ballistic strength of aramid fabric used as body armour suit. J. Text. Inst. 2021, 113, 580–588. [Google Scholar] [CrossRef]
- Shih, C.-H.; You, J.-L.; Lee, Y.-L.; Cheng, A.-Y.; Chang, C.-P.; Liu, Y.-M.; Ger, M.-D. Design and Ballistic Performance of Hybrid Plates Manufactured from Aramid Composites for Developing Multilayered Armor Systems. Polymers 2022, 14, 5026. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.S.; Wagner, N.J. Dynamic properties of shear thickening colloidal suspensions in ballistic fabrics. J. Mater. Sci. 2003, 38, 2825–2833. [Google Scholar] [CrossRef]
- Decker, M.J.; Halbach, C.J.; Nam, C.H.; Wagner, N.J.; Wetzel, E.D. Stab resistance of shear thickening fluid (STF)-treated fabrics. Compos. Sci. Technol. 2007, 67, 565–578. [Google Scholar] [CrossRef]







| Material | A (MPa) | B (MPa) | N | C | M | Reference |
|---|---|---|---|---|---|---|
| Steel 4340 (34CrNiMo6) | 792 | 510 | 0.26 | 0.014 | 1.03 | [9,12] |
| Al 7075-T6 | 503 | 260 | 0.26 | 0.015 | 1.34 | [13] |
| Nylon | 95 | 25 | 0.23 | 0.015 | 1.0 | [7] |
| Rubber | J–C not used, applied hyperelastic Mooney–Rivlin model | [14] | ||||
| PMMA (plexiglass) | 125 | 90 | 0.3 | 0.02 | 1.2 | [10] |
| Material | Penetration | Bullet Deformation | Figure |
|---|---|---|---|
| Steel 4340 | NO | Flattening |  |
| Al 7075-T6 | YES | Fragmentation | 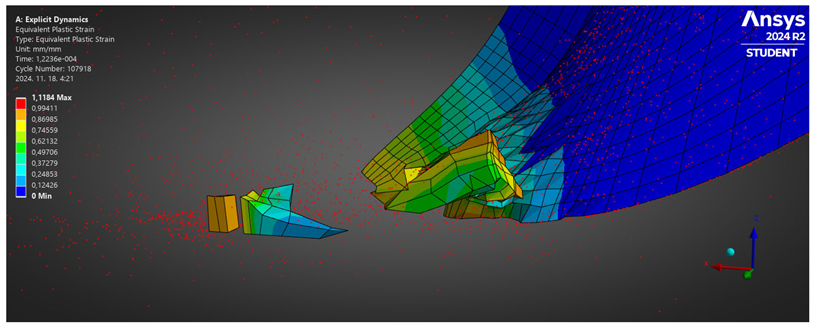 |
| Rubber | YES | Jacket Rupture |  |
| Nylon | YES | Complete Jacket Separation |  |
| Plexiglass | YES | Jacket Rupture | 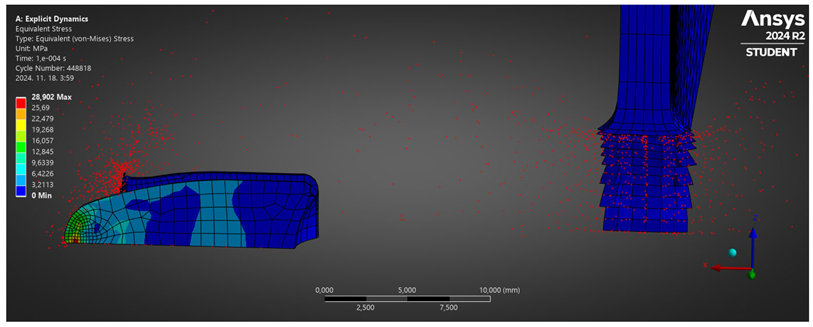 |
| Parameter | |
|---|---|
| Weight (g/m2) | 200 |
| Density (g/cm3) | 1.45 |
| Tensile strength (MPa) | 2400 |
| Tensile modulus (GPa) | 90 |
| Tensile strain (%) | 3.3 |
| Parameter | Epoxy | Polyurethan |
|---|---|---|
| Shore hardness | 55 | 30 |
| Density (cps) | 1.45 | 1.8 |
| Tensile strength (MPa) | 30 | 3.5 |
| Tensile modulus (GPa) | 75 | 100 |
| Equivalent weight (g/eq) | 140 | 125 |
| Viscosity (mPa·s) | 200 | 1800 |
| Specimen | Mass (g) | Thickness (mm) |
|---|---|---|
| 1 | 368 | 5.05 |
| 2 | 654 | 5.48 |
| 3 | 616 | 5.92 |
| Class Threat Level | Type of Bullet and Caliber | Minimum Bullet Velocity (m/s) | Number of Shots 00 | Number of Shots 300 | Minimum Penetration Depth (mm) |
|---|---|---|---|---|---|
| L1 | 0.38 Special RN | 259 | 4 | 2 | 44 |
| L1 | 0.22 LR HV | 320 | 4 | 2 | 44 |
| L2 | 0.357 Magnum JSP | 381 | 4 | 2 | 44 |
| L2 | 9 × 19 mm FMJ Parabellum | 332 | 4 | 2 | 44 |
| L3 | 0.357 Magnum JSP | 425 | 4 | 2 | 44 |
| L3 | 9 × 19 mm FMJ Parabellum | 358 | 4 | 2 | 44 |
| L4 | 44 Magnum SWC | 426 | 4 | 2 | 44 |
| L4 | 9 × 19 mm FMJ Parabellum | 426 | 4 | 2 | 25 |
| L5 | 7.62 × 54 R 39M L | 838 | 6 | 0 | 25 |
| L6 | 7.62 × 54 R 39M B32 | 868 | 1 | 0 | 25 |
| LS | specific requirements | determined by the customer | |||
| Number of Shots | Projectile Velocity (m/s) | Angle of Shot (°) | Depth of Trauma Zone (mm) | Validity |
|---|---|---|---|---|
| 1 | 428 | 0 | 17.42 | YES |
| 2 | 426 | 0 | - | NO |
| 3 | 430 | 0 | 19.25 | YES |
| Number of Shots | Projectile Velocity (m/s) | Angle of Shot (°) | Depth of Trauma Zone (mm) | Validity |
|---|---|---|---|---|
| 1 | 426 | 0 | 23.2 | YES |
| 2 | 431 | 0 | 24.8 | YES |
| 3 | 428 | 0 | 22.25 | YES |
| 4 | 433 | −30 | 23.5 | YES |
| 5 | 429 | +30 | 24.5 | YES |
| 6 | 427 | 0 | 22.84 | YES |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kondor, I.P.; Líska, J.; Kovács, Z.F. Ballistic Performance of Lightweight Armor Aramid Fabric with Different Bounding Technologies. Fibers 2025, 13, 106. https://doi.org/10.3390/fib13080106
Kondor IP, Líska J, Kovács ZF. Ballistic Performance of Lightweight Armor Aramid Fabric with Different Bounding Technologies. Fibers. 2025; 13(8):106. https://doi.org/10.3390/fib13080106
Chicago/Turabian StyleKondor, István Péter, János Líska, and Zsolt Ferenc Kovács. 2025. "Ballistic Performance of Lightweight Armor Aramid Fabric with Different Bounding Technologies" Fibers 13, no. 8: 106. https://doi.org/10.3390/fib13080106
APA StyleKondor, I. P., Líska, J., & Kovács, Z. F. (2025). Ballistic Performance of Lightweight Armor Aramid Fabric with Different Bounding Technologies. Fibers, 13(8), 106. https://doi.org/10.3390/fib13080106





