Application of Transformed Cross-Section Method for Analytical Analysis of Laminated Veneer Lumber Beams Strengthened with Composite Materials
Abstract
1. Introduction
2. Materials and Methods
2.1. Transformed Cross Section Method
- for composite parts oriented in vertical fashion:
- for composite parts oriented in horizontal fashion:
2.2. Methods
2.2.1. Modulus of Rupture (MOR)
2.2.2. Bending Stiffness EI
- A method based on the curvature of the beam during bending (conducted using experimental data);
- A method based on the characteristics of the equivalent cross-section using the elastic modulus of laminated veneer (conducted using simplified mathematical model);
- A method based on a formula that describes the deflection value of a beam loaded with two concentrated forces (conducted using experimental data).
2.2.3. Position of Neutral Axis
3. Results
3.1. Modulus of Rupture (MOR)
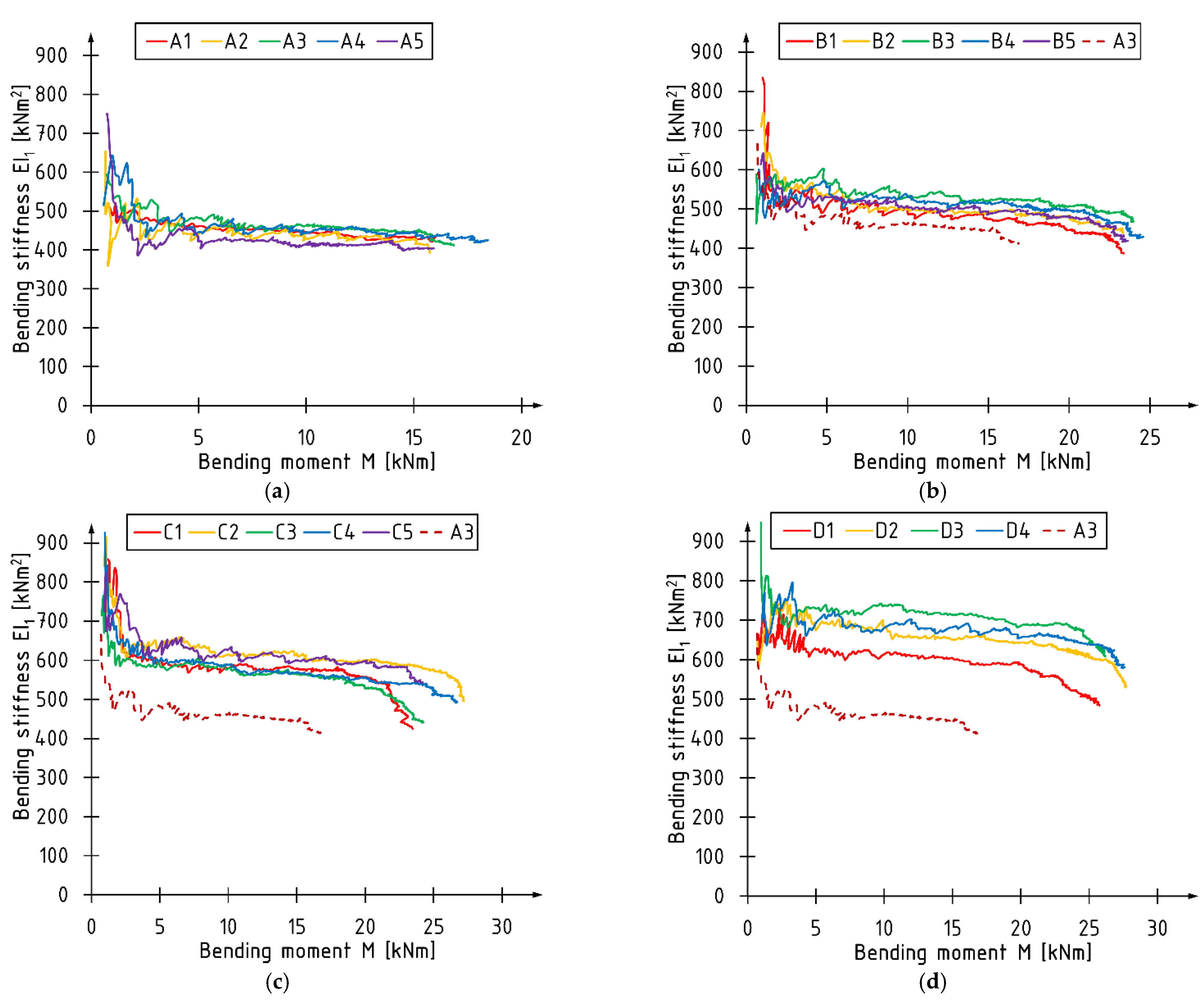
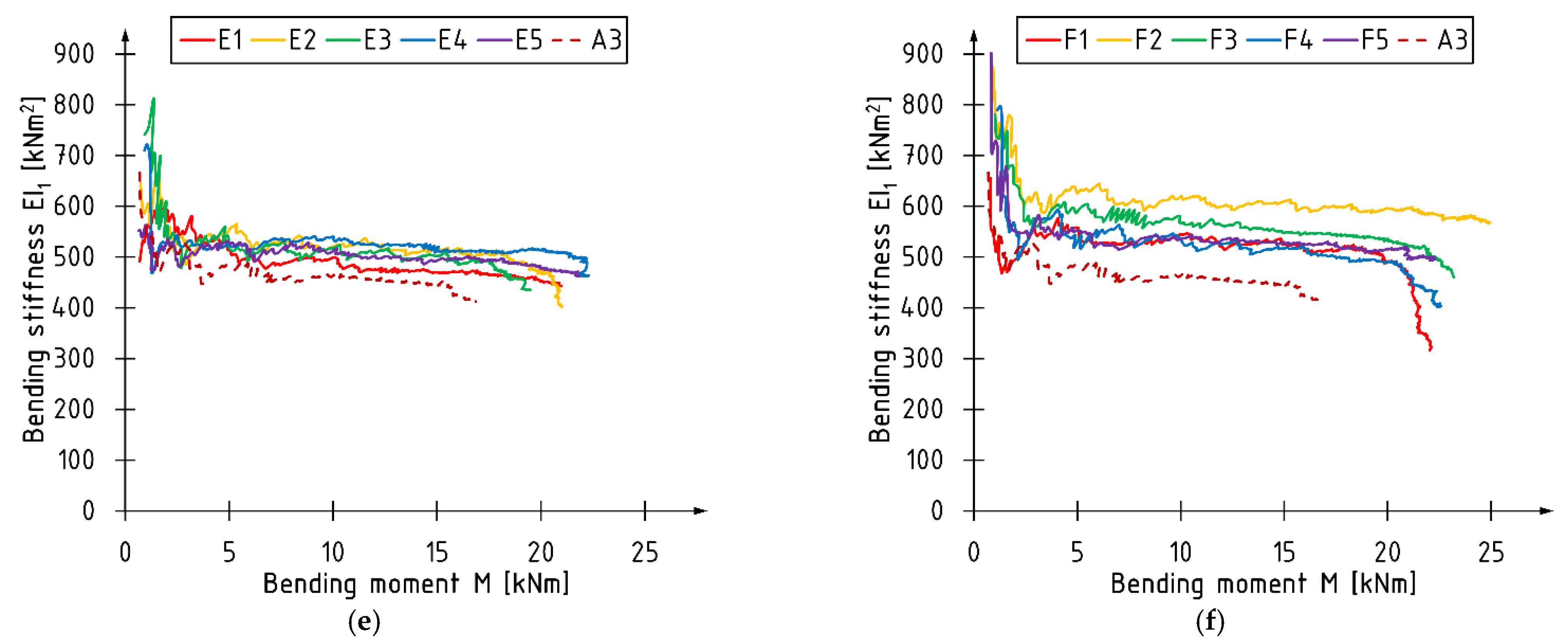
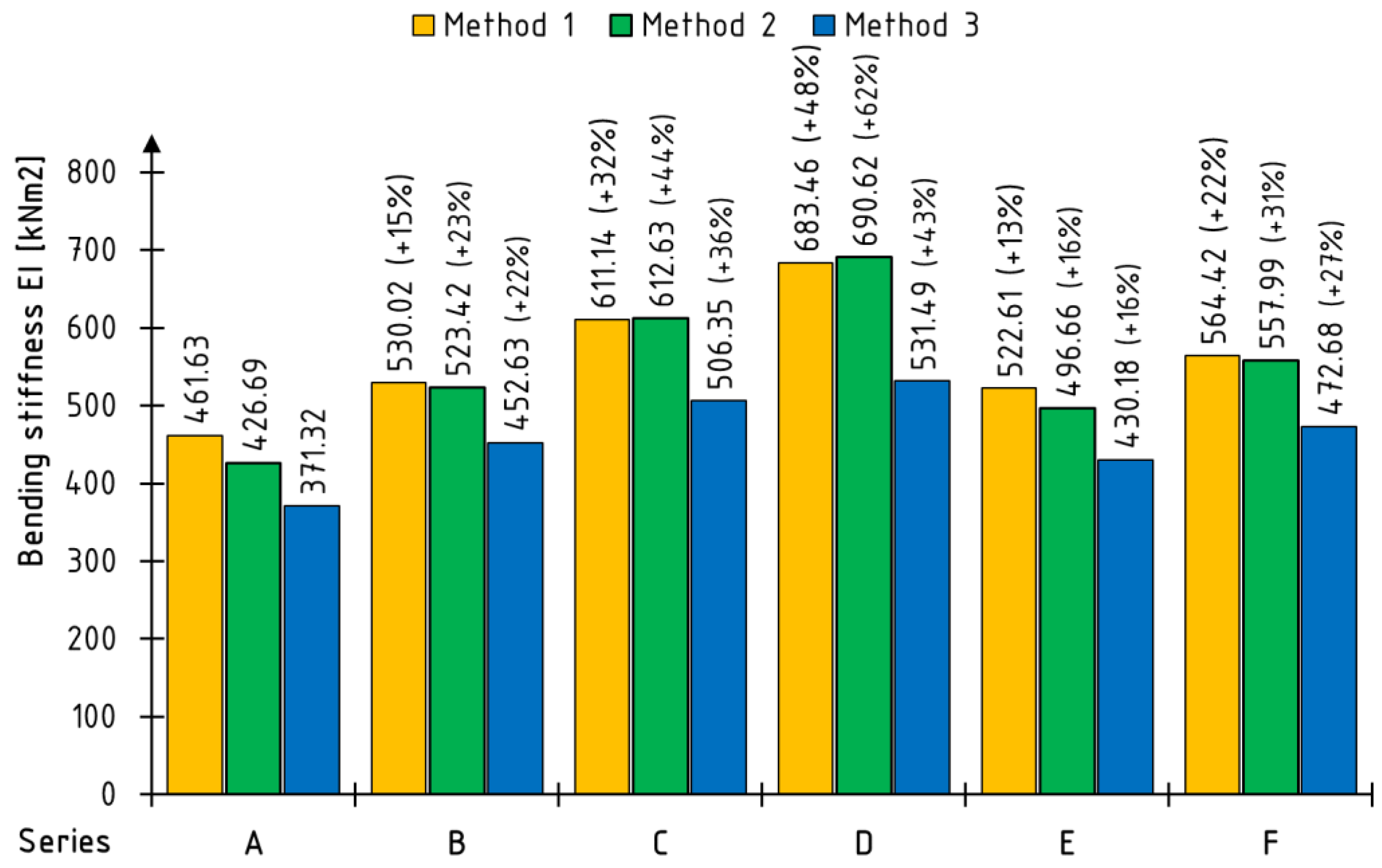
3.2. Bending Stiffness EI
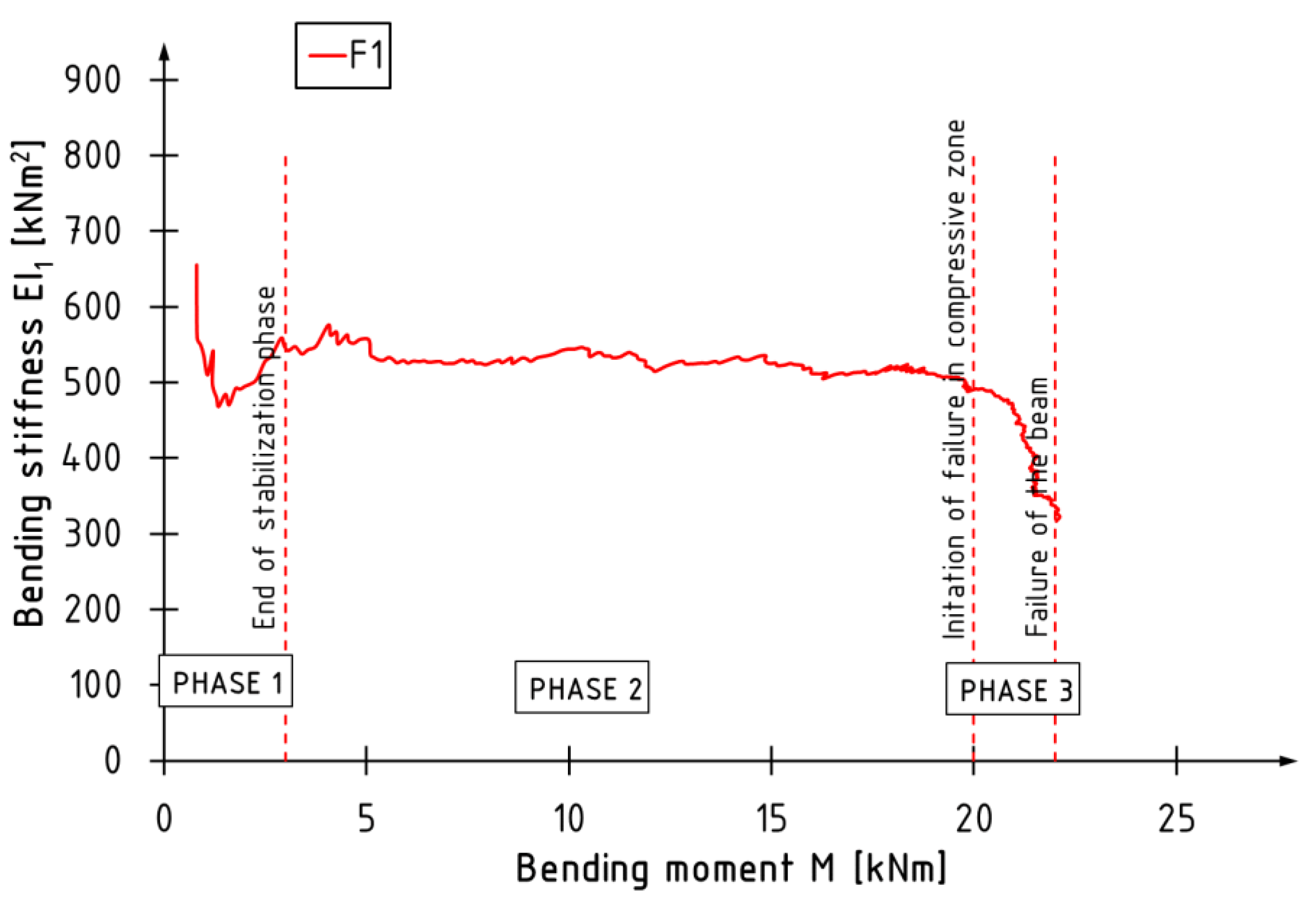
- Initial phase—rapid changes (decreases in stiffness) associated with stabilizing beams in the test stand. Typically, this phase lasts up to a load approximately equal to 5 kN;
- Middle phase—relative linear behavior, without significant changes in the curvature course;
- Final phase—begins at the point of change in the slope of the curve in the final stage of the test. The difference in slope is related to the nature of the failure and the accompanying change in stiffness, for example, due to crack propagation in the compression zone. This phase does not occur for beams whose failure occurs suddenly and is caused by exceeding the strength of the veneer in the tensile area, as is the case for unreinforced beams.
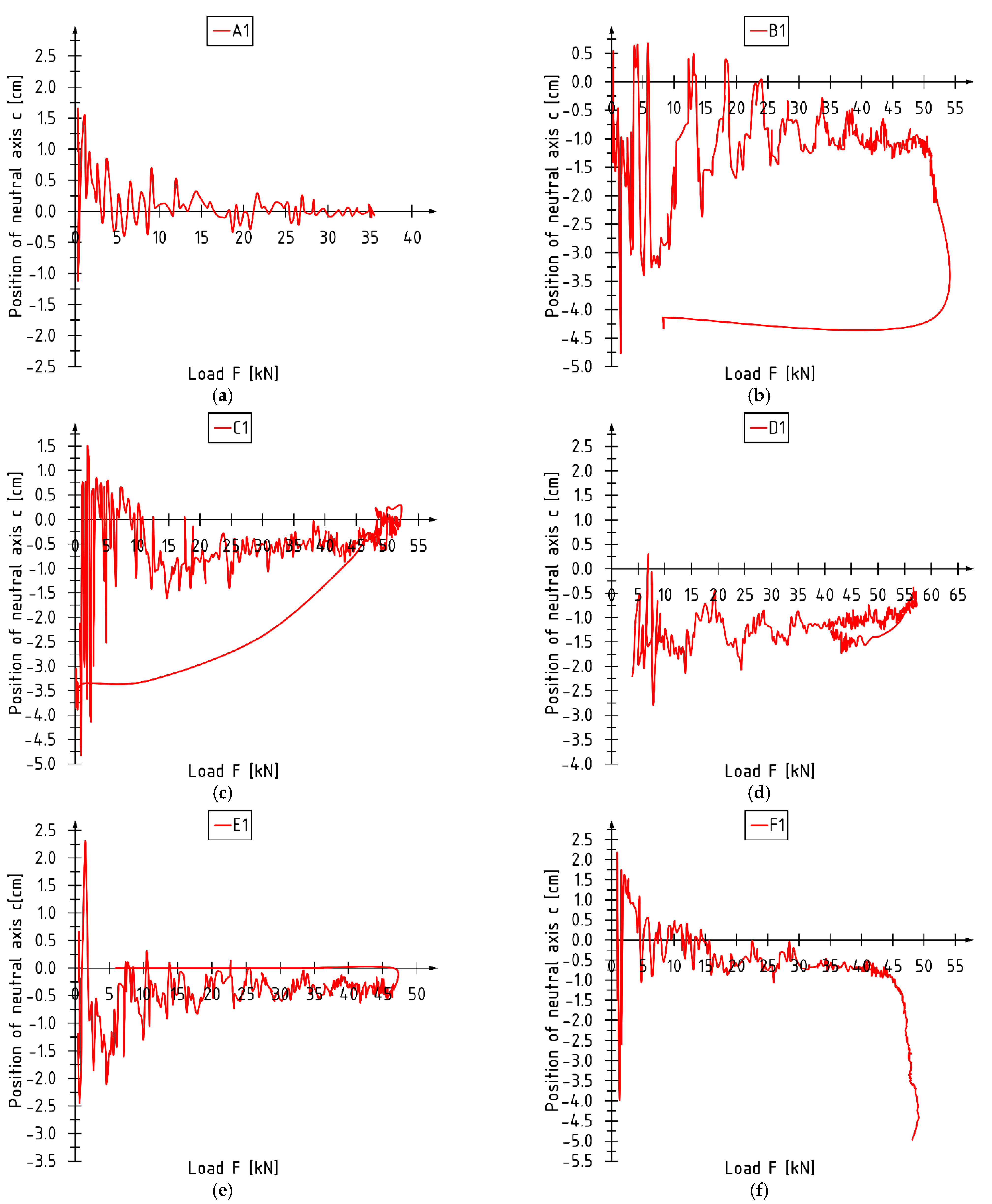
3.3. Neutral Axis Position c
4. Discussion
5. Conclusions
- The suitability of using the equivalent cross-section method to estimate the cross-sectional capacity of laminated veneers reinforced with fiber composites has not been confirmed. This is related to the assumption of a linear distribution of stresses in the compression and tension zones. In contrast, the actual distribution is linear in the tension zone and nonlinear in the compression zone. The degree of reinforcement and the way the composite reinforcement is redistributed between the compression and tensile zones greatly influence the MOR value;
- A high correspondence was obtained between the average values of EI bending stiffness estimated according to the method of equivalent characteristics (method 2) and the values derived from experimental tests (method 1). In the case of reinforcement with CFRP sheets and CFRP tapes glued to the external surface, the difference slightly exceeds 1%, and in the case of tapes glued into the grooves, less than 5%. The most significant discrepancies are recorded for reference beams—more than 7%. Of the three methods discussed for estimating the bending stiffness EI, method 3 (based on the formula for deflection at the center of the beam) differs the most from the others;
- Changes in the shape of the curves describing changes in bending stiffness as well as the position of the neutral axis can be divided into three zones: initial (stabilization), middle (constant work), and final (decrease in stiffness). The final phase occurs only in the case of reinforced beams; the failure initiated in the compression zone—a significant reduction in bending stiffness. The equivalent cross-section most accurately describes the position of the neutral axis at failure for beams reinforced with sheets glued to the outer surfaces and CFRP laminates glued into the grooves. Beams reinforced with laminates glued to the bottom surface are the worst in this respect;
- For the reinforcement simulation, using carbon sheets with an ultra-high modulus of elasticity proves the most beneficial due to the increased bending stiffness. In contrast, the least beneficial is the use of glass sheets. As the stiffness of the reinforcement and the number of sheets used increase, the effectiveness of the reinforcement increases.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Burawska, I.; Tarasovs, S. Influence of glueline parameters on the mechanical behaviour of CFRP reinforced wood—Numerical analysis. Ann. Wars. Univ. Life Sci.–SGGW For. Wood Technol. 2014, 87, 18–24. [Google Scholar]
- Kula, K.; Socha, T. Renovation and strengthening of wooden beams with CFRP bands including rheological effects. Civ. Environ. Eng. Rep. 2016, 22, 93–102. [Google Scholar] [CrossRef]
- Nowak, T.P.; Jasieńko, J.; Czepiżak, D. Experimental tests and numerical analysis of historic bent timber elements reinforced with CFRP strips. Constr. Build. Mater. 2013, 40, 197–206. [Google Scholar] [CrossRef]
- Raftery, G.M.; Harte, A.M. Nonlinear numerical modeling of FRP reinforced glued laminated timber. Compos. Part B Eng. 2013, 52, 40–50. [Google Scholar] [CrossRef]
- Ye, L.; Wang, B.; Shao, P. Experimental and Numerical Analysis of a Reinforced Wood Lap Joint. Materials 2020, 13, 4117. [Google Scholar] [CrossRef] [PubMed]
- Chybiński, M.; Polus, Ł. Experimental and numerical investigations of laminated veneer lumber. Arch. Civ. Eng. 2021, 67, 351–372. [Google Scholar] [CrossRef]
- Chybiński, M.; Polus, Ł. Experimental and numerical investigations of aluminium-timber composite beams with bolted connections. Structures 2021, 34, 1942–1960. [Google Scholar] [CrossRef]
- Chybiński, M.; Polus, Ł. Structural Behaviour of Aluminium–Timber Composite Beams with Partial Shear Connections. Appl. Sci. 2023, 13, 1603. [Google Scholar] [CrossRef]
- Işleyen, U.K.; Kesik, H.İ. Experimental and numerical analysis of compression and bending strength of old wood reinforced with CFRP strips. Structures 2021, 33, 259–271. [Google Scholar] [CrossRef]
- Khelifa, M.; Loperena, N.V.; Bleron, L.; Khennane, A. Analysis of CFRP-strengthened timber beams. J. Adhes. Sci. Technol. 2014, 28, 1–14. [Google Scholar] [CrossRef]
- Makowski, A. Impact of the type and shape of the CFRP composite reinforcement on the improvement of strength parameters of wood combined elements. Electron. J. Pol. Agric. Univ. Wood Technol. 2006, 9, #37. Available online: http://www.ejpau.media.pl/volume9/issue4/art-37.html (accessed on 29 December 2022).
- Buchanan, A.H. Bending strength of lumber. J. Struct. Eng. (ASCE) 1990, 116, 1213–1229. [Google Scholar] [CrossRef]
- Borri, A.; Corradi, M.; Grazini, A.A. A method for flexural reinforcement of old wood beams with CFRP materials. Compos. Part B Eng. 2005, 36, 143–153. [Google Scholar] [CrossRef]
- Brady, J.F.; Harte, A.M. Prestressed FRP flexural strengthening of softwood glue-laminated timber beams. In Proceedings of World Conference on Timber Engineering (WCTE08), Miyazaki, Japan, 2–5 June 2008. [Google Scholar]
- Gentile, C.; Svecova, D.; Rizkalla, S.H. Timber beams strengthened with GFRP bars: Development and applications. J. Compos. Constr. 2002, 6, 11–20. [Google Scholar] [CrossRef]
- Vahedian, A.; Shrestha, R.; Crews, K. Experimental and analytical investigation on CFRP strengthened glulam laminated timber beams: Full-scale experiments. Compos. Part B Eng. 2019, 164, 377–389. [Google Scholar] [CrossRef]
- Hernandez, R.; Davalos, J.F.; Sonti, S.S.; Kim, Y.; Moody, R.C. Strength and Stiffness of Reinforced Yellow-Poplar Glued-Laminated Beams; Research Paper FPL-RP-554; Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 1997. [Google Scholar]
- Kliger, R.; Johansson, M.; Crocetti, R.; Al-Emrani, M. Strengthening timber with CFRP or steel plates–short and long-term performance. In Proceeding of World Conference on Timber Engineering (WCTE08), Miyazaki, Japan, 2–5 June 2008. [Google Scholar]
- Chen, S.; Wei, Y.; Ding, M.; Zhao, K.; Zheng, K. Combinatorial design and flexural behavior of laminated bamboo–timber composite beams. Thin-Walled Struct. 2022, 181, 109993. [Google Scholar] [CrossRef]
- Huang, S.; Yan, L.; Kasal, B. Flexural behaviour of wood beams strengthened by flax-glass hybrid FRP subjected to hygrothermal and weathering exposures. Constr. Build. Mater. 2023, 365, 130076. [Google Scholar] [CrossRef]
- Nadir, Y.; Nagarajan, P.; Ameen, M.; Arif, M.M. Flexural stiffness and strength enhancement of horizontally glued laminated wood beams with GFRP and CFRP composite sheets. Constr. Build. Mater. 2016, 112, 547–555. [Google Scholar] [CrossRef]
- Hoseinpour, H.; Valluzzi, M.R.; Garbin, E.; Panizza, M. Analytical investigation of timber beams strengthened with composite materials. Constr. Build. Mater. 2018, 191, 1242–1251. [Google Scholar] [CrossRef]
- Shekarchi, M.; Oskouei, A.V.; Raftery, G.M. Flexural behavior of timber beams strengthened with pultruded glass fiber reinforced polymer profiles. Compos. Struct. 2020, 241, 112062. [Google Scholar] [CrossRef]
- Di, J.; Zuo, H.; Li, Y.; Wang, Z. Design method for glulam beams strengthened with flax fiber reinforced polymer sheets. Structures 2023, 49, 26–43. [Google Scholar] [CrossRef]
- Yeboah, D.; Gkantou, M. Investigation of flexural behaviour of structural timber beams strengthened with NSM basalt and glass FRP bars. Structures 2021, 33, 390–405. [Google Scholar] [CrossRef]
- Kawecki, B.; Sumorek, A. Study on Profitability of Combining Wood and CFRP into Composite Based on Mechanical Performance of Bent Beams. Appl. Sci. 2022, 12, 10304. [Google Scholar] [CrossRef]
- Timbolmas, C.; Bravo, R.; Rescalvo, F.J.; Portela, M. Transformed-section method applied to multispecies glulam timber beams subjected to pure bending. Mech. Adv. Mater. Struct. 2021, 29, 1–10. [Google Scholar] [CrossRef]
- Timbolmas, C.; Bravo, R.; Rescalvo, F.J.; Gallego, A. Development of analytical model to predict the bending behavior of composite glulam beams in tension and compression. J. Build. Eng. 2022, 45, 103471. [Google Scholar] [CrossRef]
- Halicka, A.; Ślósarz, S. Strengthening of timber beams with pretensioned CFRP strips. Structures 2021, 34, 2912–2921. [Google Scholar] [CrossRef]
- Bakalarz, M.; Kossakowski, P. Strengthening of full-scale laminated veneer lumber beams with CFRP sheets. Materials 2022, 15, 6526. [Google Scholar] [CrossRef]
- Bakalarz, M. Load bearing capacity of laminated veneer lumber beams strengthened with CFRP strips. Arch. Civ. Eng. 2021, 67, 139–155. [Google Scholar]
- Bakalarz, M.M.; Kossakowski, P.G.; Tworzewski, P. Strengthening of Bent LVL Beams with Near-Surface Mounted (NSM) FRP Reinforcement. Materials 2020, 13, 2350. [Google Scholar] [CrossRef]
- Bakalarz, M.M.; Tworzewski, P.G. Application of Digital Image Correlation to Evaluate Strain, Stiffness and Ductility of Full-Scale LVL Beams Strengthened by CFRP. Materials 2023, 16, 1309. [Google Scholar] [CrossRef]
- Masłowski, E.; Spiżewska, D. Wzmacnianie Konstrukcji Budowlanych; Wydawnictwo Arkady: Warsaw, Poland, 2000. [Google Scholar]
- Rudziński, L. Konstrukcje Drewniane. Naprawy, Wzmocnienia, Przykłady Obliczeń; Wydawnictwo Politechniki Świętokrzyskiej: Kielce, Poland, 2010. [Google Scholar]
- S&P C-Sheet 240—Technical Information. Available online: https://www.sp-reinforcement.pl/sites/default/files/field_product_col_doc_file/c-sheet_240_polska_ver20190627.pdf (accessed on 19 September 2022).
- Kossakowski, P. Materiały Pomocnicze do Laboratorium Wytrzymałości Materiałów; Wydawnictwo Politechniki Świętokrzyskiej: Kielce, Poland, 2008. [Google Scholar]
- S&P A-Sheet 120—Technical Information. Available online: https://www.sp-reinforcement.pl/sites/default/files/field_product_col_doc_file/a_sheet_120_polska_ver012019-low.pdf (accessed on 29 December 2022).
- S&P G-Sheet E 90/10, Typ B; S&P G-Sheet AR 90/10, Typ B—Technical Information. Available online: https://www.sp-reinforcement.pl/sites/default/files/field_product_col_doc_file/g_sheet_e_ar_90_10_typ_b_polska_ver012019_low.pdf (accessed on 29 December 2022).
- S&P C-Sheet 640—Technical Information. Available online: https://www.sp-reinforcement.pl/sites/default/files/field_product_col_doc_file/c-_sheet_640_polska_ver012019_low.pdf (accessed on 29 December 2022).
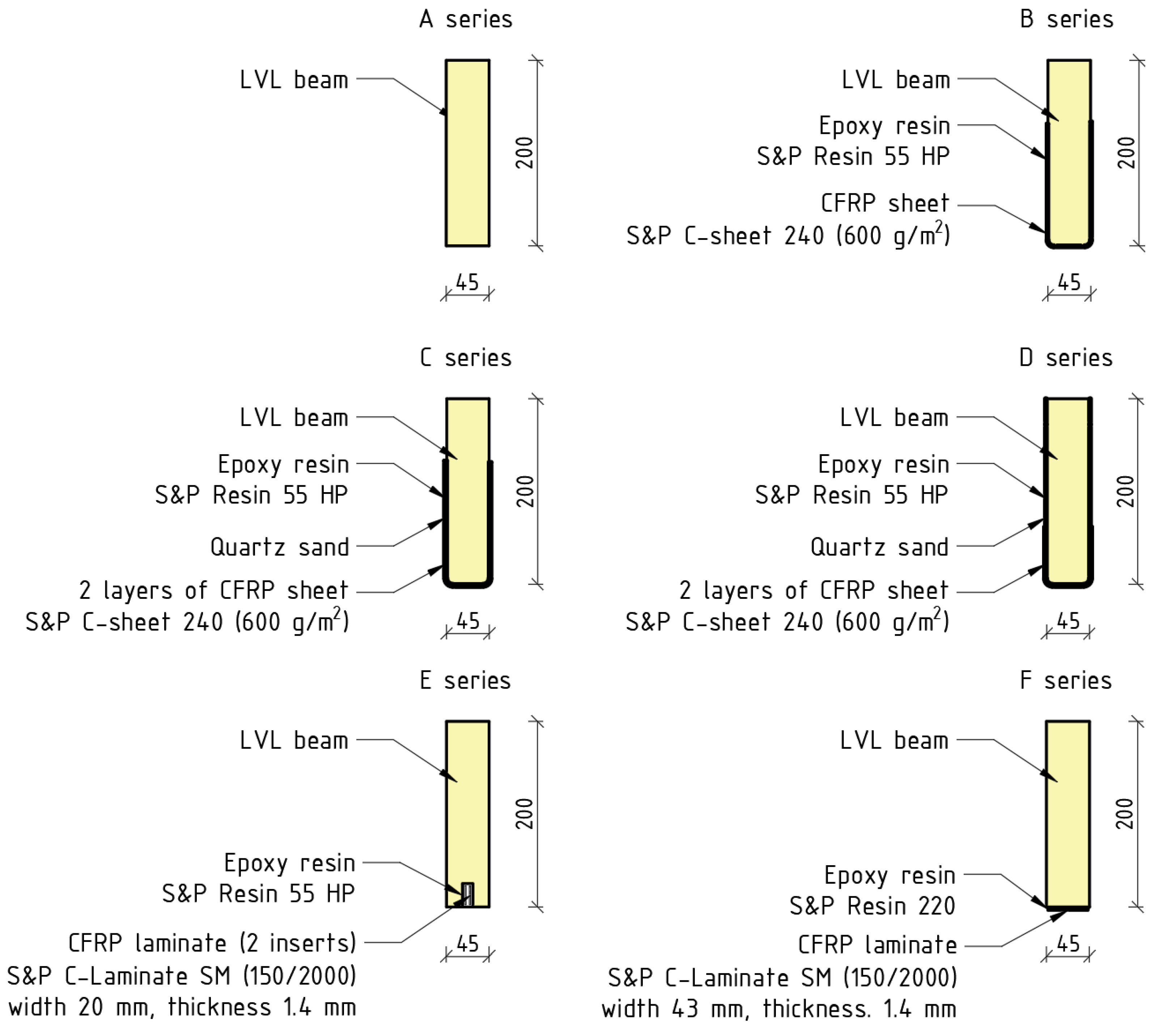

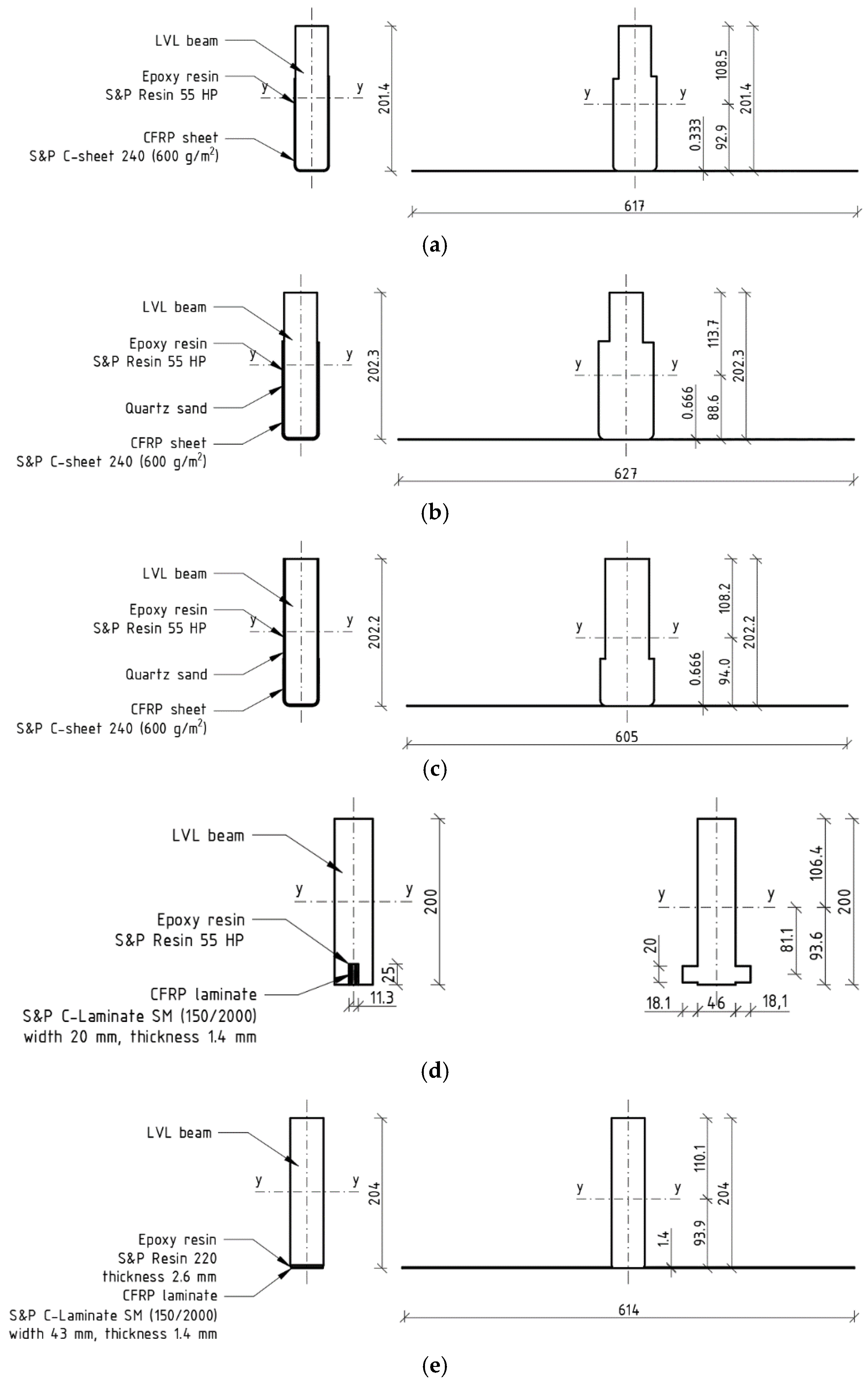
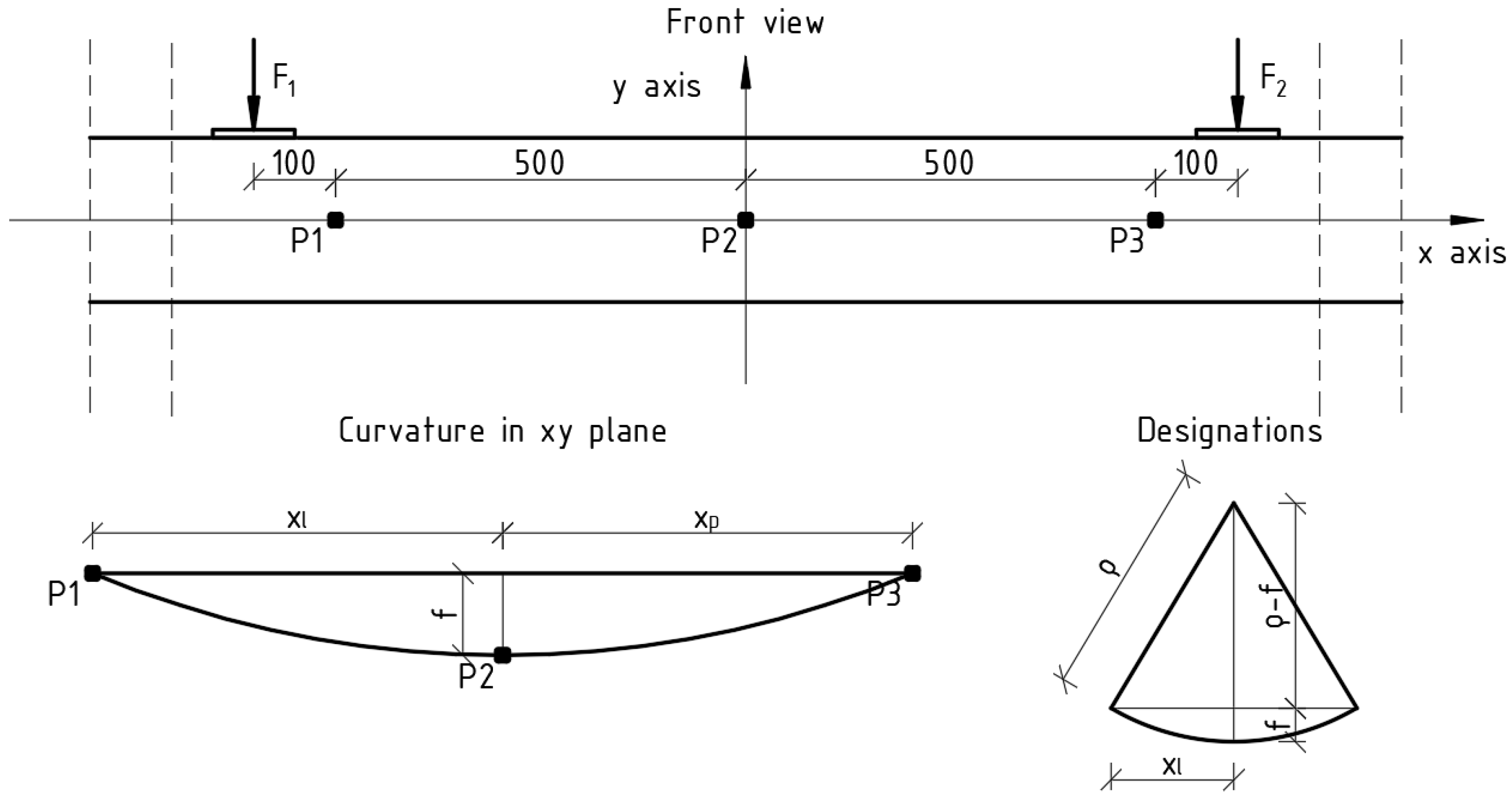
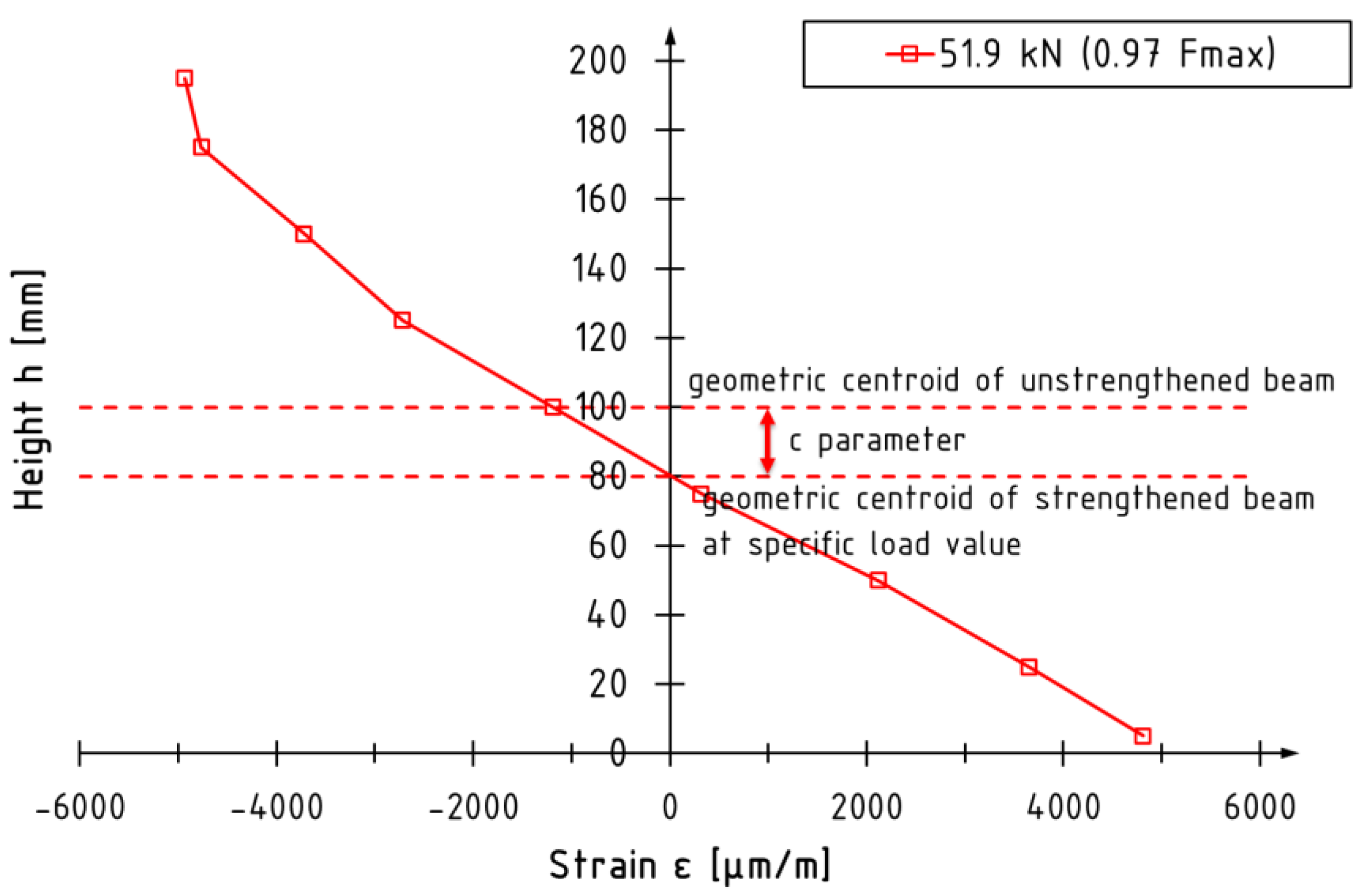


| Series | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| Method 2 | −7.57% | −1.25% | 0.24% | 1.05% | −4.97% | −1.14% |
| Method 3 | −19.56% | −14.60% | −17.15% | −22.24% | −17.69% | −16.25% |
| Series | Position of Neutral Axis c [cm] | |
|---|---|---|
| Based on Strain Distribution | Transformed Cross-Section | |
| A | 0.22 | 0.00 |
| B | −0.62 | −0.83 (−25%) |
| C | −1.12 | −1.39 (−19%) |
| D | −0.87 | −0.85 (2%) |
| E | −0.44 | −0.67 (−33%) |
| F | −2.04 | −1.01 (102%) |
| Sheet Type | AFRP Sheet S&P A-Sheet 120 | GFRP Sheet S&P G-Sheet E 90/10B | CFRP UHM Sheet S&P C-Sheet 640 |
|---|---|---|---|
| Modulus of elasticity Ef [GPa] | 120 | 73 | 640 |
| Tensile strength ft,f [MPa] | 2900 | 3400 | 2600 |
| Density ρf [kg/m3] | 1450 | 2600 | 2120 |
| Elongation at rupture εf [%] | 2.5 | 4.5 | 0.4 |
| Thickness for dimensioning tf [mm] | 0.200 | 0.308 | 0.189 |
| Sheet Type | AFRP Sheet S&P A-Sheet 120 | GFRP Sheet S&P G-Sheet E 90/10B | CFRP UHM Sheet S&P C-Sheet 640 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Number of Layers | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| Bending stiffness EI2 [kNm2] | 485 | 556 | 625 | 481 | 550 | 618 | 742 | 1051 | 1354 |
| Position of neutral axis c [cm] | −0.28 | −0.54 | −0.75 | −0.26 | −0.51 | −0.72 | −1.06 | −1.55 | −1.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bakalarz, M.M.; Kossakowski, P.G. Application of Transformed Cross-Section Method for Analytical Analysis of Laminated Veneer Lumber Beams Strengthened with Composite Materials. Fibers 2023, 11, 24. https://doi.org/10.3390/fib11030024
Bakalarz MM, Kossakowski PG. Application of Transformed Cross-Section Method for Analytical Analysis of Laminated Veneer Lumber Beams Strengthened with Composite Materials. Fibers. 2023; 11(3):24. https://doi.org/10.3390/fib11030024
Chicago/Turabian StyleBakalarz, Michał Marcin, and Paweł Grzegorz Kossakowski. 2023. "Application of Transformed Cross-Section Method for Analytical Analysis of Laminated Veneer Lumber Beams Strengthened with Composite Materials" Fibers 11, no. 3: 24. https://doi.org/10.3390/fib11030024
APA StyleBakalarz, M. M., & Kossakowski, P. G. (2023). Application of Transformed Cross-Section Method for Analytical Analysis of Laminated Veneer Lumber Beams Strengthened with Composite Materials. Fibers, 11(3), 24. https://doi.org/10.3390/fib11030024







