Abstract
This work addresses the feasibility of using waste badminton string fiber in cement and polymer matrices. A badminton racquet, once used, is torn and needs replacement with new strings. These torn strings, once cut from the badminton racquet system, become waste, and these fibers cannot be recycled and remain debris. Hence, this study examines the microstructural and mechanical properties of new fibers and old torn fibers comparatively. Scanning electron microscopy, X-ray diffraction, Fourier transform infrared spectroscopy, and energy dispersive spectroscopy are used to study the microstructural properties of the fiber. Direct tensile stress is applied to new and old fibers in the universal testing machine varying by one, three, and five strands of the fibers and varying the gauge length to 60, 80, and 100 mm, and the respective energy absorption is calculated. From investigation with a varying number of strands, similar results were observed in both old and new fibers from energy absorption and residual force ratio. From investigation with varying gauge length, the tensile stress of new fibers varies between 648.53 and 749.03 MPa, and that of old fibers is 537.40–625.55 MPa. Young’s modulus for new and old fibers is 4870.00 and 4843.50 MPa, respectively. The Weibull statistical approach is used to test the variability of test results. The Weibull modulus varies between 5.27 and 9.17, which shows lower variability. Thus, the tensile stress results obtained for the discarded badminton fibers pave way for incorporating these fibers in cement and polymer matrices to improve the matrix properties.
1. Introduction
The use of recycled fibers [1,2,3,4] as a reinforcement in cement and polymer matrices has been extensively research in the past 30 years [5,6,7,8]. The performance of concrete is enhanced by using various commercial fibers as well as recycled fibers. Among many recycled fibers such as fishing net waste [9,10,11], carpet waste [12,13,14], recycled steel wires [5,15,16], glass fibers [17,18,19], optical cable [20], and scrap nylon [21], the use of waste badminton strings as a reinforcement to the concrete is a new idea [22]. Fishing net waste [9] and recycled scrap nylon brushes [21] are twisted fibers with good tensile properties, which, when used as reinforcement in cementitious material, enhance the tensile property of concrete. Though these recycled polyamide fibers are good in long-term strength and durability behavior, researchers work on the assessment of many other recycled fibers for improvement in composites. Waste badminton string fiber (WBSF) is one such fiber that is found to have a twisted multifilament layer similar to other recycled nylon fibers. Hence, this study is aimed at determining the suitability of WBSF as a reinforcing material in concrete [22]. WBSF consist of more than 350 monofilament fibers twisted together into a single fiber and withstand very high tensile strength compared to other commercial and recycled synthetic fibers. Badminton is the second most famous sport, with over 220 million people playing badminton around the world. These strings, once used and torn, cannot be recycled, which leads to a high quantity of waste fibers that remain as debris [23].
These WBS can be used as fibers in cement and polymer matrices to strengthen their nature. WBSF does not require any additional treatment such as repolymerization when being used in concrete. WBSF just needs to be washed and properly cut for the desired aspect ratio. WBSF being used thus reduces the cost of the fiber required and is environmentally friendly. The badminton strings are a braided multifilament made up of nylon 6,6 [24,25]. Used waste badminton strings are collected from local sports shop. Many shops in different regions of the world have posted that these fibers are available as waste in abundance and can be procured for free, as shown in Figure 1 [26,27].

Figure 1.
(a) WBSF; (b) WBSF with various aspect ratios.
The key idea of incorporating these badminton fibers into cement and polymer matrices is to improve their toughness and impact resistance. Through the bridging action of this fiber with concrete, shrinkage and post-cracking are reduced [28]. Hence, the physical and microstructural properties of this fiber should be studied before incorporating it into concrete. The intermolecular bonding, crystalline phase, and elemental composition of the fibers are studied using Fourier transform infrared spectroscopy (FTIR), X-ray diffraction (XRD), and energy dispersive spectroscopy (EDS), respectively. Scanning electron microscopy (SEM) helps in the identification of the cross-sectional area and the diameter of the fiber. The SEM images are examined using ImageJ software for accuracy as the diameter of the fibers is less than 0.8 mm. Researchers have found that only 10% of the fibers in badminton racquets are damaged in the sweet spot, and the remaining undamaged fibers in the racquet show similar properties to that of new fibers [29]. WBSF in this study denotes the old fibers that are most severely damaged.
2. Methodology
In this study, old and new fibers are examined in terms of their microstructural and mechanical properties. Mechanical characteristics include the tensile strength of the fiber with varying strands (one, three, and five) and varying gauge lengths (60, 80, 100 mm) with reference to Majid Ali et al. [30] to study the energy absorption of the fiber and ASTM C-1557 [31] to study the Young’s modulus of the fiber, respectively. To determine the tensile stress of old and new fibers, the net cross-sectional area is calculated as it plays a major role. The performance of the fibers with varying strands is determined by energy absorption, whereas the performance of the fibers with varying gauge lengths can be determined by the direct tensile stress. The force distribution for fibers with varying strands (three and five) is determined by the residual force loss ratio. The Weibull distribution approach is used to determine the variability of the test results. The methodology is shown in Figure 2.
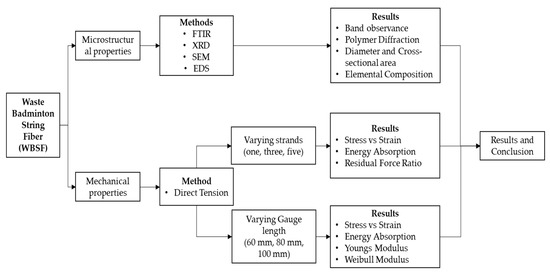
Figure 2.
Flow diagram of the methodology.
3. Experimental Methods
A microstructural analysis was conducted to study the characteristics of a multifilament nylon fiber, which was braided with more than 350+ microfibers, using FTIR [32], XRD [33], EDS [34], and SEM [35]. The mechanical characteristics were studied by conducting the direct tensile test on fibers by varying the number of strands (one, three, and five) and varying the gauge length (60, 80, and 100 mm).
3.1. Microstructural Analysis
The method followed and type of equipment used for FTIR, XRD, SEM, and EDS are given below.
3.1.1. Fourier Transform Infrared Spectroscopy
The spectrum obtained from FTIR shows the fingerprints of the structure and functional group response. A FTIR spectrum is often used to determine the material characterization of a new substance through observing various spectrum bands [36]. Infrared spectra were collected on a IR Tracer-100-Shimadzu FTIR spectrometer with a 4 cm−1 resolution, which reduces the environmental variations as it has a built-in automatic dehumidifier.
3.1.2. X-ray Diffraction
The polymer was characterized by XRD analysis to confirm its polymorphic structure. The films were studied using BRUKER USA D8 Advance, Davinci in the 2 theta range of 10°–80°.
3.1.3. Scanning Electron Microscopy and Energy Dispersion Spectroscopy
The microstructural analysis of WBSF such as SEM (for imaging) and EDS (for elemental mapping) was carried out in Thermoscientific Apreo S. The samples were prepared after washing with clean water followed by dehydration in atmospheric temperature. Among all imaging techniques, SEM is the most accurate for examining the physical properties of the fiber. The cross-sectional morphology of the fiber is examined at 200× using SEM.
3.2. Mechanical Study
The direct tensile load is applied to examine the mechanical properties. The sample preparation method, the equipment used, and the testing procedure are described in this section.
4. Results and Discussion
The results obtained from the microstructural and mechanical studies are discussed in this section.
Direct Tension Test Setup
The old and new fiber samples were gripped on an aluminum plate using a strong adhesive for a rigid gripping system [31], as shown in Figure 3. This gripping system was implemented to avoid the effect of compressive forces on the fiber due to the clamping of ends. The gauge length and spacing of the fibers were marked on a piece of paper, and then the aluminum plate (3 mm thickness; 50 mm width and length as per requirement) with fiber was positioned accordingly with a temporary adhesive. The rigid system was set by placing another plate using a strong epoxy, which ensures that the clamping force is not transferred to the fiber during testing. Proper care was taken with the epoxy used for the gripping system between the plates so that the diameter of the fiber between the plates was ensured.
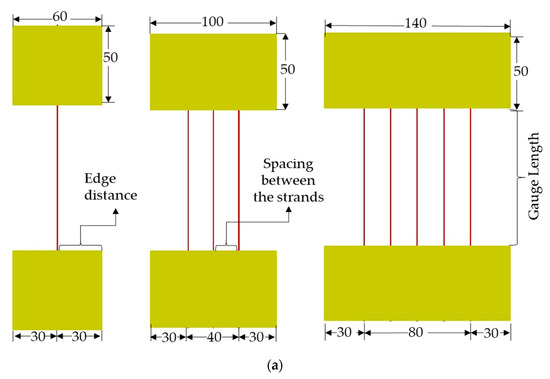
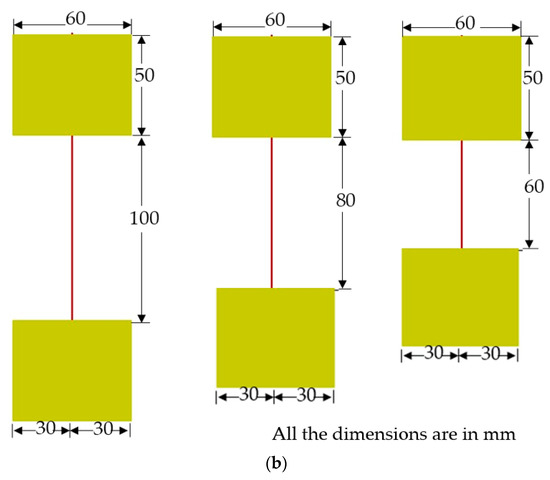
Figure 3.
Test specimen: (a) varying strands and (b) varying gauge lengths.
For the condition of varying strands (one, three and five), the gauge length was fixed as 100 mm and the edge distance and spacing between the fibers was maintained as 30 and 20 mm, respectively. For the condition of varying gauge lengths (60, 80 and 100 mm), the number of strands was fixed as a single-strand and the edge distance was maintained as 30 mm. The test specimen for varying conditions is shown in Figure 3.
The tensile test was conducted in computer-controlled universal testing machine, as shown in Figure 4. Testing was performed for samples with varying strands of the fibers and varying gauge lengths at a constant strain rate of 1 [37] and 2 mm/min [38], respectively. The fracture load was extracted with a load cell of 250 kg in capacity. The data acquired from the system are within ±1% standard uncertainty.

Figure 4.
(a) Schematic representation of test setup. (b) Test arrangement of specimen.
4.1. Microstructural Analysis
The results of WBSF obtained from FTIR, XRD, SEM and EDS are given below.
4.1.1. Fourier Transform Infrared Spectroscopy
Generally, the FTIR spectra bands are associated with both crystalline and amorphous phases, where the crystalline phase is usually sharper when compared with the amorphous phase. The three-test samples—S1, S2, and S3—also confirm the same pattern of band observance.
From the obtained band results of FTIR as shown in Figure 5, the medium peak at 3291 cm−1 can be attributed to the amino group of N-H stretch [39], and further medium peaks observed at 2920 and 2851 cm−1 show the vibration of alkane groups of asymmetric CH2 and symmetric CH2 stretch, respectively. The two strong peaks at 1635 and 1545 cm−1 were detected due to amide I and II bands [40]. Generally, the C=O stretch forms the peak between 1760 and 1665 cm−1. However, here, the peak obtained at 1635 cm−1 for the C=O stretch is due to the bonding of the amino I group with the hydrogen bond. The amide II band peak at 1545 cm−1 is due to the appearance of the N-H stretch. All the band values are given in Table 1. The peaks after 1500 cm−1 are of low intensity and the observance is weak. Hence, from the above results, the membrane shows a clear picture of the carbonyl group bonded with the hydroxyl group. This bonding reveals that the nylon 6,6 material is in its purest form.
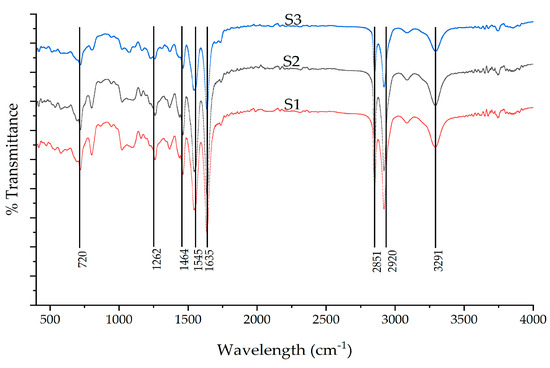
Figure 5.
FTIR response for the badminton fiber.

Table 1.
Band Assignment for the Badminton Fiber.
4.1.2. X-ray Spectroscopy
Generally, polymers contain two types of crystal—in the monoclinic α-form and in the monoclinic γ-form [41].
From the XRD pattern, two main high peaks of 2θ = 20.12° and 23.60° are visible. From this, the α-crystalline form is observed in both the high-intensity peaks, i.e., 2θ = 20.12° and 23.60°, and the γ-crystalline form is observed in the 20.12° peak. These results indicate that the crystalline structure of polyamide 6,6 is revealed [42], as shown in Figure 6.
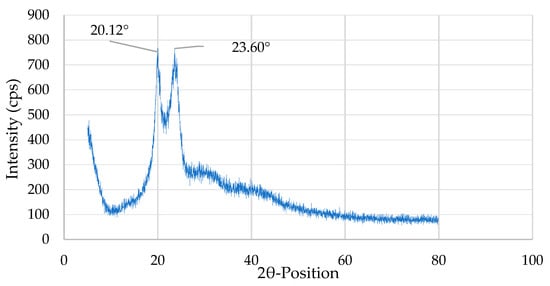
Figure 6.
XRD pattern for the badminton fiber.
4.1.3. Scanning Electron Microscopy and Energy Dispersion Spectroscopy
The fiber is cut longitudinally on the top surface to examine the layers imparted inside [43]. The typical image of WBSF from SEM is shown in Figure 7 and Figure 8.
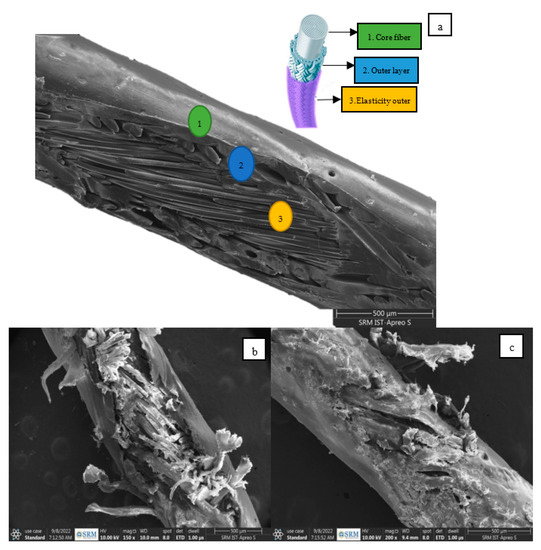
Figure 7.
WBSF observed in SEM. (a) Layers of WBSF; (b) severe damage (elasticity outer and outer layer); (c) surface damage (Elasticity outer).
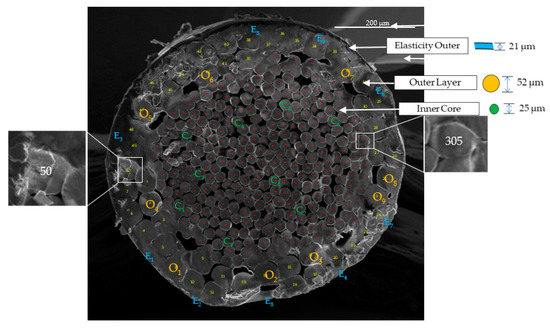
Figure 8.
Cross-sectional view of the fiber by SEM imaging.
The SEM image of the fibers reveals three distinct layers (an outer layer, an intermediate layer, and an inner layer) which are referred to as the elasticity outer, the outer layer, and the core fiber, as shown in Figure 6. In the grid system arrangement in the racquet, these fibers are subjected to more stretch. These three layers of the fibers help to withstand the high tension due to stretch. Figure 7b,c shows the SEM image of the fibers from the sweet spot of the racquet system. From the SEM image, it was noticed that only the elasticity outer and the outer layer are affected and the core fiber remains undisturbed. The elemental composition of the fiber layers is tabulated in Table 2.

Table 2.
Elemental composition of Badminton Fibers.
In elasticity outer, aluminum was detected as a minor element and the major elements detected are carbon, nitrogen, and oxygen, with a weightage of 51.53%, 25.05%, and 22.74%, respectively. In the outer layer, oxygen and silica are detected as minor elements and the major element detected is carbon, with a weightage of 88.08%. In the core fiber, sodium is detected as a minor element and the major elements detected are carbon, nitrogen, and oxygen with, a weightage of 44.39%, 25.80%, and 29.48%, respectively shown in (Supplementary Figure S1).
The entire fiber structure is arranged in such a way that nearly 350+ microfibers are bundled together. The elasticity outer of the fiber which protects the inner engineered fiber system is 21 µm in thickness, and is tabulated in Table 3.

Table 3.
Microfiber diameter in the outer layer, core fiber and thickness in the elasticity outer.
After a close examination through the outer layer and the core fiber, of the total number of microfibers, approximately 300+ are noticed in the core fiber and 50+ are noticed in the outer layer with a diameter of 25 and 52 µm, respectively. The typical pictorial representation of this system is given in Figure 8.
4.1.4. Determination of Net Cross-Sectional Area
The cross-section of the entire fiber and the microfibers in the outer and core are reasonably circular. Figure 8 shows the close image and arrangement of microfibers in the outer layer and the core fiber [44]. To characterize the diameter and area of the fiber, ImageJ software is used [45,46]. The net cross-sectional area of new and old fibers is required to determine the tensile stress and Young’s modulus of the fibers. For which, three individual sample fibers are cut in an exactly perpendicular manner and are kept vertically to perform SEM. From the SEM image, as shown in Figure 9, the cross-section borderline is traced carefully using ImageJ software. The net cross-section of the fiber is determined by deducting the area of voids from the overall cross-section of the fiber. The comparison of the net cross-sectional area of old fibers (O) and new fibers (N) is tabulated in Table 4.

Figure 9.
SEM image showing (a) the borderline and voids of new fibers; (b) the borderline and voids of old fibers.

Table 4.
Comparison of the net cross-sectional area of the fibers.
After examining three samples of new and old fibers in both the axes of symmetry, the mean diameter with standard deviation (SD) of new fibers and old fibers is 799.1 µm with 9.8 µm and 776.3 µm with 25.3 µm, respectively. A reduction in the mean diameter of the old fiber is observed, as the fiber is already tense (up to a maximum of 36 lbs) [47] at the time of stringing in the racquet system. As the old fiber is already used, so the SD in diameter is also high compared to new fibers. The diameter and SD values are tabulated in Table 4.
4.2. Mechanical Study
The mechanical properties which include stress–strain relationship, energy absorption, the residual force loss ratio, Young’s modulus, the Weibull modulus for varying strands and varying gauge lengths are discussed in this section.
4.2.1. Results of the Fibers by Varying Strands
Many samples of new and old fibers with one, three and five strands were considered for this study. The stress–strain relationship of these fibers was discussed based on the successful results of three samples under each category. For single-strand fiber samples (old and new), the maximum stress is calculated by dividing the ultimate strength of the single fiber with the net cross-sectional area of the corresponding fiber. For multi-strand fibers (old and new), the maximum stress is calculated by dividing the ultimate strength of the fiber which fails first with the net cross-sectional area of the corresponding fiber, as shown in Table 4. For all the above samples, the corresponding strain is also noted given in (Supplementary Table S1).
- (a)
- Tensile Strength of the Fiber with One Strand
The typical stress–strain curve of the fiber sample (new and old) with one strand is shown in Figure 10a. From the curve, a drop in stress was observed in three zones, namely zone 1 (elasticity outer), zone 2 (outer layer), and zone 3 (core fiber), which is due to the successive failure of three layers in the fiber. The drop in zone 1 is the failure of the elasticity outer layer, which fails at a stress approximately ranging from 200 to 350 MPa, with a corresponding approximate strain of 0.125. The drop in zone 2 is the failure of the outer layer, which fails at a stress of approximately ranging from 305 to 550 MPa, with a corresponding approximate strain of 0.16. The drop in zone 3 is the failure of the core fiber, which fails at a stress approximately ranging from 420 to 710 MPa, with a corresponding approximate strain of 0.225. Beyond this, a sudden drop to zero stress is observed. For new fibers, the average maximum stress is 654.76 MPa (standard deviation of 54.44 MPa) and its corresponding average strain is 0.21, which represents the ductile behavior of the fibers. However, for old fibers, the average maximum stress is 490.77 MPa (standard deviation of 47.66 MPa) and its corresponding average strain is 0.19. A decrease of 25% in the maximum stress and a lower difference in elongation, i.e., approximately 2%, is observed between the new and old fibers. This variation is noticed as the old fibers are stressed within the elastic limit only. The curve of stress–strain is nonlinear between the subsequent zones, due to the development of plastic strain.
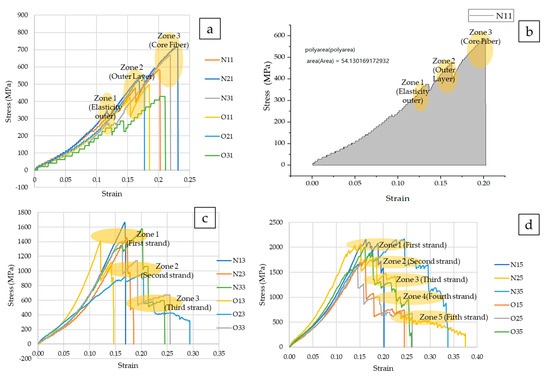
Figure 10.
(a) Stress–strain curve for one strand. (b) Energy absorption of the fiber. (c) Stress–strain curve for three strands. (d) Stress–strain curve for five strands.
The energy absorption (EA) of all fibers is calculated using Origin graphing software and the typical results for sample N11 are shown in Figure 10b. For new fibers. the average EA is 63.16 N.mm/mm3, with a standard deviation of 9.036 N.mm/mm3; and for old fibers, the average EA is 39.95 N.mm/mm3, with a standard deviation of 1.33 N.mm/mm3. As the stress and strain values of old fibers are lower than that of new fibers, a reduction of 37.63% in EA is observed in old fibers [30].
- (b)
- Tensile Strength of the Fiber with Three Strands
The typical stress–strain curve of the fiber sample (new and old) with varying three strands is shown in Figure 10c. Like single-strand fibers, a drop in stress is observed in three zones, namely zone 1 (first strand), zone 2 (second strand), and zone 3 (third strand), which is due to the successive failure of individual fibers in three strands. The maximum stress of three fibers is obtained by dividing the ultimate stress of the fiber, which fails in zone 1, to the cross-sectional area of a single fiber. For new fibers, the average maximum stress of three fibers is 1561.93 MPa (standard deviation of 87.91 MPa) and its corresponding average strain is 0.18. However, for old fibers, the average maximum stress of three fibers is 1262.53 MPa (standard deviation of 208.23 MPa) and its corresponding average strain is 0.16. As the peak load is shared among all the fibers, the maximum stress of a single fiber is calculated by dividing the maximum average stress of all fibers with the number of strands. The EA is similarly calculated from the stress–strain curve. For new fibers, the average EA is 55.34 N.mm/mm3 with a standard deviation of 3.60 N.mm/mm3, and for old fibers, the average EA is 33.65 N.mm/mm3 with a standard deviation of 3.09 N.mm/mm3. As the stress and strain values of old fibers are lower than that of new fibers, a reduction of 39.19% in EA is observed in old fibers.
- (c)
- Tensile Strength of the Fibers with Five Strands
The typical stress–strain curve of the fiber sample (new and old) with varying five strand is shown in Figure 10d. Like three-strand fibers, a drop in stress is observed in five zones, namely zone 1 (first strand), zone 2 (second strand), zone 3 (third strand), zone 4 (fourth strand) and zone 5 (fifth strand), which is due to successive failure of individual fibers in five strands. The maximum stress of five fibers is obtained by dividing the ultimate stress of the fiber which fails in zone 1 to the cross-sectional area of a single fiber. For new fibers, the average maximum stress of five fibers is 2127.19 MPa (standard deviation of 45.31 Mpa) and its corresponding average strain is 0.19. However, for old fibers, the average maximum stress of three fibers is 1738.95 Mpa (standard deviation of 109.01 Mpa) and its corresponding average strain is 0.16. As the peak load is shared among all the fibers, the maximum stress of a single fiber is calculated by dividing the maximum average stress of all fibers with the number of strands as given in Table 5. The energy absorption is similarly calculated from the stress–strain curve. For new fibers, the EA absorption is 68.04 N.mm/mm3, with a standard deviation of 12.56 N.mm/mm3, and for old fibers, the average EA is 40.09 N.mm/mm3, with a standard deviation of 2.78 N.mm/mm3. As the stress and strain values of old fibers are lower than that of new fibers, a reduction of 41.07% in EA is observed in old fibers.

Table 5.
Residual force loss ratio for varying strands.
- (d)
- Residual Force loss ratio
In multi-strand fibers, the ultimate force is reduced as the individual fibers show successive failure at different stages. A loss of force is observed due to the distribution of ultimate stress among the fibers in the strand. Thus, a better understanding of force distribution in fibers is gained by calculating the residual force loss ratio using the Equation (1) [48],
The ultimate force (Fu) and the force at different stages of break (Fur) are given in Table 5. For new fiber samples with three strands, the residual force loss percentage was 0, 35.22, 68.40, and 100.00; and for old fiber samples with three strands, the residual force loss percentage was 0, 32.48, 64.45, and 100. Similarly for samples with five strands, the residual force loss percentage of 0, 20.90, 36.44, 42.79, 61.72, 100.00 for new fibers and 0, 27.7, 40.40, 58.95, 63.88, 100 for old fibers were observed as shown in Figure 11. This loss in force is due to the successive failure of individual strands. From the results in Table 6, for multi-strand fibers (five in numbers), a minimum % of difference in observed in the residual force loss ratio as 6.35 and 4.93, which is due to the sudden failure of successive strands within a limited period.
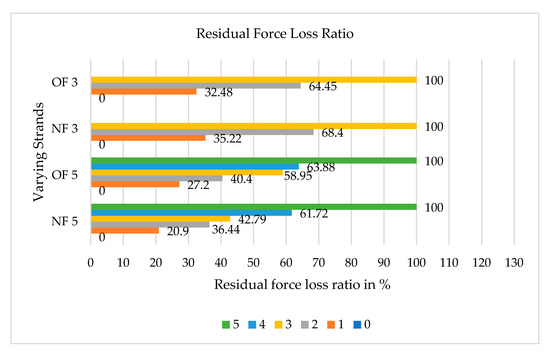
Figure 11.
Residual force loss ratio for varying fibers.

Table 6.
Weibull parameters on the performance of tensile strength.
4.2.2. Results of the Fibers by Varying Gauge Lengths
Many samples of new and old fibers with 60, 80 and 100 mm gauge length were considered for this study. The results are discussed considering two different conditions—the same gauge length with different fibers and the same fiber with different gauge lengths. The stress–strain relationship of these fibers was discussed based on the successful results of eight samples under each category given in (Supplementary Table S2).
Same Gauge Length with Different Fibers
Here, the results are compared between the same gauge length under different fibers (new and old).
- (a)
- Results of the Fiber with a 100 mm Gauge Length
The maximum and minimum values of tensile stress for new fibers with a 100 mm gauge length are 792.20 and 548.59 MPa, respectively. Additionally, the average maximum stress for new fibers is 648.53 Mpa (standard deviation of 88.02 Mpa) and its corresponding average strain is 0.23. The average energy absorption for new fibers is 66.43 N.mm/mm3, with a standard deviation of 23.58 N.mm/mm3. However, the maximum and minimum values of tensile stress for old fibers with a 100 mm gauge length are 644.37 and 458.64 MPa, respectively. Additionally, the average maximum stress for old fibers is 537.40 Mpa (standard deviation of 64.23 Mpa) and its corresponding average strain is 0.19. The average EA for old fibers is 47.06 N.mm/mm3, with a standard deviation of 33.17 N.mm/mm3. The typical stress–strain graph of the fibers with a 100 mm gauge length is represented in Figure 12a,b. The difference in average stress and average EA between the new and old fibers is 17.13% and 29.15%, respectively.
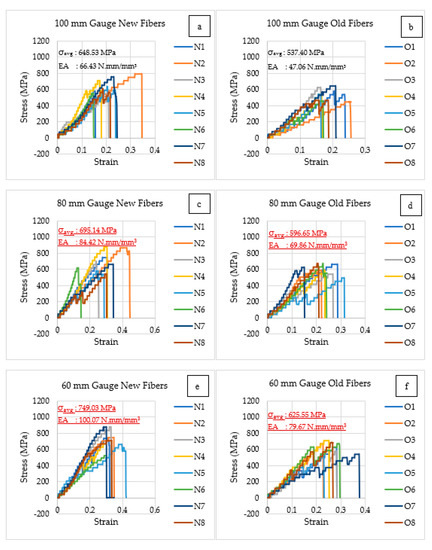
Figure 12.
Stress–strain graph of varying gauge lengths: (a) new fibers with a 100 mm gauge length, (b) old fibers with a 100 mm gauge length, (c) new fibers with a 80 mm gauge length, (d) old fibers with a 80 mm gauge length, (e) new fibers with a 60 mm gauge length, and (f) old fibers with a 60 mm gauge length.
- (b)
- Results of the Fiber with a 80 mm Gauge Length
The maximum and minimum values of tensile stress for new fibers with a 80 mm gauge length are 875.59 and 543.11 MPa, respectively. Additionally, the average maximum stress for new fibers is 695.14 MPa (standard deviation of 116.75 MPa) and its corresponding average strain is 0.30. The average EA for new fibers is 84.42 N.mm/mm3, with a standard deviation of 32.34 N.mm/mm3. However, the maximum and minimum values of tensile stress for old fibers with a 80 mm gauge length are 666.15 and 493.74 MPa, respectively. Additionally, the average maximum stress for old fibers is 596.65 MPa (standard deviation of 56.19 MPa) and its corresponding average strain is 0.25. The average EA for old fibers is 69.86 N.mm/mm3, with a standard deviation of 14.98 N.mm/mm3. The typical stress–strain graph of the fibers with a 100 mm gauge length is represented in Figure 12c,d. The difference in average stress and average EA between the new and old fibers is 14.16% and 17.24%, respectively.
- (c)
- Results of the Fiber with a 60 mm Gauge Length
The maximum and minimum values of tensile stress for new fibers with a 60 mm gauge length are 905.18 and 658.31 MPa, respectively. Additionally, the average maximum stress for new fibers is 749.03 MPa (standard deviation of 86.06 MPa) and its corresponding average strain is 0.33. The average EA for new fibers is 100.07 N.mm/mm3, with a standard deviation of 24.05 N.mm/mm3. However, the maximum and minimum values of tensile stress for old fibers with a 60 mm gauge length are 708.81 and 534.88 MPa, respectively. Additionally, the average maximum stress for old fibers is 625.55 MPa (standard deviation of 62.88 MPa) and its corresponding average strain is 0.28. The average EA for old fibers is 79.67 N.mm/mm3, with a standard deviation of 21.05 N.mm/mm3. The typical stress–strain graph of the fibers with a 60 mm gauge length is represented in Figure 12e,f. The difference in average stress and average EA between the new and old fibers is 16.48% and 20.00%, respectively.
Same Fibers with Different Gauge Lengths
Here, the results are compared between the same fibers under different gauge lengths (100, 80, and 60 mm).
- (a)
- Results of new fiber
For new fibers, an increase of 7.18% is observed in the average tensile stress of the fiber with a 80 mm gauge length compared to the fiber with a 100 mm gauge length. Additionally, an increase of 7.75% is observed in the average tensile stress of the fiber with a 60 mm gauge length compared to the fiber with a 80 mm gauge length. Similarly, there is an increase of 30.43% in the average tensile strain of the fiber with a 80 mm gauge length compared to the fiber with a 100 mm gauge length. Additionally, an increase of 10.00% is observed in the average tensile strain of the fiber with a 60 mm gauge length compared to the fiber with a 80 mm gauge length.
- (b)
- Results of old fiber
For old fibers, an increase of 11.02% is observed in the average tensile stress of the fiber with a 80 mm gauge length compared to the fiber with a 100 mm gauge length. Additionally, an increase of 4.8% is observed in the average tensile stress of the fiber with a 60 mm gauge length compared to the fiber with a 80 mm gauge length. Similarly, there is an increase of 31.57% in the average tensile strain of the fiber with a 80 mm gauge length compared to the fiber with a 100 mm gauge length. Additionally, an increase of 12.00% is observed in the average tensile strain of the fiber with a 60 mm gauge length compared to the fiber with a 80 mm gauge length.
From the above results, it was observed that both the stress and strain values increase with decreasing gauge length. The same trend has been reported by Ida maria et al., using fishing net waste fiber [49].
4.2.3. Failure of the Fibers after Tensile Testing
After being subjected to failure, the fiber sample is studied using SEM. From the image, the sequence of failure was noted. The first failure occurred in the elasticity outer layer followed by the failure of the outer layer and the core fiber, as shown in Figure 13. Thus, the trend in the failure pattern in all the graphs of the above test results also indicates a similar sequence.

Figure 13.
Failure mechanism of the fiber after tensile testing.
4.2.4. Young’s Modulus of Fiber
According to the ASTM C1557-03 standard of testing procedure, if strain is not directly measurable for Young’s modulus, then the relationship given in Equation (2) is considered [31].
—Total measured displacement,
F—Failure load,
Cs—System compliance,
—Gauge length,
E—Young’s modulus, and
A—Cross-sectional area.
The linear regression of varying gauge lengths is plotted for ΔL/F vs. lₒ/A as shown in Equation (1). The slope of the line gives the constant E and the intercept to the y-axis gives the system compliance (Cs). Figure 14a,b shows the slope 1 in E equation of new and old fibers as y = 0.0002x + 0.026 and y = 0.0002x + 0.031, respectively. From the equation, the Young’s modulus of new and old fibers is calculated as E = 4870.00 MPa and E = 4843.50 MPa, respectively. Thus, not much difference is observed between the Young’s modulus of old and new fibers. Generally, the Young’s modulus of virgin nylon 6,6 lies between 1000 and 3000 MPa [49]. Additionally, the fiber used for this study is found to have a Young’s modulus of 5000 MPa, which is observed to have higher stiffness than any other commercial nylon fibers.
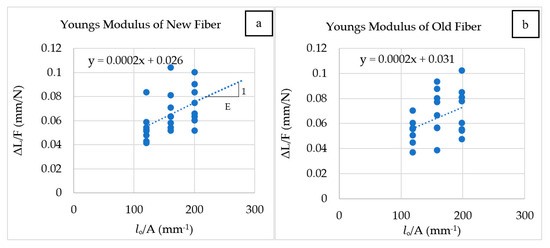
Figure 14.
Young’s modulus: (a) new fibers; (b) old fibers.
4.2.5. Validation of Results by Weibull Distribution
The statistical behavior of the tensile strength of the fiber is studied by Weibull distribution. From the Weibull analysis, the Weibull modulus (m) shows the probability of variation [50]. The probability of Weibull analysis is given by Equation (3).
where σ is the tensile strength of the fiber, m is the Weibull modulus, and σₒ is the Weibull reference strength. The fiber strength ranking for the ith value from the number of the fibers tested (N) is given by Equation (4).
P(σ)i is the probability corresponding to the ith value. Substituting Equation (4) in Equation (3) gives Equation (5).
The Weibull model is analyzed by vs. ln(σ), as shown in Figure 15a,b, which yields the Weibull parameters (m) and (σₒ).
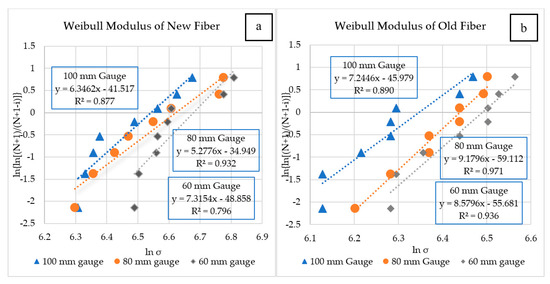
Figure 15.
Weibull modulus: (a) new fibers; (b) old fibers.
Figure 15a shows the Weibull modulus for the new fibers in varying gauge lengths. The equation of the slope y = ax + b yields a = m, which is the Weibull modulus and the Weibull reference strength, σₒ = exp(−b/a).
Generally, in measuring the Weibull modulus, the higher the (m) value, the lower the strength variability; and a Weibull modulus greater than 3 gives good results with lower variability [50,51]. Table 6 gives the Weibull parameters for varying gauge lengths of the fibers, where the Weibull modulus (m) for both old and new fibers varies between 5.27 and 9.17. Hence, the results of tensile strength exhibit lower variability. The difference in percentage between the estimated Weibull reference strength (σₒ) and the experimental average tensile strength (σAvg) is approximately 6%. From Figure 15a,b, a linear trend for new and old fibers is observed, which indicates an increase in the Weibull modulus with a decrease in gauge length [52].
5. Comparison of the Tensile Strength of WBSF with Other Recycled Nylon Fibers
Comparing the tensile strength results of WBSF with other recycled nylon fibers, WBSF has a higher tensile strength, as shown in Table 7. From the table, the tests conducted for either monofilament or multifilament recycled nylon fibers (waste fishing net, scrap paint brushes, carpet waste, etc.) show that the tensile strength ranges between 110 and 440 MPa, the elongation at break lies between 15 and 33% and the Young’s modulus ranges between 785 and 5150 MPa. However, WBSF is only of a multifilament arrangement. In this arrangement, the core layer alone is capable of withstanding a tensile strength of 490 MPa even if the outer two layers fail. This shows the highest tensile property of WBSF when compared to other recycled nylon fibers. Hence, WBSF is an efficient reinforcing material in a cement matrix.

Table 7.
Comparison of the tensile strength of recycled nylon fibers.
6. Conclusions
The microstructural properties and tensile behavior of new and old fibers have been investigated. Their physical and mechanical properties are related to the morphology of new and old fibers. The Weibull statistical approach was studied. The following results are concluded from this work.
- Microstructural analysis using EDS, FTIR, and XRD reveals that nylon 6,6 is the purest form of the fiber.
- From the SEM imaging of the fibers, the overall diameter and the net cross-sectional area are 799.10 μm and 504,786.30 μm2, respectively, for new fibers and 776.30 μm and 498,125.00 μm2, respectively, for old fibers.
- From the various strand fibers, the average energy absorption of a single fiber ranges from 68.04 to 55.34 N.mm/mm3 for new fibers and 40.09 to 33.65 N.mm/mm3 for old fibers.
- The pattern of the residual force loss percentage for new and old fibers with three strands was similar and calculated as 0, 35.22, 68.40, 100.00 and 0, 32.48, 64.45, and 100, respectively.
- The pattern of the residual force loss percentage for new and old fibers with five strands was similar and calculated as 0, 20.90, 36.44, 42.79, 61.72, and 100.00, and 0, 27.7, 40.40, 58.95, 63.88, and 100.00, respectively.
- From the varying gauge lengths, the difference in the average stress and average energy absorption between the new and old fibers is 17.13% and 29.15% for a 100 mm gauge length, 14.16% and 17.24% for a 80 mm gauge length, and 16.48% and 20.00% for a 60 mm length, respectively.
- The Young’s modulus of new and old fibers is 4870.00 and 4843.50 MPa, respectively, and no significant difference was observed.
- The Weibull modulus (m) varies between 5.27 and 9.17, which shows a lower variability of tensile test results for both new and old fibers.
- The tensile strength of WBSF is 490.00 MPa, which is higher when compared to other recycled nylon fibers.
- Therefore, the feasibility of incorporating WBSF in polymer and cement matrices would be a better idea, which would effectively improve the toughness and impact strength.
- Furthermore, the use of recycled fibers from industrial or post-consumer waste offers additional advantages of waste reduction and resource conservation. These advantages can be realized through the incorporation of WBSF.
7. Patents
An Indian patent was published from this research work under the title “Multifilament Nylon Cutter with various aspect ratio for embedding in Concrete Mixtures for reinforcement” on 8 July 2022. Patent publication no. 202241037954 A.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/fib11030025/s1, Figure S1: Energy Dispersion Spectroscopy of WBSF (a) Core Fiber (b) Outer Layer (c) Elasticity Outer. Table S1: Tensile properties of fibers by varying strands. Table S2: Tensile properties and energy absorption by varying the gauge length.
Author Contributions
Conceptualization and methodology, writing—original draft preparation, K.M.; validation, editing and supervision, S.S.N.; data curation and supervision, A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
We acknowledge the XRD FACILITY at SRMIST setup with support from MNRE (Project No. 31/03/2014-15/PVSE-R&D), Government of India. We acknowledge SRMIST for the high-resolution scanning electron microscopy (HR-SEM) facility and Fourier transform infrared spectroscopy (FTIR).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kanan, M.; Wannassi, B.; Barham, A.S.; Ben Hassen, M.; Assaf, R. The Quality of Blended Cotton and Denim Waste Fibres: The Effect of Blend Ratio and Waste Category. Fibers 2022, 10, 76. [Google Scholar] [CrossRef]
- Farinha, C.B.; Silvestre, J.D.; de Brito, J.; Veiga, M.D.R. Life cycle assessment of mortars with incorporation of industrial wastes. Fibers 2019, 7, 59. [Google Scholar] [CrossRef]
- Signorini, C.; Volpini, V. Mechanical performance of fiber reinforced cement composites including fully-recycled plastic fibers. Fibers 2021, 9, 16. [Google Scholar] [CrossRef]
- Maia Pederneiras, C.; Veiga, R.; de Brito, J. Impact Resistance of Rendering Mortars with Natural and Textile-Acrylic Waste Fibres. Fibers 2022, 10, 44. [Google Scholar] [CrossRef]
- Pachideh, G.; Gholhaki, M. An experimental investigation into effect of temperature rise on mechanical and visual characteristics of concrete containing recycled metal spring. Struct. Concr. 2021, 22, 550–565. [Google Scholar] [CrossRef]
- Park, J.K.; Kim, M.O.; Kim, D.J. Pullout behavior of recycled waste fishing net fibers embedded in cement mortar. Materials 2020, 13, 4195. [Google Scholar] [CrossRef]
- Kowsalya, M.; Sindhu Nachiar, S.; Sekar, A.; Ravichandran, P.T. Study on Mechanical and Microstructural Properties of Concrete with Fly Ash Cenosphere as Fine Aggregate—A Sustainable Approach. Buildings 2022, 12, 1679. [Google Scholar] [CrossRef]
- Ivars, J.; Labanieh, A.R.; Soulat, D. Effect of the Fibre Orientation Distribution on the Mechanical and Preforming Behaviour of Nonwoven Preform Made of Recycled Carbon Fibres. Fibers 2021, 9, 82. [Google Scholar] [CrossRef]
- Orasutthikul, S.; Unno, D.; Yokota, H. Effectiveness of recycled nylon fiber from waste fishing net with respect to fiber reinforced mortar. Constr. Build. Mater. 2017, 146, 594–602. [Google Scholar] [CrossRef]
- Srimahachota, T.; Yokota, H.; Akira, Y. Recycled nylon fiber from waste fishing nets as reinforcement in polymer cement mortar for the repair of corroded RC beams. Materials 2020, 13, 4276. [Google Scholar] [CrossRef]
- Park, J.K.; Kim, D.J.; Kim, M.O. Mechanical behavior of waste fishing net fiber-reinforced cementitious composites subjected to direct tension. J. Build. Eng. 2021, 33, 101622. [Google Scholar] [CrossRef]
- Marinelli, S.; Butturi, M.A.; Rimini, B.; Gamberini, R.; Sellitto, M.A. Estimating the circularity performance of an emerging industrial symbiosis network: The case of recycled plastic fibers in reinforced concrete. Sustainability 2021, 13, 10257. [Google Scholar] [CrossRef]
- Ahmed, H.U.; Faraj, R.H.; Hilal, N.; Mohammed, A.A.; Sherwani, A.F.H. Use of recycled fibers in concrete composites: A systematic comprehensive review. Compos. Part B Eng. 2021, 215, 108769. [Google Scholar] [CrossRef]
- Ming, Y.; Chen, P.; Li, L.; Gan, G.; Pan, G. A comprehensive review on the utilization of recycled waste fibers in cement-based composites. Materials 2021, 14, 3643. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, L. Influence of tire-recycled steel fibers on strength and flexural behavior of reinforced concrete. Adv. Mater. Sci. Eng. 2020, 2020, 6363105. [Google Scholar] [CrossRef]
- Yang, J.; Peng, G.F.; Shui, G.S.; Zhang, G. Mechanical properties and anti-spalling behavior of ultra-high performance concrete with recycled and industrial steel fibers. Materials 2019, 12, 783. [Google Scholar] [CrossRef]
- Neira Medina, A.L.; Garcia, J.A.; Castellanos, N.T. Flexural behavior of environmentally friendly ultra-high-performance concrete with locally available low-cost synthetic fibers. Eur. J. Environ. Civ. Eng. 2022, 26, 6281–6304. [Google Scholar] [CrossRef]
- Yang, S.L.; Millard, S.G.; Soutsos, M.N.; Barnett, S.J.; Le, T.T. Influence of aggregate and curing regime on the mechanical properties of ultra-high performance fibre reinforced concrete (UHPFRC). Constr. Build. Mater. 2009, 23, 2291–2298. [Google Scholar] [CrossRef]
- Criado, M.; García-Díaz, I.; Bastidas, J.M.; Alguacil, F.J.; López, F.A.; Monticelli, C. Effect of recycled glass fiber on the corrosion behavior of reinforced mortar. Constr. Build. Mater. 2014, 64, 261–269. [Google Scholar] [CrossRef]
- Suchorab, Z.; Franus, M.; Barnat-Hunek, D. Properties of fibrous concrete made with plastic optical fibers from E-Waste. Materials 2020, 13, 2414. [Google Scholar] [CrossRef]
- Farooq, M.A.; Fahad, M.; Ali, B.; El Ouni, M.H.; Elhag, A.B. Influence of nylon fibers recycled from the scrap brushes on the properties of concrete: Valorization of plastic waste in concrete. Case Stud. Constr. Mater. 2022, 16, e01089. [Google Scholar] [CrossRef]
- Kumaresan, M.; Nachiar, S.S.; Anandh, S. Implementation of waste recycled fibers in concrete: A review. Mater. Today Proc. 2022, 68, 1988–1994. [Google Scholar] [CrossRef]
- Yin, S.-R.; Chang, H.-C.; Cheng, K.B. Impact Characteristics of a Badminton Racket with Realistic Finite Element Modeling. Multidiscip. Digit. Publ. Inst. Proc. 2020, 49, 106. [Google Scholar] [CrossRef]
- Zhu, Q. Perceiving the affordance of string tension for power strokes in badminton: Expertise allows effective use of all string tensions. J. Sport. Sci. 2013, 31, 1187–1196. [Google Scholar] [CrossRef]
- Fakhrizal, A.N.; Ardiyansyah, S.; Harun, M.N.; Kadir, M.R.A.; Omar, A.H. Finite-element study on effect of string tension toward coefficient of restitution of a badminton racket string-bed. Adv. Mater. Res. 2013, 845, 417–420. [Google Scholar] [CrossRef]
- Racquet Network. We Recycle Racquet String. 2018. Available online: https://racquetnetwork.com/we-recycle-racquet-string/ (accessed on 29 January 2023).
- Tennis Express. Inside Look at Wilson’s 2019 US Open Stringing Team. 2019. Available online: https://www.tennisexpress.com/blog/inside-look-at-wilsons-2019-us-open-stringing-team/ (accessed on 29 January 2023).
- Zainal, S.M.I.S.; Hejazi, F.; Aziz, F.N.A.A.; Jaafar, M.S. Effects of hybridized synthetic fibers on the shear properties of cement composites. Materials 2020, 13, 5055. [Google Scholar] [CrossRef]
- Nasruddin, F.A.; Harun, M.N.; Syahrom, A.; Kadir, M.R.A.; Omar, A.H.; Öchsner, A. Finite Element Analysis on Badminton Racket Design Parameters; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Ali, M.; Chouw, N. Experimental investigations on coconut-fibre rope tensile strength and pullout from coconut fibre reinforced concrete. Constr. Build. Mater. 2013, 41, 681–690. [Google Scholar] [CrossRef]
- ASTM C1557−14; Standard Test Method for Tensile Strength and Young’s Modulus of Fibers. ASTM International: West Conshohocken, PA, USA, 2015. [CrossRef]
- Kisler-Rao, A. Comparison of nylon, polyester, and olefin fibers using FTIR and melting point analysis. J. Am. Soc. Trace Evid. Exam. 2015, 6, 3–20. [Google Scholar]
- Madhu, P.; Sanjay, M.R.; Senthamaraikannan, P.; Pradeep, S.; Saravanakumar, S.S.; Yogesha, B. A review on synthesis and characterization of commercially available natural fibers: Part II. J. Nat. Fibers 2019, 16, 25–36. [Google Scholar] [CrossRef]
- Obada, D.O.; Kuburi, L.S.; Dauda, M.; Dodoo-Arhin, D.; Iorpenda, M.J.; Hou, Y.; Balogun, M.B.; Iliyasu, I.; Umaru, S.; Bansod, N.D.; et al. Microstructural evolution and hardness properties of coir-coconut husk powder reinforced polymer composites subjected to an acidic environment. Procedia Manuf. 2019, 35, 737–742. [Google Scholar] [CrossRef]
- Khan, A.; Vijay, R.; Singaravelu, D.L.; Sanjay, M.R.; Siengchin, S.; Jawaid, M.; Alamry, K.A.; Asiri, A.M. Extraction and characterization of natural fibers from Citrullus lanatus climber. J. Nat. Fibers 2022, 19, 621–629. [Google Scholar] [CrossRef]
- Fan, C.; Huang, Y.Z.; Lin, J.N.; Li, J. Microplastic constituent identification from admixtures by Fourier-transform infrared (FTIR) spectroscopy: The use of polyethylene terephthalate (PET), polyethylene (PE), polypropylene (PP), polyvinyl chloride (PVC) and nylon (NY) as the model constituents. Environ. Technol. Innov. 2021, 23, 101798. [Google Scholar] [CrossRef]
- Nahar, S.; Hasan, M. Effect of chemical composition, anatomy and cell wall structure on tensile properties of bamboo fiber. Eng. J. 2013, 17, 61–68. [Google Scholar] [CrossRef]
- Rajkumar, G.R.; Krishna, M.; Narasimhamurthy, H.N.; Keshavamurthy, Y.C.; Nataraj, J.R. Investigation of tensile and bending behavior of aluminum based hybrid fiber metal laminates. Procedia Mater. Sci. 2014, 5, 60–68. [Google Scholar] [CrossRef]
- Vasanthan, N. Crystallinity determination of nylon 66 by density measurement and fourier transform infrared (FTIR) spectroscopy. J. Chem. Educ. 2012, 89, 387–390. [Google Scholar] [CrossRef]
- Vasanthan, N.; Salem, D.R. FTIR spectroscopic characterization of structural changes in polyamide-6 fibers during annealing and drawing. J. Polym. Sci. Part B Polym. Phys. 2001, 39, 536–547. [Google Scholar] [CrossRef]
- Zarrini, K.; Rahimi, A.A.; Alihosseini, F.; Fashandi, H. Highly efficient dye adsorbent based on polyaniline-coated nylon-6 nanofibers. J. Clean. Prod. 2017, 142, 3645–3654. [Google Scholar] [CrossRef]
- Mohammadhosseini, H.; Tahir, M.M.; Sayyed, M.I. Strength and transport properties of concrete composites incorporating waste carpet fibres and palm oil fuel ash. J. Build. Eng. 2018, 20, 156–165. [Google Scholar] [CrossRef]
- El-Newehy, M.H.; Al-Deyab, S.S.; Kenawy, E.R.; Abdel-Megeed, A. Nanospider technology for the production of nylon-6 nanofibers for biomedical applications. J. Nanomater. 2011, 2011, 626589. [Google Scholar] [CrossRef]
- Munawar, S.S.; Umemura, K.; Kawai, S. Characterization of the morphological, physical, and mechanical properties of seven nonwood plant fiber bundles. J. Wood Sci. 2007, 53, 108–113. [Google Scholar] [CrossRef]
- Mazzoli, A.; Monosi, S.; Plescia, E.S. Evaluation of the early-age-shrinkage of Fiber Reinforced Concrete (FRC) using image analysis methods. Constr. Build. Mater. 2015, 101, 596–601. [Google Scholar] [CrossRef]
- Cai, Z.; Chattopadhyay, N.; Liu, W.J.; Chan, C.; Pignol, J.P.; Reilly, R.M. Optimized digital counting colonies of clonogenic assays using ImageJ software and customized macros: Comparison with manual counting. Int. J. Radiat. Biol. 2011, 87, 1135–1146. [Google Scholar] [CrossRef]
- Sanusi, S.H.; Azman, A.N. Performance Analysis of Different Polymer Core for Badminton String Application. Res. Prog. Mech. Manuf. Eng. 2021, 2, 152–158. [Google Scholar]
- Mouradi, H.; El Barkany, A.; El Biyaali, A. Steel wire ropes failure analysis: Experimental study. Eng. Fail. Anal. 2018, 91, 234–242. [Google Scholar] [CrossRef]
- Bertelsen, I.M.G.; Ottosen, L.M. Engineering properties of fibres from waste fishing nets. In Proceedings of the International Conference on Materials, Systems and Structures in Civil Engineering: Conference Workshop on Cold Region Engineering, Lyngby, Denmark, 22–24 August 2016. [Google Scholar]
- Wang, F.; Shao, J. Modified Weibull distribution for analyzing the tensile strength of bamboo fibers. Polymers 2014, 6, 3005–3018. [Google Scholar] [CrossRef]
- Meng, C.; Li, W.; Cai, L.; Shi, X.; Jiang, C. Experimental research on durability of high-performance synthetic fibers reinforced concrete: Resistance to sulfate attack and freezing-thawing. Constr. Build. Mater. 2020, 262, 120055. [Google Scholar] [CrossRef]
- Fidelis, M.E.A.; Pereira, T.V.C.; Gomes, O.D.F.M.; de Andrade Silva, F.; Toledo Filho, R.D. The effect of fiber morphology on the tensile strength of natural fibers. J. Mater. Res. Technol. 2013, 2, 149–157. [Google Scholar] [CrossRef]
- Spadea, S.; Farina, I.; Carrafiello, A.; Fraternali, F. Recycled nylon fibers as cement mortar reinforcement. Constr. Build. Mater. 2015, 80, 200–209. [Google Scholar] [CrossRef]
- Balea, A.; Fuente, E.; Monte, M.C.; Blanco, A.; Negro, C. Recycled fibers for sustainable hybrid fiber cement based material: A review. Materials 2021, 14, 2408. [Google Scholar] [CrossRef]
- Tran, N.P.; Gunasekara, C.; Law, D.W.; Houshyar, S.; Setunge, S.; Cwirzen, A. Comprehensive review on sustainable fiber reinforced concrete incorporating recycled textile waste. J. Sustain. Cem.-Based Mater. 2022, 11, 41–61. [Google Scholar] [CrossRef]
- Pakravan, H.R.; Jeddi, A.A.A.; Jamshidi, M.; Memarian, F.; Saghafi, A.M. Properties of recycled carpet fiber reinforced concrete. In Use of Recycled Plastics in Eco-Efficient Concrete; Woodhead Publishing: Sawston, UK, 2019; pp. 411–425. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).