Thin-Layer Fibre-Reinforced Concrete Sandwich Walls: Numerical Evaluation †
Abstract
:1. Introduction
2. Materials and Methods
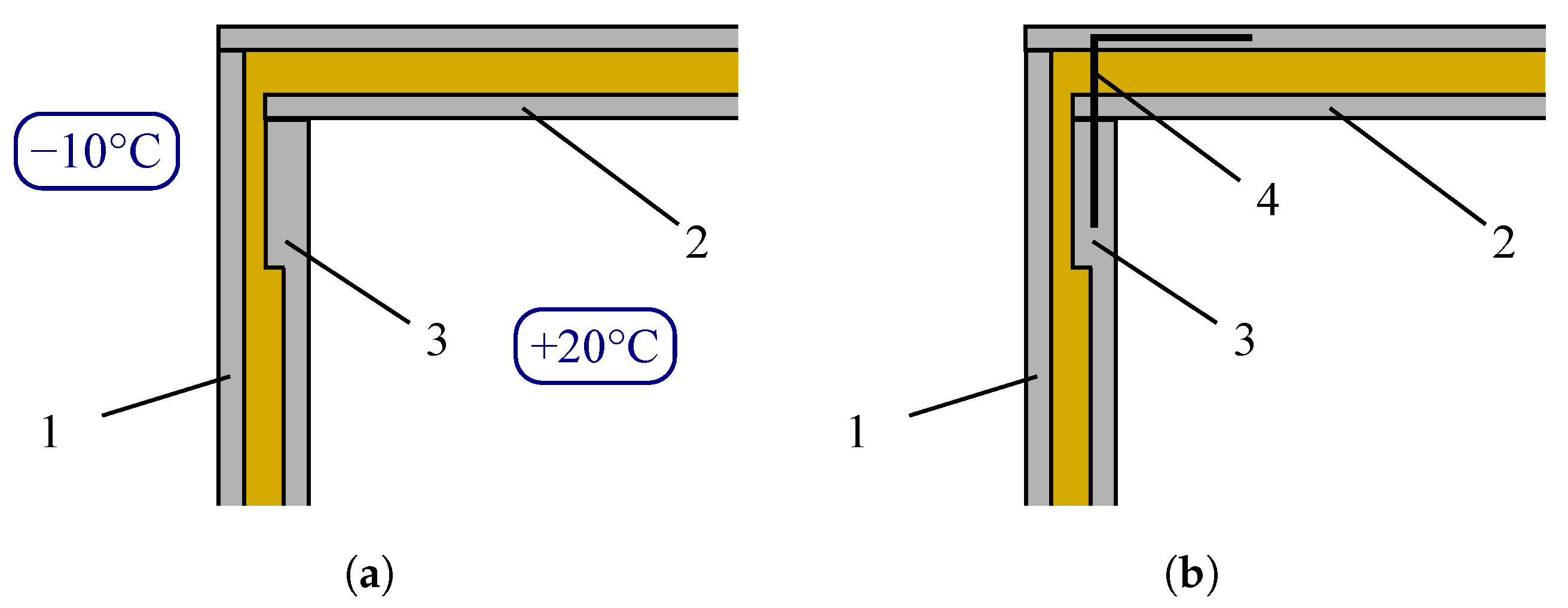
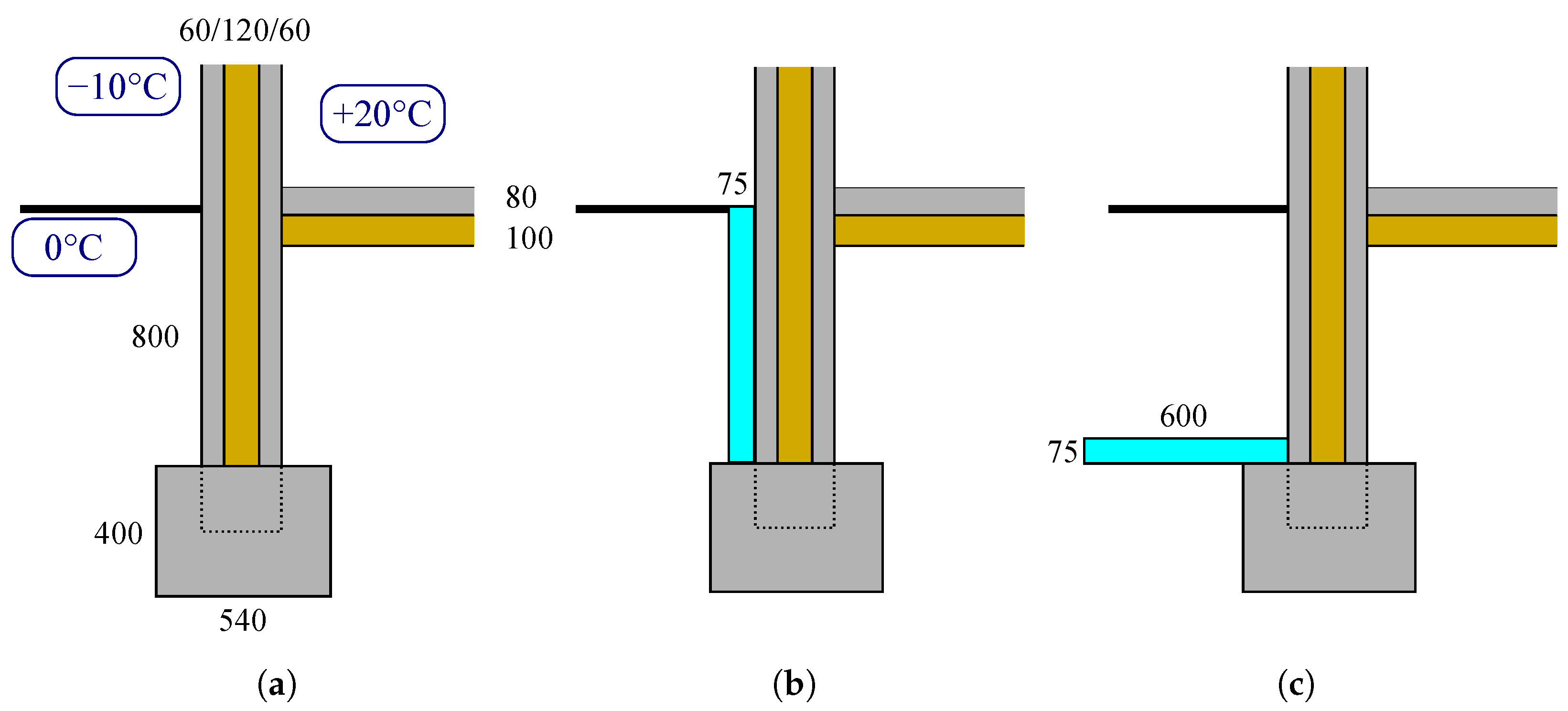
2.1. Thermal Analysis
2.2. Sound Insulation Analysis
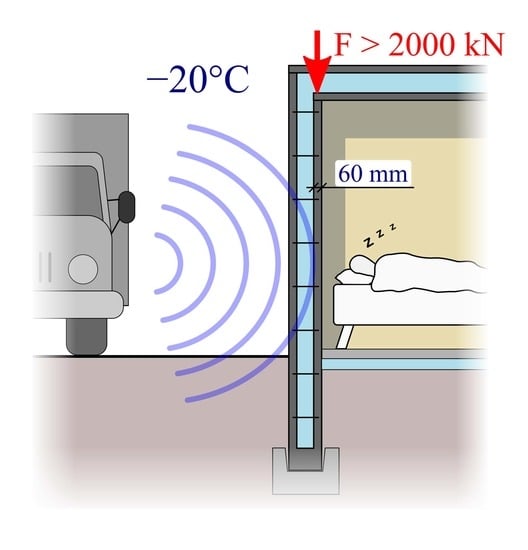
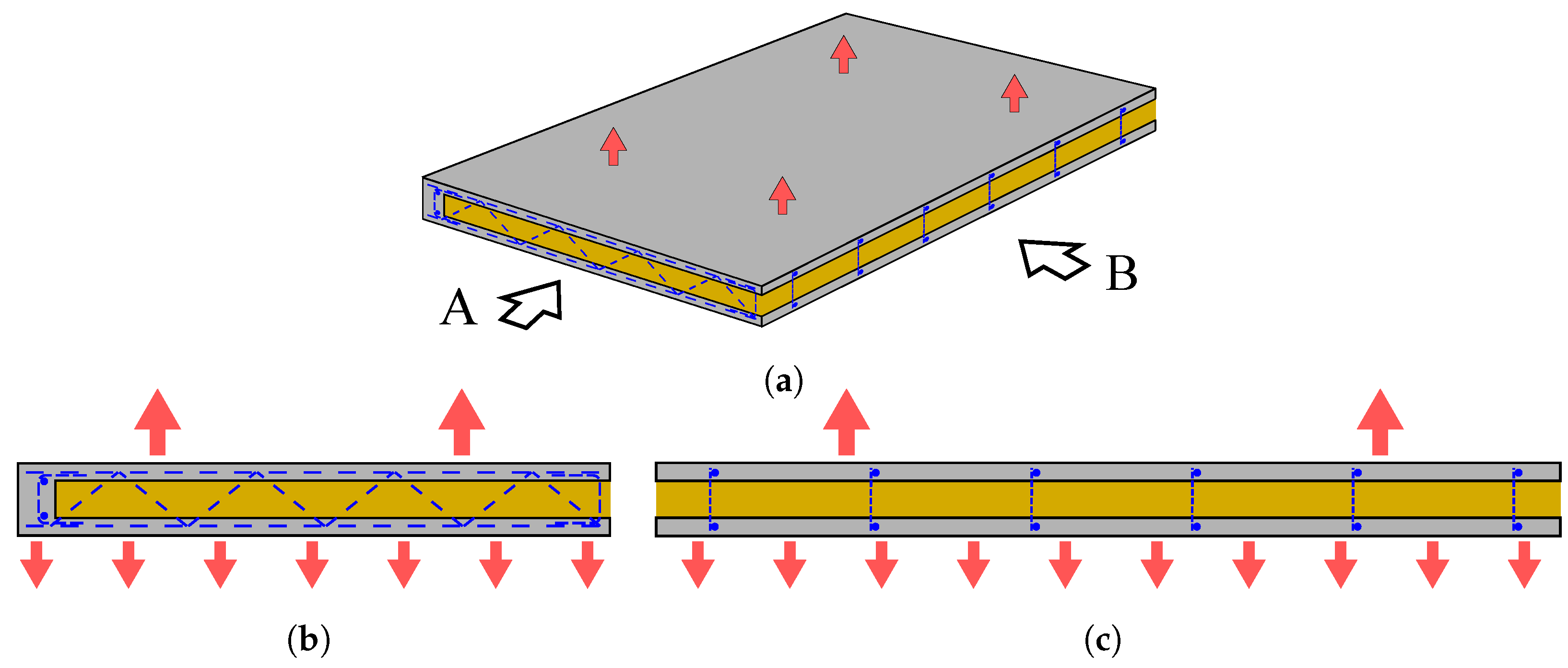
2.3. Structural Analysis and Design
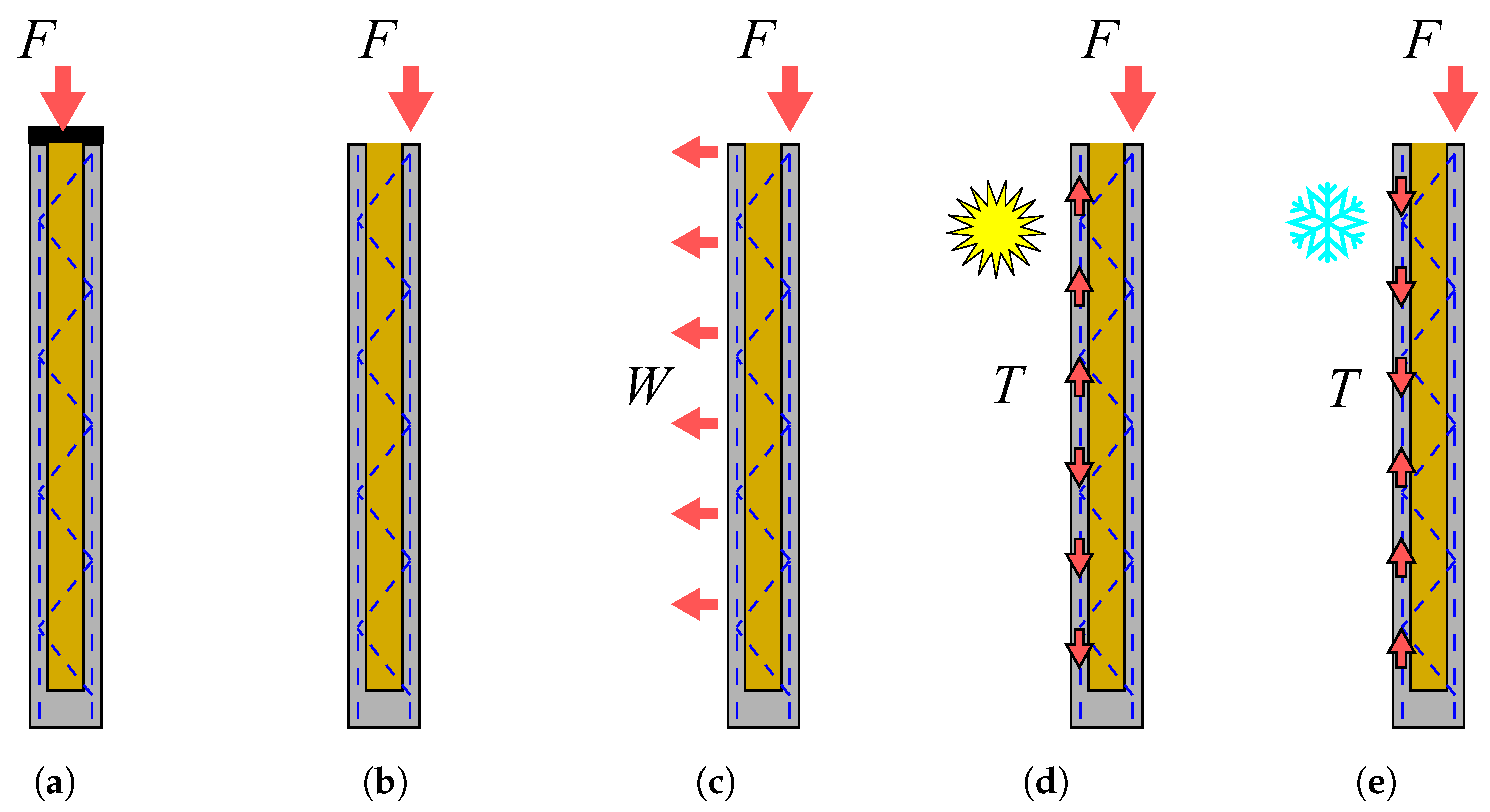
Actions
2.4. Nonlinear FEM Analysis
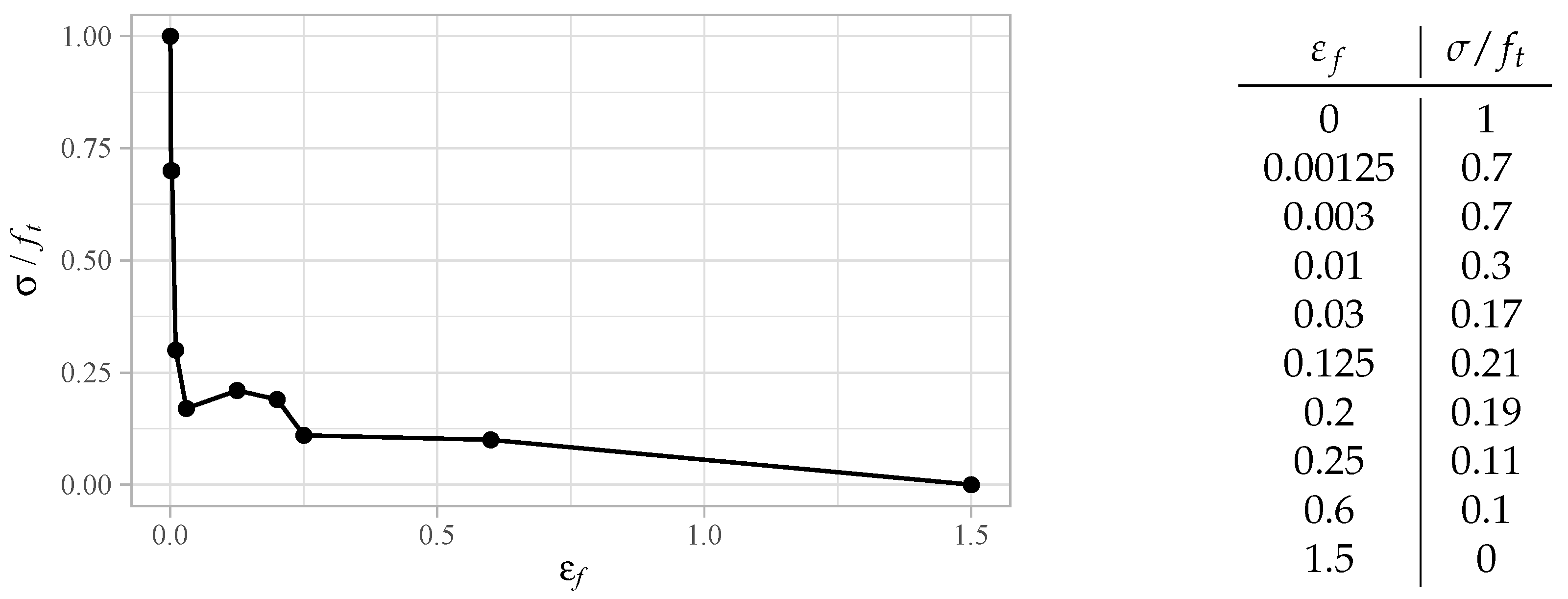
2.4.1. Materials
2.4.2. Mesh
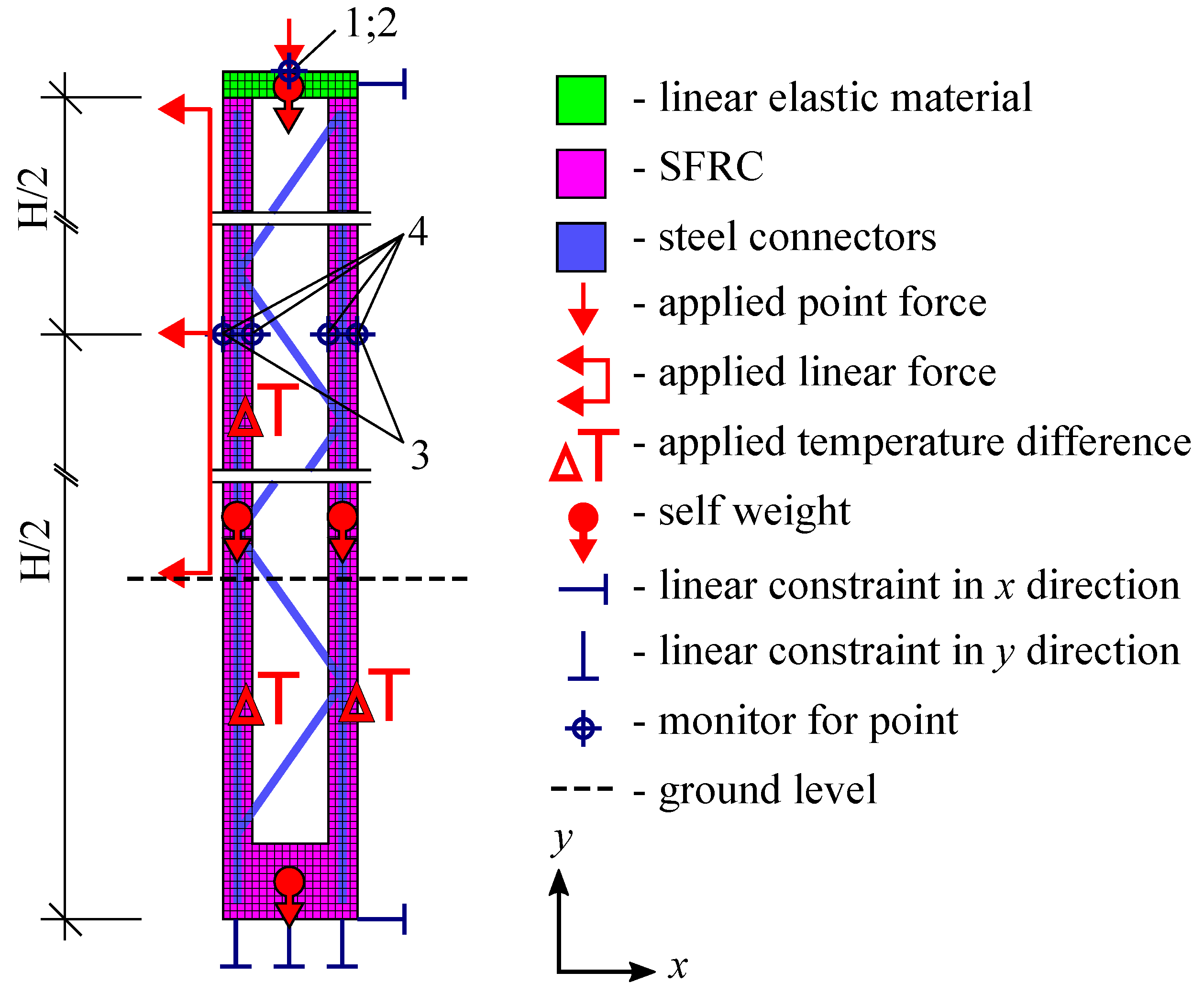
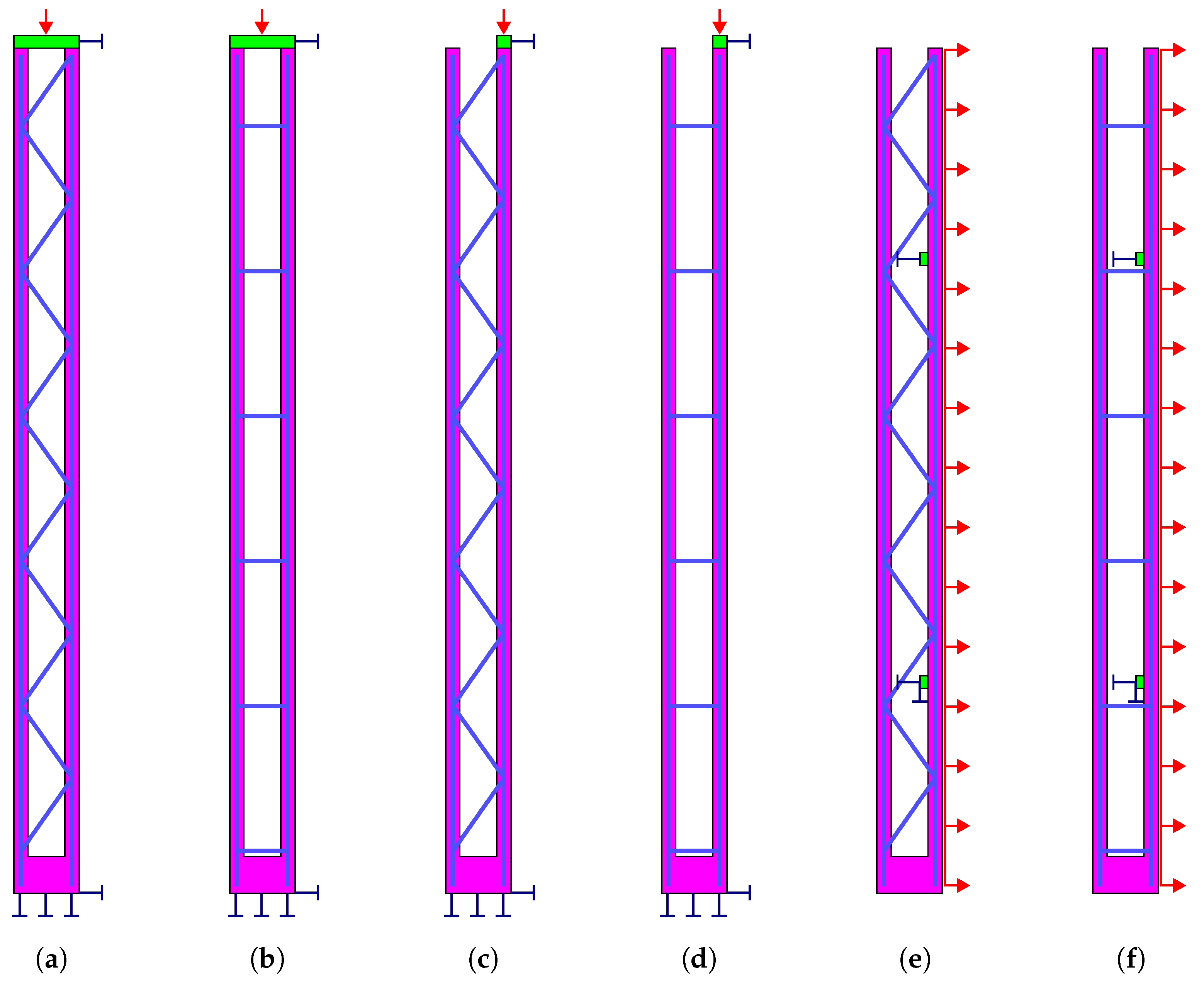
2.4.3. Boundary Conditions and Load Application
3. Results
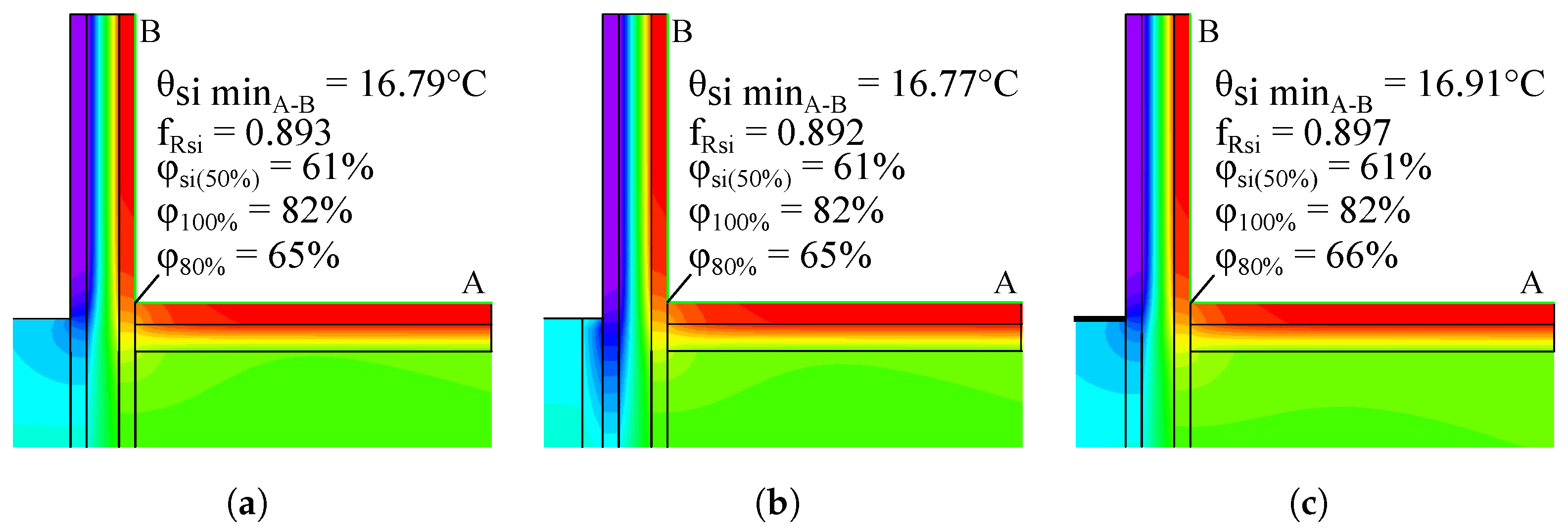
3.1. Thermal Performance
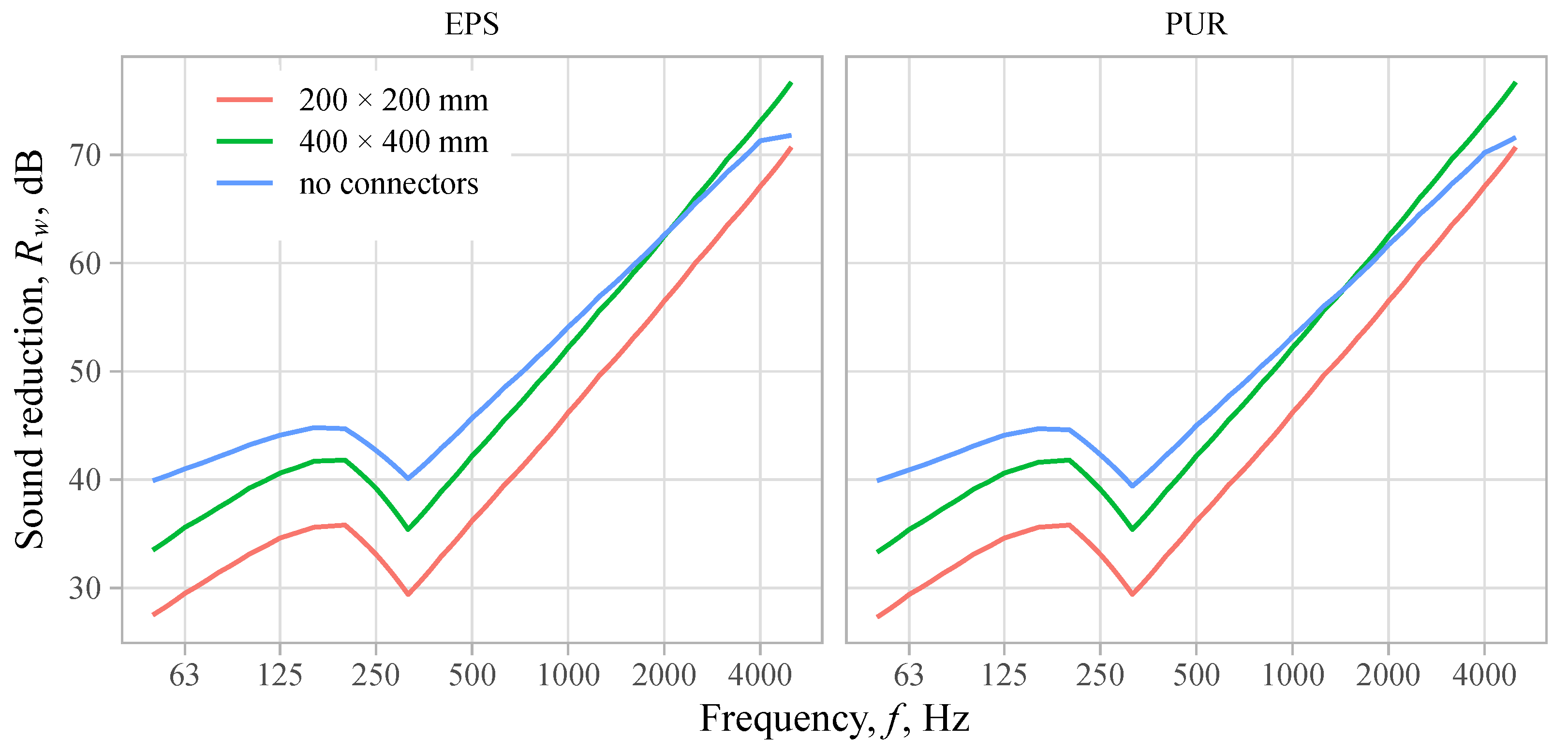
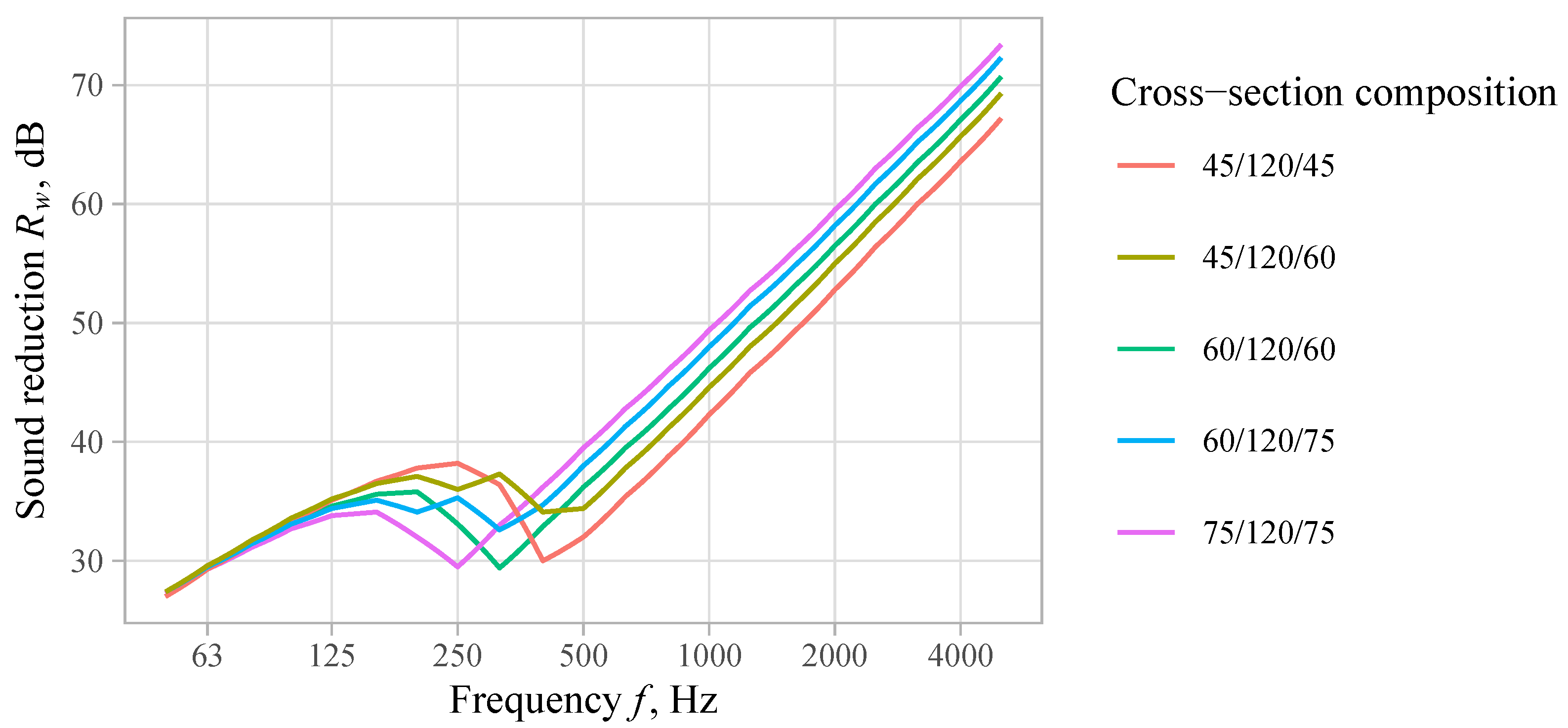
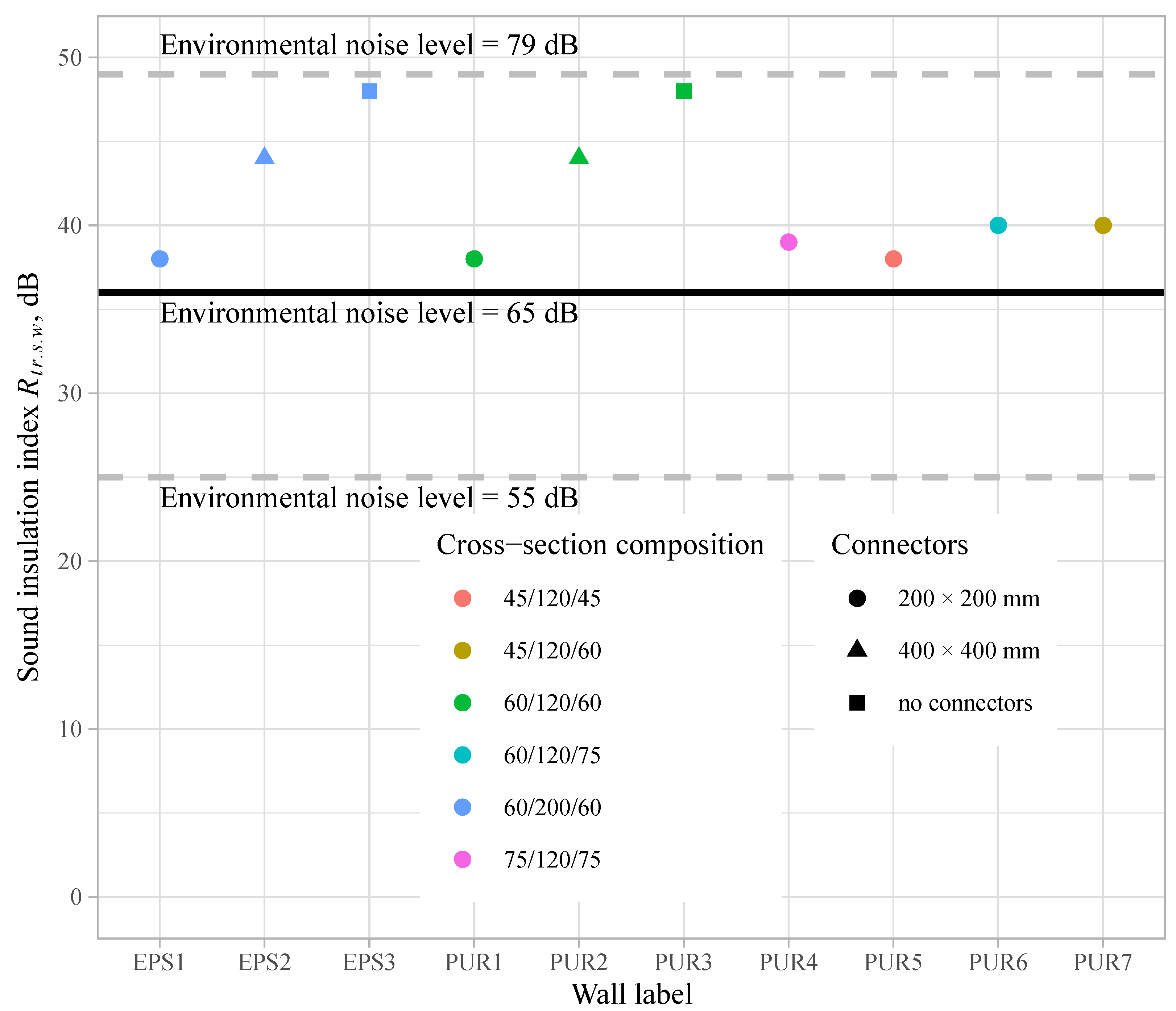
3.2. Sound Insulation Performance
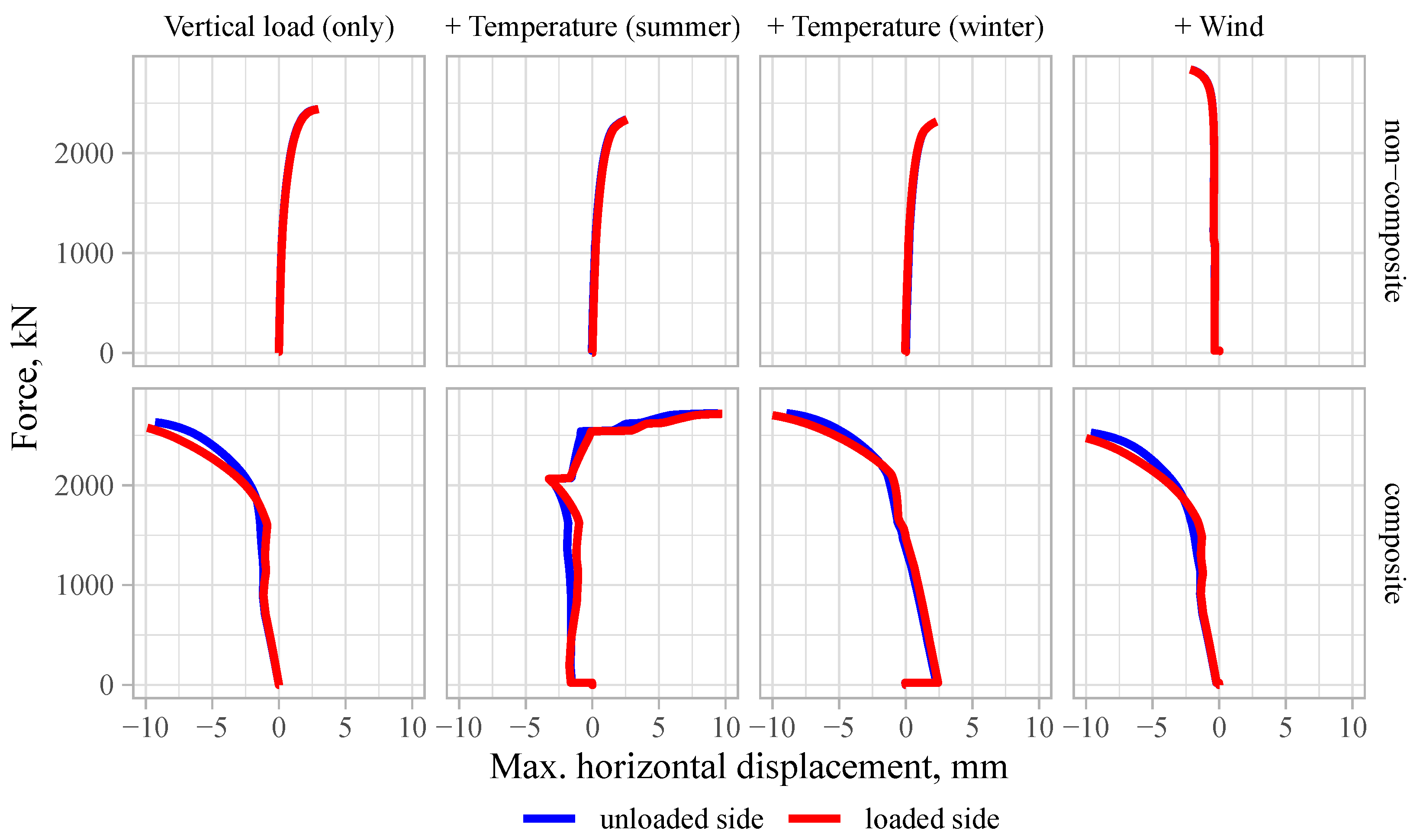
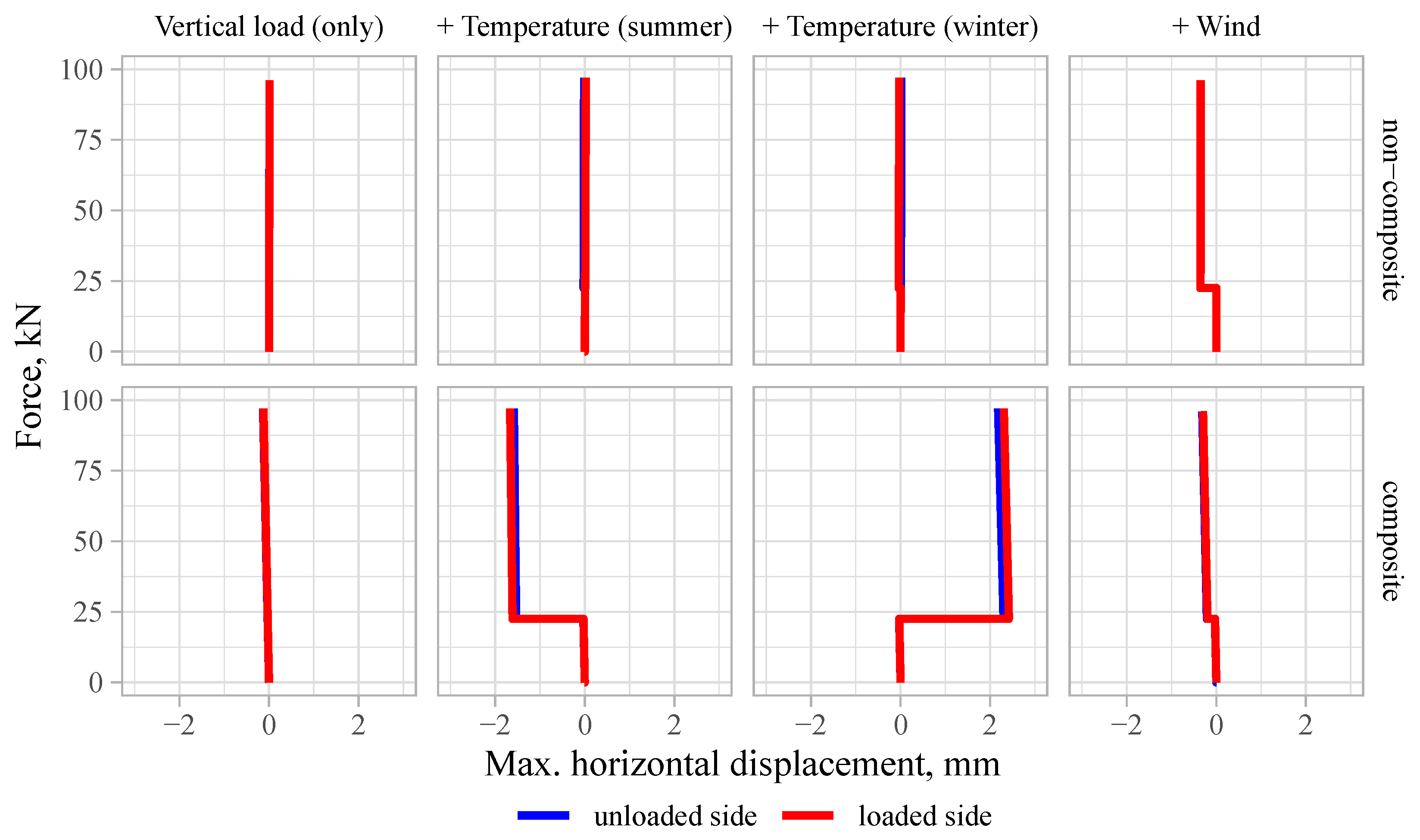
3.3. Structural Performance
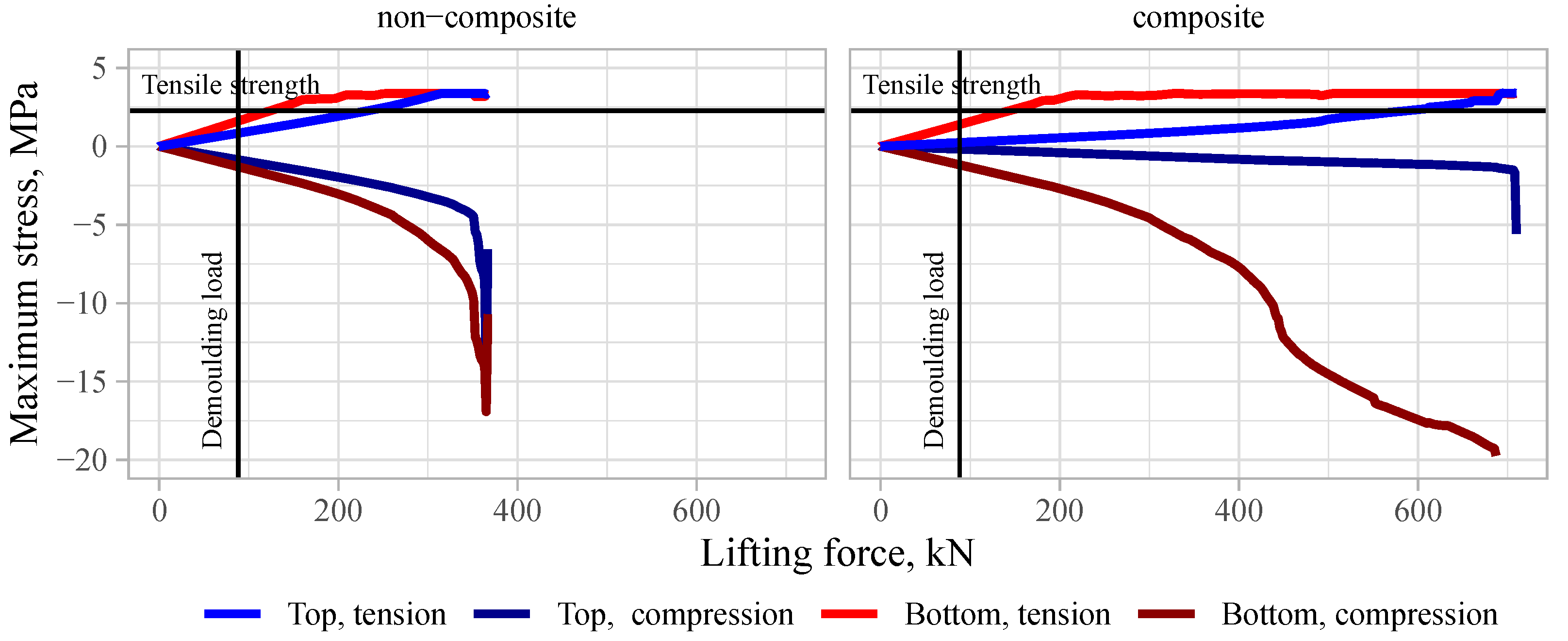
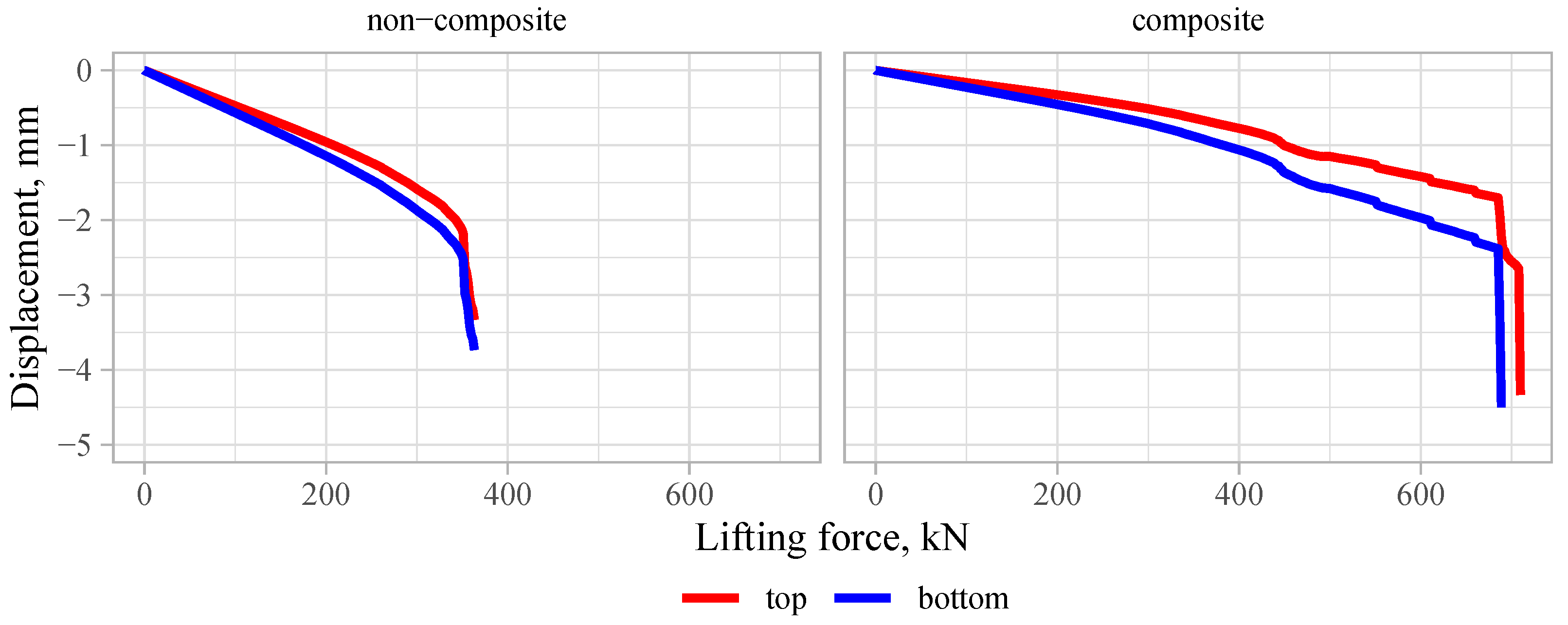
3.3.1. Demoulding
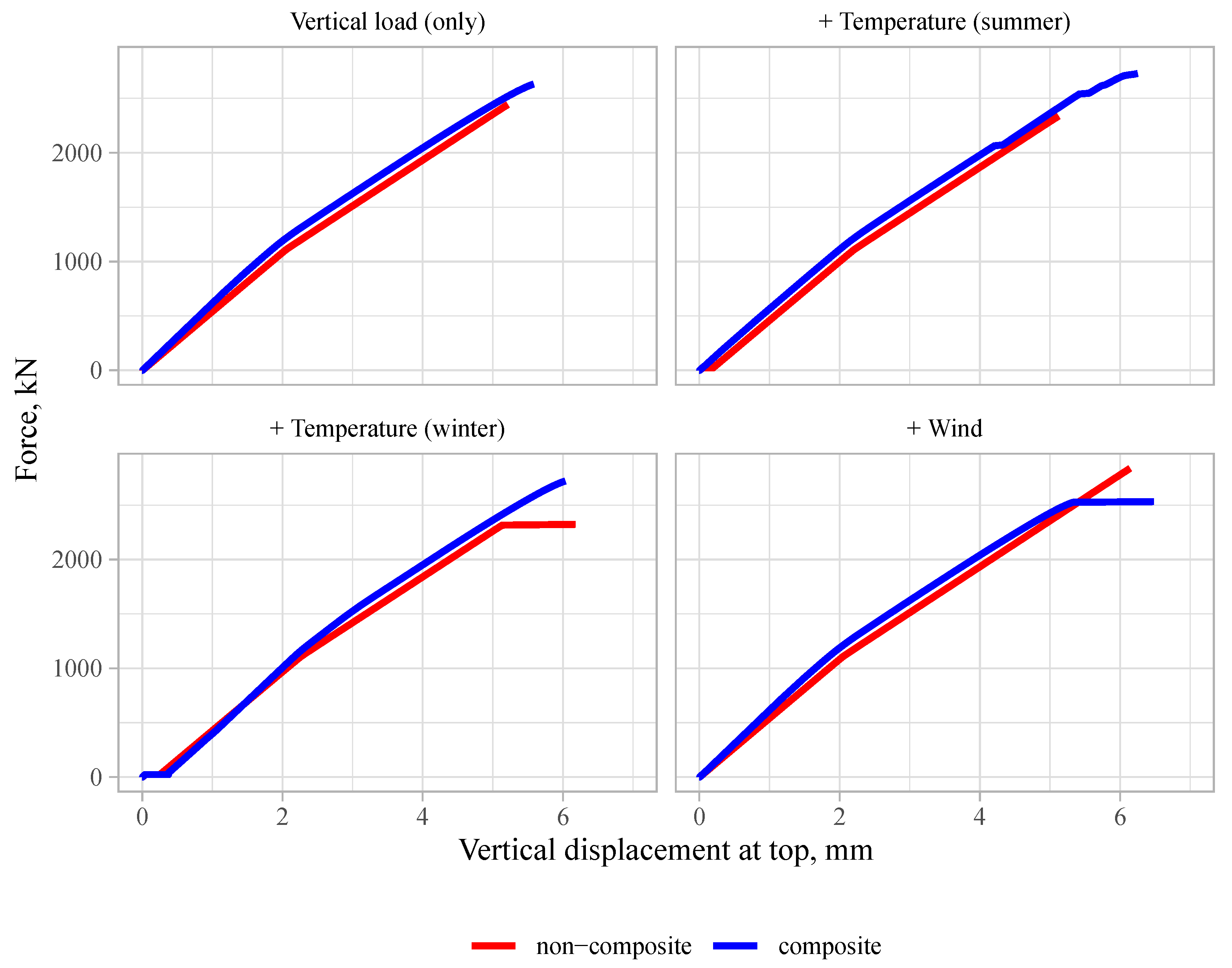
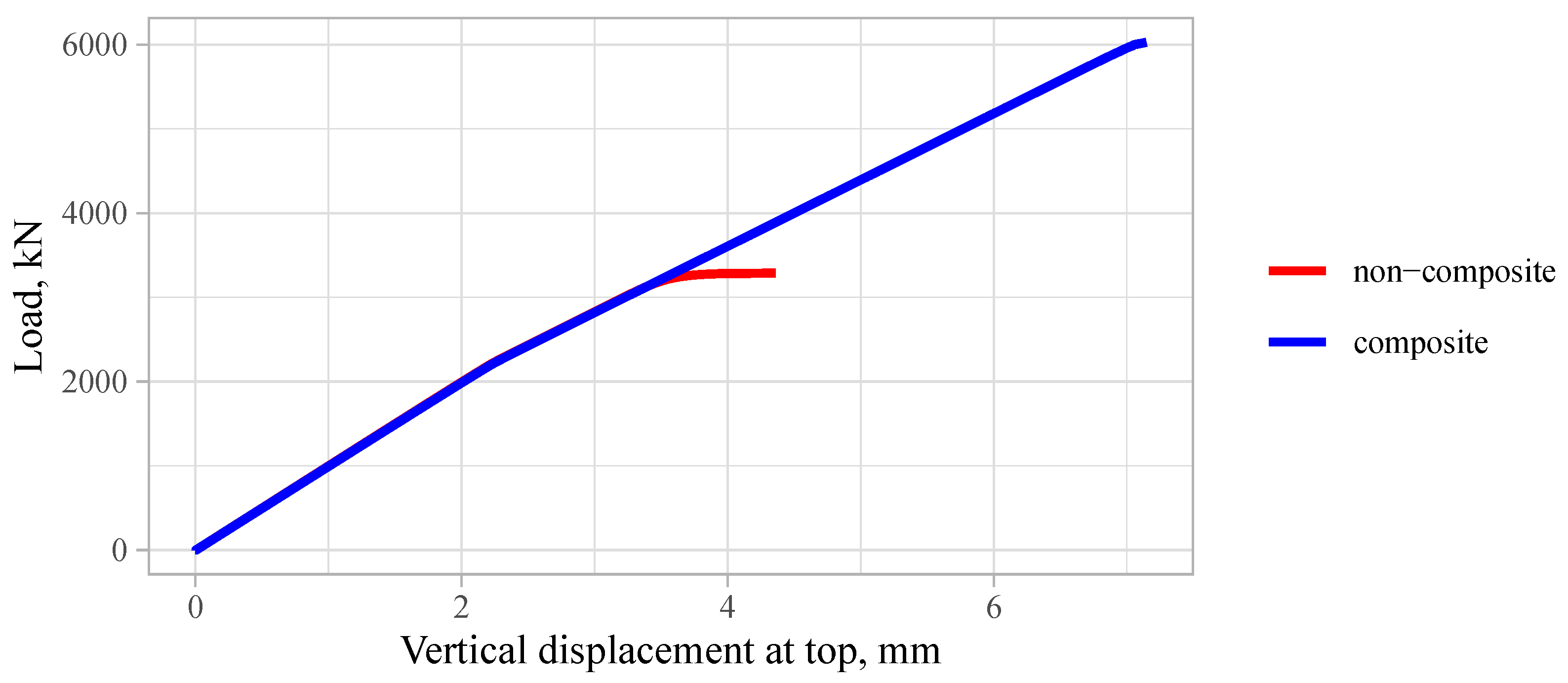
3.3.2. Persistent Design Situation
4. Discussion
4.1. Load-Bearing Capacity
4.2. Composite Action
4.3. Thermal and Sound Reduction Performance
5. Conclusions
- Short fibres can substitute for conventional reinforcement mesh in SW panels and maintain a high load-bearing capacity, even with the increased distance between wythes resulting from the required thickness of thermal insulation.
- In the case of a family house, the core layer of the exterior SW must be at least 120 or 200 mm if polyurethane (PUR) or expended polystyrene (EPS) is used, respectively.
- The theoretical load-bearing capacity estimated by nonlinear finite element analysis exceeds the design loads significantly—by up to 100 times.
- An SW with a non-composite cross-section exhibited the same load-bearing capacity as the ones with a composite cross-section, reaching 55–77% of the load-bearing capacity of the loaded wythe cross-section.
- An SW with a fully composite cross-section can have unfavourable effects in cases of extreme temperature loads, in which high tensile stresses are developed.
- The thermal bridge analysis showed that the temperature distributions at the top and bottom of the wall are satisfactory; however, use of steel connectors resulted in possible condensation of the surface of the SW.
- The sound insulation properties of the analysed thin-layer SW satisfy the requirements set by the Latvian Building Regulations if maximum admissible environmental noise levels are not exceeded.
- In cases of higher environmental noise levels, the requirements for sound insulation can lead to SWs needing thicker wythes. A positive effect can be achieved also by reducing the amount of connectors and using wythes with different thicknesses.
- The thickness of the thermal insulation layer does not have any noticeable effect on the sound reduction of the SW due to its low density.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CMOD | Crack mouth opening distance |
| EPS | Expended polystyrene |
| FRP | Fibre reinforced polymer |
| PUR | Polyurethane |
| SFRC | Steel-fibre-reinforced concrete |
| SW | Sandwich wall |
References
- Losch, E.D.; Hynes, P.W.; Andrews, R., Jr.; Browning, R.; Cardone, P.; Devalapura, R.; Donahey, R.; Freedman, S.; Gleich, H.A.; Goettsche, G.; et al. State of the art of precast/prestressed concrete sandwich wall panels. PCI J. 2011, 56, 131–176. [Google Scholar]
- Ordóñez, D.; Fernández, A.; Cladera, B. Prefabrication for Affordable Housing; Fib Bulletin No. 60; Fib: Lausanne, Switzerland, 2011; p. 123. [Google Scholar]
- Mugahed Amran, Y.; El-Zeadani, M.; Huei Lee, Y.; Yong Lee, Y.; Murali, G.; Feduik, R. Design innovation, efficiency and applications of structural insulated panels: A review. Structures 2020, 27, 1358–1379. [Google Scholar] [CrossRef]
- O’Hegarty, R.; Kinnane, O. Review of precast concrete sandwich panels and their innovations. Constr. Build. Mater. 2020, 233, 117145. [Google Scholar] [CrossRef]
- Tawil, H.; Tan, C.G.; Sulong, N.H.R.; Nazri, F.M.; Sherif, M.M.; El-Shafie, A. Mechanical and Thermal Properties of Composite Precast Concrete Sandwich Panels: A Review. Buildings 2022, 12, 1429. [Google Scholar] [CrossRef]
- Serpilli, M.; Clementi, F.; Lenci, S. An experimental and numerical study on the in-plane axial and shear behavior of sprayed in-situ concrete sandwich panels. Eng. Struct. 2021, 232, 111814. [Google Scholar] [CrossRef]
- Benayoune, A.; Samad, A.A.; Trikha, D.; Ali, A.A.; Ellinna, S. Flexural behaviour of pre-cast concrete sandwich composite panel – Experimental and theoretical investigations. Constr. Build. Mater. 2008, 22, 580–592. [Google Scholar] [CrossRef]
- Kumar, S.; Chen, B.; Xu, Y.; Dai, J.G. Axial-flexural behavior of FRP grid-reinforced geopolymer concrete sandwich wall panels enabled with FRP connectors. J. Build. Eng. 2022, 47, 103907. [Google Scholar] [CrossRef]
- O’Hegarty, R.; Kinnane, O.; Grimes, M.; Newell, J.; Clifford, M.; West, R. Development of thin precast concrete sandwich panels: Challenges and outcomes. Constr. Build. Mater. 2021, 267, 120981. [Google Scholar] [CrossRef]
- Mercedes, L.; Bernat-Maso, E.; Gil, L. Bending and compression performance of full-scale sandwich panels of hemp fabric reinforced cementitious matrix. Eng. Struct. 2023, 275, 115241. [Google Scholar] [CrossRef]
- Shin, D.H.; Kim, H.J. Composite effects of shear connectors used for lightweight-foamed-concrete sandwich wall panels. J. Build. Eng. 2020, 29, 101108. [Google Scholar] [CrossRef]
- Sylaj, V.; Fam, A. UHPC sandwich panels with GFRP shear connectors tested under combined bending and axial loads. Eng. Struct. 2021, 248, 113287. [Google Scholar] [CrossRef]
- O’Hegarty, R.; West, R.; Reilly, A.; Kinnane, O. Composite behaviour of fibre-reinforced concrete sandwich panels with FRP shear connectors. Eng. Struct. 2019, 198, 109475. [Google Scholar] [CrossRef]
- Gara, F.; Ragni, L.; Roia, D.; Dezi, L. Experimental tests and numerical modelling of wall sandwich panels. Eng. Struct. 2012, 37, 193–204. [Google Scholar] [CrossRef]
- Lameiras, R.; Barros, J.A.; Valente, I.B.; Poletti, E.; Azevedo, M.; Azenha, M. Seismic behaviour of precast sandwich wall panels of steel fibre reinforced concrete layers and fibre reinforced polymer connectors. Eng. Struct. 2021, 237, 112149. [Google Scholar] [CrossRef]
- Graziani, L.; Quagliarini, E.; D’Orazio, M.; Lenci, S.; Scalbi, A. A More Sustainable Way for Producing RC Sandwich Panels On-Site and in Developing Countries. Sustainability 2017, 9, 472. [Google Scholar] [CrossRef]
- Choi, I.; Kim, J.; Kim, H.R. Composite Behavior of Insulated Concrete Sandwich Wall Panels Subjected to Wind Pressure and Suction. Materials 2015, 8, 1264–1282. [Google Scholar] [CrossRef]
- Choi, I.; Kim, J.; Kim, H.R. Composite Behavior of a Novel Insulated Concrete Sandwich Wall Panel Reinforced with GFRP Shear Grids: Effects of Insulation Types. Materials 2015, 8, 899–913. [Google Scholar] [CrossRef]
- Barros, J.; Pereira, E.; Santos, S. Lightweight Panels of Steel Fiber-Reinforced Self-Compacting Concrete. J. Mater. Civ. Eng. 2007, 19, 295–304. [Google Scholar]
- Lameiras, R.; Barros, J.; Valente, I.B.; Azenha, M. Development of sandwich panels combining fibre reinforced concrete layers and fibre reinforced polymer connectors. Part I: Conception and pull-out tests. Compos. Struct. 2013, 105, 446–459. [Google Scholar] [CrossRef]
- Lameiras, R.M. Sandwich Structural Panels Comprising Thin-Walled SFRSCC and GFRP Connectors: From Material Features to Structural Behaviour. Ph.D. Thesis, Universidade do Minho, Guimeraes, Portugal, 2015. [Google Scholar]
- Thomas, D.; Gregory, L. Flexural Behavior of Composite Precast Concrete Sandwich Panels With Continuous Truss Connectors. PCI J. 1994, 39, 112–121. [Google Scholar]
- Tomlinson, D.G.; Teixeira, N. Behaviour of Partially Composite Precast Concrete Sandwich Panels under Flexural and Axial Loads. Ph.D. Thesis, Queen’s University, Kingston, ON, Canada, 2015. [Google Scholar]
- Chen, J.; Hamed, E.; Gilbert, R.I. Structural performance of concrete sandwich panels under fire. Fire Saf. J. 2021, 121, 103293. [Google Scholar] [CrossRef]
- PCI IH Committee. PCI Handbook Precast Prestressed Concrete, 6th ed.; PCI: Chicago, IL, USA, 2004. [Google Scholar]
- Woltman, G.; Noel, M.; Fam, A. Experimental and numerical investigations of thermal properties of insulated concrete sandwich panels with fiberglass shear connectors. Energy Build. 2017, 145, 22–31. [Google Scholar] [CrossRef]
- Künzel, H. WUFI Pro. 2022. Available online: https://wufi.de/en/software/what-is-wufi/ (accessed on 27 December 2022).
- EN 15026:2007; Hygrothermal Performance of Building Components and Building Elements—Assessment of Moisture Transfer by Numerical Simulation. CEN: Brussels, Belgium, 2007.
- Infomind Ltd. Flixo. 2022. Available online: https://www.flixo.com/ (accessed on 28 December 2022).
- EN ISO 10211:2017; Thermal Bridges in Building Construction—Heat Flows and Surface Temperatures—Detailed Calculations. CEN: Brussels, Belgium, 2017.
- EN ISO 10077-2:2017; Thermal Performance of Windows, Doors and Shutters—Calculation of Thermal Transmittance—Part 2: Numerical Method for Frames. CEN: Brussels, Belgium, 2017.
- LBN 002-19; Regulations Regarding the Latvian Construction Standard LBN 002-19, Thermotechnics of Building Envelopes. Regulation No. 280; Cabinet of Ministers: Riga, Latvia, 2019.
- Marshall Day Acoustics. Sound Insulation Prediction Program INSUL 9.0, User Manual. 2017. Available online: https://www.insul.co.nz/media/30049/Insul-Manual-2017-word-version.pdf (accessed on 30 December 2022).
- Marshall Day Acoustics. Sound Insulation Prediction Program INSUL 9.0. 2022. Available online: https://www.insul.co.nz/ (accessed on 30 December 2022).
- Long, M. Architectural Acoustics; Academic Press: Boston, MA, USA, 2006. [Google Scholar]
- LBN 016-15; Regulations Regarding the Latvian Construction Standard LBN 016-15, Building Acoustic. Latvian Construction Standard LBN 016-15. Cabinet of Ministers: Riga, Latvia, 2015.
- Regulations of the Cabinet of Ministers. Noise Assessment and Management Procedure; Regulation No. 16; Cabinet of Ministers: Riga, Latvia, 2014. [Google Scholar]
- Eurocode 1; Eurocode 1: Actions on Structures—Part 1-5: General Actions— Thermal Actions. European Standard LVS EN 579 1991-1-5. CEN: Brussels, Belgium, 2004.
- Eurocode 1/NA:2014; Eurocode 1: Actions on Structures—Part 1-5: General Actions—Thermal Actions—National Annex. Latvian Standard LVS EN 1991-1-5:2004/NA:2014. LVS: Riga, Latvia, 2014.
- Červenka, V.; Červenka, J. ATENA Science Software. 2022. Available online: www.cervenka.cz (accessed on 2 January 2023).
- Federation International du Beton. Fib Model Code for Concrete Structures 2010; Ernst & Sohn GmbH & Co., KG.: Berlin, Germany, 2013; ISBN 9783433030615. [Google Scholar]
- European Standard EN 14651:2005; Test Method for Metallic Fibre Concrete—Measuring the Flexural Tensile Strength (Limit of Proportionality (LOP), Residual). CEN: Brussels, Belgium, 2007.
- Miskinis, K.; Dikavicius, V.; Buska, A.; Banionis, K. Influence of EPS, mineral wool and plaster layers on sound and thermal insulation of a wall: A case study. Appl. Acoust. 2018, 137, 62–68. [Google Scholar] [CrossRef]
- Wang, J.; Du, B.; Huang, Y. Experimental study on airborne sound insulation performance of lightweight double leaf panels. Appl. Acoust. 2022, 197, 108907. [Google Scholar] [CrossRef]
- Alchaar, A.; Abed, F. Finite element analysis of a thin-shell concrete sandwich panel under eccentric loading. J. Build. Eng. 2020, 32, 101804. [Google Scholar] [CrossRef]
- Eurocode 2; Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. European Standard EN 1992-1-1. CEN: Brussels, Belgium, 2004.
- Flansbjer, M.; Williams Portal, N.; Vennetti, D.; Mueller, U. Composite Behaviour of Textile Reinforced Reactive Powder Concrete Sandwich Façade Elements. Int. J. Concr. Struct. Mater. 2018, 12, 71. [Google Scholar] [CrossRef]
- Chen, D.; Li, K.; Yuan, Z.; Cheng, B.; Kang, X. Shear Behavior of FRP Connectors in Precast Sandwich Insulation Wall Panels. Buildings 2022, 12, 1095. [Google Scholar] [CrossRef]
- Haffke, M.; Pahn, M.; Thiele, C.; Grzesiak, S. Experimental Investigation of Concrete Sandwich Walls with Glass-Fiber-Composite Connectors Exposed to Fire and Mechanical Loading. Appl. Sci. 2022, 12, 3872. [Google Scholar] [CrossRef]



| Property | Unit | Concrete | EPS | PUR |
|---|---|---|---|---|
| Density | kg/m | 2400 | 30 | 40 |
| Porosity | m/m | 0.18 | 0.95 | 0.95 |
| Specific Heat Capacity (dry) | J/(kg K) | 850 | 1500 | 1500 |
| Thermal Conductivity (dry, 10 C) | W/(m K) | 2.2 | 0.04 | 0.025 |
| Water Vapour Diffusion Resistance Factor | - | 180 | 50 | 50 |
| Moisture-dep. Thermal Cond. Supplement | %/M.-% | 8 | - | - |
| Temp-dep. Thermal Cond. Supplement | W/(m K) | 0.0002 | 0.0002 | 0.0002 |
| Type 1 | Type 2 | |
|---|---|---|
| Composition | concrete–EPS–concrete | concrete–PUR–concrete |
| Thickness (mm) | 60-200-60 | 60-120-60 |
| Total thickness (mm) | 320 | 240 |
| R-value (mK/W) | 5.04 | 4.81 |
| U-value (W/(mK)) | 0.191 | 0.2 |
| Label | Cross-Section Composition | Insulation | Connector Spacing, mm |
|---|---|---|---|
| EPS1 | 60/200/60 | EPS | no connectors |
| EPS2 | 60/200/60 | EPS | 400 × 400 |
| EPS3 | 60/200/60 | EPS | 200 × 200 |
| PUR1 | 60/120/60 | PUR | no connectors |
| PUR2 | 60/120/60 | PUR | 400 × 400 |
| PUR3 | 60/120/60 | PUR | 200 × 200 |
| PUR4 | 75/120/75 | PUR | 200 × 200 |
| PUR5 | 45/120/45 | PUR | 200 × 200 |
| PUR6 | 60/120/75 | PUR | 200 × 200 |
| PUR7 | 45/120/60 | PUR | 200 × 200 |
| Load Type | Load Design Value, kN/m |
|---|---|
| Dead load of roof slab | 5.85 |
| Snow load | 1.50 |
| Wind suction load | 1.00 |
| Loading Situation | Intervals and Number of Steps | ||||||
|---|---|---|---|---|---|---|---|
| BC | SW | F | W | T | 3F | Failure | |
| Centric | 1 | 10 | 200 | - | - | 200 | 1000 |
| Eccentric | 1 | 10 | 200 | - | - | 200 | 1000 |
| Eccentric + wind | 1 | 10 | 200 | 20 | - | 200 | 1000 |
| Eccentric + temperature (winter) | 1 | 10 | 200 | - | 30 | 200 | 1000 |
| Eccentric + temperature (summer) | 1 | 10 | 200 | - | 30 | 200 | 1000 |
| Demoulding(vertical section) | 1 | - | 200 | - | - | 200 | 1000 |
| Demoulding(horizontal section) | 1 | - | 200 | - | - | 200 | 1000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skadiņš, U.; Kuļevskis, K.; Vulāns, A.; Brencis, R. Thin-Layer Fibre-Reinforced Concrete Sandwich Walls: Numerical Evaluation. Fibers 2023, 11, 19. https://doi.org/10.3390/fib11020019
Skadiņš U, Kuļevskis K, Vulāns A, Brencis R. Thin-Layer Fibre-Reinforced Concrete Sandwich Walls: Numerical Evaluation. Fibers. 2023; 11(2):19. https://doi.org/10.3390/fib11020019
Chicago/Turabian StyleSkadiņš, Ulvis, Kristens Kuļevskis, Andris Vulāns, and Raitis Brencis. 2023. "Thin-Layer Fibre-Reinforced Concrete Sandwich Walls: Numerical Evaluation" Fibers 11, no. 2: 19. https://doi.org/10.3390/fib11020019
APA StyleSkadiņš, U., Kuļevskis, K., Vulāns, A., & Brencis, R. (2023). Thin-Layer Fibre-Reinforced Concrete Sandwich Walls: Numerical Evaluation. Fibers, 11(2), 19. https://doi.org/10.3390/fib11020019