On the Design of Permanent Rock Support Using Fibre-Reinforced Shotcrete
Abstract
1. Introduction
2. Design of Shotcrete as Permanent Rock Support
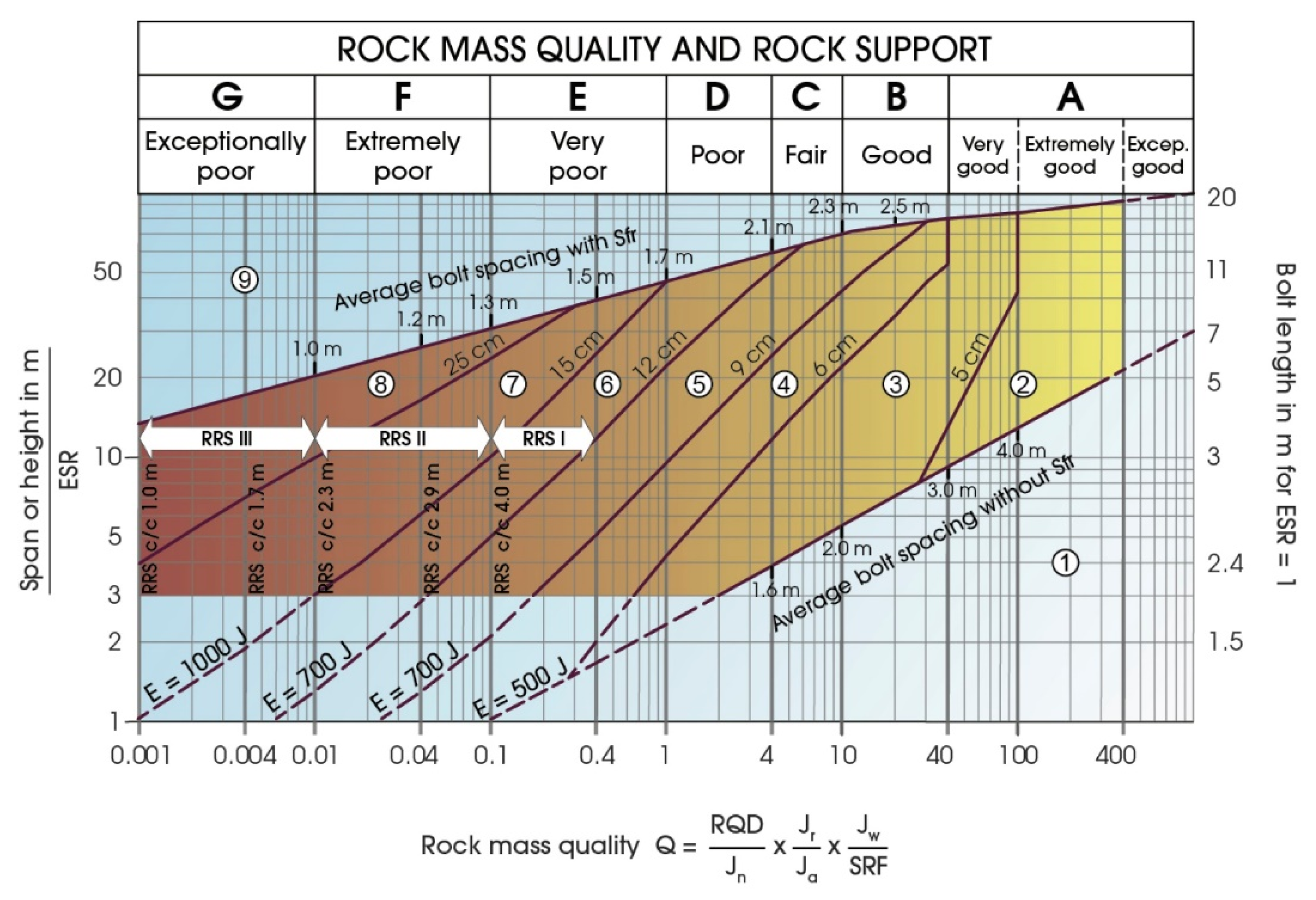
2.1. Design with the Q-Method
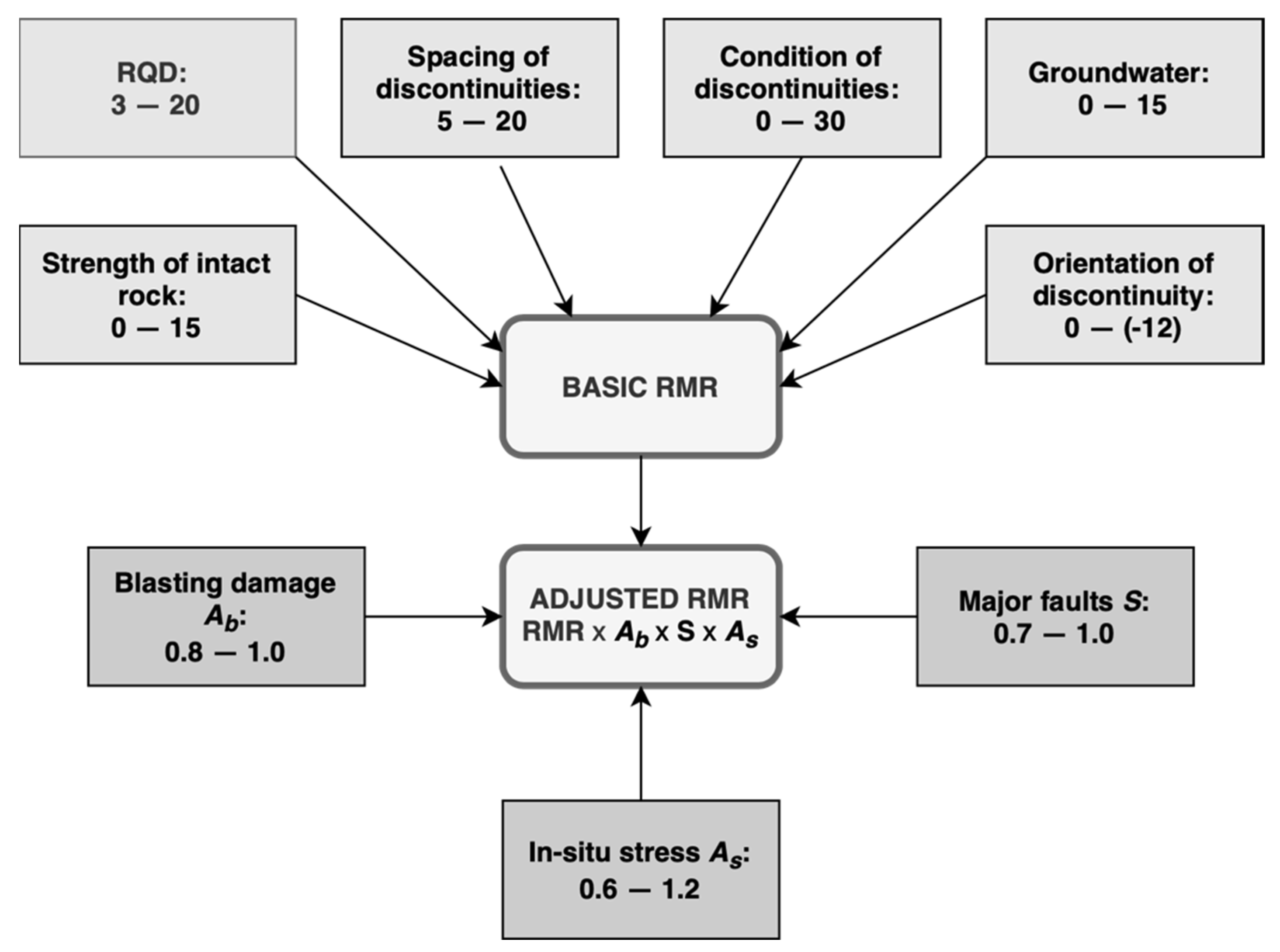
2.2. Design with the RMR-Method
2.3. Design with the National Guidelines
2.4. Design with Analytical Equations
3. Experimental Campaign
3.1. Overview
3.2. Preparation of Specimens
4. Case Study of Tunnel Design
- Design with Q-method: The required energy absorption for the shotcrete was based on the geometry, ESR- and Q-value. First, the required energy absorption was taken from the Q-chart shown in Figure 1 and then converted according to .
- TPL design: Based on the Q-value, a rock class was determined based on the Q-chart. The correlation between rock class and toughness performance level (TPL) was used to determine a required residual strength .
- Australian design: Here, it was assumed that small deformations were expected for Q = 20 and large deformations when Q = 1.5. Hence, the design was based on a residual strength for Q = 20 and an energy absorption for Q = 1.5 based on Australian standards (ACS2010).
- Swedish design: The requirements of the shotcrete were based on a recommended residual strength based on Swedish guidelines .
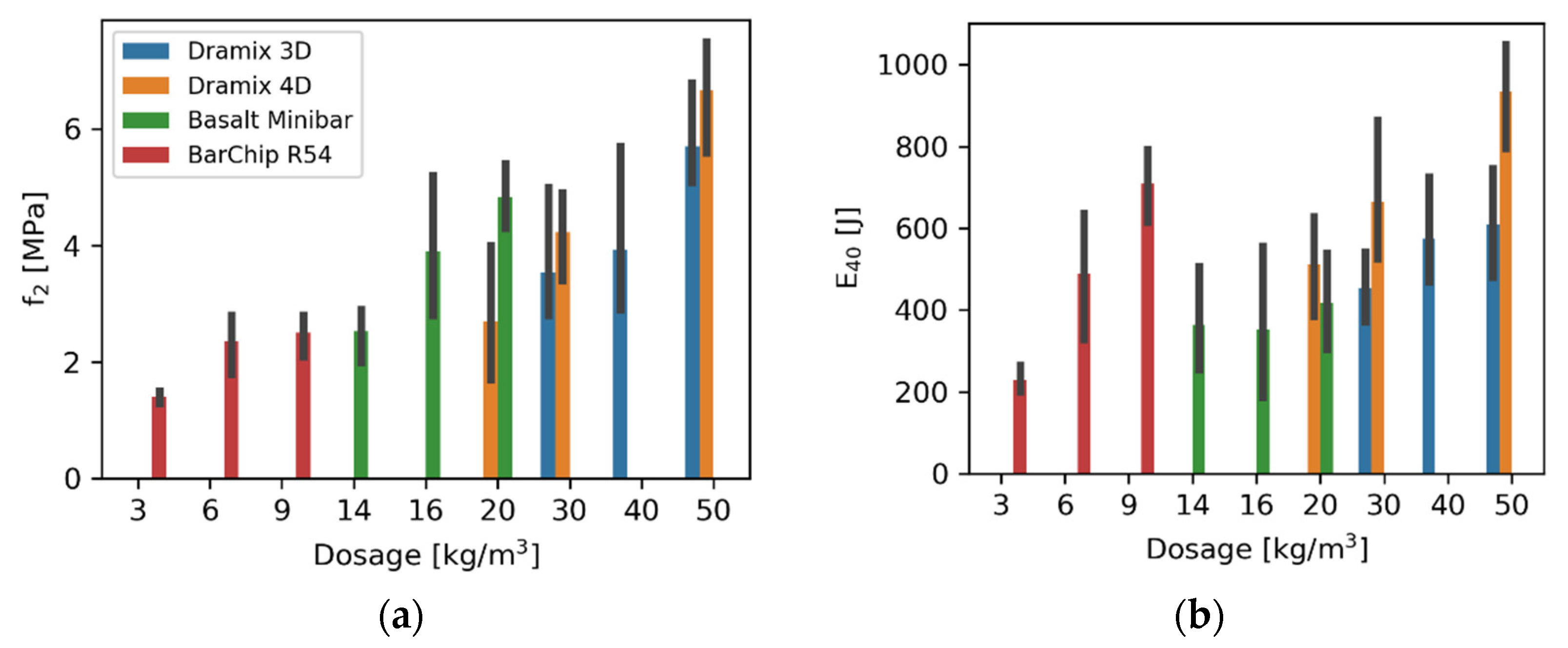
- Dosage of fibres: Based on the results from the experimental campaign presented in Section 5, the minimum dosage of fibres that fulfilled the design criterion was selected for each design alternative.
5. Results and Discussion
5.1. Experimental Results
5.2. Structural Performance
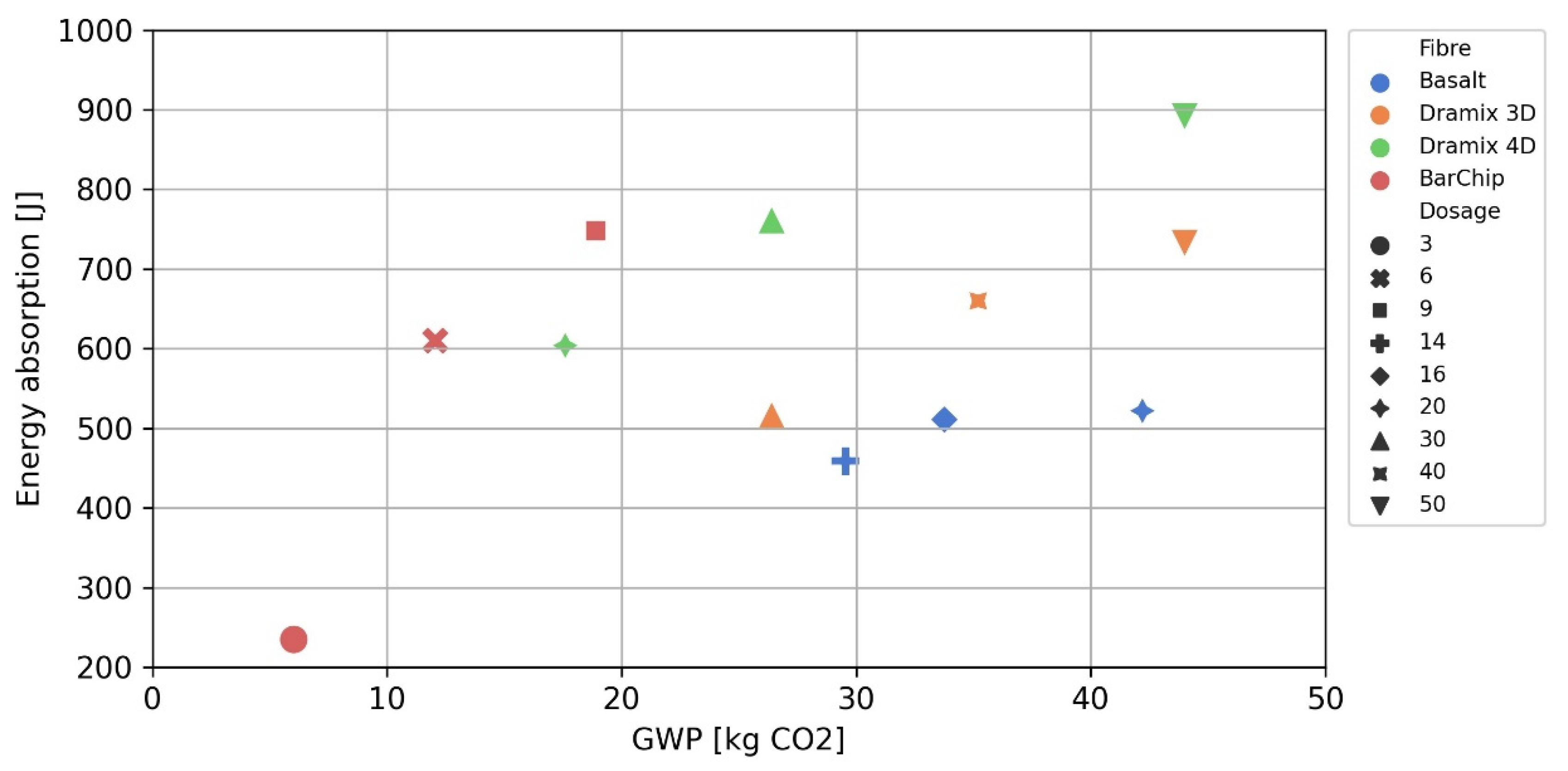
5.3. Environmental Performance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Johansson, F.; Roslin, M.; Josefosson, J. Evaluation of Glass-Fibre Bolt as Permanent Rock Support; Technical report; KTH Royal Institute of Technology: Stockholm, Sweden, 2020. (In Swedish) [Google Scholar]
- Bjureland, W.; Johansson, F.; Sjölander, A.; Spross, J.; Larsson, S. Probability distributions of shotcrete parameters for reliability-based analyses of rock tunnel support. Tunn. Undergr. Space Technol. 2019, 87, 15–26. [Google Scholar] [CrossRef]
- Wetlesen, T.; Krutrök, B. Measurment of shotcrete thickness in tunnel with Bever 3D laser scanner operated from robot. In Proceedings of the 7th International Symposium on Sprayed Concrete, Sandefjord, Norway, 16–19 June 2014. [Google Scholar]
- Solla, M.; Pérez-Gracia, V.; Fontul, S. A Review of GPR Application on Transport Infrastructures: Troubleshooting and Best Practices. Remote Sens. 2021, 13, 672. [Google Scholar] [CrossRef]
- Belloni, V.; Sjölander, A.; Ravanelli, R.; Crespi, M.; Nascetti, A. Tack project: Tunnel and bridge automatic crack monitoring using deep learning and photogrammetry. ISPRS—Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2020, XLIII-B4-2, 741–745. [Google Scholar] [CrossRef]
- Insa-Iglesias, M.; Jenkins, M.D.; Morison, G. 3D visual inspection system framework for structural condition monitoring and analysis. Autom. Constr. 2021, 128, 103755. [Google Scholar] [CrossRef]
- Sjölander, A. Structural Behaviour of Shotcrete in Hard Rock Tunnels. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2020. [Google Scholar]
- Myren, S.; Bjøntegard, Ø.; Hagelia, P. The ban of polymer fibre in FRS in Norwegian road tunnels. In Proceedings of the 8th International Symposium on Sprayed Concrete, Trondheim, Norway, 11–14 June 2018. [Google Scholar]
- Ansell, A. Dynamically Loaded Rock Reinforcement. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 1999. [Google Scholar]
- Bryne, L.E. Time Dependent Material Properties of Shotcrete for Hard Rock Tunneling. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2014. [Google Scholar]
- Holmgren, J. Punch-Loaded Shotcrete Linings on Hard Rock; Technical report; Rock Engineering Research Foundation (BeFo): Stockholm, Sweden, 1979. [Google Scholar]
- Malmgren, L. Interaction between Shotcrete and Rock: Experimental and Numerical Study. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 2005. [Google Scholar]
- Nordström, E. Durability of sprayed concrete–Steel fibre corrosion in cracks. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 2005. [Google Scholar]
- Bernard, E. Design of fibre reinforced shotcrete linings with macro-synthetic fibres. In Proceedings of the 11th Shotcrete for Underground Support, Davos, Switzerland, 7–10 June 2009. [Google Scholar]
- Monaldo, E.; Nerilli, F.; Vairo, G. Basal-based fiber-reinforced materials and structural applications in civil engineering. Compos. Struct. 2019, 214, 246–263. [Google Scholar] [CrossRef]
- Mohaghegh, A. Structural Performance of High-Performance Macro Basalt Fibre Concrete: Flexural, shear, Punching Shear and Fire Spalling. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2018. [Google Scholar]
- Afroz, M.; Patnaikuni, I.; Venkatesan, S. Chemical durability and performance of modified basalt fiber in concrete medium. Constr. Build. Mater. 2017, 154, 191–203. [Google Scholar] [CrossRef]
- Fiore, V.; Scalici, T.; Di Bella, G.; Valenza, A. A review on basalt fibre and its composites. Compos. Part B Eng. 2015, 74, 74–94. [Google Scholar] [CrossRef]
- EN 1997-1; Eurocode 7: Geotechnical Design Part 1: General Rules. Technical standard. EU: Brussels, Belgium, 2004.
- Bieniawski, Z. Engineering classification of jointed rock masses. Civ. Eng. S. Afr. 1973, 15, 333–343. [Google Scholar]
- Barton, N.; Lien, R.; Lunde, J. Engineering classification of rock masses for the design of tunnel support. Rock Mech. Rock Eng. 1974, 6, 189–236. [Google Scholar] [CrossRef]
- Terzaghi, K. Rock defects and loads on tunnel supports. In Rock Tunneling with Steel Supports; Proctor, R., White, T., Eds.; Publication 418–Soil mechanics series 25; Harvard University: Boston, MA, USA, 1946. [Google Scholar]
- Grimstad, E.; Barton, N. Updating the Q-System for NMT; Norwegian Geotechnical Institute: Oslo, Norway, 1993. [Google Scholar]
- Grimstad, E.; Kankes, K.; Bhasin, R.; Magnussen, A.W.; Kaynia, A. Rock mass quality Q used in designing reinforced ribs of sprayed concrete and energy absorption. In Proceedings of the 4th International Symposium on Sprayed Concrete, Davos, Switzerland, 22–26 September 2002. [Google Scholar]
- NGI. Using the Q-System: Rock Mass Classification and Support Design; TDOK2016:0231; NGI: Oslo, Norway, 2016. [Google Scholar]
- EFNARC. European Specification for Sprayed Concrete; Technical report; EFNARC: Surrey, UK, 1996. [Google Scholar]
- Bieniawski, Z.T. Rock mass classification in rock engineering. In Proceedings of the Symposium on Exploration for Rock Engineering, Cape Town, South Africa, 1–5 November 1976. [Google Scholar]
- Bieniawski, Z.T. The geomechanics classification in rock engineering applications. In Proceedings of the 4th International Congress on Rock Mechanics, Rotterdam, The Netherlands, 1 January 1979; Volume 2, pp. 41–48. [Google Scholar]
- Aksoy, C.O. Review of rock mass rating classification: Historical developments, applications, and restrictions. J. Min. Sci. 2008, 44, 51–63. [Google Scholar] [CrossRef]
- Singh, B.; Goel, R.K. Engineering Rock Mass Classification: Tunneling, Foundations and Landslides; Butterworth-Heinemann: Amsterdam, The Netherlands, 2011; pp. 45–62. ISBN 9780123858788. [Google Scholar] [CrossRef]
- Hudson, J.A. Rock Testing and Site Characterization; Pergamon: Amsterdam, The Netherlands, 1995; ISBN 9780080420660. [Google Scholar] [CrossRef]
- Papworth, F. Design guidelines for the use of fibre-reinforced shotcrete in ground support. Shotcrete Mag. 2002, 1, 16–21. [Google Scholar]
- Heere, R.; Morgan, D.R. Specification of shotcrete toughness. Shotcrete Magazine, Fall. 2003; 14–16. [Google Scholar]
- Trafikverket. Projektering av Bergkonstruktioner; Planning of Structures in Rock, Trafikverket: Borlänge, Sweden, 2015. (In Swedish) [Google Scholar]
- EN 14488-3; Testing Sprayed Concrete Part 3: Flexural Strengths (First, Peak and Residual) of Fibre Reinforced Concrete Beam Specimens. Technical Standard. EU: Brussels, Belgium, 2006.
- AuSS. Recommended Practice Shotcreting in Australia; Technical Report; Concrete Institute of Australia: Rhodes, Australia, 2010. [Google Scholar]
- ASTM C1550-19; Standard Test Method for Flexural Toughness of Fibre-Reinforced Concrete. Technical Standard. ASTM: West Conshohocken, PA, USA, 2019.
- Mao, D.; Bjorn, N.; Lu, M. Numerical analysis of rock fall at Hanekleiv road tunnel. Bull. Eng. Geol. Environ. 2012, 71, 783–790. [Google Scholar] [CrossRef]
- Morton, E.; Thompson, A.G.; Villaecusa, E.; Howard, D. Static testing of shotcrete. In Proceedings of the 13th Australian Tunnel Conference, Melbourne, Australia, 4–7 May 2008. [Google Scholar]
- Barrett, S.; McCreath, D. Shortcrete support design in blocky ground: Towards a deterministic approach. Tunn. Undergr. Space Technol. 1995, 10, 79–89. [Google Scholar] [CrossRef]
- Fernandez-Delgado, G.; Cording, E.J.; Mahar, J.W. Shotcrete: Structural Testing of Thin Liners; Technical report; University of Illinois: Washington, DC, USA, 1975. [Google Scholar]
- Holmgren, J. Bolt-anchored, steel-fibre-reinforced shotcrete linings. Tunn. Undergr. Space Technol. 1987, 2, 319–333. [Google Scholar] [CrossRef]
- Sjölander, A.; Hellgren, R.; Malm, R.; Ansell, A. Verification of failure mechanisms and design philosophy for a bolt-anchored and fibre-reinforced shotcrete lining. Eng. Fail. Anal. 2020, 116, 104741. [Google Scholar] [CrossRef]
- EN 14487-1; Sprayed Concrete Part 1: Definitions, Specifications and Conformity. Technical Standard. EU: Brussels, Belgium, 2005.
- Brodd, E.; Östlund, L. Environmental and Technical Evaluation of Cement Reduction and Test Methods for Fibre Reinforced Shotcrete in Tunnels. Master’s Science Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2022. [Google Scholar]
- EN 12390-3; Testing Hardened Concrete Part 3: Compressive Strength of Test Specimens. Technical Standard. EU: Brussels, Belgium, 2019.
- EN 12390-1; Testing Hardened Concrete Part 1: Shape, Dimensions and Other Requirements for Specimens and Moulds. Technical Standard. EU: Brussels, Belgium, 2019.
- EPD. BarChip 48, BarChip 54, and BarChip 60 Macro Synthetic Fibres; Environmental Product Declaration, 2020; Available online: https://www.environdec.com/library/epd2054 (accessed on 29 March 2022).
- EPD. Dramix Steel Fibres for Concrete Reinforcement; Environmental Product Declaration, 2021; Available online: www.itb.pl (accessed on 29 March 2022).
- EPD. Reforcetech Basalt MiniBar; Environmental Product Declaration, 2022; Available online: https://www.epd-norge.no/stal-armering-aluminiumskonstruksjoner/basalt-minibars-tm-article3823-323.htmlTM%281%29.pdf (accessed on 29 March 2022).
- EN 14025; Environmental Labels and Declarations–Type III Environmental Declarations–Principles and Procedures. Technical Standard. EU: Brussels, Belgium, 2010.
- EN 15804; Sustainability of Construction Works–Environmental Product Declarations–Core Rules for the Product Category of Construction Products. Technical Standard. EU: Brussels, Belgium, 2010.
- Sjölander, A.; Ansell, A.; Nordström, E. Data from Structural Testing of Sprayed and Cast Shotcrete Reinforced with Fibres of Steel, Basalt and Synthetic Material. Mendeley Data, V1. 2022. Available online: https://data.mendeley.com/datasets/d7n5mvb2sg (accessed on 1 December 2022).
- Sjölander, A. Analyses of Shotcrete Stress States due to Varying Lining Thickness and Irregular Rock Surfaces. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2017. [Google Scholar]
- Ansell, A. Investigation of shrinkage cracking in shotcrete on tunnel drains. Tunn. Undergr. Space Technol. 2010, 25, 607–613. [Google Scholar] [CrossRef]
- Sjölander, A.; Ansell, A. In-Situ and Laboratory Investigation on Leaching and Effects of Early Curing of Shotcrete. Nord. Concr. Res. 2019, 61, 23–37. [Google Scholar] [CrossRef]
- Anand, S. Evaluation of Environmental and Technical Performance of Alternate Fibres for Shotcrete in Tunnels. Master’s Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2022. [Google Scholar]



| RMR | Rock Support |
|---|---|
| 81–100 | Occasional spot bolting. |
| 61–80 | Local bolts in crown, = 2.5 m, = 50 mm was needed |
| 41–60 | Systematic bolts in crown and wall, = 1.5–2.0 m, = 50–100 mm and = 30 mm |
| 21–40 | Systematic bolts in crown and wall, = 1.0–1.5 m, = 100–150 mm and = 100 mm |
| 0–20 | Systematic bolts in crown and wall, = 1.0–1.5 m, = 150–200 mm and = 150 mm |
| Rock Class | TPL | (J) | (J) | (-) | (MPa) | (MPa) | (MPa) | (J) |
|---|---|---|---|---|---|---|---|---|
| A | 0 | 0 | 0 | 0 | 0 | 3.5–4.0 | 3.0 | |
| B | 1 | >500 | >200 | 0.1–0.25 | 0.4–1.0 | 3.5–4.0 | 3.0 | |
| C | 2 | >500 | >200 | 0.25–0.47 | 1.0–1.9 | 3.5–4.0 | 400 | |
| D | 3 | >700 | >280 | 0.47–0.67 | 1.9–2.7 | 3.5–4.0 | 400 | |
| E | 4 | >1000 | >400 | 0.67–1.0 | 2.7–4.0 | 3.5–4.0 | 400 | |
| F | 4 | >1400 | >560 | 0.67–1.0 | >4.0 | 3.5–4.0 | 400 |
| Fibre | Material | Dosage (kg/m3) | Beams (-) | Panels (-) | Cubes (-) |
|---|---|---|---|---|---|
| Dramix 3D | Steel | 30/40/50 | 3/3/3 | 3/3/3 | 3/3/3 |
| Dramix 4D | Steel | 20/30/40 | 3/3/3 | 3/3/3 | 3/3/3 |
| Basalt Minibar | Basalt | 14/16/20 | 3/3/3 | 3/3/3 | 3/3/3 |
| BarChip 54 | Synthetic | 3/6/9 | 3/3/3 | 3/3/3 | 3/3/3 |
| Material | Quantity | Unit (-) |
|---|---|---|
| Cement | 500 | kg/m3 |
| Water | 204 | kg/m3 |
| w/c | 0.41 | - |
| Aggregate 0–2 mm | 489 | kg/m3 |
| Aggregate 0–8 mm | 1141 | kg/m3 |
| Release agent 1 | 1.6 | kg/m3 |
| Plasticizer 2 | 5.0 | kg/m3 |
| Air 3 | 4.5–5.1 | % |
| Slump 3 | 80–160 | mm |
| Fibre | Density (kg/m3) | E (GPa) | (MPa) | l (mm) | d (mm) | l/d (-) |
|---|---|---|---|---|---|---|
| Dramix 3D | 7850 | 200 | 1800 | 35 | 0.5 | 65 |
| Dramix 4D | 7850 | 200 | 1600 | 35 | 0.5 | 65 |
| Basalt Minibar | 2000 | 42 | >1000 | 43 | 0.7 | 61 |
| BarChip 54 | 900 | 12 | 640 | 54 | 0.6 | 90 |
| CO2 Eq. to Produce 1 kg of Fibre | |||
|---|---|---|---|
| Indicator | Dramix | BarChip | MiniBar |
| Global Warming Potential (GWP) | 0.88 kg | 2.01 kg | 2.11 kg |
| Cubes | Beams EN 14488-3 (MPa) | Panels (J) | |||||
|---|---|---|---|---|---|---|---|
| Fibre | Dosage (kg/m3) | (MPa) | Mean | Mean | |||
| Dramix 3D | 50 | 57/63/64 | 5.1/5.2/6.8 | 5.7 | 4.9/5.1/6.4 | 5.5 | 709/764/724 |
| Dramix 3D | 40 | 60/63/65 | 2.9/3.2/5.7 | 3.9 | 2.7/3.1/5.2 | 3.7 | 592/597/792 |
| Dramix 3D | 30 | 56/61/63 | 2.8/2.8/5.0 | 3.5 | 2.4/2.7/4.5 | 3.2 | 472/516/564 |
| Dramix 4D | 50 | 57/57/59 | 5.6/6.9/7.5 | 6.7 | 4.8/5.0/8.1 | 6.7 | 737/957/979 |
| Dramix 4D | 30 | 58/59/62 | 3.4/4.4/4.9 | 4.2 | 3.5/4.4/4.5 | 4.2 | 525 */825/927 |
| Dramix 4D | 20 | 59/61/61 | 1.7/2.4/4.0 | 2.7 | 1.7/2.3/3.7 | 2.7 | 577/583/653 |
| Basalt Minibar | 20 | 58/62/64 | 4.3/4.8/5.4 | 4.8 | 4.0/4.9/5.3 | 4.7 | 475/536/557 |
| Basalt Minibar | 16 | 63/63/64 | 2.8/3.7/5.2 | 3.9 | 2.9/4.0/5.8 | 4.2 | 379/511/644 |
| Basalt Minibar | 14 | 63/63/64 | 2.0/2.7/2.9 | 2.5 | 1.9/2.7/3.1 | 2.6 | 362/503/514 |
| BarChip 54 | 9 | 55/55/57 | 2.1/2.6/2.7 | 2.5 | 2.3/2.9/3.1 | 2.8 | 703/736/806 |
| BarChip 54 | 6 | 55/61/64 | 1.8/2.5/2.8 | 2.4 | 2.1/2.9/3.2 | 2.7 | 558/610/662 |
| BarChip 54 | 3 | 49/51/54 | 1.3/1.4/1.5 | 1.4 | 1.4/1.5/1.6 | 1.5 | 202/233/272 |
| Dramix 3D | Dramix 4D | MiniBar | BarChip | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Design | Q (-) | RC (-) | Dosage (kg/m3) | GWP (kg CO2) | Dosage (kg/m3) | GWP (kg CO2) | Dosage (kg/m3) | GWP (kg CO2) | Dosage (kg/m3) | GWP (kg CO2) |
| —200 J | 20 | B | 30 * | 26 | 20 * | 18 | 14 * | 30 | 3 | 6 |
| —TPL I | 20 | B | 30 * | 26 | 20 * | 18 | 14 * | 30 | 6 * | 12 |
| —3.0 MPa | 20 | B | 30 | 26 | 30 | 26 | 16 | 34 | - | - |
| —4.0 MPa | 20 | B | 50 | 44 | 30 | 26 | 20 | 42 | - | - |
| —280 J | 1.5 | D | 30 * | 26 | 20 * | 18 | 14 * | 30 | 6 * | 12 |
| —TPL III | 1.5 | D | 50 | 44 | 50 | 44 | - | - | - | - |
| —400 J | 1.5 | D | 30 | 26 | 20 | 18 | 14 | 30 | 6 | 12 |
| —4.0 MPa | 1.5 | D | 50 | 44 | 30 | 26 | 20 | 42 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sjölander, A.; Ansell, A.; Nordström, E. On the Design of Permanent Rock Support Using Fibre-Reinforced Shotcrete. Fibers 2023, 11, 20. https://doi.org/10.3390/fib11020020
Sjölander A, Ansell A, Nordström E. On the Design of Permanent Rock Support Using Fibre-Reinforced Shotcrete. Fibers. 2023; 11(2):20. https://doi.org/10.3390/fib11020020
Chicago/Turabian StyleSjölander, Andreas, Anders Ansell, and Erik Nordström. 2023. "On the Design of Permanent Rock Support Using Fibre-Reinforced Shotcrete" Fibers 11, no. 2: 20. https://doi.org/10.3390/fib11020020
APA StyleSjölander, A., Ansell, A., & Nordström, E. (2023). On the Design of Permanent Rock Support Using Fibre-Reinforced Shotcrete. Fibers, 11(2), 20. https://doi.org/10.3390/fib11020020








