Effectiveness of Hybrid Fibers on the Fracture and Shear Behavior of Prestressed Concrete Beams
Abstract
:1. Introduction
2. Research Significance and Objectives
- Understanding the variations in deformation characteristics and failure modes of prestressed concrete beams due to hybrid fibers.
- Studying the influences of different volume fractions of hybrid fibers on crack kinematics, such as crack opening (Uw) and crack slip (Us).
- Analyzing the effects of hybrid fiber reinforcement on fracture energy and the crack arresting mechanism in Mode-I fractures, and the latter’s inter-relation with the shear behavior of prestressed concrete beams.
3. Materials and Methods
4. Results and Discussion
4.1. Fracture Behavior of Hybrid FRC Beams
4.1.1. Residual Flexural Strength Calculations Using RILEM Recommendations
4.1.2. Fracture Energy Calculations Using JCI Provisions
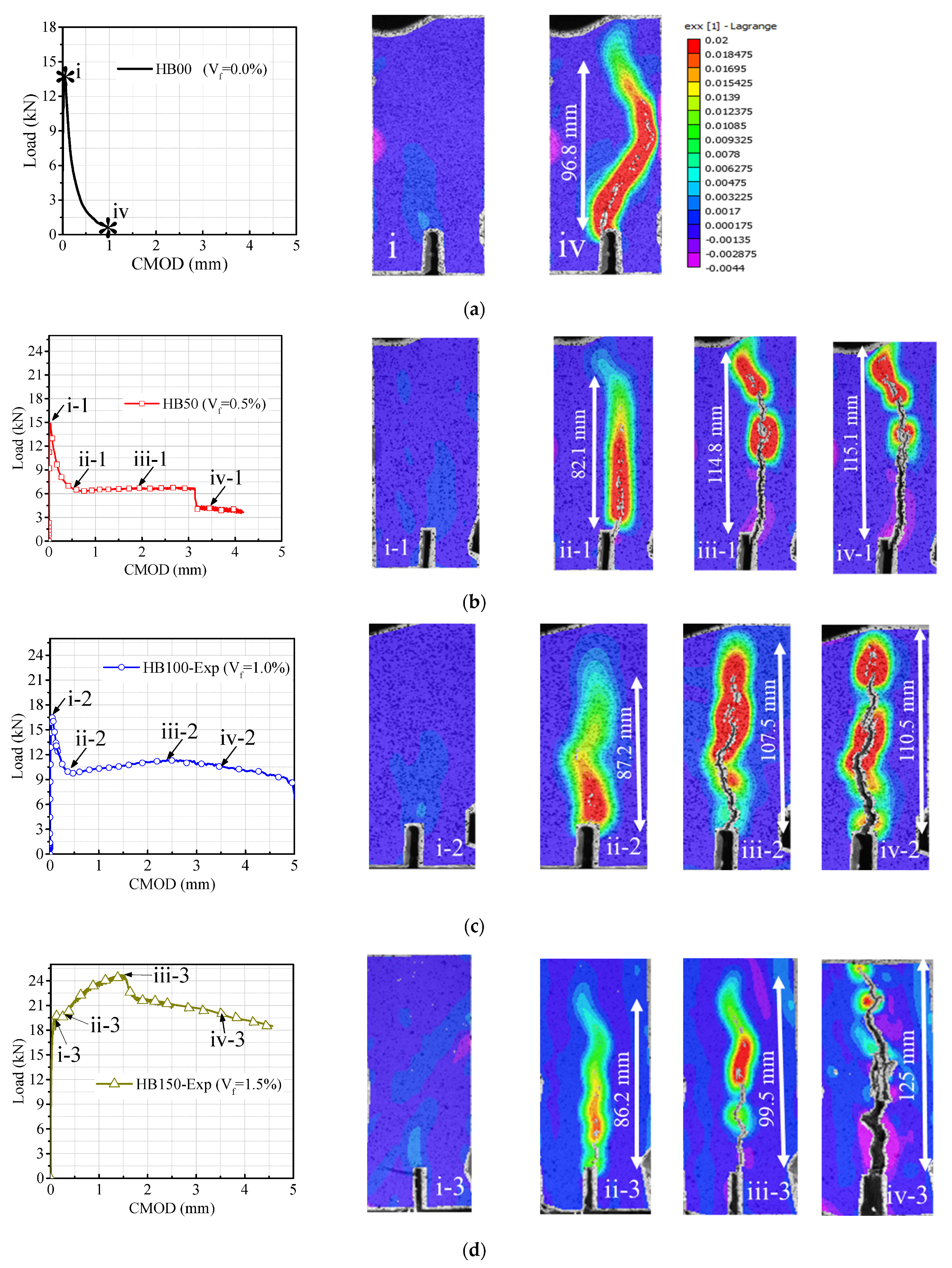
4.1.3. Calibration of Digital Image Correlation (DIC) Results
4.1.4. Evaluation of Crack Arresting Mechanisms of HFRC Prisms Using DIC
4.2. Shear Behavior of HFRC Prestressed Concrete Beams
4.2.1. Test Setup and Instrumentation Details
4.2.2. Load–Deflection Behavior
Control Specimen (HB00)
HB50 Beams
HB100 Beams
HB150 Beams
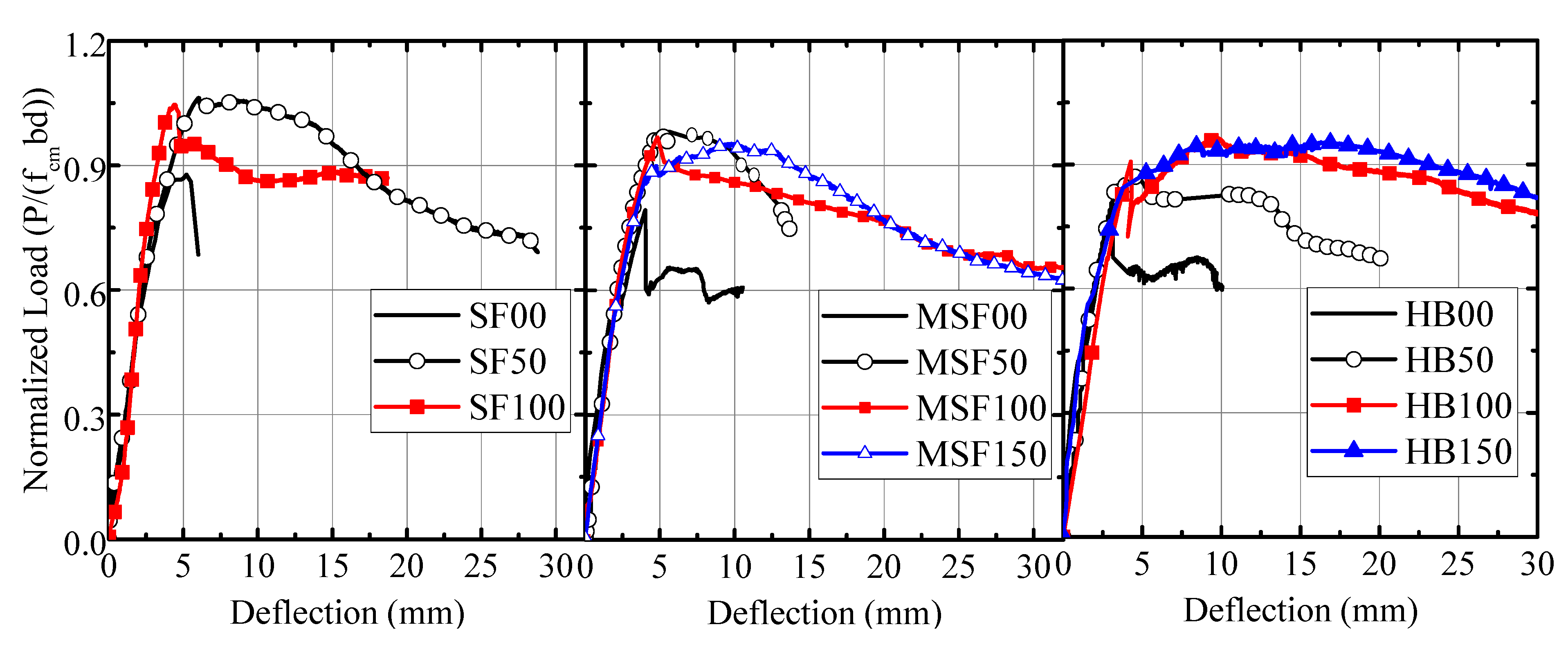
4.2.3. Comparison of Normalized Load–Deflection Behavior of SF, MSF, and HB Beams
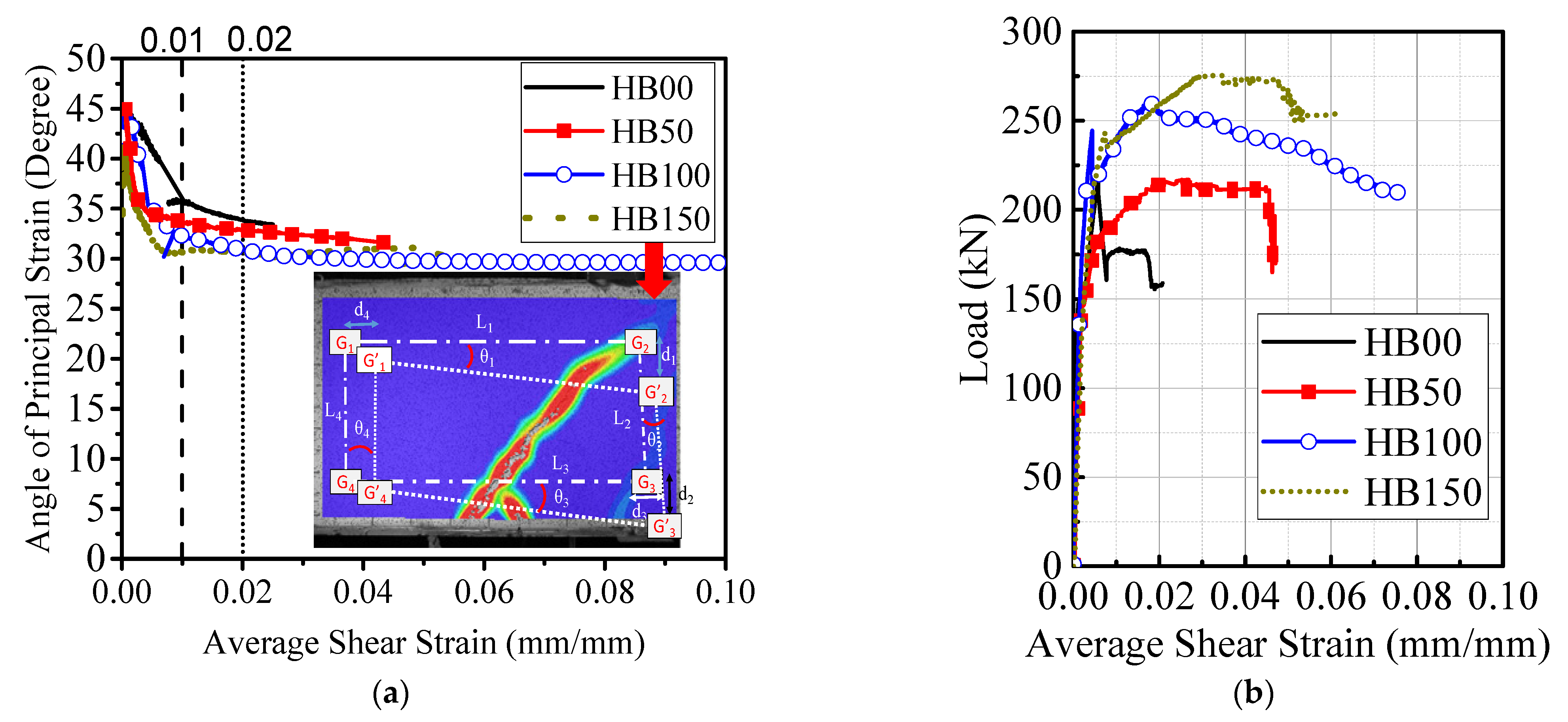
4.2.4. Analysis of Average Shear Strain and Angle of Principal Strain Using DIC
4.2.5. Evaluation of Concrete Principal Strain at Different Load Levels
4.3. Measurement of Shear Parameters from DIC Analysis
4.3.1. Identification of Crack Pattern
4.3.2. Kinematics of Critical Shear Crack
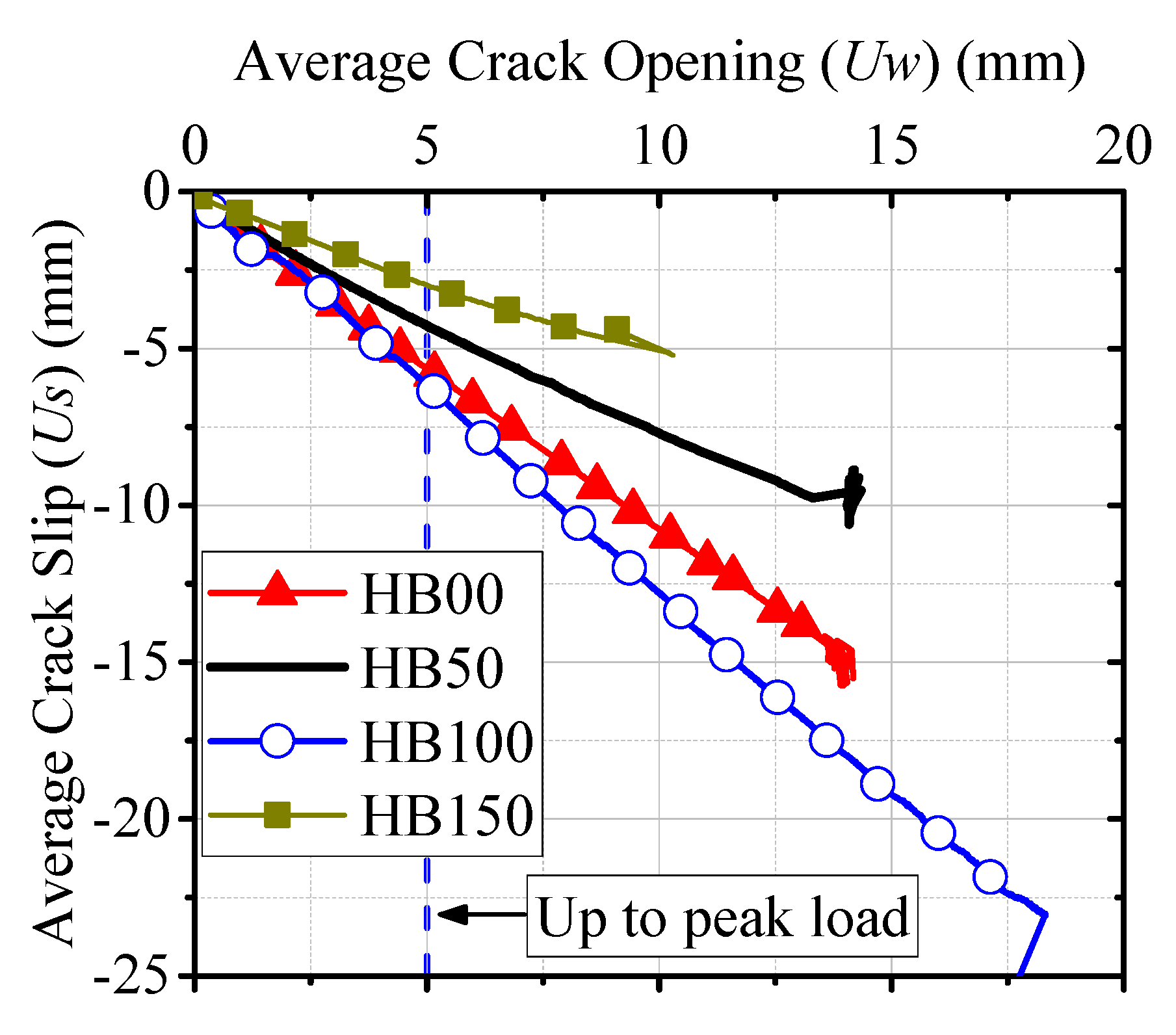
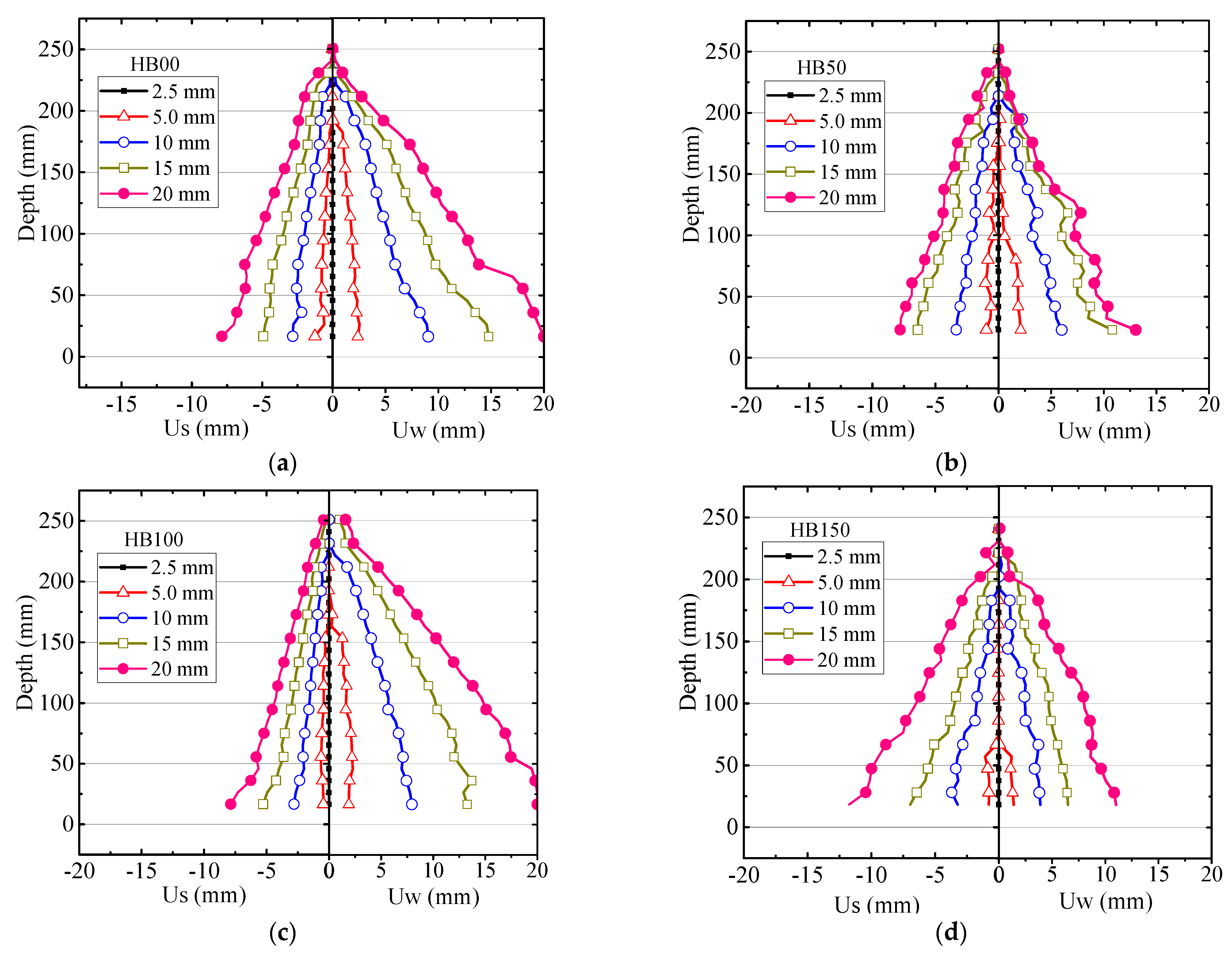
4.3.3. Variations in Crack Opening and Crack Slip across the Depth of Beam
4.4. Shear Capacity Predictions Using Code Provisions
4.4.1. RILEM Provisions
4.4.2. Fib-MC2010 Code Provisions for Shear Capacity
- 1.
- Reinforcement ratio of longitudinal bars (ρl).
- 2.
- Size effect factor (K).
- 3.
- Compressive strength of concrete (fck).
- 4.
- Average stress (σcp) on the cross-section of concrete due to prestressing.
- 5.
- Ultimate residual tensile strength (fFtuk) (Fracture parameter).
- 6.
- The characteristic value of tensile strength of concrete matrix (fctk).
5. Scope for Further Work
6. Conclusions
- Fracture test results of the HFRC prism specimens showed an extended softening response compared to control specimens. Similarly, the residual flexural tensile strengths of hybrid fiber reinforced concrete compared to control concrete were 3.2, 4.7, and 10.35 times for HB50, HB100, and HB150 beams. The measurement of the residual strength of HFRC is critical for shear capacity calculations.
- The comparison of the load–deflection responses of steel, macro-synthetic, and hybrid fiber-reinforced beams shows that the performance of hybrid FRC beams was high. They had good ductility due to their better workability in the fresh state.
- All the tested beams initially cracked from flexure. However, the final failure was because of a critical shear crack forming at an angle of 36°–60° to the longitudinal axis of the member. The failure mode changed from brittle shear to less brittle flexure-shear with an increase in fiber dosage.
- With an increase in fiber volume fraction in HFRPC beams, the crack opening and crack propagation depth in prestressed beams reduced at any specific load point, indicating effective crack bridging action.
- Only a marginal influence of hybrid fibers was observed on the dilatancy behavior up to the peak load. However, hybrid fibers significantly influenced the shear dilatancy response in the post-peak regime from peak load until final failure.
- The experimental to shear capacity predictions using RILEM recommendations vary from 1.6 to 2. However, fib-MC2010 code predictions are 1.5 times those of experimental results. Comparisons indicate that predictions using RILEM are more conservative than the fib-MC2010 provisions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Notations
| Alig | = | Area of the ligament (b × h) | (mm2) |
| As | = | Area of the tension reinforcement extending not less than ‘d + anchorage length’ beyond the section considered | (mm2) |
| b’ | = | Width of the prism specimen | (mm) |
| b | = | Width of the prestressed concrete beam | (mm) |
| bf | = | Width of the flange | (mm) |
| bw | = | Minimum width of the section over the effective depth | (mm) |
| CMODC | = | Crack mouth opening displacement at the time of rupture | (mm) |
| D | = | The effective depth of the prestressed concrete beam | (mm) |
| d1 | = | Vertical displacement of virtual gauge in DIC | (mm) |
| d2 | = | Vertical displacement of virtual gauge in DIC | (mm) |
| Ec | = | Modulus of elasticity of concrete | (MPa) |
| ex | = | Strain in x-direction (ΔL3/L3) | (mm/mm) |
| ey | = | Strain in x-direction (ΔL4/L4) | (mm/mm) |
| EAC | = | The energy absorption capacity of prestressed concrete beam | (Joule) |
| EACc | = | The energy absorption capacity of the prestressed concrete control beam | (Joule) |
| fc’ | = | Average cylinder compressive strength | (MPa) |
| fctk | = | Characteristic tensile strength of concrete | (MPa) |
| fcm | = | Average compressive strength of concrete | (MPa) |
| fFtu | = | The ultimate residual tensile strength at 1.5 mm crack width | (MPa) |
| fctm | = | Mean axial tensile strength of concrete | (MPa) |
| ffctm,fl | = | Mean flexural tensile strength | (MPa) |
| = | jth residual strength | (MPa) | |
| = | Residual flexural strength of FRC at CMOD of 0.5 mm and 3.5 mm respectively | (MPa) | |
| = | Gravitational acceleration (9.807) | (m/s2) | |
| Gf | = | Fracture energy of notched beams | (N/mm) |
| Gfc | = | Fracture energy of notched control beam | (N/mm) |
| hsp | = | Distance between the tip of the notch to the top of cross-section | (mm) |
| k | = | Size effect factor = 1 + ≤ 2.0 | |
| Kh | = | Size factor | - |
| Kf | = | Flange factor for considering flange effect in a T-section | - |
| L | = | The total span of the notched beams for fracture test | (mm) |
| L1 | = | The horizontal displacement of virtual gauges G1-G2 in DIC | (mm) |
| L3 | = | The horizontal displacement of virtual gauges G4-G3 in DIC | (mm) |
| m1 | = | Mass of the specimen | (kg) |
| m2 | = | Mass of the jig not attached to the machine but placed on the specimen until rupture | (kg) |
| Nsd | = | Longitudinal force in the section due to loading or prestressing | (N) |
| S | = | Loading span of the beam used in fracture test | (mm) |
| Tf | = | The toughness of notched beams | (kN-mm) |
| Vcd | = | Concrete contribution in total shear | (kN) |
| VEXP | = | Experimental shear capacity | (kN) |
| Vfd | = | Fibers contribution in total shear | (kN) |
| VRILEM | = | Predicted total shear capacity by RILEM approach | (kN) |
| Vwd | = | The contribution of shear reinforcement due to stirrups and inclined bars | (kN) |
| Vfib | = | Predicted total shear capacity by fib-MC2010 approach | (kN) |
| Wo | = | The area below CMOD curve up to rupture of the specimen | (N-mm) |
| W1 | = | Work done by the dead weight of the specimen and loading jig | (N-mm) |
| xo | = | Distance from support to crack in shear span | (mm) |
| ey | = | Strain in x-direction (ΔL4/L4) | (mm/mm) |
| γxy | = | Shear strain in concrete | (mm/mm) |
| θps | = | The angle of principal strain | (degrees) |
| τfd | = | The design value of the increased shear strain due to steel fibers | (kN) |
References
- Kani, G. How Safe are Our Large Reinforced Concrete Beams? ACI J. Proc. 1967, 64, 128–141. [Google Scholar] [CrossRef]
- Birrcher, D.B.; Tuchscherer, R.G.; Huizinga, M.; Bayrak, O. Minimum Web Reinforcement in Deep Beams. ACI Struct. J. 2013, 110, 297–306. [Google Scholar] [CrossRef]
- Shahnewaz, M.; Alam, M.S. Improved Shear Equations for Steel Fiber-Reinforced Concrete Deep and Slender Beams. ACI Struct. J. 2014, 111, 851–860. [Google Scholar] [CrossRef]
- Mihaylov, B.I.; Liu, J.; Simionopoulos, K.; Bentz, E.C.; Collins, M.P. Effect of Member Size and Tendon Layout on Shear Behavior of Post-Tensioned Beams. ACI Struct. J. 2019, 116, 265–274. [Google Scholar] [CrossRef]
- Isojeh, B.; El-Zeghayar, M.; Vecchio, F.J. Fatigue Resistance of Steel Fiber-Reinforced Concrete Deep Beams. ACI Struct. J. 2017, 114, 1215–1226. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, S.; Bhargava, P. Shear Strength Models for Reinforced Concrete Slender Beams: A Comparative Study. Structures 2018, 16, 119–128. [Google Scholar] [CrossRef]
- Bhosale, A.B.; Lakavath, C.; Prakash, S.S. Multi-linear tensile stress-crack width relationships for hybrid fibre reinforced concrete using inverse analysis and digital image correlation. Eng. Struct. 2020, 225, 111275. [Google Scholar] [CrossRef]
- Karimipour, A.; Ghalehnovi, M. Comparison of the effect of the steel and polypropylene fibres on the flexural behaviour of recycled aggregate concrete beams. Structures 2021, 29, 129–146. [Google Scholar] [CrossRef]
- Sharma, A.; Reddy, G.R.; Varshney, L.; Bharathkumar, H.; Vaze, K.K.; Ghosh, A.K.; Kushwaha, H.S.; Krishnamoorthy, T.S. Experimental investigations on mechanical and radiation shielding properties of hybrid lead–steel fiber reinforced concrete. Nucl. Eng. Des. 2009, 239, 1180–1185. [Google Scholar] [CrossRef]
- Bošnjak, J.; Sharma, A.; Grauf, K. Mechanical Properties of Concrete with Steel and Polypropylene Fibres at Elevated Temperatures. Fibers 2019, 7, 9. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Wang, Q.; Wang, Z. Properties of Polyvinyl Alcohol-Steel Hybrid Fiber-Reinforced Composite with High-Strength Cement Matrix. J. Mater. Civ. Eng. 2017, 29, 04017026. [Google Scholar] [CrossRef]
- Padmarajaiah, S.K.; Ramaswamy, A. Flexural strength predictions of steel fiber reinforced high-strength concrete in fully/partially prestressed beam specimens. Cement Concrete Compos. 2004, 26, 275–290. [Google Scholar] [CrossRef]
- Yoo, D.-Y.; Lee, J.-Y.; Shin, H.-O.; Yang, J.-M.; Yoon, Y.-S. Effects of blast furnace slag and steel fiber on the impact resistance of railway prestressed concrete sleepers. Cement Concrete Compos. 2019, 99, 151–164. [Google Scholar] [CrossRef]
- Vakili, S.E.; Homami, P.; Esfahani, M.R. Effect of fibers and hybrid fibers on the shear strength of lightweight concrete beams reinforced with GFRP bars. Structures 2019, 20, 290–297. [Google Scholar] [CrossRef]
- Patil, G.M.; Suriya Prakash, S. Effect of Macrosynthetic and Hybrid Fibers on the Behavior of Square Concrete Columns Reinforced with GFRP Rebars under Axial Compression. J. Compos. Constr. 2021, 25, 04021053. [Google Scholar] [CrossRef]
- Bhosale, A.; Rasheed, M.A.; Prakash, S.S.; Raju, G. A study on the efficiency of steel vs. synthetic vs. hybrid fibers on fracture behavior of concrete in flexure using acoustic emission. Constr. Build. Mater. 2019, 199, 256–268. [Google Scholar] [CrossRef]
- Curosu, I.; Liebscher, M.; Mechtcherine, V.; Bellmann, C.; Michel, S. Tensile behavior of high-strength strain-hardening cement-based composites (HS-SHCC) made with high-performance polyethylene, aramid and PBO fibers. Cement Concrete Res. 2017, 98, 71–81. [Google Scholar] [CrossRef]
- Bhowmik, S.; Ray, S. An experimental approach for characterization of fracture process zone in concrete. Eng. Fract. Mech. 2019, 211, 401–419. [Google Scholar] [CrossRef]
- Das, S.; Aguayo, M.; Sant, G.; Mobasher, B.; Neithalath, N. Fracture process zone and tensile behavior of blended binders containing limestone powder. Cement Concrete Res. 2015, 73, 51–62. [Google Scholar] [CrossRef]
- Abadel, A.; Abbas, H.; Almusallam, T.; Al-Salloum, Y.; Siddiqui, N. Mechanical properties of hybrid fibre-reinforced concrete—Analytical modelling and experimental behaviour. Mag. Concr. Res. 2016, 68, 823–843. [Google Scholar] [CrossRef]
- Sivakumar, A.; Santhanam, M. Mechanical properties of high strength concrete reinforced with metallic and non-metallic fibres. Cement Concrete Compos. 2007, 29, 603–608. [Google Scholar] [CrossRef]
- Shao, Y.; Billington, S.L. Impact of UHPC Tensile Behavior on Steel Reinforced UHPC Flexural Behavior. J. Struct. Eng. 2022, 148, 04021244. [Google Scholar] [CrossRef]
- Witchukreangkrai, E.; Mutsuyoshi, H.; Takag, M.; De Silva, S. Evaluation of Shear Crack Width in Partially Prestressed Concrete Members. Proc. JCI 2006, 28, 823–828. [Google Scholar]
- Joshi, S.S.; Thammishetti, N.; Prakash, S.S. Efficiency of steel and macro-synthetic structural fibers on the flexure-shear behaviour of prestressed concrete beams. Eng. Struct. 2018, 171, 47–55. [Google Scholar] [CrossRef]
- Sagi, M.S.V.; Lakavath, C.; Prakash, S.S.; Sharma, A. Experimental Study on Evaluation of Replacing Minimum Web Reinforcement with Discrete Fibers in RC Deep Beams. Fibers 2021, 9, 73. [Google Scholar] [CrossRef]
- Zarate Garnica, G. Analysis of Shear Transfer Mechanisms in Concrete Members without Shear Reinforcement Based on Kinematic Measurements; TU Delft: Delft, The Netherlands, 2018. [Google Scholar]
- Gali, S.; Subramaniam, K.V.L. Shear Behavior of Slender and Non-Slender Steel Fiber-Reinforced Concrete Beams. ACI Struct. J. 2019, 116, 149–158. [Google Scholar] [CrossRef]
- Torres, J.A.; Lantsoght, E.O. Influence of Fiber Content on Shear Capacity of Steel Fiber-Reinforced Concrete Beams. Fibers 2019, 7, 102. [Google Scholar] [CrossRef] [Green Version]
- Abambres, M.; Lantsoght, E.O. ANN-Based Shear Capacity of Steel Fiber-Reinforced Concrete Beams without Stirrups. Fibers 2019, 7, 88. [Google Scholar] [CrossRef] [Green Version]
- Lantsoght, E.O.L. Database of Shear Experiments on Steel Fiber Reinforced Concrete Beams without Stirrups. Materials 2019, 12, 917. [Google Scholar] [CrossRef] [Green Version]
- Guerini, V.; Conforti, A.; Plizzari, G.; Kawashima, S. Influence of Steel and Macro-Synthetic Fibers on Concrete Properties. Fibers 2018, 6, 47. [Google Scholar] [CrossRef] [Green Version]
- Lakavath, C.; Joshi, S.S.; Prakash, S.S. Investigation of the effect of steel fibers on the shear crack-opening and crack-slip behavior of prestressed concrete beams using digital image correlation. Eng. Struct. 2019, 193, 28–42. [Google Scholar] [CrossRef]
- Tan, K.H.; Murugappan, K.; Paramasivam, P. Shear Behavior of Steel Fiber Reinforced Concrete Beams. ACI Struct. J. 1993, 90, 176–184. [Google Scholar] [CrossRef]
- Lakavath, C.; Prakash, S.S.; Dirar, S. Experimental and numerical studies on shear behaviour of macro-synthetic fibre reinforced prestressed concrete beams. Constr. Build. Mater. 2021, 291, 123313. [Google Scholar] [CrossRef]
- JCI-S-002-2003; Method of Test for Load-Displacement Curve of Fiber Reinforced Concrete by Use of Notched Beam. Japan Concrete Institute: Tokyo, Japan, 2003; pp. 3–8. Available online: https://www.jci-net.or.jp/j/jci/study/jci_standard/JCI-S-001-2003-e.pdf (accessed on 13 January 2019).
- Test Method for Metallic Fiber Concrete—Measuring the Flexural Tensile Strength (Limit of Proportionality (LOP), Residual); EN 14651:2005+A1:2007; British Standards Institution: London, UK, 2008.
- Gustafsson, P.J.; Hillerborg, A. Sensitivity in Shear Strength of Longitudinally Reinforced Concrete Beams to Fracture Energy of Concrete. ACI Struct. J. 1988, 85, 286–294. [Google Scholar]
- Foster, S.J.; Agarwal, A.; Amin, A. Design of steel fiber reinforced concrete beams for shear using inverse analysis for determination of residual tensile strength. Struct. Concr. 2018, 19, 129–140. [Google Scholar] [CrossRef]
- Sahoo, S.; Lakavath, C.; Prakash, S.S. Experimental and Analytical Studies on Fracture Behavior of Fiber-Reinforced Structural Lightweight Aggregate Concrete. J. Mater. Civ. Eng. 2021, 33, 04021074. [Google Scholar] [CrossRef]
- Rilem Tc 162-Tdf: Test and design methods for steel fibre reinforced concrete. Mater. Struct. 2003, 36, 560–567. [CrossRef]
- JCI-S-001-2003; Method of Test for Fracture Energy of Concrete by Use of Notched Beam. Japan Concrete Institute: Tokyo, Japan, 2003; Volume 2, pp. 1–14.
- Enfedaque, A.; Alberti, M.G.; Galvez, J. Influence of Fiber Distribution and Orientation in the Fracture Behavior of Polyolefin Fiber-Reinforced Concrete. Materials 2019, 12, 220. [Google Scholar] [CrossRef] [Green Version]
- Kang, S.-T.; Kim, J.-K. The relation between fiber orientation and tensile behavior in an Ultra High Performance Fiber Reinforced Cementitious Composites (UHPFRCC). Cement Concrete Res. 2011, 41, 1001–1014. [Google Scholar] [CrossRef]
- Laranjeira, F.; Aguado, A.; Molins, C.; Grünewald, S.; Walraven, J.; Cavalaro, S. Framework to predict the orientation of fibers in FRC: A novel philosophy. Cement Concrete Res. 2012, 42, 752–768. [Google Scholar] [CrossRef]
- Abrishambaf, A.; Pimentel, M.; Nunes, S. Influence of fibre orientation on the tensile behaviour of ultra-high performance fibre reinforced cementitious composites. Cement Concrete Res. 2017, 97, 28–40. [Google Scholar] [CrossRef]
- Yang, T.; Dashlejeh, A.A.; Arabzadeh, A.; Hizaji, R. New model for prediction of ultimate load of prestressed RC deep beams. Structures 2020, 23, 509–517. [Google Scholar] [CrossRef]
- Ramirez-Garcia, A.T.; Floyd, R.W.; Hale, W.M.; Martí-Vargas, J. Effect of concrete compressive strength on transfer length. Structures 2016, 5, 131–140. [Google Scholar] [CrossRef]
- Kani, G.N.J. Basic Facts Concerning Shear Failure. ACI J. Proc. 1966, 63, 675–692. [Google Scholar] [CrossRef]
- Juárez, C.; Valdez-Tamez, P.L.; Durán, A.; Sobolev, K. The diagonal tension behavior of fiber reinforced concrete beams. Cement Concrete Compos. 2007, 29, 402–408. [Google Scholar] [CrossRef]
- Amin, A.; Foster, S. Shear strength of steel fibre reinforced concrete beams with stirrups. Eng. Struct. 2016, 111, 323–332. [Google Scholar] [CrossRef]
- Perceka, W.; Liao, W.-C.; Wu, Y.-F. Shear Strength Prediction Equations and Experimental Study of High Strength Steel Fiber-Reinforced Concrete Beams with Different Shear Span-to-Depth Ratios. Appl. Sci. 2019, 9, 4790. [Google Scholar] [CrossRef] [Green Version]
- Hwang, J.-H.; Lee, D.H.; Ju, H.; Kim, K.S.; Kang, T.H.-K.; Pan, Z. Shear Deformation of Steel Fiber-Reinforced Prestressed Concrete Beams. Int. J. Concr. Struct. Mater. 2016, 10, 53–63. [Google Scholar] [CrossRef] [Green Version]
- Tadepalli, P.R.; Hoffman, N.; Hsu, T.T.; Mo, Y.L. Steel Fiber Replacement of Mild Steel in Prestressed Concrete Beams (No. FHWA/TX-09/0-5255-2); University of Houston: Houston, TX, USA, 2011. [Google Scholar]
- Vecchio, F.J.; Collins, M.P. Modified Compression-Field Theory for Reinforced Concrete Elements Subjected To Shear. J. Am. Concr. Inst. 1986, 83, 219–231. [Google Scholar] [CrossRef]
- Khan, M.A.; Ahmed, F.S. Effect of Web Reinforcement On Ultimate Strength Of Reinforced Concrete Deep Beams. ACI Struct. J. 1997, 94, 572–581. [Google Scholar]
- Smith, K.N.; Vantsiotis, A.S. Shear Strength of Deep Beams. J. Am. Concr. Inst. 1982, 79, 201–213. [Google Scholar] [CrossRef]
- Adebar, P.; Van Leeuwen, J. Side-Face Reinforcement for Flexural and Diagonal Cracking in Large Concrete Beams. ACI Struct. J. 1999, 96, 693–704. [Google Scholar] [CrossRef]
- Susanto, T.; Ma, W.; Fang, W. Shear strength of high-strength concrete deep beams under Fatigue Loading. ACI Struct. J. 2000, 97, 572–580. [Google Scholar]
- Sahoo, D.R.; Bhagat, S.; Reddy, T.C.V. Experimental study on shear-span to effective-depth ratio of steel fiber reinforced concrete T-beams. Mater. Struct. Constr. 2016, 49, 3815–3830. [Google Scholar] [CrossRef]
- Devalapura, R.K.; Tadros, M.K. Stress-Strain Modeling of 270 ksi Low-Relaxation Prestressing Strands. PCI J. 1992, 37, 100–106. [Google Scholar] [CrossRef]
- Model Code 2010-First Complete Draft-Volume 2: Model Code; Fédération Internationale du Béton (fib): Lausanne, Switzerland, 2010; Volume 56, ISBN 964-7445-88-1.
- Alberti, M.; Enfedaque, A.; Gálvez, J. On the prediction of the orientation factor and fibre distribution of steel and macro-synthetic fibres for fibre-reinforced concrete. Cement Concrete Compos. 2017, 77, 29–48. [Google Scholar] [CrossRef]
- Mudadu, A.; Tiberti, G.; Germano, F.; Plizzari, G.A.; Morbi, A. The effect of fiber orientation on the post-cracking behavior of steel fiber reinforced concrete under bending and uniaxial tensile tests. Cement Concrete Compos. 2018, 93, 274–288. [Google Scholar] [CrossRef]
- Reddy, K.C.; Subramaniam, K. Analysis for multi-linear stress-crack opening cohesive relationship: Application to macro-synthetic fiber reinforced concrete. Eng. Fract. Mech. 2017, 169, 128–145. [Google Scholar] [CrossRef]
- Stephen, S.J.; Raphael, B.; Gettu, R.; Jose, S. Determination of the tensile constitutive relations of fiber reinforced concrete using inverse analysis. Constr. Build. Mater. 2019, 195, 405–414. [Google Scholar] [CrossRef]
- Kaufmann, W.; Amin, A.; Beck, A.; Lee, M. Shear transfer across cracks in steel fibre reinforced concrete. Eng. Struct. 2019, 186, 508–524. [Google Scholar] [CrossRef]
- El-Helou, R.G.; Graybeal, B.A. Shear Behavior of Ultrahigh-Performance Concrete Pretensioned Bridge Girders. J. Struct. Eng. 2022, 148, 04022017. [Google Scholar] [CrossRef]
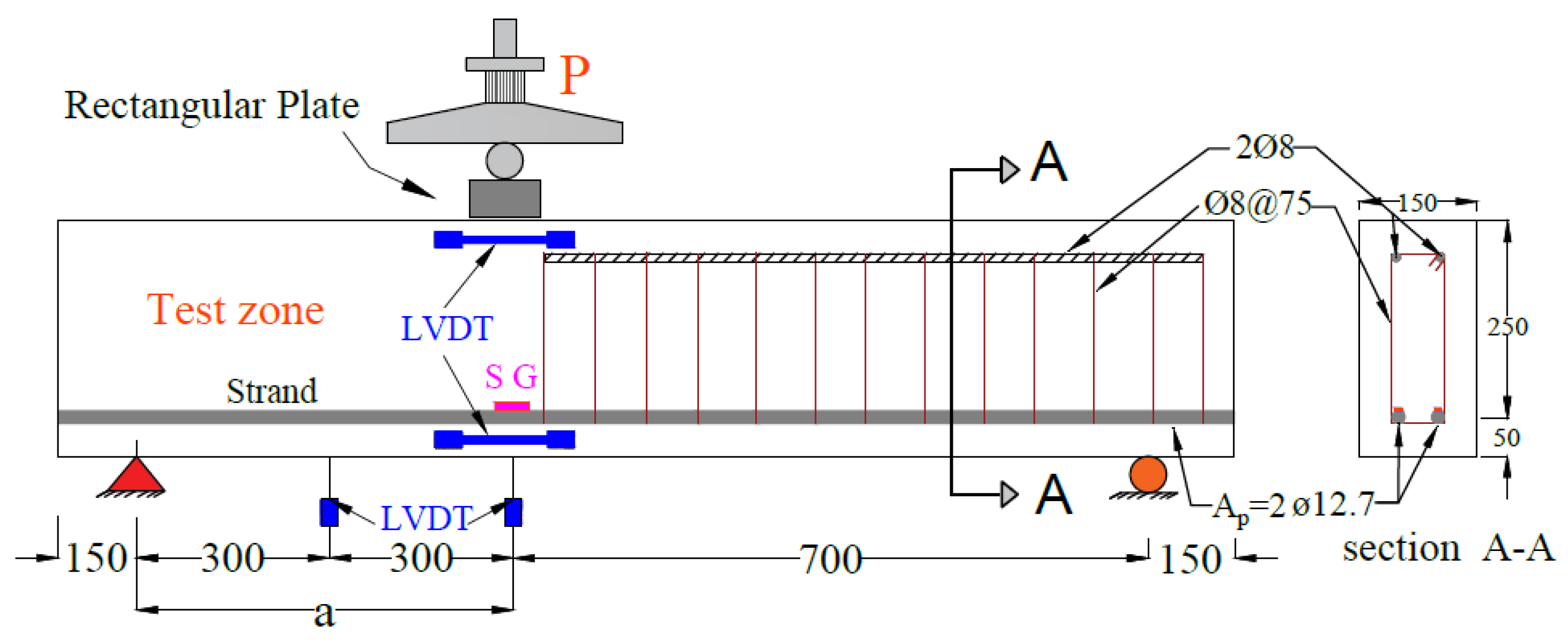
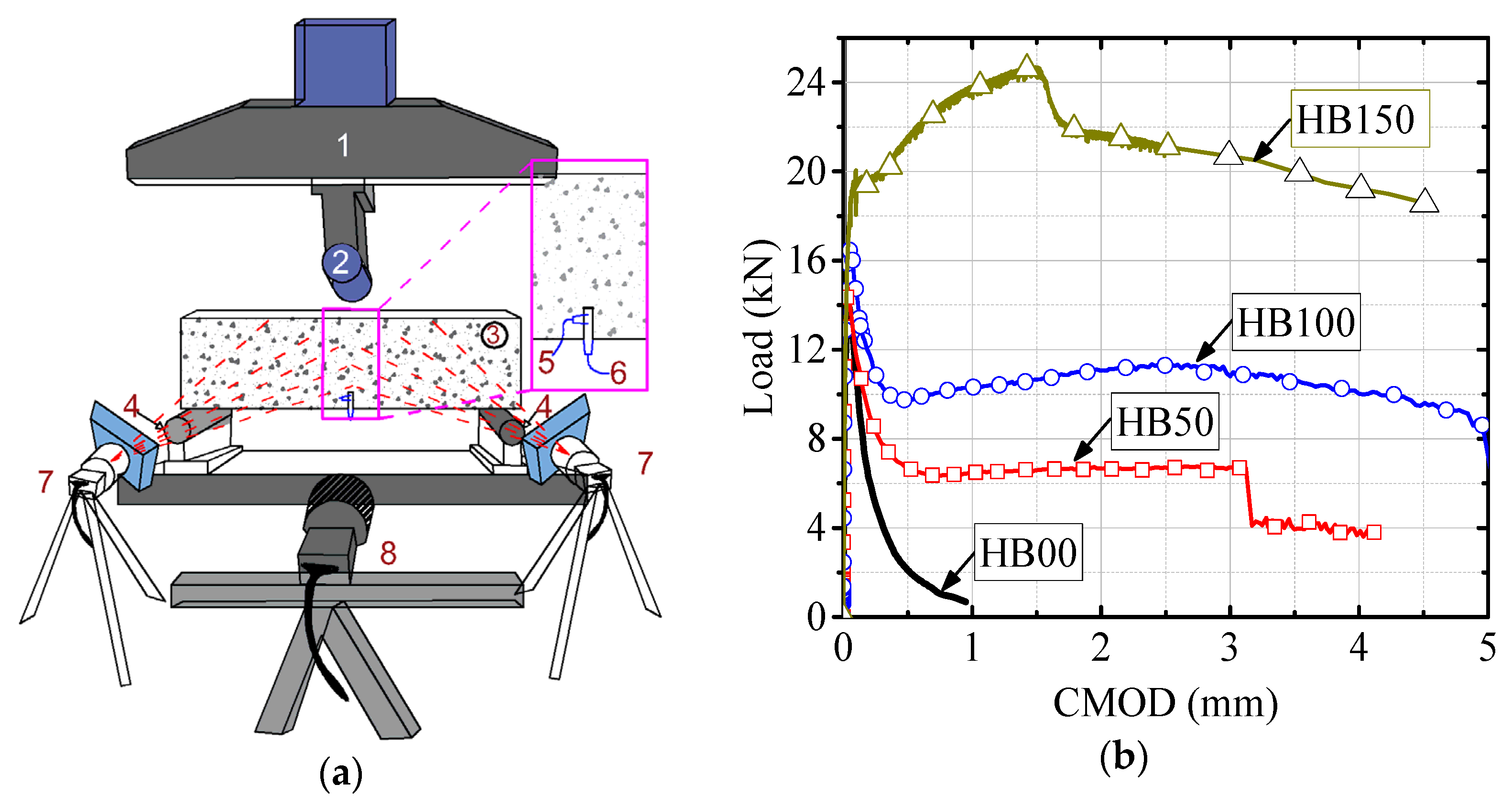
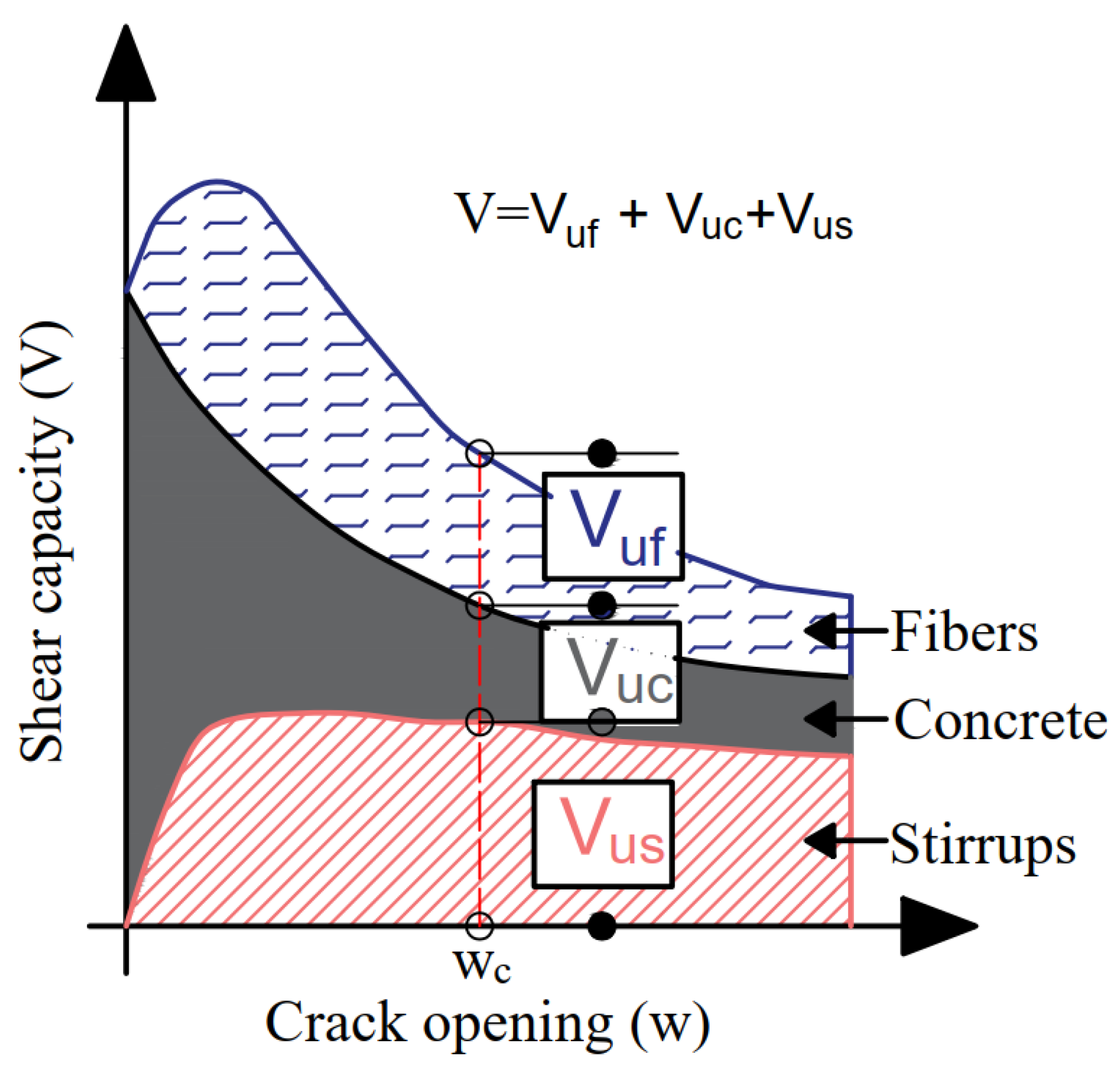
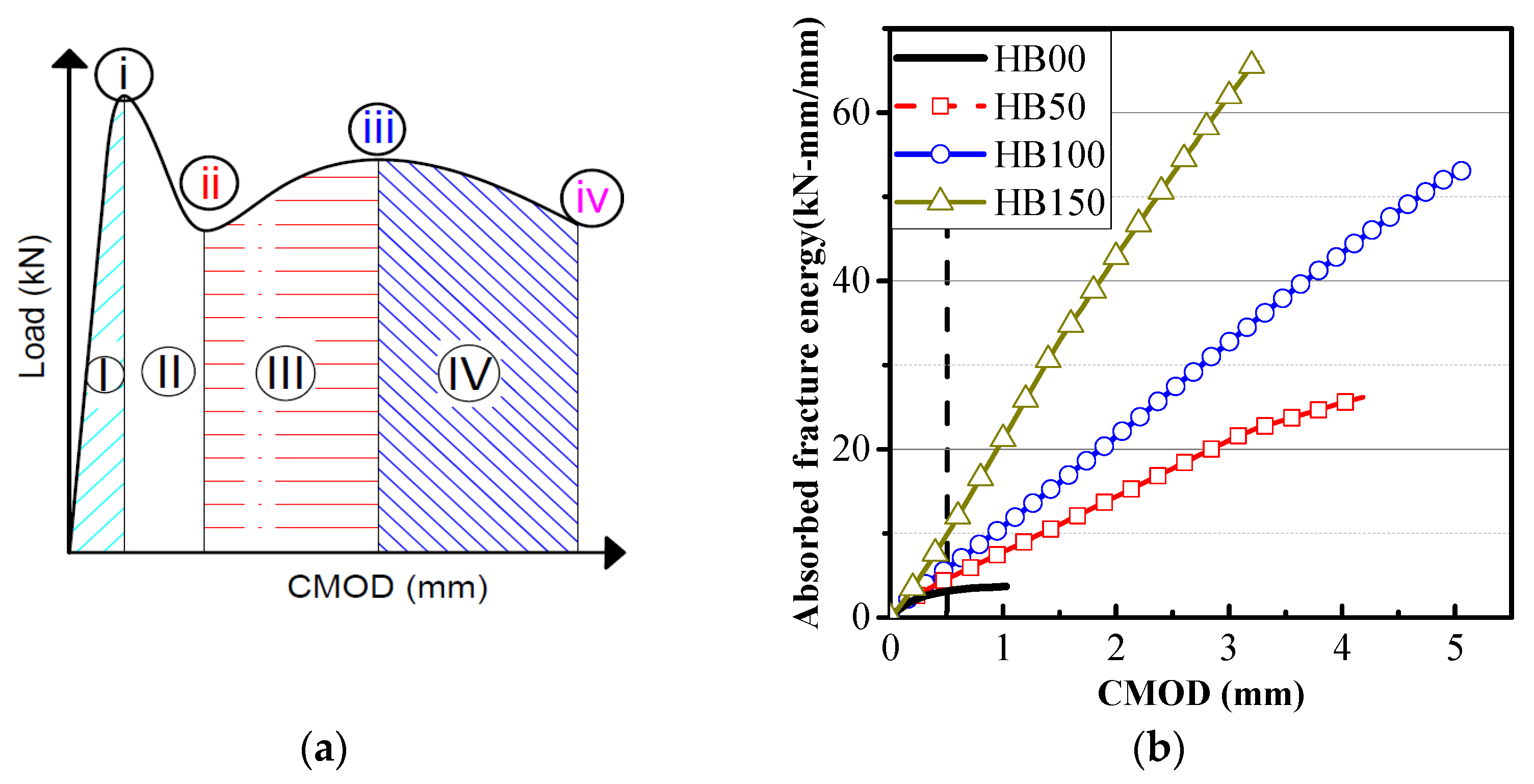




| Specimen |  Steel Fiber (SF) |  Macro-Synthetic Fiber (MSF) | Prestressing Strand |
|---|---|---|---|
| Specific gravity | 7.85 | 0.91 | 7.85 |
| Length (mm) | 30 | 50 | - |
| Diameter (mm) | 0.60 | 0.50 | 12.70 |
| Aspect ratio | 50 | 100 | - |
| Specified tensile strength (MPa) | 1000 | 618 | 1860.00 |
| Specified Modulus of elasticity (GPa) | 200 | 10 | 196.50 |
| Mix ID | C | CSS | NRS | SP | Water | CA | Hybrid Fiber Combination | ||
|---|---|---|---|---|---|---|---|---|---|
| 20 mm | 10 mm | SF | PO | ||||||
| HB00 | 450 | 415 | 312 | 2.6 | 152 | 755 | 355 | 0 | 0 |
| HB50 | 450 | 415 | 312 | 2.6 | 152 | 755 | 355 | 19.65 | 2.27 |
| HB100 | 450 | 415 | 312 | 2.6 | 152 | 755 | 355 | 39.25 | 4.55 |
| HB150 | 450 | 415 | 312 | 2.6 | 152 | 755 | 355 | 58.87 | 2.27 |
| Mix ID | fcm (S.D) | Residual Flexural Tensile Strength (MPa) | Total Fracture Energy Gf (N/mm) | Toughness Tf × 10−3 (kN-mm) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| fR1 | fR3 | fR4 | I | II | III | IV | Total (Tf) | ||||
| HB00 | 45.30 (1.73) | 0.60 | - | - | 0.156 | 1.00 | 0.53 | 3.14 | - | - | 3.67 |
| HB50 | 47.21 (1.52) | 1.93 | 1.93 | 1.15 | 0.976 | 6.25 | 0.35 | 6.29 | 13.36 | 3.59 | 23.60 |
| HB100 | 51.70 (1.63) | 2.81 | 3.26 | 3.09 | 1.484 | 9.51 | 0.78 | 5.19 | 22.21 | 10.25 | 38.43 |
| HB150 | 56.12 (1.80) | 6.21 | 6.07 | 5.76 | 3.063 | 19.63 | 1.58 | 4.51 | 27.52 | 42.10 | 75.70 |
| HB00-1 | HB50-1 | HB50-2 | HB100-1 | HB100-2 | HB150-1 | HB150-2 | |
|---|---|---|---|---|---|---|---|
| Flexure Cracking Load (kN) | 150.4 | 145.8 | 143.5 | 150.4 | 150.8 | 150.9 | 153.7 |
| Deflection at Flexure Cracking Load (mm) | 2.30 | 1.51 | 1.65 | 2.26 | 2.20 | 1.65 | 1.73 |
| Shear Crack Load (kN) | 178.3 | 148.5 | 150.3 | 204.8 | 207.1 | 217.8 | 153.7 |
| Deflection at Shear Crack Load (mm) | 2.96 | 1.70 | 1.73 | 3.30 | 3.11 | 1.65 | 1.73 |
| Peak Load (kN) | 215.9 | 216.9 | 224.4 | 260.6 | 276.9 | 275.5 | 268.1 |
| Deflection at Peak Load (mm) | 4.01 | 9.61 | 4.77 | 9.66 | 6.79 | 13.35 | 16.65 |
| Ultimate Load (0.8× Peak Load) (kN) | 172.7 | 173.5 | 179.6 | 208.5 | 221.5 | 220.4 | 214.57 |
| Deflection at Ultimate Load (mm) | 5.19 | 20.80 | 17.74 | 30.71 | 12.72 | 31.05 | 35.52 |
| % increase in peak load compared to HB00, ∆P (%) | 0 | 0.5 | 3.9 | 20.7 | 28.3 | 27.6 | 24.2 |
| Post-peak stiffness in load–deflection curve from peak load to ultimate load, K′ (kN/mm) | −36.6 | −3.9 | −3.5 | −2.5 | −9.3 | −3.1 | −2.8 |
| % increase in post-peak stiffness, ∆K′ (%) | 0 | 89.4 | 90.4 | 93.2 | 74.6 | 91.5 | 92.3 |
| Energy absorption capacity, EAC (Joules) | 643 | 3931 | 3371 | 6828 | 3667 | 7862 | 8509 |
| 1 | 6.1 | 5.3 | 10.6 | 6.0 | 12.2 | 13.2 | |
| Crack failure angle, θ° | 40.8° | 42.8° | 39.2° | 35.9° | 40.4° | 59.3° | 56.7° |
| Failure Mode | DST | DST | DST | DST | DST | DST | DST |
| Beam ID | VEXP kN | Vcd kN | Vfd kN | VRILEM kN | VEXP/VRILEM | Vfib-MC2010 | VEXP/Vfib-MC2010 |
|---|---|---|---|---|---|---|---|
| HB00 | 215.9 | 109.0 | 0 | 109.0 | 1.9 | 136.8 | 1.5 |
| HB50 | 220.6 | 109.0 | 12.8 | 121.6 | 1.8 | 156.0 | 1.4 |
| HB100 | 268.7 | 109.0 | 34.0 | 142.8 | 1.8 | 165.8 | 1.6 |
| HB150 | 271.8 | 109.0 | 63.8 | 172.73 | 1.6 | 183.5 | 1.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lakavath, C.; Bhosale, A.B.; Prakash, S.S.; Sharma, A. Effectiveness of Hybrid Fibers on the Fracture and Shear Behavior of Prestressed Concrete Beams. Fibers 2022, 10, 26. https://doi.org/10.3390/fib10030026
Lakavath C, Bhosale AB, Prakash SS, Sharma A. Effectiveness of Hybrid Fibers on the Fracture and Shear Behavior of Prestressed Concrete Beams. Fibers. 2022; 10(3):26. https://doi.org/10.3390/fib10030026
Chicago/Turabian StyleLakavath, Chandrashekhar, Aniket B. Bhosale, S. Suriya Prakash, and Akanshu Sharma. 2022. "Effectiveness of Hybrid Fibers on the Fracture and Shear Behavior of Prestressed Concrete Beams" Fibers 10, no. 3: 26. https://doi.org/10.3390/fib10030026
APA StyleLakavath, C., Bhosale, A. B., Prakash, S. S., & Sharma, A. (2022). Effectiveness of Hybrid Fibers on the Fracture and Shear Behavior of Prestressed Concrete Beams. Fibers, 10(3), 26. https://doi.org/10.3390/fib10030026








