Study of Birefringence and Stress Distribution of SiO2 Film Optical Waveguide on Silicon Wafer
Abstract
:1. Introduction
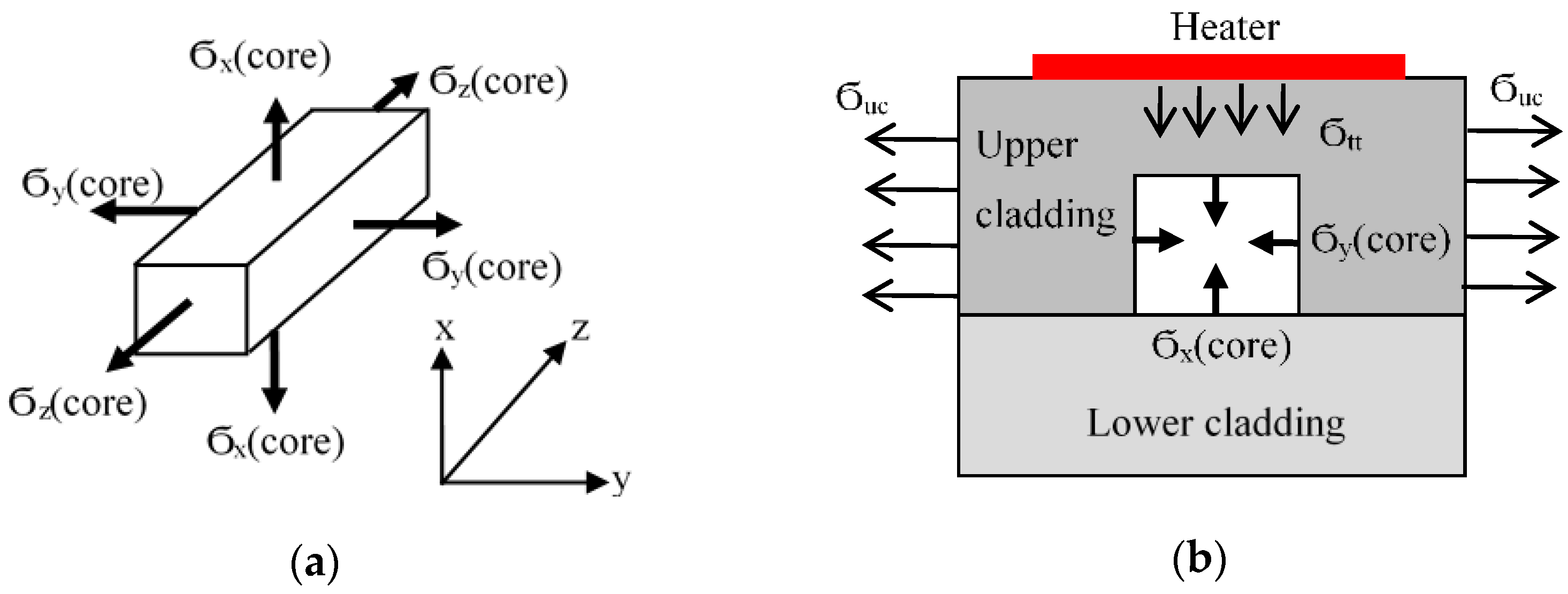
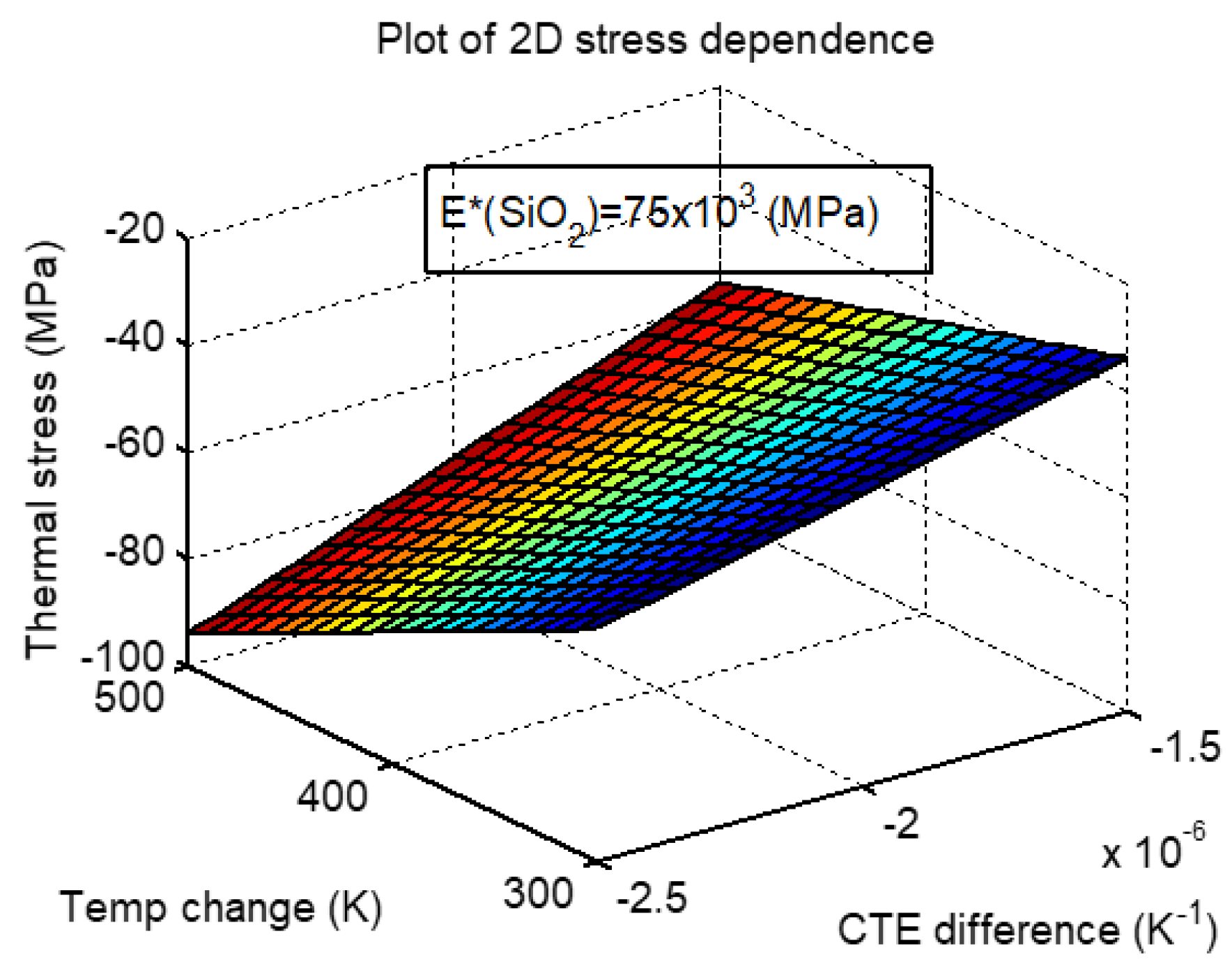
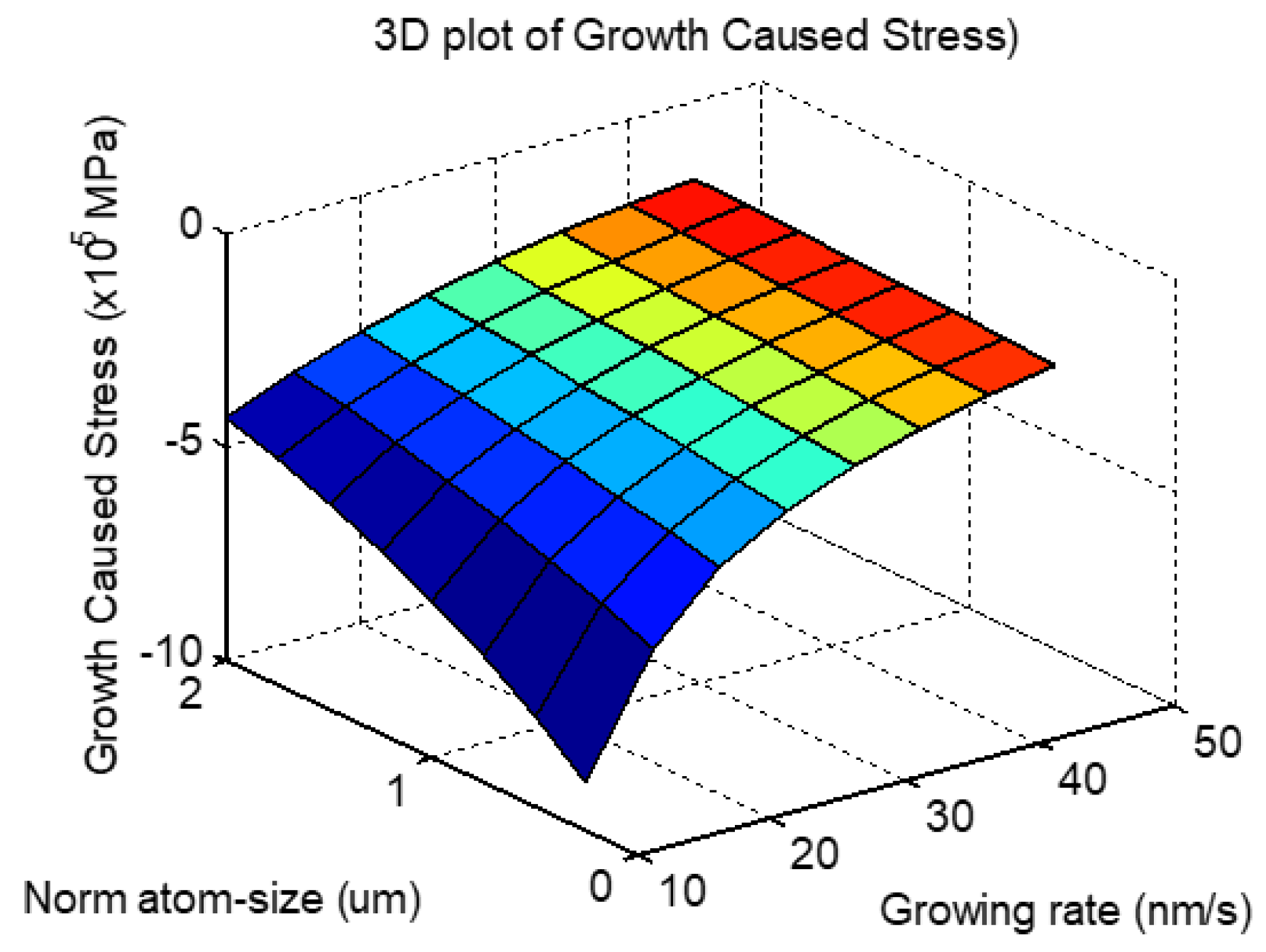
2. Theoretical Model
3. Results and Discussion
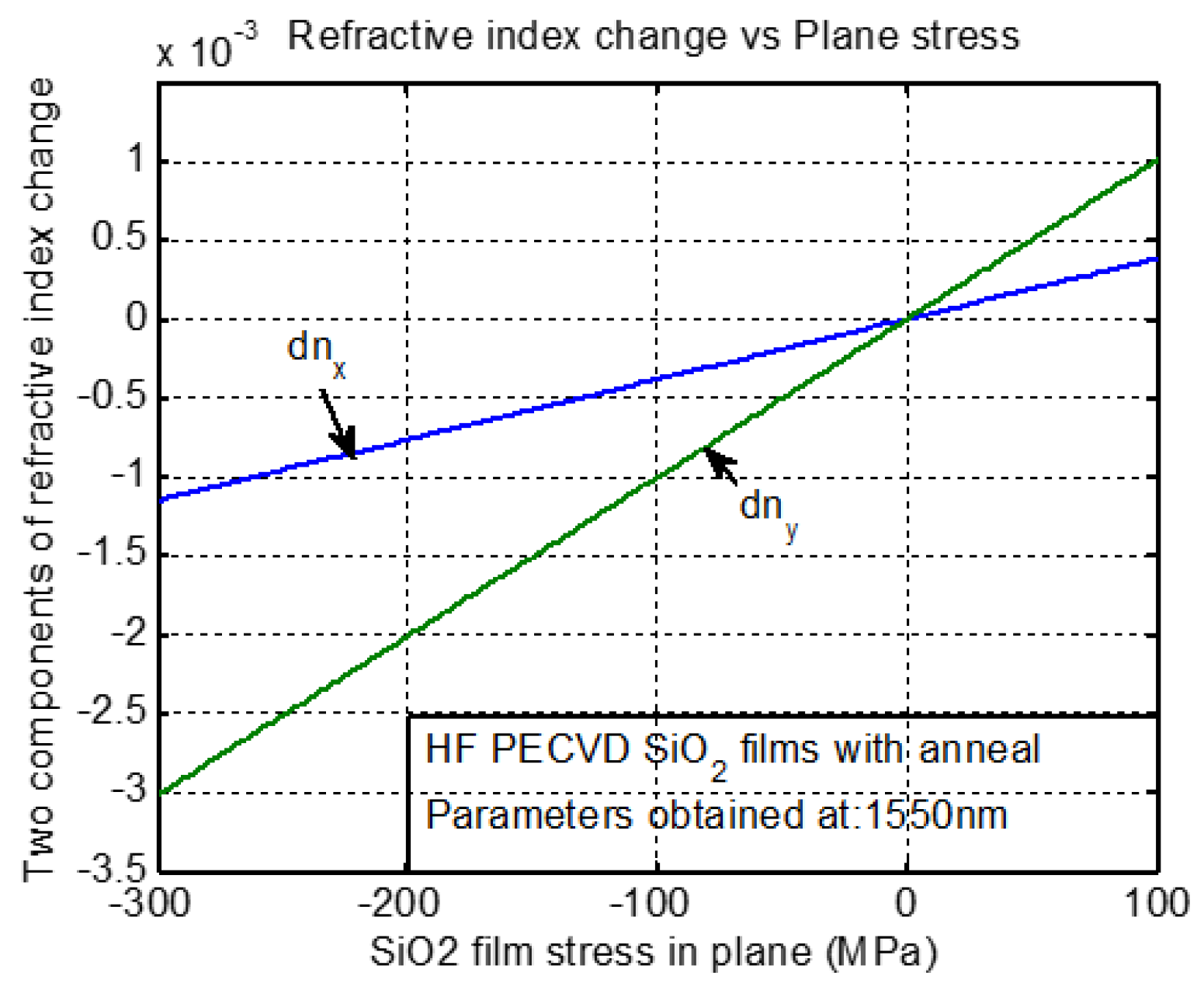
3.1. Numerical Calculations
3.2. Experimental Measurements
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Doerr, C.R.; Okamoto, K. Optical Fiber Telecommunications V A; Academic Press/Elsevier: New York, NY, USA, 2008; pp. 269–341. [Google Scholar]
- Wu, X.P.; Liu, W.; Yuan, Z.L.; Liang, X.R.; Chen, H.; Xu, X.H.; Tang, F.F. Low power consumption VOA array with air trenches and curved waveguide. IEEE Photon. J. 2018, 10, 7201308. [Google Scholar] [CrossRef]
- Wang, J.; Yi, J.; Guo, L.J.; Liu, P.; Hall, T.J.; Sun, D.G. Improved silica-PLC MZI type optical switches with error dependence compensation of directional coupler. Opt. Las Technol. 2017, 89, 208–213. [Google Scholar] [CrossRef]
- Okamoto, K. Planar Lightwave Circuits (PLCs). In Fundamentals of Optical Waveguides, 1st ed.; Academic Press: New York, NY, USA, 2000; pp. 341–400. [Google Scholar]
- Tomlinson, W. Evolution of passive optical component technologies for fiber-optic communication systems. J. Lightwave Technol. 2008, 26, 1046–1063. [Google Scholar] [CrossRef]
- Takato, N.; Jinguiji, K.; Yasu, M.; Toba, H.; Kawachi, M. Silica-based single-mode waveguides on silicon and their application to guided-wave optical interferometers. J. Lightwave Technol. 1988, 6, 1003–1010. [Google Scholar] [CrossRef]
- Huang, M. Analytical solutions for thermal stress in buried channel waveguides on silicon and their application to guided-wave optical interferometers. IEEE J. Quantum Electron. 2004, 40, 1562–1568. [Google Scholar] [CrossRef]
- Guan, D.; Bruccoleri, A.R.; Heilmann, R.K.; Schattenburg, M.L. Stress control of plasma enhanced chemical vapor deposited silicon dioxide from tetraethoxysilane. J. Micfromech. Microeng. 2013, 24, 027001. [Google Scholar] [CrossRef]
- Wu, F.; Lagally, M.G. Ge-induced reversal of surface stress anisotropy on Si (001). Phys. Rev. Lett. 1995, 75, 2534–2537. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Wolf, I.D. Study of damage and stress induced by backgrinding in Si wafers. Semicond. Sci. Technol. 2003, 18, 261–268. [Google Scholar] [CrossRef]
- Yao, Y.W.; Chalifoux, B.D.; Heilmann, R.K.; Schattenburg, M.L. Thermal oxide patterning method for compensating coating stress in silicon substrates. Opt. Express. 2019, 27, 1010–1025. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.S.; Zhang, X.; Lin, S.Y. Intrinsic stress generation and relaxation deposited oxide during deposition and subsequent thermal cycling. Thin Solid Films. 2003, 434, 190–202. [Google Scholar] [CrossRef]
- Chason, E.; Shin, J.W.; Hearne, S.J.; Freund, L.B. Kinetic model for dependence of thin film stress on growth rate, temperature, and microstructure. J. Appl. Phys. 2012, 111, 083520. [Google Scholar] [CrossRef]
- Sun, D.G.; Sun, Q.Y.; Xing, W.C.; Sun, Z.Y.; Shang, H.P.; Chang, L.Y.; Wang, X.P.; Liu, P.; Hall, T.J. Investigation for the structural stress of SiO2 thin films and its distribution on the large-wafer created by plasma enhanced chemical vapor deposition. AIP Adv. 2018, 8, 085217. [Google Scholar] [CrossRef]
- Watanabe, K.; Kasahama, R.; Hashizume, Y. Extremely-low-power-consumption Thermo-optic Switch with silicon-silica hybrid structure. NTT Technol. Rev. 2010, 8, 1–5. [Google Scholar]
- Morinaki, O.; Noguchi, K.; Takahashi, H.; Sakamoto, T.; Sato, K.I.; Hasegawa, H.; Okuno, M.; Ohmori, Y. Multihop signal transmission experiments employing PLC-based hierarchical optical cross-connect system. IEEE Photon. Technol. Lett. 2010, 22, 1586–1588. [Google Scholar] [CrossRef]
- Watanabe, T.; Suzuki, K.; Takahashi, T. Silica-based PLC transponder aggregators for colorless, directionless, and contentionless ROADM. In Proceedings of the Optical Fiber Communication Conference & Exposition, OSA Technical Digest (OSA, 2012), LA, CA, USA, 4–8 March 2012. Paper OTh3D.1. [Google Scholar]
- Choi, J.K.; Lee, J.; Yoo, J.B.; Maeng, J.S.; Kim, Y.M. Residual stress analysis of SiO2 films deposited by plasma-enhanced chemical vapor deposition. Surf. Coat. Technol. 2000, 131, 153–157. [Google Scholar] [CrossRef]
- Okuno, M.; Sugita, A.; Jinguli, K.; Kawachi, M. Birefringence control of silica waveguides on Si and its application to polarization beam splitter/switch. J. Lightwave Technol. 1994, 12, 625–633. [Google Scholar] [CrossRef]
- Zhao, X.; Xu, Y.Z.; Li, C. Birefringence control in optical planar waveguides. J. Lightwave Technol. 2003, 21, 2352–2356. [Google Scholar] [CrossRef]
- Ye, W.N.; Xu, D.X.; Janz, S.; Cheben, P.; Picard, M.J.; Lamontagne, B.; Tarr, N.G. Birefringence control using stress engineering in silicon-on-insulator (SOI) waveguides. J. Lightwave Technol. 2005, 23, 1308–1318. [Google Scholar] [CrossRef]
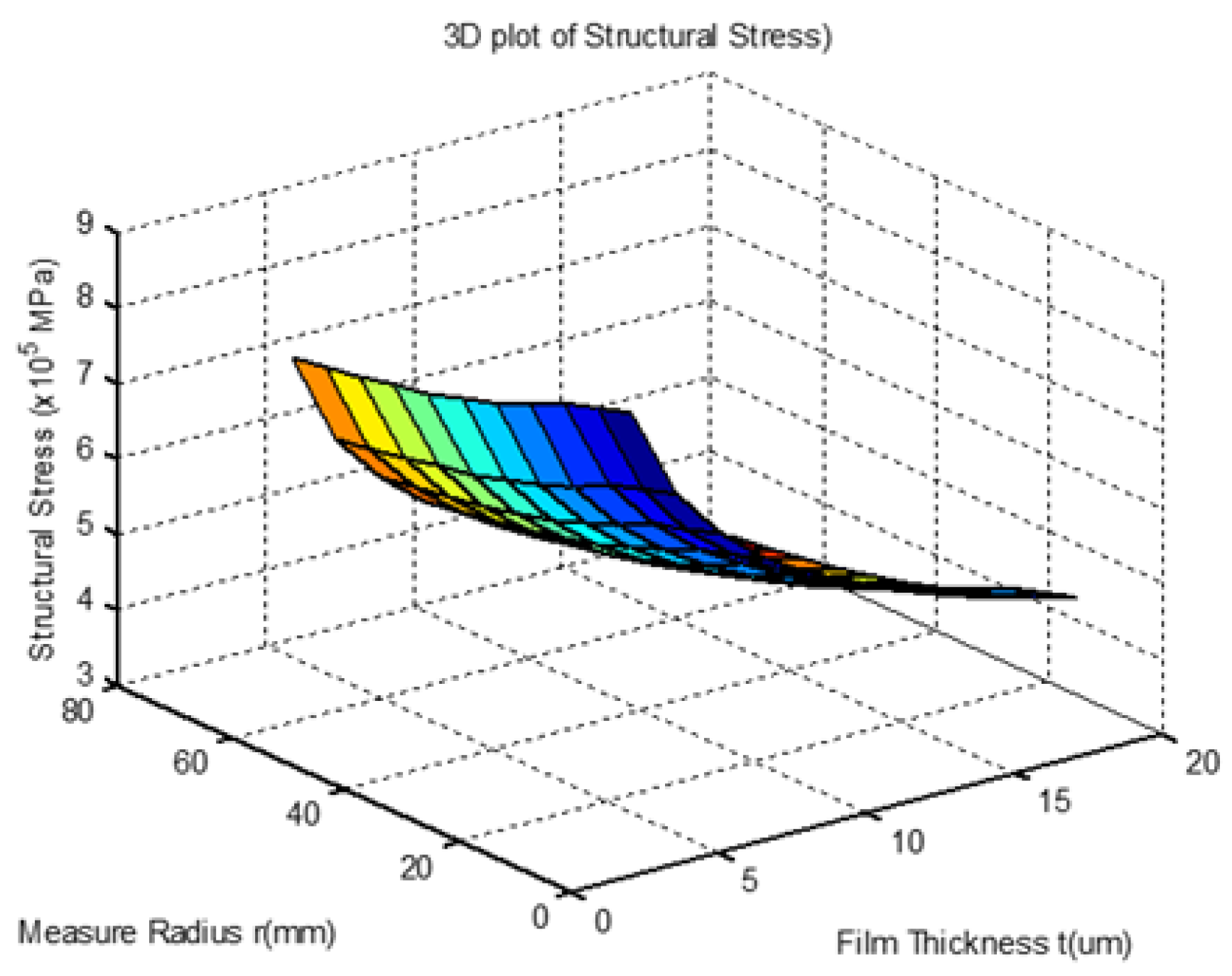
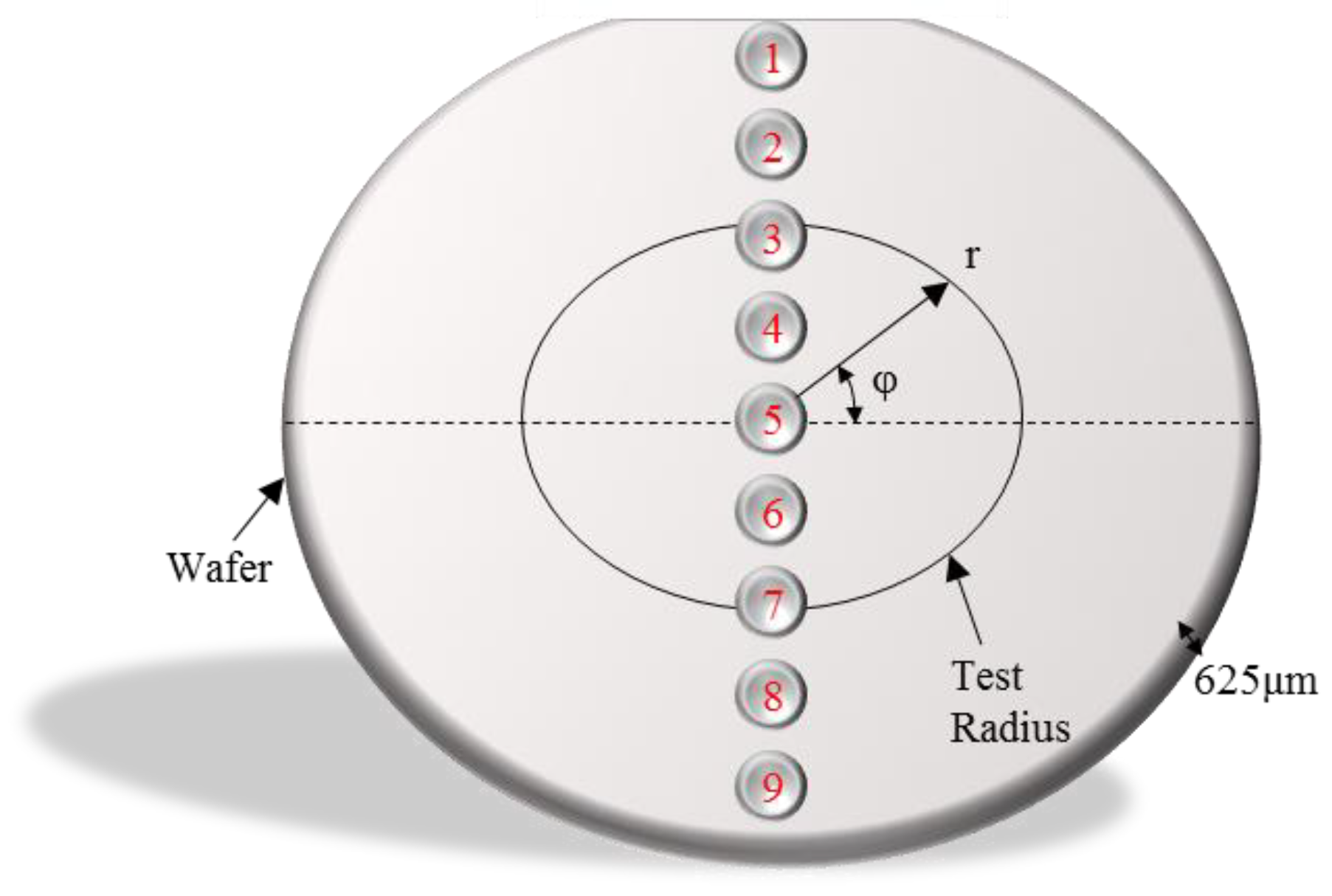

| ϕ(π) | 1/4 (Diameter) (kgf/mm2) | 1/2 (Diameter) (kgf/mm2) | 1/1 (Diameter) (kgf/mm2) |
|---|---|---|---|
| 0.0 | 0.0009 | 0.0009 | 0.0042 |
| 0.5 | 0.0006 | 0.0009 | 0.0038 |
| ϕ(π) | 1/4 (Diameter) (kgf/mm2) | 1/2 (Diameter) (kgf/mm2) | 1/1 (Diameter) (kgf/mm2) |
|---|---|---|---|
| 0.0 | −26.8 | −26.8 | −130.0 |
| 0.5 | −17.9 | −26.8 | −110.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Q.; Sun, D.; Shang, H.; Yu, T.; Chang, L.; Sun, Z.; Xing, W.; Dong, M. Study of Birefringence and Stress Distribution of SiO2 Film Optical Waveguide on Silicon Wafer. Coatings 2019, 9, 316. https://doi.org/10.3390/coatings9050316
Sun Q, Sun D, Shang H, Yu T, Chang L, Sun Z, Xing W, Dong M. Study of Birefringence and Stress Distribution of SiO2 Film Optical Waveguide on Silicon Wafer. Coatings. 2019; 9(5):316. https://doi.org/10.3390/coatings9050316
Chicago/Turabian StyleSun, Qingyu, DeGui Sun, Hongpeng Shang, Ting Yu, Liyuan Chang, Zheyu Sun, Wenchao Xing, and Mingxue Dong. 2019. "Study of Birefringence and Stress Distribution of SiO2 Film Optical Waveguide on Silicon Wafer" Coatings 9, no. 5: 316. https://doi.org/10.3390/coatings9050316
APA StyleSun, Q., Sun, D., Shang, H., Yu, T., Chang, L., Sun, Z., Xing, W., & Dong, M. (2019). Study of Birefringence and Stress Distribution of SiO2 Film Optical Waveguide on Silicon Wafer. Coatings, 9(5), 316. https://doi.org/10.3390/coatings9050316




