Theoretical Approach of Stability and Mechanical Properties in (TiZrHf)1−x(AB)x (AB = NbTa, NbMo, MoTa) Refractory High-Entropy Alloys
Abstract
1. Introduction
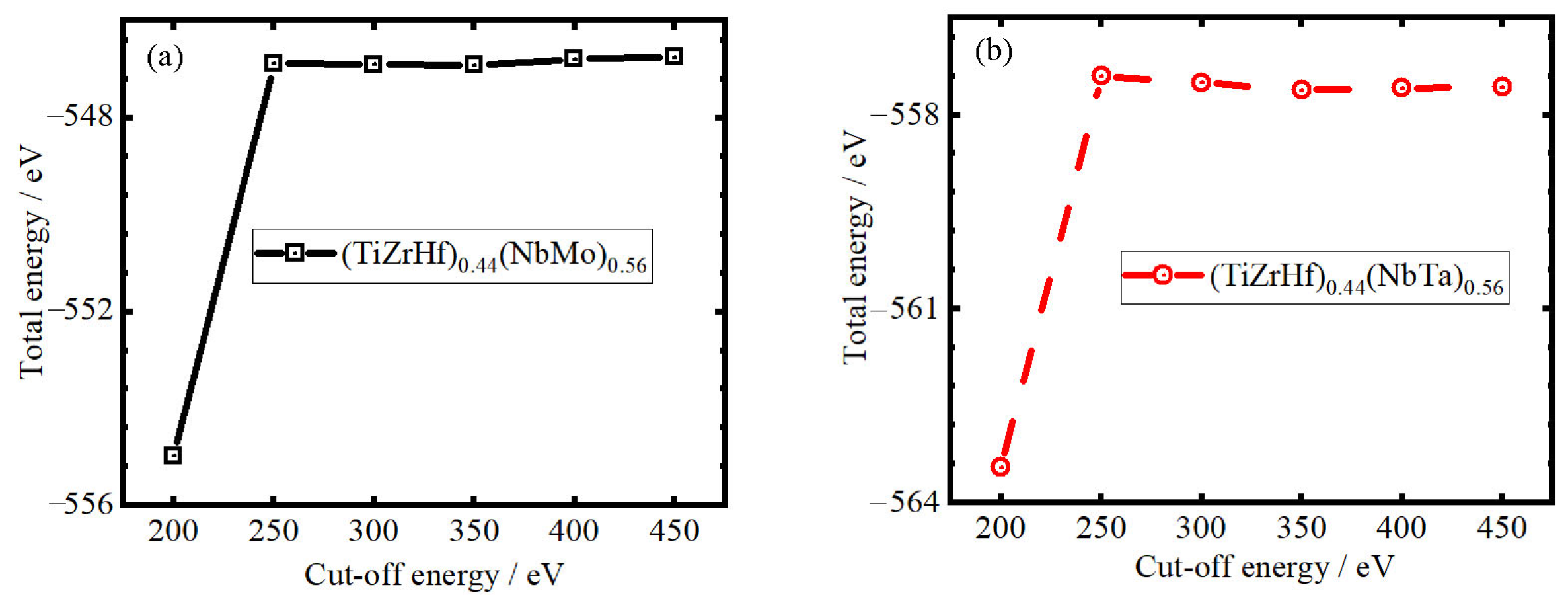
2. Calculation Details
3. Results and Discussion
3.1. Formation and Stability
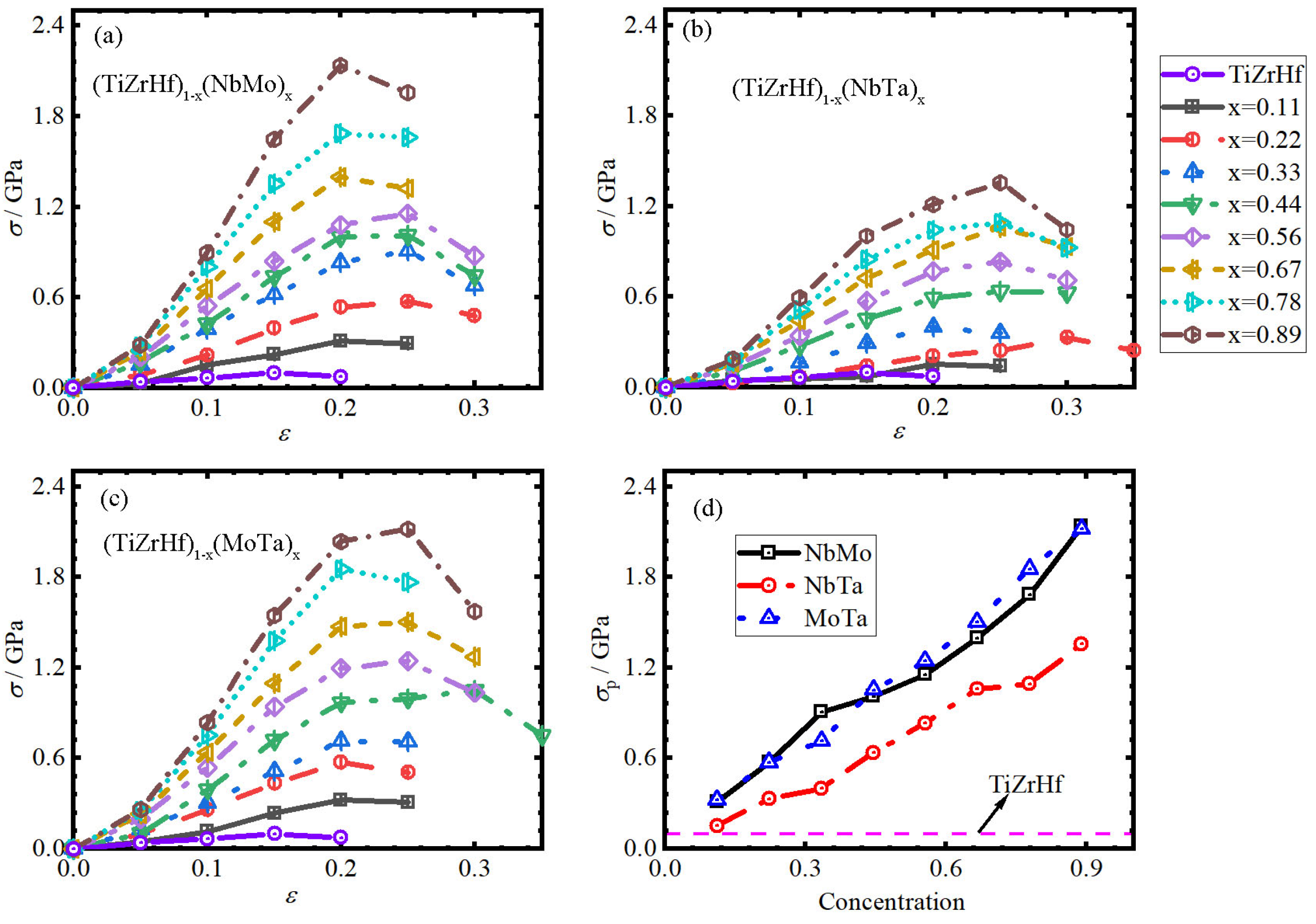
3.2. Ideal Strength
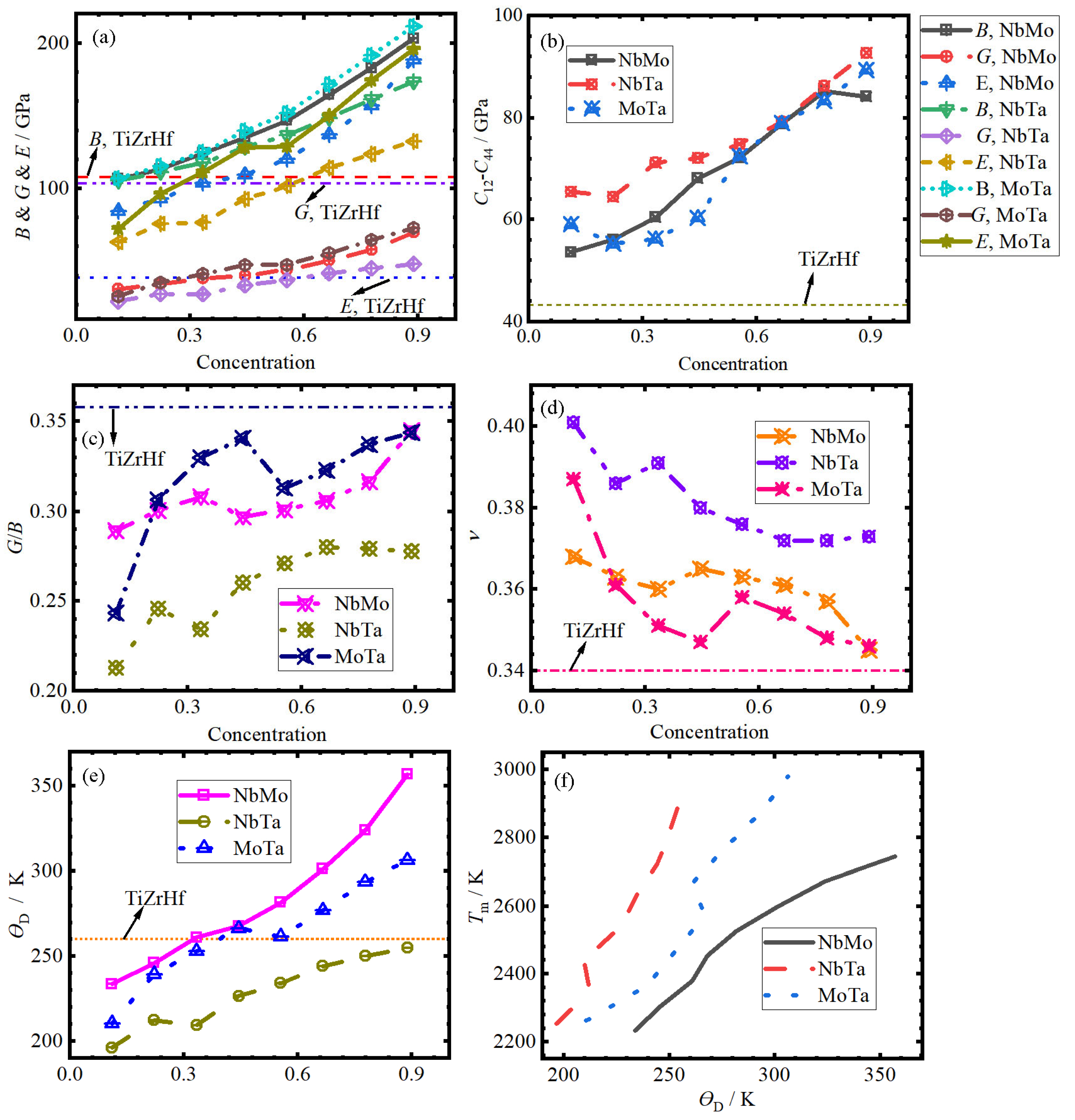
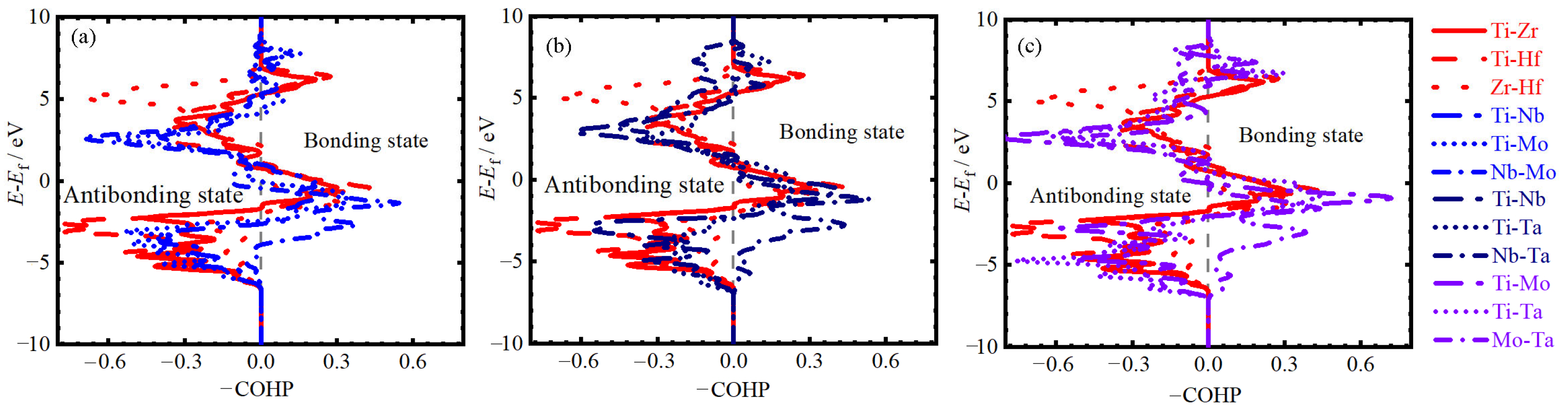
3.3. Elastic Property
4. Conclusions
- (1)
- The ΔHmix of (TiZrHf)1−x(AB)x (AB = NbMo, MoTa) linearly decreases, whereas both ΔHmix and ΔSmix of (TiZrHf)1−x(NbTa)x increase initially and subsequently decrease, with the crossover occurring at x = 0.56. The ΔHmix of (TiZrHf)1−x(NbTa)x and (TiZrHf)1−x(AB)x (AB = NbMo, MoTa) alloys are larger and lower than that of TiZrHf, respectively, while the ΔSmix of all (TiZrHf)1−x(AB)x is larger than that of TiZrHf.
- (2)
- The Ω of all (TiZrHf)1−x(AB)x (AB = NbMo, MoTa) first decreases sharply, followed by a gradual decrease. And the δ remains relatively stable around x = 0.56 for all cases, after which it decreases sharply until x = 0.89. The δ value of (TiZrHf)1−x(AB)x is higher than that of TiZrHf for x < 0.56 but becomes lower beyond this composition.
- (3)
- The VEC increases linearly from x = 0.11 to 0.89 while the ΔHf shows the opposite, except for (TiZrHf)0.67(NbTa)0.33. The VEC of all (TiZrHf)1−x(AB)x alloys increases, whereas their ΔHf decreases compared to that of TiZrHf.
- (4)
- The σp of (TiZrHf)1−x(AB)x increases linearly, reaching approximately 2.12 GPa, and the σp of all (TiZrHf)1−x(AB)x is larger than that of TiZrHf. B, E, and G also exhibit linear increases, and their values in all (TiZrHf)1−x(AB)x alloys are higher than those of TiZrHf, with some exceptions.
- (5)
- The C12–C44 and G/B of all (TiZrHf)1−x(AB)x alloys increase, whereas the ν exhibits the opposite trend. Moreover, The C12–C44 and G/B ratio of TiZrHf are lower and higher, respectively, than those of (TiZrHf)1−x(AB)x, and the ν of TiZrHf is lower than that of (TiZrHf)1−x(AB)x.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Miracle, D.B.; Senkov, O.N. A critical review of high entropy alloys and related concepts. Acta Mater. 2017, 122, 448–511. [Google Scholar] [CrossRef]
- Wang, S.; Wu, D.; She, H.; Wu, M.; Shu, D.; Dong, A.; Lai, H.; Sun, B. Design of high-ductile medium entropy alloys for dental implants. Mater. Sci. Eng. C 2020, 113, 110959. [Google Scholar] [CrossRef] [PubMed]
- Pink, E.; Eck, R. Refractory Metals and Their Alloys. In Materials Science and Technology: A Comprehensive Treatment, The Classic ed.; Wiley-VCH: Weinheim, Germany, 2006. [Google Scholar] [CrossRef]
- Praveen, S.; Kim, H.S. High-Entropy Alloys: Potential Candidates for High-Temperature Applications—An Overview. Adv. Eng. Mater. 2018, 20, 1700645. [Google Scholar] [CrossRef]
- Zhou, J.-L.; Cheng, Y.-H.; Chen, H.; Ma, K.; Wan, Y.-X.; Yang, J.-Y. Strengthening mechanisms and high-temperature oxidation properties of laser-clad TaNbZrTi refractory high entropy alloy coatings. J. Mater. Sci. 2023, 58, 16822–16840. [Google Scholar] [CrossRef]
- Zhao, Y.; Shi, W.; Huang, J. Microstructure evolution and performance effect of composite carbide (W,Ti)C enhanced Ni-based coatings fabricated by laser cladding. J. Mater. Res. Technol. 2025, 35, 298–307. [Google Scholar] [CrossRef]
- Yamabe-Mitarai, Y.; Yanao, K.; Toda, Y.; Ohnuma, I.; Matsunaga, T. Phase stability of Ti-containing high-entropy alloys with a bcc or hcp structure. J. Alloys Compd. 2022, 911, 164849. [Google Scholar] [CrossRef]
- Yeh, J.-W. Alloy Design Strategies and Future Trends in High-Entropy Alloys. JOM 2013, 65, 1759–1771. [Google Scholar] [CrossRef]
- Rogal, Ł.; Czerwinski, F.; Jochym, P.T.; Litynska-Dobrzynska, L. Microstructure and mechanical properties of the novel Hf25Sc25Ti25Zr25 equiatomic alloy with hexagonal solid solutions. Mater. Des. 2016, 92, 8–17. [Google Scholar] [CrossRef]
- Senkov, O.N.; Wilks, G.B.; Scott, J.M.; Miracle, D.B. Mechanical properties of Nb25Mo25Ta25W25 and V20Nb20Mo20Ta20W20 refractory high entropy alloys. Intermetallics 2011, 19, 698–706. [Google Scholar] [CrossRef]
- Qi, L.; Chrzan, D.C. Tuning Ideal Tensile Strengths and Intrinsic Ductility of bcc Refractory Alloys. Phys. Rev. Lett. 2014, 112, 115503. [Google Scholar] [CrossRef]
- Sheikh, S.; Shafeie, S.; Hu, Q.; Ahlström, J.; Persson, C.; Veselý, J.; Zýka, J.; Klement, U.; Guo, S. Alloy design for intrinsically ductile refractory high-entropy alloys. J. Appl. Phys. 2016, 120, 164902. [Google Scholar] [CrossRef]
- Dirras, G.; Lilensten, L.; Djemia, P.; Laurent-Brocq, M.; Tingaud, D.; Couzinié, J.P.; Perrière, L.; Chauveau, T.; Guillot, I. Elastic and plastic properties of as-cast equimolar TiHfZrTaNb high-entropy alloy. Mater. Sci. Eng. A 2016, 654, 30–38. [Google Scholar] [CrossRef]
- Rogal, L.; Ikeda, Y.; Lai, M.; Körmann, F.; Kalinowska, A.; Grabowski, B. Design of a dual-phase hcp-bcc high entropy alloy strengthened by ω nanoprecipitates in the Sc-Ti-Zr-Hf-Re system. Mater. Des. 2020, 192, 108716. [Google Scholar] [CrossRef]
- Zhang, L.; Fu, H.; Ge, S.; Zhu, Z.; Li, H.; Zhang, H.; Wang, A.; Zhang, H. Phase transformations in body-centered cubic NbxHfZrTi high-entropy alloys. Mater. Charact. 2018, 142, 443–448. [Google Scholar] [CrossRef]
- Ikeda, Y.; Gubaev, K.; Neugebauer, J.; Grabowski, B.; Körmann, F. Chemically induced local lattice distortions versus structural phase transformations in compositionally complex alloys. npj Comput. Mater. 2021, 7, 34. [Google Scholar] [CrossRef]
- Clatterbuck, D.M.; Krenn, C.R.; Cohen, M.L.; Morris, J.W. Phonon Instabilities and the Ideal Strength of Aluminum. Phys. Rev. Lett. 2003, 91, 135501. [Google Scholar] [CrossRef]
- Iijima, Y.; Nagase, T.; Matsugaki, A.; Wang, P.; Ameyama, K.; Nakano, T. Design and development of Ti–Zr–Hf–Nb–Ta–Mo high-entropy alloys for metallic biomaterials. Mater. Des. 2021, 202, 109548. [Google Scholar] [CrossRef]
- Yurchenko, N.; Panina, E.; Shaysultanov, D.; Zherebtsov, S.; Stepanov, N. Refractory high entropy alloy with ductile intermetallic B2 matrix/hard bcc particles and exceptional strain hardening capacity. Materialia 2021, 20, 101225. [Google Scholar] [CrossRef]
- Nagase, T.; Todai, M.; Wang, P.; Sun, S.-H.; Nakano, T. Design and development of (Ti, Zr, Hf)-Al based medium entropy alloys and high entropy alloys. Mater. Chem. Phys. 2022, 276, 125409. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, K.; Fang, D.; Qiu, X.; Tang, D.; Meng, J. Microstructure, tensile properties, and creep behavior of high-pressure die-cast Mg–4Al–4RE–0.4 Mn (RE = La, Ce) alloys. J. Mater. Sci. 2009, 44, 2046–2054. [Google Scholar] [CrossRef]
- Mahmudi, R.; Kabirian, F.; Nematollahi, Z. Microstructural stability and high-temperature mechanical properties of AZ91 and AZ91 + 2RE magnesium alloys. Mater. Des. 2011, 32, 2583–2589. [Google Scholar] [CrossRef]
- Jin, L.; Kevorkov, D.; Medraj, M.; Chartrand, P. Al–Mg–RE (RE = La, Sm) systems: Thermodynamic evaluations and optimizations coupled with key experiments and Miedema’s model estimations. J. Chem. Thermodyn. 2013, 58, 166–195. [Google Scholar] [CrossRef]
- Sun, S.P.; Li, X.P.; Wang, H.J.; Jiang, H.F.; Yi, D.Q. First-principles investigations on the electronic properties and stabilities of low-index surfaces of L12-Al3Sc intermetallic. Appl. Surf. Sci. 2014, 288, 609–618. [Google Scholar] [CrossRef]
- Finnis, M.W. The theory of metal-ceramic interfaces. J. Phys. Condens. Matter 1996, 8, 5811–5836. [Google Scholar] [CrossRef]
- Wang, C.; Wang, C.Y. Ni/Ni3Al interface: A density functional theory study. Appl. Surf. Sci. 2009, 255, 3669–3675. [Google Scholar] [CrossRef]
- Zhou, W.F.; Ren, X.D.; Ren, Y.P.; Yuan, S.Q.; Ren, N.F.; Yang, X.Q.; Adu-Gyamfi, S. Initial dislocation density effect on strain hardening in FCC aluminium alloy under laser shock peening. Philos. Mag. 2017, 97, 917–929. [Google Scholar] [CrossRef]
- Zhao, S.J.; Stocks, G.M.; Zhang, Y.W. Stacking fault energies of face-centered cubic concentrated solid solution alloys. Acta Mater. 2017, 134, 334–345. [Google Scholar] [CrossRef]
- Dong, T.H.; Zhang, X.D.; Yang, L.M.; Wang, F. Effect of structural vacancies on lattice vibration, mechanical, electronic, and thermodynamic properties of Cr5BSi3. Chin. Phys. B 2022, 31, 026101. [Google Scholar] [CrossRef]
- Li, X. Phase stability and micromechanical properties of TiZrHf-based refractory high-entropy alloys: A first-principles study. Phys. Rev. Mater. 2023, 7, 113604. [Google Scholar] [CrossRef]
- Chen, S.-M.; Ma, Z.-J.; Qiu, S.; Zhang, L.-J.; Zhang, S.-Z.; Yang, R.; Hu, Q.-M. Phase decomposition and strengthening in HfNbTaTiZr high entropy alloy from first-principles calculations. Acta Mater. 2022, 225, 117582. [Google Scholar] [CrossRef]
- Meng, H.; Duan, J.-M.; Chen, X.-T.; Jiang, S.; Shao, L.; Tang, B.-Y. Influence of Local Lattice Distortion on Elastic Properties of Hexagonal Close-Packed TiZrHf and TiZrHfSc Refractory Alloys. Phys. Status Solidi 2021, 258, 2100025. [Google Scholar] [CrossRef]
- Hafner, J. Ab-initio simulations of materials using VASP: Density-functional theory and beyond. J. Comput. Chem. 2008, 29, 2044–2078. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projected augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 1996, 54, 16533. [Google Scholar] [CrossRef]
- Feynman, R.P. Forces in Molecules. Phys. Rev. 1939, 56, 340. [Google Scholar] [CrossRef]
- Van de Walle, A.; Tiwary, P.; De Jong, M.; Olmsted, D.; Asta, M.; Dick, A.; Shin, D.; Wang, Y.; Chen, L.-Q.; Liu, Z.-K. Efficient stochastic generation of special quasirandom structures. Calphad 2013, 42, 13–18. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Nutor, R.K.; Cao, Q.; Wang, X.; Zhang, D.; Fang, Y.; Zhang, Y.; Jiang, J.-Z.; Selection, P. Phase Selection, Lattice Distortions, and Mechanical Properties in High-Entropy Alloys. Adv. Eng. Mater. 2020, 22, 2000466. [Google Scholar] [CrossRef]
- Takeuchi, A.; Inoue, A. Classification of Bulk Metallic Glasses by Atomic Size Difference, Heat of Mixing and Period of Constituent Elements and Its Application to Characterization of the Main Alloying Element. Mater. Trans. 2005, 46, 2817–2829. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y. Prediction of high-entropy stabilized solid-solution in multi-component alloys. Mater. Chem. Phys. 2012, 132, 233–238. [Google Scholar] [CrossRef]
- Cheng, C.; Zhang, X.; Haché, M.J.R.; Zou, Y. Magnetron co-sputtering synthesis and nanoindentation studies of nanocrystalline (TiZrHf)x(NbTa)1−x high-entropy alloy thin films. Nano Res. 2022, 15, 4873–4879. [Google Scholar] [CrossRef]
- Guo, N.N.; Wang, L.; Luo, L.S.; Li, X.Z.; Chen, R.R.; Su, Y.Q.; Guo, J.J.; Fu, H.Z. Effect of composing element on microstructure and mechanical properties in Mo–Nb–Hf–Zr–Ti multi-principle component alloys. Intermetallics 2016, 69, 13–20. [Google Scholar] [CrossRef]
- Hobhaydar, A.; Wang, X.; Wang, Y.; Li, H.; Van Tran, N.; Zhu, H. Effect of tungsten doping on the irradiation resistance of FeCrV-based refractory medium entropy alloy for potential nuclear applications. J. Alloys Compd. 2023, 966, 171635. [Google Scholar] [CrossRef]
- Chen, L.; Li, Y.; Xiao, B.; Gao, Y.; Zhao, S. Chemical bonding, thermodynamic stability and mechanical strength of Ni3Ti/α-Al2O3 interfaces by first-principles study. Scr. Mater. 2021, 190, 57–62. [Google Scholar] [CrossRef]
- Han, F.; Yuan, M.; Wei, Z.; Yao, Y.; Yao, L.; Xin, L.; Shen, X. First-principles study of the Ti/Al3Ti interfacial properties. Appl. Surf. Sci. 2021, 544, 148960. [Google Scholar] [CrossRef]
- Klimashin, F.F.; Lobmaier, L.; Koutná, N.; Holec, D.; Mayrhofer, P.H. The MoN–TaN system: Role of vacancies in phase stability and mechanical properties. Mater. Des. 2021, 202, 109568. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, Y. Mechanical, thermodynamic, and electronic studies on the Al3V/Al interface based on the density functional theory. Surf. Interfaces 2021, 25, 101212. [Google Scholar] [CrossRef]
- Otero-De-La-Roza, A.; Abbasi-Pérez, D.; Luaña, V. Gibbs2: A new version of the quasiharmonic model code. II. Models for solid-state thermodynamics, features and implementation. Comput. Phys. Commun. 2011, 182, 2232–2248. [Google Scholar] [CrossRef]
- Liu, T.; Ma, T.; Li, Y.; Ren, Y.; Liu, W. Stabilities, mechanical and thermodynamic properties of Al–RE intermetallics: A first-principles study. J. Rare Earths 2022, 40, 345–352. [Google Scholar] [CrossRef]
- Vasilyev, D.; Ikhsanov, R.S.; Zheleznyi, M.; Kartsev, A. Calculations of elastic and thermal properties of the strengthening C14 Fe6Nb4Al2 Laves phase using the density functional theory. J. Mater. Sci. 2025, 60, 5427–5441. [Google Scholar] [CrossRef]
- Benmakhlouf, A.; Daoud, S.; Bouarissa, N.; Allaoui, O. Elastic constants and thermophysical properties of CuPd: First-principles study. Rev. Mex. Física 2025, 71, 020501. [Google Scholar] [CrossRef]
- El Galta, A.; Masrour, R. First-principles calculations to investigate structural, magneto-electronic, elastic, thermodynamic, and thermoelectric properties of Co2LuY (Y = Zr, Hf) alloys for potential industrial application. Solid State Commun. 2025, 404, 116028. [Google Scholar] [CrossRef]
- Johnson, R.A. Analytic nearest-neighbor model for fcc metals. Phys. Rev. B 1988, 37, 3924–3931. [Google Scholar] [CrossRef]
- Fu, H.; Zhao, Z.; Liu, W.; Peng, F.; Gao, T.; Cheng, X. Ab initio calculations of elastic constants and thermodynamic properties of γ-TiAl under high pressures. Intermetallics 2010, 18, 761–766. [Google Scholar] [CrossRef]
- Frantsevich, I.N.; Voronov, F.F.; Bokuta, S.A. Elastic Constants and Elastic Moduli of Metals and Insulators Handbook; Naukova Dumka: Kiev, Ukraine, 1983. [Google Scholar]
- Dronskowski, R.; Bloechl, P.E. Crystal orbital Hamilton populations (COHP): Energy-resolved visualization of chemical bonding in solids based on density-functional calculations. J. Phys. Chem. 1993, 97, 8617–8624. [Google Scholar] [CrossRef]
- Deringer, V.L.; Tchougréeff, A.L.; Dronskowski, R. Crystal Orbital Hamilton Population (COHP) Analysis As Projected from Plane-Wave Basis Sets. J. Phys. Chem. A 2011, 115, 5461–5466. [Google Scholar] [CrossRef]
- Nelson, R.; Ertural, C.; George, J.; Deringer, V.L.; Hautier, G.; Dronskowski, R. LOBSTER: Local orbital projections; atomic charges, and chemical-bonding analysis from projector-augmented-wave-based density-functional theory. J. Comput. Chem. 2020, 41, 1931–1940. [Google Scholar] [CrossRef]



| Alloys | ΔHmix | ΔSmix | Tm | Ω | δ | VEC | ΔHf |
|---|---|---|---|---|---|---|---|
| TiZrHf | 0 | 9.13 | 2160.48 | − | 11.67 | 4.00 | 5.40 |
| (TiZrHf)0.89(NbMo)0.11 | −0.34 | 11.66 | 2233.61 | 77.18 | 13.26 | 4.17 | 5.05 |
| (TiZrHf)0.78(NbMo)0.22 | −0.76 | 12.79 | 2306.74 | 38.96 | 13.92 | 4.33 | 3.89 |
| (TiZrHf)0.67(NbMo)0.33 | −1.26 | 13.30 | 2379.87 | 25.14 | 14.75 | 4.50 | 1.96 |
| (TiZrHf)0.56(NbMo)0.44 | −1.84 | 13.35 | 2453.00 | 17.76 | 14.02 | 4.67 | 1.51 |
| (TiZrHf)0.44(NbMo)0.56 | −2.51 | 12.97 | 2526.13 | 13.05 | 13.71 | 4.83 | 0.77 |
| (TiZrHf)0.33(NbMo)0.67 | −3.26 | 12.18 | 2599.26 | 9.71 | 10.42 | 5.00 | −0.87 |
| (TiZrHf)0.22(NbMo)0.78 | −4.09 | 10.92 | 2672.39 | 7.13 | 8.29 | 5.17 | −2.54 |
| (TiZrHf)0.11(NbMo)0.89 | −5.00 | 9.04 | 2745.52 | 4.96 | 4.99 | 5.33 | −4.92 |
| (TiZrHf)0.89(NbTa)0.11 | 1.12 | 11.66 | 2254.34 | 23.48 | 13.10 | 4.11 | 6.97 |
| (TiZrHf)0.78(NbTa)0.22 | 1.96 | 12.79 | 2348.19 | 15.33 | 13.01 | 4.22 | 7.42 |
| (TiZrHf)0.67(NbTa)0.33 | 2.52 | 13.30 | 2442.04 | 12.90 | 15.86 | 4.33 | 7.71 |
| (TiZrHf)0.56(NbTa)0.44 | 2.80 | 13.35 | 2535.89 | 12.10 | 14.62 | 4.44 | 5.95 |
| (TiZrHf)0.44(NbTa)0.56 | 2.80 | 12.97 | 2629.74 | 12.19 | 15.43 | 4.56 | 5.28 |
| (TiZrHf)0.33(NbTa)0.67 | 2.52 | 12.18 | 2723.59 | 13.17 | 11.48 | 4.67 | 3.39 |
| (TiZrHf)0.22(NbTa)0.78 | 1.96 | 10.92 | 2817.45 | 15.70 | 10.22 | 4.78 | 2.15 |
| (TiZrHf)0.11(NbTa)0.89 | 1.12 | 9.04 | 2911.30 | 23.51 | 5.45 | 4.89 | 0.52 |
| (TiZrHf)0.89(MoTa)0.11 | −0.52 | 11.66 | 2262.95 | 50.49 | 12.34 | 4.17 | 5.07 |
| (TiZrHf)0.78(MoTa)0.22 | −1.05 | 12.79 | 2365.41 | 28.72 | 13.28 | 4.33 | 4.60 |
| (TiZrHf)0.67(MoTa)0.33 | −1.59 | 13.30 | 2467.87 | 20.61 | 13.81 | 4.50 | 4.47 |
| (TiZrHf)0.56(MoTa)0.44 | −2.14 | 13.35 | 2570.34 | 16.03 | 14.60 | 4.67 | 1.93 |
| (TiZrHf)0.44(MoTa)0.56 | −2.70 | 12.97 | 2672.80 | 12.86 | 12.26 | 4.83 | 1.30 |
| (TiZrHf)0.33(MoTa)0.67 | −3.26 | 12.18 | 2775.26 | 10.37 | 11.34 | 5.00 | −0.70 |
| (TiZrHf)0.22(MoTa)0.78 | −3.83 | 10.92 | 2877.72 | 8.20 | 9.15 | 5.17 | −4.43 |
| (TiZrHf)0.11(MoTa)0.89 | −4.41 | 9.04 | 2980.19 | 6.11 | 7.14 | 5.33 | −5.98 |
| Alloys | C11 | C12 | C44 | C12–C44 |
|---|---|---|---|---|
| TiZrHf | 155.60 | 84.20 | 40.86 | 43.30 |
| (TiZrHf)0.89(NbMo)0.11 | 136.86 | 91.65 | 38.04 | 53.61 |
| (TiZrHf)0.78(NbMo)0.22 | 152.01 | 94.06 | 37.99 | 56.07 |
| (TiZrHf)0.67(NbMo)0.33 | 172.86 | 100.04 | 39.60 | 60.44 |
| (TiZrHf)0.56(NbMo)0.44 | 190.43 | 107.40 | 39.25 | 68.16 |
| (TiZrHf)0.44(NbMo)0.56 | 218.76 | 110.81 | 38.63 | 72.19 |
| (TiZrHf)0.33(NbMo)0.67 | 251.02 | 121.27 | 42.47 | 78.80 |
| (TiZrHf)0.22(NbMo)0.78 | 275.92 | 136.40 | 51.10 | 85.30 |
| (TiZrHf)0.11(NbMo)0.89 | 321.77 | 143.82 | 59.66 | 84.16 |
| (TiZrHf)0.89(NbTa)0.11 | 124.48 | 96.16 | 30.66 | 65.49 |
| (TiZrHf)0.78(NbTa)0.22 | 138.71 | 97.73 | 33.24 | 64.49 |
| (TiZrHf)0.67(NbTa)0.33 | 148.50 | 102.31 | 31.06 | 71.25 |
| (TiZrHf)0.56(NbTa)0.44 | 165.37 | 110.51 | 38.36 | 72.16 |
| (TiZrHf)0.44(NbTa)0.56 | 183.87 | 113.11 | 38.23 | 74.88 |
| (TiZrHf)0.33(NbTa)0.67 | 204.55 | 120.73 | 41.49 | 79.23 |
| (TiZrHf)0.22(NbTa)0.78 | 223.90 | 130.25 | 43.96 | 86.28 |
| (TiZrHf)0.11(NbTa)0.89 | 247.21 | 136.94 | 44.18 | 92.76 |
| (TiZrHf)0.89(MoTa)0.11 | 126.70 | 97.22 | 38.12 | 59.10 |
| (TiZrHf)0.78(MoTa)0.22 | 152.38 | 97.07 | 41.77 | 55.30 |
| (TiZrHf)0.67(MoTa)0.33 | 177.56 | 98.84 | 42.57 | 56.28 |
| (TiZrHf)0.56(MoTa)0.44 | 202.47 | 108.42 | 48.03 | 60.39 |
| (TiZrHf)0.44(MoTa)0.56 | 218.00 | 118.67 | 46.15 | 72.52 |
| (TiZrHf)0.33(MoTa)0.67 | 254.04 | 130.62 | 51.65 | 78.97 |
| (TiZrHf)0.22(MoTa)0.78 | 289.34 | 142.80 | 59.41 | 83.39 |
| (TiZrHf)0.11(MoTa)0.89 | 324.49 | 155.10 | 65.70 | 89.40 |
| Alloys | B | G | E | G/B | υ | ϴD |
|---|---|---|---|---|---|---|
| TiZrHf | 108.00 | 38.71 | 103.74 | 0.358 | 0.340 | 260.01 |
| (TiZrHf)0.89(NbMo)0.11 | 106.72 | 30.87 | 84.47 | 0.289 | 0.368 | 233.74 |
| (TiZrHf)0.78(NbMo)0.22 | 113.38 | 34.09 | 92.95 | 0.301 | 0.363 | 245.99 |
| (TiZrHf)0.67(NbMo)0.33 | 124.31 | 38.29 | 104.18 | 0.308 | 0.360 | 261.00 |
| (TiZrHf)0.56(NbMo)0.44 | 135.08 | 40.14 | 109.56 | 0.297 | 0.365 | 267.96 |
| (TiZrHf)0.44(NbMo)0.56 | 146.79 | 44.18 | 120.44 | 0.301 | 0.363 | 281.68 |
| (TiZrHf)0.33(NbMo)0.67 | 164.52 | 50.36 | 137.08 | 0.306 | 0.361 | 301.40 |
| (TiZrHf)0.22(NbMo)0.78 | 182.91 | 57.90 | 157.11 | 0.317 | 0.357 | 323.88 |
| (TiZrHf)0.11(NbMo)0.89 | 203.14 | 70.05 | 188.49 | 0.345 | 0.345 | 356.87 |
| (TiZrHf)0.89(NbTa)0.11 | 105.60 | 22.49 | 62.99 | 0.213 | 0.401 | 196.34 |
| (TiZrHf)0.78(NbTa)0.22 | 111.39 | 27.38 | 75.91 | 0.246 | 0.386 | 212.33 |
| (TiZrHf)0.67(NbTa)0.33 | 117.71 | 27.58 | 76.75 | 0.234 | 0.391 | 209.42 |
| (TiZrHf)0.56(NbTa)0.44 | 128.80 | 33.53 | 92.57 | 0.260 | 0.380 | 226.71 |
| (TiZrHf)0.44(NbTa)0.56 | 136.70 | 37.07 | 101.98 | 0.271 | 0.376 | 234.25 |
| (TiZrHf)0.33(NbTa)0.67 | 148.67 | 41.66 | 114.31 | 0.280 | 0.372 | 244.26 |
| (TiZrHf)0.22(NbTa)0.78 | 161.46 | 45.09 | 123.74 | 0.279 | 0.372 | 250.10 |
| (TiZrHf)0.11(NbTa)0.89 | 173.70 | 48.28 | 132.55 | 0.278 | 0.373 | 254.90 |
| (TiZrHf)0.89(MoTa)0.11 | 107.05 | 26.05 | 72.27 | 0.243 | 0.387 | 210.56 |
| (TiZrHf)0.78(MoTa)0.22 | 115.50 | 35.40 | 96.37 | 0.307 | 0.361 | 239.44 |
| (TiZrHf)0.67(MoTa)0.33 | 125.08 | 41.25 | 111.50 | 0.330 | 0.351 | 252.94 |
| (TiZrHf)0.56(MoTa)0.44 | 139.77 | 47.63 | 128.30 | 0.341 | 0.347 | 266.39 |
| (TiZrHf)0.44(MoTa)0.56 | 151.78 | 47.52 | 129.10 | 0.313 | 0.358 | 261.59 |
| (TiZrHf)0.33(MoTa)0.67 | 171.76 | 55.47 | 150.23 | 0.323 | 0.354 | 277.22 |
| (TiZrHf)0.22(MoTa)0.78 | 191.65 | 64.61 | 174.26 | 0.337 | 0.348 | 293.83 |
| (TiZrHf)0.11(MoTa)0.89 | 211.56 | 72.74 | 195.77 | 0.344 | 0.346 | 306.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, H.; Zhang, Y.; Ruan, Z.; Fan, T.; Hu, T.; Yan, H. Theoretical Approach of Stability and Mechanical Properties in (TiZrHf)1−x(AB)x (AB = NbTa, NbMo, MoTa) Refractory High-Entropy Alloys. Coatings 2025, 15, 1092. https://doi.org/10.3390/coatings15091092
Luo H, Zhang Y, Ruan Z, Fan T, Hu T, Yan H. Theoretical Approach of Stability and Mechanical Properties in (TiZrHf)1−x(AB)x (AB = NbTa, NbMo, MoTa) Refractory High-Entropy Alloys. Coatings. 2025; 15(9):1092. https://doi.org/10.3390/coatings15091092
Chicago/Turabian StyleLuo, Heng, Yuanyuan Zhang, Zixiong Ruan, Touwen Fan, Te Hu, and Hongge Yan. 2025. "Theoretical Approach of Stability and Mechanical Properties in (TiZrHf)1−x(AB)x (AB = NbTa, NbMo, MoTa) Refractory High-Entropy Alloys" Coatings 15, no. 9: 1092. https://doi.org/10.3390/coatings15091092
APA StyleLuo, H., Zhang, Y., Ruan, Z., Fan, T., Hu, T., & Yan, H. (2025). Theoretical Approach of Stability and Mechanical Properties in (TiZrHf)1−x(AB)x (AB = NbTa, NbMo, MoTa) Refractory High-Entropy Alloys. Coatings, 15(9), 1092. https://doi.org/10.3390/coatings15091092







