Characterizing Asphalt Binder Phase Transitions via Dynamic Mechanical Analysis: Performance Implications and SARA Fraction Correlations
Abstract
1. Introduction
2. Materials and Methods
2.1. Asphalt Binder Samples
2.2. Test and Analysis Methods
2.2.1. Basic Performance Test
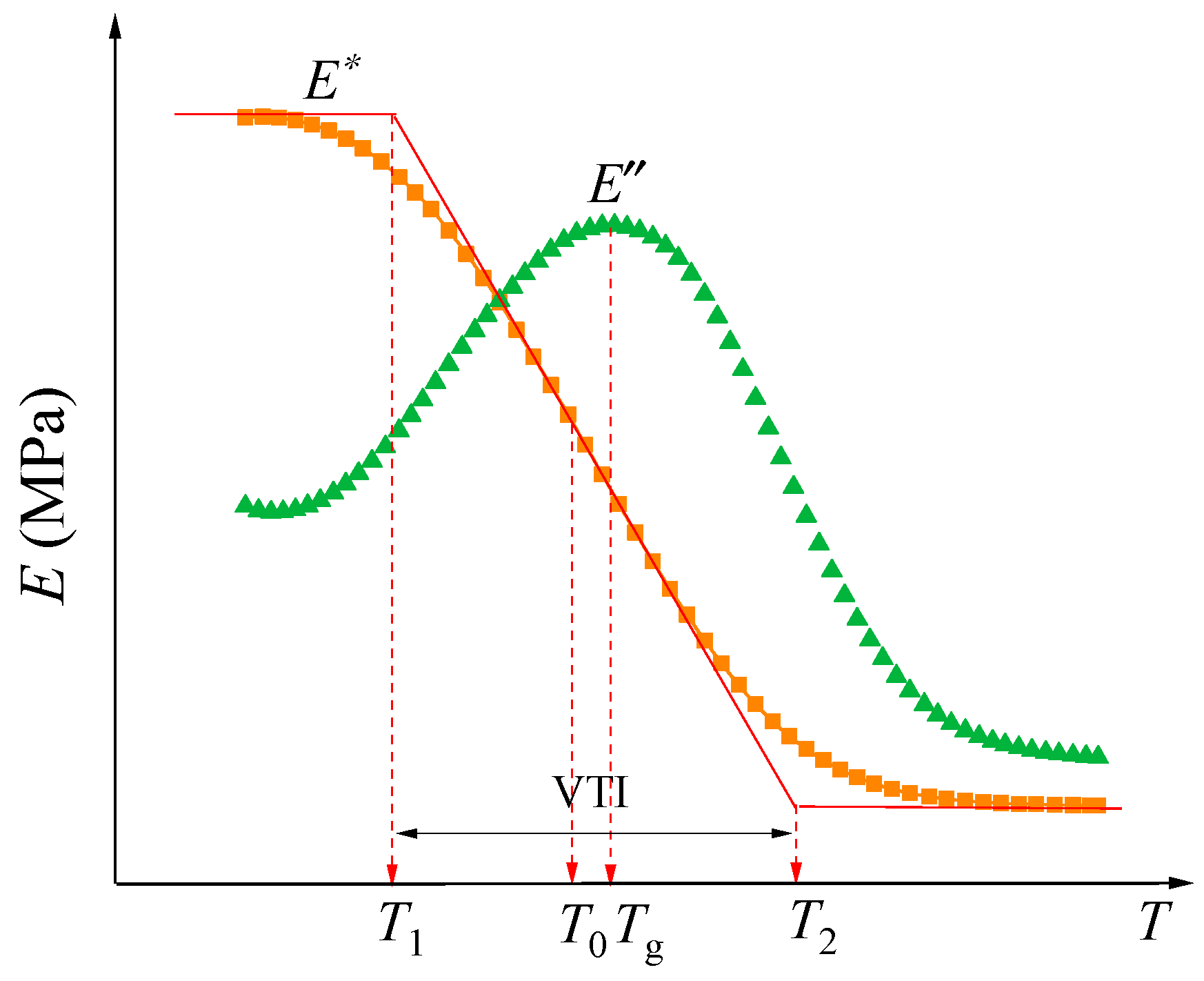
2.2.2. DMA Test
- The temperatures corresponding to the midpoint of the complex modulus curve are defined as and ;
- The temperature at which the midpoint tangent of the complex modulus curve intersects the low-temperature asymptote is designated T1, ;
- The temperature at which the midpoint tangent of the complex modulus curve intersects the high-temperature asymptote is denoted as T2, .
- The temperature interval between T1 and T2 is the viscoelastic temperature interval (VTI) of the asphalt binder. During this phase, the asphalt binder exhibits certain deformation resistance and elastic recovery capabilities. .
3. Results and Discussion
3.1. Evaluation of Asphalt Binder Phase Transition Characteristics
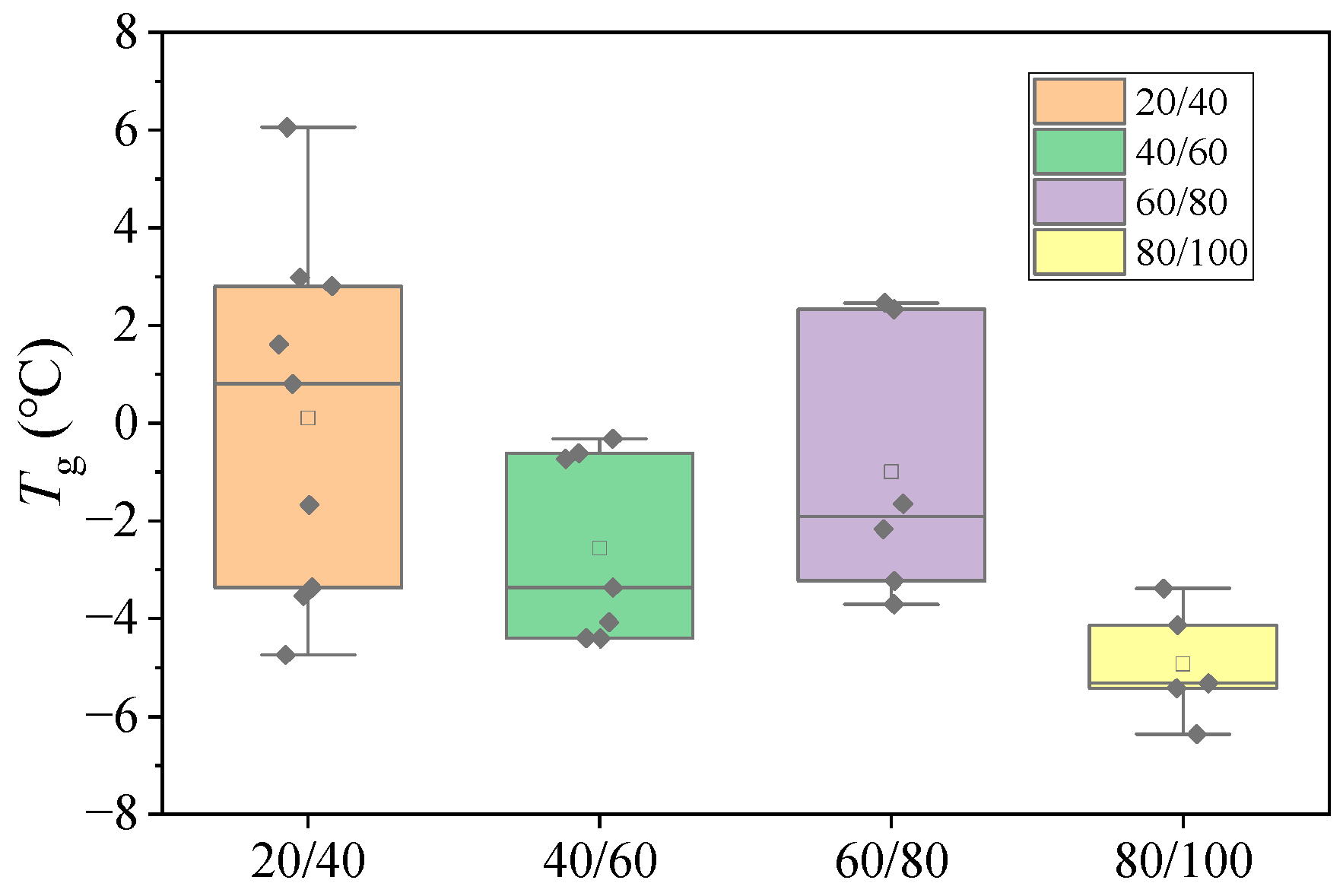
3.1.1. PTTs of Asphalt Binder
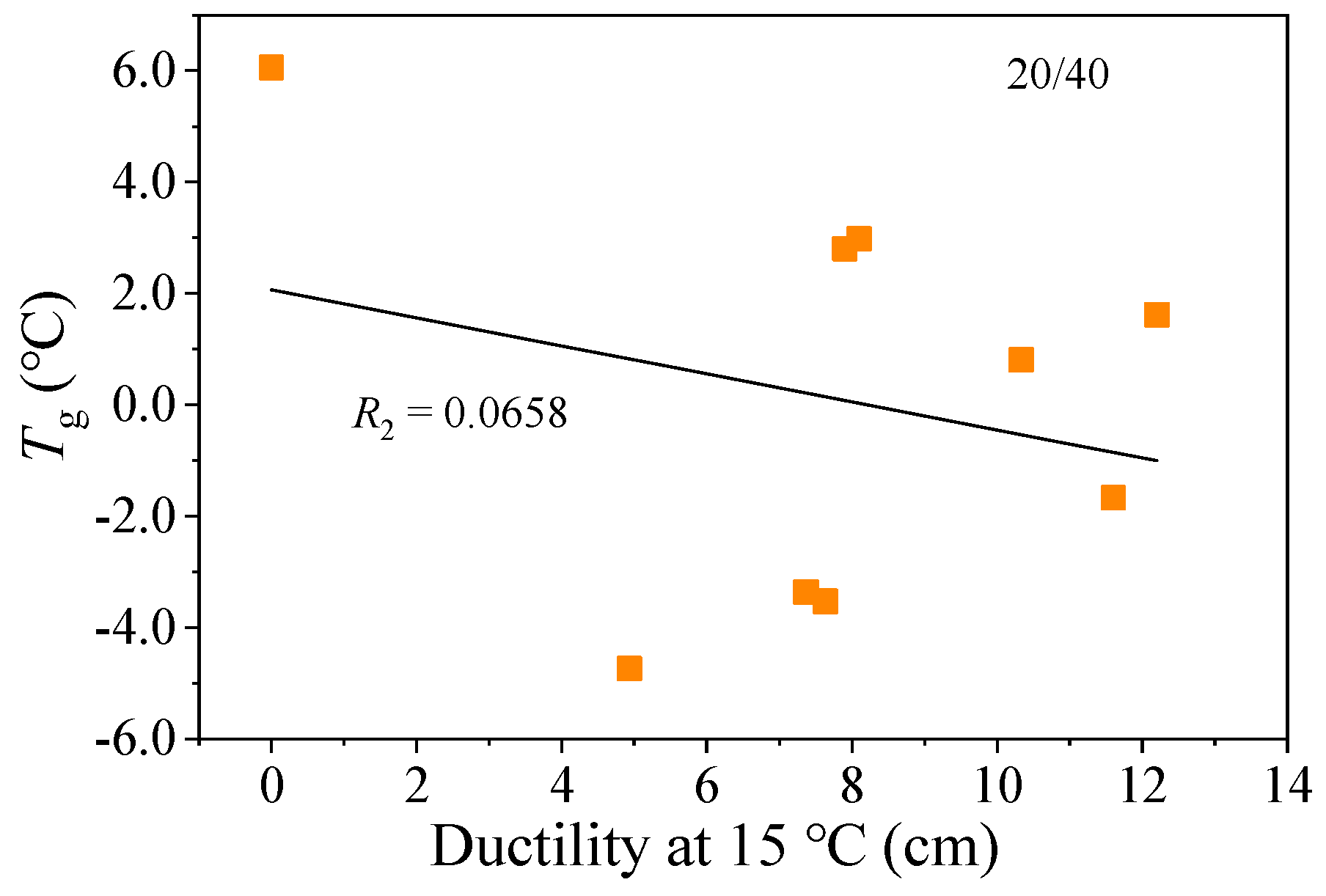
- Asphalt binder A1 displayed a ductility of 0 cm at 15 °C, indicating the poorest low-temperature performance, consistent with its PTT evaluation.
- Asphalt binder E1, conversely, showed a ductility of 5 cm at 15 °C—lower than other 20/40-grade asphalt binders—but exhibited the lowest Tg, which contradicts the PTT assessment.
- Asphalt binders B1, C1, and D5 all recorded identical ductility values (8 cm), yet their PTTs differed by 6.5 °C.
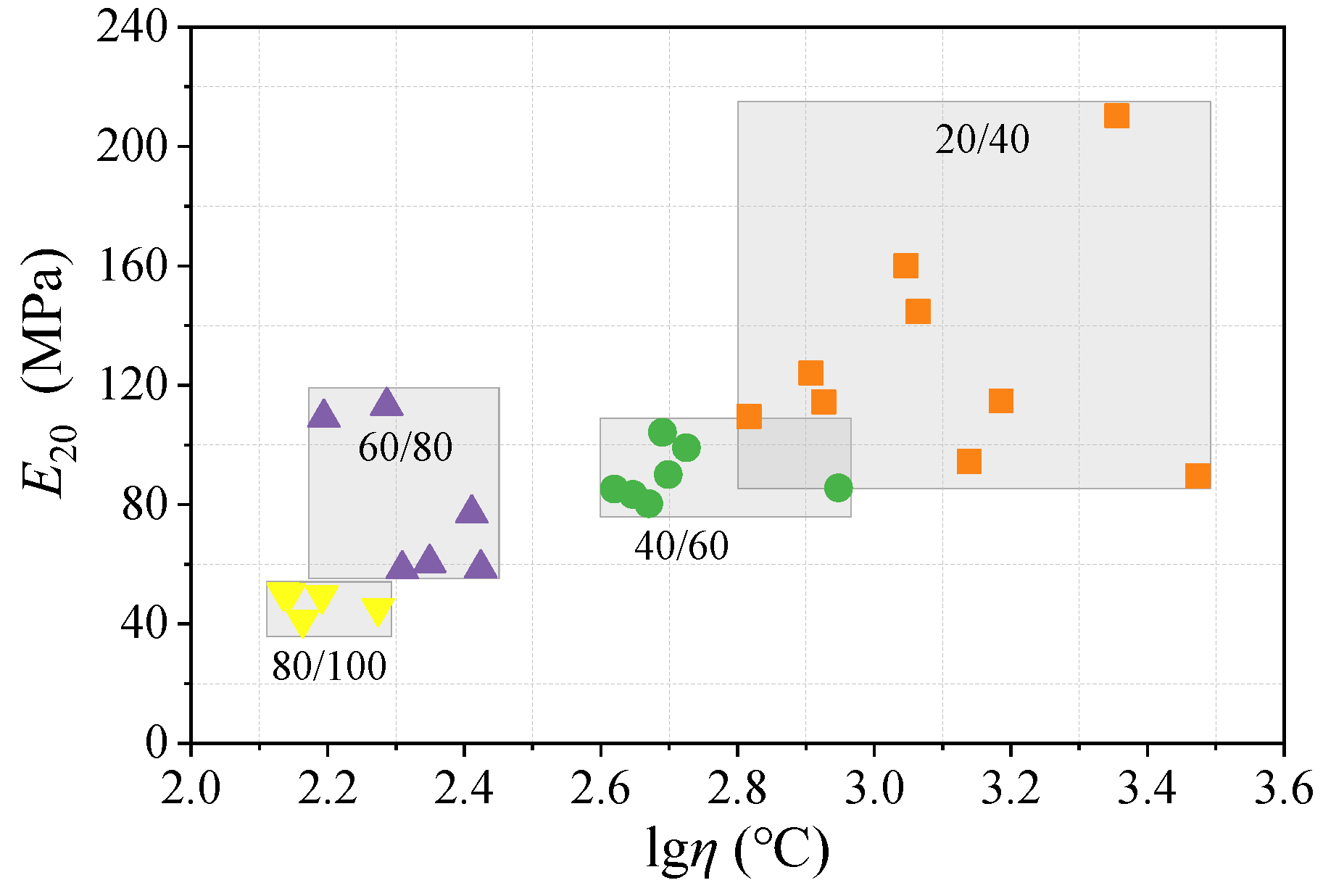
3.1.2. Characteristic Modulus of Asphalt Binders
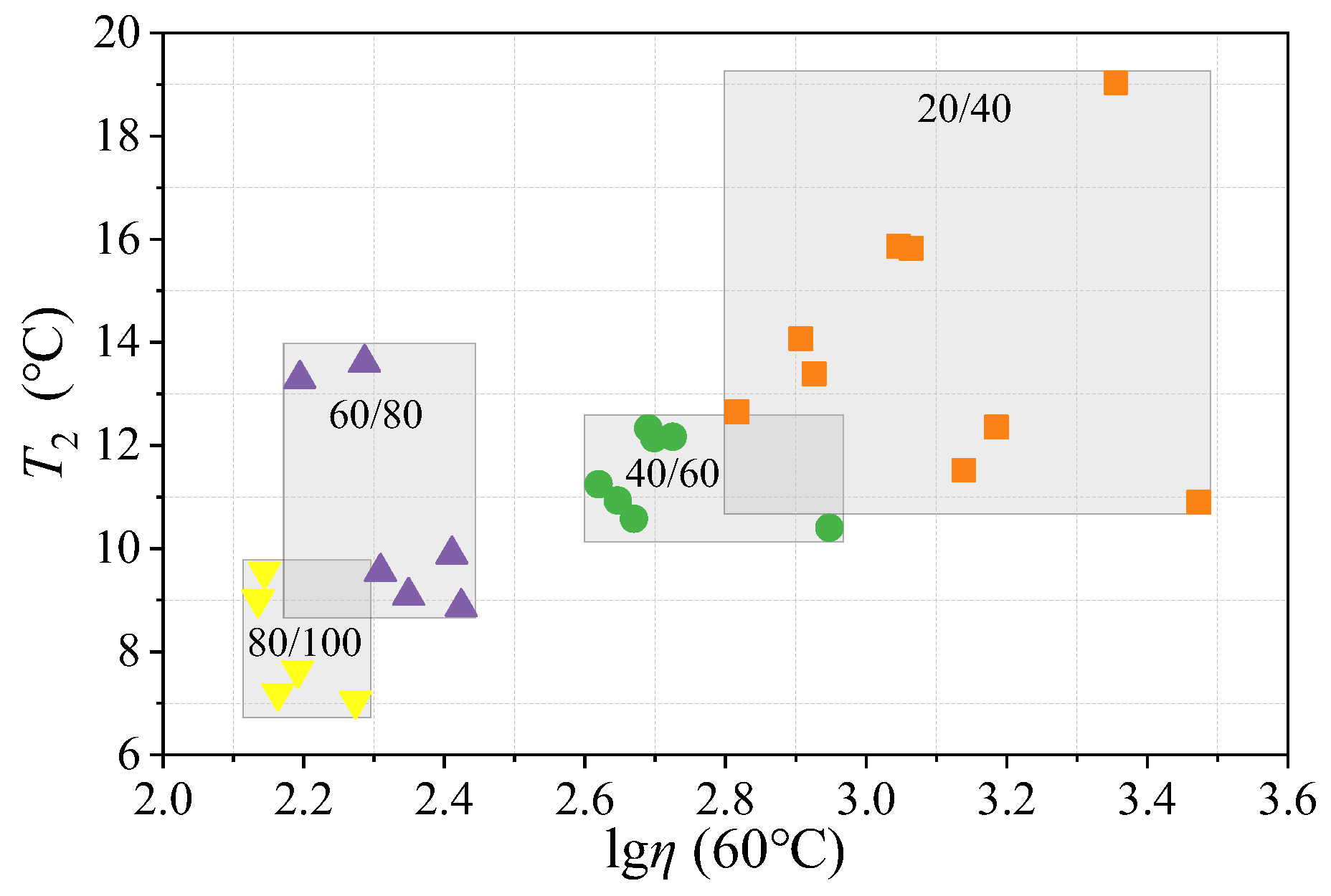
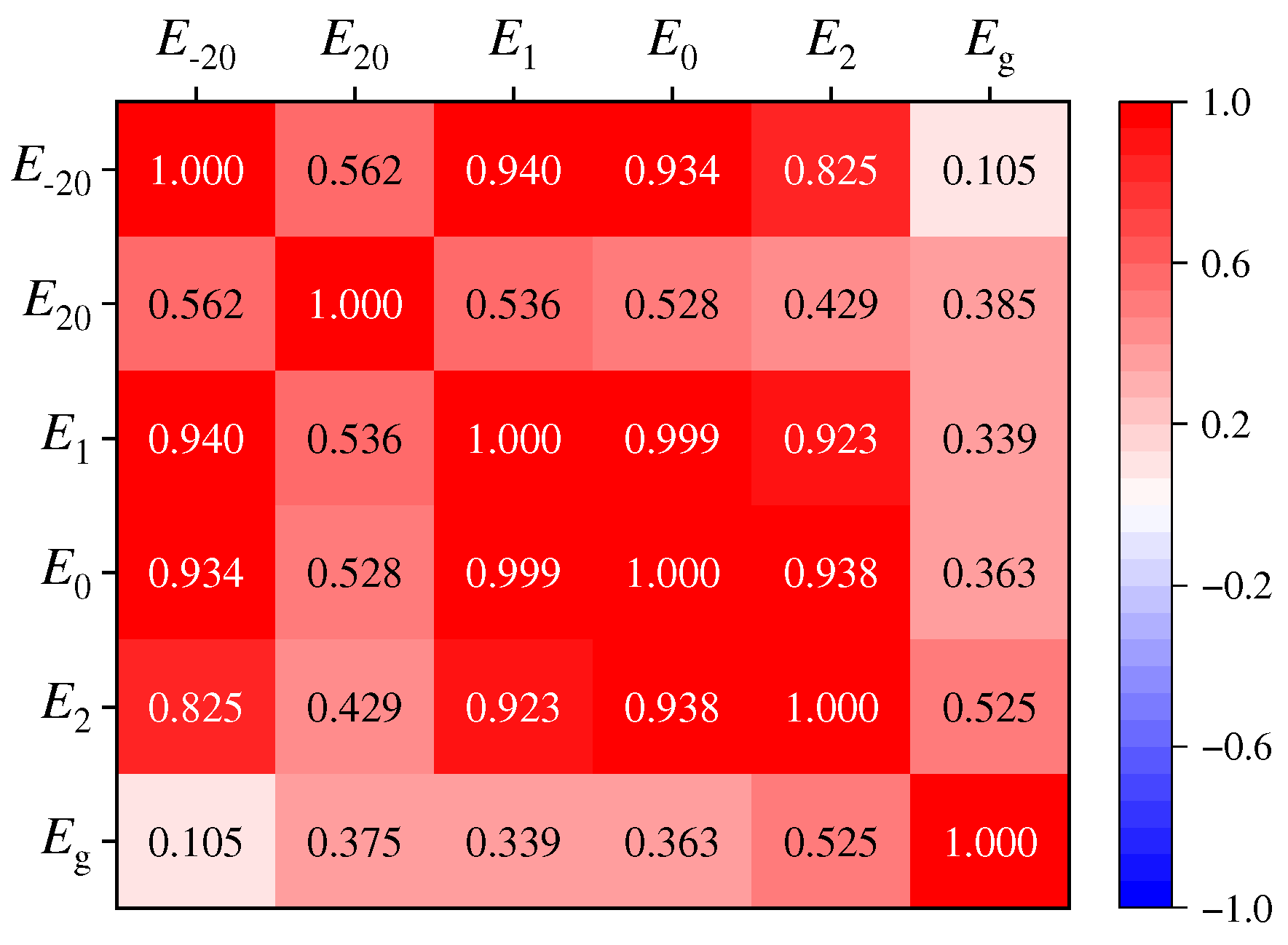
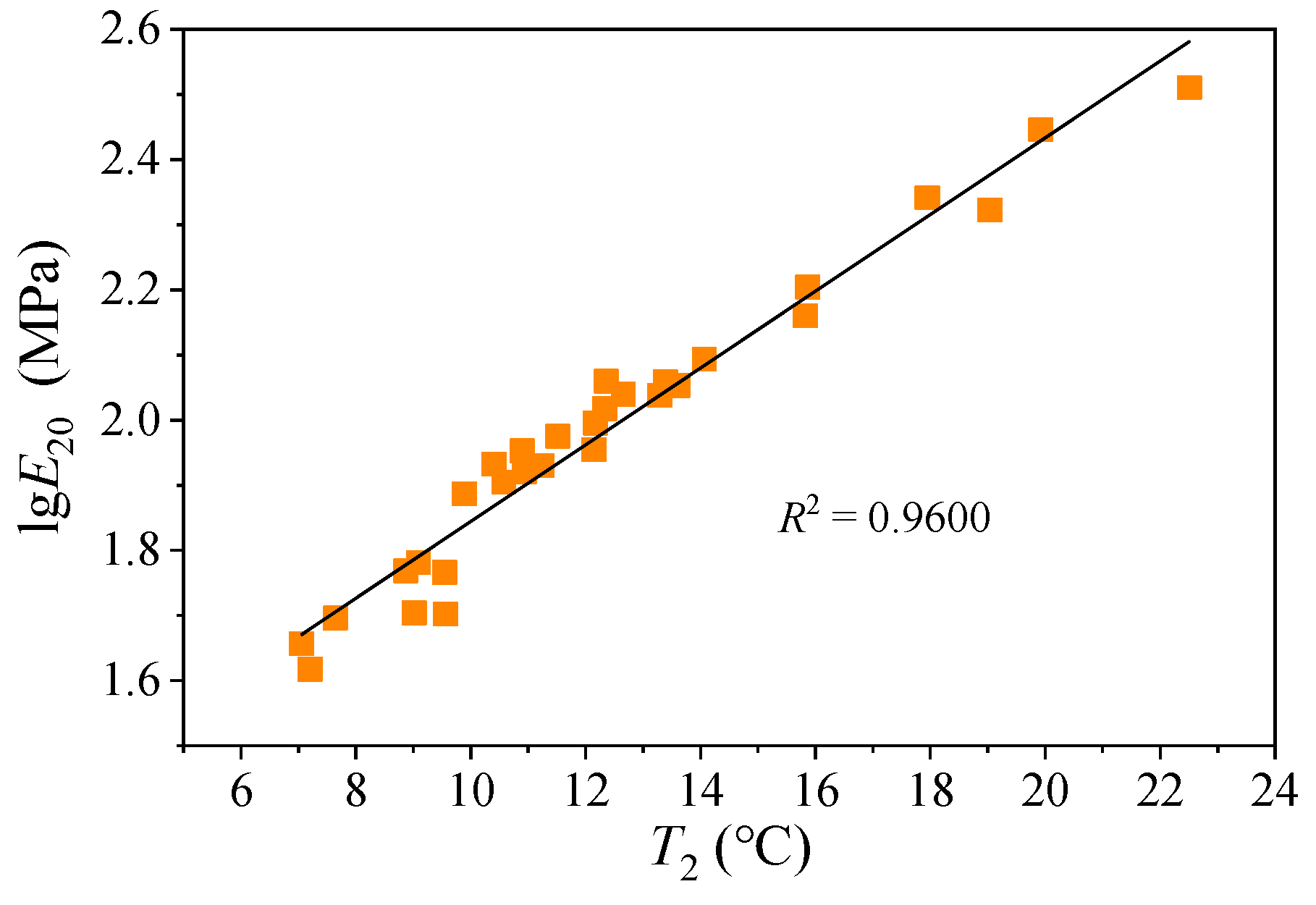
3.2. The Relationship Between Phase Transition Characteristic Index and Conventional Performance Index
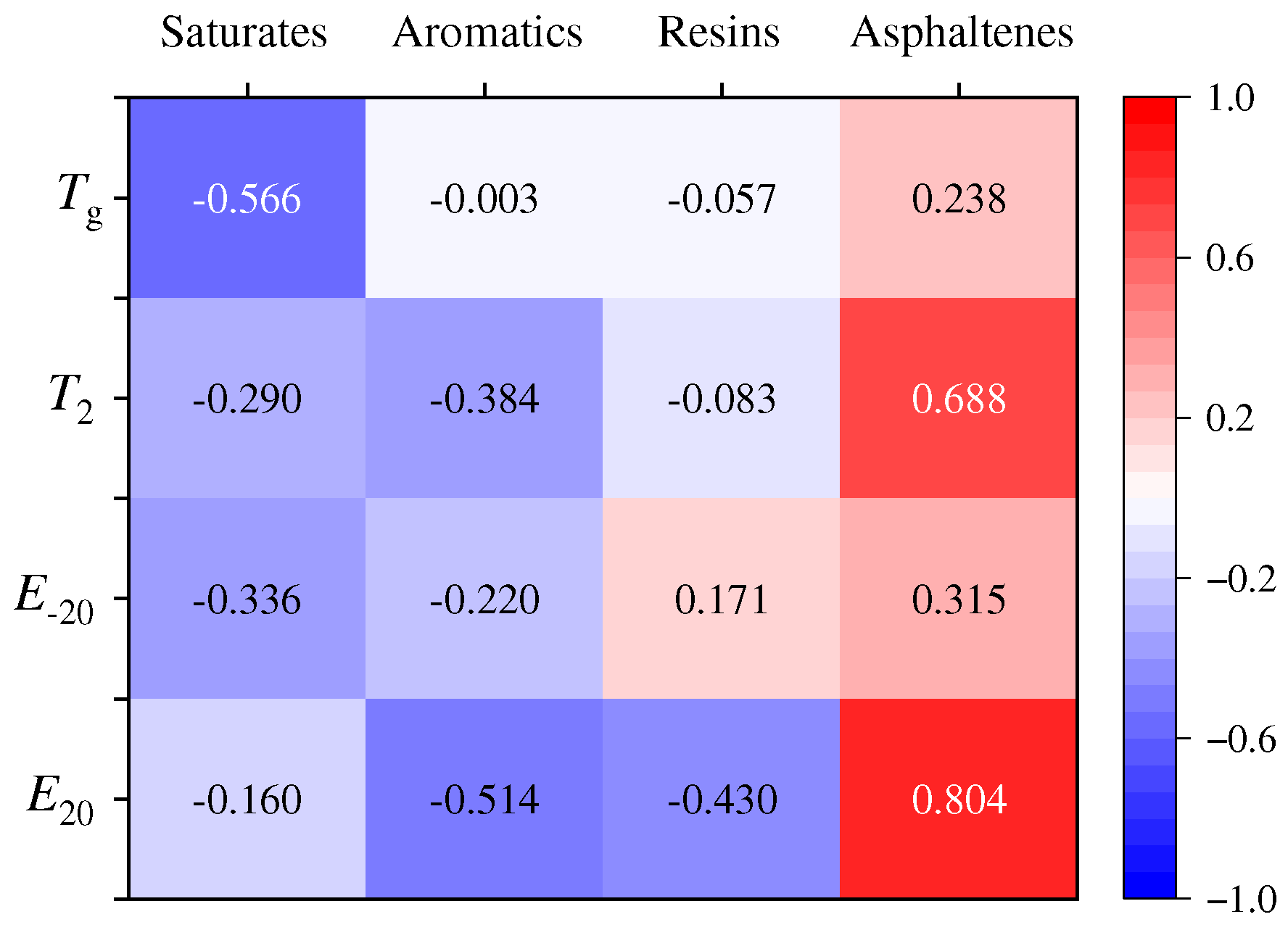
3.3. Relationship Analysis Between Phase Transition Characteristics and Asphalt Binder Components
3.3.1. Single Factor Correlation Analysis
3.3.2. Multiple Linear Regression Analysis
4. Conclusions
- Low-temperature performance: Tg effectively distinguishes asphalt binder behavior even when ductility values exceed 100 cm or brittle fracture is observed, addressing empirical limitations.
- High-temperature performance: Strong correlations between T2, E20, and viscosity validate their utility in predicting rutting resistance; however, overlapping ranges with penetration grades suggest complementary use.
- Chemical composition: Saturates reduce Tg, enhancing low-temperature flexibility, while asphaltenes elevate E20, improving high-temperature stiffness. Nonetheless, the weak correlations between individual SARA fractions and low-temperature indices highlight the necessity for a holistic compositional analysis.
- Integration into existing grading systems: The proposed DMA-based phase-transition indicators (Tg, T2, E−20, E20) can be incorporated into current binder specifications as supplementary performance criteria. For instance, Tg could serve as a low-temperature performance grade supplement, especially for regions experiencing extreme cold, while T2 and E20 could enhance high-temperature performance grade classification. This dual approach—combining empirical metrics with mechanistic indicators—would provide a more comprehensive evaluation framework, enabling better material selection tailored to specific climatic and loading conditions.
- Practical implications: DMA-based phase-transition indicators bridge the gap between empirical specifications and mechanistic understanding, facilitating precise material selection for diverse climatic conditions. It should be noted that the findings and models presented in this study are based on laboratory testing of neat asphalt binders under controlled conditions. The applicability to modified asphalt binders or real-world pavement environments may require further validation. Future work should explore modified asphalt binders and conduct a field validation to refine these models for broader engineering applications.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DMA | Dynamic Mechanical Analysis |
| SARA | Saturate, Aromatic, Resin, and Asphaltene |
| PTT | Phase Transition Temperature |
| TTSP | Time–Temperature Superposition Principle |
| DSC | Differential Scanning Calorimetry |
| VTI | Viscoelastic Temperature Interval |
References
- Liu, J.; Sun, Y.; Wang, W.; Chen, J. Using the viscoelastic parameters to estimate the glass transition temperature of asphalt binders. Constr. Build. Mater. 2017, 153, 908–917. [Google Scholar] [CrossRef]
- Tan, Y.; Guo, M. Study on the phase behavior of asphalt mastic. Constr. Build. Mater. 2013, 47, 311–317. [Google Scholar] [CrossRef]
- Guo, M. Dynamic Mechanical Thermal Analysis of Polymers and Composites; Chemical Industry Press: Beijing, China, 2002. [Google Scholar]
- Elseifi, M.A.; Mohammad, L.N.; Glover, I.; Negulescu, I.; Daly, W.H.; Abadie, C. Relationship between Molecular Compositions and Rheological Properties of Neat Asphalt Binder at Low and Intermediate Temperatures. J. Mater. Civ. Eng. 2010, 22, 1288–1294. [Google Scholar] [CrossRef]
- Kriz, P.; Stastna, J.; Zanzotto, L. Glass Transition and Phase Stability in Asphalt Binders. Road Mater. Pavement Des. 2008, 9 (Suppl. 1), 37–65. [Google Scholar] [CrossRef]
- Sun, Y.; Huang, B.; Chen, J.; Jia, X.; Ding, Y. Characterizing rheological behavior of asphalt binder over a complete range of pavement service loading frequency and temperature. Constr. Build. Mater. 2016, 123, 661–672. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Ma, Z.; Shan, L.; Zhang, C. Evaluation of the High- and Low-Temperature Performance of Asphalt Mortar Based on the DMA Method. Materials 2022, 15, 3341. [Google Scholar] [CrossRef]
- Caro, S.; Sánchez, D.B.; Caicedo, B. Methodology to characterise non-standard asphalt materials using DMA testing: Application to natural asphalt mixtures. Int. J. Pavement Eng. 2014, 16, 1–10. [Google Scholar] [CrossRef]
- Kang, Y.; Song, M.; Pu, L.; Liu, T. Rheological behaviors of epoxy asphalt binder in comparison of base asphalt binder and SBS modified asphalt binder. Constr. Build. Mater. 2015, 76, 343–350. [Google Scholar] [CrossRef]
- Wang, D.; Falchetto, A.C.; Riccardi, C.; Wistuba, M.P. Investigation on the low temperature properties of asphalt binder: Glass transition temperature and modulus shift factor. Constr. Build. Mater. 2020, 245, 118351. [Google Scholar] [CrossRef]
- Xu, J.; Fan, Z.; Lin, J.; Yang, X.; Wang, D.; Oeser, M. Predicting the low-temperature performance of asphalt binder based on rheological model. Constr. Build. Mater. 2021, 302, 124401. [Google Scholar] [CrossRef]
- Gunay, T.; Tomkovic, T.; Hatzikiriakos, S.G. Thermorheological properties of asphalt binders. Can. J. Chem. Eng. 2020, 98, 1803–1814. [Google Scholar] [CrossRef]
- Ayanarayanan, K.; Rasana, N.; Mishra, R.K. Chapter 6-Dynamic Mechanical Thermal Analysis of Polymer Nanocomposites. In Thermal and Rheological Measurement Techniques for Nanomaterials Characterization; Elsevier: Amsterdam, The Netherlands, 2017; pp. 123–157. [Google Scholar] [CrossRef]
- Yuan, Q.; Liu, W.; Pan, Y.; Deng, D.; Liu, Z. Characterization of Cement Asphalt Mortar for Slab Track by Dynamic Mechanical Thermoanalysis. J. Mater. Civ. Eng. 2016, 28, 04015154. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, P.; Wu, J. Dynamic Mechanical Properties of EVA Polymer-Modified Cement Paste at Early Age. Phys. Procedia 2012, 25, 305–310. [Google Scholar] [CrossRef]
- Fu, Q.; Xie, Y.; Long, G.; Niu, D.; Song, H. Dynamic mechanical thermo-analysis of cement and asphalt mortar. Powder Technol. 2017, 313, 36–43. [Google Scholar] [CrossRef]
- Morlat, R.; Godard, P.; Bomal, Y.; Orange, G. Dynamic mechanical thermoanalysis of latexes in cement paste. Cem. Concr. Res. 1999, 29, 847–853. [Google Scholar] [CrossRef]
- Yang, G.; Wang, X.; Zhou, X.; Wang, Y. Experimental Study on the Phase Transition Characteristics of Asphalt Mixture for Stress Absorbing Membrane Interlayer. Materials 2020, 13, 474. [Google Scholar] [CrossRef]
- You, L.; Spyriouni, T.; Dai, Q.; You, Z.; Khanal, A. Experimental and molecular dynamics simulation study on thermal, transport, and rheological properties of asphalt. Constr. Build. Mater. 2020, 265, 120358. [Google Scholar] [CrossRef]
- Apostolidis, P.; Elwardany, M.; Porot, L.; Vansteenkiste, S.; Chailleux, E. Glass transitions in bituminous binders. Mater. Struct. 2021, 54, 132. [Google Scholar] [CrossRef]
- Sultana, S.; Bhasin, A. Effect of chemical composition on rheology and mechanical properties of asphalt binder. Constr. Build. Mater. 2014, 72, 293–300. [Google Scholar] [CrossRef]
- Oyekunle, L.O. Influence of Chemical Composition on the Physical Characteristics of Paving Asphalts. Pet. Sci. Technol. 2007, 25, 1401–1414. [Google Scholar] [CrossRef]
- Zhang, M.; Hao, P.; Dong, S.; Li, Y.; Yuan, G. Asphalt binder micro-characterization and testing approaches: A review. Meas. J. Int. Meas. Confed. 2020, 151, 107255. [Google Scholar] [CrossRef]
- Guo, M.; Liang, M.; Sreeram, A.; Bhasin, A.; Luo, D. Characterisation of rejuvenation of various modified asphalt binders based on simplified chromatographic techniques. Int. J. Pavement Eng. 2022, 23, 4333–4343. [Google Scholar] [CrossRef]
- Handle, F.; Füssl, J.; Neudl, S.; Grossegger, D.; Eberhardsteiner, L.; Hofko, B.; Hospodka, M.; Blab, R.; Grothe, H. The bitumen microstructure: A fluorescent approach. Mater. Struct. 2016, 49, 167–180. [Google Scholar] [CrossRef]
- Wei, J.; Dong, F.; Li, Y.; Zhang, Y. Relationship analysis between surface free energy and chemical composition of asphalt binder. Constr. Build. Mater. 2014, 71, 116–123. [Google Scholar] [CrossRef]
- Wang, J.; Wang, T.; Hou, X.; Xiao, F. Modelling of rheological and chemical properties of asphalt binder considering SARA fraction. Fuel 2019, 238, 320–330. [Google Scholar] [CrossRef]
- Weigel, S.; Stephan, D. Relationships between the chemistry and the physical properties of bitumen. Road Mater. Pavement Des. 2018, 19, 1636–1650. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Wang, L. Understanding the relationships between rheology and chemistry of asphalt binders: A review. Constr. Build. Mater. 2022, 329, 127161. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Y. Physico-chemo-rheological characterization of neat and polymer-modified asphalt binders. Constr. Build. Mater. 2019, 199, 471–482. [Google Scholar] [CrossRef]
- Jiang, J.; Lu, F.; Guo, X.; Hao, P.; Wang, W.; Yu, J. Effect of SARA Fractions on Fatigue Properties of Hard Asphalt. Materials 2024, 17, 2713. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Zhan, E.; Shan, L. Effect of SARA on Rheological Properties of Asphalt Binders. J. Mater. Civ. Eng. 2019, 31, 4019086. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Zhang, J.; Li, Z.; Chen, Z.; Pei, J.; Wang, M. Examining the rheological and adhesion performance of asphalt: Insights into the influence of SARA components. Case Stud. Constr. Mater. 2024, 21, e03427. [Google Scholar] [CrossRef]
- Wang, T.; Wang, J.; Hou, X.; Xiao, F. Effects of SARA fractions on low temperature properties of asphalt binders. Road Mater. Pavement Des. 2021, 22, 539–556. [Google Scholar] [CrossRef]
- Martin Wieser, A.; Schaur, S.H. Unterberger, Polymer-Bitumen Interaction: A Correlation Study with Six Different Bitumens to Investigate the Influence of SARA Fractions on the Phase Stability, Swelling, and Thermo-Rheological Properties of SBS-PmB. Materials 2021, 14, 1273. [Google Scholar] [CrossRef]
- JTG E20-2011; Standard Test Methods of Bitumen and Bituminous Mixtures for Highway Engineering. China Communications Press: Beijing, China, 2011.






| Asphalt Binder | Pen. (25 °C) /0.1 mm | Softening Point/°C | Ductility (15 °C) /cm | Ductility (10 °C) /cm | Dynamic Viscosity (60 °C)/Pa∙s | Component Analysis/% | |||
|---|---|---|---|---|---|---|---|---|---|
| Saturates | Aromatics | Resins | Asphaltenes | ||||||
| A1 | 22 | 61.1 | 0 | 0 | 2266 | 7.7 | 38.8 | 37.3 | 16.2 |
| A2 | 49 | 52.2 | >100 | 10 | 500 | 10.2 | 40.2 | 35.0 | 14.6 |
| A3 | 67 | 49.0 | >100 | >100 | 224 | 11.8 | 41.0 | 34.3 | 12.9 |
| B1 | 30 | 59.0 | 8 | 0 | 1159 | 11.1 | 43.3 | 30.9 | 14.7 |
| B2 | 37 | 57.2 | 10 | 0 | 843 | 9.7 | 41.0 | 34.7 | 14.6 |
| B3 | 46 | 53.2 | 53 | 0 | 531 | 11.4 | 40.0 | 34.4 | 14.2 |
| B4 | 70 | 45.4 | >100 | 69 | 266 | 12.1 | 37.7 | 37.0 | 13.2 |
| B5 | 88 | 44.0 | >100 | 38 | 188 | 10.9 | 42.0 | 35.5 | 13.6 |
| C1 | 31 | 59.6 | 8 | 0 | 1113 | 8.6 | 40.8 | 35.1 | 15.5 |
| C2 | 37 | 57.7 | 12 | 0 | 808 | 10.4 | 40.8 | 33.8 | 15.0 |
| C3 | 47 | 53.7 | 48 | 0 | 490 | 9.6 | 40.5 | 35.3 | 14.6 |
| C4 | 71 | 46.1 | >100 | 85 | 198 | 11.0 | 43.4 | 32.0 | 13.6 |
| C5 | 90 | 44.7 | >100 | 51 | 146 | 11.1 | 39.5 | 35.8 | 13.6 |
| D1 | 11 | 98.9 | 0 | 0 | - | 10.6 | 29.4 | 32.1 | 27.9 |
| D2 | 16 | 80.2 | 0 | 0 | 59,214 | 11.1 | 32.5 | 31.8 | 24.6 |
| D3 | 16 | 80.4 | 0 | 0 | 52,809 | 11.1 | 32.5 | 32.2 | 24.2 |
| D4 | 34 | 59.8 | 7 | 0 | 1533 | 11.7 | 37.2 | 32.9 | 18.2 |
| D5 | 35 | 60.0 | 8 | 0 | 1377 | 11.6 | 37.6 | 33.4 | 17.4 |
| D6 | 42 | 56.7 | 9 | 0 | 887 | 11.6 | 38.6 | 33.1 | 16.7 |
| E1 | 27 | 64.3 | 5 | 0 | 3403 | 10.1 | 39.5 | 32.5 | 17.9 |
| E2 | 47 | 54.6 | 24 | 8 | 468 | 11.2 | 41.4 | 30.7 | 16.7 |
| E3 | 47 | 50.5 | 17 | 5 | 417 | 10.9 | 40.5 | 33.4 | 15.2 |
| E4 | 47 | 50.2 | 37 | 0 | 443 | 10.0 | 47.0 | 31.7 | 11.3 |
| E5 | 37 | 53.7 | 12 | 0 | 656 | 11.2 | 42.6 | 32.8 | 13.4 |
| F1 | 69 | 46.9 | >100 | 88 | 258 | 9.5 | 40.6 | 36.1 | 13.8 |
| F2 | 71 | 46.7 | >100 | >100 | 194 | 6.2 | 56.1 | 27.3 | 10.4 |
| F3 | 74 | 46.8 | >100 | >100 | 157 | 6.0 | 56.1 | 28.6 | 9.3 |
| G1 | 87 | 43.7 | >100 | 55 | 137 | 9.5 | 50.4 | 28.9 | 11.2 |
| G2 | 88 | 43.7 | >100 | >100 | 139 | 9.5 | 49.0 | 30.4 | 11.1 |
| G3 | 87 | 44.3 | >100 | >100 | 156 | 13.9 | 40.5 | 32.0 | 13.6 |
| Strain Amplitude | Frequency | Heating Rate | Temperature Range |
|---|---|---|---|
| 25 με | 10 Hz | 2 °C/min | −35 °C to 35 °C |
| Asphalt Binder | Phase Transition Temperature/°C | VTI/°C | Characteristic Modulus/MPa | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| T1 | T0 | T2 | Tg | E1 | E0 | E2 | Eg | E−20 | E20 | ||
| A1 | −13.5 | 2.8 | 19.0 | 6.1 | 32.5 | 1910 | 1073 | 236 | 854 | 2046 | 210 |
| A2 | −16.4 | −2.1 | 12.1 | −0.3 | 28.6 | 1838 | 1043 | 249 | 911 | 1928 | 90 |
| A3 | −18.6 | −4.8 | 9.1 | −3.2 | 27.7 | 1864 | 1060 | 255 | 942 | 1905 | 60 |
| B1 | −14.9 | 0.5 | 15.8 | 3.0 | 30.7 | 1806 | 1023 | 240 | 856 | 1917 | 145 |
| B2 | −16.3 | −1.5 | 13.4 | 0.8 | 29.7 | 1897 | 1077 | 258 | 914 | 1989 | 114 |
| B3 | −17.2 | −2.5 | 12.2 | −0.6 | 29.4 | 1928 | 1095 | 262 | 955 | 2004 | 99 |
| B4 | −17.7 | −4.4 | 8.9 | −3.7 | 26.6 | 1777 | 1012 | 248 | 959 | 1840 | 59 |
| B5 | −19.1 | −6.0 | 7.1 | −6.4 | 26.1 | 1641 | 936 | 232 | 960 | 1666 | 45 |
| C1 | −16.2 | −0.2 | 15.9 | 2.8 | 32.0 | 2018 | 1140 | 263 | 930 | 2114 | 160 |
| C2 | −16.4 | −1.2 | 14.1 | 1.6 | 30.5 | 1951 | 1105 | 259 | 904 | 2043 | 124 |
| C3 | −17.6 | −2.6 | 12.3 | −0.7 | 29.9 | 1993 | 1131 | 269 | 989 | 2062 | 104 |
| C4 | −14.2 | −2.3 | 9.5 | −1.6 | 23.7 | 1698 | 970 | 243 | 918 | 1834 | 58 |
| C5 | −18.5 | −5.7 | 7.2 | −5.3 | 25.7 | 1792 | 1019 | 246 | 992 | 1810 | 41 |
| D1 | −16.2 | 3.2 | 22.5 | 2.4 | 38.7 | 1887 | 1073 | 260 | 1117 | 1963 | 324 |
| D2 | −18.6 | 0.7 | 19.9 | 1.6 | 38.5 | 2069 | 1175 | 281 | 1118 | 2102 | 279 |
| D3 | −18.7 | −0.4 | 17.9 | 0.3 | 36.6 | 1965 | 1116 | 268 | 1075 | 1997 | 219 |
| D4 | −19.5 | −3.6 | 12.4 | −3.4 | 31.8 | 2020 | 1147 | 275 | 1134 | 2035 | 115 |
| D5 | −20.2 | −4.3 | 11.5 | −3.5 | 31.7 | 1850 | 1051 | 252 | 999 | 1846 | 95 |
| D6 | −20.3 | −4.9 | 10.4 | −4.1 | 30.7 | 1950 | 1109 | 267 | 1046 | 1941 | 86 |
| E1 | −21.4 | −5.3 | 10.9 | −4.7 | 32.3 | 1844 | 1047 | 251 | 1013 | 1802 | 90 |
| E2 | −20.1 | −4.8 | 10.6 | −3.4 | 30.7 | 1880 | 1067 | 253 | 969 | 1876 | 80 |
| E3 | −19.8 | −4.3 | 11.2 | −4.4 | 31.0 | 1692 | 963 | 233 | 971 | 1698 | 85 |
| E4 | −20.2 | −4.6 | 10.9 | −4.4 | 31.1 | 1733 | 986 | 238 | 971 | 1728 | 83 |
| E5 | −19.5 | −3.4 | 12.7 | −1.7 | 32.1 | 1923 | 1090 | 258 | 972 | 1937 | 110 |
| F1 | −18.3 | −4.2 | 9.9 | −2.2 | 28.1 | 2049 | 1165 | 281 | 1000 | 2104 | 77 |
| F2 | −15.4 | −0.9 | 13.6 | 2.5 | 29.0 | 1916 | 1087 | 257 | 838 | 2029 | 113 |
| F3 | −15.6 | −1.2 | 13.3 | 2.3 | 28.9 | 1899 | 1078 | 257 | 822 | 2007 | 109 |
| G1 | −18.0 | −4.5 | 9.0 | −4.1 | 27.0 | 1662 | 944 | 226 | 920 | 1715 | 51 |
| G2 | −17.9 | −4.2 | 9.6 | −3.4 | 27.4 | 1650 | 935 | 220 | 882 | 1704 | 50 |
| G3 | −18.3 | −5.3 | 7.6 | −5.4 | 25.9 | 1699 | 970 | 240 | 978 | 1748 | 50 |
| Goodness of Fit Results | ||||
|---|---|---|---|---|
| Tg | T2 | E−20 | E20 | |
| Multiple R | 0.7591 | 0.8830 | 0.7043 | 0.9149 |
| R2 | 0.5763 | 0.7798 | 0.4960 | 0.8370 |
| Adjusted R2 | 0.5085 | 0.7445 | 0.4154 | 0.8109 |
| Standard error | 2.2136 | 1.9071 | 102.3 | 29.4 |
| Observations | 30 | 30 | 30 | 30 |
| DS | SS | MS | F | p | ||
|---|---|---|---|---|---|---|
| Tg | Regression | 4 | 166.6 | 41.7 | 8.50 | 1.8 × 10−4 |
| Residual | 25 | 122.5 | 4.9 | |||
| Total | 29 | 289.1 | ||||
| T2 | Regression | 4 | 321.9 | 80.5 | 22.13 | 6.6 × 10−8 |
| Residual | 25 | 90.9 | 3.6 | |||
| Total | 29 | 412.9 | ||||
| E−20 | Regression | 4 | 257,519.0 | 64,379.7 | 6.15 | 1.4 × 10−3 |
| Residual | 25 | 261,632.4 | 10,465.3 | |||
| Total | 29 | 519,151.4 | ||||
| E20 | Regression | 4 | 111,246.1 | 27,811.5 | 32.10 | 1.6 × 10−9 |
| Residual | 25 | 21,662.3 | 866.5 | |||
| Total | 29 | 132,908.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wei, J.; Xu, X.; Xu, Q.; Sun, Y.; Liu, N.; Zhang, Z. Characterizing Asphalt Binder Phase Transitions via Dynamic Mechanical Analysis: Performance Implications and SARA Fraction Correlations. Coatings 2025, 15, 1046. https://doi.org/10.3390/coatings15091046
Wang Y, Wei J, Xu X, Xu Q, Sun Y, Liu N, Zhang Z. Characterizing Asphalt Binder Phase Transitions via Dynamic Mechanical Analysis: Performance Implications and SARA Fraction Correlations. Coatings. 2025; 15(9):1046. https://doi.org/10.3390/coatings15091046
Chicago/Turabian StyleWang, Yanzhu, Jincheng Wei, Xizhong Xu, Qinsheng Xu, Yue Sun, Na Liu, and Zhengchao Zhang. 2025. "Characterizing Asphalt Binder Phase Transitions via Dynamic Mechanical Analysis: Performance Implications and SARA Fraction Correlations" Coatings 15, no. 9: 1046. https://doi.org/10.3390/coatings15091046
APA StyleWang, Y., Wei, J., Xu, X., Xu, Q., Sun, Y., Liu, N., & Zhang, Z. (2025). Characterizing Asphalt Binder Phase Transitions via Dynamic Mechanical Analysis: Performance Implications and SARA Fraction Correlations. Coatings, 15(9), 1046. https://doi.org/10.3390/coatings15091046






