Crack Propagation Mechanism in Thermal Barrier Coatings Containing Different Residual Grit Particles Under Thermal Cycling
Abstract
1. Introduction
2. Model Description
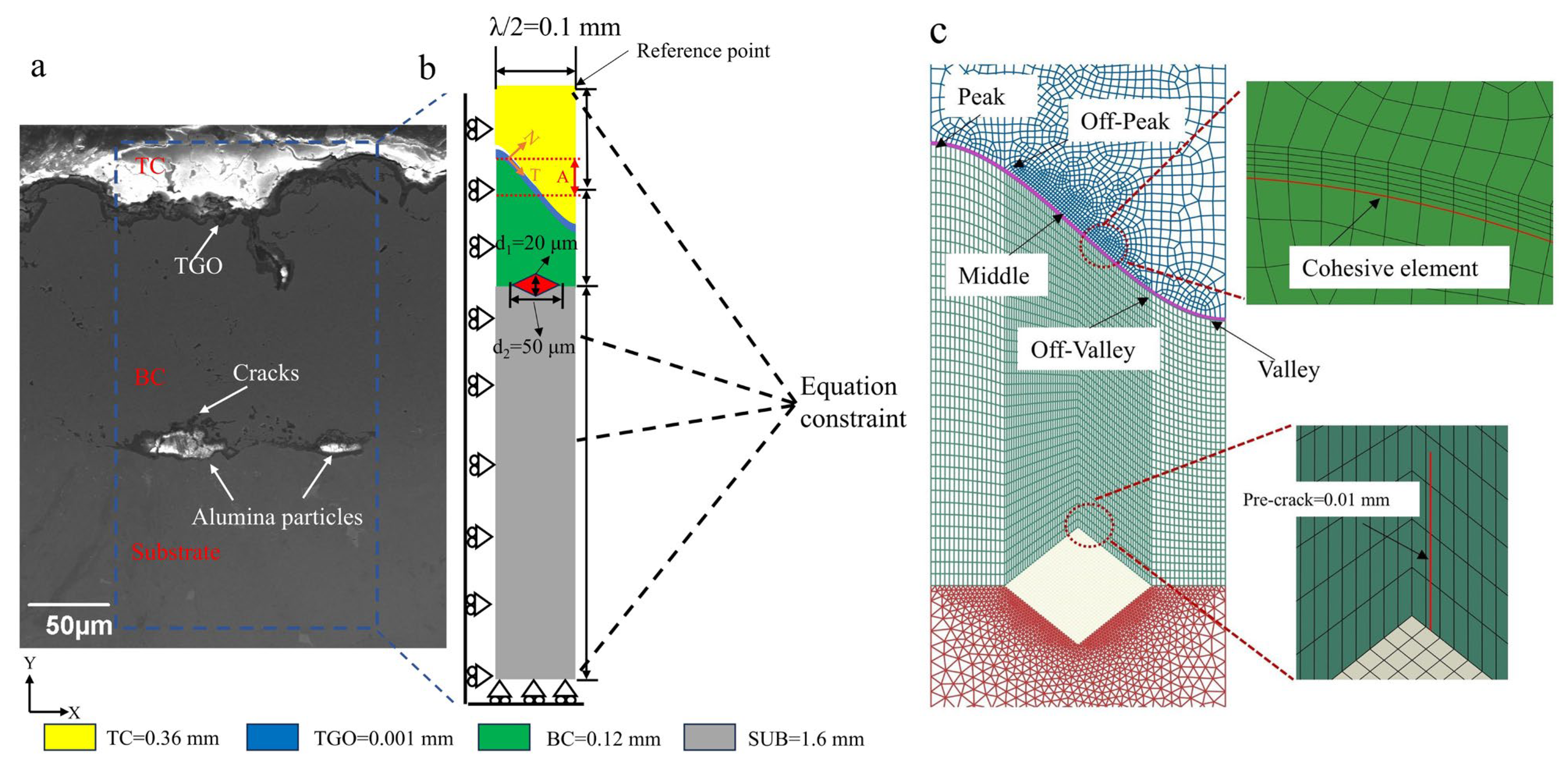
2.1. Geometry Model
2.2. Boundary Condition and Meshing
2.3. Material Property
2.4. Thermal Cycling History
2.5. Crack Initiation and Growth Criterion
3. Results and Discussion
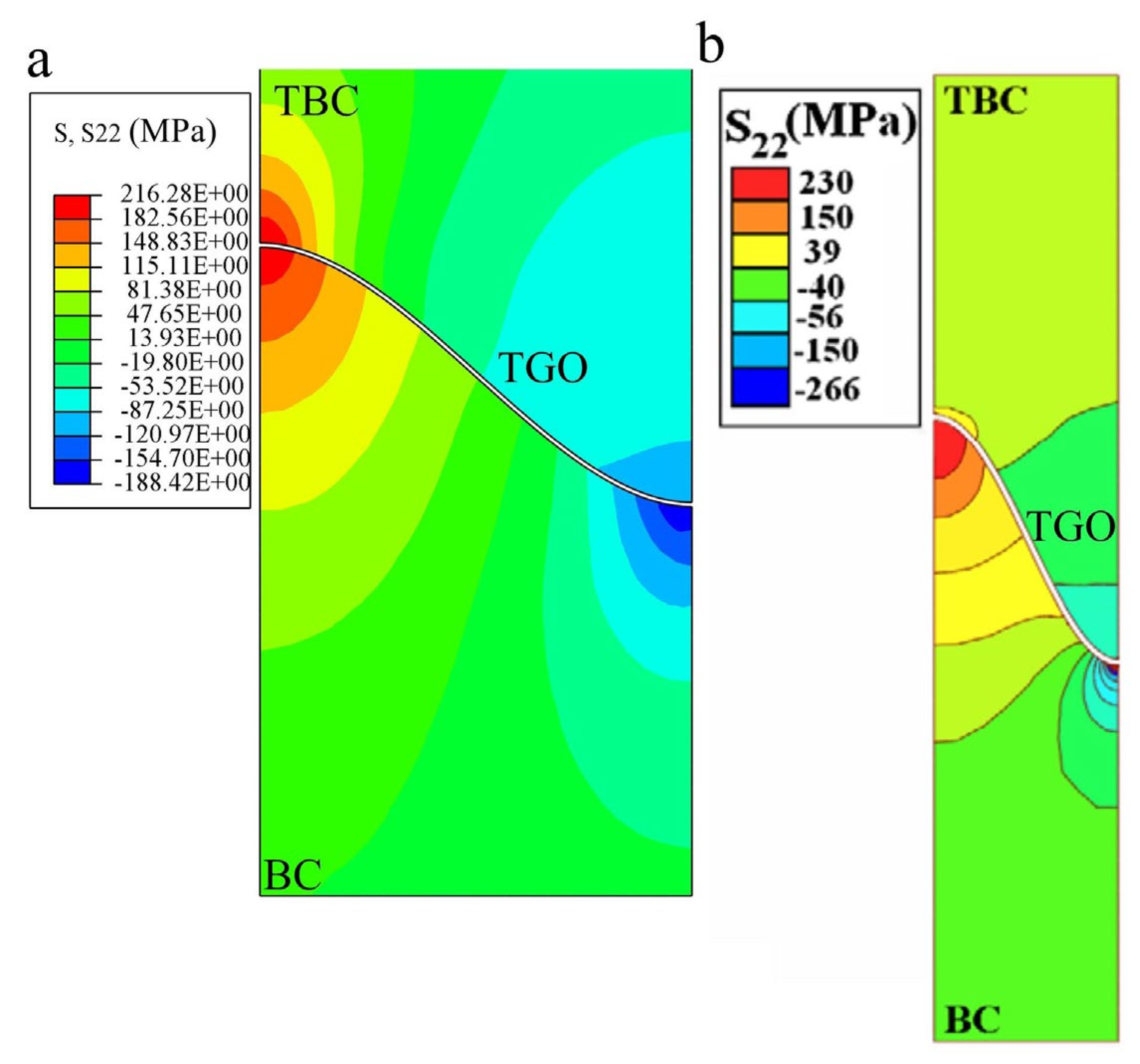
3.1. Stress Distribution During Thermal Cycling
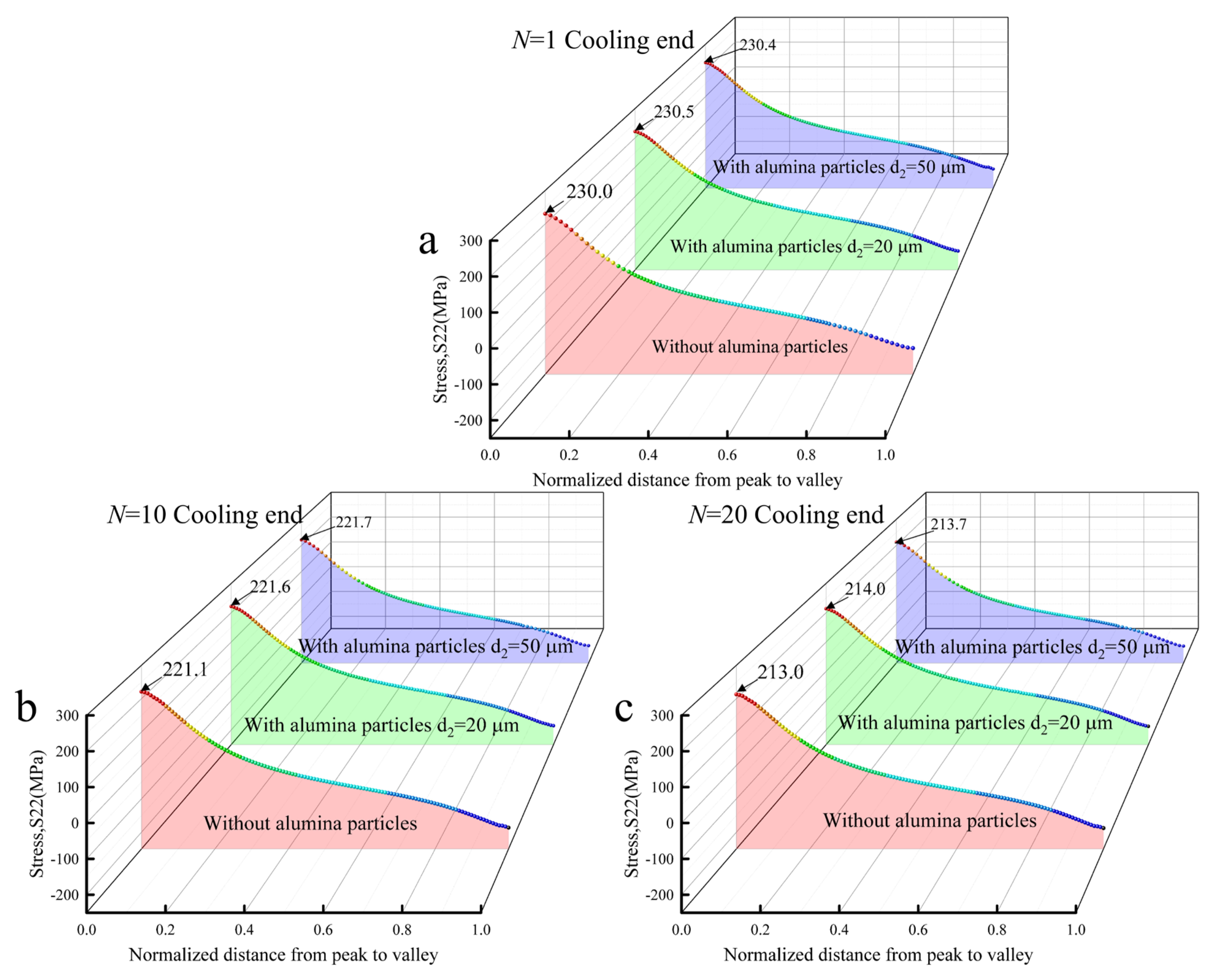
3.2. Effect of Grit Particles on BC/TGO Interfacial Crack Propagation
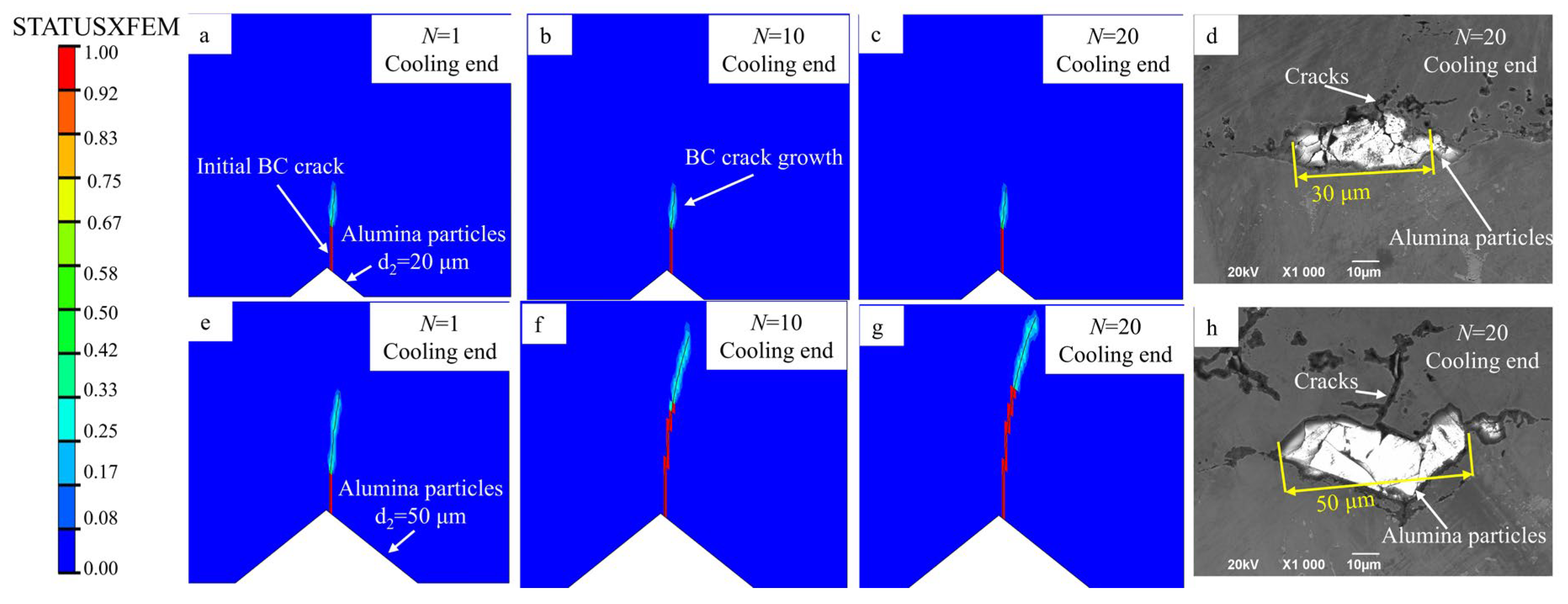
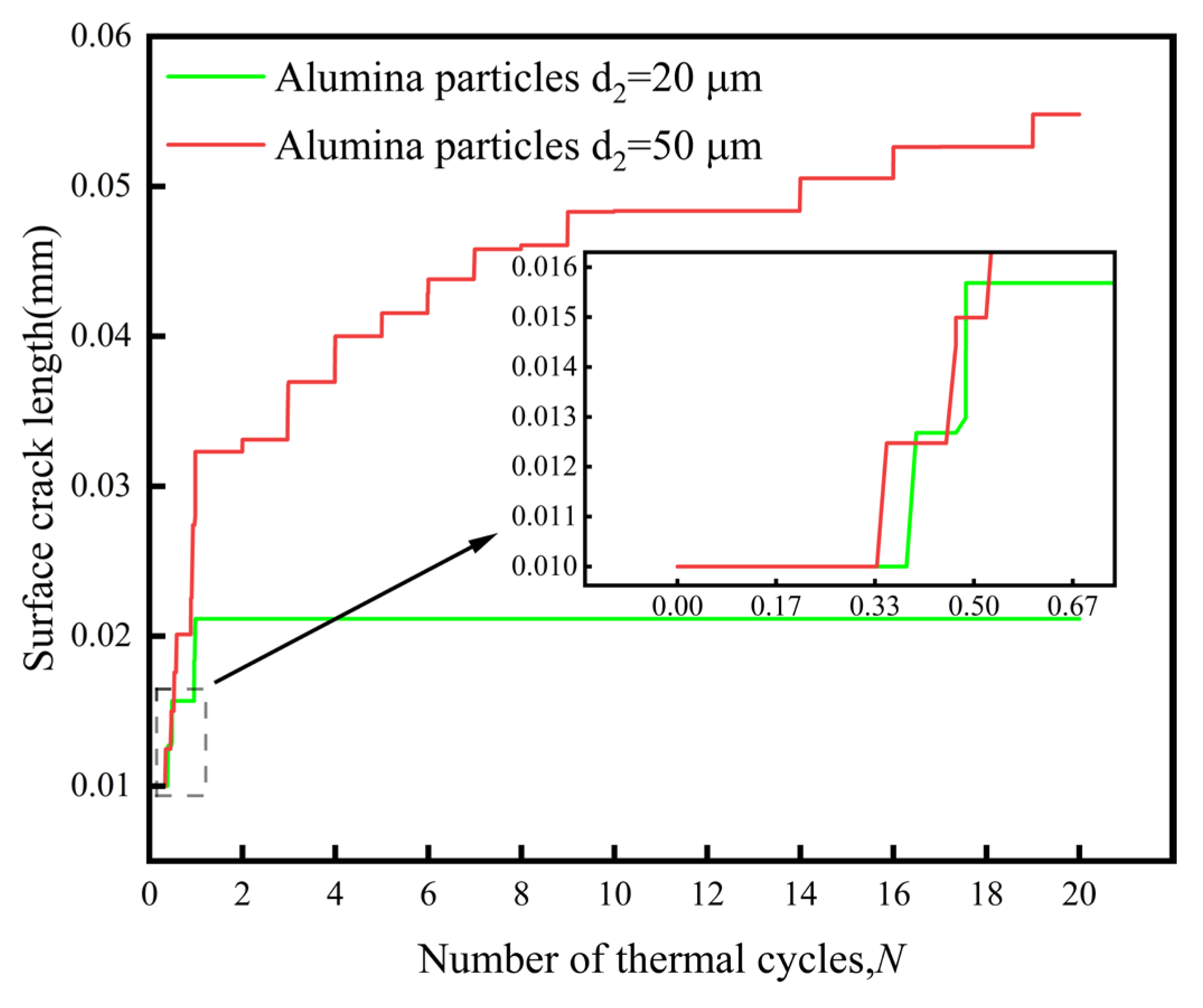
3.3. Effect of Grit Particles on Crack Propagation Within the BC Layer
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Long, H.; Mao, S.; Liu, Y.; Zhang, Z.; Han, X. Microstructural and compositional design of Ni-based single crystalline superalloys―A review. J. Alloys Compd. 2018, 743, 203–220. [Google Scholar] [CrossRef]
- Padture, N.P.; Gell, M.; Jordan, E.H. Thermal Barrier Coatings for Gas-Turbine Engine Applications. Science 2002, 296, 280–284. [Google Scholar] [CrossRef] [PubMed]
- Clarke, D.R.; Oechsner, M.; Padture, N.P. Thermal-barrier coatings for more efficient gas-turbine engines. MRS Bull. 2012, 37, 891–898. [Google Scholar] [CrossRef]
- Thakare, J.G.; Pandey, C.; Mahapatra, M.M.; Mulik, R.S. Thermal Barrier Coatings—A State of the Art Review. Met. Mater. Int. 2021, 27, 1947–1968. [Google Scholar] [CrossRef]
- Liu, K.; Du, Y.; Guo, X.; Ma, J.; He, W.; Cao, Y.; Du, J. Study of stress-driven cracking behavior and competitive crack growth in functionally graded thermal barrier coatings. Surf. Coat. Technol. 2023, 473, 129969. [Google Scholar] [CrossRef]
- Ranjbar-far, M.; Absi, J.; Mariaux, G.; Smith, D.S. Crack propagation modeling on the interfaces of thermal barrier coating system with different thickness of the oxide layer and different interface morphologies. Mater. Des. 2011, 32, 4961–4969. [Google Scholar] [CrossRef]
- Wei, Z.; Cai, H.; Feng, R.; Zhang, H. The Combined Effect of Creep and TGO Growth on the Cracking Driving Force in a Plasma-Sprayed Thermal Barrier System. J. Therm. Spray Technol. 2019, 28, 1000–1016. [Google Scholar] [CrossRef]
- Abdelgawad, A.; Al-Athel, K.; Albinmousa, J. Analysis of crack initiation and propagation in Thermal Barrier Coatings using SEM-Based geometrical model with extended finite element method. Ceram. Int. 2021, 47, 33140–33151. [Google Scholar] [CrossRef]
- Shi, D.; Song, J.; Li, S.; Qi, H.; Yang, X. Cracking behaviors of EB-PVD thermal barrier coating under temperature gradient. Ceram. Int. 2019, 45, 18518–18528. [Google Scholar] [CrossRef]
- Mohammadi, Z.; Ziaei-Moayyed, A.A.; Mesgar, A.S.-M. Grit blasting of Ti–6Al–4V alloy: Optimization and its effect on adhesion strength of plasma-sprayed hydroxyapatite coatings. J. Mater. Process. Technol. 2007, 194, 15–23. [Google Scholar] [CrossRef]
- Moreau, C.; Gougeon, P.; Lamontagne, M. Influence of substrate preparation on the flattening and cooling of plasma-sprayed particles. J. Therm. Spray Technol. 1995, 4, 25–33. [Google Scholar] [CrossRef]
- Giouse, J.B.; White, K.; Tromas, C. Nanoindentation characterization of the surface mechanical properties of a 17-4PH stainless steel substrate treated with grit blasting and coated with a Cr3C2-NiCr coating. Surf. Coat. Technol. 2019, 368, 119–125. [Google Scholar] [CrossRef]
- Nowak, W.J.; Ochał, K.; Wierzba, P.; Gancarczyk, K.; Wierzba, B. Effect of Substrate Roughness on Oxidation Resistance of an Aluminized Ni-Base Superalloy. Metals 2019, 9, 782. [Google Scholar] [CrossRef]
- Abbas, M.; Smith, G.M.; Munroe, P.R. Microstructural study of HVOF sprayed Ni particles on a grit-blasted stainless-steel substrate. Surf. Coat. Technol. 2021, 409, 126832. [Google Scholar] [CrossRef]
- Hernández, L.; Oliveira, F.; Berríos, J.A.; Villalobos, C.; Pertuz, A.; Puchi Cabrera, E.S. Fatigue properties of a 4340 steel coated with a Colmonoy 88 deposit applied by high-velocity oxygen fuel. Surf. Coat. Technol. 2000, 133–134, 68–77. [Google Scholar] [CrossRef]
- Antoš, J.; Duliškovič, J.; Bejblíková, S. Aluminium oxide grid blasting: Grid size and blasting pressure influence on the substrate surface contamination, roughness and ceramic plasma spray coating adhesion strength. J. Phys. Conf. Ser. 2023, 2572, 012009. [Google Scholar] [CrossRef]
- Lai, J.; Shen, X.; Yuan, X.; Li, D.; Gong, X.; Zhao, F.; Liao, X.; Yu, J. The Effect of Shot Blasting Abrasive Particles on the Microstructure of Thermal Barrier Coatings Containing Ni-Based Superalloy. Coatings 2024, 14, 1312. [Google Scholar] [CrossRef]
- ABAQUS Analysis User’s Guide, version 6.22; Dassault Systèmes: Vélizy-Villacoublay, France, 2022; Available online: https://help.3ds.com/HelpProductsDS.aspx (accessed on 20 June 2025.).
- Cen, L.; Qin, W.; Yu, Q. A three-dimensional finite element model for the oxide growth mechanism and growth-induced stress within thermal barrier system. Mater. Today Commun. 2021, 29, 102790. [Google Scholar] [CrossRef]
- Wei, Z.; Liu, Y.; Cheng, B.; Tahir, A. Influence of non-uniform feature of thermally grown oxide thickness on the local stress state and cracking behavior in TBC. Surf. Coat. Technol. 2022, 443, 128607. [Google Scholar] [CrossRef]
- Xiao, Y.Q.; Yang, L.; Zhu, W.; Zhou, Y.C.; Pi, Z.P.; Wei, Y.G. Delamination mechanism of thermal barrier coatings induced by thermal cycling and growth stresses. Eng. Fail. Anal. 2021, 121, 105202. [Google Scholar] [CrossRef]
- Aktaa, J.; Sfar, K.; Munz, D. Assessment of TBC systems failure mechanisms using a fracture mechanics approach. Acta Mater. 2005, 53, 4399–4413. [Google Scholar] [CrossRef]
- Song, J.; Qi, H.; Shi, D.; Yang, X.; Li, S. Effect of non-uniform growth of TGO layer on cracking behaviors in thermal barrier coatings: A numerical study. Surf. Coat. Technol. 2019, 370, 113–124. [Google Scholar] [CrossRef]
- Yu, Q.M.; Zhou, H.L.; Wang, L.B. Influences of interface morphology and thermally grown oxide thickness on residual stress distribution in thermal barrier coating system. Ceram. Int. 2016, 42, 8338–8350. [Google Scholar] [CrossRef]
- Białas, M. Finite element analysis of stress distribution in thermal barrier coatings. Surf. Coat. Technol. 2008, 202, 6002–6010. [Google Scholar] [CrossRef]
- Jiang, J.; Wang, W.; Zhao, X.; Liu, Y.; Cao, Z.; Xiao, P. Numerical analyses of the residual stress and top coat cracking behavior in thermal barrier coatings under cyclic thermal loading. Eng. Fract. Mech. 2018, 196, 191–205. [Google Scholar] [CrossRef]
- Wei, Z.; Cai, H.; Li, C. Comprehensive dynamic failure mechanism of thermal barrier coatings based on a novel crack propagation and TGO growth coupling model. Ceram. Int. 2018, 44, 22556–22566. [Google Scholar] [CrossRef]
- Bostancı, S.M.; Gürses, E.; Çöker, D. Finite Element Modelling of TBC Failure Mechanisms by Using XFEM and CZM. Procedia Struct. Integr. 2019, 21, 91–100. [Google Scholar] [CrossRef]
- Zhu, W.; Zhang, Z.B.; Yang, L.; Zhou, Y.C.; Wei, Y.G. Spallation of thermal barrier coatings with real thermally grown oxide morphology under thermal stress. Mater. Des. 2018, 146, 180–193. [Google Scholar] [CrossRef]
- Fartash, A.H.; Lyavoli, H.F.; Poursaeidi, E.; Schmauder, S. Interfacial delamination of porous thermal barrier coatings based on SEM image processing in finite element model. Theor. Appl. Fract. Mech. 2023, 125, 103915. [Google Scholar] [CrossRef]
- Wang, L.; Li, D.C.; Yang, J.S.; Shao, F.; Zhong, X.H.; Zhao, H.Y.; Yang, K.; Tao, S.Y.; Wang, Y. Modeling of thermal properties and failure of thermal barrier coatings with the use of finite element methods: A review. J. Eur. Ceram. Soc. 2016, 36, 1313–1331. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T.A. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Zhou, Q.Q.; Yang, L.; Luo, C.; Chen, F.W.; Zhou, Y.C.; Wei, Y.G. Thermal barrier coatings failure mechanism during the interfacial oxidation process under the interaction between interface by cohesive zone model and brittle fracture by phase-field. Int. J. Solids Struct. 2021, 214–215, 18–34. [Google Scholar] [CrossRef]
- Li, B.; Fan, X.; Okada, H.; Wang, T. Mechanisms governing the failure modes of dense vertically cracked thermal barrier coatings. Eng. Fract. Mech. 2018, 189, 451–480. [Google Scholar] [CrossRef]
- Ranjbar-Far, M.; Absi, J.; Shahidi, S.; Mariaux, G. Impact of the non-homogenous temperature distribution and the coatings process modeling on the thermal barrier coatings system. Mater. Des. 2011, 32, 728–735. [Google Scholar] [CrossRef]
- Ranjbar-Far, M.; Absi, J.; Mariaux, G.; Dubois, F. Simulation of the effect of material properties and interface roughness on the stress distribution in thermal barrier coatings using finite element method. Mater. Des. 2010, 31, 772–781. [Google Scholar] [CrossRef]
- Rösler, J.; Bäker, M.; Aufzug, K. A parametric study of the stress state of thermal barrier coatings: Part I: Creep relaxation. Acta Mater. 2004, 52, 4809–4817. [Google Scholar] [CrossRef]
- Wei, Z.; Cai, Y.; Li, F.; Huang, H.; Wang, M. Heterogeneous multilayered delamination of thermally grown oxide accelerating spallation of thermal barrier coatings. Ceram. Int. 2024, 50, 49300–49310. [Google Scholar] [CrossRef]
- Bäker, M.; Rösler, J.; Heinze, G. A parametric study of the stress state of thermal barrier coatings Part II: Cooling stresses. Acta Mater. 2005, 53, 469–476. [Google Scholar] [CrossRef]





| Plastic Parameters | Temperature/(°C) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 400 | 600 | 800 | 900 | 1000 | ||||||
| σ/(Mpa) | 1100 | 2500 | 1100 | 2200 | 300 | 380 | 45 | 60 | 10 | 15 |
| εp | 0 | 0.23 | 0 | 0.30 | 0 | 0.02 | 0 | 0.02 | 0 | 0.01 |
| Material | Temperature/ (°C) | Elastic Modulus/ (GPa) | μ | Density/ (kg∙m−3) | CTE/ 10−6∙°C−1 |
|---|---|---|---|---|---|
| TC (8YSZ) | 20 | 48 | 0.10 | 5280 | 9.0 |
| 200 | 47 | 0.10 | 5280 | 9.2 | |
| 600 | 40 | 0.10 | 5280 | 10.1 | |
| 800 | 34 | 0.11 | 5280 | 10.8 | |
| 1100 | 22 | 0.12 | 5280 | 12.2 | |
| BC (MCrAlY) | 20 | 200 | 0.30 | 8100 | 13.6 |
| 200 | 190 | 0.30 | 8100 | 14.2 | |
| 600 | 160 | 0.31 | 8100 | 15.2 | |
| 800 | 145 | 0.32 | 8100 | 16.1 | |
| 1100 | 110 | 0.35 | 8100 | 17.6 | |
| TGO (α-Al2O3) | 20 | 400 | 0.23 | 4000 | 8.0 |
| 200 | 390 | 0.23 | 4000 | 8.2 | |
| 600 | 370 | 0.32 | 4000 | 8.7 | |
| 800 | 355 | 0.32 | 4000 | 9.0 | |
| 1100 | 320 | 0.33 | 4000 | 9.6 | |
| SUB (Inconel DZ125) | 20 | 220 | 0.31 | 8200 | 14.8 |
| 200 | 210 | 0.32 | 8200 | 15.2 | |
| 600 | 170 | 0.33 | 8200 | 16.2 | |
| 800 | 155 | 0.34 | 8200 | 16.9 | |
| 1100 | 120 | 0.35 | 8200 | 18.0 | |
| Alumina particle (Al2O3) | 20 | 380 | 0.27 | 38,700 | 5.08 |
| 220 | 369 | 0.27 | 38,700 | 5.90 | |
| 420 | 370 | 0.27 | 38,700 | 6.73 | |
| 620 | 355 | 0.27 | 38,700 | 7.55 | |
| 1020 | 320 | 0.27 | 38,700 | 9.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, X.; Wei, Z.; Jiang, Z.; Zhang, J.; Li, D.; Gong, X.; Li, Q.; Zhao, F.; Lai, J.; Yu, J. Crack Propagation Mechanism in Thermal Barrier Coatings Containing Different Residual Grit Particles Under Thermal Cycling. Coatings 2025, 15, 747. https://doi.org/10.3390/coatings15070747
Shen X, Wei Z, Jiang Z, Zhang J, Li D, Gong X, Li Q, Zhao F, Lai J, Yu J. Crack Propagation Mechanism in Thermal Barrier Coatings Containing Different Residual Grit Particles Under Thermal Cycling. Coatings. 2025; 15(7):747. https://doi.org/10.3390/coatings15070747
Chicago/Turabian StyleShen, Xin, Zhiyuan Wei, Zhenghao Jiang, Jianpu Zhang, Dingjun Li, Xiufang Gong, Qiyuan Li, Fei Zhao, Jianping Lai, and Jiaxin Yu. 2025. "Crack Propagation Mechanism in Thermal Barrier Coatings Containing Different Residual Grit Particles Under Thermal Cycling" Coatings 15, no. 7: 747. https://doi.org/10.3390/coatings15070747
APA StyleShen, X., Wei, Z., Jiang, Z., Zhang, J., Li, D., Gong, X., Li, Q., Zhao, F., Lai, J., & Yu, J. (2025). Crack Propagation Mechanism in Thermal Barrier Coatings Containing Different Residual Grit Particles Under Thermal Cycling. Coatings, 15(7), 747. https://doi.org/10.3390/coatings15070747





