Abstract
Fujian Tulou, a UNESCO World Heritage Site, is highly vulnerable to environmental and anthropogenic stresses, with its earthen walls prone to surface cracking that threatens both structural stability and cultural value. Traditional manual inspection is inefficient, subjective, and may disturb fragile surfaces, highlighting the need for non-destructive and automated solutions. This study proposes a dual-path framework that integrates lightweight crack detection with independent physical simulation. On the detection side, an improved YOLOv12 model is developed to achieve lightweight and accurate recognition of multiple crack types under complex wall textures. On the simulation side, a two-layer RFPA3D model was employed to parameterize loading conditions and material thickness, reproducing the four-stage crack evolution process, and aligning well with field observations. Quantitative validation across paired samples demonstrates improved consistency in morphology, geometry, and topology compared with baseline models. Overall, the framework offers an effective and interpretable solution for standardized crack documentation and mechanistic interpretation, providing practical benefits for the preventive conservation and sustainable management of Fujian Tulou.
1. Introduction
Fujian Tulou, as a representative form of traditional rammed-earth architecture in China, has been inscribed on the UNESCO World Heritage List due to its distinctive defensive structure, ecological adaptability, and socio-cultural significance [1]. However, prolonged exposure to natural weathering and anthropogenic disturbances inevitably leads to surface deterioration of the earthen walls, manifesting as strip cracks, intersecting fissures, polygonal crack networks, exfoliation, and discoloration [2]. These forms of damage not only compromise structural stability but also diminish cultural and historical value, and in severe cases may trigger partial or overall collapse, posing safety risks [3,4]. Thus, the accurate detection and reliable prediction of crack initiation and evolution are crucial for the long-term preservation and scientific conservation of earthen heritage sites.
Structural health monitoring (SHM) has long considered cracking as a core research topic [5]. Traditional inspection methods largely rely on visual surveys or manual interpretation of surface morphology, sometimes assisted by basic image processing operations such as grayscale enhancement, histogram equalization, edge detection (e.g., Canny), or threshold segmentation [6,7]. For example, grayscale enhancement and histogram equalization can highlight surface crack features [8,9], the Canny algorithm can assist in edge recognition [10], and threshold segmentation can be used for crack area extraction [11]. While effective in controlled laboratory conditions, these methods are highly sensitive to lighting, shadows, and material heterogeneity, and require extensive manual parameter tuning, limiting their applicability in complex heritage environments.
The rapid development of deep learning has provided new opportunities for non-contact, automated detection of surface damage in cultural heritage [5]. Non-destructive techniques such as drones, video monitoring, and smartphone imaging, when combined with convolutional neural networks, allow efficient remote crack detection. Two-stage detectors (e.g., Fast R-CNN) can achieve high accuracy in complex scenarios but struggle to meet real-time monitoring needs [12]. In contrast, single-stage detectors such as SSD, RetinaNet, and the YOLO family offer a better trade-off between speed, accuracy, and cross-platform deployment [13,14]. With successive iterations, YOLO models have achieved competitive performance in small-scale crack detection under challenging textures [15,16]. For example, studies on materials such as steel and concrete have shown that the improved YOLO model can significantly improve the detection capabilities of small-scale cracks and complex texture backgrounds [17,18,19]. Nevertheless, due to the heterogeneity of earthen materials and the complexity of weathered surfaces, current YOLO-based methods remain limited in capturing early crack initiation and reproducing full-scale crack evolution.
Beyond detection accuracy, recent advances emphasize that AI technologies can also play a broader role in the real-time monitoring and digital management of heritage structures [20,21]. In this regard, the integration of computer vision outputs into Heritage Building Information Modeling (HBIM) frameworks has gained increasing attention [22]. HBIM provides a comprehensive and user-friendly platform that federates geometric data, environmental conditions, structural monitoring records, and conservation histories, thereby offering interpretable tools for both researchers and practitioners [23,24,25]. For example, HBIM can incorporate parametric modeling scripts to represent complex architectural geometries [26,27], and Revit plug-ins now enable integration with real-time data collected from IoT devices and AI models, improving both workflow efficiency and monitoring accuracy [28]. Such environments have already been coupled with sensor networks and analysis modules to visualize real-time conditions, generate automatic reports, and support preventive decision-making [29]. Furthermore, AI-assisted model updating has demonstrated the potential to turn monitoring data into reliable numerical surrogates for decision support, for instance by calibrating finite element models with modal parameters optimized through swarm intelligence algorithms [30,31]. These studies highlight that the value of AI lies not only in enhancing detection but also in linking field evidence to digital twins that integrate monitoring, simulation, and conservation planning. However, despite these advances, existing studies remain largely fragmented. Most research efforts focus either on improving the accuracy of AI-based crack detection or on integrating monitoring data into HBIM and digital twin platforms, but rarely address both dimensions in a unified framework. Moreover, current approaches often treat cracks as static surface features, lacking mechanisms to explain or predict their progressive evolution. This study differs from previous work by introducing a dual-path framework. By linking detection outputs with mechanistic parameters, the framework not only standardizes multi-class crack documentation but also reproduces the four-stage evolution process observed in situ. To the best of our knowledge, this is the first attempt to establish such a detection–simulation loop tailored for earthen heritage architecture, thereby extending AI applications from isolated recognition tasks to interpretable, evolution-aware, and conservation-oriented decision support.
Building on these advances, this study proposes a dual-path parallel framework. The first path employs an improved YOLOv12 detection model (YOLOv12-MLE) for multi-class identification and standardized documentation of cracks on Tulou facades, covering strip, intersecting, and polygonal patterns. The second path introduces an independent physical simulation using RFPA3D, parameterizing the loading ratio (λ = Δy/Δx) and overlay thickness (t) to mechanistically reproduce the four crack evolution stages—initiation, propagation, coalescence, and saturation—and validate against field observations. Both outputs can be integrated into HBIM-centered workflows, thereby extending the applicability of AI beyond isolated detection tasks.
The framework offers three main innovations: (i) a lightweight YOLOv12-MLE model enabling accurate, edge-deployable detection of Tulou cracks, benchmarked against mainstream detectors using F1, precision, recall, and mAP@50; (ii) a parameterized RFPA3D simulation protocol systematically examining the effects of λ and t on crack morphology, density, and stage transitions, yielding qualitative consistency with on-site observations; and (iii) a cross-validation strategy linking detection results with physical mechanisms, producing reusable datasets and visual reports to support targeted conservation strategies such as thickness control and localized reinforcement.
In summary, the proposed dual-path framework not only extends the application of deep learning in cultural heritage conservation but also provides an efficient, interpretable, and scientifically grounded approach for the standardized recording and mechanistic study of crack evolution in Fujian Tulou. The remainder of this paper is organized as follows: Section 2 presents the framework architecture, experimental design, dataset construction, and evaluation metrics; Section 3 discusses the results and analysis; Section 4 concludes the contributions and outlines future research directions.
2. Materials and Methods
2.1. Case Study Description
The samples for this study were collected from the Gaopi and Nanxi tulou clusters in southern Fujian, including Chaoyang, Chengqi, Fuxing, Kuiju, Yanxiang, and Zhencheng, as shown in Figure 1. These Fujian tulou were officially inscribed on the UNESCO World Heritage List in 2008. Chengqi and Zhencheng are among Fujian’s most representative and renowned tulou [32]. These large, multi-story dwellings, characterized by circular or rectangular layouts, combined defensive functions with communal living spaces, reflecting their ecological adaptability and sociocultural traditions [33]. Despite their historical and architectural significance, tulou are highly susceptible to environmental and human influences. Long-term exposure to rainfall, temperature fluctuations, and human intervention leads to the gradual deterioration of earthen walls, often manifesting as linear cracks, intersecting fissures, and polygonal crack networks [34]. These defects not only compromise the structural stability of the walls but also threaten the cultural value and authenticity of these heritage sites.

Figure 1.
Case studies from the Gaopi and Nanxi Tulou. (a) Chaoyang tulou; (b) Zhencheng tulou; (c) Yanxiang tulou; (d) Kuiju tulou; (e) Chengqi tulou; (f) Fuxing tulou.
Field investigations revealed a wide range of crack patterns, from thin surface fissures in the plaster overlay to large-scale vertical cracks propagating through the rammed-earth substrate, as shown in Figure 2. In panel (a), thin polygonal cracks are visible in the plaster overlay, with widths generally below 2 mm. These micro-cracks often result from surface shrinkage and represent the initiation stage of deterioration. In panel (b), localized surface loss and cavity formation are observed, due to long-term moisture penetration and material erosion. Such defects can accelerate crack propagation and undermine the protective surface layer. Panel (c) illustrates a large vertical crack penetrating the rammed-earth substrate, with a width exceeding 10 mm. This type of through-crack is strongly correlated with differential settlement or thermal stresses, posing significant risks to structural stability. These examples highlight the heterogeneity of Tulou wall degradation, where both fine-scale surface cracks and deep structural fissures coexist. Documenting such variations provides essential ground-truth evidence for validating the YOLOv12-MLE crack detection model and supports the parameterized RFPA3D simulations in replicating progressive crack evolution.

Figure 2.
Representative crack types observed in Fujian Tulou. (a) Polygonal cracks forming irregular networks on the wall surface; (b) Surface erosion and cavity-like defects caused by material loss; (c) Vertical linear crack extending along the earthen wall.
To support standardized recording and physics-aware interpretation, we classify cracks by width and report representative cases observed in Yongding and Nanjing clusters together with indicative environmental and structural parameters, as shown in Table 1. (i) Micro cracks (<1 mm). Frequently observed as fine polygonal patterns on well-maintained facades (e.g., Zhencheng Tulou). Dominant drivers are seasonal humidity swings (annual RH ≈ 70%–85% with ±10%–20% excursions) and daily solar heating (ΔT ≈ 10–15 °C), causing reversible surface shrink-swell. Typical seasonal widening is 0.1–0.3 mm in sun-exposed sectors; wall-thickness transitions around openings act as stress concentrators. (ii) Small cracks (1–5 mm). Common on inner walls of square Tulou (e.g., Wenchang building at Tianluokeng). Moisture variability (valley RH ≈ 80%, ±20% seasonally) and minor differential settlement (≈ 0.5–1 mm/yr) jointly drive 2–4 mm openings; legacy cement patches (1950s–1980s) can introduce interface incompatibility, adding ≈ 0.5–1 mm. (iii) Moderate cracks (5–20 mm). Observed on tall or slightly leaning walls (e.g., Yuchang). Thick-to-thin wall gradients (base 2.0 m → top 0.8 m) amplify tensile demand; high moisture near rivers (RH swing up to 30%) plus settlement (≈ 5 mm/yr) and historic cement jackets (5–10 cm) lead to 10–15 mm openings and debonding along repair interfaces. (iv) Large cracks (>20 mm). Found on neglected/abandoned sections (e.g., remnants in the Gaobei area). Lack of maintenance, intense wetting–drying cycles (±25% RH), and extreme temperatures (−2 to 38 °C) accelerate fabric degradation and foundation softening; annual widening can exceed 10 mm, with local collapse risk.

Table 1.
Crack width classes, typical causes, and indicative parameters in Fujian Tulou.
The width-based typology provides standardized labels for the detection pipeline (training/validation strata) and priors for the IEIoU-enhanced localization of long, high-aspect-ratio cracks. The parameter ranges (RH, ΔT, thickness) give physically plausible bounds for RFPA3D, easing calibration of λ and t. The representative cases create repeatable test patches for cross-checking prediction consistency (skeleton IoU, Chamfer, Hausdorff, spacing MAE, orientation EMD) against real façades.
2.2. Data Prepossessing and Dataset Construction
To support crack detection and evolution prediction in Fujian Tulou, a high-quality image dataset of earthen-site cracks was constructed and annotated. Given the variability of rammed-earth materials across climates, construction techniques, and historical periods, crack patterns exhibit significant complexity and diversity. Based on conservation practice and fracture mechanics theory, a multi-class semantic labeling scheme was established, as shown in Figure 3, covering strip cracks, intersecting cracks, and polygonal crack networks to provide standardized samples for deep learning models.

Figure 3.
Crack semantic annotation system.
The final dataset comprised 2800 images, annotated into four evolutionary stages: initiation (700), propagation (700), coalescence (700), and saturation (700). Images were sourced from three complementary channels: (i) Digital archives from heritage agencies (38%, 1064 images), primarily from the National Cultural Heritage Administration platform and the Fujian Tulou Conservation Center; (ii) High-resolution field surveys (27%, 756 images) conducted by conservation technicians at representative Tulou sites; (iii) Open-access resources (35%, 980 images), including Wikimedia Commons, academic databases, and archaeological repositories, restricted to Fujian Tulou or structurally equivalent rammed-earth heritage buildings. This combination ensured that the dataset not only reflected authentic case-study conditions but also captured broader variations in crack morphology, surface texture, and environmental contexts. Such integration of multiple sources was essential to improve model robustness and generalization, reducing overfitting to a single site and enabling applicability to a wider range of Tulou structures.
To improve data quality and adaptability, the GrabCut algorithm was applied to remove complex backgrounds, and all images were resized to 512 × 512 pixels for compatibility with YOLO models and mainstream detectors. Data augmentation strategies including rotation, mirroring, color perturbation, and perspective transformation were employed to expand sample distributions across crack stages and alleviate imbalance in saturation samples.
Annotation was conducted collaboratively by heritage conservation experts, structural engineers, and computer vision specialists. Each image was independently labeled by two experts, cross-validated, and refined through three rounds of review. The inter-annotator agreement reached a Cohen’s Kappa of 0.88, indicating high consistency. All bounding boxes and labels were converted into a unified JSON format compatible with YOLOv12 and RFPA3D inputs. To further optimize anchor box matching, K-means clustering was applied to the distribution of bounding box dimensions, yielding improved detection accuracy and convergence. Consistency evaluation was performed using IoU ≥ 0.5 as the matching criterion, with each region annotated by three experts; the mean κ value was 0.89, confirming robust agreement. To prevent data leakage, time-series images of the same crack object were assigned to the same subset. The dataset was finally split into training (80%) and validation (20%) sets, with 20% of the training set reserved as a tuning subset. Early stopping was adopted to terminate training if validation loss failed to improve for five consecutive epochs, effectively reducing overfitting and enhancing generalization.
2.3. Model Comparison and Improvement
To validate the effectiveness of the proposed improvements, we conducted both ablation studies and comparative experiments with mainstream object detection models, including YOLOv5, YOLOv6, YOLOv7, YOLOv9, YOLOv10, YOLOv11, YOLOv12, DEtection TRansformer (DETR), Faster R-CNN, and SSD. These algorithms vary in precision, speed, generalization capacity, and computational cost, and were selected to provide a comprehensive benchmark on the Fujian Tulou crack dataset. The evaluation considered: (i) capability to identify multiple crack types (e.g., vertical, horizontal, step-shaped, ring, and radial cracks); (ii) robustness to complex wall backgrounds, as Tulou facades consist of rammed earth, timber beams, and cobblestone with highly heterogeneous textures; and (iii) adaptability to cultural heritage scenarios, which was evaluated through dataset diversity and robustness testing. Specifically, the crack dataset incorporated images from multiple sources (digital archives, field surveys, and open-access repositories), covering a wide range of wall conditions such as variations in thickness, moisture stains, and historical repair traces. To enhance adaptability, data augmentation techniques (e.g., rotation, mirroring, color perturbation, perspective transformation) were applied to simulate heterogeneous surfaces and environmental interferences. Furthermore, stratified cross-validation ensured that each subset of wall conditions was represented in both training and validation sets, allowing performance indicators (F1, precision, recall, mAP@50) to be systematically compared across scenarios.
Based on overall performance, YOLOv12 was chosen as the baseline model, upon which we developed an improved framework, YOLO-MLE (YOLO for Multi-scale Long-crack Extraction), specifically tailored for Tulou crack detection, as shown in Figure 4. YOLO-MLE employs MobileNetV4 as a lightweight yet effective backbone, structured into five hierarchical blocks (Block1–Block5) to extract multi-scale features from 512 × 512 × 3 input images. Shallow-to-deep features capture low-level textures through to high-level semantics, while skip connections preserve spatial detail and facilitate cross-scale information flow. To enhance spatial representation and semantic refinement, A2C2f modules are embedded after feature cascades at levels P3, P4, and P5, integrating channel and spatial attention for improved context fusion.
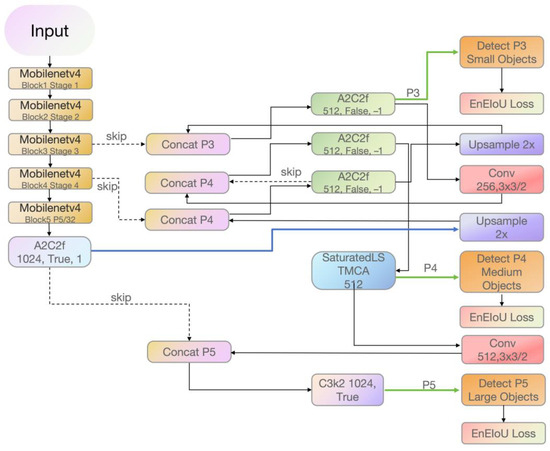
Figure 4.
YOLO-MLE framework diagram. The architecture integrates a MobileNetV4 backbone with an Improved Multi-channel Attention (IMCA) module and an Enhanced EIoU loss function. The diagram shows five hierarchical feature extraction blocks (Block1–Block5) with skip connections, three-scale detection heads (P3, P4, P5), and sequential modeling via a SaturatedLSTMCA module. This design enables multi-scale feature extraction, enhances sensitivity to elongated cracks, and improves localization under heterogeneous Tulou wall textures.
In the intermediate layer (P4), a SaturatedLSTMCA module is introduced to perform sequential modeling on flattened spatial vectors, enabling the network to capture long-range spatial dependencies. This design is particularly suited for thin, elongated, or curved cracks exhibiting sequential patterns on Tulou facades. The detection head operates at three scales: P3 (8 × 8 grid) for small targets, P4 (16 × 16) for medium targets, and P5 (32 × 32) for large targets. Each branch outputs classification and localization predictions supervised by an enhanced EIoU loss function (EnEIoU). Unlike standard IoU-based losses, EnEIoU incorporates geometric priors, including aspect ratio sensitivity, directional consistency, and adaptive weight adjustment, making it highly effective for crack-like targets with high aspect ratios and directional variance. Detailed implementation steps are provided in the Supplementary Materials.
Specifically, lightweight, and efficient MobileNetV4 was selected as the backbone to support high-precision feature extraction of Fujian Tulou cracks across multiple structural scales, as shown in Figure 5. As a UNESCO World Heritage Site, Tulou walls are composed of rammed earth, timber beams, and cobblestones, resulting in highly complex textures, strong noise, and pronounced material heterogeneity. Crack patterns are diverse, ranging from micro-surface fissures to vertical, horizontal, radial, and penetrating structural cracks. Therefore, the YOLOv12-MLE framework must strike a balance between lightweight design and robust performance to ensure accurate crack recognition under mobile deployment conditions.
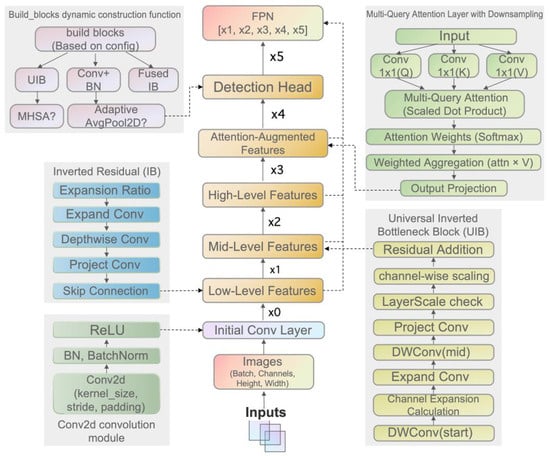
Figure 5.
MobileNetV4 backbone network framework diagram. The backbone employs Universal Inverted Bottleneck (UIB) blocks across four convolutional stages, balancing computational efficiency and feature richness. Depthwise and expansion convolutions capture surface textures and crack patterns, while projection layers compress features for lightweight deployment. The figure also highlights the integration of Multi-Query Attention modules and a dual-path down-sampling mechanism, which strengthen spatial context modeling under noisy wall conditions.
The architecture employs Universal Inverted Bottleneck (UIB) blocks with variable depth configurations, organized into a four-stage convolutional structure to balance computational efficiency and representational power. First, initial depth wise convolutions capture low-level surface textures such as rammed-earth imprints and timber grain. Second, expansion convolutions increase channel capacity to extract multi-scale crack details. Third, intermediate depth wise convolutions model higher-order interactions between cracks and earthen textures. Finally, projection convolutions compress high-dimensional features, reducing computational cost while preserving critical crack semantics.
At key stages, Multi-Query Attention modules are embedded and combined with a dual-path down-sampling mechanism, significantly enhancing spatial context modeling under noisy wall backgrounds. This design is particularly effective for low-contrast cracks and highly textured surfaces. Additionally, a Layer Scale module introduces a learnable parameter () to fine-tune channel-level feature responses, allowing the model to adaptively adjust crack detection sensitivity across varying Tulou materials and illumination conditions.
The backbone adopts a hierarchical feature extraction strategy, ultimately producing a five-level feature pyramid that provides rich multi-scale semantics for downstream crack detection and evolution modeling. To ensure real-time inference on edge devices such as Jetson AGX Orin, convolution channel numbers are optimized with the make divisible function to multiples of eight, maintaining high performance while preserving lightweight efficiency.
The improved multi-channel attention mechanism (IMCA) was designed to enhance the representational power of conventional attention modules by incorporating a complete LSTM sequence encoder, a dual-path adaptive fusion strategy, and dimensional alignment, as illustrated in Figure 6. This module was specifically optimized for crack detection on Fujian Tulou walls, where surfaces are composed of rammed earth, timber beams, and cobblestones, characterized by complex textures, high noise levels, and strong heterogeneity. Crack patterns are diverse and exhibit long-range dependencies and staged variations, including initiation, propagation, coalescence, and saturation.
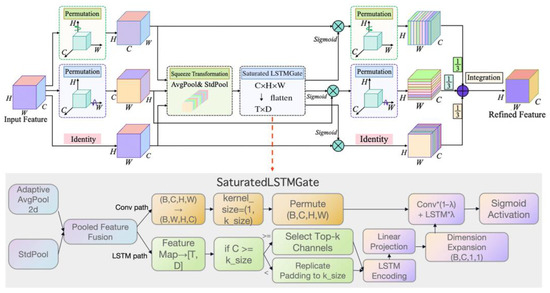
Figure 6.
Improved Channel Attention Mechanism (MCA) framework diagram. The figure illustrates the feature modeling strategy: (i) statistical pooling operations (average, max, and standard deviation) fused adaptively to enhance global descriptors; and (ii) a lightweight LSTM path for spatial sequence modeling to capture crack directionality. Outputs are combined through learnable fusion coefficients and generate spatial attention maps, shown as highlighted regions emphasizing cracks while suppressing background noise; Conv*(1 − λ) + LSTM*λ represents a weighted sum of convolutional and LSTM paths, where * denotes element-wise scaling.
IMCA employs a dual-path feature modeling strategy to balance global context and local crack detail. In the first path, multiple statistical pooling operations (average, max, and standard deviation pooling) are used to extract complementary global descriptors, which are then adaptively fused through a learnable weighting scheme. This design significantly improves discrimination of crack features under noisy Tulou wall backgrounds. In the second path, a lightweight LSTM network models spatial sequences along rows or columns of feature maps, capturing crack directionality and continuity. To ensure compatibility across feature layers, an adaptive sequence processing strategy is introduced, automatically padding or truncating inputs for stable multi-level modeling.
After dual-path modeling, outputs are integrated via learnable fusion coefficients and a Sigmoid activation function to generate spatial attention maps. These maps emphasize crack-related regions while suppressing high-frequency noise caused by rammed-earth imprints, timber grains, and repair marks. To further enhance modeling of crack anisotropy, IMCA computes and fuses attention responses along both height and width axes, thereby improving sensitivity to vertical, radial, and curved cracks typical of Tulou walls.
In the Fujian Tulou crack detection task, IMCA demonstrated clear advantages: it effectively suppressed false detections under noisy rammed-earth backgrounds, improved modeling of crack directionality and morphology, and supported differentiation of crack evolution stages. In the Fujian Tulou crack detection task, the improved multi-head cross-attention (IMCA) module demonstrated clear advantages. As shown in the ablation experiments (Table 2), introducing IMCA into the baseline model increased the F1 score from 85.5% to 87.4% and improved precision from 88.7% to 90.9%, while also enhancing recall to 84.1%. These gains indicate that IMCA effectively suppresses false detections under noisy rammed-earth backgrounds and improves the modeling of crack directionality and morphology. Moreover, when IMCA was combined with MobileNetV4 and EnEIoU, the full YOLOv12-MLE framework achieved the best overall performance (F1 = 91.8%, mAP@50 = 95.5%), supporting the claim that IMCA contributes not only to geometric feature extraction but also to distinguishing different crack evolution stages.

Table 2.
Ablation experiment results.
Furthermore, its lightweight design enables real-time performance on mobile and edge devices, offering reliable technical support for non-destructive crack detection and structural health assessment in earthen heritage conservation.
The enhanced EIoU loss function introduces an aspect-ratio-sensitive mechanism and a directional consistency penalty, as shown in Figure 7. This design is particularly suited for the linear crack patterns commonly observed on Tulou walls, strengthening the model’s ability to capture complex geometric morphologies. Specifically, the squared differences in width () and height () between the predicted and ground-truth boxes are first computed and normalized by the diagonal length of the minimum enclosing box, ensuring scale invariance. Next, an aspect-ratio discrepancy metric is introduced as a criterion for identifying elongated structures. When the detected target exceeds a predefined aspect-ratio threshold, a linear mask is activated to further determine whether the object corresponds to a slender crack.
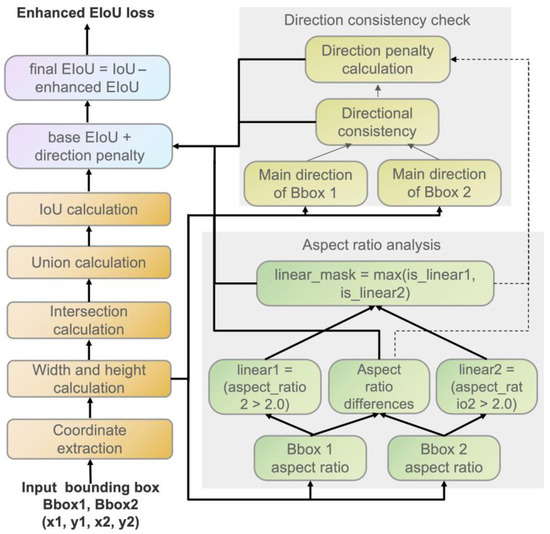
Figure 7.
Enhanced EIoU loss function framework.
On this basis, a directional consistency penalty is constructed to evaluate the angular deviation between the principal axes of predicted and ground-truth boxes. Even when IoU values are high, large orientation discrepancies are penalized, preventing misclassification of elongated cracks due to incorrect alignment. Finally, the overall EIoU loss is formulated as a weighted combination of the baseline EIoU term and the proposed orientation penalty, as expressed in Equation (1):
where is a weight coefficient adaptively adjusted based on the target’s geometric characteristics, enabling the model to dynamically adjust the optimized center of gravity for targets of varying morphology. This improvement is particularly critical in crack detection tasks, especially in linear crack structures caused by stress evolution, which often exhibit distinct directionality and high aspect ratios. By incorporating these geometric prior constraints into the loss function, not only does it improve detection accuracy, but it also enhances the model’s structural interpretation capabilities, aligning with the actual evolution of cracks in cultural heritage sites.
2.4. Evaluation Metrics and Statistical Formulations
To ensure the robustness and statistical validity of our results, we conducted ablation and comparison experiments for the YOLOv12-MLE configuration. In each run, we trained and evaluated the model using a fixed train-test split and different random seeds. For each performance metric (F1 score, precision, recall, and mAP@50), the formula is as follows:
Precision measures the proportion of correctly classified “crack” features among all predicted instances, as shown in Equation (2):
The recall rate evaluates the model’s ability to correctly retrieve all relevant crack attributes, as shown in Equation (3):
The F1-Score is a balanced metric that combines precision and recall. It comprehensively evaluates a model’s ability to accurately identify small cracks and fully cover all types of cracks in the Fujian Tulou crack detection task. It is particularly suitable for evaluating the model’s robustness and generalization performance in high-noise and complex texture backgrounds, as shown in Equation (4):
Object Detection Metrics (Bounding Box Evaluation). Because YOLOv12 performs both classification and object localization, bounding box accuracy must be evaluated using the following metric: mean average precision at an intersection-over-union (IoU) of 0.5 (mAP@50). This metric evaluates the model’s object detection performance by measuring the average precision at which the predicted bounding box achieves at least 50% accuracy. The intersection-over-union (IoU) with the ground truth reflects the model’s ability to correctly detect and classify cracks at moderate localization thresholds. A higher mAP@50 score indicates greater accuracy in identifying and localizing crack classes, as shown in Equation (5):
2.5. Crack Prediction Method and Model Description
After incorporating the proposed improvements, the YOLOv12-MLE model achieved finer-grained feature parsing in the Fujian Tulou crack detection task. Unlike conventional detectors that only output bounding boxes, the improved framework additionally classifies crack evolution stages and estimates the orientation angle (θ), thereby providing richer inputs for subsequent physical modeling and three-dimensional crack evolution simulations. Based on this output, the detected crack coordinates and orientation information are translated into the initial defect distribution of RFPA3D, combined with boundary loading conditions to conduct quasi-static evolution simulations. Specifically, the orientation angle θ is used to initialize the crack growth direction, while the stage labels are mapped to the damage variable D, controlling the rate of crack evolution across different loading steps.
Within the modeling framework, RFPA3D [35] identifies tensile or shear damage of material elements under three-dimensional stress states and quantifies crack development through the damage variable D, as shown in Figure 8. By parameterizing the loading ratio (λ = Δy/Δx) and overlay thickness (t), the model extrapolates the transition from micro-scale damage propagation to macro-scale crack patterns—ranging from parallel cracks to ladder-like networks and polygonal crack meshes. This achieves a unified modeling objective of “physics-driven mechanisms coupled with structural response regulation.”
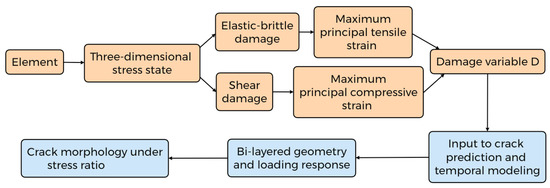
Figure 8.
Crack evolution modeling process based on three-dimensional damage mechanism (RFPA3D) and double-layer structure model. The figure depicts the simulation workflow used to reproduce four stages of crack evolution. The bi-layer slab model includes a brittle overlay and a ductile rammed-earth substrate, with loading ratio (λ) and thickness (t) as key parameters. Stress distribution and crack propagation pathways are shown step-by-step, illustrating how RFPA3D captures micro-to-macro transitions consistent with field observations.
RFPA3D adopts a finite element method based on elastic damage theory to simulate the progressive failure of quasi-brittle materials such as rock, rammed-earth walls, and ceramic fragments under external disturbances. The essence of the crack evolution process lies in the heterogeneous development of element-level damage. To reflect the inherent heterogeneity of Tulou materials, RFPA3D assigns a strength threshold to each mesoscopic element according to a Weibull probability distribution function, as shown in Equation (6):
is the average mechanical parameter of the element (such as strength, Young’s modulus, etc.). is the material homogeneity index, where → ∞ indicates complete homogeneity and m → 0 indicates high heterogeneity. is the failure probability density function of the element. RFPA3D, based on the elastic-brittle damage theory, defines the following elastic modulus degradation model for each element, as shown in Equation (7):
is the original elastic modulus. is the damage variable ( = 0 indicates no damage, = 1 indicates complete failure). When → 1, to avoid solution interruption, the system sets a minimum value of E ≥ 5–10.
When the tensile strain reaches the threshold , the element begins to damage. The damage evolution expression is shown in Equation (8):
is the residual tensile stress. and are the damage initiation strain and ultimate strain, respectively. For failure in shear and compression modes, the Mohr-Coulomb criterion is used, with a threshold of the maximum compressive strain set to control compressive-shear failure.
To simulate the crack evolution mechanism of the surface layer of Tulou under various loading conditions, this paper comprehensively considers the two dominant failure mechanisms, tensile failure, and compressive-shear failure, in the RFPA3D three-dimensional finite element system based on the elastic-brittle damage constitutive theory. Under one-dimensional uniaxial tension, the evolution of the damage variable is defined as above. When the crack propagates into a three-dimensional stress state, the constitutive relationship must introduce an equivalent principal tensile strain to replace the uniaxial tensile strain, as shown in Equation (9):
, , and are the principal strains. This approach allows damage evolution to preserve the tensile-dominated failure characteristics of heterogeneous materials.
To reflect the crack initiation and propagation behavior of an element under compression and shear stress, this paper introduces the Mohr-Coulomb criterion as a second damage threshold. If the element is not damaged in tension, the following expression is used to determine whether shear damage has occurred, as shown in Equation (10):
where is the three-dimensional principal compressive strain. is the ultimate compressive principal strain of the material under uniaxial compressive stress. is the residual strength; and is the initial Young’s modulus.
For the Tulou surface material, considering that the surface plaster and rammed earth matrix are typical quasi-brittle materials, their compression and shear behavior will affect the crack morphology and propagation direction. Therefore, is calculated based on the following Equation (11) [36]:
is uniaxial compressive strength of the material. are the secondary principal stress and minimum principal stress. is Angle of internal friction. is Poisson’s ratio.
The proposed model not only reproduces the four-stage crack evolution process (initiation–propagation–coalescence–saturation) under various stress states but also allows physical labels to be embedded into the crack prediction model (e.g., YOLOv12), thereby enhancing structural interpretability and trend-fitting accuracy. To further simulate the cracking behavior of Tulou walls, a flat double-layer model was adopted following Helgeson and Aydin [37], representing in-plane tensile stresses on the surface layer of the structure. In this model, the upper layer corresponds to plaster or decorative coatings, which are more brittle and prone to cracking, while the lower layer represents the rammed-earth substrate that provides structural support and constraint.
To examine the influence of overlay thickness (t) on crack spacing and propagation, four thickness settings were used: t = {5, 10, 15, 30 mm}, with substrate thicknesses T = {15, 20, 25, 30 mm}, following standard ratios in layered material fracture studies. Each model was discretized into mesoscopic elements of 1 × 1 × 1 mm3. For example, the case of t = 5 mm and T = 15 mm consisted of a 160 × 160 × 20 mm3 slab subdivided into eight-node hexahedral elements, as shown in Figure 9.
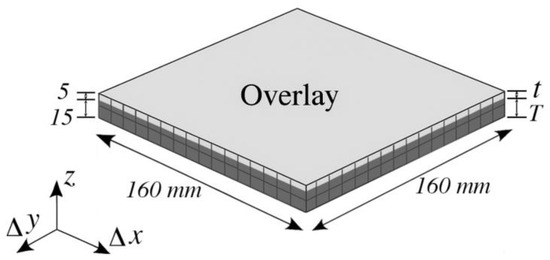
Figure 9.
Dimensions and boundary conditions for the double-layer plate model.
To simulate environmental stresses such as thermal expansion–contraction, drying shrinkage, and structural displacement, quasi-static biaxial tensile loads were applied. Displacement increments were imposed in both x and y directions, generating in-plane tensile stresses. The loading ratio λ was defined as the ratio of orthogonal displacement increments, as shown in Equation (12):
with fixed at 0.004% and set to 0, 0.0008%, 0.002%, and 0.004%, corresponding to λ = 0, 0.2, 0.5, and 1.0. λ = 0 represents uniaxial tension, while λ = 1 approximates isotropic biaxial tension, which reproduces the polygonal crack patterns commonly observed on Tulou surfaces under natural weathering [38].
To further examine the influence of geometric proportions, the ratio η = t/T was introduced, where t is overlay thickness and T is substrate thickness. Four sets of slab models were constructed with t = {5, 10, 15, 30 mm} and T = {15, 30, 45, 90 mm}, maintaining η ≈ 0.33 as a standard layered ratio. The η parameter reflects the mechanical dominance of the cracking region; higher η values imply stronger deformation capacity of the overlay and greater potential for pattern transitions and saturation. This model thus captures the transition of crack networks from parallel to ladder-like and eventually polygonal configurations under asymmetric thickness and biaxial loading, providing a meso-scale physical foundation for coupling with deep learning-based crack detection and evolution prediction.
The material properties of the double-layer Tulou wall model are summarized in Table 3. The overlay represents plaster or coating layers with high material heterogeneity, lower compressive strength, and brittle characteristics, making them more susceptible to cracking under minor perturbations. The substrate simulates the rammed-earth base with higher strength, better uniformity, and greater ductility, providing effective constraint and support. During loading, cracks predominantly initiate and develop within the overlay. The homogeneity index m characterizes material variability, with smaller values indicating greater heterogeneity. To better approximate real Tulou conditions, the overlay Young’s modulus was set higher than that of the substrate, ensuring that cracks preferentially nucleate in the overlay under the same applied stress, while the substrate—possessing significantly higher compressive strength—remains intact to provide structural resistance.

Table 3.
Tulou crack model material parameters.
2.6. Quantitative Validation and Cross-Check
To overcome the subjectivity of relying solely on visual similarity and expert interpretation, a three-tier quantitative evaluation system was established, comprising: (i) morphological consistency (pixel/skeleton level), (ii) geometric statistical consistency (spacing/orientation), and (iii) topological consistency (loops/connectivity). The evaluation was conducted on binary crack maps derived from both simulated predictions and field observations (or subsequent-stage images).
Specifically, for the same Tulou wall surface or regions under comparable conditions, pairs of “early-stage” images () and “late-stage” images () were selected as the validation set. The detection features (spacing, density, and orientation) extracted from early-stage cracks were used to drive the RFPA3D simulation, generating predicted binary crack maps . The crack binary image obtained by detection is used as the “quasi-true value”. To reduce the influence of segmentation thickness, the binary image is morphologically skeletonized S().
Tier 1: Morphological consistency (pixel/skeleton level): The skeleton Intersection-over-Union (IoU) was employed, as defined in Equation (13):
is the set of pixels in the predicted crack skeleton. is the set of pixels in the actual crack skeleton. This is an “overlap” metric, like the intersection-over-union ratio of two shapes, but only for the crack skeleton. The value range is from 0 to 1, with values closer to 1 indicating a closer match between the predicted and actual skeletons.
Tier 2: Bidirectional Chamfer distance, as shown in Equation (14):
is the predicted skeleton point set, and is the predicted true skeleton point set. For each predicted point p, find the nearest true point q, calculate the distance, and then average the distance across all points. This bidirectional calculation ensures that both the predicted and true points can find each other.
Tier 3: Hausdorff Distance, as shown in Equation (15):
The Hausdorff distance captures the worst-case error, defined as the maximum distance from any point on the predicted skeleton to the closest point on the ground-truth skeleton, and vice versa. Full implementation details and parameter settings are provided in the Appendix A.
In summary, the three morphological metrics serve complementary purposes: (i) IoU evaluates global overlap, answering whether “the predicted cracks align with the ground truth”. (ii) Chamfer distance measures average error, assessing “how precisely the aligned cracks match”. (iii) Hausdorff distance quantifies extreme deviations, indicating “how large the worst-case error is.” Together, these measures provide a comprehensive evaluation of crack evolution predictions, capturing global consistency, average accuracy, and worst-case performance.
Next, this study designed two validation protocols. Protocol P1 (real-time post-test control): The metrics were run for each plot (, ), reporting the mean ± standard deviation with a 95% CI. These metrics were compared to a baseline of uncalibrated physical parameters (e.g., fixed λ = 1), with paired t-tests and significance stars. Protocol P2 (synthetic-measured hybrid): A batch of synthetic “post-tests” was generated in RFPA3D and parameters (λ, t, m) were perturbed to test the metrics’ sensitivity to parameter deviations and generate robustness curves. Parameter inversion and calibration: Using as the objective function, grid search and Bayesian optimization of λ and t were performed to minimize the difference. The improvement and cost of the metrics before and after calibration were reported.
All results are reported as mean ± standard deviation with 95% CI. The Shapiro–Wilk test was used for normality assessment. Depending on distribution characteristics, paired t-tests or Wilcoxon signed-rank tests were applied. Effect sizes (Cohen’s d) were further reported. All evaluation steps—including image binarization, skeletonization, orientation estimation, distance transforms, and topological analysis—were implemented in Python (v3.10.12) using OpenCV, scikit-image, and SciPy. Thresholds and algorithmic parameters are detailed in the Table A1 to ensure reproducibility.
3. Results
3.1. Ablation Experiments
An ablation study was conducted to systematically evaluate the contributions of the MobileNetV4 backbone (Mv4), the improved multi-head cross-attention module (IMCA), and the EnEIoU to overall detection performance. The baseline model achieved an F1 score of 83.2%, precision (P) of 85.6%, recall (R) of 80.1%, and mAP@50 of 84.7%, serving as a performance reference for subsequent improvements, as shown in Table 2.
The best performance was obtained when all three modules (Mv4 + IMCA + EnEIoU) were combined, yielding an F1 score of 91.8%, precision of 91.5%, recall of 92.0%, and mAP@50 of 95.5%. In addition to significantly surpassing the baseline in detection accuracy, this configuration accurately captured the full crack evolution pathway (initiation–propagation–coalescence–saturation). Importantly, these gains were achieved while maintaining computational efficiency, requiring only 4.68 GFLOPs and 2.21 MB of parameters, highlighting the lightweight and deployable nature of the framework. This makes it particularly suitable for real-time crack detection on edge devices deployed in heritage conservation sites.
For individual modules, introducing only the MobileNetV4 backbone improved performance to an F1 score of 89.1% and mAP@50 of 93.7%, while reducing computational cost from 5.99 GFLOPs to 4.68 GFLOPs, confirming the backbone’s role in balancing efficiency and accuracy. The EnEIoU loss alone also led to a notable improvement (F1 = 89.0%, mAP@50 = 94.0%), whereas IMCA contributed more modestly (F1 = 87.4%). When IMCA and EnEIoU were combined without Mv4, performance was relatively lower (F1 = 88.2%, mAP@50 = 93.9%) and computational complexity was the highest (5.99 GFLOPs, 2.52 MB). These findings demonstrate that while each module enhances detection accuracy to some extent, their synergistic integration is most effective, and that the lightweight MobileNetV4 backbone plays a critical role in strengthening feature representation while optimizing computational efficiency.
3.2. Model Comparison Results
As shown in Table 4, the models exhibited substantial differences in performance on the tasks of Tulou surface defect detection and crack prediction. Overall, YOLOv12-MLE (YOLO for Multi-scale Long-crack Extraction) achieved the best results across all metrics, with an F1 score of 91.8% and mAP@50 of 95.5%. It maintained an excellent balance between precision and recall, while requiring only 4.68 GFLOPs and 2.21 MB of parameters, demonstrating outstanding lightweight efficiency. These characteristics make it particularly well-suited for deployment on edge devices or in real-time heritage monitoring scenarios.

Table 4.
Model comparison results.
By contrast, DETR achieved competitive accuracy (F1 = 85.2%, mAP@50 = 89.9%) but demanded 54.12 GFLOPs and 19.01 MB, limiting its applicability in resource-constrained or low-latency conservation contexts. Within the YOLO family, YOLOv12n also performed strongly, offering a favorable trade-off between accuracy and efficiency. YOLOv11n and YOLOv5n obtained F1 scores of 83.3% and 84.0%, with mAP@50 values of 89.5% and 90.0%, respectively, making them viable for real-time crack detection. In contrast, YOLOv10n and YOLOv9n showed weaker performance (F1 = 74.5% and 78.0%; mAP@50 = 81.0% and 84.4%), and despite lower computational costs (8.41 and 7.86 GFLOPs), they lack sufficient accuracy for demanding Tulou crack prediction tasks. YOLOv6n delivered moderate results (F1 = 80.5%, mAP@50 = 87.2%) but required more computational resources than YOLOv5n and YOLOv12n, reducing its efficiency advantage.
In summary, while some YOLO models outperform larger detectors such as DETR in terms of lightweight efficiency and detection accuracy, the improved YOLOv12-MLE demonstrated the most balanced performance. Its high accuracy, low computational cost, and compact size make it particularly suitable for on-site real-time protection and long-term monitoring of Fujian Tulou.
3.3. Performance Evaluation of CAM, Grad-CAM, XGrad-CAM, SSCAM for Deep Learning Model
In practical deployment, the proposed system operates by capturing façade images of Tulou walls through fixed cameras which are then processed in real time by the YOLOv12-MLE detection model to identify cracks and by the RFPA3D module to simulate their likely evolution. This workflow provides conservation teams with rapid diagnostic outputs directly on site. As illustrated in Figure 10, four mainstream class activation mapping techniques (CAM, Grad-CAM, SSCAM, and XGrad-CAM) were employed to enhance model interpretability in the Fujian Tulou crack detection task. These methods were used to compare the spatial focus and discriminative regions of the baseline YOLOv12n with the improved YOLOv12-MLE. Results show that YOLOv12-MLE consistently exhibited stronger structural focus and boundary sensitivity across all visualization methods, enabling more accurate localization of crack-related regions. Compared with YOLOv12n, YOLOv12-MLE produced more concentrated attention responses and significantly suppressed background texture interference, particularly in regions with wall cavities and surface roughness. This demonstrates the model’s ability to effectively distinguish cracks from non-crack features, thereby improving robustness under the highly heterogeneous conditions of earthen wall surfaces.
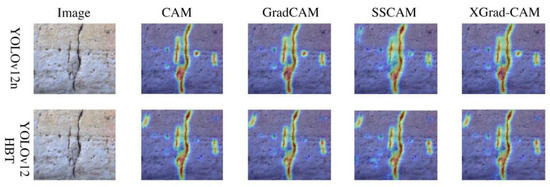
Figure 10.
Visualization of attention maps for YOLOv12n and YOLOv12-MLE using CAM, GradCAM, SSCAM, and XGrad-CAM. In the attention maps, red and yellow regions indicate areas of high model attention corresponding to crack features, while blue regions represent low attention or background areas.
Closer examination of Grad-CAM and SSCAM results further indicated that the high-response areas of YOLOv12-MLE aligned closely with main crack trunks and branching fissures, whereas YOLOv12n displayed dispersed attention and false hotspots. These findings confirm that the improved model not only enhances semantic focus on crack structures but also achieves greater sensitivity in capturing boundary features, providing transparent and traceable visual evidence for crack detection and evolution prediction.
Despite these advantages, certain limitations were observed in complex scenarios. As shown in Figure 11, the input image depicts an outer Tulou wall with multiple intersecting cracks accompanied by windows, material heterogeneity, and illumination reflections. Under such conditions, YOLOv12-MLE attention maps generated by CAM, XGrad-CAM, Grad-CAM, and SSCAM were primarily concentrated on large, salient cracks and structural openings (e.g., vertical crack trunks and window edges), while failing to adequately activate fine branching cracks or subtle micro-fissures at higher wall elevations. Particularly in Grad-CAM, attention hotspots were overly concentrated and neglected peripheral micro-cracks that often represent early indicators of material deterioration.

Figure 11.
Visualization of YOLOv12-MLE revealing attention limitations under occlusion and ambiguous postures using CAM, GradCAM, SSCAM, and XGrad-CAM. In the attention maps, red and yellow regions indicate areas of high model attention, while blue regions represent low attention or background areas.
Notably, strong activations were also observed around window frames and small openings, suggesting a tendency toward misclassification. Since Tulou walls frequently contain small windows, ventilation holes, or repair marks, which share visual similarities with cracks in terms of vertical, high-contrast edges, the model occasionally misidentified these features as defects. This highlights a limitation in distinguishing high-contrast non-crack features from true crack signals.
Overall, these observations indicate that the model’s semantic focus mechanism tends to prioritize high-contrast, large-scale, or opening-adjacent regions, while devoting less attention to low-contrast, dispersed, or peripheral crack signals. In other words, the spatial sensitivity and feature separation capacity of the current model diminish under noisy or occluded conditions. This suggests a potential blind spot in practical Tulou conservation: although YOLOv12-MLE performs reliably on prominent cracks, it remains vulnerable to incomplete focus and interpretability gaps when dealing with complex wall environments or early-stage micro-cracks.
In addition to these interpretability findings, it is important to consider how the system would operate under real field conditions. Data acquisition in Fujian Tulou environments is often affected by variable illumination, surface moisture, vegetation occlusion, and restricted accessibility of higher wall sections. While YOLOv12-MLE showed strong robustness for large and salient cracks, its performance decreased for microcracks and shaded or partially occluded regions, indicating the necessity of standardized acquisition protocols and potentially multi-modal sensing (e.g., UAV-based photogrammetry, multi-spectral or thermal imaging) to ensure reliable input quality. Furthermore, maintaining model performance in practice is challenging because crack morphology evolves with seasonal weathering and conservation interventions. This requires periodic dataset updates and retraining to prevent performance degradation, as well as lightweight strategies such as model compression and distillation to support long-term operation on edge devices. Addressing these practical challenges will be essential for ensuring sustainable monitoring and decision support in heritage conservation workflows.
3.4. Crack Simulation Results
In RFPA3D, quasi-static biaxial tensile loading was applied to the double-layer slab model, with Δx fixed at 0.004% and Δy set to 0, 0.0008%, 0.002%, and 0.004%, corresponding to four typical loading ratios: λ = 0, 0.2, 0.5, and 1.0. To investigate the influence of overlay thickness on crack density, the overlay thickness was varied as t = {5,10,15,30} mm, while the substrate thickness was fixed as T = {15,20,25,30} mm. As summarized in Table 5, crack morphology was strongly controlled by the loading ratio λ. At λ = 0, uniaxial strain generated parallel cracks, consistent with the strip-shaped cracking patterns often observed in Tulou walls under unidirectional stress or temperature gradients. When λ increased to 0.2–0.5, cracks evolved into ladder-like or intersecting networks, closely resembling field observations of intersecting cracks caused by uneven settlement or biaxial loading of outer walls. At λ = 1.0, representing isotropic biaxial tension, the morphology further developed into closed polygonal crack networks, consistent with the surface cracking observed on Tulou facades under long-term thermal expansion–contraction or multi-axial stress constraints.

Table 5.
Different fracture patterns of models with varying overlay thicknesses (5, 10, 15, and 20 mm) under different loading ratios (λ = 0, 0.2, 0.5, 1). The 3D schematic blocks illustrate simulated crack morphologies: darker/red regions correspond to more severe fracture development, while lighter and yellow regions indicate relatively intact areas.
The simulations also revealed the effect of overlay thickness on crack density. In thinner overlays (e.g., t = 5 mm, T = 15 mm), cracks were significantly more numerous, forming dense polygonal networks. In contrast, in thicker overlays (e.g., t = 30 mm, T = 30 mm), the number of cracks was greatly reduced, although the critical λ-dependent transitions in crack morphology remained unchanged. This finding aligns with in situ observations of Fujian Tulou: plaster layers on facades (typically 5–10 mm thick) tend to generate dense crack networks, whereas thicker rammed-earth substrates (exceeding 30 mm) show fewer cracks, though their morphology is still primarily governed by the loading ratio λ. The strong consistency between simulations and field observations reinforces the reliability of the proposed dual-path framework combining YOLOv12-MLE detection and RFPA3D simulation for predicting crack evolution in earthen heritage structures.
On this basis, to further elucidate the evolution of cracks from microscopic defects to macroscopic patterns, Figure 12 presents the progressive four-stage failure process and maximum principal stress (σ1) distribution for a representative case with λ = 1, overlay thickness t = 5 mm, and substrate thickness T = 15 mm.
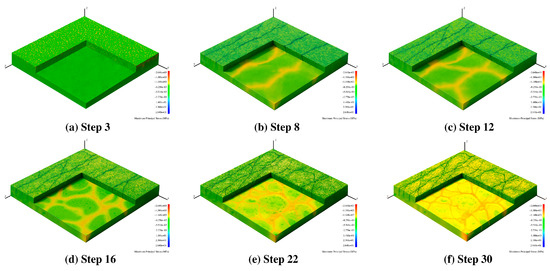
Figure 12.
Stress distribution and crack evolution at different simulation steps in the bi-layered slab model under biaxial loading (λ = 1, t = 5 mm, T = 15 mm). Subfigures (a–f) correspond to Step 3, 8, 12, 16, 22, and 30, respectively, illustrating the progressive formation and propagation of cracks. The color bar represents the maximum principal stress (MPa), where values are shown in scientific notation (e.g., −2.640e+03). Red indicates regions of high tensile stress, while blue indicates compressive or low-stress areas.
In the initial stage (Step 3), the inherent heterogeneity of Tulou wall materials produced uneven stress distributions, with local weak zones experiencing elevated tensile stresses, serving as potential crack nucleation sites. By Step 8–12, micro-cracks gradually emerged and extended along the direction of maximum principal tensile stress, forming skeleton-like crack patterns like the orthogonal fissures observed on Tulou facades. During the propagation stage (Step 16–22), crack density increased, and coalescence became evident: on the one hand, secondary cracks merged into primary ones at near-right angles, leading to localized block segmentation; on the other hand, sequential connections between parallel cracks promoted the development of honeycomb-like or polygonal crack networks, resembling typical field patterns on Tulou walls. Finally, in the saturation stage (Step 30), cracks penetrated the interface between layers, inducing overlay detachment and forming isolated “island” units. Stress was progressively released, marking the transition into the saturation phase.
This simulation not only reveals the progressive evolution of cracks, from stress concentration to interfacial delamination, but also provides a mechanistic explanation of defect formation in Tulou walls. The strong agreement between simulated results and observed crack morphologies validates the physical fidelity of the proposed framework.
3.5. Quantitative Results of Evolutionary Predictions
Quantitative validation of the proposed dual-path framework (YOLOv12-MLE + RFPA3D) was conducted on 20 paired “early–late” Tulou wall crack samples. Results demonstrated stable performance across three evaluation levels: global morphological consistency, geometric statistical consistency, and topological agreement.
As shown in Table 6, calibrated predictions achieved a skeleton IoU of 0.80 ± 0.05 (baseline is 0.72 ± 0.06), significantly improving overall crack skeleton overlap. The Chamfer distance decreased from 5.9 px to 3.7 px, while the Hausdorff distance was reduced from 15.2 px to 9.8 px, indicating improvements in both mean and extreme deviations. Geometric metrics also showed consistent gains: spacing MAE was controlled at 0.95 mm, orientation EMD decreased to 0.09, and density error was reduced to 3.2%. These results confirm that the framework effectively reproduces the spatial distribution and geometric features of Tulou cracks.

Table 6.
Performance metrics for paired Tulou crack samples (mean ± SD).
In the parameter sensitivity analysis, predictive performance declined sharply when overlay thickness t and loading ratio λ deviated from true conditions, but calibration effectively restored accuracy (Table 7). For example, at λ = 0.5, the skeleton IoU dropped to 0.69; after calibration (λ ≈ 1.1, t ≈ 1.0 cm), it recovered to 0.79.

Table 7.
Parameter sensitivity and calibration effects.
Overall, these findings demonstrate that the proposed framework not only reproduces overall crack morphology but also quantitatively aligns spatial distribution, orientation features, and topological structures. Parameter calibration further confirmed the intrinsic coupling between the model and physical constraints, highlighting the framework’s interpretability and potential for generalization.
4. Discussion
This study proposes a dual-path framework tailored for Fujian Tulou conservation: (i) lightweight crack detection based on YOLOv12-MLE and (ii) independent physical simulation using RFPA3D. The two paths are designed to complement each other, with the shared goal of providing reliable detection outcomes and mechanistic insights for heritage protection.
In the detection path, ablation and comparative experiments demonstrated that YOLOv12-MLE, through the integration of the MobileNetV4 backbone, the improved multi-head cross-attention module (IMCA), and the EnEIoU loss, achieved superior detection accuracy and robustness under heterogeneous wall textures while maintaining a compact and edge-deployable architecture. Class activation mapping further confirmed the model’s spatial focus, showing enhanced crack localization and boundary sensitivity under complex backgrounds. Nevertheless, limitations remain: the model exhibited insufficient activation for fine-scale cracks and occasional misclassification of small openings or windows as cracks. Thus, interpretability analysis both validated the effectiveness of the improvements and revealed directions for future optimization.
In the simulation path, RFPA3D reproduced crack evolution patterns strongly gov-erned by the loading ratio (λ), while crack density was primarily influenced by overlay thickness (t). These findings closely match field observations of strip-shaped, ladder-like, and polygonal cracks on Tulou facades, indicating that the combined detection–simulation strategy provides a mechanistic explanatory framework and physically validates observed crack generation and propagation.
From a conservation perspective, the proposed framework offers three major advantages: (i) structured crack archives that facilitate cross-temporal comparison and rapid reinspection; (ii) mechanistic evidence for differentiated effects of λ and t, informing thickness control, localized reinforcement, and boundary-zone interventions; and (iii) a lightweight and interpretable detection model deployable on mobile or unattended devices, meeting real-time and sustainable monitoring requirements in heritage sites. Compared with previous studies that focused primarily on either detection accuracy or HBIM integration, our approach establishes a detection–simulation loop that not only identifies cracks but also explains their physical evolution. This novelty extends AI applications from isolated recognition tasks to interpretable, mechanism-aware, and decision-oriented conservation tools.
Quantitative evaluation further confirmed consistency at multiple levels. Skeleton IoU, Chamfer, and Hausdorff distances demonstrated strong agreement with observed crack morphologies; orientation EMD and spacing MAE validated alignment of directional and spacing statistics; and topological measures (e.g., Betti number β1 and loop rate) revealed consistent trends in connectivity. It is emphasized that these assessments represent cross-sectional consistency diagnostics rather than strict temporal prediction. Since current paired samples approximate temporal evolution rather than deriving from long-term monitoring, future work should integrate multi-epoch fixed-point imaging and thermo–hydro–mechanical coupled field measurements, as well as explicit parameter-mapping protocols, to test parameter identifiability and move toward quantifiable prediction.
5. Conclusions
This study introduced a dual-path framework for the conservation of Fujian Tulou, integrating lightweight crack detection with YOLOv12-MLE and physics-based simulation with RFPA3D. Compared with previous studies that have focused mainly on either detection performance or digital model integration, our framework establishes a detection–simulation loop that both identifies cracks and explains their underlying physical mechanisms. This novelty extends the role of AI in heritage protection from isolated recognition tasks to an integrated, mechanism-aware, and decision-support system.
Despite promising results, limitations remain. RFPA3D simulations rely on an idealized double-layer slab assumption and neglect the multilayered composite structure, pore heterogeneity, and environmental degradation processes of Tulou walls, potentially leading to bias under extreme climate conditions. Future studies should incorporate high-resolution 3D modeling, microstructural characterization, and multi-physics coupling to improve physical accuracy. Moreover, this study focused mainly on geometric crack features (direction, spacing, density) while omitting factors such as moisture, salt migration, and repair traces. Multi-modal data sources (e.g., hyperspectral imaging, thermal infrared, and 3D scanning) could be integrated with deep learning to construct a more comprehensive predictive framework. Finally, although YOLOv12-MLE achieved lightweight performance, further optimization is required for ultra-low power and extreme environments. Techniques such as model distillation, quantization, and neural architecture search (NAS) may facilitate efficient deployment under highly constrained computational resources.
Supplementary Materials
The following supporting information can be downloaded at website: https://www.mdpi.com/article/10.3390/coatings15101156/s1.
Author Contributions
Conceptualization, Y.H. and S.C. (Shaokang Chen); methodology, Y.H.; software, S.C. (Shaokang Chen); validation, Y.H., S.C. (Si Cheng) and S.C. (Shaokang Chen); formal analysis, S.C. (Si Cheng); investigation, Y.H.; resources, Z.Z.; data curation, S.C. (Si Cheng); writing—original draft preparation, Y.H.; writing—review and editing, S.C. (Shaokang Chen) and Z.Z.; visualization, S.C. (Shaokang Chen); supervision, Z.Z.; project administration, Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data supporting the findings of this study are openly available in Figshare at https://doi.org/10.6084/m9.figshare.30104506 (accessed on 20 September 2025).
Conflicts of Interest
Authors Zhuang Zhao is employed by the company Sydney Water Corporation. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as potential conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| YOLO | You Only Look Once |
| SSD | Single Shot MultiBox Detector |
| DETR | DEtection TRansformer |
| RFPA3D | Realistic Failure Process Analysis in 3D |
| CAM | Class Activation Mapping |
| Grad-CAM | Gradient-weighted Class Activation Mapping |
| SSCAM | Score-Weighted Class Activation Mapping |
| XGrad-CAM | Extended Gradient-weighted Class Activation Mapping |
| IoU | Intersection over Union |
| mAP@50 | Mean Average Precision at 50% IoU threshold |
| GFLOPs | Giga Floating Point Operations per Second |
| UIB | Universal Inverted Bottleneck |
| IMCA | Improved Multi-head Cross Attention |
| EnEIoU | Enhanced Efficient Intersection over Union |
| LSTM | Long Short-Term Memory |
| SaturatedLSTMCA | Saturated Long Short-Term Memory Convolutional Attention |
| MAE | Mean Absolute Error |
| EMD | Earth Mover’s Distance |
Appendix A
Table A1 summarizes the parameter settings used in the quantitative evaluation workflow for Fujian Tulou crack detection and evolution prediction. The workflow integrates image preprocessing, skeletonization, feature extraction, and quantitative metrics, ensuring reproducibility of results and consistency across validation protocols. Each step is listed with the corresponding algorithm, key parameters, and implementation notes, covering operations from binary conversion and skeleton IoU to Chamfer/Hausdorff distances and topological analysis (e.g., Betti numbers, loop ratio).

Table A1.
Parameter settings for quantitative evaluation workflow.
Table A1.
Parameter settings for quantitative evaluation workflow.
| Step | Operation | Algorithm/Function | Parameters | Notes |
|---|---|---|---|---|
| Binary conversion | Otsu thresholding | cv2.threshold (…, cv2.THRESH_OTSU) | N/A | Remove small regions <20 px |
| Skeletonization | Thinning | Zhang-Suen/cv2.ximgproc.thinning | mode = THINNING_ZHANGSUEN | Produces 1-pixel skeleton |
| Orientation estimation | Structure tensor | 3 × 3 window | Histogram bins = 18 (10° per bin) | Orientation in [0°, 180°) |
| Spacing extraction | Euclidean distance transform | cv2.distanceTransform | Pixel to mm scaling factor = s | Ridge detection = local maxima |
| Density calculation | Skeleton length/area | np.count_nonzero (skeleton) | Normalize by area | Gives cracks per cm2 |
| Skeleton IoU | Intersection over union | Binary maps | N/A | Evaluates overlap |
| Chamfer distance | Symmetric Chamfer | cv2.distanceTransform + NN search | N/A | Average distance both ways |
| Hausdorff distance | Max distance | scipy.spatial.cKDTree | N/A | Worst-case mismatch |
| Betti numbers | Connected components and loops | scipy.ndimage.label + contour hierarchy | N/A | Gives β0\beta_0, β1\beta_1 |
| Graph abstraction | Skeleton to graph | Nodes = endpoints/branchpoints | N/A | Compute avg. degree, loop ratio |
| Statistics | Significance tests | Paired t-test/Wilcoxon | α = 0.05 | With Shapiro–Wilk normality check |
| Binary conversion | Otsu thresholding | cv2.threshold (…, cv2.THRESH_OTSU) | N/A | Remove small regions <20 px |
| Skeletonization | Thinning | Zhang-Suen/cv2.ximgproc.thinning | mode = THINNING_ZHANGSUEN | Produces 1-pixel skeleton |
| Orientation estimation | Structure tensor | 3 × 3 window | Histogram bins = 18 (10° per bin) | Orientation in [0°, 180°) |
| Spacing extraction | Euclidean distance transform | cv2.distanceTransform | Pixel to mm scaling factor = s | Ridge detection = local maxima |
| Density calculation | Skeleton length / area | np.count_nonzero (skeleton) | Normalize by area | Gives cracks per cm2 |
| Skeleton IoU | Intersection over union | Binary maps | N/A | Evaluates overlap |
| Chamfer distance | Symmetric Chamfer | cv2.distanceTransform + NN search | N/A | Average distance both ways |
| Hausdorff distance | Max distance | scipy.spatial.cKDTree | N/A | Worst-case mismatch |
| Betti numbers | Connected components and loops | scipy.ndimage.label + contour hierarchy | N/A | Gives β0\beta_0, β1\beta_1 |
| Graph abstraction | Skeleton to graph | Nodes = endpoints/branchpoints | N/A | Compute avg. degree, loop ratio |
| Statistics | Significance tests | Paired t-test/Wilcoxon | α = 0.05 | With Shapiro–Wilk normality check |
References
- Porretta, P.; Pallottino, E.; Colafranceschi, E. Minnan and Hakka Tulou: Functional, typological and construction features of the rammed earth dwellings of Fujian (China). Int. J. Archit. Herit. 2022, 16, 899–922. [Google Scholar] [CrossRef]
- Chen, W.; Yan, B.; Guo, S.; Liu, Y.; Yang, F.; Zhang, K.; Mao, W. An in-situ conservation method of the rammed earth sites using a new silica protective agent. Constr. Build. Mater. 2024, 452, 138960. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, S.; Quan, D.; Fang, K.; Wang, B.; Ma, Z. Properties of sustainable earth construction materials: A state-of-the-art review. Sustainability 2024, 16, 670. [Google Scholar] [CrossRef]
- Golewski, G.L. The phenomenon of cracking in cement concretes and reinforced concrete structures: Mechanisms, causes, types, and detection methods—A review. Buildings 2023, 13, 765. [Google Scholar] [CrossRef]
- Azouz, Z.; Honarvar Shakibaei Asli, B.; Khan, M. Evolution of crack analysis in structures using image processing technique: A review. Electronics 2023, 12, 3862. [Google Scholar] [CrossRef]
- Pala, G.K.; Kesana, N.S.; Gopalapurapu, K.S. Advancements in optimizing the quality assurance and crack detection by leveraging the application of emerging artificial intelligence trends for enrichment of civil infrastructure—A recapitulation. In Recent Developments and Innovations in the Sustainable Production of Concrete; Woodhead Publishing: Cambridge, UK, 2025; pp. 635–655. [Google Scholar]
- Miao, P.; Srimahachota, T. Cost-effective system for detection and quantification of concrete surface cracks by combination of convolutional neural network and image processing techniques. Constr. Build. Mater. 2021, 293, 123549. [Google Scholar] [CrossRef]
- Vijayan, V.; Joy, C.M.; Shailesh, S. A survey on surface crack detection in concretes using traditional, image processing, machine learning, and deep learning techniques. In Proceedings of the 2021 International Conference on Communication, Control and Information Sciences (ICCISc), Idukki, India, 16–18 June 2021; Volume 1, pp. 1–6. [Google Scholar]
- Sun, Z.; Caetano, E.; Pereira, S.; Moutinho, C. Employing histogram of oriented gradient to enhance concrete crack detection performance with classification algorithm and Bayesian optimization. Eng. Fail. Anal. 2023, 150, 107351. [Google Scholar] [CrossRef]
- Han, H.; Deng, H.; Dong, Q.; Gu, X.; Zhang, T.; Wang, Y. An advanced Otsu method integrated with edge detection and decision tree for crack detection in highway transportation infrastructure. Adv. Mater. Sci. Eng. 2021, 2021, 9205509. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.Y.; Liu, J.X.; Zhang, Y.; Chen, Z.P.; Li, C.G.; Yan, R.B. Research on crack detection algorithm of the concrete bridge based on image processing. Procedia Comput. Sci. 2019, 154, 610–616. [Google Scholar] [CrossRef]
- Xu, X.; Zhao, M.; Shi, P.; Ren, R.; He, X.; Wei, X.; Yang, H. Crack detection and comparison study based on faster R-CNN and mask R-CNN. Sensors 2022, 22, 1215. [Google Scholar] [CrossRef]
- Yu, F.; Du, C.; Hua, A.; Jiang, M.; Wei, X.; Peng, T.; Hu, X. EnCaps: Clothing image classification based on enhanced capsule network. Appl. Sci. 2021, 11, 11024. [Google Scholar] [CrossRef]
- Kim, H.J.; Lee, D.H.; Niaz, A.; Kim, C.Y.; Memon, A.A.; Choi, K.N. Multiple-clothing detection and fashion landmark estimation using a single-stage detector. IEEE Access 2021, 9, 11694–11704. [Google Scholar] [CrossRef]
- Sohaib, M.; Arif, M.; Kim, J.M. Evaluating YOLO models for efficient crack detection in concrete structures using transfer learning. Buildings 2024, 14, 3928. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, T.; Xu, J.; Hong, Y.; Pu, Q.; Wen, X. Rotating target detection method of concrete bridge crack based on YOLOv5. Appl. Sci. 2023, 13, 11118. [Google Scholar] [CrossRef]
- Yin, Z.; Li, H.; Qi, B.; Shan, G. BBW YOLO: Intelligent detection algorithms for aluminium profile material surface defects. Coatings 2025, 15, 684. [Google Scholar] [CrossRef]
- Karimi, N.; Mishra, M.; Lourenço, P.B. Automated surface crack detection in historical constructions with various materials using deep learning-based YOLO network. Int. J. Archit. Herit. 2025, 19, 581–597. [Google Scholar] [CrossRef]
- Ren, W.; Zhong, Z. LBA-YOLO: A novel lightweight approach for detecting micro-cracks in building structures. PLoS ONE 2025, 20, e0321640. [Google Scholar] [CrossRef]
- Bruno, S.; Galantucci, R.A.; Musicco, A. Decay detection in historic buildings through image-based deep learning. Vitruvio 2023, 8, 6–17. [Google Scholar] [CrossRef]
- Croce, V.; Caroti, G.; Piemonte, A.; De Luca, L.; Véron, P. H-BIM and Artificial Intelligence: Classification of Architectural Heritage for Semi-Automatic Scan-to-BIM Reconstruction. Sensors 2023, 23, 2497. [Google Scholar] [CrossRef] [PubMed]
- Laohaviraphap, N.; Waroonkun, T. Integrating Artificial Intelligence and the Internet of Things in Cultural Heritage Preservation: A Systematic Review of Risk Management and Environmental Monitoring Strategies. Buildings 2024, 14, 3979. [Google Scholar] [CrossRef]
- Odgers, D.; Henry, A. Practical Building Conservation: Stone; Ashgate: Farnham, UK, 2012; p. 338. [Google Scholar]
- D’Agostino, D.; Congedo, P.M.; Cataldo, R. Computational Fluid Dynamics (CFD) Modeling of Microclimate for Salts Crystallization Control and Artworks Conservation. J. Cult. Herit. 2014, 15, 448–457. [Google Scholar] [CrossRef]
- Pocobelli, D.P.; Boehm, J.; Bryan, P.; Still, J.; Grau-Bové, J. BIM for Heritage Science: A Review. Herit. Sci. 2018, 6, 30. [Google Scholar] [CrossRef]
- Ceccarelli, L.; Bevilacqua, M.G.; Caroti, G.; Castiglia, R.B.F.; Croce, V. Semantic Segmentation through Artificial Intelligence from Raw Point Clouds to H-BIM Representation. Disegnarecon 2023, 16, 171–178. [Google Scholar] [CrossRef]
- Yiğit, A.Y.; Uysal, M. Automatic Crack Detection and Structural Inspection of Cultural Heritage Buildings Using UAV Photogrammetry and Digital Twin Technology. J. Build. Eng. 2024, 94, 109952. [Google Scholar] [CrossRef]
- Rodrigues, F.; Cotella, V.; Rodrigues, H.; Rocha, E.; Freitas, F.; Matos, R. Application of Deep Learning Approach for the Classification of Buildings’ Degradation State in a BIM Methodology. Appl. Sci. 2022, 12, 7403. [Google Scholar] [CrossRef]
- Standoli, G.; Salachoris, G.P.; Masciotta, M.G.; Clementi, F. Modal-Based FE Model Updating via Genetic Algorithms: Exploiting Artificial Intelligence to Build Realistic Numerical Models of Historical Structures. Constr. Build. Mater. 2021, 303, 124393. [Google Scholar] [CrossRef]
- Gara, F.; Nicoletti, V.; Arezzo, D.; Cipriani, L.; Leoni, G. Model Updating of Cultural Heritage Buildings through Swarm Intelligence Algorithms. Int. J. Archit. Herit. 2025, 19, 259–275. [Google Scholar] [CrossRef]
- Salehi, H.; Burgueño, R. Emerging Artificial Intelligence Methods in Structural Engineering. Eng. Struct. 2018, 171, 170–189. [Google Scholar] [CrossRef]
- Fan, J.; Chen, Y.; Zheng, L. Artificial Intelligence for Routine Heritage Monitoring and Sustainable Planning of the Conservation of Historic Districts: A Case Study on Fujian Earthen Houses (Tulou). Buildings 2024, 14, 1915. [Google Scholar] [CrossRef]
- Luo, Y.; Yin, B.; Peng, X.; Xu, Y.; Zhang, L. Wind-Rain Erosion of Fujian Tulou Hakka Earth Buildings. Sustain. Cities Soc. 2019, 50, 101666. [Google Scholar] [CrossRef]
- Zhou, Q. Research on Traditional Reinforcement Techniques for Rammed Earth Walls in China. Int. J. Archit. Herit. 2025, 19, 496–514. [Google Scholar] [CrossRef]
- Tang, C.A. Numerical simulation of progressive rock failure and associated seismicity. Int. J. Rock Mech. Min. Sci. 1997, 34, 249–261. [Google Scholar] [CrossRef]
- Tang, C.A.; Liang, Z.Z.; Zhang, Y.B.; Xu, T. Three-dimensional material failure process analysis. Key Eng. Mater. 2005, 297–300, 1196–1201. [Google Scholar] [CrossRef]
- Helgeson, D.E.; Aydin, A. Characteristics of joint propagation across layer interfaces in sedimentary rocks. J. Struct. Geol. 1991, 13, 897–911. [Google Scholar] [CrossRef]
- Tang, C.A.; Zhang, Y.B.; Liang, Z.Z.; Xu, T.; Tham, L.G.; Lindqvist, P.-A.; Kou, S.Q.; Liu, H.Y. Fracture spacing in layered materials and pattern transition from parallel to polygonal fractures. Phys. Rev. E 2006, 73, 056120. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).















