Pavement Performance and Mechanism of Asphalt Mixtures Reinforced with Different Diameters of Basalt Fibers for the Surface Layer
Abstract
1. Introduction
2. Materials and Methods
2.1. Raw Materials
2.1.1. Asphalt Binder
2.1.2. Aggregates and Fillers
2.1.3. Basalt Fiber
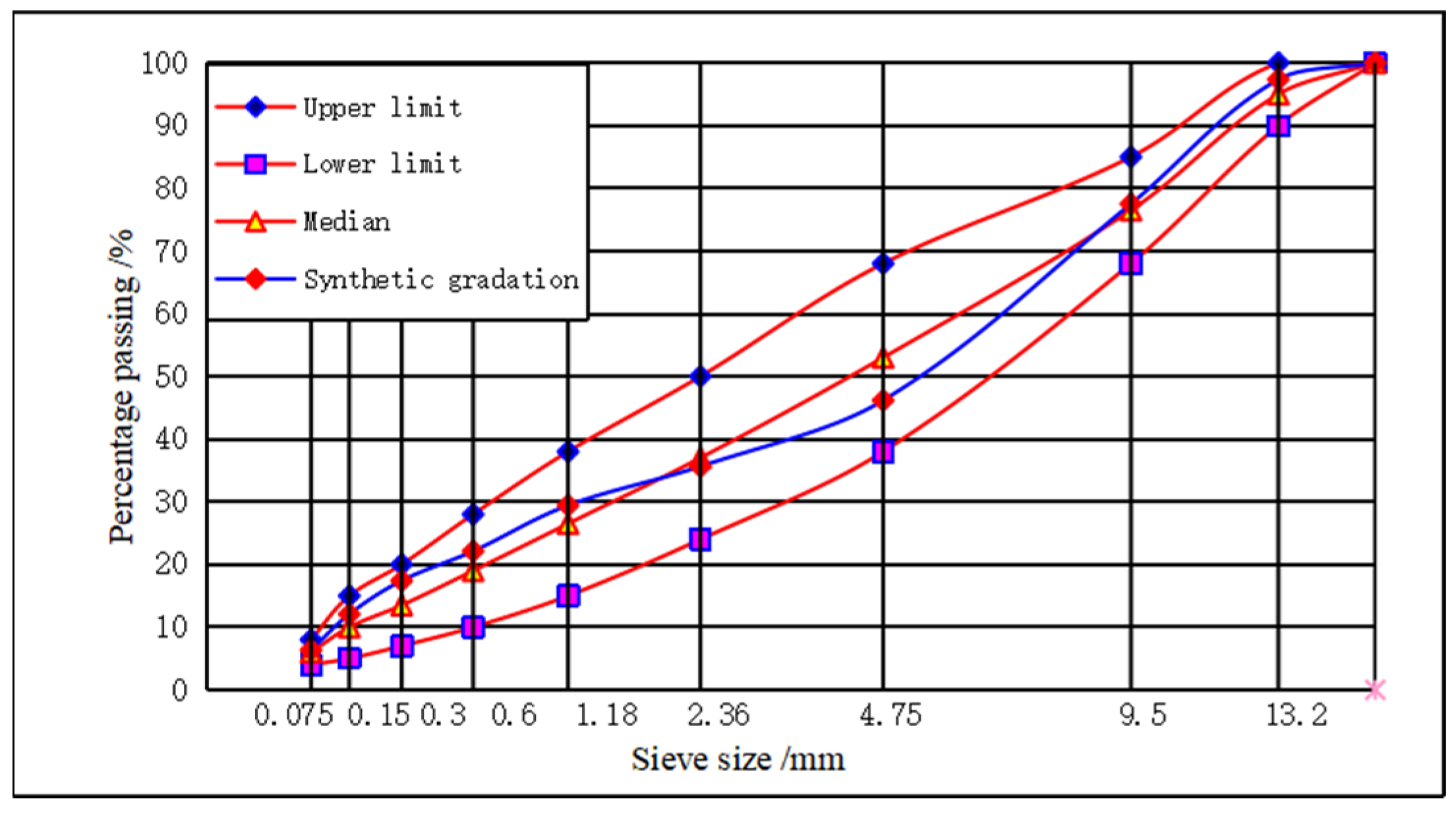
2.1.4. Mixture Gradation
2.2. Test Methods
2.2.1. Rutting Test
2.2.2. Low Temperature Beam Bending Test
2.2.3. Immersion Marshall Test
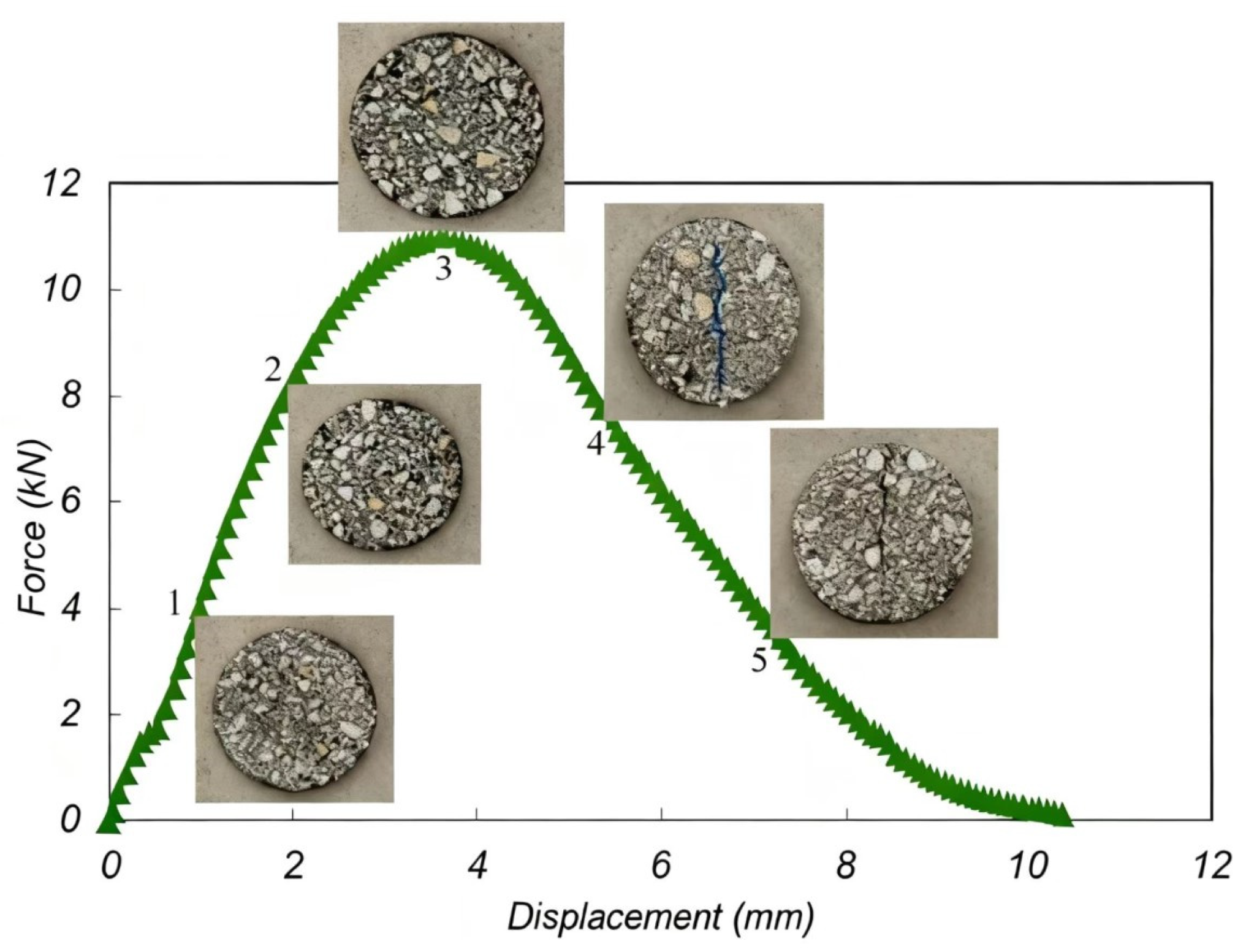
2.2.4. IDEAL Cracking Test
2.2.5. Triaxial Shear Test
2.2.6. Dynamic Creep Test
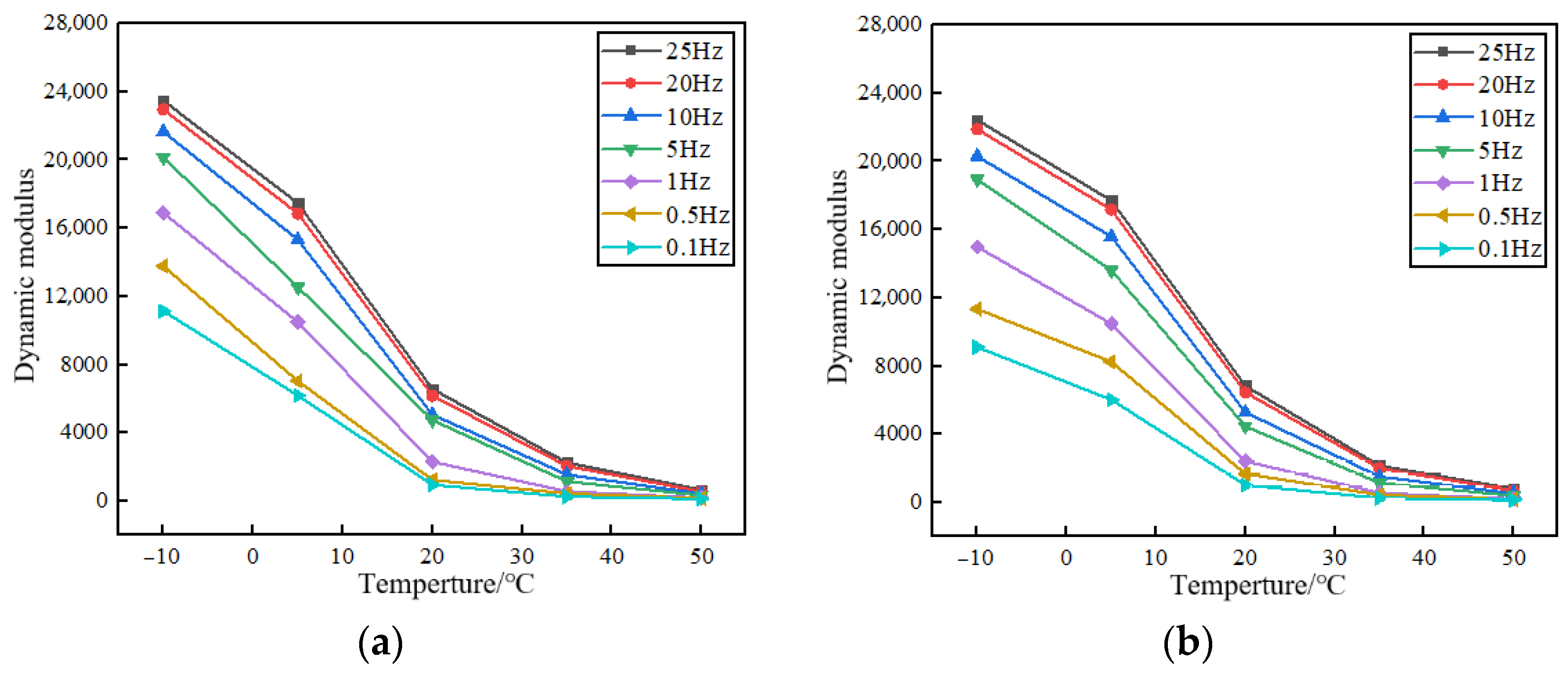
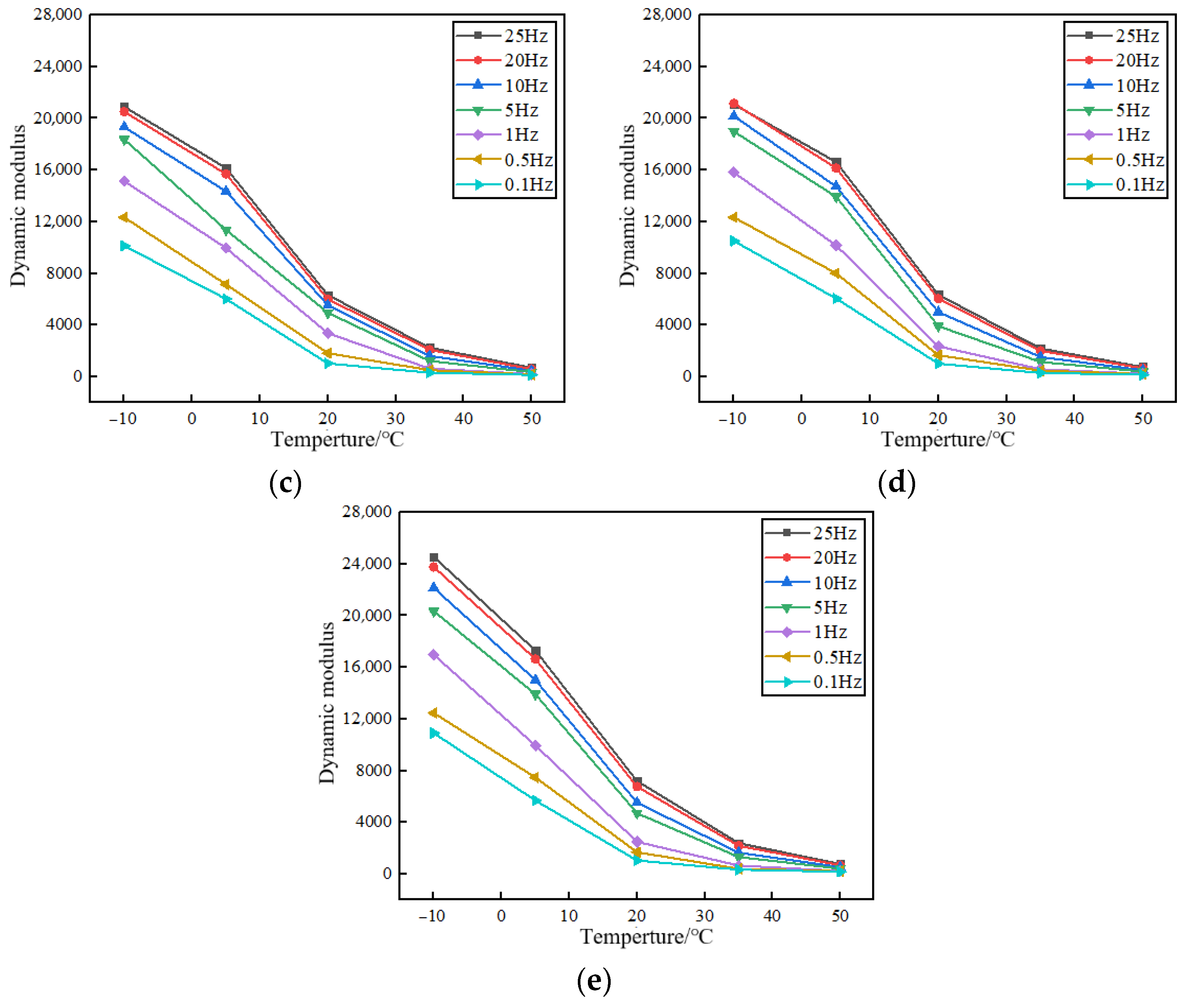
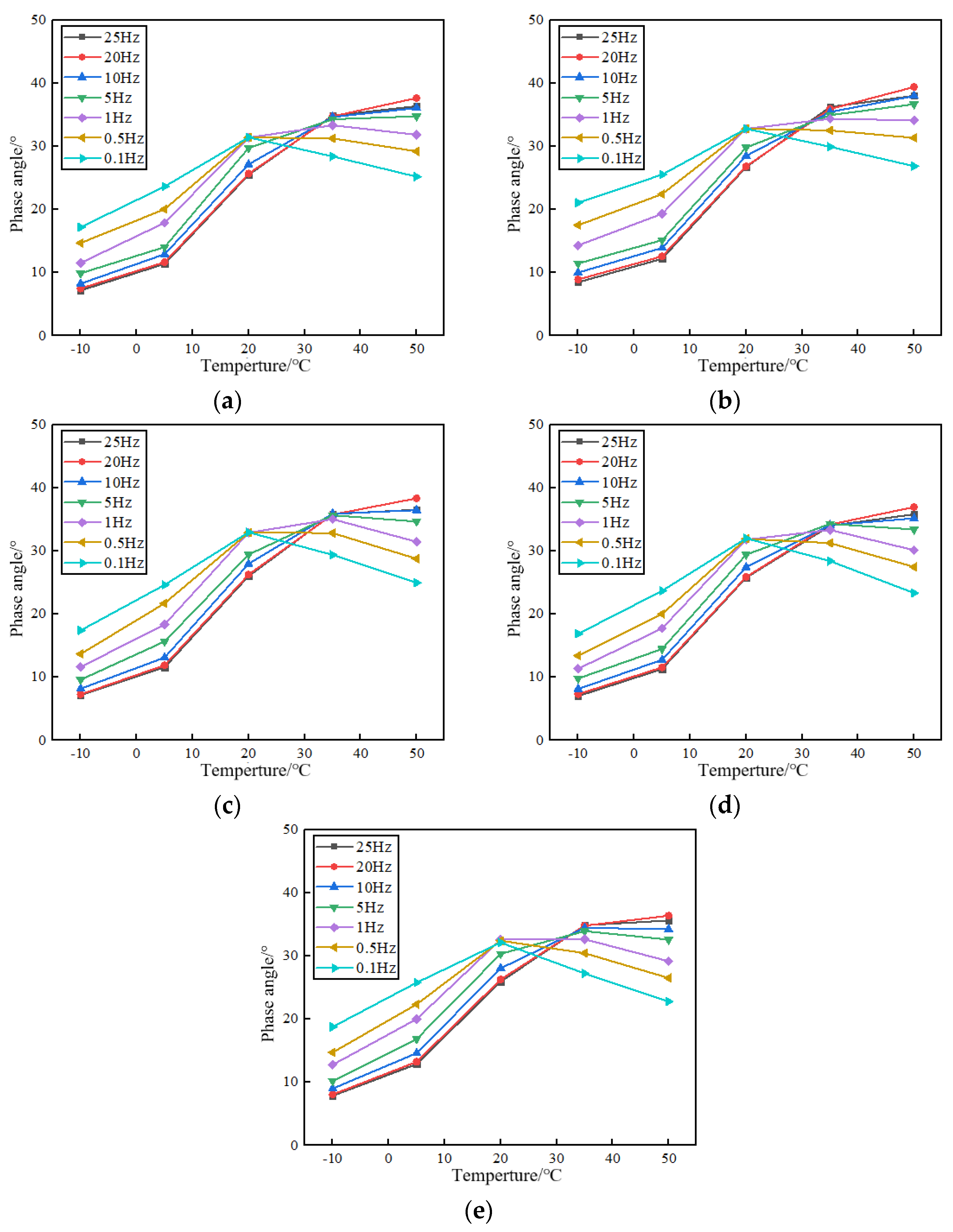
2.2.7. Dynamic Modulus Test
3. Results and Discussion
3.1. Optimum Asphalt–Aggregate Ratio
3.2. Effect of Basalt Fiber on the Performance of Asphalt Mixture
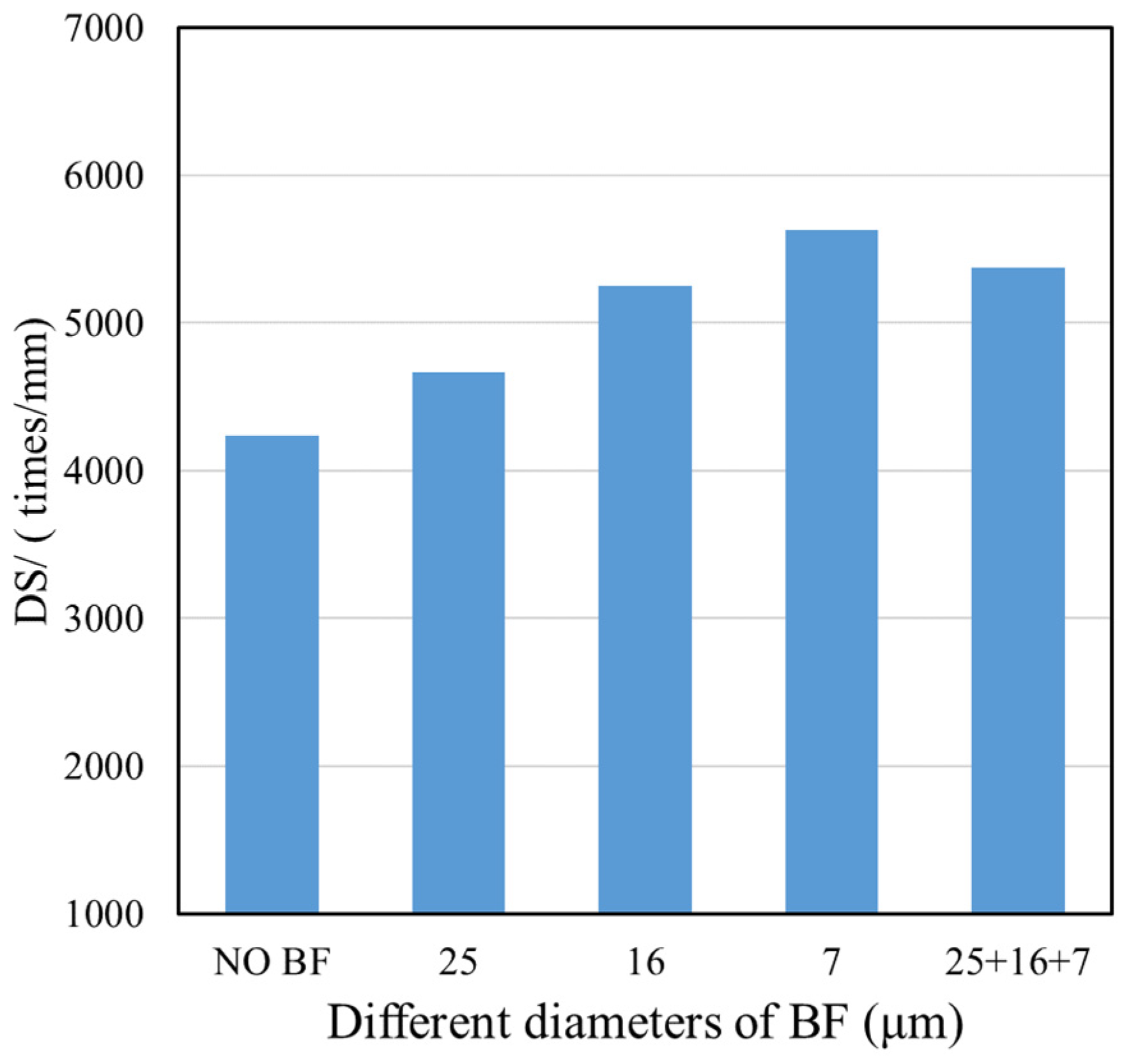
3.2.1. High Temperature Deformation Resistance
3.2.2. Low Temperature Crack Resistance
3.2.3. Water Stability
3.3. Mechanical Property Analysis
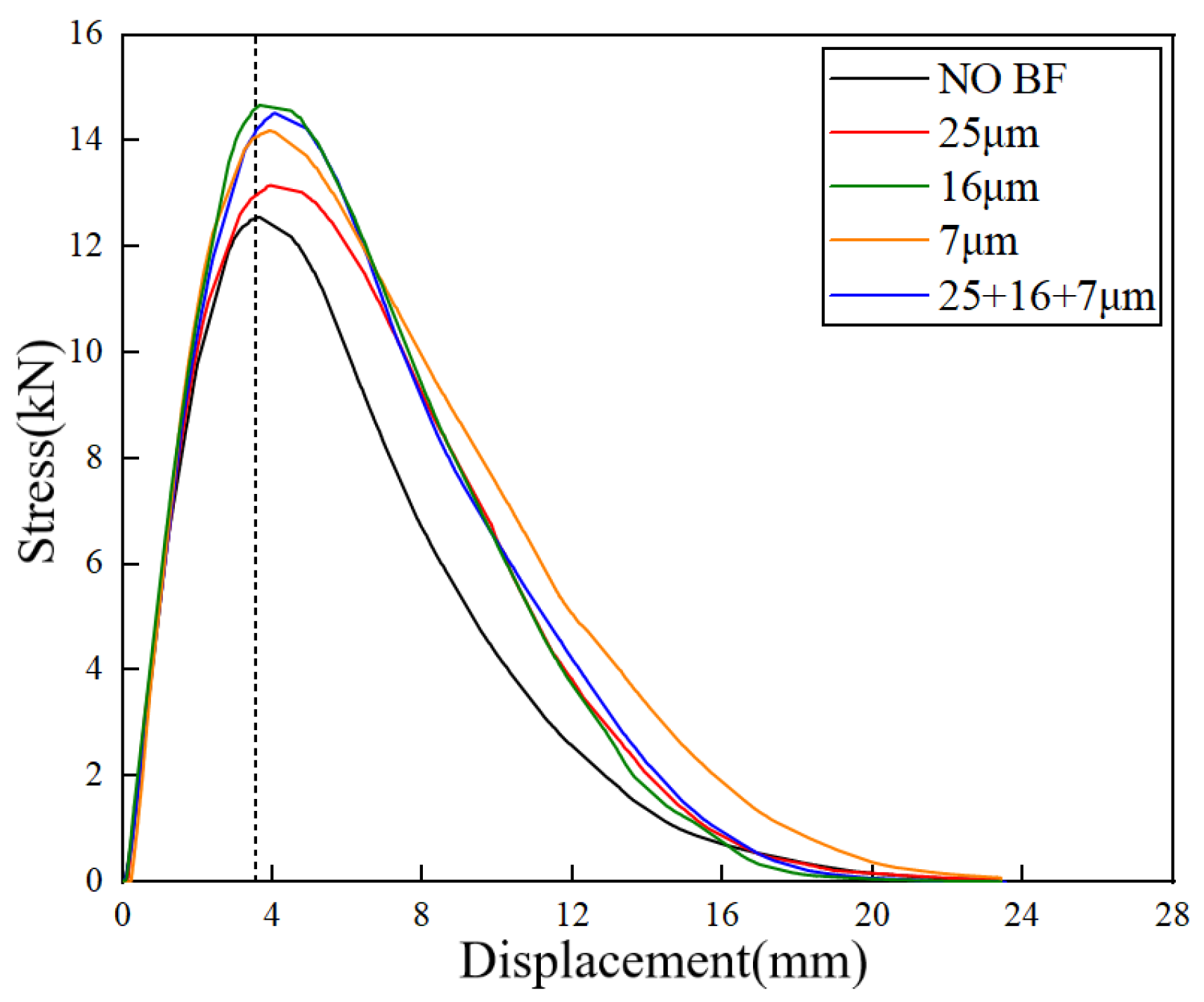
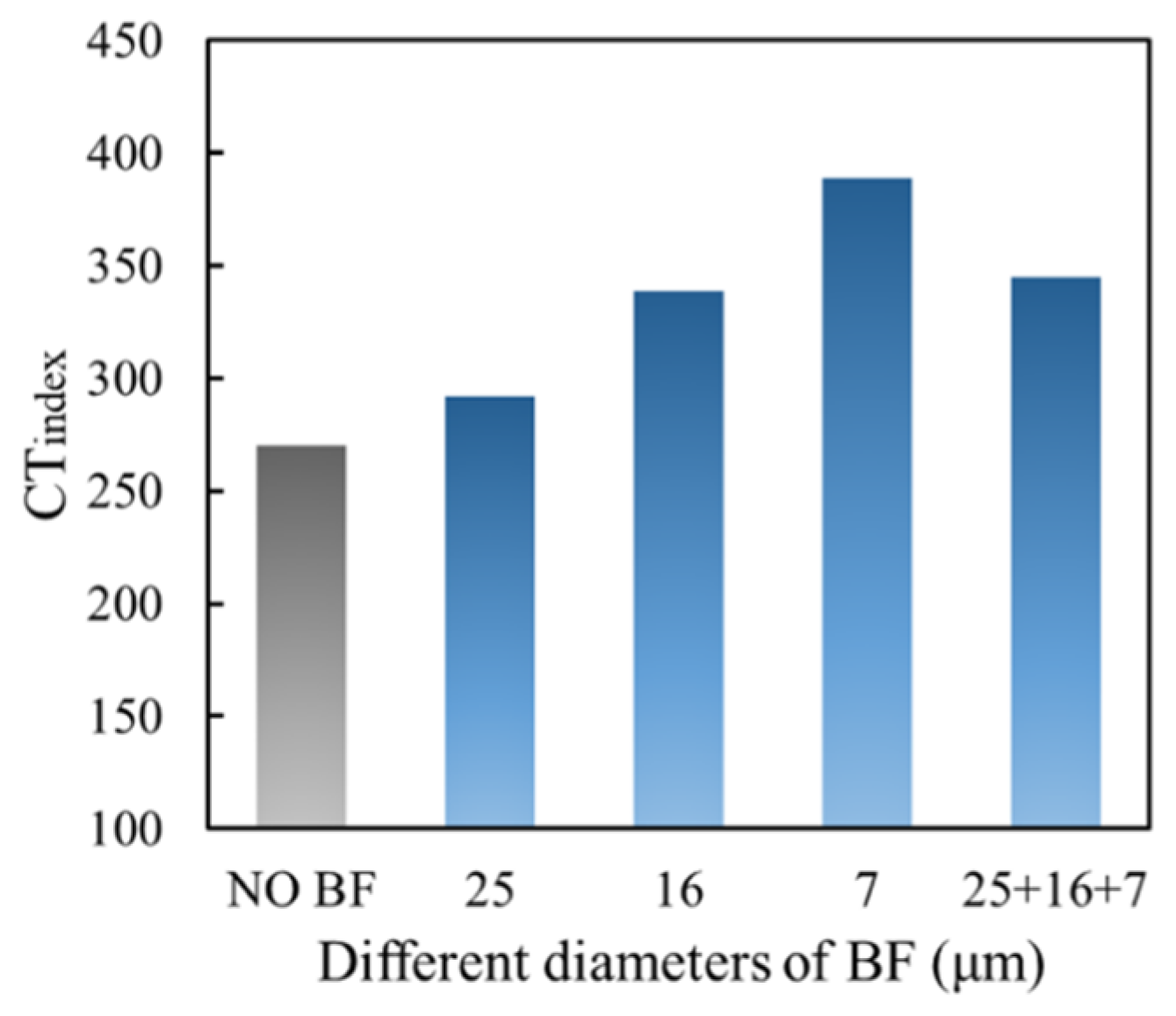
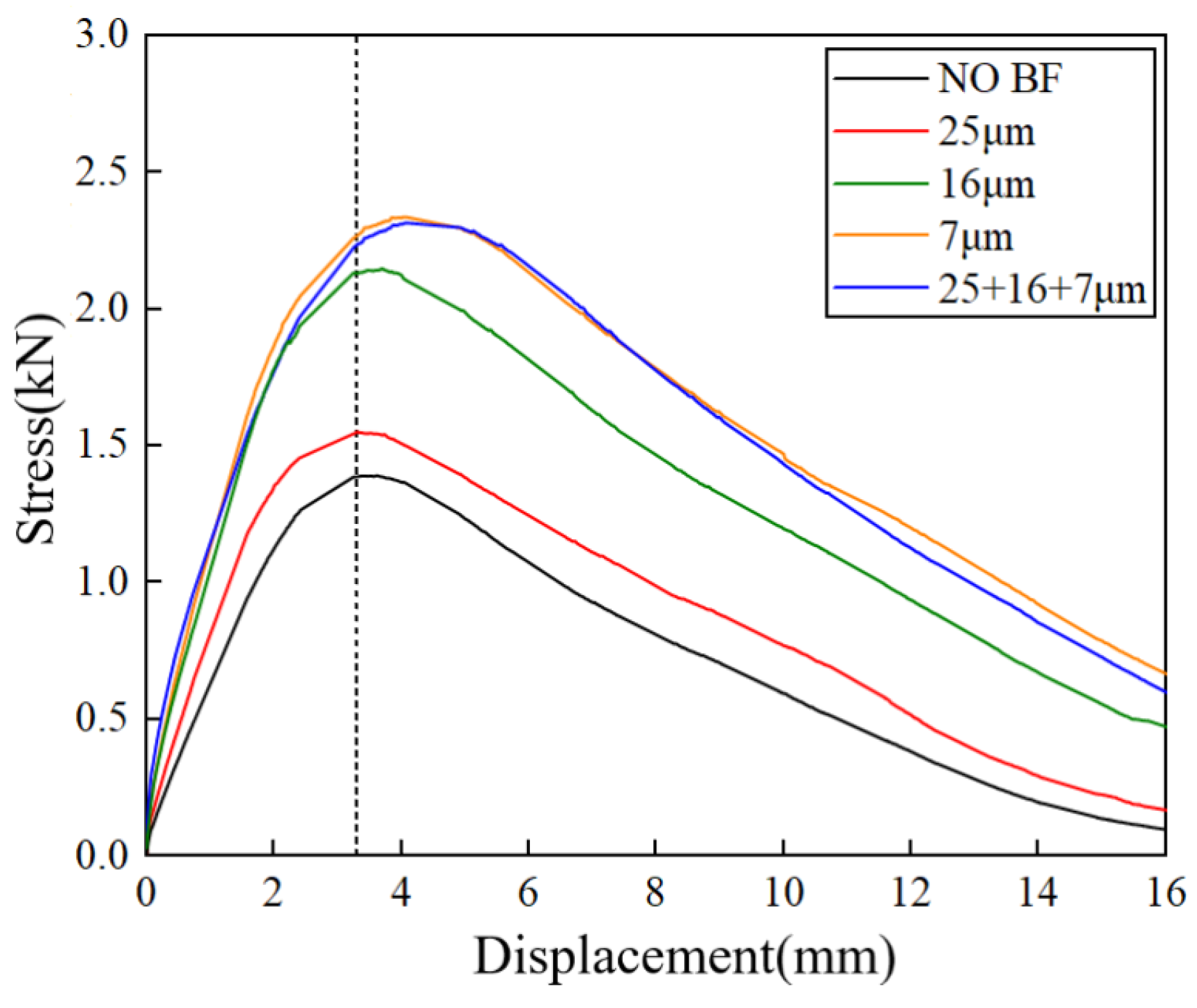
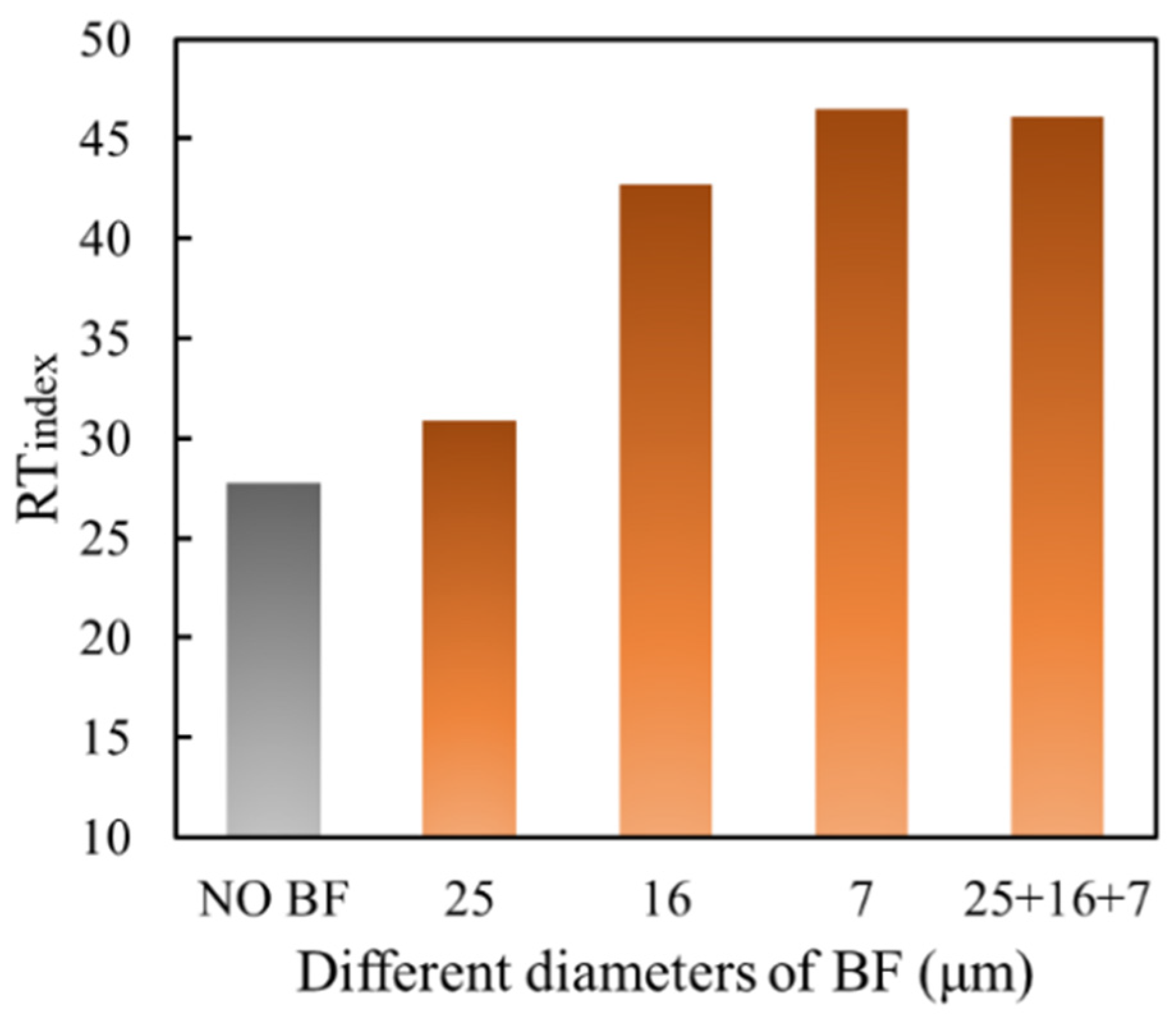
3.3.1. Anti-Cracking Performance
3.3.2. Shear Resistance
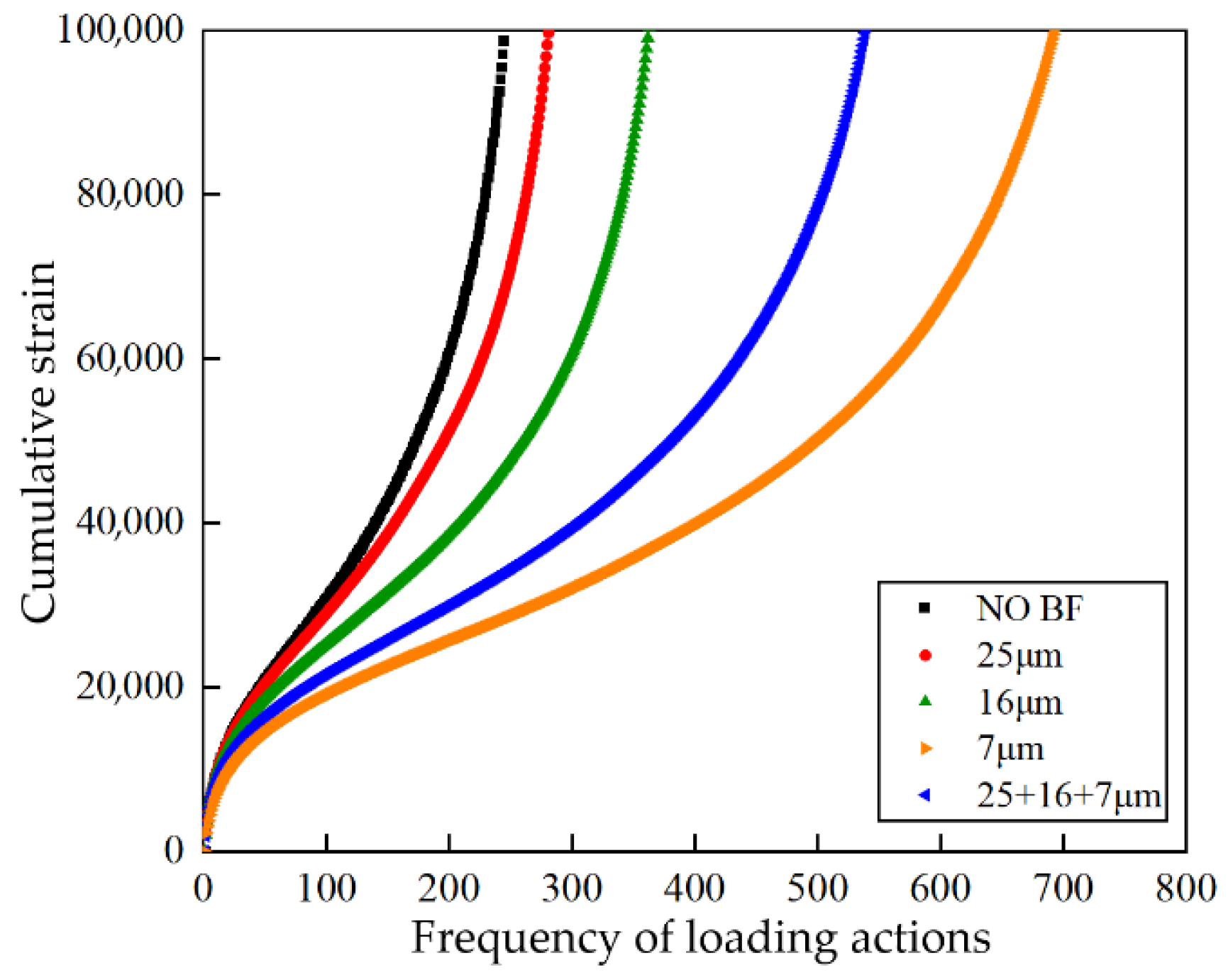
3.3.3. Creep Performance
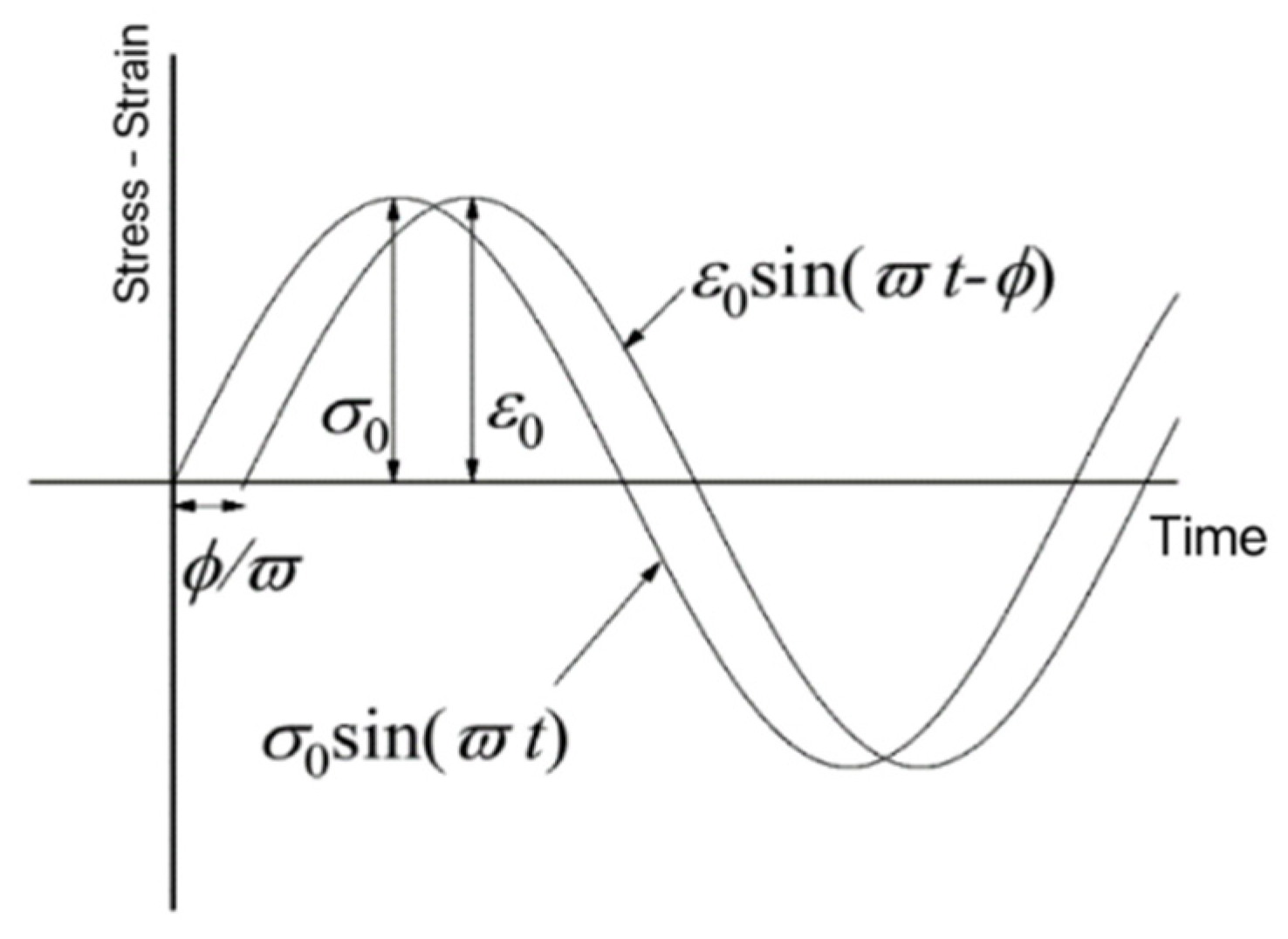
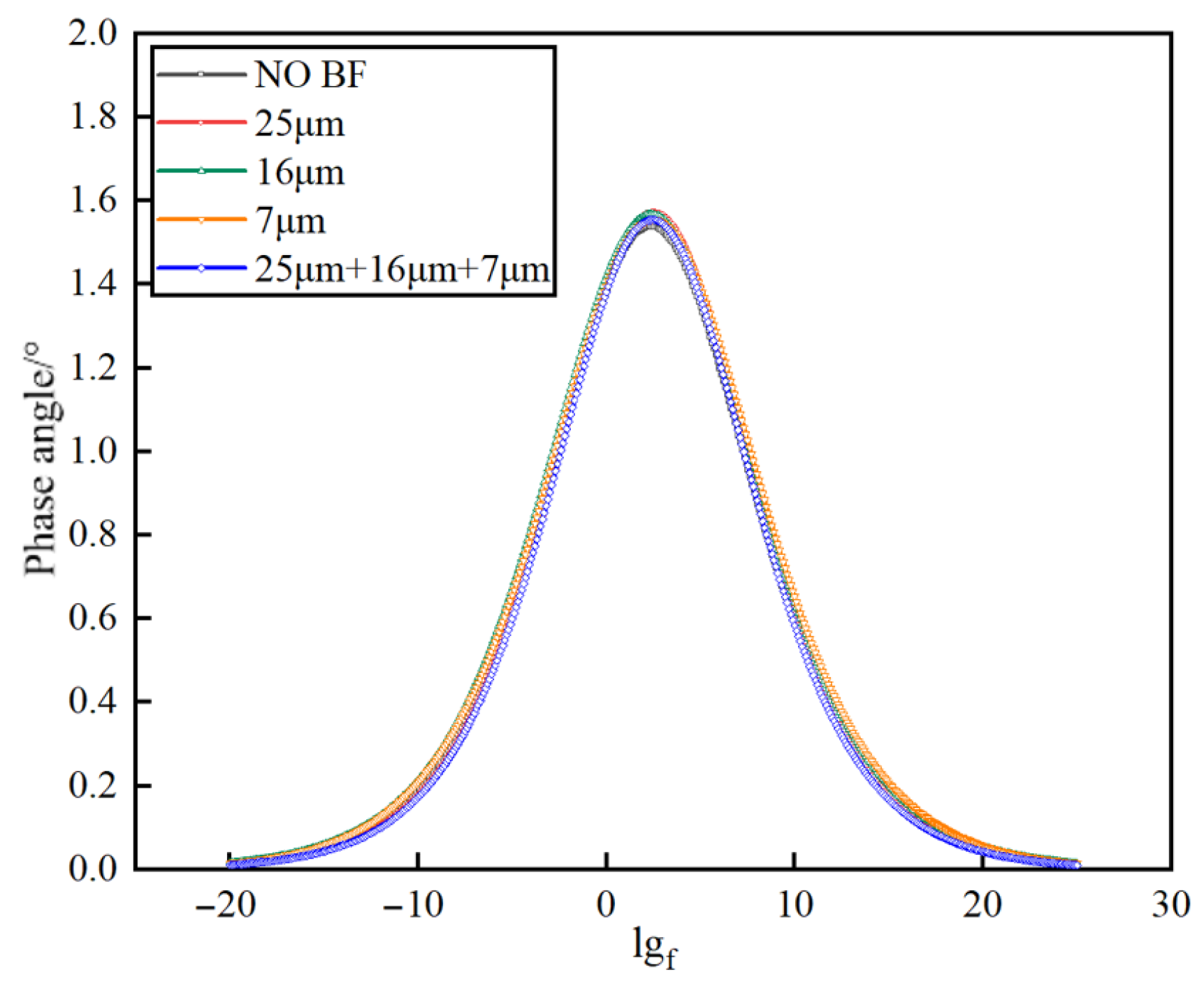
3.3.4. Viscoelastic Property
3.4. Mechanism Analysis Using the Equal Cross-Section Theory
3.4.1. Equal Cross-Section Theory
3.4.2. Relationship Between the TTCR of the BFs and the Performance and Mechanism of the Asphalt Mixture
4. Conclusions
- (1)
- Adding BFs can effectively improve the performance of the asphalt mixture, and the fiber diameter is a significant factor. The five types of BFs with different diameters present different reinforcing effects on the mixture performance, from excellent to poor, which are in the following order: 7 μm, mixed diameter, 16 μm, and 25 μm, indicating that smaller diameter BFs exhibit more remarkable improvements in asphalt mixture performance.
- (2)
- BFs with a diameter of 7 μm demonstrate the best improvement in mixture performance. The dynamic stability of the asphalt mixture containing 7 μm BF increased by 32.7%, the maximum bending tensile strain improved by 21.5%, the increase in the percentage of the Marshall stability improved from 37.7% to 40.5%, the CTindex improved by 44.1%, the RTindex improved by 67.8%, the cohesion improved by 61.5%, the creep rate attained a range of 64 to 349, and the dynamic modulus rose by 99.7 MPa (50 °C, 10 Hz), respectively.
- (3)
- The performance of a mixed diameter BFAM is better than 16 µm, and slightly worse than 7 μm, indicates that a mixed diameter BF (7 μm: 16 μm: 25 μm = 1:1:1) has an excellent reinforcing effect on the mixture performance.
- (4)
- The TTCR of fibers with different diameters are ranked from high to low as follows: 7 μm, mixed diameter, 16 μm, and 25 μm, which shows that the 7 μm BF presents the best reinforcement effect for the mixture, which is consistent with the performance test results of the asphalt mixture. According to the results of the equal cross-section theory, it will help to improve the performance of the asphalt mixture when the Young’s modulus of the fiber is relatively high and the diameter of the fiber is relatively small.
- (5)
- According to the equal cross-section theory, when the fiber diameter is smaller, the number of fibers increases under the same dosage, and the fibers are wound with each other to form a denser fiber frame, thus adsorbing more structural asphalt, making the asphalt mixture performance better. When the BFAM is subjected to external load, the fiber–asphalt blend can fully absorb external energy by its own synergistic deformation, thereby preventing the relative displacement between fiber and asphalt, asphalt and aggregate, and aggregate and aggregate. This phenomenon plays a certain role in delaying or even preventing the damage of the BFAM. This effect is more pronounced under high temperature conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviation | Full Name |
| ACCD | Asphalt Concrete Cracking Device |
| BF | Basalt Fiber |
| BFAM | Basalt Fiber Asphalt Mixture |
| CTindex | Cracking Index |
| DS | Dynamic Stability |
| E* | Composite Dynamic Modulus |
| E’ | Storage Modulus |
| E’’ | Loss Modulus |
| Gf | Fracture Energy |
| IDEAL-CT | IDEAL Cracking Test |
| IDEAL-RT | IDEAL Rutting Test |
| IDT | Indirect Tensile Test |
| ISDT | In Situ Direct Tension Test |
| MS | Marshall Stability |
| MS0 | Immersion Residual Stability |
| PB | Maximum Failure Load |
| RTindex | Rutting Index |
| RTFOT | Rolling Thin Film Oven Test |
| SB | Bending Stiffness Modulus |
| SCB | Semi-Circular Bending Test |
| SBS | Styrene–Butadiene–Styrene Block Copolymer |
| TCR | Transformed Cross-Sectional Area |
| TTCR | Total Transformed Cross-Section |
| VFA | Asphalt Saturation |
| VMA | Mineral Aggregate Gap Rate |
| VV | Void Ratio |
| Symbol | Description |
| a, b, c, d, f | Fitting coefficients |
| b | Width of the specimen mid-span section |
| C1, C2 | Correction coefficients of the rutting test machine |
| d | Mid-span deflection of the specimen at failure |
| d1, d2 | Deformation depths of the specimen at t1 and t2 |
| D | Diameter of cylindrical specimens |
| Ef | Young’s modulus of basalt fiber |
| EAC | Young’s modulus of asphalt concrete |
| f | Loading frequency |
| Fn | Rheological times |
| h | Height of the specimen section |
| l75 | Displacement of the specimen corresponding to 75% post-peak load |
| L | Span of the prismatic beam specimen |
| |m75| | Absolute value of the slope of the load-displacement curve at 75% post-peak load |
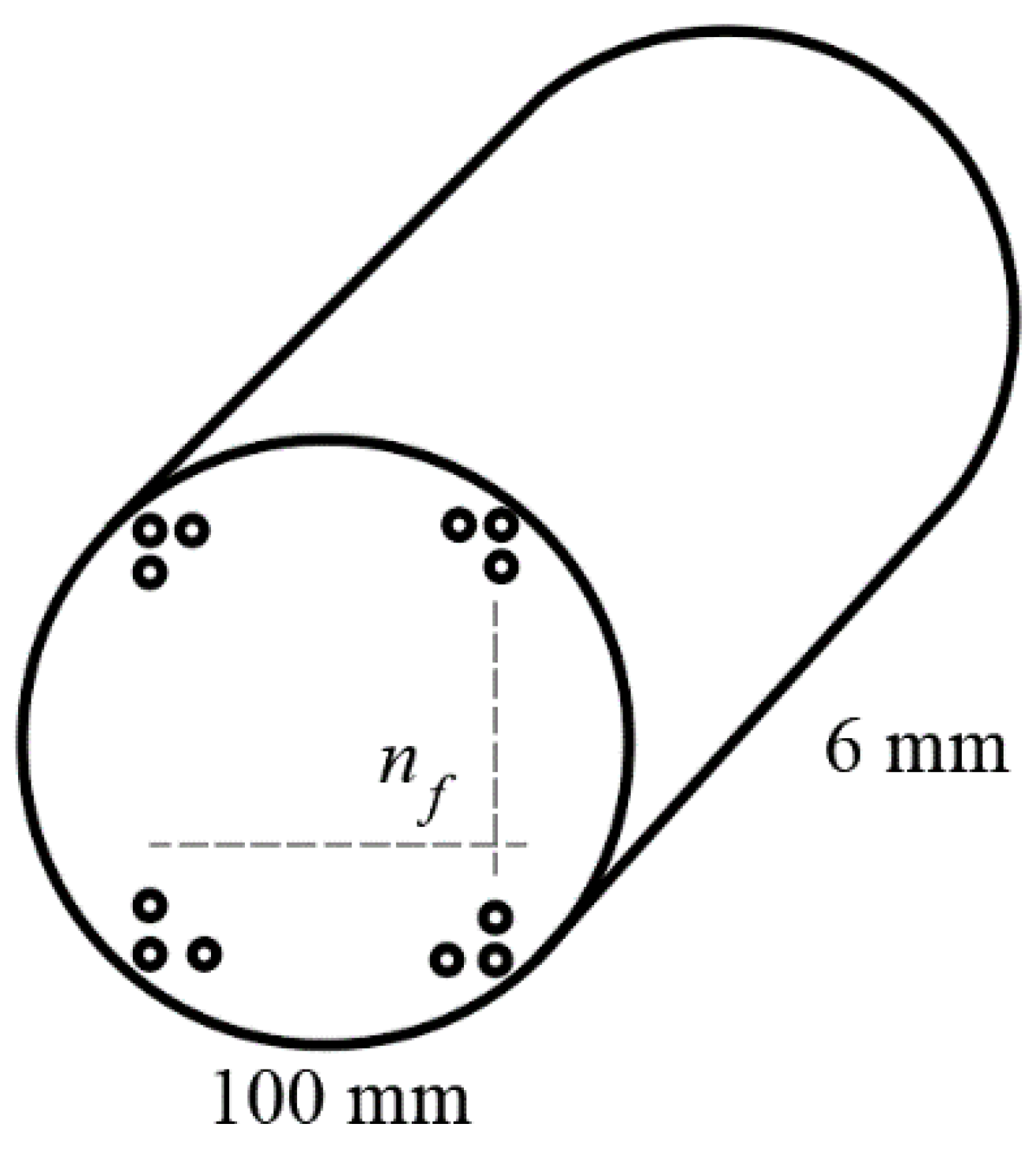
| nf | Number of fibers per row/column in the cube unit |
| N | Number of wheel pressure reciprocations (rutting test); load cycles (dynamic creep test) |
| Nps | Critical load cycles at the transition from compaction stage to stable stage (creep) |
| Nst | Critical load cycles at the transition from stable stage to destruction stage (creep) |
| Pmax | Maximum load applied to the specimen |
| σ | Sinusoidal applied stress |
| σ0 | Maximum amplitude of sinusoidal stress |
| ε | Sinusoidal feedback strain |
| ε0 | Maximum amplitude of sinusoidal strain |
| εB | Maximum bending tensile strain at the bottom of the beam |
| εp | Cumulative microstrain of the specimen |
| εps | Cumulative microstrain at the start of the stable creep stage |
| εst | Cumulative microstrain at the end of the stable creep stage |
| Φ | Phase angle |
| sf | Cross-sectional area of a single basalt fiber |
| Sf | Total cross-sectional area of all transverse fibers in the cube unit |
| t | Test time (dynamic modulus test); specimen thickness (IDEAL-CT/RT tests) |
| t1, t2 | Test times (45 min and 60 min, respectively) in the rutting test |
| w | Width of the upper load strip in the IDEAL-RT test |
| ω | Angular velocity of sinusoidal loading |
| Unit | Applicable Equations/Sections |
| Dimensionless | Equations (10)–(12) |
| mm | Equation (2) |
| Dimensionless | Equation (1) |
| mm | Equation (3) |
| mm | Equation (1) |
| mm | Equations (6), (8), and (9) |
| MPa | Equation (16) |
| MPa | Equation (16) |
| Hz | Equations (13)–(15); Figure 14 |
| Cycles | Table 8 |
| mm | Equations (2) and (3) |
| mm | Equations (6) and (8) |
| mm | Equations (2) and (3) |
| kN/mm | Equations (6)–(8) |
| Dimensionless | Equation (16) |
| Cycles/min (rutting); Cycles (creep) | Equation (1); Equations (10)–(12) (creep) |
| Cycles | Equations (10) and (11) (dynamic creep test) |
| Cycles | Equations (11) and (12) (dynamic creep test) |
| kN | Equation (9) |
| MPa | Equations (13)–(15) |
| MPa | Equations (13)–(15) (dynamic modulus test) |
| με | Equations (13)–(15) (dynamic modulus test) |
| με | Equations (13)–(15) (dynamic modulus test) |
| με | Equation (3) (low-temperature beam bending test) |
| με | Equations (10)–(12) (dynamic creep test) |
| με | Equations (11) and (12) (dynamic creep test) |
| με | Equations (11) and (12 |
| Degree (°) | Equations (13)–(15); Figure 13 |
| Mm2 | Equation (16) |
| mm2 | Equation (16) |
| s (dynamic modulus); mm (IDEAL tests) | Equations (6), (8), and (9); Equations (13)–(15) |
| min | Equation (1) |
| m | Equation (9) |
| rad/s | Equations (13)–(15) |
References
- Sun, X.; Wang, H.; Liu, S. Research on road performance of fiber-reinforced semi-flexible pavement materials. J. China Foreign Highway 2024, 45, 106–117. [Google Scholar] [CrossRef]
- Xu, T.; Gu, X.; Ni, F. Test and performance study of basalt fiber reinforced asphalt concrete. J. Transp. Eng. Inf. 2011, 69, 115–121. [Google Scholar]
- Xiao, P.; Wu, B.; Xu, Y.; Jiang, D. Experimental study on road performance of SMA using different fibers. J. China Foreign Highway 2014, 34, 302–306. [Google Scholar]
- Wu, Z.; Jiang, D.; Lv, Y.; Xiao, P.; Ding, Z.; Yu, H. Toughness research and mechanism analysis of basalt fiber asphalt mixture. J. Nanjing Univ. Sci. Technol. 2015, 39, 500–505. [Google Scholar]
- Wu, S.; Haji, A.; Adkins, I. State of art review on the incorporation of fibres in asphalt pavements. Road Mater. Pavement Des. 2022, 24, 1559–1594. [Google Scholar] [CrossRef]
- Zhang, X. Study on neutral energy of basalt fiber in pavement application. Highway Traffic Sci. Technol. (Appl. Technol. Ed.) 2015, 11, 113–115. [Google Scholar]
- Yan, J.; Wang, G.; Zheng, J. Study on pavement performance of basalt fiber asphalt concrete under different pavement environment. J. Phys. Conf. Ser. 2020, 1654, 012119. [Google Scholar] [CrossRef]
- Dai, J.J.; Jia, X.D. Fatigue performance of high-modulus basalt fiber reinforced asphalt mixture. J. Appl. Sci. Eng. 2022, 26, 1187–1193. [Google Scholar]
- Yang, C.; Liu, L.; Liu, Z.; Huang, Y.; Yu, S.; Fu, Y. Study on the mechanism of bond strength generation and debonding failure between basalt fiber and asphalt based on molecular dynamics. Case Stud. Constr. Mater. 2023, 19, e02493. [Google Scholar] [CrossRef]
- Zahedi, M.; Zarei, M. Studying the simultaneous effect of black Nanocarbon and Polyester fibers with high stability on mechanical properties of asphalt mixture. Turk. Online. J. Des. Art Commun. 2016, 4, 188–195. [Google Scholar]
- He, Y.; Zhang, J.; Zhao, X.; Wang, M.; Xiong, K.; Hu, Q. Study on design optimization, road performance verification and preparation process selection of hybrid fiber reinforced asphalt mixture composite. Constr. Build. Mater. 2024, 448, 138245. [Google Scholar] [CrossRef]
- Long, A.X.; Sun, X.J.; Yu, Z.P.; Zhang, B.; Zhang, G.; Huang, P.; Wang, J. Experimental study and mechanism analysis on the basic mechanical properties of hydraulic basalt fiber asphalt concrete. Mater. Struct. 2018, 55, 161. [Google Scholar] [CrossRef]
- Liu, X. Research on road performance of basalt fiber asphalt mixture. J. China Foreign Highway 2018, 38, 252–255. [Google Scholar]
- Hu, Z.; Zhou, Z. Experimental study on pavement performance of fiber asphalt mortar and asphalt mixture. Highway Eng. 2014, 39, 124–127. [Google Scholar]
- Andronov, S.; Vasiliev, Y.; Kotlyarsky, E.; Kokodeeva, N.; Kochetkov, A. Impact Study of Basalt and Polyacrylonitrile Fibers on Performance Characteristics of Asphalt Concrete. Adv. Intell. Syst. Comput. 2021, 1258, 473–485. [Google Scholar]
- Zhang, X.Y.; Liu, J.X. Viscoelastic creep properties and mesostructure modeling of basalt fiber-reinforced asphalt concrete. Constr. Build. Mater. 2020, 259, 119680. [Google Scholar] [CrossRef]
- Wang, W.; Cheng, Y.; Tan, G. Design optimization of SBS-modified asphalt mixture reinforced with eco-friendly basalt fiber based on response surface methodology. Materials 2018, 11, 1311. [Google Scholar] [CrossRef]
- Hui, Y.; Men, G.; Xiao, P.; Tang, Q.; Han, F.; Kang, A.; Wu, Z. Recent advances in basalt fiber reinforced asphalt mixture for pavement applications. Materials 2022, 15, 6826. [Google Scholar] [CrossRef]
- Xu, J.; Liu, M.; Kang, A.; Wu, Z.; Kou, C.; Zhang, Y.; Xiao, P. Effect of fiber characteristic parameters on the synergistic action and mechanism of basalt fiber asphalt mortar. Constr. Build. Mater. 2024, 438, 137234. [Google Scholar] [CrossRef]
- Zhao, Y.; Tan, Y.; Yu, X. Study on stress dependence of mechanical properties of asphalt mixture. J. Huazhong Univ. Sci. Technol. 2010, 38, 124–127. [Google Scholar]
- Liu, J.; Wang, B.; Yang, W.; Ping, J.; Zhuang, C. Study on the influence of specimen type and loading mode on dynamic modulus of asphalt mixture. Highway 2021, 66, 255–260. [Google Scholar]
- Jiang, Y.; Zhang, Y. Factors influencing the shear strength of asphalt mixture. Highway Transp. Sci. Technol. 2012, 29, 9–14. [Google Scholar]
- Wang, W.; Yang, L.; Cui, H.; Wu, F.; Cheng, Y.; Liang, C. Freeze-thaw damage mechanism analysis of SBS asphalt mixture containing basalt fiber and lignocellulosic fiber based on microscopic void characteristics. Polymers 2023, 15, 3887. [Google Scholar] [CrossRef]
- Li, Q.; Li, G.; Wang, H. Influence of stress mode on dynamic modulus of asphalt mixture. J. Build. Mater. 2014, 17, 816–822. [Google Scholar]
- Xue, Y.; Li, P.; Gao, P.; Yang, L.; Shen, M. Comparative analysis of master curve method of dynamic modulus of asphalt mixture. J. Guangxi Univ. (Nat. Sci. Ed.) 2020, 45, 1–9. [Google Scholar]
- Wu, B.; Pei, Z.; Xiao, P.; Lou, K.; Wu, X. Influence of fiber-asphalt interface property on crack resistance of asphalt mixture. Case Stud. Constr. Mater. 2022, 17, 01703. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, Y.; Wang, X.; Li, S.; Liu, J. Analysis of the influence of strain level on dynamic modulus and viscoelasticity of asphalt mixture. J. China Foreign Highway 2017, 37, 188–192. [Google Scholar]
- Li, B.; Zhou, Y.; Kang, A. Research on fracture behavior of fiber-asphalt mixtures using digital image correlation technology. Materials 2023, 16, 6825. [Google Scholar] [CrossRef]
- Phung, B.N.; Le, T.; Nguyen, T.A.; Ly, H.B. Advancing basalt fiber asphalt concrete design: A novel approach using gradient boosting and metaheuristic algorithms. Case Stud. Constr. Mater. 2023, 19, 02528. [Google Scholar] [CrossRef]
- Huang, Q.; Kang, X.; Chen, P. Characterization of viscoelastic behavior of basalt fiber asphalt mixtures based on discrete and continuous spectrum models. PLoS ONE 2024, 19, 0296087. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.; Kanstad, T.; Jacobsen, S.; Ji, G. Bonding property between fiber and cementitious matrix: A critical review. Constr. Build. Mater. 2023, 378, 131169. [Google Scholar] [CrossRef]
- Barbhuiya, S.; Das, B.B.; Kanavaris, F. A review of fracture propagation in concrete: Fundamentals, experimental techniques, modelling and applications. Mag. Concr. Res. 2023, 76, 482–514. [Google Scholar] [CrossRef]
- Hejazi, S.M.; Abtahi, S.M.; Sheikhzadeh, M.; Semnani, D. Introducing two simple models for predicting fiber-reinforced asphalt concrete behavior during longitudinal loads. J. Appl. Polym. Sci. 2008, 109, 2872–2881. [Google Scholar] [CrossRef]
- Qin, X.; Shen, A.; Guo, Y.; Li, Z.; Lv, Z. Characterization of asphalt mastics reinforced with basalt fibers. Constr. Build. Mater. 2018, 159, 508–516. [Google Scholar] [CrossRef]
- Abiola, O.S.; Kupolati, W.K.; Sadiku, E.R.; Ndambuki, J.M. Utilization of natural fiber as modifier in bituminous mixes: A review. Constr. Build. Mater. 2014, 54, 305–312. [Google Scholar] [CrossRef]
- Oda, S.; Fernandes, J.L.; Ildefonso, J.S. Analysis of use of natural fibers and asphalt rubber binder in discontinuous asphalt mixtures. Constr. Build. Mater. 2012, 26, 13–20. [Google Scholar] [CrossRef]
- Xie, T.; Wang, L. Optimization of Carbon Fiber Length and Content for Asphalt Mastics Based on Rheological Measurements. J. Mater. Civ. Eng. 2023, 35, 04023461. [Google Scholar] [CrossRef]
- Zhou, F.J.; Im, S.; Sun, L.J. Development of an IDEAL cracking test for asphalt mix design and QC/QA. Road Mater. Pavement Des. 2017, 18, 405–427. [Google Scholar] [CrossRef]



| Test Items | Test Result | Method | Specification Requirements | |
|---|---|---|---|---|
| Penetration (25 °C), 0.1 mm | 71 | T0604 | 60~80 | |
| Softening point, °C | 86 | T0606 | ≮55 | |
| Ductility (5 cm/min, 5 °C), cm | 48 | T0605 | ≮30 | |
| Penetration index | 0.5 | T0604 | −0.4~1.0 | |
| Softening point difference, °C | 1.4 | T0661 | ≯2.5 | |
| Elastic recovery (25 °C), % | 76 | T0662 | ≮65 | |
| Residue after RTFOT | Mass change, % | −0.08 | ±1.0 | T0610 |
| Penetration, % | 86 | ≮60 | T0604 | |
| Residual ductility (15 °C), cm | 37 | ≮20 | T0605 | |
| Aggregates | Apparent Relative Density | Gross Volume Relative Density | |
|---|---|---|---|
| Basalt aggregates | 4.75–16 mm | 2.910 | 2.855 |
| Limestone aggregates | 2.36–13.2 mm | 2.911 | 2.835 |
| 1.18–4.75 mm | 2.902 | / | |
| 0.075–2.36 mm | 2.596 | / | |
| Test Items | Test Results | Requirements | Test Methods | |
|---|---|---|---|---|
| Moisture content/% | 0.3 | ≤1 | Dying method | |
| Relative density | 2.654 | ≥2.5 | Chinese standard T0352 | |
| Hydrophilic coefficient | 0.63 | <1 | Chinese standard T0353 | |
| Particle size range | <0.6 mm | 100 | 100 | Chinese standard T0351 |
| <0.15 mm | 92.6 | 90~100 | ||
| <0.075 mm | 79.2 | 75~100 | ||
| Test Items | Specification Requirements | Test Results | ||
|---|---|---|---|---|
| 25 μm | 16 μm | 7 μm | ||
| Density, g·cm−3 | ≥2.600 | 2.71 | 2.71 | 2.71 |
| Breaking strength, MPa | ≥1000 | 1940 | 2318 | 3200 |
| Elongation at break, % | 2.0–3.0 | 2.67 | 2.68 | 2.71 |
| Elastic modulus, GPa | ≥80 | 101 | 101 | 101 |
| Retention rate of breaking strength, % | ≥85 | 93 | 92 | 91 |
| Water absorption, % | ≤0.2 | 0.11 | 0.12 | 0.13 |
| Number | Basalt Fiber Diameter, μm | Fiber Content, % | Optimum Asphalt– Aggregate Ratio, % |
|---|---|---|---|
| 1 | control group | / | 4.9 |
| 2 | 25 | 0.3 | 5.0 |
| 3 | 16 | 0.3 | 5.1 |
| 4 | 7 | 0.3 | 5.2 |
| 5 | mixed diameter | 0.3 | 5.1 |
| Oil Stone Ratio/% | Gross Bulk Density/g cm−3 | Void Ratio VV/% | Mineral Aggregate Gap Rate VMA/% | Asphalt Saturation VFA/% | Stability/kN | Flow Value/mm |
|---|---|---|---|---|---|---|
| 4.9 | 2.414 | 4.2 | 14.3 | 70.8 | 10.74 | 4.68 |
| 5.0 | 2.402 | 4.5 | 14.7 | 69.3 | 9.71 | 4.48 |
| 5.1 | 2.397 | 4.6 | 14.9 | 69.2 | 9.63 | 4.89 |
| 5.2 | 2.416 | 3.7 | 14.2 | 74.3 | 10.19 | 4.24 |
| 5.1 | 2.400 | 4.5 | 14.6 | 69.4 | 10.02 | 4.95 |
| Specification requirements | / | 3~6 | ≥13.0 | 65~75 | ≥8.0 | ≥4.0 |
| Fiber Diameter, μm | Marshall Stability/kN | Immersion Marshall Stability/kN | Soaking Residual Stability/% |
|---|---|---|---|
| control group | 10.02 | 9.07 | 90.52 |
| 25 | 11.43 | 10.39 | 90.90 |
| 16 | 12.71 | 11.62 | 91.42 |
| 7 | 13.80 | 12.74 | 92.32 |
| mixed diameter | 13.25 | 12.15 | 91.70 |
| Type of Mixture | Phase II Model | R2 | Creep Rate | Rheological Times Fn |
|---|---|---|---|---|
| control group | y = 198x + 10,245 | 0.999 | 198 | 139 |
| 25 μm | y = 183x + 10,725 | 0.997 | 183 | 158 |
| 16 μm | y = 132x + 12,423 | 0.995 | 132 | 228 |
| 7 μm | y = 64x + 12,644 | 0.998 | 64 | 349 |
| mixed diameter | y = 87x + 12,830 | 0.997 | 87 | 301 |
| Fiber Diameter/μm | sf/mm2 | nf | Ef/MPa | EAC/MPa | TCR/mm2 | TTCR/mm2 |
|---|---|---|---|---|---|---|
| 25 | 4.91 × 10−6 | 394 | 101,250 | 3076 | 0.064 | 25.311 |
| 16 | 2.01 × 10−6 | 963 | 101,250 | 4003 | 0.049 | 47.177 |
| 7 | 3.85 × 10−7 | 5031 | 101,250 | 4534 | 0.043 | 217.609 |
| mixed diameter | 2.44 × 10−6 | 792 | 101,250 | 3174 | 0.062 | 48.944 |
| Test Name | Evaluating Indicator | Fiber Diameter | |||
|---|---|---|---|---|---|
| 25 | 16 | 7 | Mixed Diameter | ||
| Rutting test | Dynamic stability DS, times, mm | 4666.7 | 5250.3 | 5625.8 | 5373.7 |
| Low temperature beam bending | Maximum bending tensile strain, εB | 3001 | 3447 | 3727 | 3670 |
| Immersed Marshall | Soaking residual stability, % | 90.90 | 91.42 | 92.32 | 91.70 |
| IDEAL-CT | CTindex | 291.8 | 338.7 | 388.7 | 344.7 |
| Triaxial shear | Cohesion c, kPa | 292.0 | 317.2 | 338.1 | 325.7 |
| Dynamic creep | Rheological times Fn | 158 | 228 | 349 | 301 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kou, C.; Xu, S.; Sun, J.; Wang, D.; Chen, Z.; Kang, A. Pavement Performance and Mechanism of Asphalt Mixtures Reinforced with Different Diameters of Basalt Fibers for the Surface Layer. Coatings 2025, 15, 1153. https://doi.org/10.3390/coatings15101153
Kou C, Xu S, Sun J, Wang D, Chen Z, Kang A. Pavement Performance and Mechanism of Asphalt Mixtures Reinforced with Different Diameters of Basalt Fibers for the Surface Layer. Coatings. 2025; 15(10):1153. https://doi.org/10.3390/coatings15101153
Chicago/Turabian StyleKou, Changjiang, Shuxiang Xu, Jiyang Sun, Di Wang, Zikai Chen, and Aihong Kang. 2025. "Pavement Performance and Mechanism of Asphalt Mixtures Reinforced with Different Diameters of Basalt Fibers for the Surface Layer" Coatings 15, no. 10: 1153. https://doi.org/10.3390/coatings15101153
APA StyleKou, C., Xu, S., Sun, J., Wang, D., Chen, Z., & Kang, A. (2025). Pavement Performance and Mechanism of Asphalt Mixtures Reinforced with Different Diameters of Basalt Fibers for the Surface Layer. Coatings, 15(10), 1153. https://doi.org/10.3390/coatings15101153








