Flow of Maxwell Fluid with Heat Transfer through Porous Medium with Thermophoresis Particle Deposition and Soret–Dufour Effects: Numerical Solution

Abstract

In this paper, we study the magnetohydrodynamics of Darcy flow in a non-Newtonian liquid. The influence of thermophoresis on particle deposition is examined in the Darcy flow of a Maxwell nanofluid. In our model, the temperature distribution is generated by the Fourier law of heat conduction with nonlinear thermal radiation and heat sink/source. We also examine the Soret–Dufour effects in the mass concentration equations. The Brownian and thermophoretic diffusions are assumed to be generated by nanoparticle dispersion in the fluid. The similarity method is used to transform the partial differential equations into nonlinear ordinary differential equations. The transformed flow equations were solved numerically using the BVP Midrich scheme. The results of the computation are displayed graphically and in tabular form. The results obtained show that increasing the Deborah number leads to a decline in radial and angular motion and a decrease in the magnitude of axial flow. As expected, the strength of the heat source and the values of the thermal radiation parameters determine the temperature of the liquid. We also found that as the Soret number rises (or the Dufour number falls), so does the mass transfer rate.

1. Introduction

Using a range of computational, numerical and theoretical approaches, [1,2,3] we investigated fluid flow with a perspective of engineering applications. Understanding the flow characteristics of non-Newtonian liquids is needed in numerous applications. For such liquids, the Navier–Stokes theory is inadequate, and there is no single constitutive equation that reflects all fluid features in the literature. As a result, a number of non-Newtonian liquid models have been proposed. Among these models, the one that has gained the most interest is the Maxwell fluid model. This model is a simplified subdivision of the rate-type of non-Newtonian fluids that allows for an authentic approximation of the phenomenon being studied. This model is named viscoelastic fluid due to its elasticity and viscosity effects and was initially proposed by James Clerk Maxwell in 1867. The Maxwell model was modeled for the purpose of predicting the elastic and viscous behavior of air [4]. However, some researchers have repeatedly applied the Maxwell model to the response of various viscoelastic fluids, ranging from polymeric fluids to the Earth’s mantle. The Maxwell fluid’s rheological properties were discussed by Olsson et al. [5]. Choi et al. [6] examined the Maxwell fluid flow behavior within a channel. Maxwell fluid models were investigated by Fetecau et al. [7,8], who found new analytical solutions. Mustafa [9] investigated the features of the modified Fourier law on non-Newtonian liquid using a Maxwell fluid model. The convective and radiative Maxwell fluid flow is studied by Mabood et al. [10]. The chemically reactive flow of Maxwell liquid along with heat source and Joule heating was examined by Hosseinzadeh et al. [11]. Ijaz and Ayub [12] examined the stratified flow of Maxwell nanofluid in the presence of activation energy. In [13], Mabood et al. examine the Maxwell fluid model with variable thermal conductivity. The latter paper considered the swirling motion of the liquid in a rotating disk. Recently, Devi and Maboob [14] discussed the swirling flow with heat and mass transfer featuring the relaxation time effects and obtained a numerical solution using the shooting technique. Several researchers have focused on Maxwell fluid flow analysis with various physical aspects applicable to a variety of situations [15,16,17,18,19,20,21,22,23,24].

The novel aspect of this paper lies in examining the rotation and Darcy flow of non-Newtonian fluid caused by a rotating disk; a topic that has received little attention in the past. The heat and mass transport are analyzed along with the features of the Dufour and Soret effects. The flow analysis took into account thermal radiation, heat source/sink and Joule heating effects. The conversion of the governing equations into nonlinear ordinary differential equations is carried out using the von Kármán similarity procedure. The problem is numerically integrated using the Maple BVP Midrich package. A comparison of the outcome of our computations with previously reported work is tabulated.

2. Formulation

In this study, we examine the steady incompressible chemically reactive Darcy flow of a Maxwell fluid influenced by Joule heating. Cylindrical coordinates (r,φ,z) are used in the mathematical modeling of the physical problem. We modeled the motion of the fluid as a disk rotating about the $z$-axis with uniform angular velocity. The disk is porous with mass flux velocity $w_0$ ($w_0$> 0 for injection and $w_0$< 0 for suction). A uniform beam of magnetic field $B_0$ is imposed along the z-axis. The thermophoresis effect is used to better model the fluctuation of mass deposition on the surface. The flow is axisymmetric along the $z$-axis. The heat and mass transport are analyzed along with the Dufour–Soret effects. The flow mechanism is shown in Figure 1.

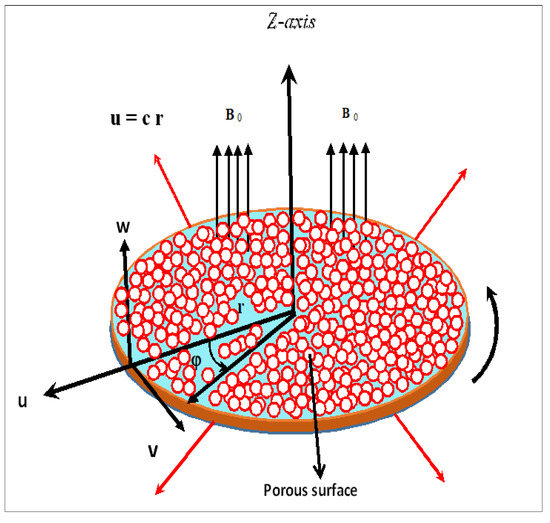
Figure 1. Flow diagram [25].

Our assumptions, given above, result in the following governing equations:

$$\frac{\partial u}{\partial r}+\frac{u}{r}+\frac{\partial w}{\partial z}=0,$$

(1)

$$\begin{array}{l}u\frac{\partial u}{\partial r}-\frac{v^2}{r}+w\frac{\partial u}{\partial z}=\nu \frac{{\partial }^{2}u}{\partial z^2}-\frac{{\sigma }_1}{\rho }{B}_0{}^2\left[u+{\lambda }_{1}w\frac{\partial u}{\partial z}\right]-\frac{{\varphi }_1\nu }{K}u\\ -{\lambda }_1\left[u^2\frac{{\partial }^{2}u}{\partial r^2}+w^2\frac{{\partial }^{2}u}{\partial z^2}+2uw\frac{{\partial }^{2}u}{\partial r\partial z}-\frac{2uv}{r}\frac{\partial v}{\partial r}-\frac{2vw}{r}\frac{\partial v}{\partial z}+\frac{u{v}^2}{r^2}+\frac{v^2}{r}\frac{\partial u}{\partial r}\right],\end{array}$$

(2)

$$\begin{array}{l}u\frac{\partial v}{\partial r}+\frac{uv}{r}+w\frac{\partial v}{\partial z}=\nu \frac{{\partial }^{2}v}{\partial z^2}-\frac{{\sigma }_1}{\rho }{B}_0{}^2\left[v+{\lambda }_{1}w\frac{\partial v}{\partial z}\right]-\frac{{\varphi }_1\nu }{K}v\\ -{\lambda }_1\left[u^2\frac{{\partial }^{2}v}{\partial r^2}+w^2\frac{{\partial }^{2}v}{\partial z^2}+2uw\frac{{\partial }^{2}v}{\partial r\partial z}+\frac{2uv}{r}\frac{\partial u}{\partial r}+\frac{2vw}{r}\frac{\partial u}{\partial z}-2\frac{u^{2}v}{r^2}-\frac{v^3}{r^2}+\frac{v^2}{r}\frac{\partial v}{\partial r}\right],\end{array}$$

(3)

$$u\frac{\partial T}{\partial r}+w\frac{\partial T}{\partial z}=\frac{k}{\rho c_p}\left(\frac{{\partial }^{2}T}{\partial z^2}\right)-\frac{1}{\rho c_p}\frac{\partial q_{rad}}{\partial z}+\frac{{\sigma }_1{B}_0{}^2}{\rho }\left(u^2+v^2\right)+\frac{D{k}_T}{c_s{c}_p}\frac{{\partial }^{2}C}{\partial z^2}+\frac{Q_0}{\rho c_p}\left(T-T_{\infty }\right),$$

(4)

$$u\frac{\partial C}{\partial r}+w\frac{\partial C}{\partial z}=D_m\frac{{\partial }^{2}C}{\partial z^2}+\frac{D_m{k}_T}{T_m}\frac{{\partial }^{2}T}{\partial z^2}-K_{1}C-\frac{\partial \left(U_{T}C\right)}{\partial r}-\frac{\partial \left(W_{T}C\right)}{\partial z},$$

(5)

The radiative flux $q_{rad}$ is given by

$$q_{rad}=-\frac{4}{3}\frac{{\sigma }^{*}}{k^{*}}\frac{\partial T^4}{\partial z}=-\frac{16}{3}\frac{{\sigma }^{*}{T}_{\infty }^3}{k^{*}}\frac{\partial T}{\partial z},$$

(6)

The thermophoretic velocities are

$$U_T=-k\nu \frac{1}{T}\frac{\partial T}{\partial r} \mathrm{and} W_T=-k\nu \frac{1}{T}\frac{\partial T}{\partial z},$$

(7)

where $k$ is the thermophoretic coefficient whose value is usually taken to fall in the range of $0.2–1.2$ and, according to Batchelor and Shen [26] and Talbot et al. [27], is given by

$$k=\frac{2C_s\left({\lambda }_g/{\lambda }_p+C_{t}Kn\right)\left[1+Kn\left(C_1+C_2{e}^{-C_3/kn}\right)\right]}{\left(1+3C_{m}Kn\right)\left[1+{\lambda }_g/{\lambda }_p+2C_{t}Kn\right]},$$

(8)

where $\left(C_s, C_t, C_m, C_1, C_2, C_3\right)=\left(1.147, 2.20, 1.146, 1.2, 0.41, 0.88\right)$ are constants, $Kn$ is the Knudsen number, and ${\lambda }_p, {\lambda }_g$ are the thermal conductivities of the diffusion particles and the fluid, respectively. The boundary conditions are

$$\begin{array}{c}u=u_w=cr, v=\mathsf{\Omega }\mathrm{r}, \mathrm{w}=w_0, -k_{*}\frac{\partial T}{\partial z}=h_f\left(T_f-T\right), C=C_w \mathrm{at} z=0,\\ u\to 0, v\to 0, T\to T_{\infty }, C\to C_{\infty } \mathrm{as} z\to \infty .\end{array}$$

(9)

Using the similarity variables [28],

$$\left(\eta ,u,v,w\right)=\left(\sqrt{\frac{\mathsf{\Omega }}{\nu }}z, \mathsf{\Omega }rF, \mathsf{\Omega }rG, \sqrt{\mathsf{\Omega }\nu }H\right),\left[T,C,\mathsf{\Delta }T\right]=\left[T_{\infty }+\mathsf{\Delta }T\theta , C_{\infty }\varphi , T_f-T_{\infty }\right].$$

(10)

Substituting Equation (10) into Equations (1)–(5), we obtain

$$H^{\prime }+2F=0,$$

(11)

$$F^2-G^2+F^{\prime }H-F^{″}+\gamma F+\beta \left(F^{″}{H}^2+2F{F}^{\prime }H-2G{G}^{\prime }H\right)+M\left(F+{\beta }_1{F}^{\prime }H\right)=0,$$

(12)

$$2FG+G^{\prime }H-G^{″}+\gamma G+\beta \left(G^{″}{H}^2+2\left(F{G}^{\prime }+F^{\prime }G\right)H\right)+M\left(G+{\beta }_1{G}^{\prime }H\right)=0,$$

(13)

$$\begin{array}{l}{\theta }^{″}+4Rd\left({\theta }_w-1\right){\left[1+\left({\theta }_w-1\right)\theta \right]}^2+\frac{4}{3}Rd{\left[1+\left({\theta }_w-1\right)\theta \right]}^3{\theta }^{″}-\mathrm{Pr}H{\theta }^{\prime }\\ +\mathrm{Pr} Du {\varphi }^{″}+\mathrm{Pr} \delta \theta +\mathrm{Pr} MEc\left(F^2+G^2\right)=0,\end{array}$$

(14)

$$\frac{1}{Sc}{\varphi }^{″}-H{\varphi }^{\prime }-K_r\varphi +S_r{\theta }^{″}+\frac{kNt}{\left(1+Nt\theta \right)}{\theta }^{″}\varphi -\frac{k{\left(Nt\right)}^2}{{\left(1+Nt\theta \right)}^2}{{\theta }^{\prime }}^2\varphi +\frac{kNt}{\left(1+Nt\theta \right)}{\theta }^{\prime }{\varphi }^{\prime }=0.$$

(15)

The transformed BCs are

$$\begin{array}{c}F\left(\eta \right)=R, G\left(\eta \right)=1, H\left(\eta \right)=s, {\theta }^{\prime }\left(\eta \right)=-Bi\left(1-\theta \left(\eta \right)\right), \varphi \left(\eta \right)=0 \mathrm{at} \eta =0,\\ F\left(\eta \right)\to 0, G\left(\eta \right)\to 0, \theta \left(\eta \right)\to 0, \varphi \left(\eta \right)\to 1 \mathrm{as} \eta \to \infty \end{array}$$

(16)

In (16), prime denotes differentiation with respect to $\eta .$

The parameters are expressed as

$M=\left(\frac{{\sigma }_{1B_0^2}}{\rho \mathsf{\Omega }}\right),$	$R=\left(\frac{c}{\mathsf{\Omega }}\right),$	$\beta =\left({\lambda }_1\mathsf{\Omega }\right),$	$\gamma =\left(\frac{\nu {\varphi }_1}{\mathsf{\Omega }K}\right),$	$s=\left(\frac{w_0}{\sqrt{\mathsf{\Omega }\nu }}\right),$	$Rd=\left(\frac{4}{3}\frac{{\sigma }^{*}{T}_{\infty }^3}{k_{*}{k}^{*}}\right)$
$Bi=\left(\frac{h_f\sqrt{\frac{\nu }{\mathsf{\Omega }}}}{k_{*}}\right)$	${\theta }_w=\left(\frac{T_f}{T_{\infty }}\right),$	$\delta =\left(\frac{Q_0}{\mathsf{\Omega }\rho c_p}\right),$	$Ec=\left(\frac{u_w^2}{c_p\mathsf{\Delta }T}\right),$	$K_r=\left(\frac{K_1}{\mathsf{\Omega }}\right),$	$Du=\left(\frac{D_m{k}_T}{c_s{c}_p\nu }\frac{C_{\infty }}{\Delta \mathrm{T}}\right)$
$Sr=\left(\frac{D_m{k}_T}{T_m\nu }\frac{\Delta \mathrm{T}}{C_{\infty }}\right)$	$\mathrm{Pr}=\left(\frac{\nu \left(\rho c_p\right)}{k_{*}}\right)$	$Sc=\left(\frac{\nu }{D_m}\right)$	and	$Nt=\left(\frac{\Delta \mathrm{T}}{T_{\infty }}\right).$

Here, $M$ is the magnetic field parameter, $R$ the stretching parameter, $\beta$ the Deborah number, $\gamma$ the porosity parameter,$s$ the mass transfer parameter, $Rd$ the radiation parameter, $Bi$ the Biot number, ${\theta }_w$ the temperature ratio parameter, $\delta$ the heat source/sink parameter, $Ec$ the Eckert number, $Du$ the Dufour number, $K_r$the chemical reaction parameter, $Sr$ the Soret number, $\mathrm{Pr}$ the Prandtl number and $Sc$ the Schmidt number. Finally, $Nt$ is the relative temperature difference parameter, which is negative for a heated surface, positive for a cooled surface and zero for surfaces at ambient temperature.

The physical parameters are defined as:

$$N{u}_r=-\frac{r{k}_{*}{\left(\left[\frac{\partial T}{\partial z}\right]+q_{rad}\right)}_{z=0}}{k_{*}\left(T_f-T_{\infty }\right)}, \mathrm{and} S{h}_r=\frac{r{D}_m{\left(\frac{\partial C}{\partial z}\right)}_{z=0}}{D_m\left(C_w-C_{\infty }\right)},$$

(17)

where $N{u}_r$ is the Nusselt number, and $S{h}_r$ is Sherwood number. Their dimensionless forms are

$$R{e}^{-\frac{1}{2}} N{u}_r=-\left\{1+\frac{4Rd}{3}{\left[1+\left({\theta }_w-1\right)\theta \left(0\right)\right]}^3\right\}{\theta }^{\prime }\left(0\right) , \mathrm{and} R{e}^{-\frac{1}{2}} S{h}_r=-{\varphi }^{\prime }\left(0\right),$$

(18)

in which $Re=\left(\frac{r^2\mathsf{\Omega }}{\nu }\right)$ is the local Reynold number.

3. Results and Discussion

In this section, we examine the effects of the above parameters on the flow fields, temperature and concentration distributions. To do this, the governing Equations (11–15) and conditions (16) were numerically solved using the Maple BVP function with Midrich method. The results are shown by graphing all the governing parameters, namely the magnetic field parameters, the relaxation time parameter, the Soret number, the porosity parameter, the Dufour parameter, the Biot number, the Prandtl number, the chemical reaction parameter, the suction parameter and the Schmidt number against the fluid’s velocities, temperature and concentration distributions, as shown in Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6. For all the computations, the leading parameters are assigned fixed values:

$$\begin{array}{c} M=1.0, \beta =0.05, R=1.3, s=0.1, \mathrm{Pr}=6.5, Sc=6.5, Sr=0.1, K_2=0.01, Du=0.1, \\ \gamma =0.1, Ec=0.7, {\theta }_w=1.1, Rd=0.1, Bi=0.1, \delta =0.1, k=0.2, \mathrm{and} Nt=0.1.\end{array}$$

(19)

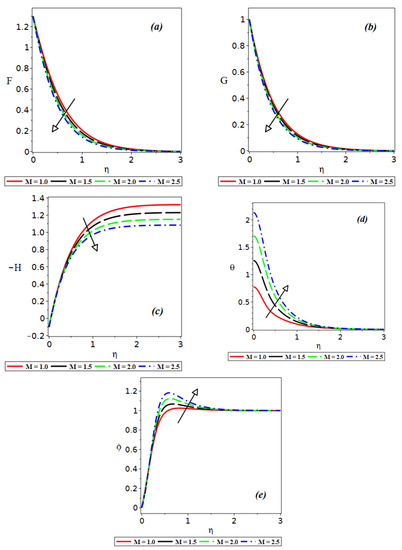
Figure 2. Effect of $M$ on $F, G, \left\{-H\right\}, \theta$ and $\varphi$.

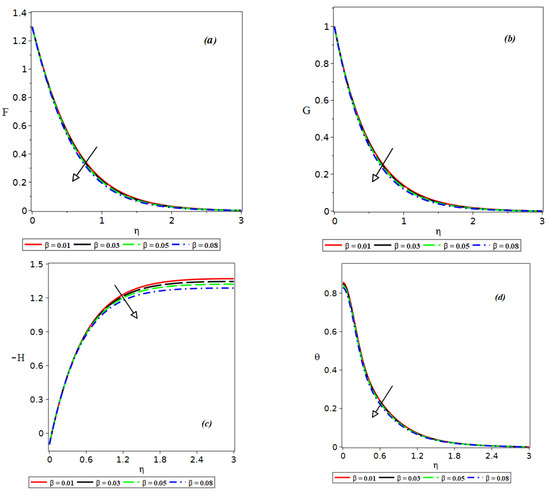
Figure 3. Effect of $\beta$ on $F, G, \left\{-H\right\}, \mathrm{and} \theta$.

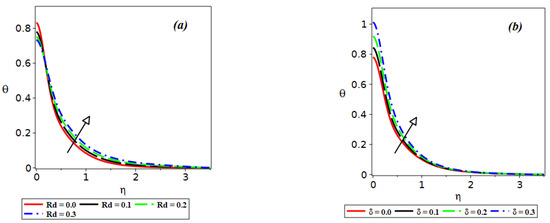
Figure 4. Variation of $\theta \left(\eta \right)$ on $Rd$ and $\delta$.

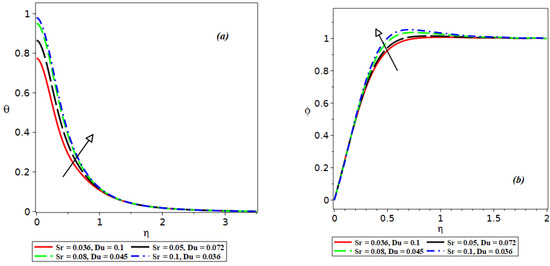
Figure 5. Effect of $\left\{Sr, Du\right\}$ on $\theta \left(\eta \right)$ and $\varphi \left(\eta \right)$.

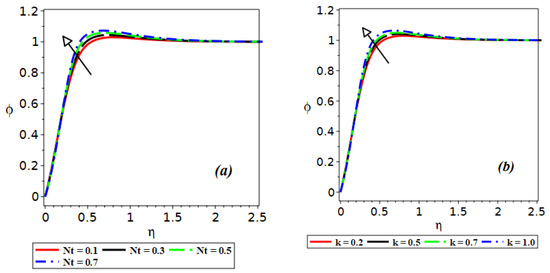
Figure 6. Variation of $\varphi \left(\eta \right)$ on $Nt$ and $k$.

Figure 2a–e depict the effect of magnetic parameter $M$ on the functional dependence of the flow components, temperature and concentration distribution on the dimensionless variable $\eta$. In an electrically conducting fluid, a drag force, which is essentially a resistive force, is produced by the magnetic field. This resistive force tends to reduce the movement of fluid and increase the temperature on the surface of the disk. This explains the decrease in the values of radial $F\left(\eta \right)$, azimuthal $G\left(\eta \right)$ and the magnitude of the axial velocity $H\left(\eta \right)$ seen in Figure 2a–c. The increase in the temperature and mass concentration of the fluid is shown in Figure 2d,e.

Figure 3a–c show the effect of the Deborah number $\beta$ on velocity components in radial, azimuthal and axial directions. These figures show a decrease in all three velocity components as the value of the Deborah number $\beta$ is increased. As a result, the hydrodynamic boundary layer thins out. Increasing the value of $\beta$ causes the fluid to behave more like a solid, causing the decrease in the velocities $\left(F,G,H\right)$. The effect of the Deborah number on temperature distribution is displayed in Figure 3d, where it can be seen that the temperature decreases with the increasing $\beta .$

An increase in the thermal radiation parameter, as can be expected, results in an increase in the temperature of the liquid, as seen in Figure 4a. To maintain the heat transportation in the liquid, heat source/sink effects are applied. As seen in Figure 4b, an upward shift in the temperature profile is shown as the values of $\delta$ increase from 0.0 to 0.3.

The influence of the Dufour number $Du$ and the Soret number $Sr$ on the temperature distribution is shown in Figure 5a. In this figure, one sees an upward shift of the thermal curves $\theta \left(\eta \right)$ with increasing $Sr$. Figure 5b shows the effect of the Dufour number $Du$ and the Soret number $Sr$ on the solutal concentration. Increasing the Soret $Sr$, while decreasing the Dufour number $Du$, results in an upward shift of mass concentration. Figure 6a,b show that the solutal concentration increases by increasing the values of $Nt$ and $k$.

Table 1 displays the variation in $R{e}^{-1/2}N{u}_r$ (Nusselt number) with $Rd,Bi,Sr,Du$ and $Ec$. Increasing the values of $Rd,Bi$ and $Du$, the heat transfer rate rises while the effect of $Sr$ and $Ec$ are to reduce the heat transfer rate in the liquid. The tabular results of the Sherwood number against $\gamma , K_r, k$ and $Nt$ are shown in Table 2. As can be seen in Table 2, increasing the values $\gamma , K_r, k$ and $Nt$ decreases the mass transfer rate. Finally, Table 3 shows the relationship between the results obtained in this paper and past results [29,30].

Table 1. Variation of $R{e}^{-\frac{1}{2}}N{u}_r$ with $Rd, Bi, Sr, Du$ and $Ec$.

$\mathit{R}\mathit{d}$	Bi	Sr	Du	Ec	$\mathit{R}{\mathit{e}}^{-\frac{1}{2}}\mathit{N}{\mathit{u}}_{\mathit{r}}$
0.1	0.1	0.1	0.1	0.7	0.01516
0.2					0.04803
0.3					0.06370
0.1	0.3				0.04269
	0.5				0.06705
	0.7				0.08869
0.1	0.1	0.1			0.01516
		0.15			−0.02639
		0.2			−0.25054
0.1	01	0.1	0.1		0.01516
			0.11		0.01695
			0.12		0.01809
				0.1	0.12427
				0.3	0.09894
				0.5	0.06806

Table 2. Variation of $R{e}^{-\frac{1}{2}}S{h}_r$ with $\gamma , K_r, S_r, k$ and $Nt$.

$\mathit{\gamma }$	${\mathit{K}}_{\mathit{r}}$	${\mathit{S}}_{\mathit{r}}$	$\mathit{k}$	$\mathit{N}\mathit{t}$	$\mathit{R}{\mathit{e}}^{-\frac{1}{2}}\mathit{S}{\mathit{h}}_{\mathit{r}}$
0.1	0.01	0.1	0.2	0.1	−1.897503
0.2					−1.894312
0.3					−1.891150
0.1	0.02				−1.837879
	0.03				−1.779653
	0.04				−1.722789
0.1	0.01	0.1			−1.897504
		0.15			−1.349949
		0.2			0.205047
0.1	0.01	0.1	0.3		−1.864637
			0.5		−1.792577
			0.7		−1.714251
0.1	0.01	0.1	0.7	0.2	−1.836673
				0.3	−1.777058
				0.5	−1.664599

Table 3. The relationship between [29,30] and the current paper on fixed $\mathrm{Pr}=6.5$ and $M=0=\gamma =R=s=\beta =Rd=\delta =Ec=Du$.

	[29]	[30]	Present Result
$F^{\prime }\left(0\right)$	0.5102	0.51023262	0.5101162643
$-G^{\prime }\left(0\right)$	0.6159	0.61592201	0.6158492796
$-{\theta }^{\prime }\left(0\right)$	0.9337	0.93387794	0.9336941128

4. Conclusions

The Darcy flow of Maxwell fluid surrounding a porous disk is analyzed under a variety of physical parameter values. Heat and mass transfer properties are examined in the presence of diffusion. The key findings are as below:

• The presence of a magnetic parameter impedes the movement of the liquid and enhances its temperature;
• Increasing the Soret number results in a significant increase in the mass concentration of the fluid;
• The solutal profile increases monotonically by increasing the values of the relative temperature difference parameter and the thermophoretic coefficient;
• The mass transportation in the Maxwell fluid seems to increase by increasing the values of the chemical reaction parameter.