Effect of Intermediate Principal Stress on the Bearing Capacity of Footings in Soft Rock
Abstract
:1. Introduction
2. Materials, Theories and Methods
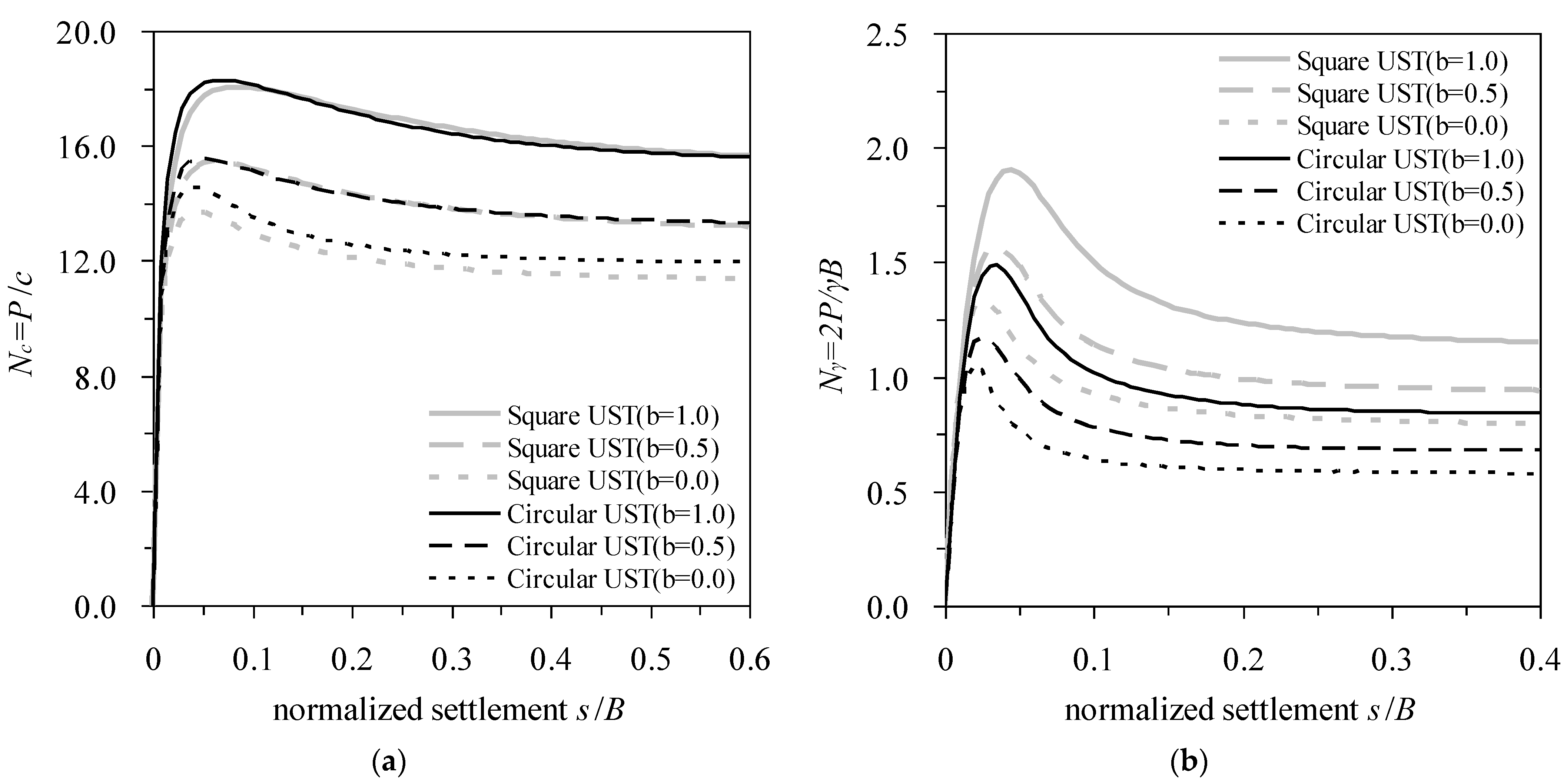
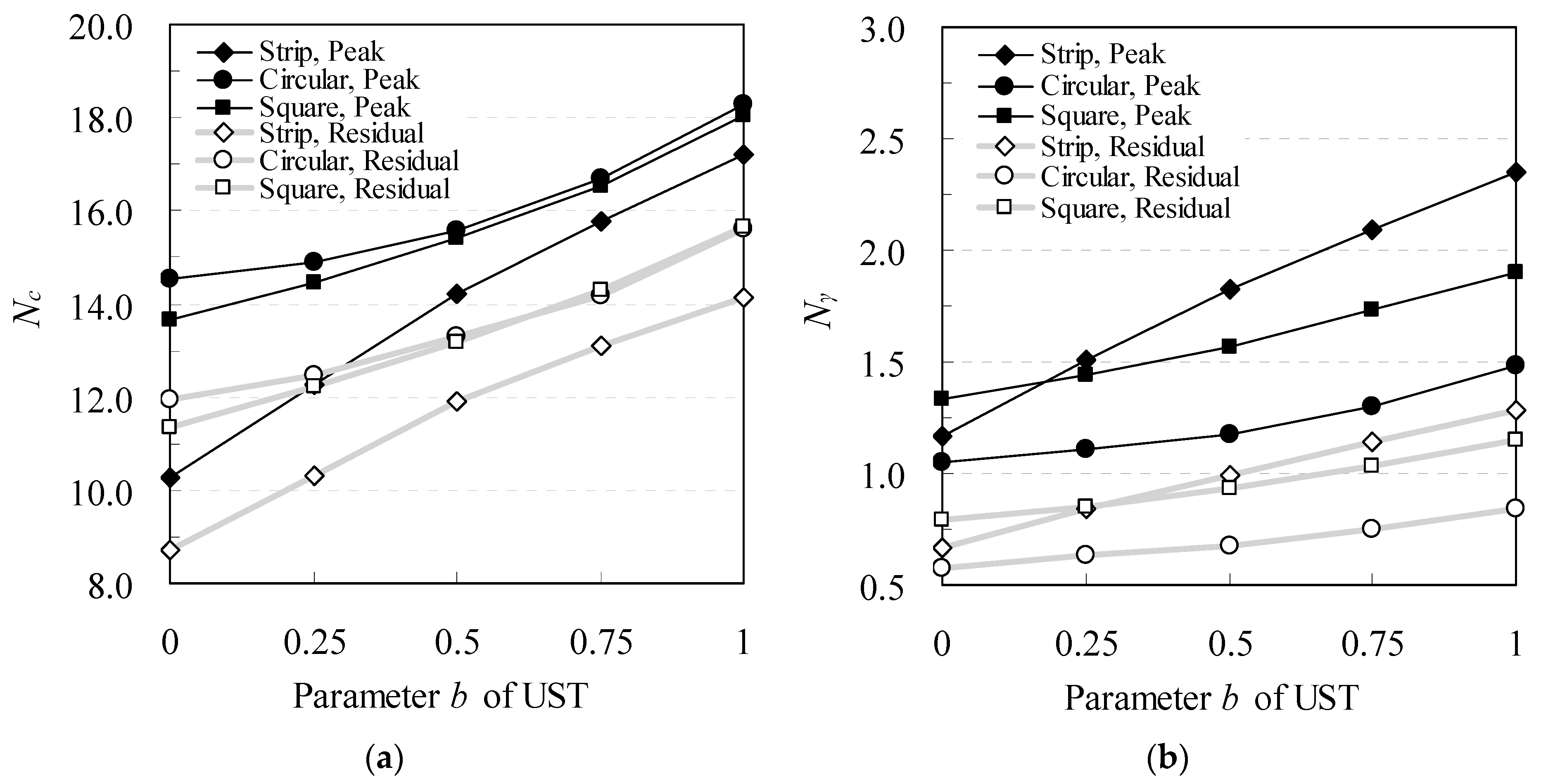
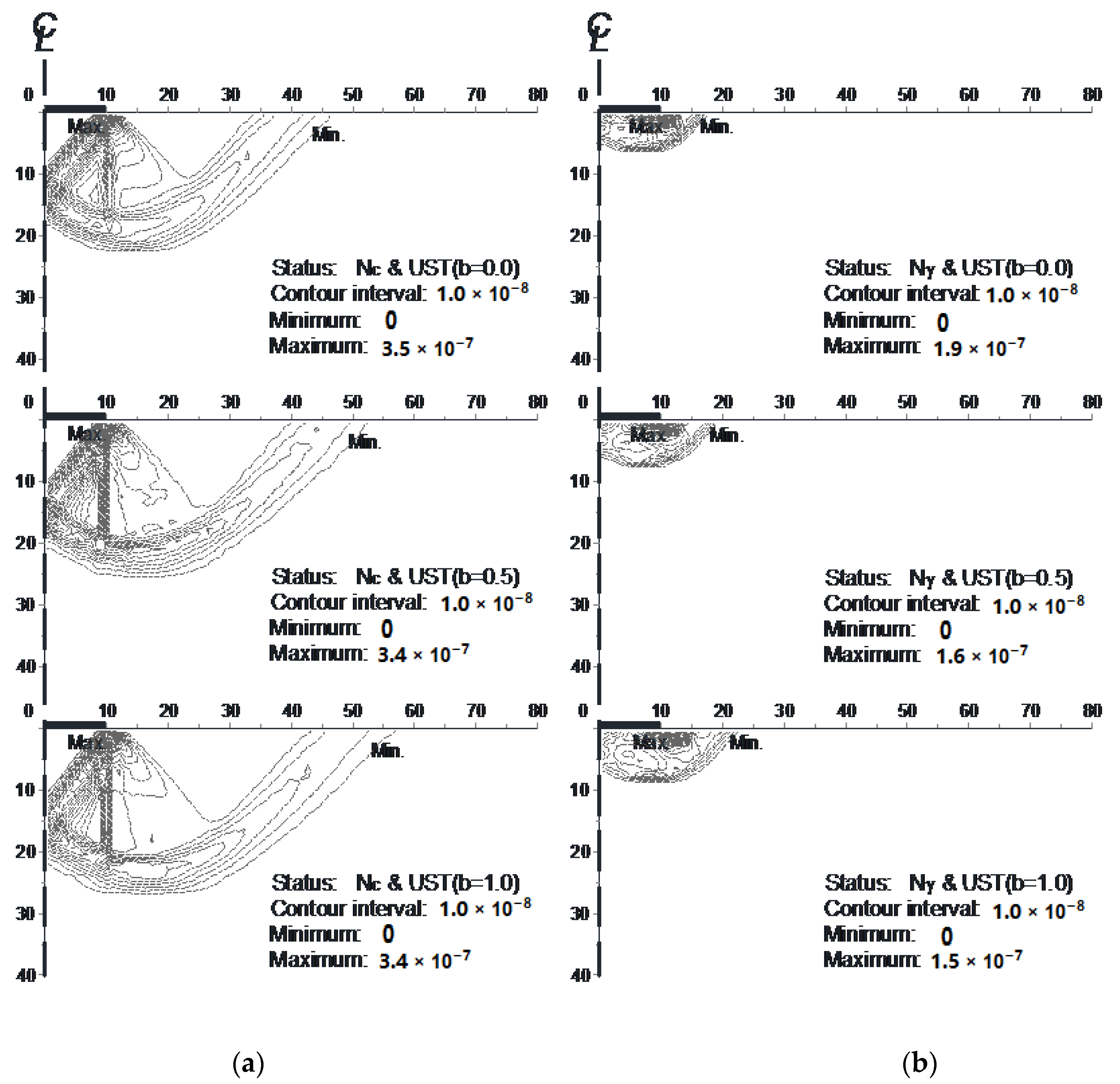
3. Calculations and Results
4. Discussion
5. Conclusions
- (1)
- A strain hardening/softening constitutive model which takes the influence of the intermediate principal stress into account was established in this study. The mechanical behavior of the strain-softening material under the complex stress state can be analyzed using this model.
- (2)
- The intermediate principal stress significantly influences a soft rock foundation’s bearing capacity and failure mechanisms. The intermediate principal stress has less influence on the bearing capacity of footing when gravity is neglected. The influence of the intermediate principal stress on the bearing capacity for strip footing is much more significant than that of circular and square footings. The size of the failure area in the soft rock foundation increases with the increased effect of the intermediate principal stress.
- (3)
- The research works of our study would benefit the reasonable estimation of the bearing capacity of footings in a soft rock medium. In our future research, taking the nonlinear failure envelope on the meridian plane into account, the influence of the intermediate principal stress effect on soft rock material will be investigated.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- British Standards Institution. Geotechnical Investigation and Testing—Identification and Classification of Rock; ISO14689: 2017; British Standards Institution: London, UK, 2018. [Google Scholar]
- International Society for Rock Mechanics (ISRM). The ISRM Suggested Methods for Rock Characterization, Testing and Monitoring: 2007–2014; Ulusay, R., Ed.; Pergamon Press: Oxford, UK, 2015. [Google Scholar]
- Berre, T. Triaxial Testing of Soft Rocks. Geotech. Test. J. 2011, 34, 61–75. [Google Scholar] [CrossRef]
- Liao, H.J.; Su, L.J.; Pu, W.C.; Yin, J.H. Test and numerical analysis of the constitutive relation of a diatomaceous soft rock. Mar. Geotechnol. 2003, 21, 183–200. [Google Scholar] [CrossRef]
- Jovičić, V.; Lapčević, R.; Bogdanović, S. Preservation of Historical Underground Sites in Soft Rock: A Case Example. Geosciences 2020, 10, 256. [Google Scholar] [CrossRef]
- Liu, B.; Jiang, X. Consolidation and deformation characteristics of soft rock foundation in hydrological wetland environment. Earth Sci. Res. J. 2020, 24, 183–190. [Google Scholar] [CrossRef]
- Zhu, H.; Ye, B.; Cai, Y.; Feng, Z. An elasto-viscoplastic model for soft rock around tunnels considering overconsolidation and structure effects. Comput. Geotech. 2013, 50, 6–16. [Google Scholar] [CrossRef]
- Tokiwa, T.; Tsusaka, K.; Matsubara, M.; Ishikawa, T. Fracture characterization around a gallery in soft sedimentary rock in horonobe url of japan. Int. J. Rock Mech. Min. Sci. 2014, 65, 1–7. [Google Scholar] [CrossRef]
- Erickson, H.L.; Drescher, A. Bearing capacity of circular footings. J. Geotech. Geoenvironmental Eng. 2002, 128, 38–43. [Google Scholar] [CrossRef]
- Frydman, S.; Burd, H. Numerical studies of bearing-capacity factor ngamma. J. Geotech. Geoenvironmental Eng. 1997, 123, 20–29. [Google Scholar] [CrossRef]
- Loukidis, D.; Salgado, R. Bearing capacity of strip and circular footings in sand using finite elements. Comput. Geotech. 2009, 36, 871–879. [Google Scholar] [CrossRef]
- Salgado, R.; Lyamin, A.V.; Sloan, S.W.; Yu, H.S. Two and three-dimensional bearing capacity of foundations in clay. Géotechnique 2004, 54, 297–306. [Google Scholar] [CrossRef]
- Sukmak, G.; Sukmak, P.; Horpibulsuk, S.; Hoy, M.; Arulrajah, A. Load Bearing Capacity of Cohesive-Frictional Soils Reinforced with Full-Wraparound Geotextiles: Experimental and Numerical Investigation. Appl. Sci. 2021, 11, 2973. [Google Scholar] [CrossRef]
- Hosamo, H.; Sliteen, I.; Ding, S. Numerical Analysis of Bearing Capacity of a Ring Footing on Geogrid Reinforced Sand. Buildings 2021, 11, 68. [Google Scholar] [CrossRef]
- Galindo, R.; Alencar, A.; Isik, N.S.; Olalla Marañón, C. Assessment of the Bearing Capacity of Foundations on Rock Masses Subjected to Seismic and Seepage Loads. Sustainability 2020, 12, 10063. [Google Scholar] [CrossRef]
- Ma, Z.Y.; Liao, H.J.; Dang, F.N. Effect of intermediate principal stress on strength of soft rock under complex stress states. J. Cent. South Univ. 2014, 21, 1583–1593. [Google Scholar] [CrossRef]
- Ma, Z.Y.; Liao, H.J.; Dang, F.N. Influence of intermediate principal stress on the bearing capacity of strip and circular footings. J. Eng. Mech. ASCE 2014, 140, 04014041. [Google Scholar] [CrossRef]
- Lade, P.V. Assessment of test data for selection of 3-d failure criterion for sand. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 307–333. [Google Scholar] [CrossRef]
- You, M. True-triaxial strength criteria for rock. Int. J. Rock Mech. Min. Sci. 2009, 46, 115–127. [Google Scholar] [CrossRef]
- Sutherland, H.B.; Mesdary, M.S. The influence of the intermediate principal stress on the strength of sand. In Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering, Mexico City, Mexico, 12–16 January 1969; pp. 391–399. [Google Scholar]
- Mogi, K. Effect of the intermediate principal stress on rock failure. J. Geophys. Res. 1967, 72, 5117–5131. [Google Scholar] [CrossRef]
- Xue, Y.; Liu, J.; Ranjith, P.G.; Liang, X.; Wang, S. Investigation of the influence of gas fracturing on fracturing characteristics of coal mass and gas extraction efficiency based on a multi-physical field model. J. Pet. Sci. Eng. 2021, 206, 109018. [Google Scholar] [CrossRef]
- Kulatilake, P.H.S.W. 3-D Rock Mass Strength Criteria—A Review of the Current Status. Geotechnics 2021, 1, 7. [Google Scholar] [CrossRef]
- Xu, P.; Sun, Z.; Shao, S.; Fang, L. Comparative Analysis of Common Strength Criteria of Soil Materials. Materials 2021, 14, 4302. [Google Scholar] [CrossRef]
- Liu, Y.; Liao, X.; Li, L.; Mao, H. Discrete Element Modelling of the Mechanical Behavior of Sand–Rubber Mixtures under True Triaxial Tests. Materials 2020, 13, 5716. [Google Scholar] [CrossRef]
- Song, Z.; Li, M.; Yin, G.; Ranjith, P.G.; Zhang, D.; Liu, C. Effect of Intermediate Principal Stress on the Strength, Deformation, and Permeability of Sandstone. Energies 2018, 11, 2694. [Google Scholar] [CrossRef] [Green Version]
- Guan, H.-X.; Wang, H.-Q.; Liu, H.; Yan, J.-J.; Lin, M. The Effect of Intermediate Principal Stress on Compressive Strength of Different Cement Content of Cement-Stabilized Macadam and Different Gradation of AC-13 Mixture. Appl. Sci. 2018, 8, 2000. [Google Scholar] [CrossRef] [Green Version]
- Rukhaiyar, S.; Sajwan, G.; Samadhiya, N.K. Strength behavior of plain cement concrete subjected to true triaxial compression. Can. J. Civ. Eng. 2018, 45, 179–196. [Google Scholar] [CrossRef] [Green Version]
- Yang, Q.; Zan, Y.; Xie, L.G. Comparative analysis of the nonlinear unified strength criterion for rocks and other three-dimensional Hoek–Brown strength criteria. Geomech. Geophys. Geo-Energy Geo-Resour. 2018, 4, 29–37. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Pande, G.N. Finite Elements in Geomechanics; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Matsuoka, H.; Nakai, T. Relationship among tresca, mises, mohr-coulomb and matsuoka-nakai failure criteria. Soils Found. 1985, 25, 123–128. [Google Scholar] [CrossRef] [Green Version]
- Yu, M.H. Unified Strength Theory and Its Applications; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Itasca Consulting Group Inc. FLAC-Fast Lagrangian Analysis of Continua (Version 8.1) User’s Manual; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 2019. [Google Scholar]
- Itasca Consulting Group Inc. FLAC3D-Fast Lagrangian Analysis of Continua in 3 Dimensions (Version 7.0) User’s Manual; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 2019. [Google Scholar]
- Ma, Z.Y.; Liao, H.J.; Dang, F.N. Unified elastoplastic finite difference and its application. Appl. Math. Mech. 2013, 34, 457–474. [Google Scholar] [CrossRef]
- Ma, Z.Y.; Dang, F.N.; Liao, H.J. Numerical study of the dynamic compaction of gravel soil ground using the discrete element method. Granul. Matter 2014, 16, 881–889. [Google Scholar] [CrossRef]
- Vermeer, P.A.; Borst, D. Non-associated plasticity for soils, concrete and rocks. Heron 1984, 29, 3–64. [Google Scholar] [CrossRef] [Green Version]
- Li, H.Z.; Liao, H.J.; Kong, L.W.; Leng, X.L. Experimental study on stress-strain relationship of expansive mud-stone. Yantu Lixue/Rock Soil Mech. 2007, 28, 107–110. (In Chinese) [Google Scholar]
- Kang, X.S.; Liao, H.J. A Bounding Surface Plasticity Model Considering Spacing Ratio for Overconsolidated Jointed Soft Rocks. Rock Mech. Rock Eng. 2020, 53, 59–69. [Google Scholar] [CrossRef]
- Vesic, A.S. Analysis of ultimate loads of shallow foundations. J. Soil Mech. Found. Div. ASCE 1973, 99, 45–73. [Google Scholar] [CrossRef]
- Terzaghi, K. Theoretical Soil Mechanics; Wiley: New York, NY, USA, 1943. [Google Scholar]
- Eason, G.; Shield, R.T. The plastic indentation of a semi-infinite solid by a perfectly rough circular punch. Z. Angew. Math. Phys. Zamp 1960, 11, 33–43. [Google Scholar] [CrossRef]
- Cox, A.D. Axially-symmetric plastic deformation in soils—II. indentation of ponderable soils. Int. J. Mech. Sci. 1962, 4, 371–380. [Google Scholar] [CrossRef]
- Dixit, M.S.; Patil, K.A. Experimental estimate of nγ values and corresponding settlements for square footings on finite layer of sand. Geomech. Eng. 2013, 5, 363–377. [Google Scholar] [CrossRef]
- Puzakov, V.; Drescher, A.; Michalowski, R.L. Shape factor for shallow footings. Geomech. Eng. 2009, 1, 113–120. [Google Scholar] [CrossRef]
- Long, Y.; Liu, J.; Kong, X.J.; Hu, Y. Three-dimensional large deformation fe analysis of square footings in two-layered clays. J. Geotech. Geoenviron. Eng. ASCE 2011, 137, 52–58. [Google Scholar] [CrossRef]
- Zhu, M.; Radoslaw, L.; Michalowski, R.L. Shape factors for limit loads on square and rectangular footings. J. Geotech. Geoenviron. Eng. 2005, 131, 223–231. [Google Scholar] [CrossRef]
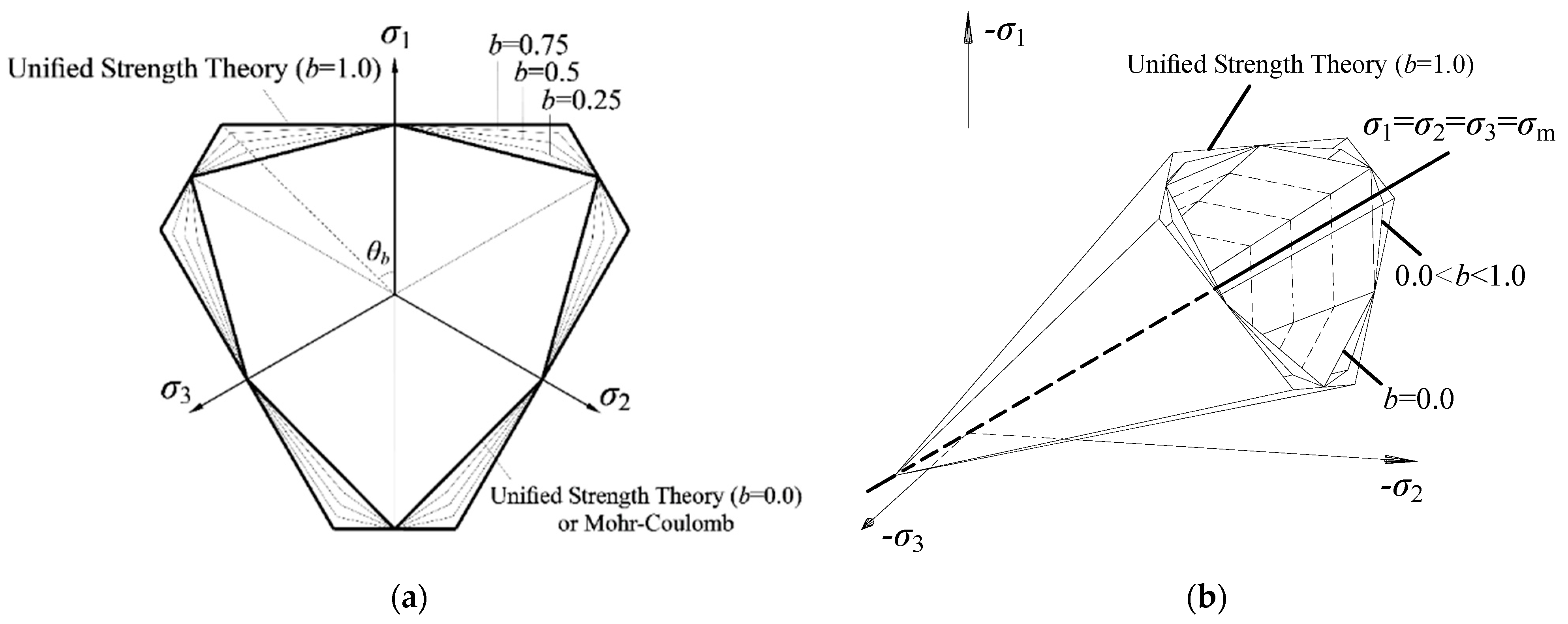
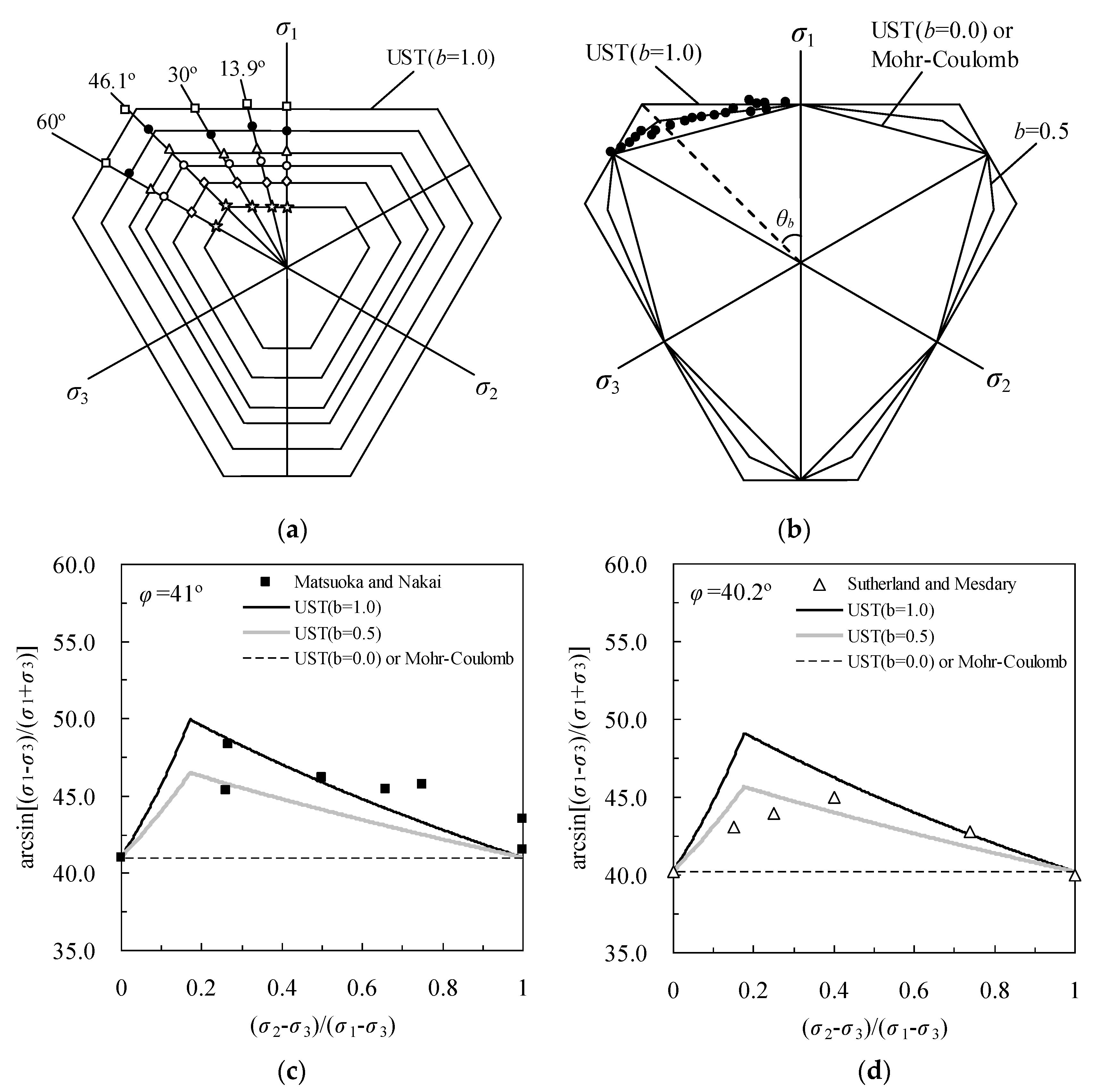
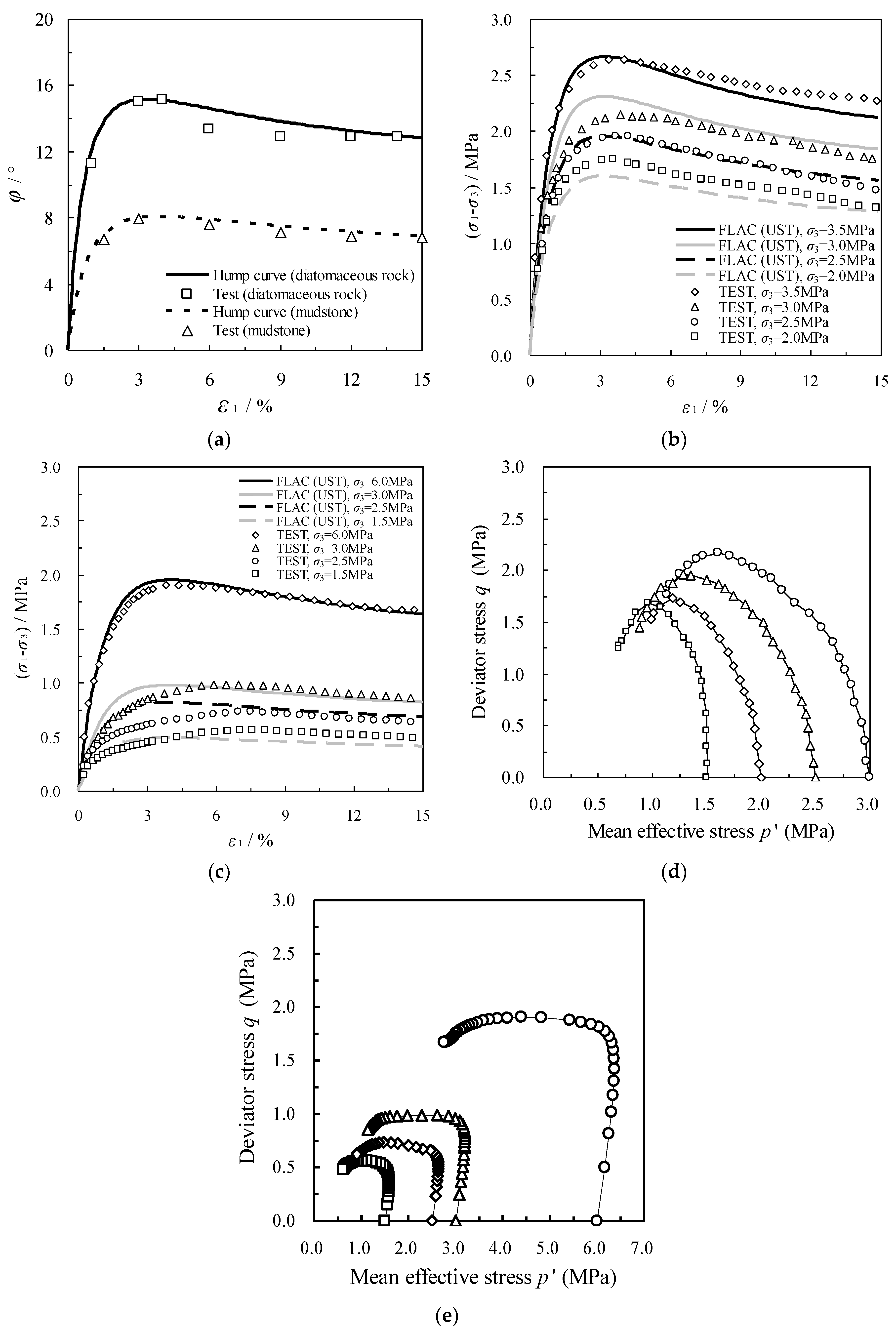
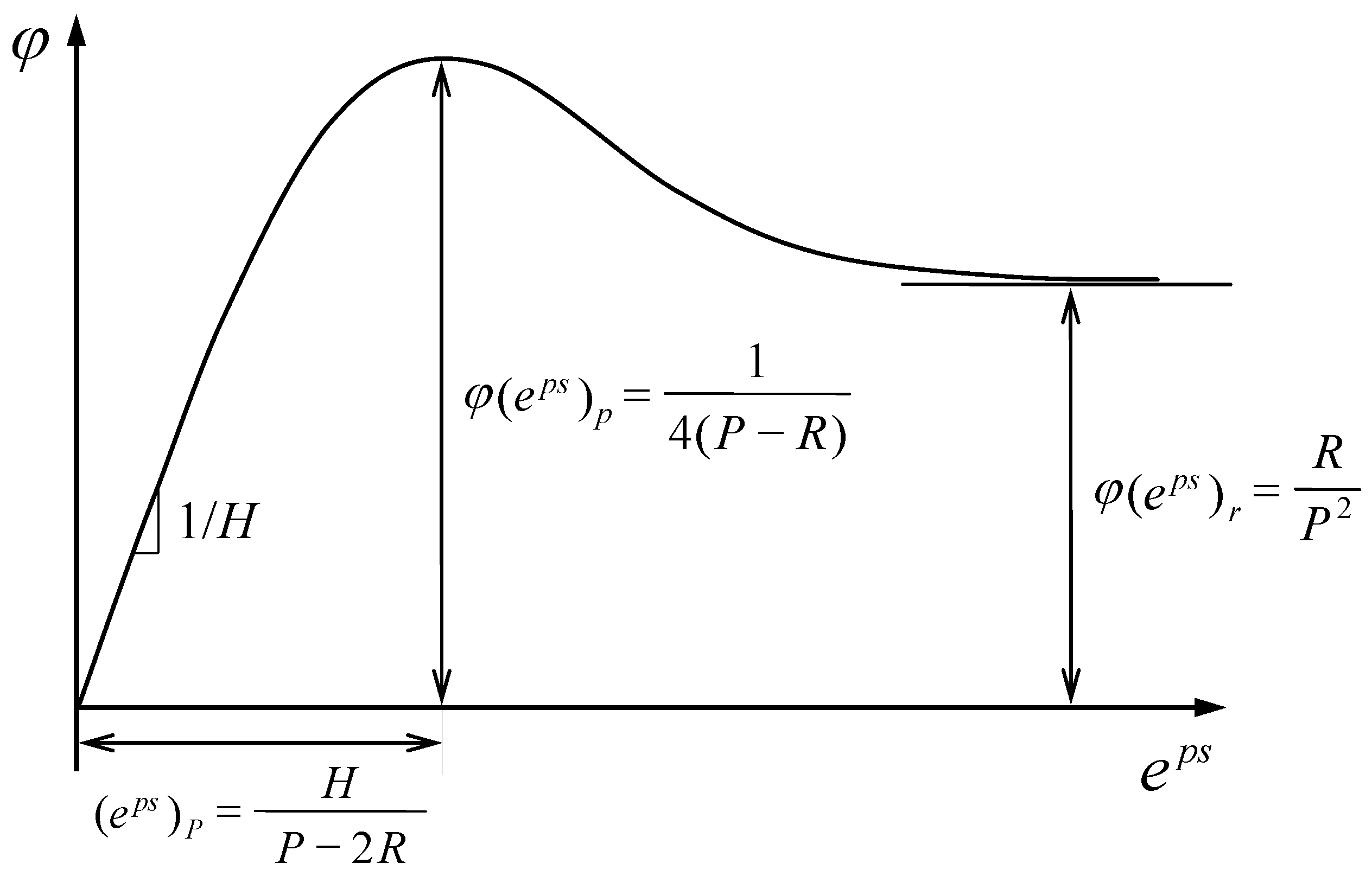
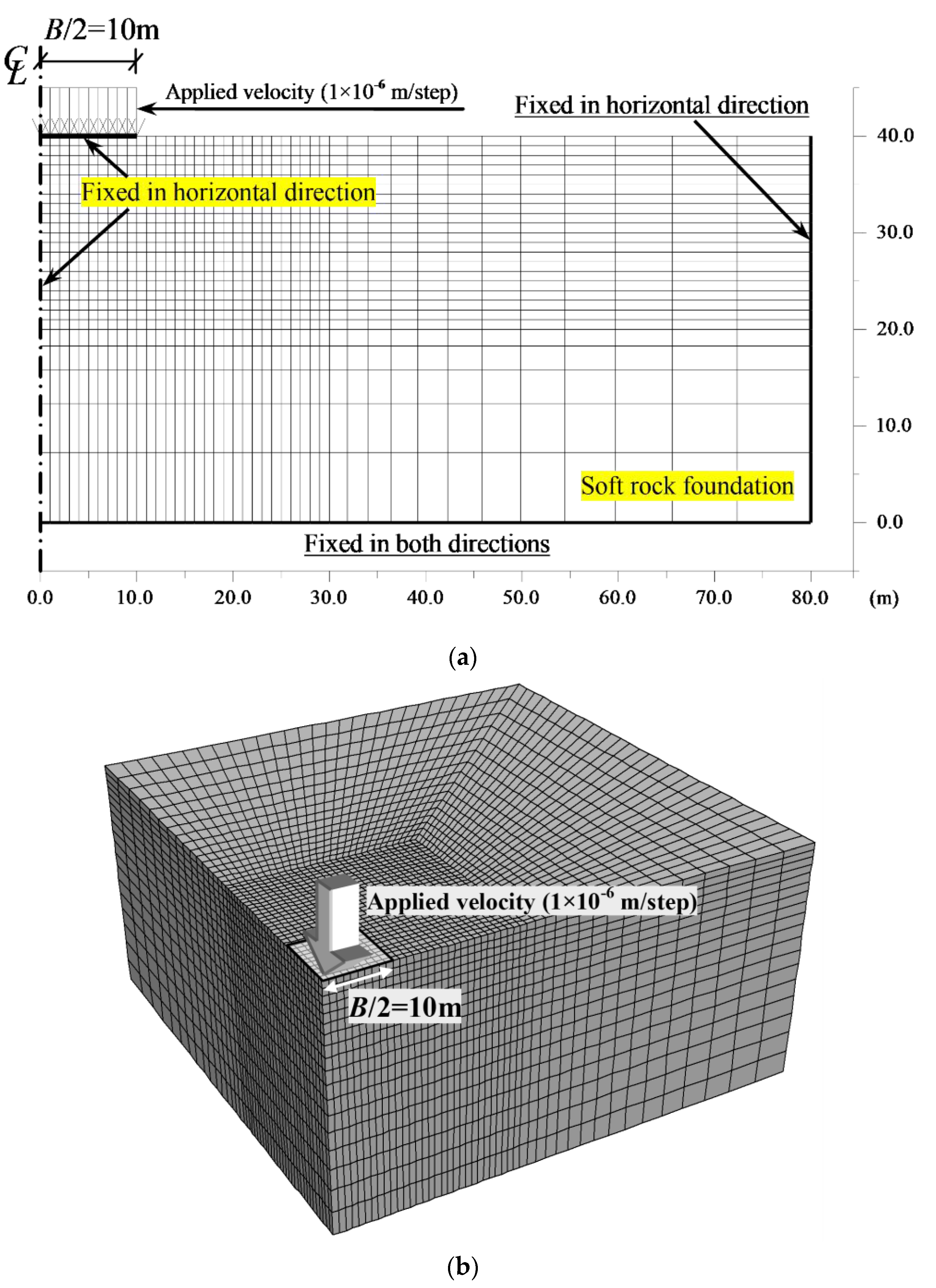

| Name | Density ρ (kg/m3) | Elastic Modulus E (MPa) | Poisson’s Ratio ν | Cohesion c (kPa) | Peak Friction Angle (°) | Residual Friction Angle (°) | P | H | R |
|---|---|---|---|---|---|---|---|---|---|
| Diatomaceous soft rock | 2183 | 500 | 0.25 | 40 | 15.1 | 12.8 | 0.021 | 0.04 | 0.0045 |
| Mudstone | 2032 | 500 | 0.25 | 1.2 | 8.0 | 6.8 | 0.039 | 0.09 | 0.0079 |
| Geometry | Strip | Circular | Square | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| UST | b = 0.0 | b = 0.25 | b = 0.5 | b = 0.75 | b = 1.0 | b = 0.75 | b = 1.0 | b = 0.5 | b = 0.75 | b = 1.0 | b = 0.0 | b = 0.25 | b = 0.5 | b = 0.75 | b = 1.0 |
| Peak values | 10.27 | 12.27 | 14.22 | 15.77 | 17.20 | 14.56 | 14.88 | 15.57 | 16.69 | 18.28 | 13.68 | 14.45 | 15.43 | 16.55 | 18.05 |
| Residual values | 8.72 | 10.30 | 11.90 | 13.10 | 14.16 | 11.94 | 12.46 | 13.32 | 14.17 | 15.60 | 11.34 | 12.21 | 13.17 | 14.31 | 15.65 |
| Geometry | Strip | Circular | Square | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| UST | b = 0.0 | b = 0.25 | b = 0.5 | b = 0.75 | b = 1.0 | b = 0.0 | b = 0.25 | b = 0.5 | b = 0.75 | b = 1.0 | b = 0.0 | b = 0.25 | b = 0.5 | b = 0.75 | b = 1.0 |
| Peak values | 1.17 | 1.51 | 1.83 | 2.09 | 2.35 | 1.05 | 1.11 | 1.18 | 1.30 | 1.49 | 1.33 | 1.44 | 1.57 | 1.73 | 1.90 |
| Residual values | 0.67 | 0.86 | 0.99 | 1.14 | 1.28 | 0.58 | 0.63 | 0.68 | 0.75 | 0.84 | 0.79 | 0.85 | 0.94 | 1.03 | 1.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Z.; Dang, F.; Liao, H. Effect of Intermediate Principal Stress on the Bearing Capacity of Footings in Soft Rock. Coatings 2021, 11, 1019. https://doi.org/10.3390/coatings11091019
Ma Z, Dang F, Liao H. Effect of Intermediate Principal Stress on the Bearing Capacity of Footings in Soft Rock. Coatings. 2021; 11(9):1019. https://doi.org/10.3390/coatings11091019
Chicago/Turabian StyleMa, Zongyuan, Faning Dang, and Hongjian Liao. 2021. "Effect of Intermediate Principal Stress on the Bearing Capacity of Footings in Soft Rock" Coatings 11, no. 9: 1019. https://doi.org/10.3390/coatings11091019
APA StyleMa, Z., Dang, F., & Liao, H. (2021). Effect of Intermediate Principal Stress on the Bearing Capacity of Footings in Soft Rock. Coatings, 11(9), 1019. https://doi.org/10.3390/coatings11091019






