Providing a Specified Level of Electromagnetic Shielding with Nickel Thin Films Formed by DC Magnetron Sputtering
Abstract
:1. Introduction
- Compressive stresses appearing with an increase of the volume of the oxide film (Vox/Vm ˃ 1);
- Compressive stresses arising in the oxide film growing on a rough surface and causing tearing forces;
- Stresses arising due to different values of the expansion coefficients of the metal and the oxide film [18].
- The possibility of film deposition at a sufficiently low (below melting point) substrate temperature;
- High adhesion rate of a thin film to the substrate;
- The growth rate of the film, allowing deposition of layers up to submicron thicknesses in a minimum time interval;
- Uniformity of thickness on plane substrates with an area of up to several square millimeters;
- Absence of impurities and droplet phase;
- Uniformity of the film over its thickness.
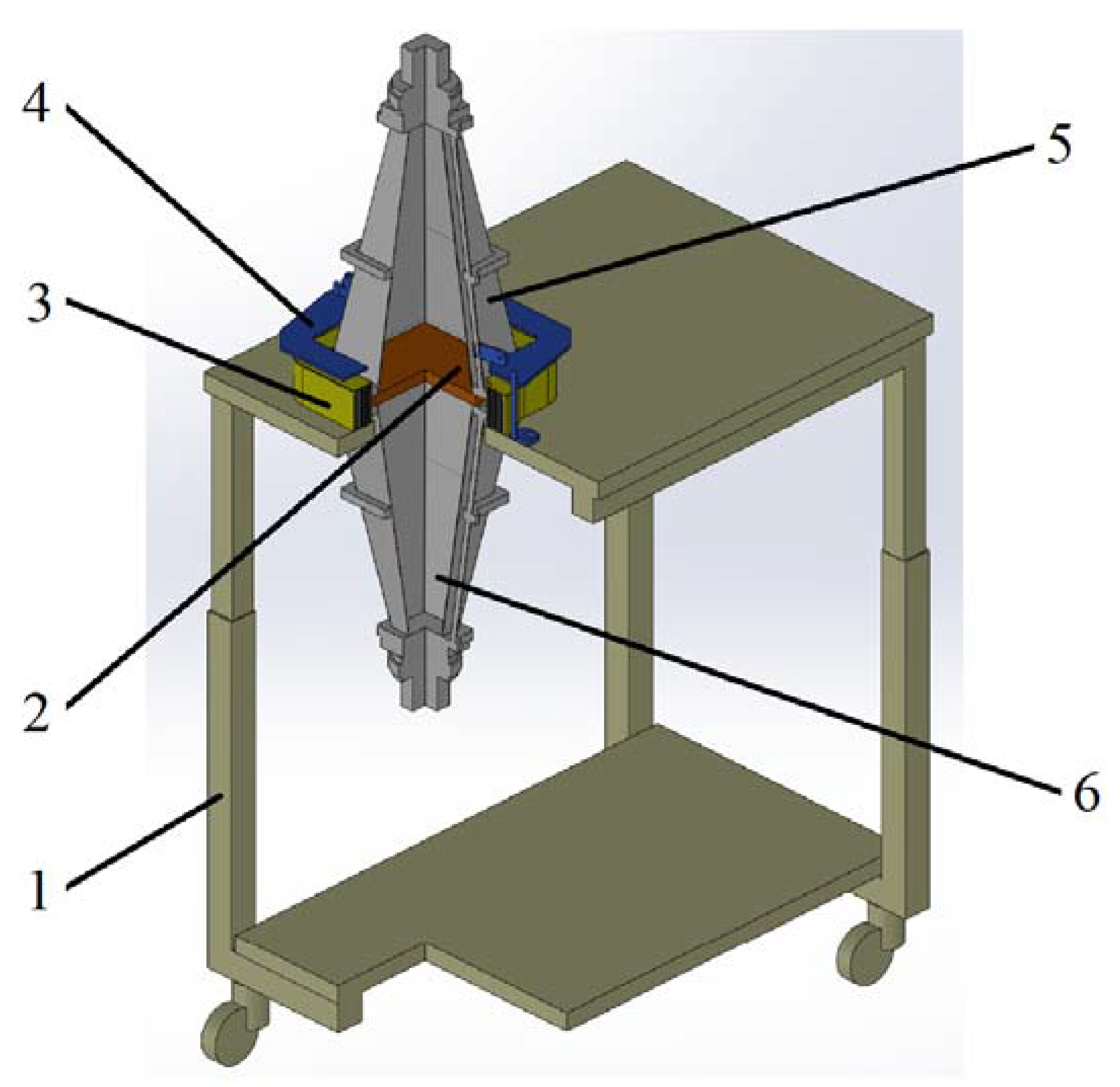
2. Materials and Methods
3. Results and Discussion
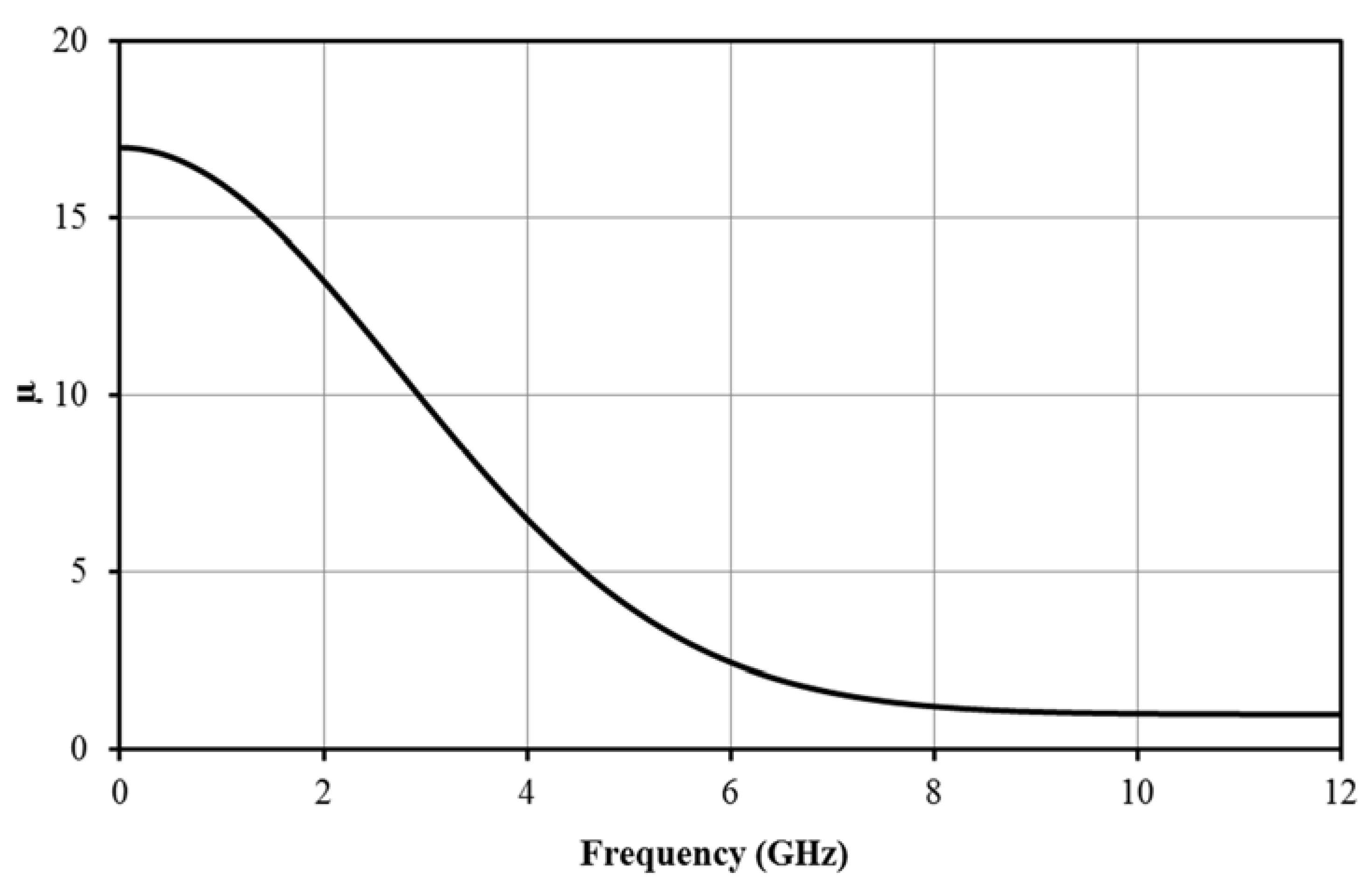
3.1. Frequency Dependencies of Magnetic Permeability and Skin Depth
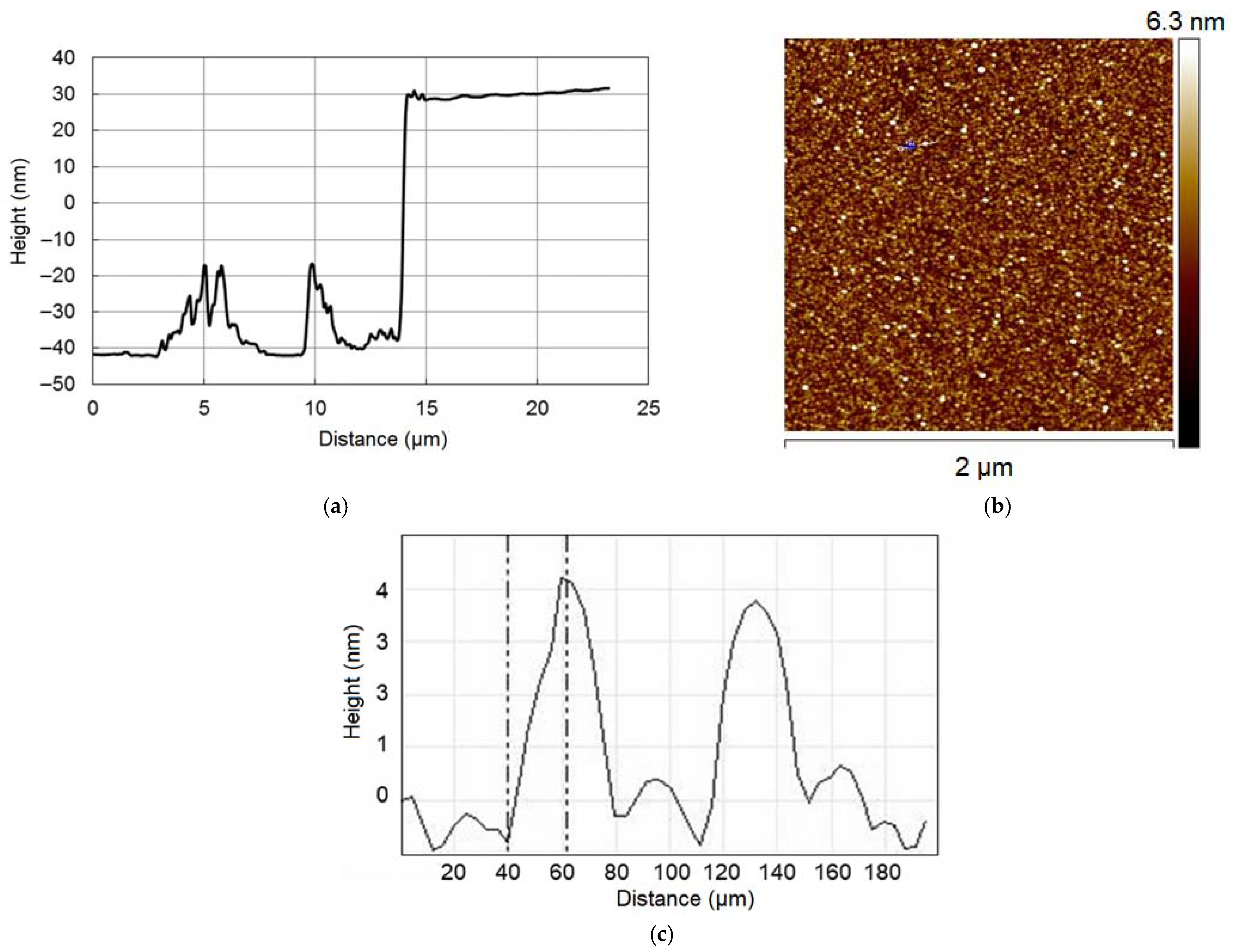
3.2. Surface Morphology
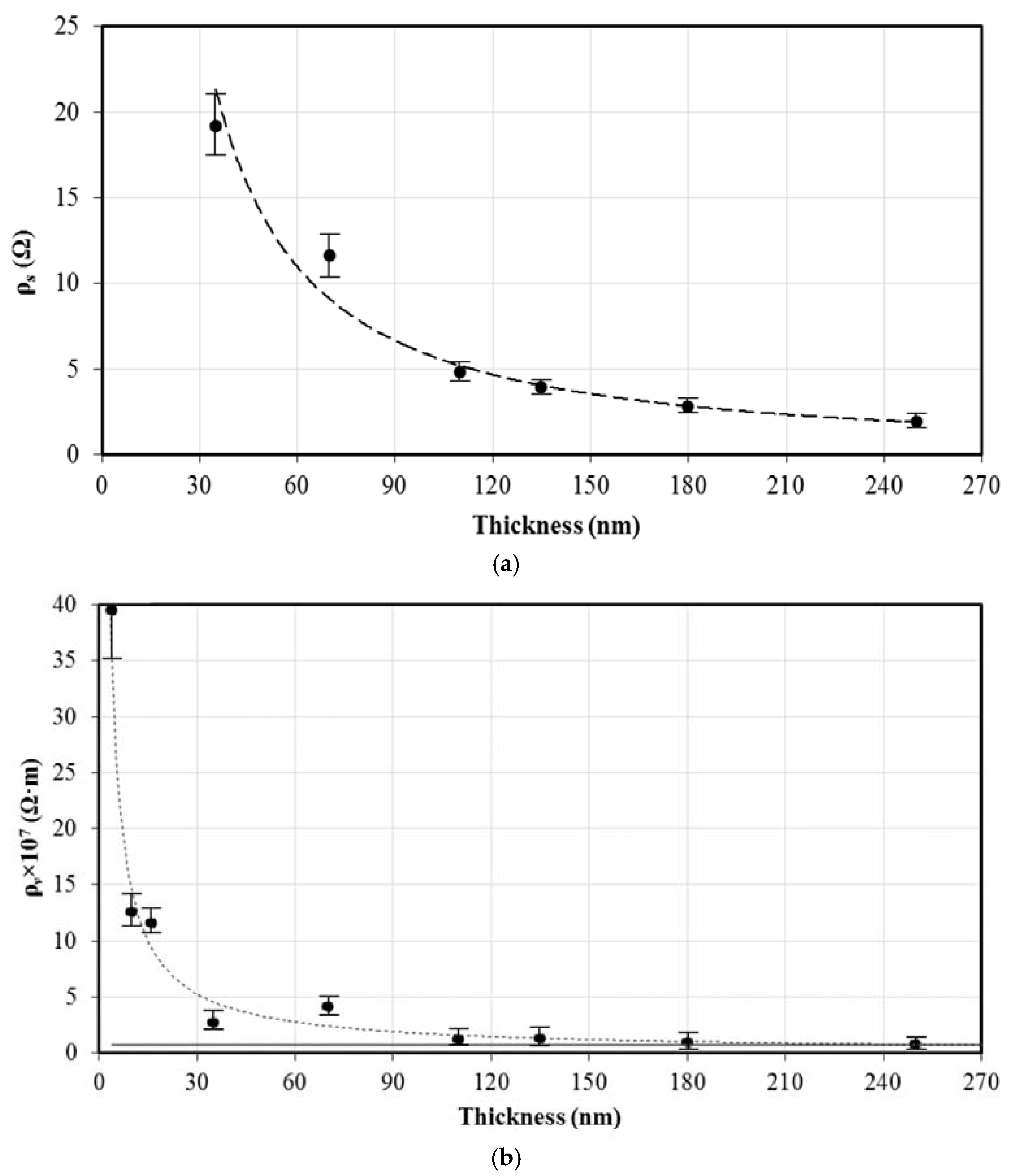
3.3. Electrical Resistivity
3.4. Electromagnetic Shielding Effectiveness
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ott, H.W. Electromagnetic Compatibility Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2009; pp. 243–252. [Google Scholar]
- Jiang, Z.; Zhao, S.; Huang, W.; Chen, L.; Liu, Y. Embedded flexible and transparent double-layer nickel-mesh for high shielding efficiency. Opt. Express 2020, 28, 26531–26542. [Google Scholar] [CrossRef] [PubMed]
- Angappan, M.; Bora, P.J.; Vinoy, K.J.; Ramamurthy, P.C.; Vijayaraju, K. Tailorable electromagnetic interference shielding using nickel coated glass fabric-epoxy composite with excellent mechanical property. Compos. Commun. 2018, 10, 110–115. [Google Scholar] [CrossRef]
- Chung, D.D.L. Electromagnetic interference shielding effectiveness of carbon materials. Carbon 2001, 39, 279–285. [Google Scholar] [CrossRef]
- Jiyong, H.; Guohao, L.; Junhui, S.; Xudong, Y.; Xin, D. Improving the electromagnetic shielding of nickel/polyaniline coated polytrimethylene-terephthalate knitted fabric by optimizing the electroless plating conditions. Text. Res. J. 2017, 87, 902–912. [Google Scholar] [CrossRef]
- Yu, X.; Shen, Z. The electromagnetic shielding of Ni films deposited on cenosphere particles by magnetron sputtering method. J. Magn. Magn. Mater. 2009, 321, 2890–2895. [Google Scholar] [CrossRef]
- Dravid, S.V.; Bhosale, S.D.; Datar, S.; Goyal, R.K. Nickel Nanoparticle-Filled High-Performance Polymeric Nanocomposites for EMI Shielding Applications. J. Electron. Mater. 2020, 49, 1630–1637. [Google Scholar] [CrossRef]
- Geetha, S.; Kumar, K.K.S.; Rao, C.R.K.; Vijayan, M.; Trivedi, D.C. EMI shielding: Methods and materials—A review. J. Appl. Polym. Sci. 2009, 112, 2073–2086. [Google Scholar] [CrossRef]
- Jiang, S.X.; Guo, R.H. Electromagnetic shielding and corrosion resistance of electroless Ni-P/Cu-Ni multilayer plated polyester fabric. Surf. Coat. Technol. 2011, 205, 4274–4279. [Google Scholar] [CrossRef]
- Ding, X.; Wang, W.; Wang, Y.; Xu, R.; Yu, D. High-performance flexible electromagnetic shielding polyimide fabric prepared by nickel-tungsten-phosphorus electroless plating. J. Alloys Compd. 2019, 777, 1265–1273. [Google Scholar] [CrossRef]
- Tran, V.V.; Nguyen, D.D.; Nguyen, A.T.; Hofmann, M.; Hsieh, Y.P.; Kan, H.C.; Hsu, C.C. Electromagnetic Interference Shielding by Transparent Graphene/Nickel Mesh Films. ACS Appl. Nano Mater. 2020, 3, 7474–7481. [Google Scholar] [CrossRef]
- Jordan, L.; Swanger, W.H. The properties of pure nickel. Bur. Stand. J. Res. 1930, 5, 1291–1307. [Google Scholar] [CrossRef]
- Lide, D.R. Handbook of Chemistry and Physics, 84th ed.; CRC Press: Boca Raton, FL, USA, 2004; pp. 1988–1990. [Google Scholar]
- Bogoroditsky, N.P.; Pasynkov, V.V.; Tareev, B.M. Electrical Engineering Materials; Mir Publishers: Moscow, Russia, 1979; p. 232. [Google Scholar]
- Dizenko, E.I.; Novoselov, V.F.; Tugunov, P.I.; Yufin, V.A. Corrosion Protection of Pipelines and Tanks; Nedra: Moscow, Russia, 1978; p. 24. (In Russian) [Google Scholar]
- Roberge, P.R. Handbook of Corrosion Engineering; McGraw-Hill: New York, NY, USA, 2000; p. 233. [Google Scholar]
- Revie, R.W.; Uhlig, H.H. Corrosion and Corrosion Control: An Introduction to Corrosion Science and Engineering, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2008; p. 220. [Google Scholar]
- Zhuk, N.P. A Course on the Theory of Corrosion and Protection of Metals; Metallurgiya: Moscow, Russia, 1976; pp. 32, 75, 76. (In Russian) [Google Scholar]
- Krynetskiĭ, I.B.; Gizhevskiĭ, B.A.; Naumov, S.V.; Kozlov, E.A. Size effect of the thermal expansion of nanostructural copper oxide. Phys. Solid State 2008, 50, 756–758. [Google Scholar] [CrossRef]
- Kazantsev, E.I. Industrial Ovens. Reference Guide for Calculations and Design, 2nd ed.; Supplemented and Revised; Metallurgiya: Moscow, Russia, 1975; p. 46. (In Russian) [Google Scholar]
- Gadzhiev, G.G. The thermal and elastic properties of zinc oxide-based ceramics at high temperatures. High Temp. 2003, 41, 778–782. [Google Scholar] [CrossRef]
- Shapiro, D.N. Fundamentals of the Theory of Electromagnetic Shielding; Energiya: Leningrad, Russia, 1975; p. 21. (In Russian) [Google Scholar]
- Maskaeva, L.N.; Fedorova, E.A.; Markov, V.F. Thin Film and Coating Technology; Publishing House of the Ural University: Yekaterinburg, Russia, 2019; pp. 11–14. (In Russian) [Google Scholar]
- Jackson, B.C.; Shawhan, G. Current review of the performance characteristics of conductive coatings for EMI control. In Proceedings of the IEEE International Symposium on Electromagnetic Compatibility, Denver, CO, USA, 24–28 August 1998; Volume 1, pp. 567–572. [Google Scholar] [CrossRef]
- Smits, F.M. Measurement of Sheet Resistivities with the Four-Point Probe. Bell Syst. Tech. J. 1958, 37, 711–718. [Google Scholar] [CrossRef]
- Haldor Topsoe Semiconductor Division. Geometric Factors in Four Point Resistivity Measurement; Bulletin No. 472-13; Haldor Topsøe: Vedbæk, Denmark, 1966; Volume 472, p. 15. [Google Scholar]
- Marvin, A.C.; Dawson, L.; Flintoft, I.D.; Dawson, J.F. A method for the measurement of shielding effectiveness of planar samples requiring no sample edge preparation or contact. IEEE Trans. Electromagn. Compat. 2009, 51, 255–262. [Google Scholar] [CrossRef] [Green Version]
- Volski, V.; Vandenbosch, G.A.E.; Vasylchenko, A. A dedicated technique to measure shielding effectiveness of textiles using a two-horn antenna set-up. J. Text. Inst. 2011, 102, 164–171. [Google Scholar] [CrossRef]
- Wang, L.-B.; Zhang, J.-W.; See, K.Y.; Svimonishvili, T. Ultra-Thin and Flexible Multi-Band Rejection EMI Shield. J. Electromagn. Anal. Appl. 2014, 6, 163–173. [Google Scholar] [CrossRef] [Green Version]
- Cui, Y. A New Measure for Evaluating Shielding Performance of an Equipment Enclosure at Frequencies above 1 GHz. Ph.D. Thesis, Department of Electronics, University of York, York, UK, 2007. [Google Scholar]
- Andryushchenko, M.S.; Gusakovskii, V.E.; Shtager, E.A.; Shtager, D.E.; Shchesnyak, S.S. Methods of Analysis of EMI Protection of Radioelectronic Systems; VVM: St. Petersburg, Russia, 2016; pp. 271–273. (In Russian) [Google Scholar]
- Gareev, K.G.; Luchinin, V.V.; Sevost’yanov, E.N.; Testov, I.O.; Testov, O.A. Frequency Dependence of an Electromagnetic Absorption Coefficient in Magnetic Fluid. Tech. Phys. 2019, 64, 893–896. [Google Scholar] [CrossRef]
- Tao, Y.; Scharf, F. Revisiting the Effect of Nickel Characteristics on High-Speed Interconnect Performance. IEEE Trans. Microw. Theory Tech. 2016, 64, 2447–2453. [Google Scholar] [CrossRef]
- Timsit, R.S. High speed electronic connector design: A review of electrical and electromagnetic properties of passive contact. IEICE Trans. Electron. 2008, E91-C, 1178–1191. [Google Scholar] [CrossRef]
- Glathart, J.L. The inner, initial, magnetic permeability of iron and nickel at ultra-high radiofrequencies. Phys. Rev. 1939, 55, 833–838. [Google Scholar] [CrossRef]
- Hoag, J.B.; Glathart, J.L. The outer, initial permeability of nickel from 10 to 70 megacycles. Phys. Rev. 1940, 57, 240. [Google Scholar] [CrossRef]
- Nonaka, Y.; Nakane, H.; Maeda, T.; Hasuike, K. Simultaneous Measurement of the Resistivity and Permeability of a Film Sample with a Double Coil. IEEE Trans. Instrum. Meas. 1995, 44, 679–682. [Google Scholar] [CrossRef]
- Lucyszyn, S. Microwave characterization of nickel. In Proceedings of the Progress in Electromagnetics Research Symposium, Hangzhou, China, 24–28 March 2008; pp. 879–883. [Google Scholar]
- Choi, H.S.; Suh, S.J.; Kim, S.W.; Kim, H.J.; Park, J.W. Transparent electromagnetic shielding film utilizing imprinting-based micro patterning technology. Polymers 2021, 13, 738. [Google Scholar] [CrossRef]
- Liao, S.Y. Light Transmittance and RF Shielding Effectiveness of a Gold Film on a Glass Substrate. IEEE Trans. Electromagn. Compat. 1975, EMC-17, 211–216. [Google Scholar] [CrossRef]
- Liu, H.D.; Zhao, Y.P.; Ramanath, G.; Murarka, S.P.; Wang, G.C. Thickness dependent electrical resistivity of ultrathin (<40 nm) Cu films. Thin Solid Film. 2001, 384, 151–156. [Google Scholar] [CrossRef]
- Antonets, I.V.; Kotov, L.N.; Shavrov, V.G.; Shcheglov, V.I. Conducting and reflecting properties of nanometer-width films of various metals. J. Commun. Technol. Electron. 2006, 51, 1394–1400. [Google Scholar] [CrossRef]
- Schulz, R.B.; Plantz, V.C.; Brush, D.R. Shielding Theory and Practice. IEEE Trans. Electromagn. Compat. 1988, 30, 187–201. [Google Scholar] [CrossRef]
- Unutulmazsoy, Y.; Merkle, R.; Fischer, D.; Mannhart, J.; Maier, J. The oxidation kinetics of thin nickel films between 250 and 500 °C. Phys. Chem. Chem. Phys. 2017, 19, 9045–9052. [Google Scholar] [CrossRef] [PubMed] [Green Version]

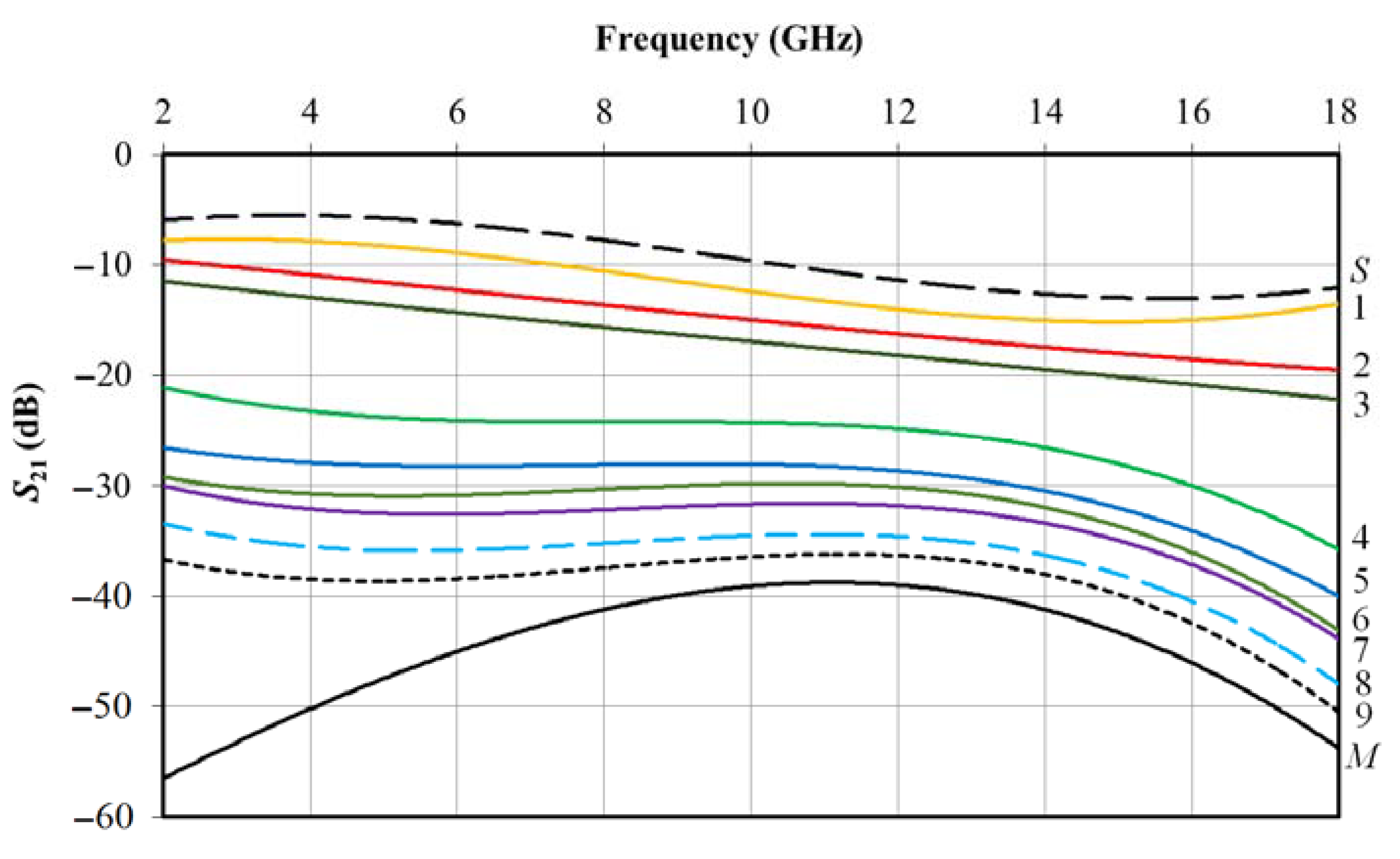
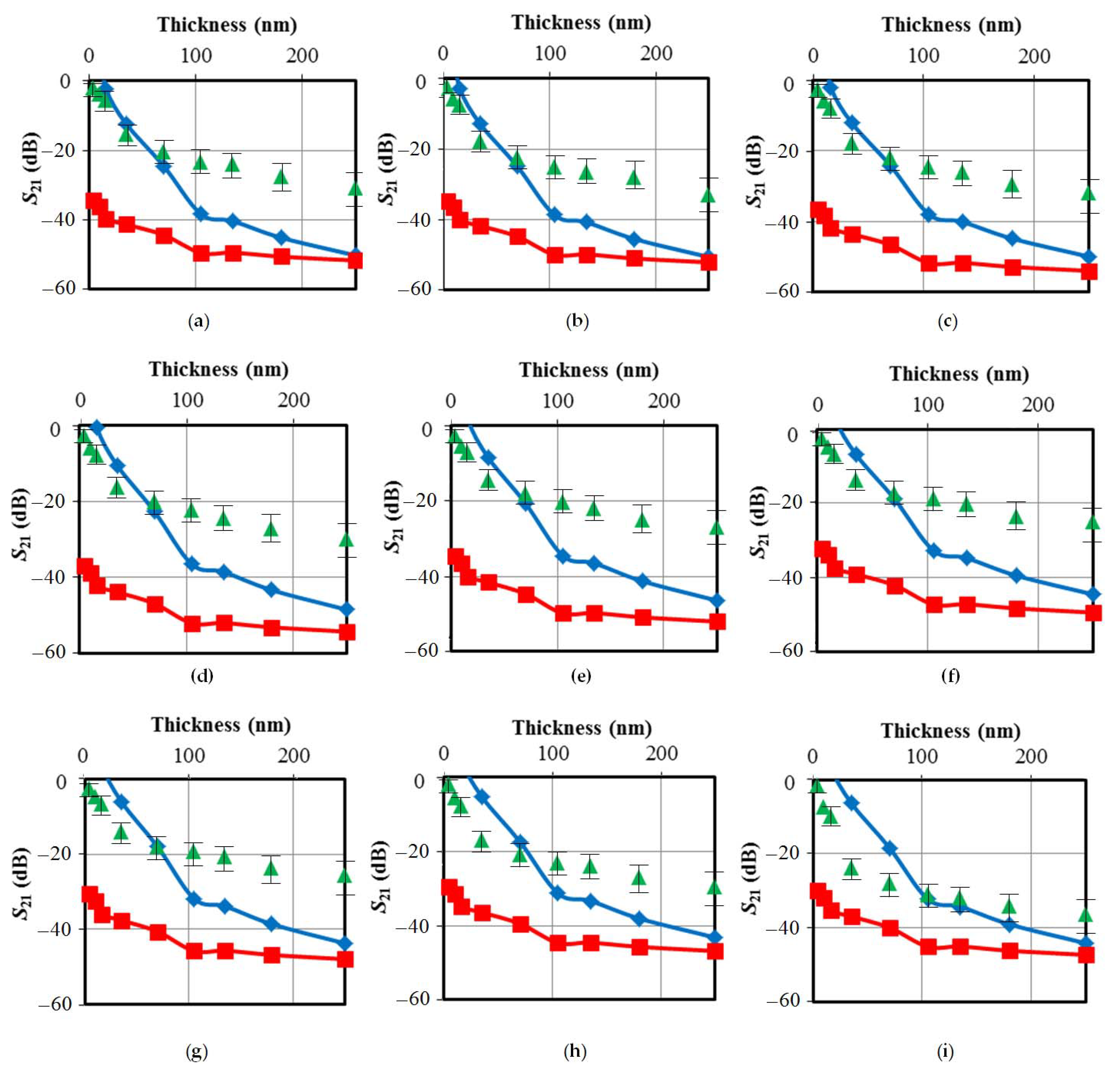
| Sample No. | Thickness (nm) |
|---|---|
| 1 | 4 |
| 2 | 10 |
| 3 | 16 |
| 4 | 35 |
| 5 | 70 |
| 6 | 110 |
| 7 | 135 |
| 8 | 180 |
| 9 | 250 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Testov, O.A.; Komlev, A.E.; Gareev, K.G.; Khmelnitskiy, I.K.; Luchinin, V.V.; Sevost’yanov, E.N.; Testov, I.O. Providing a Specified Level of Electromagnetic Shielding with Nickel Thin Films Formed by DC Magnetron Sputtering. Coatings 2021, 11, 1455. https://doi.org/10.3390/coatings11121455
Testov OA, Komlev AE, Gareev KG, Khmelnitskiy IK, Luchinin VV, Sevost’yanov EN, Testov IO. Providing a Specified Level of Electromagnetic Shielding with Nickel Thin Films Formed by DC Magnetron Sputtering. Coatings. 2021; 11(12):1455. https://doi.org/10.3390/coatings11121455
Chicago/Turabian StyleTestov, Oleg A., Andrey E. Komlev, Kamil G. Gareev, Ivan K. Khmelnitskiy, Victor V. Luchinin, Eugeniy N. Sevost’yanov, and Igor O. Testov. 2021. "Providing a Specified Level of Electromagnetic Shielding with Nickel Thin Films Formed by DC Magnetron Sputtering" Coatings 11, no. 12: 1455. https://doi.org/10.3390/coatings11121455
APA StyleTestov, O. A., Komlev, A. E., Gareev, K. G., Khmelnitskiy, I. K., Luchinin, V. V., Sevost’yanov, E. N., & Testov, I. O. (2021). Providing a Specified Level of Electromagnetic Shielding with Nickel Thin Films Formed by DC Magnetron Sputtering. Coatings, 11(12), 1455. https://doi.org/10.3390/coatings11121455