Cattaneo-Christov Heat Flux Model for Second Grade Nanofluid Flow with Hall Effect through Entropy Generation over Stretchable Rotating Disk
Abstract
:1. Introduction
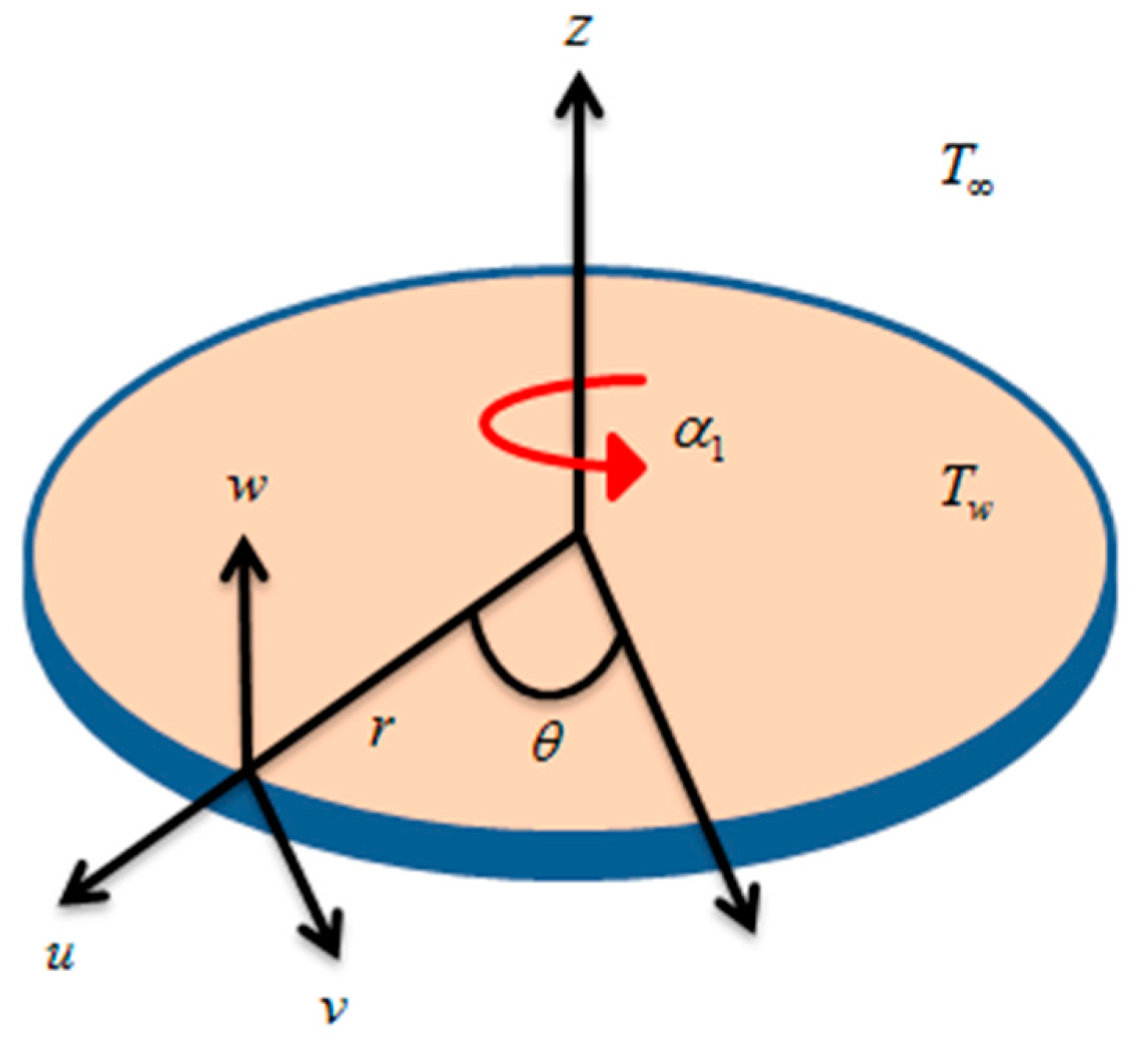
2. Problem Modeling
2.1. Skin Friction and Nusselt Number
2.2. Entropy Generation
3. HAM Solution
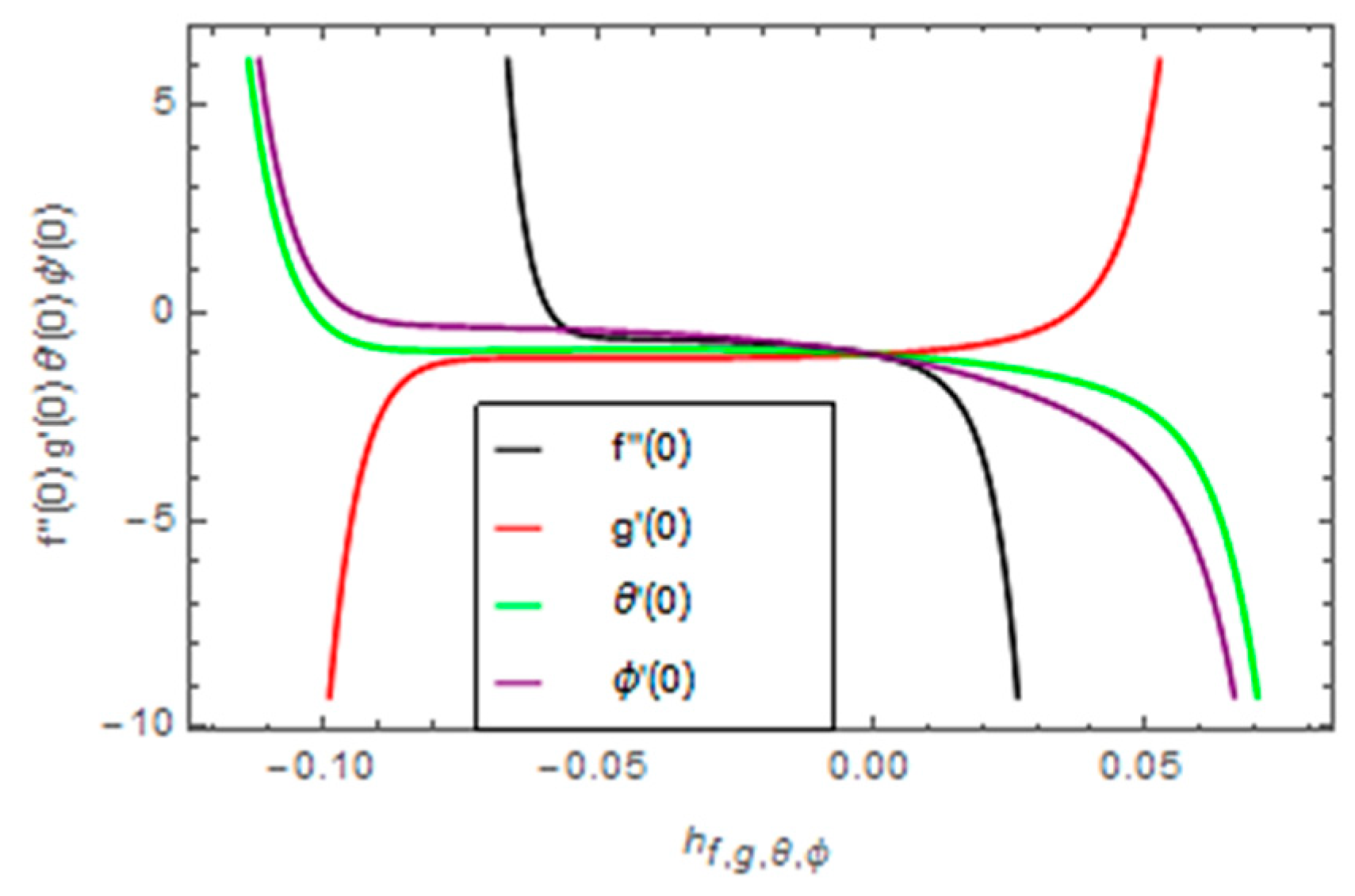
Convergence Investigation
4. Results and Discussion
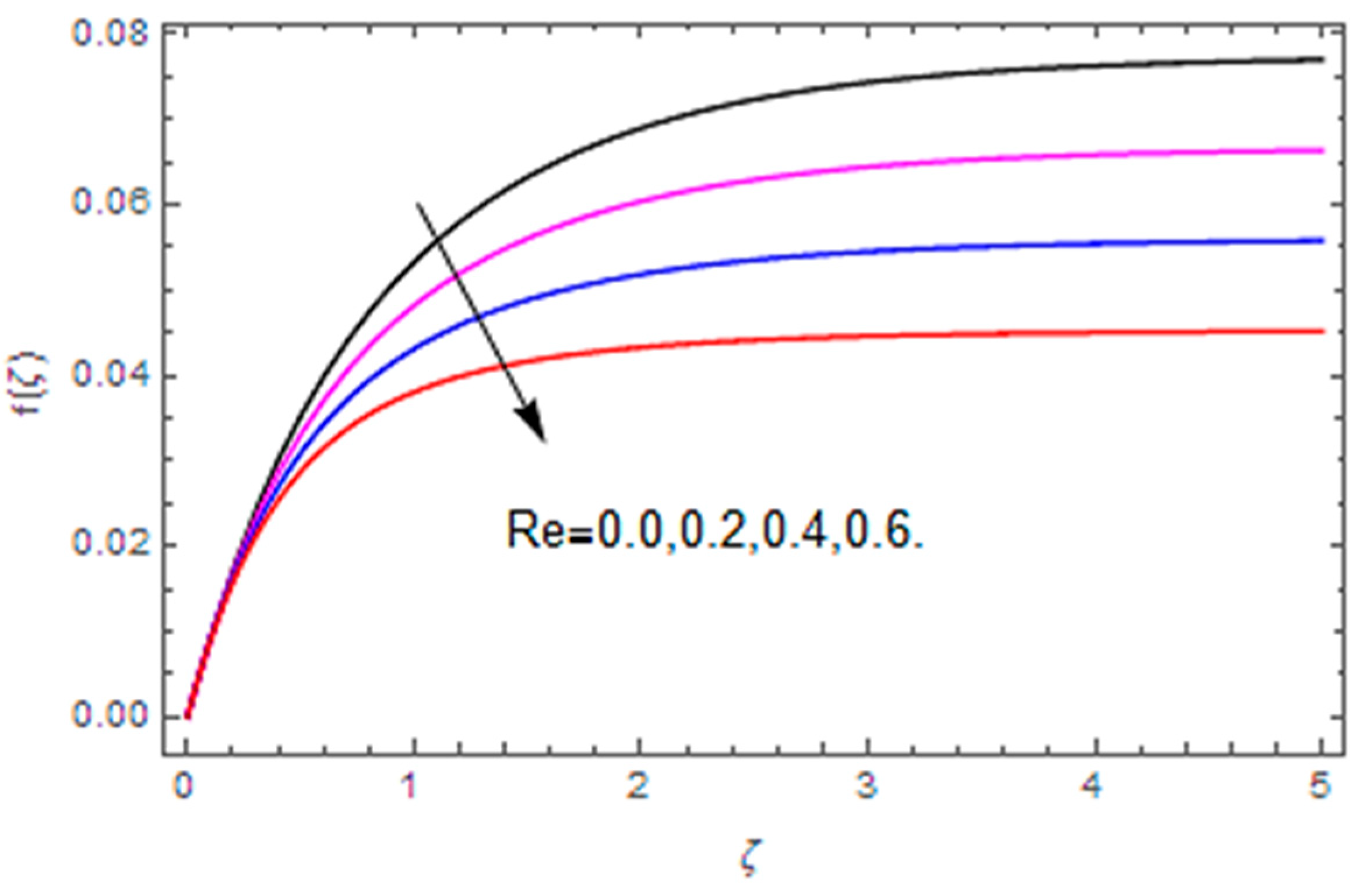
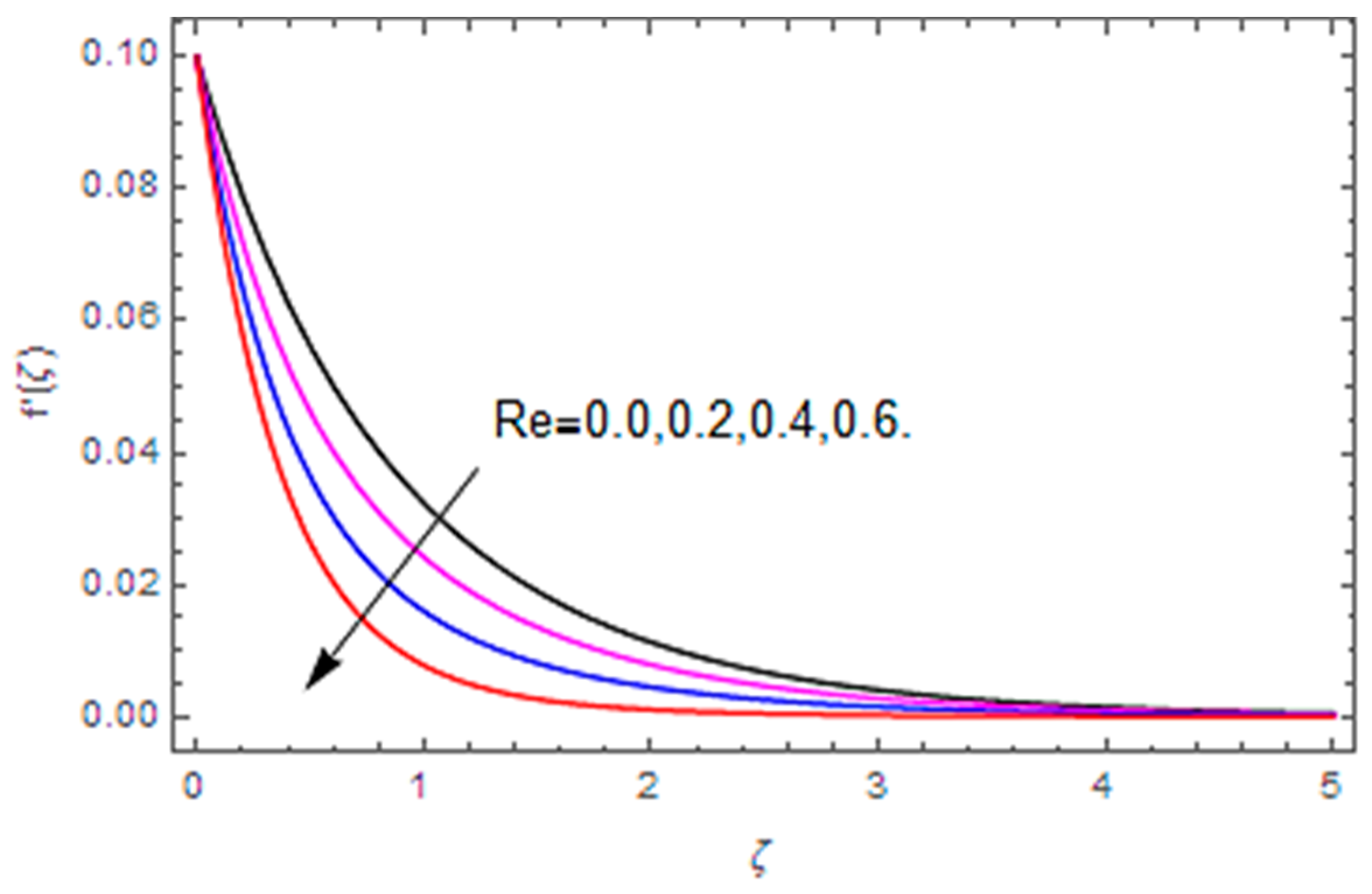
4.1. Velocities, Temperature and Concentration Fields
4.2. Entropy Optimization and Bejan Number
4.3. Physical Quantities
5. Conclusions
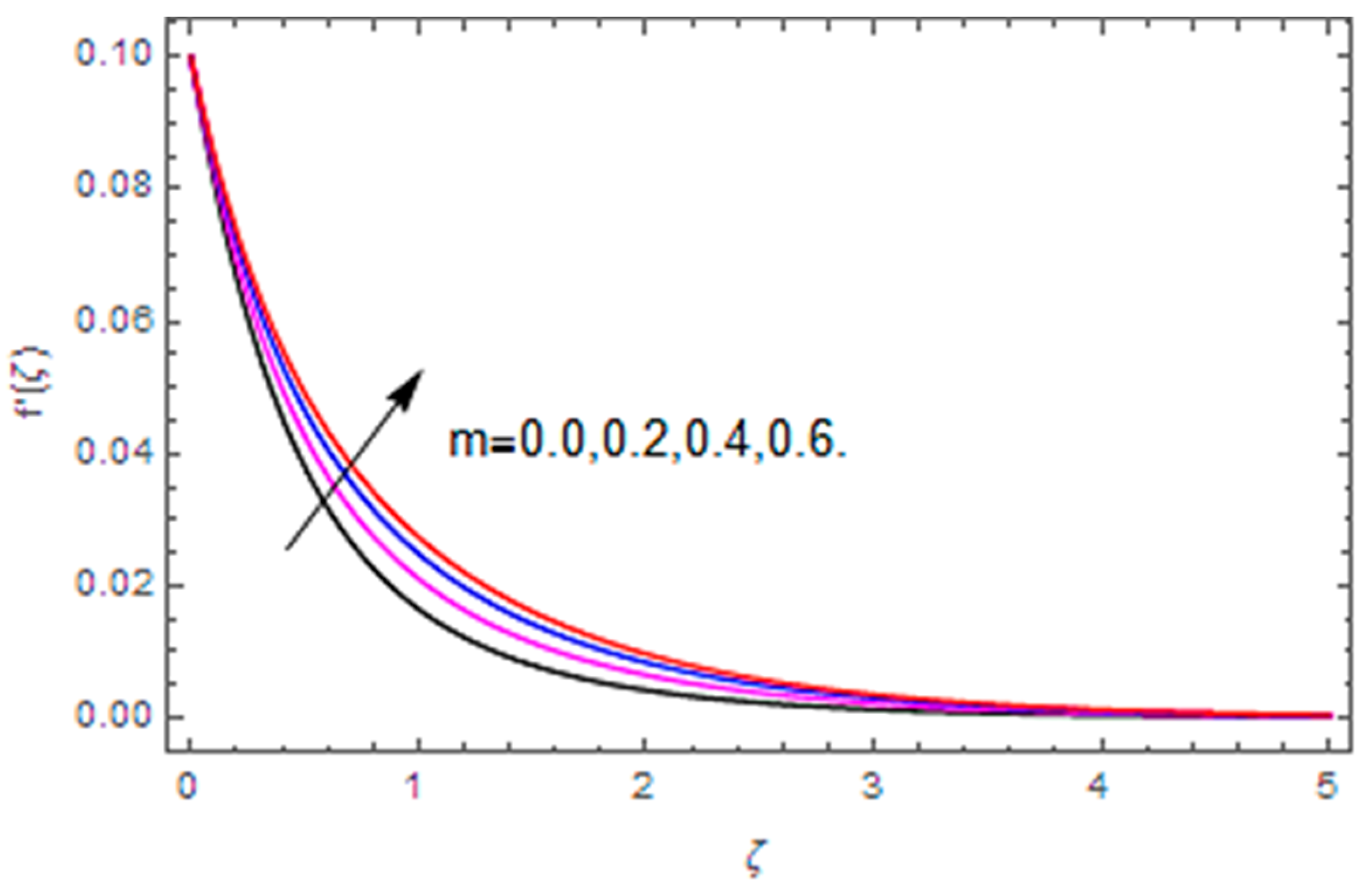
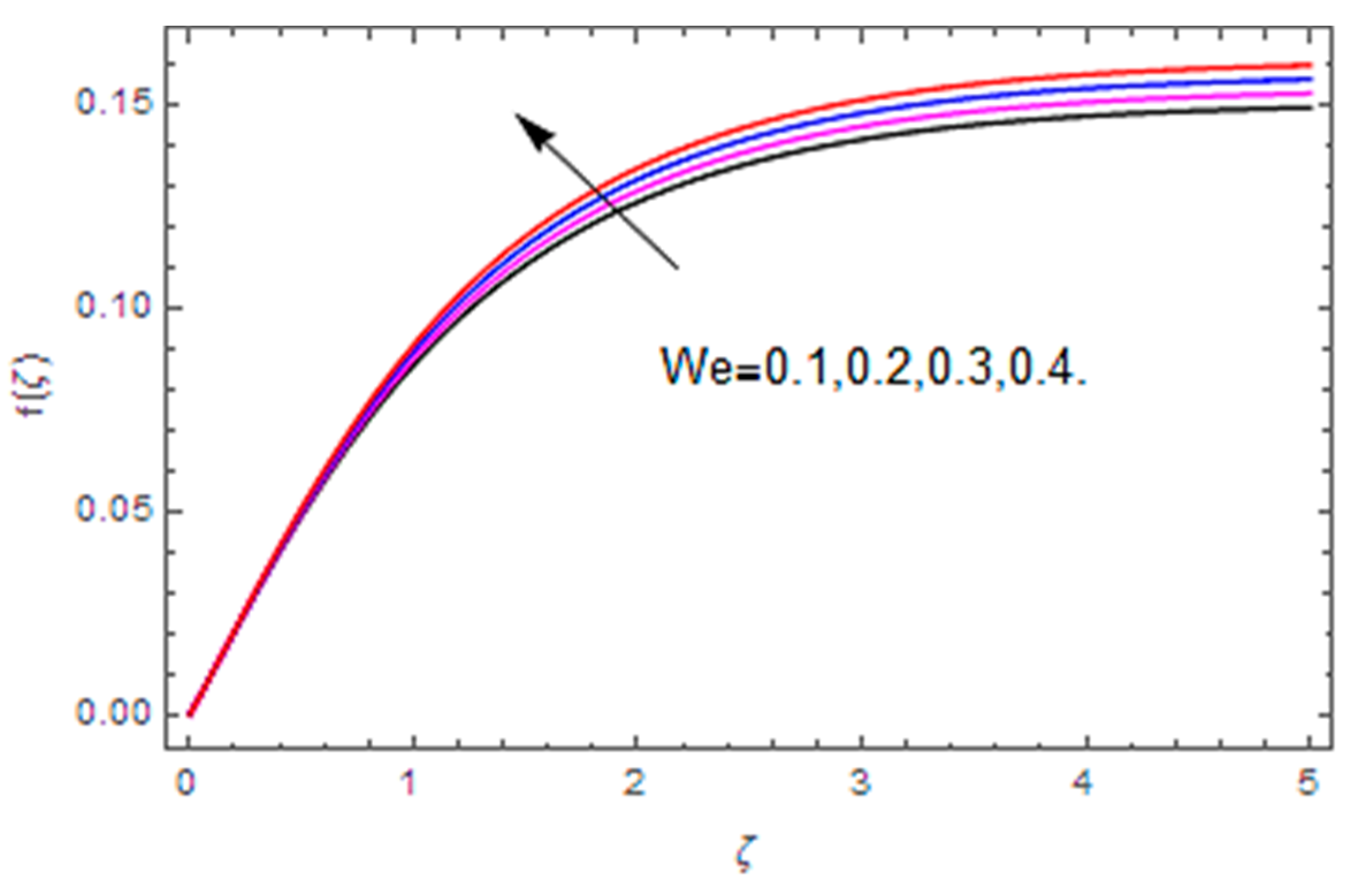
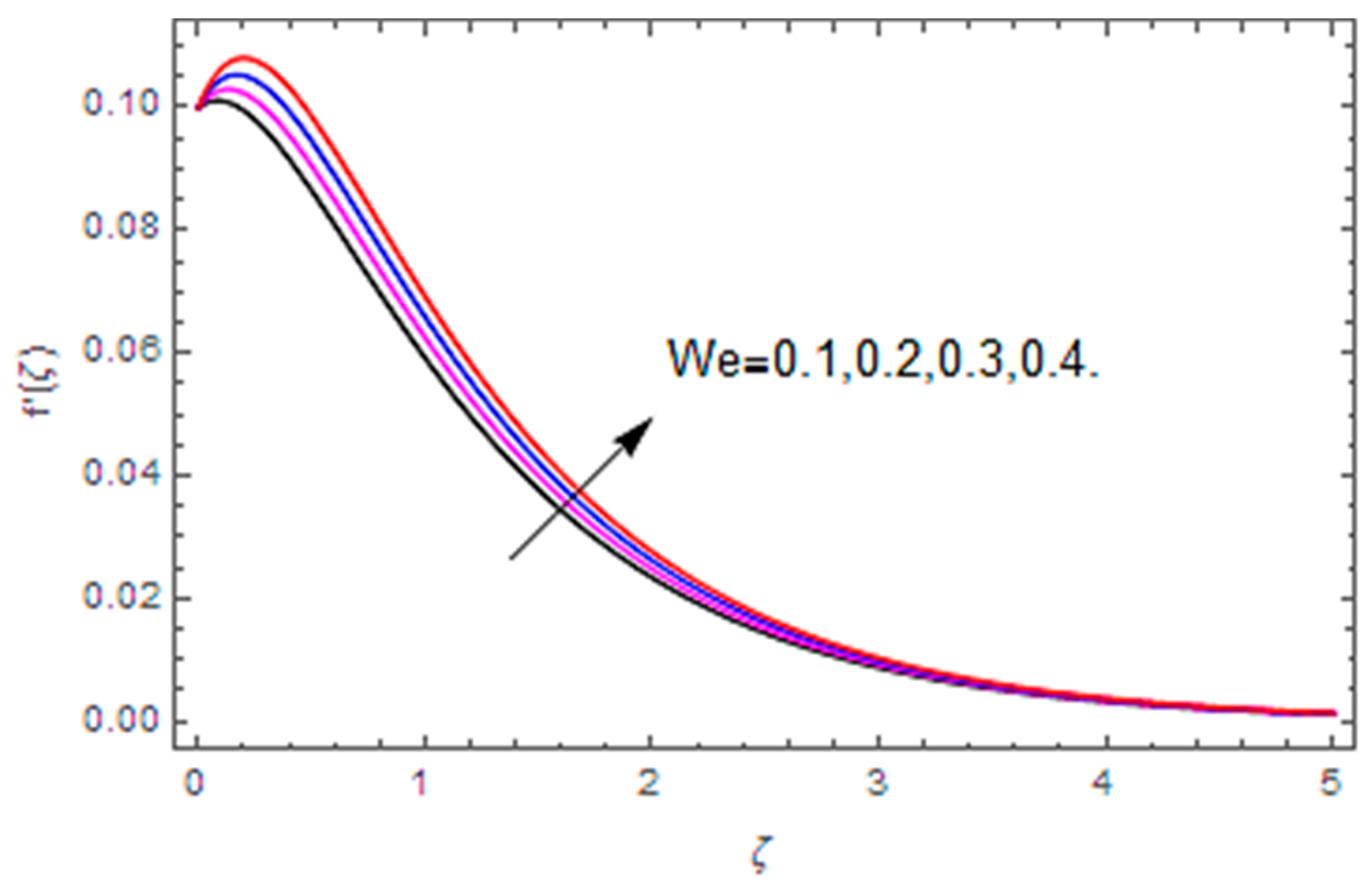
- Velocity along the radial direction is enhanced with the Weissenberg number and stretching parameter, however, the conflicting influence is observed via the Reynolds number.
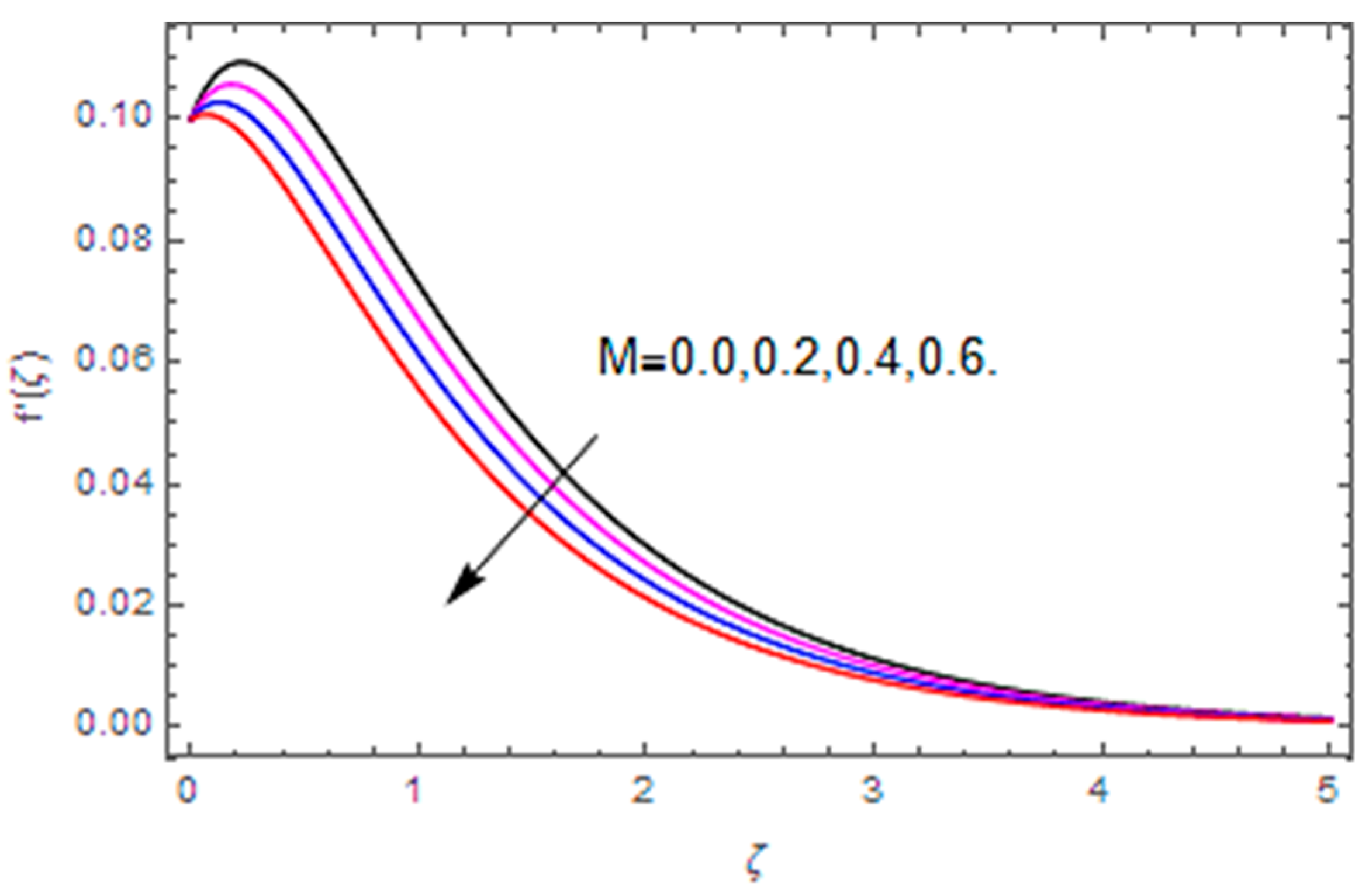
- Velocity along the axial direction is heightened with the Hall parameter and Weissenberg number, while it is decreased with the magnetic parameter and the Reynolds number.
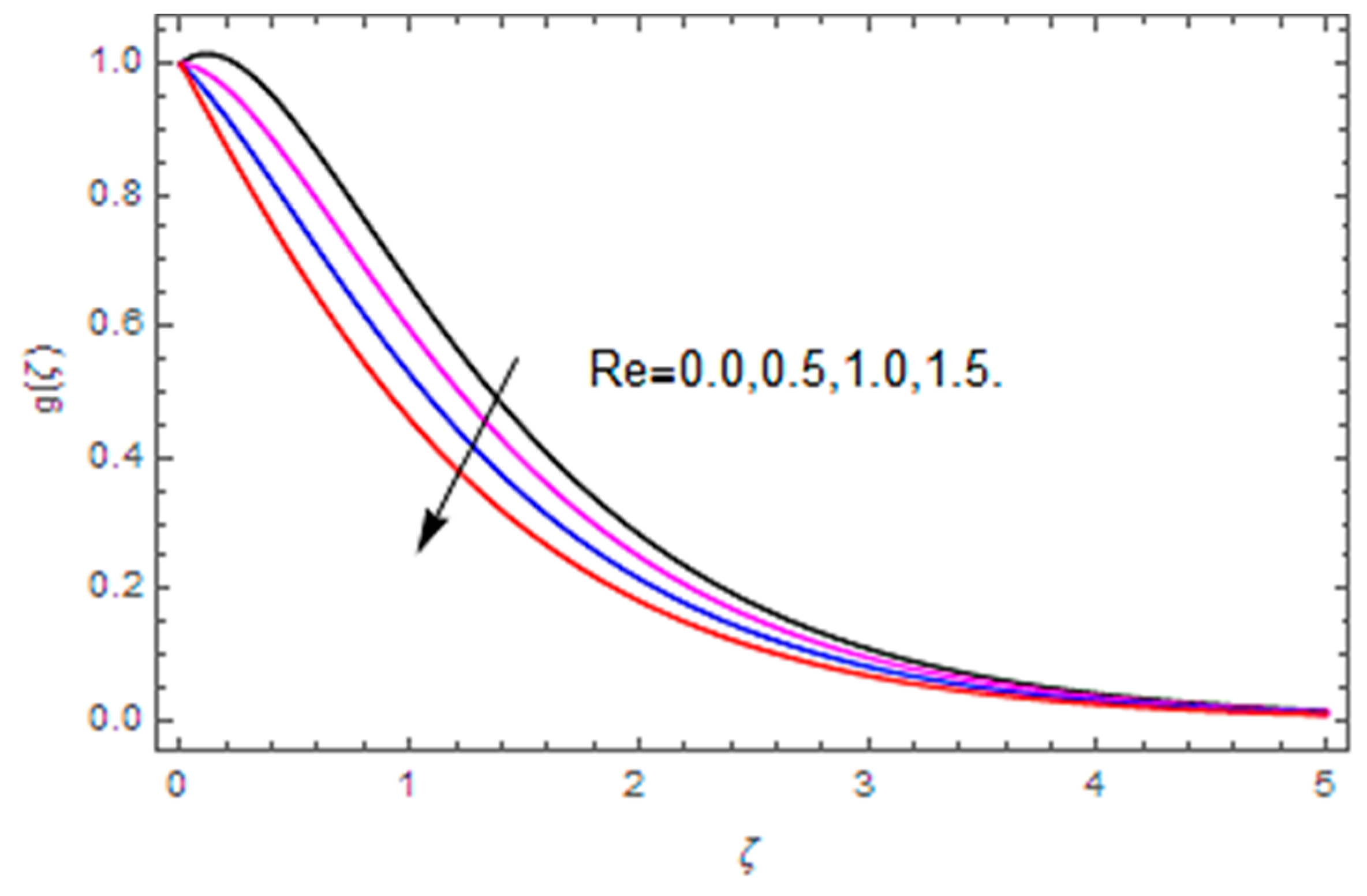
- Velocity along the tangential direction is escalated with the Hall parameter, while it decays with the magnetic parameter, Reynolds number and stretching parameter.
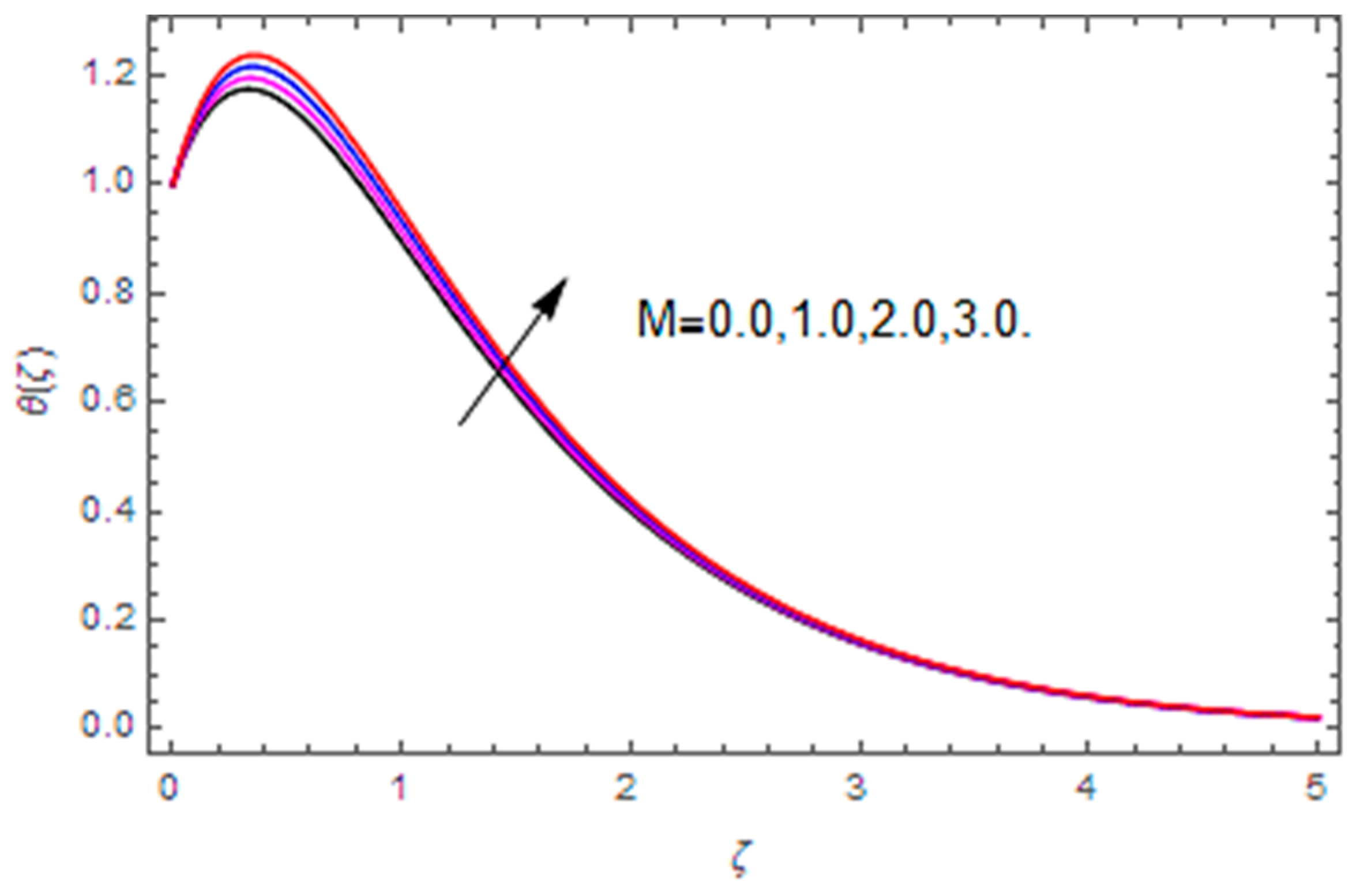
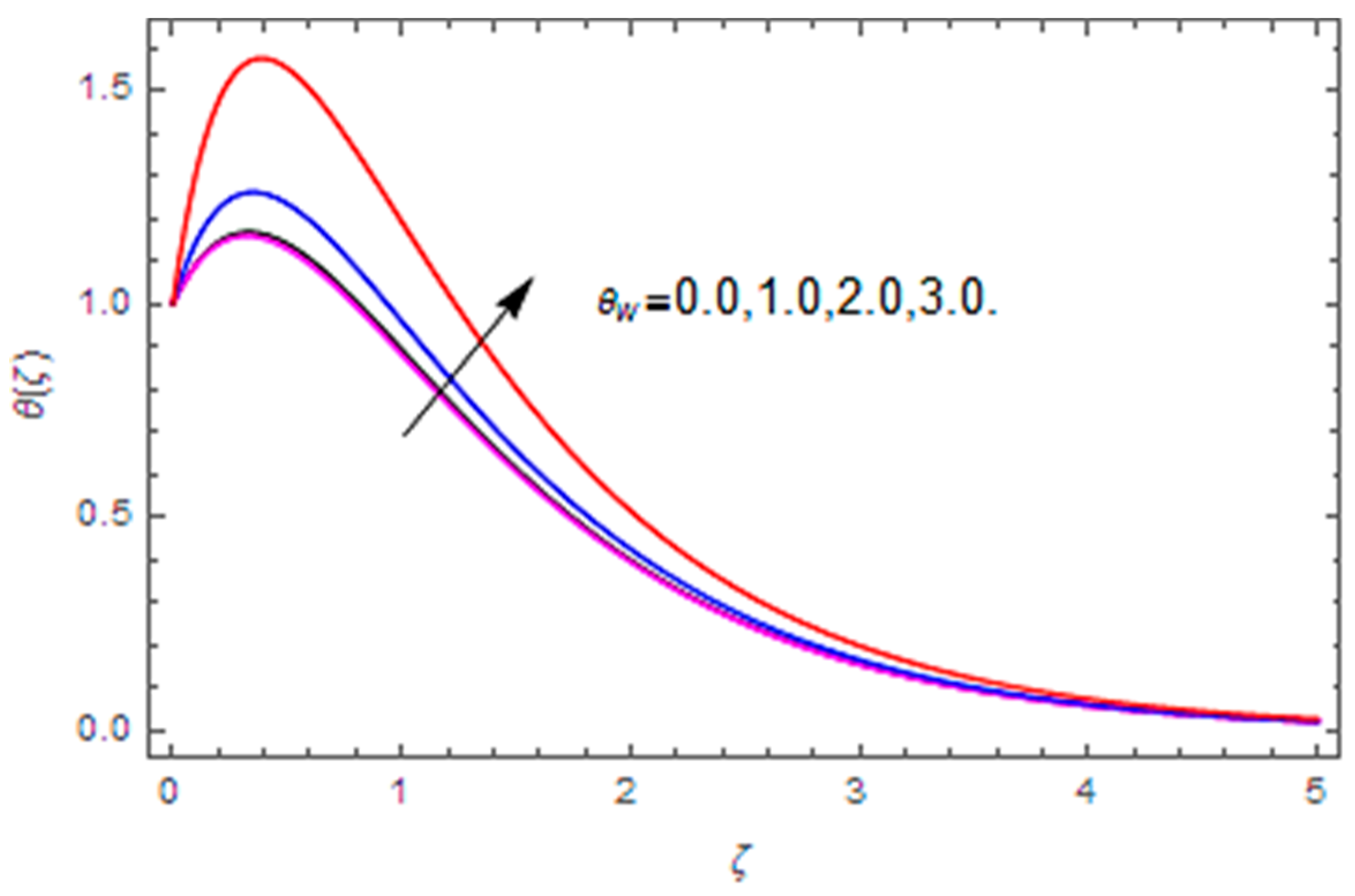
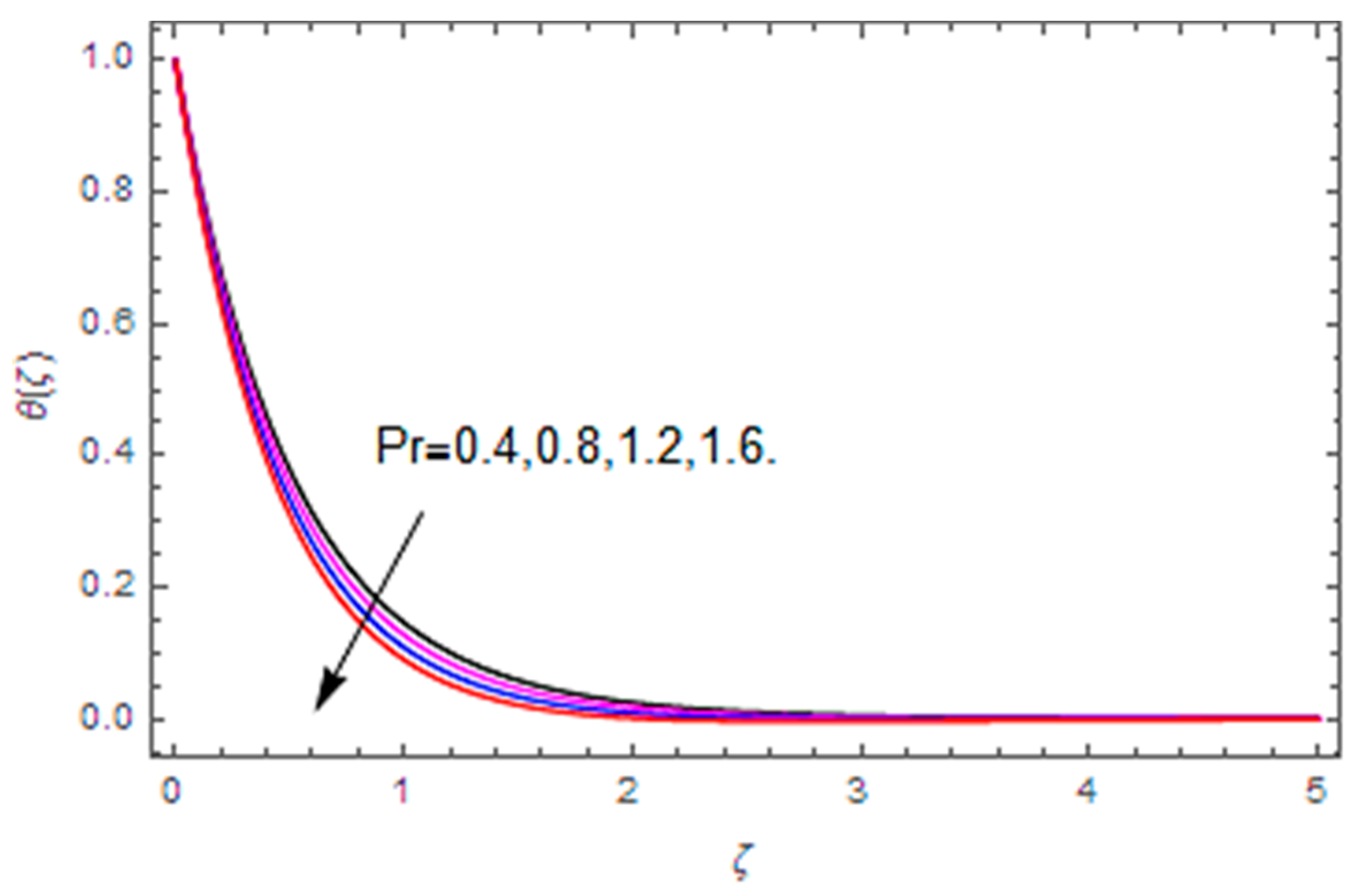
- The temperature profile is increased with the magnetic parameter, Brownian motion parameter, thermophoresis parameter, temperature difference and heat generation/absorption parameter, whereas it is reduced with the Hall parameter, thermal relaxation parameter and Prandtl number.
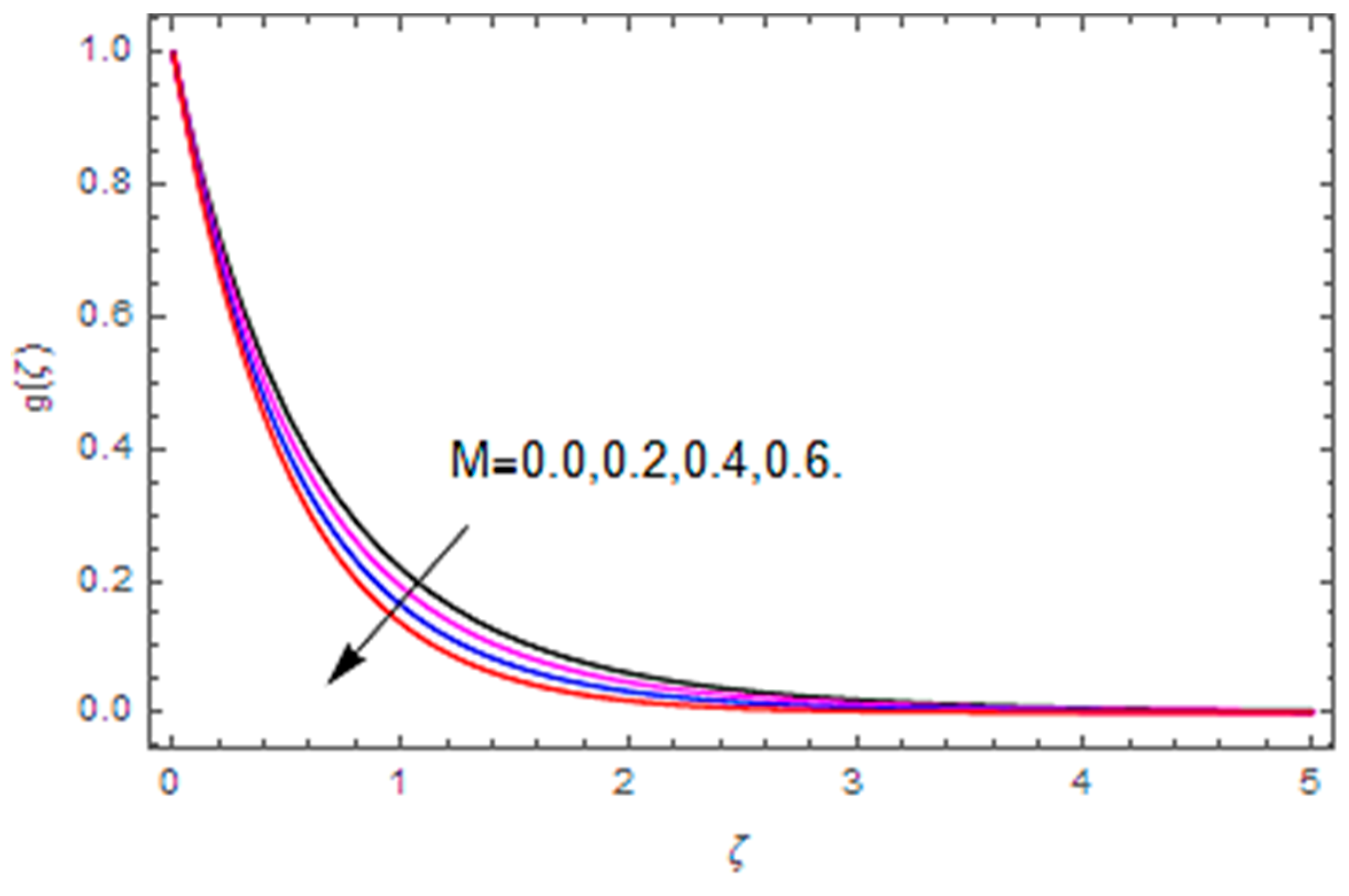
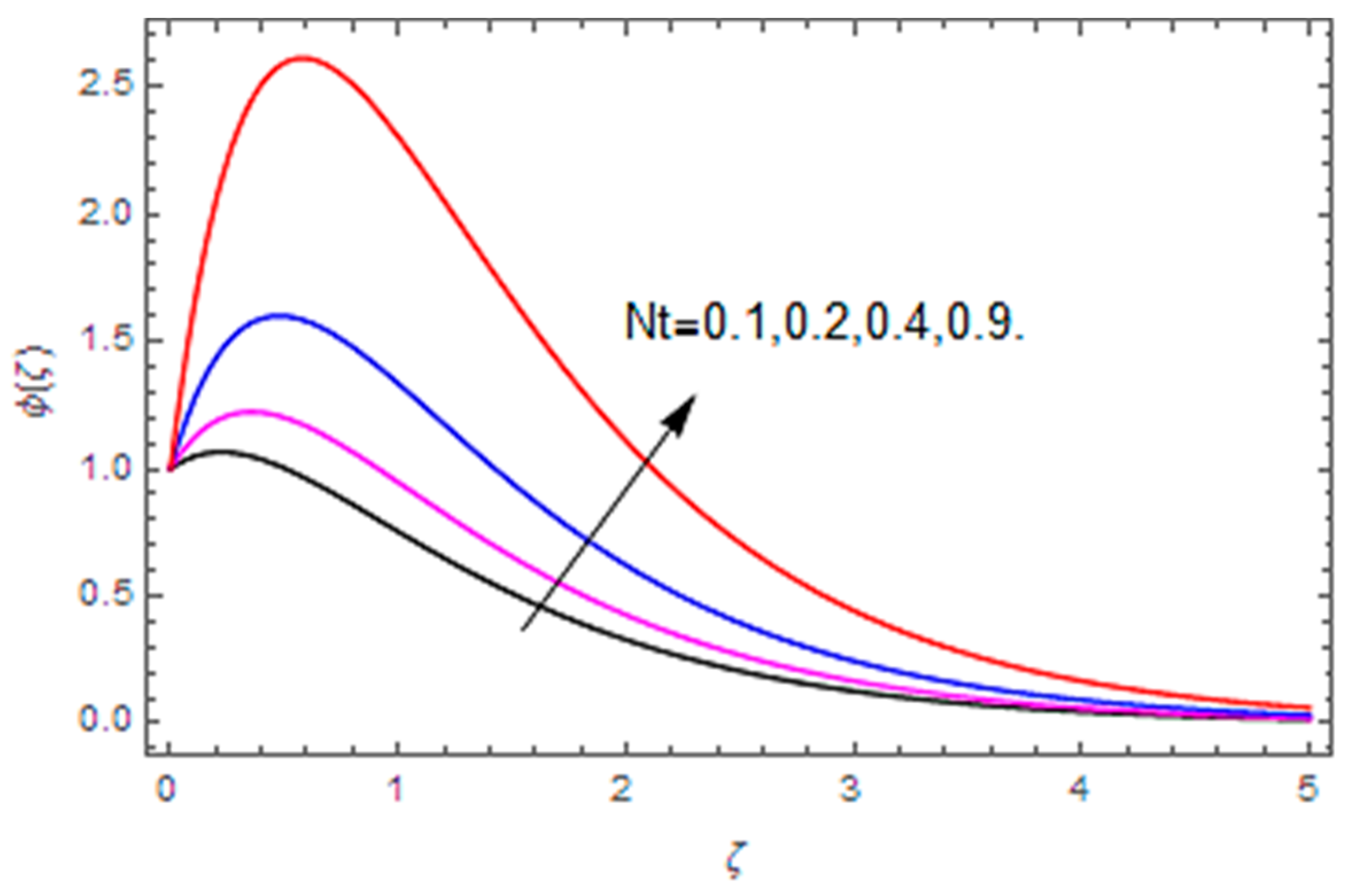
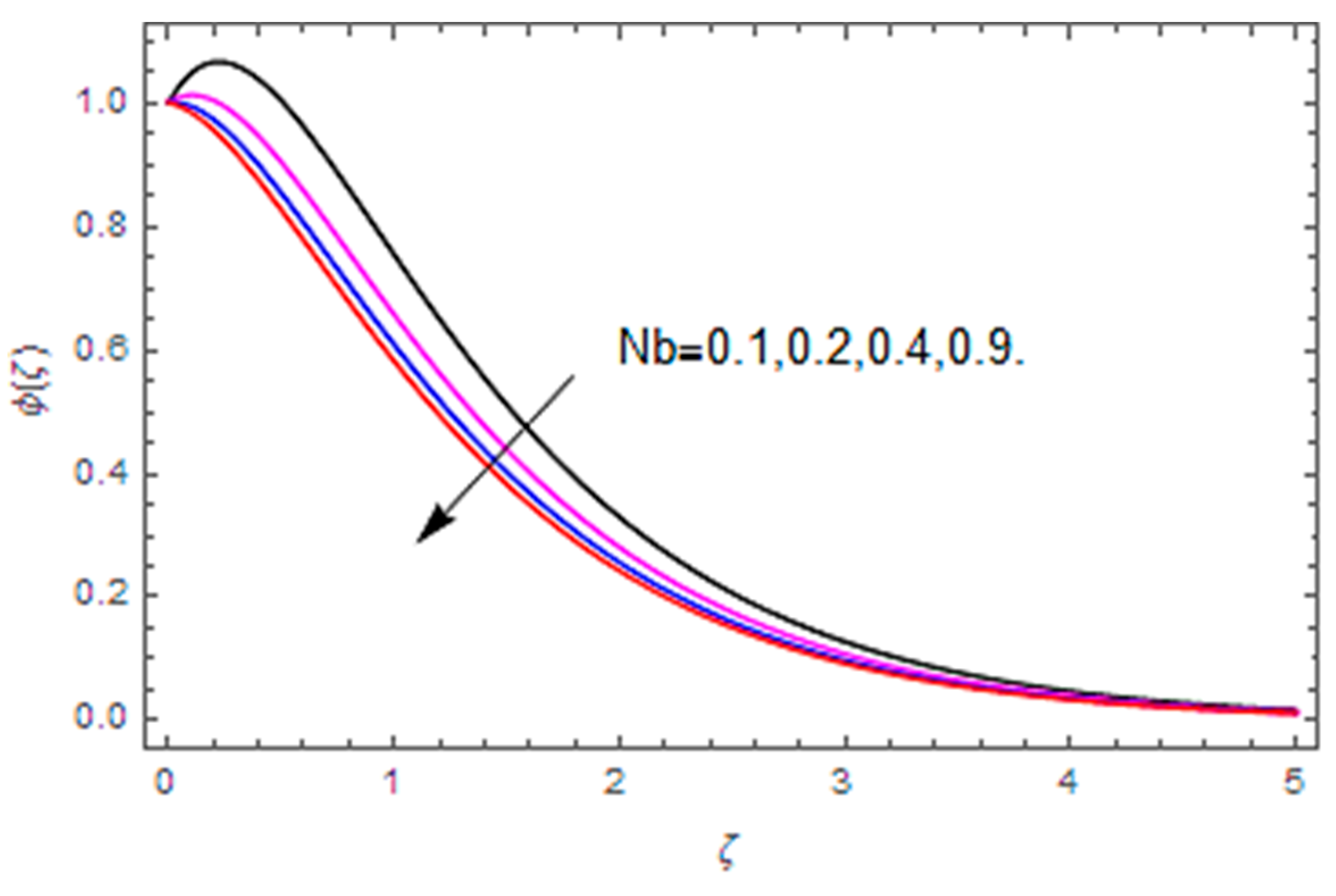
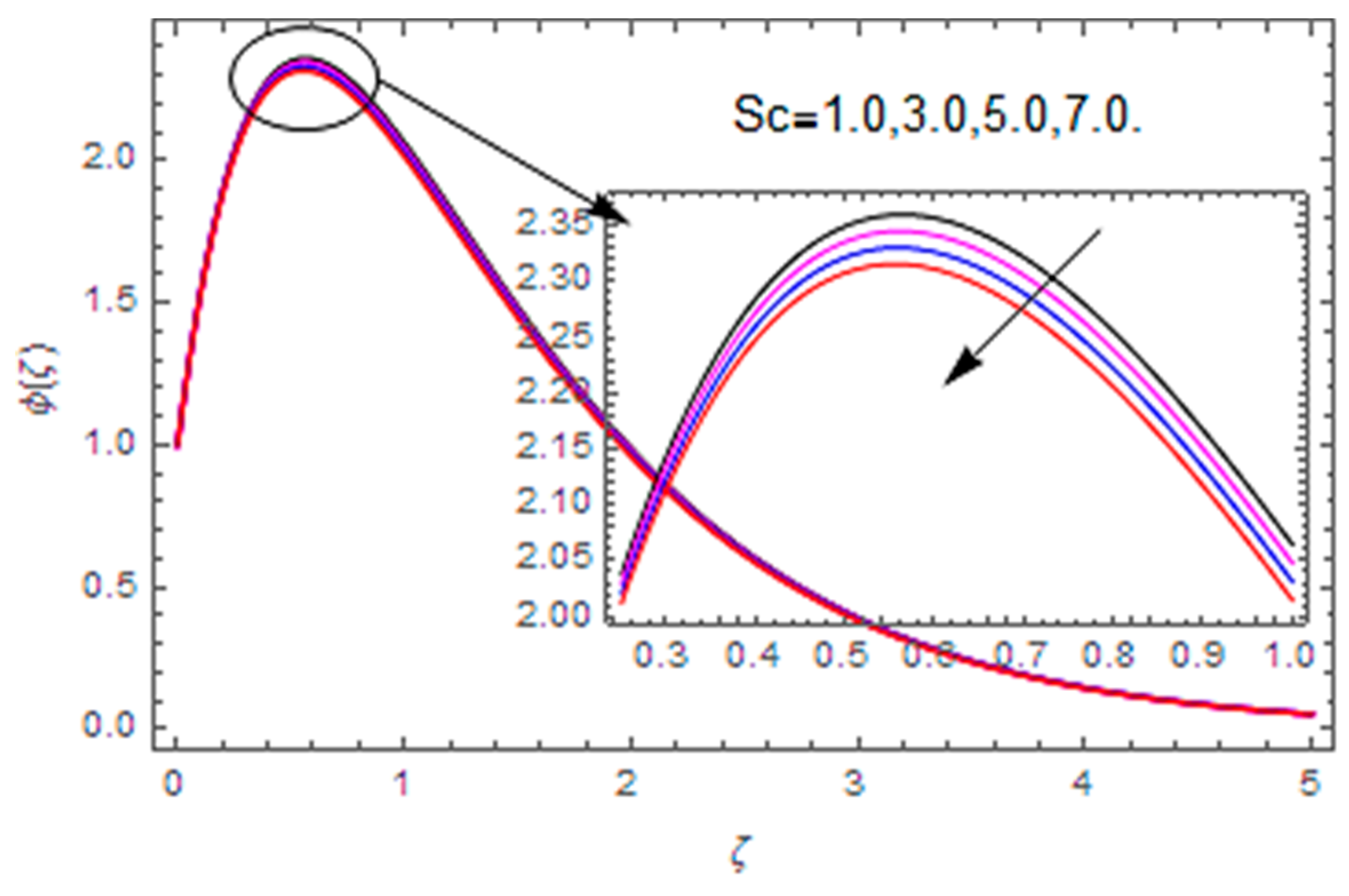
- The concentration profile is increased with the thermophoresis parameter, while it is reduced with the Brownian motion parameter and the Schmidt number.
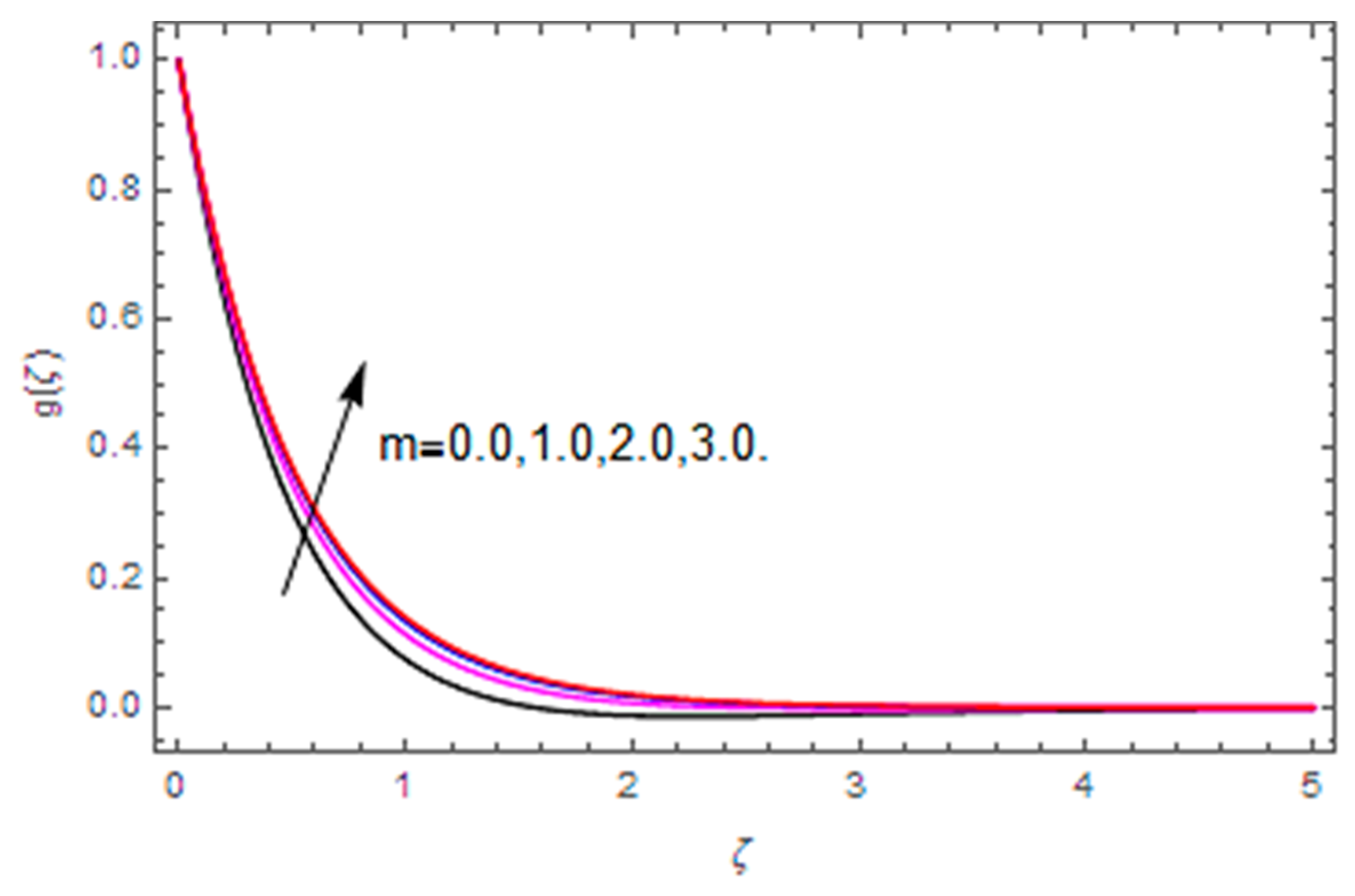
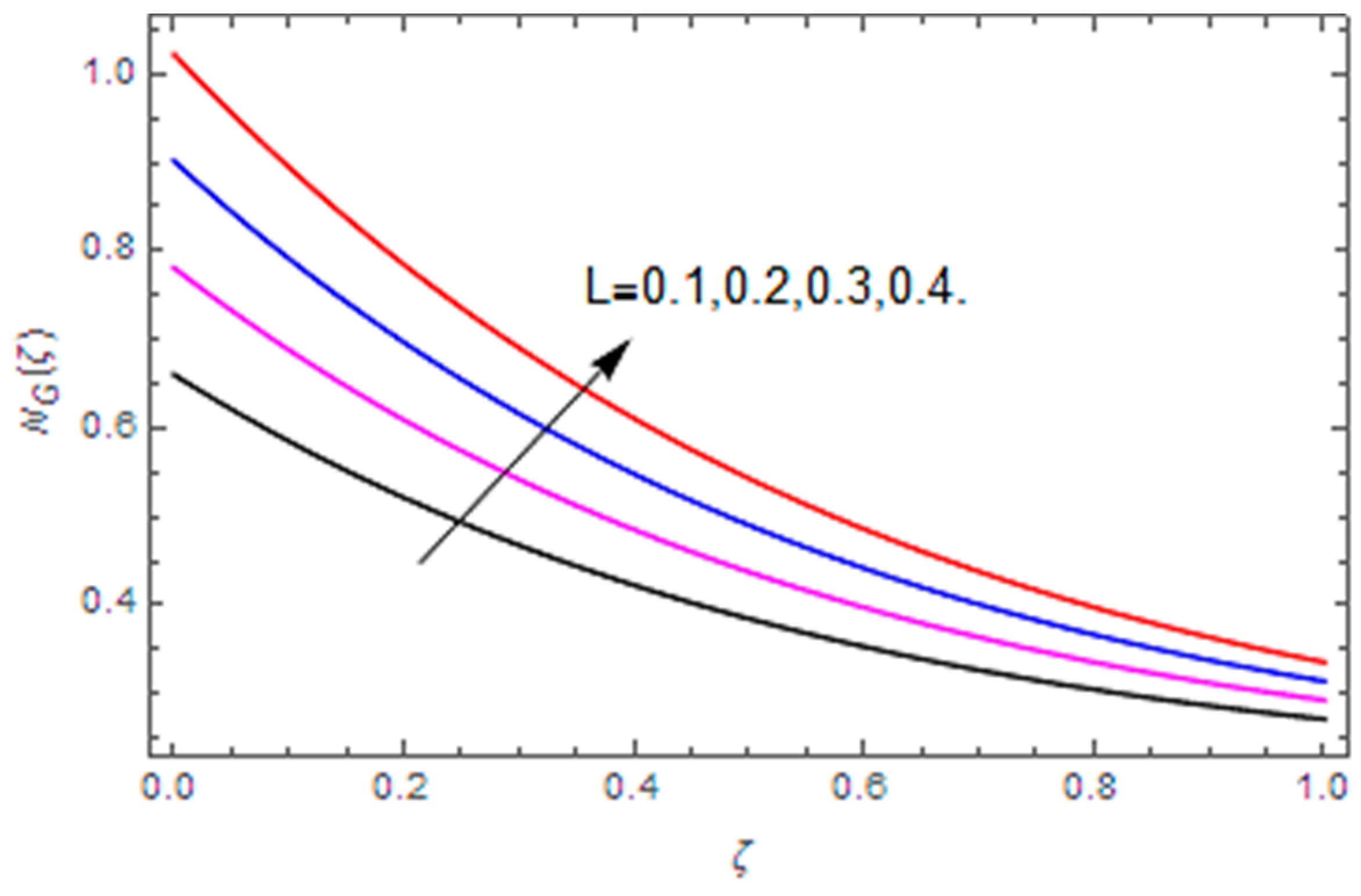
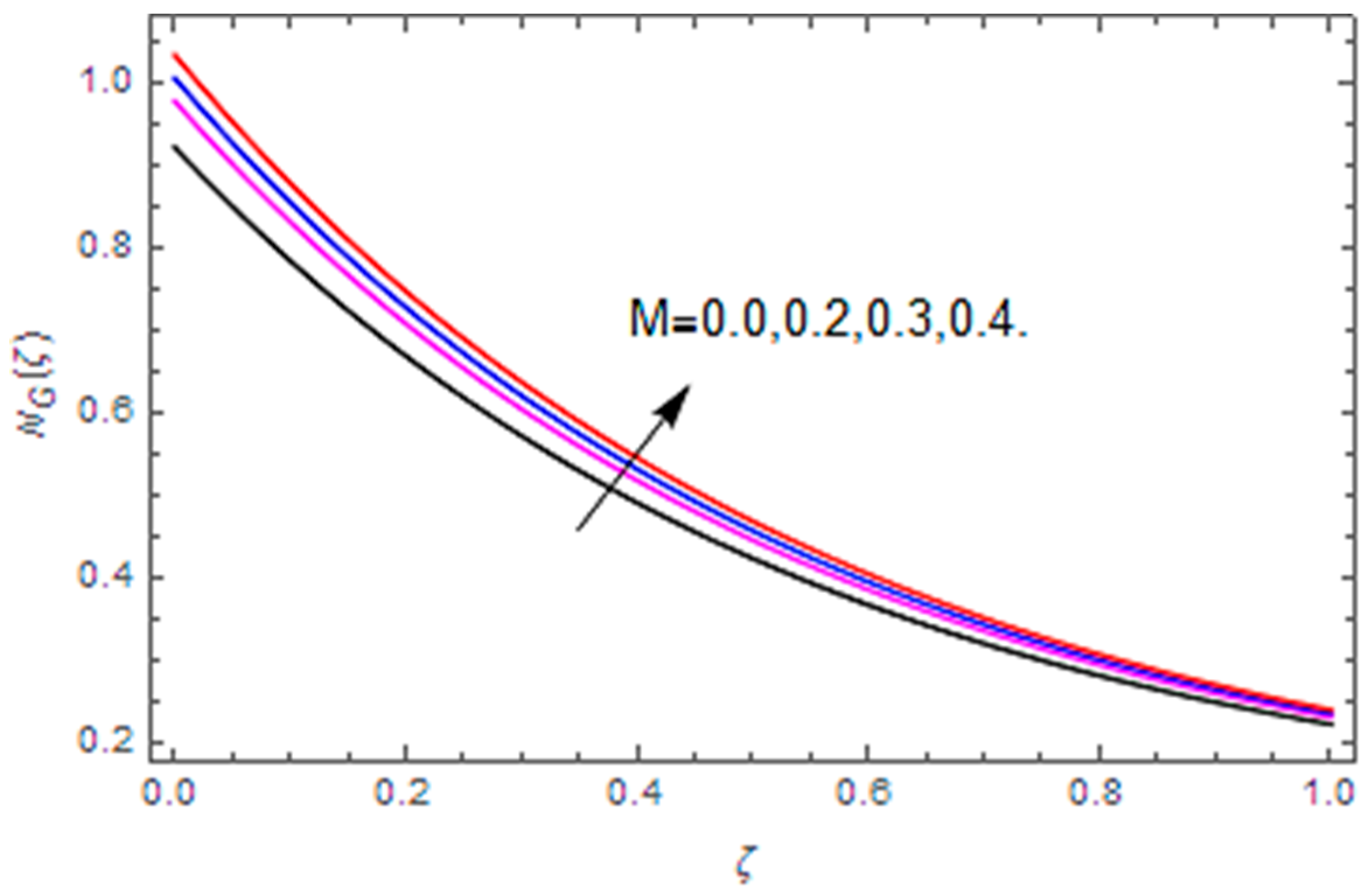
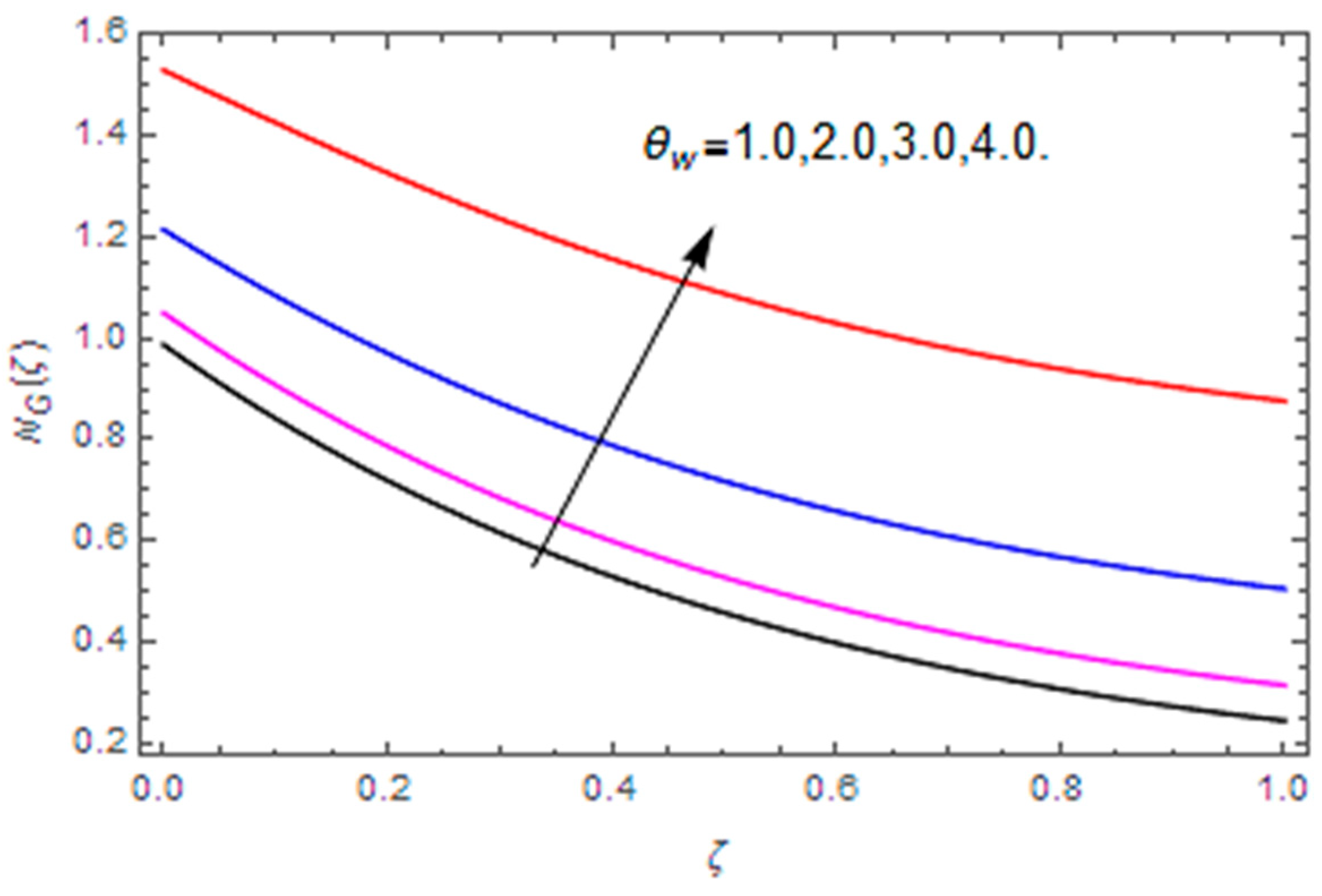
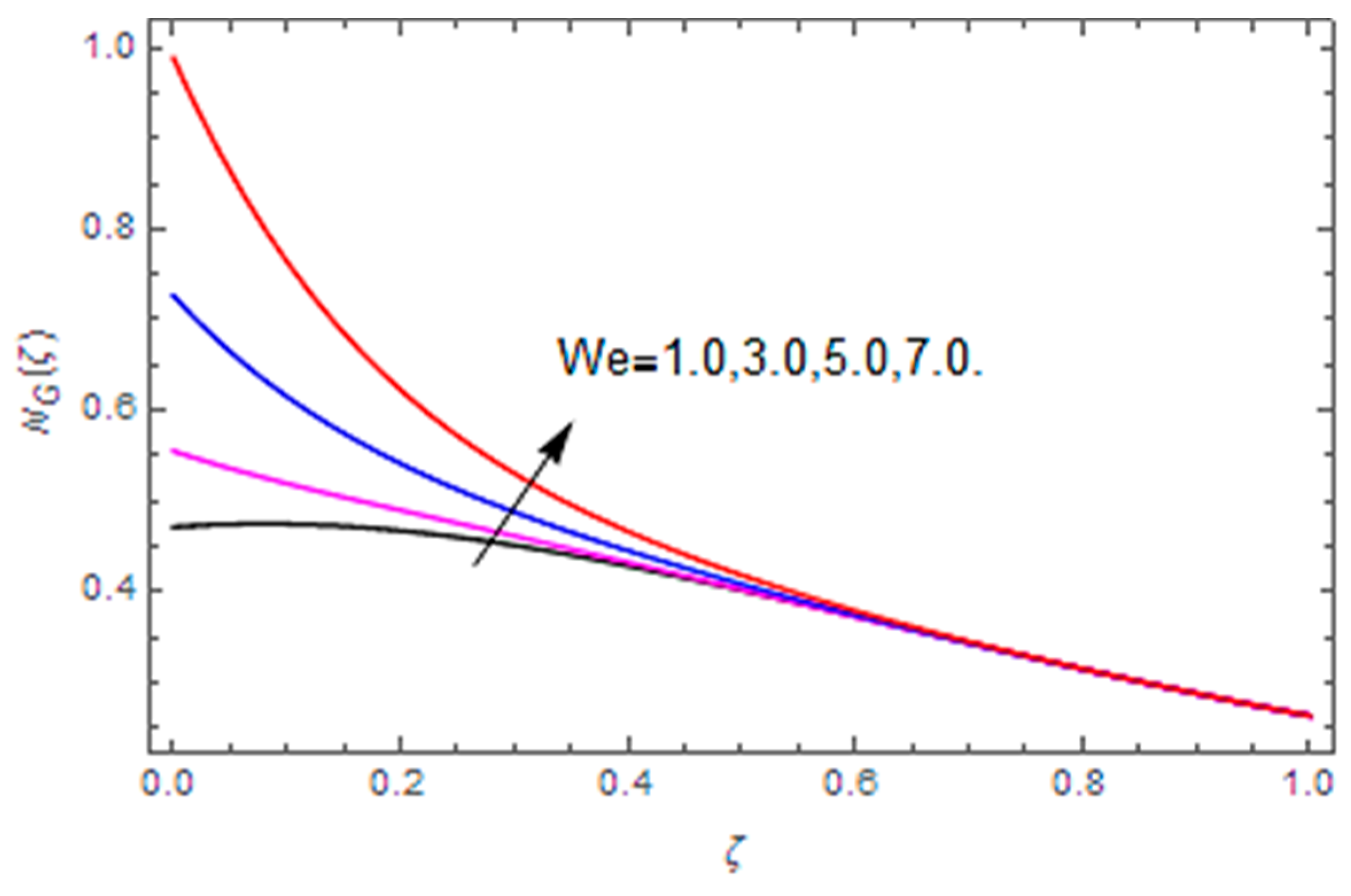
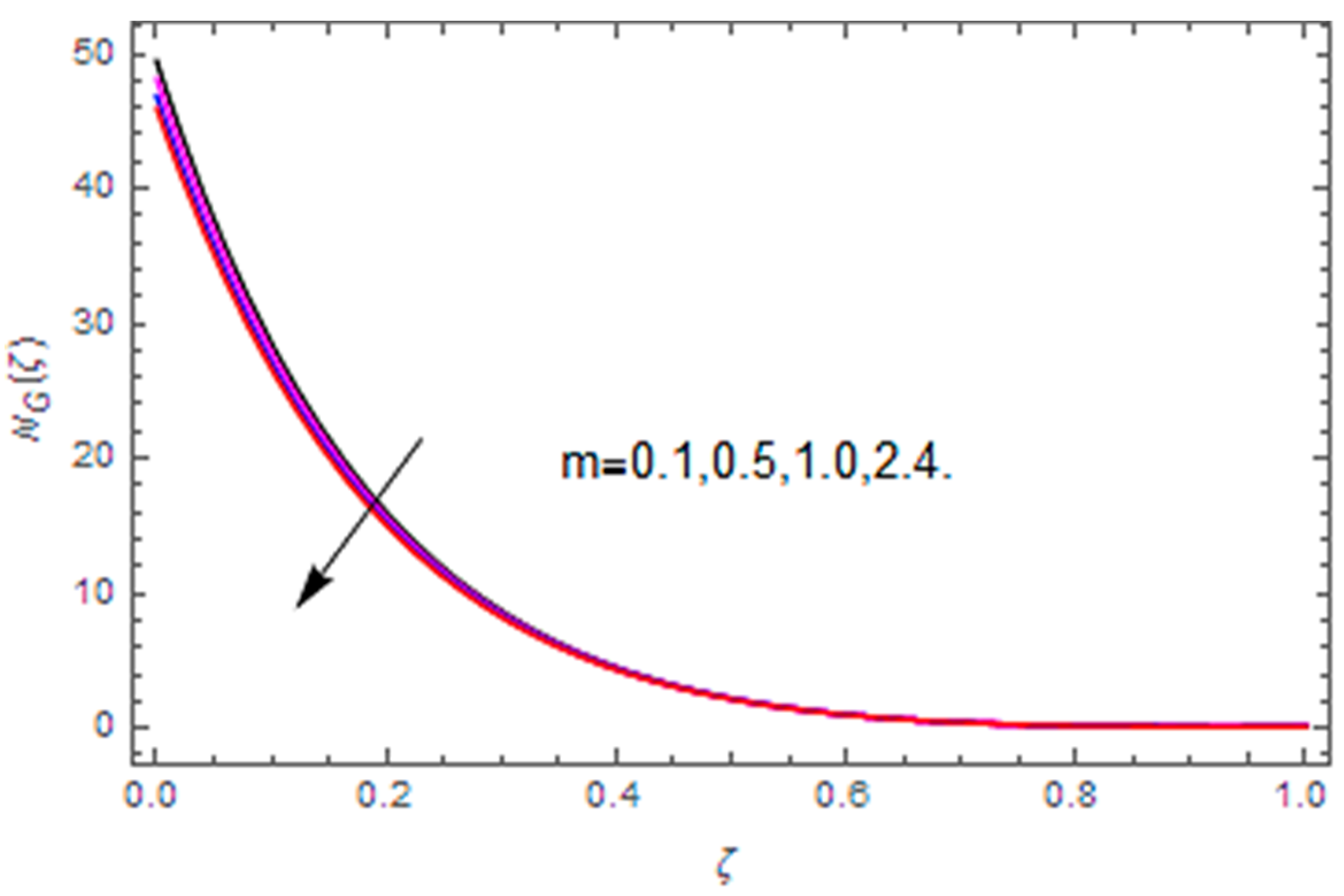
- The total entropy profile is enhanced with the Brinkman number, diffusion parameter, magnetic parameter, temperature difference and Weissenberg number, while a declining influence is detected via the Hall parameter.
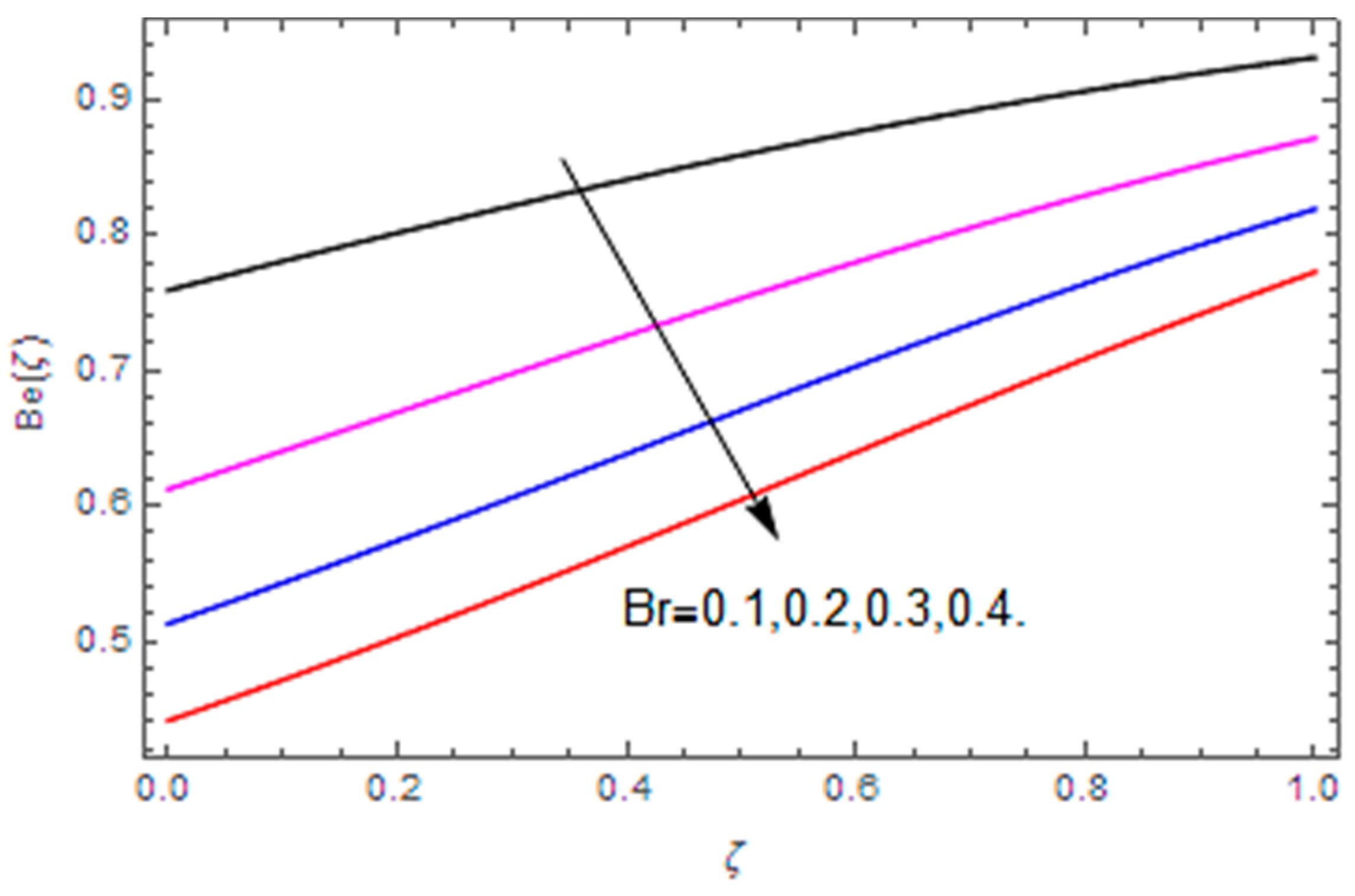
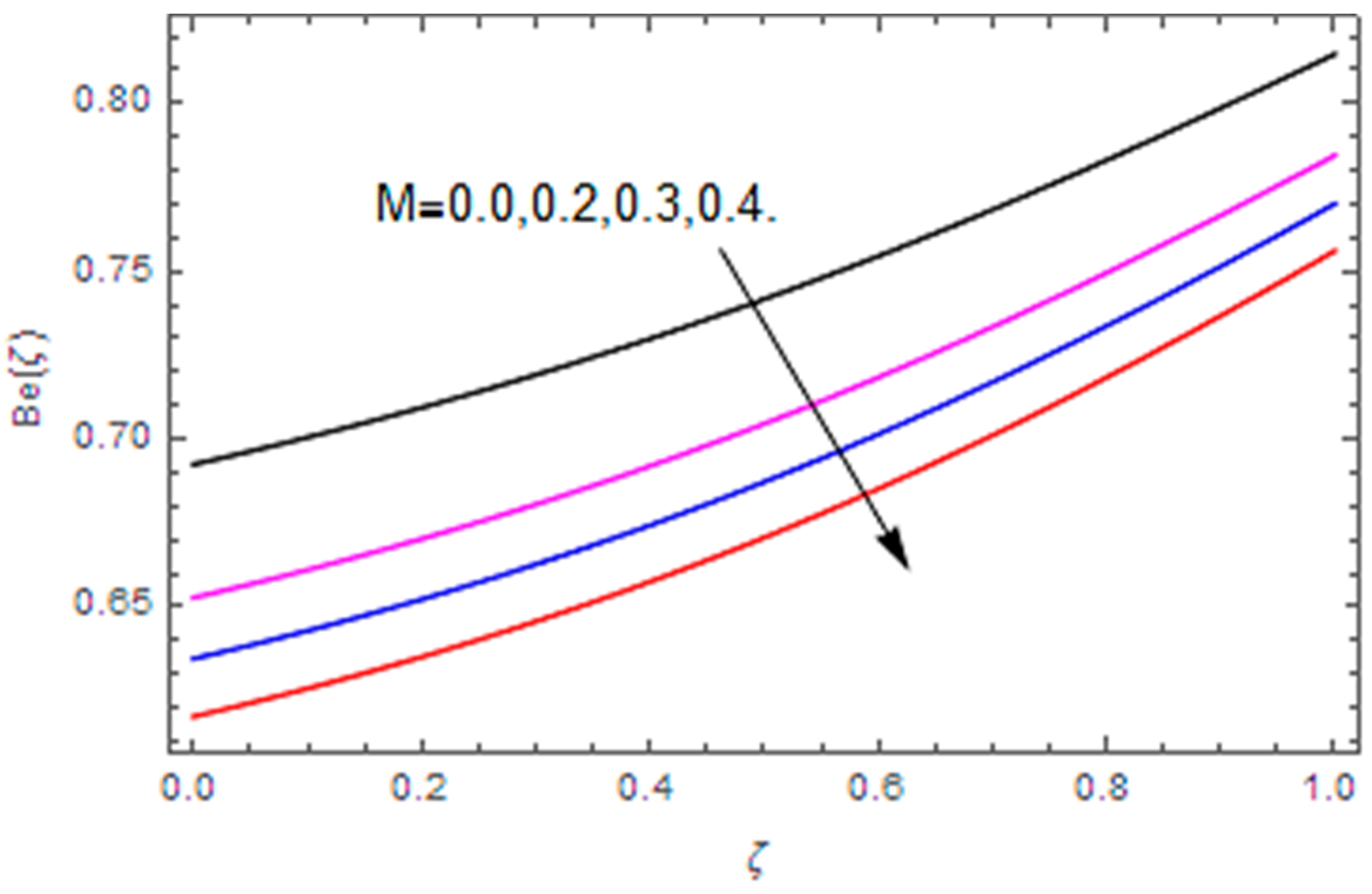
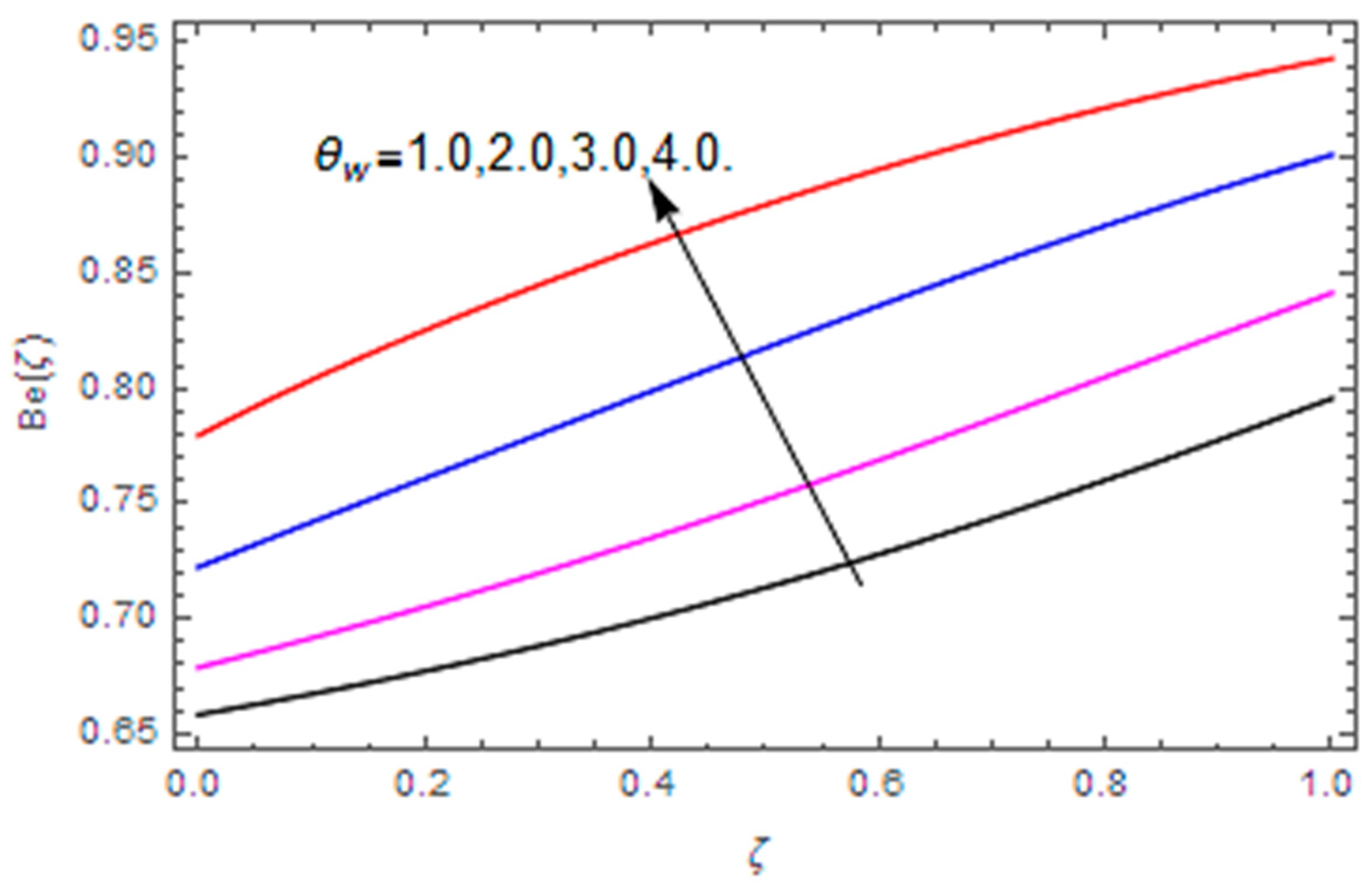
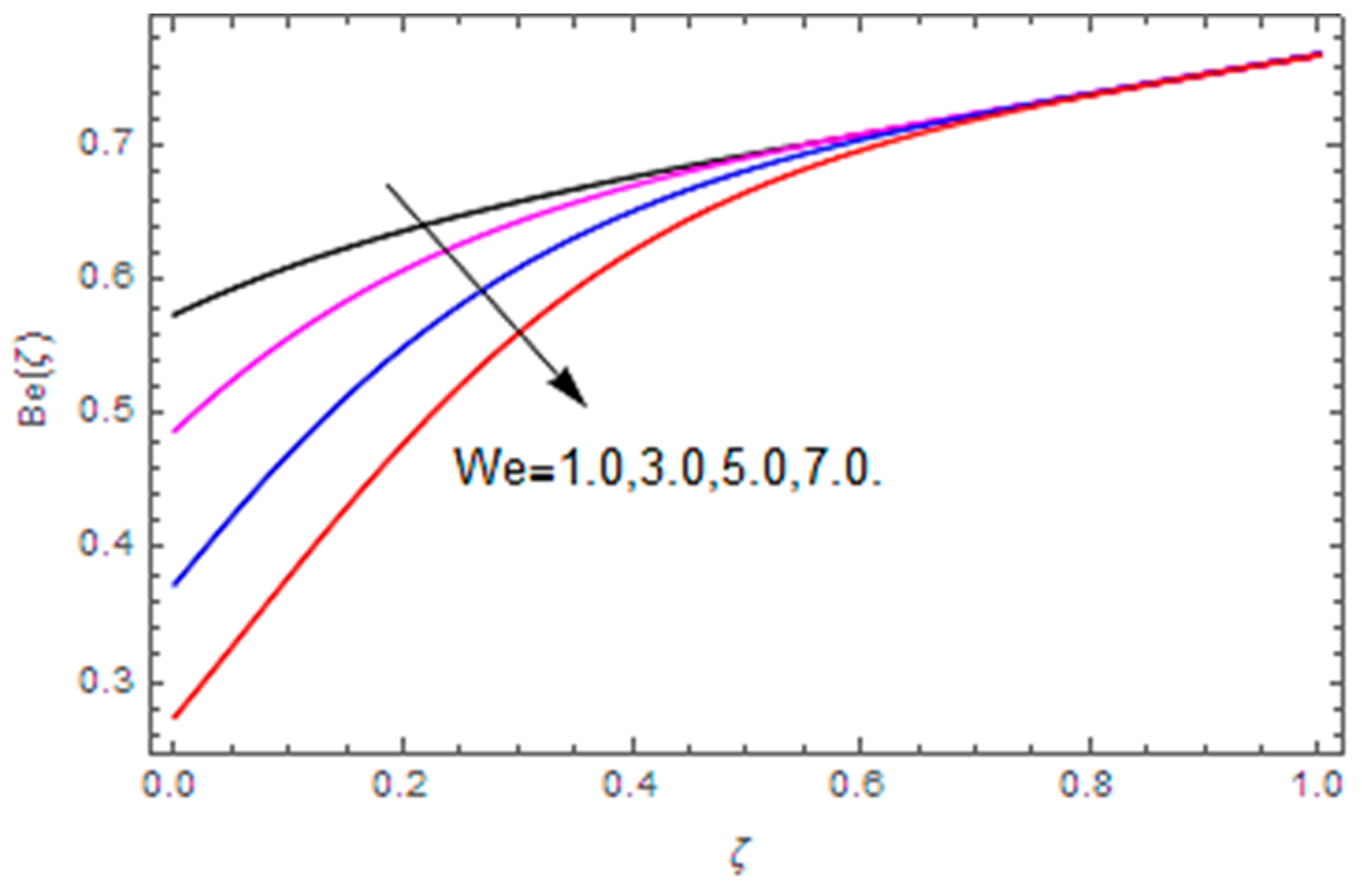
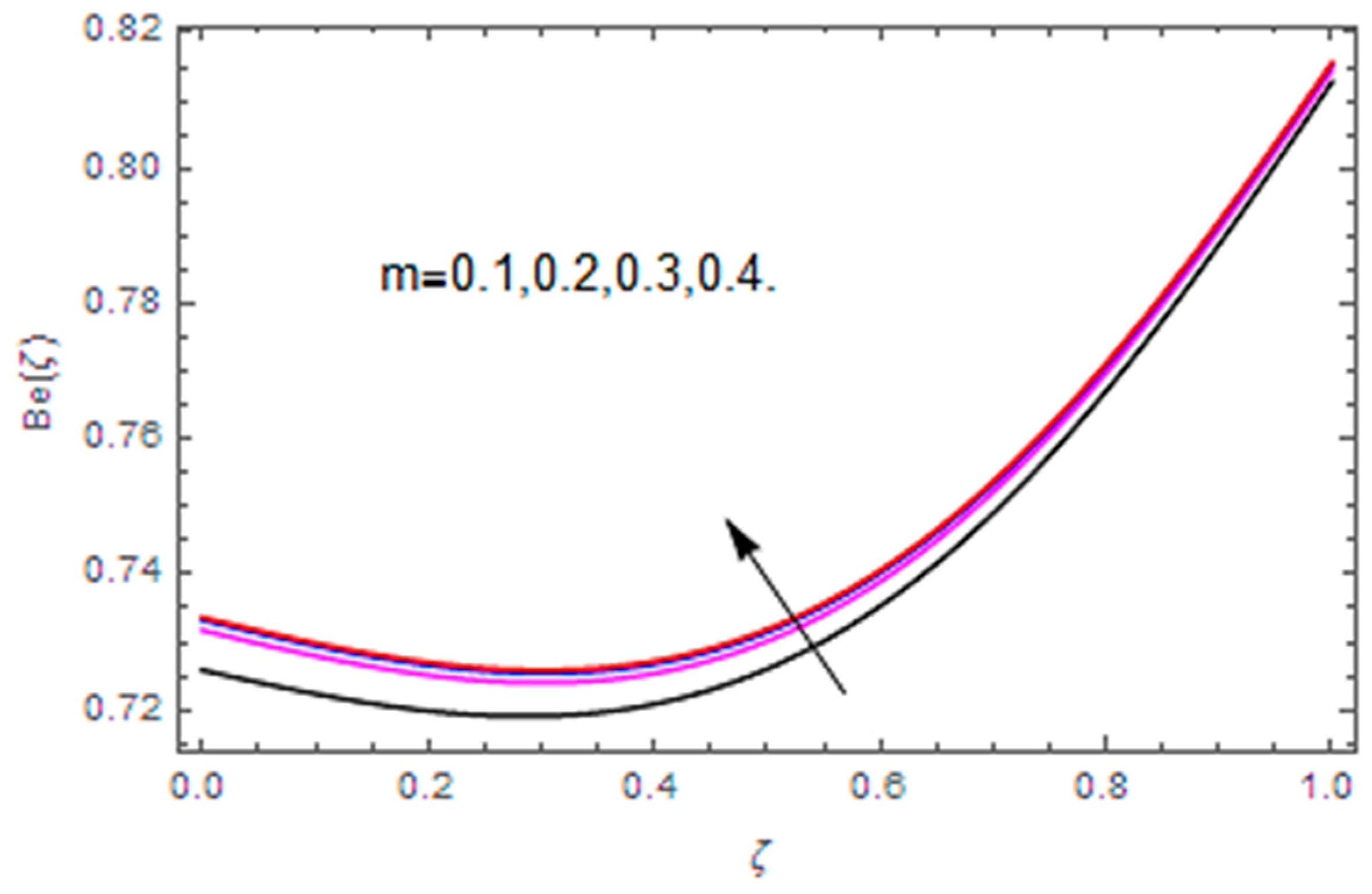
- The Bejan number profile is heightened with diffusion parameter, temperature difference and Hall parameter, while it is diminished with the Brinkman number, magnetic parameter and Weissenberg number.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; No. ANL/MSD/CP-84938; CONF-951135-29; Argonne National Lab.: Cass Ave, IL, USA, 1995. [Google Scholar]
- Farooq, M.; Khan, M.I.; Waqas, M.; Hayat, T.; Alsaedi, A.; Khan, M.I. MHD stagnation point flow of viscoelastic nanofluid with non-linear radiation effects. J. Molecul. Liq. 2016, 221, 1097–1103. [Google Scholar] [CrossRef]
- Sajid, M.; Iqbal, S.A.; Naveed, M.; Abbas, Z. Effect of homogeneous-heterogeneous reactions and magnetohydrodynamics on Fe3O4 nanofluid for the Blasius flow with thermal radiations. J. Molecul. Liq. 2017, 233, 115–121. [Google Scholar] [CrossRef]
- Sreedevi, P.; Reddy, P.S.; Chamkha, A.J. Heat and mass transfer analysis of nanofluid over linear and non-linear stretching surfaces with thermal radiation and chemical reaction. Powder Technol. 2017, 315, 194–204. [Google Scholar] [CrossRef]
- Qayyum, S.; Khan, M.I.; Hayat, T.; Alsaedi, A. A framework for nonlinear thermal radiation and homogeneous-heterogeneous reactions flow based on silver-water and copper-water nanoparticles: A numerical model for probable error. Results Phys. 2017, 7, 1907–1914. [Google Scholar] [CrossRef]
- Hayat, T.; Qayyum, S.; Imtiaz, M.; Alsaedi, A. Comparative study of silver and copper water nanofluids with mixed convection and nonlinear thermal radiation. Int. J. Heat Mass Transf. 2016, 102, 723–732. [Google Scholar] [CrossRef]
- Goodarzi, M.; Amiri, A.; Goodarzi, M.S.; Safaei, M.R.; Karimipour, A.; Languri, E.M.; Dahari, M. Investigation of heat transfer and pressure drop of a counter flow corrugated plate heat exchanger using MWCNT based nanofluids. Int. Commun. Heat Mass Transf. 2015, 66, 172–179. [Google Scholar] [CrossRef]
- Goshayeshi, H.R.; Goodarzi, M.; Safaei, M.R.; Dahari, M. Experimental study on the effect of inclination angle on heat transfer enhancement of a ferrofluid in a closed loop oscillating heat pipe under magnetic field. Exp. Therm. Fluid Sci. 2016, 74, 265–270. [Google Scholar] [CrossRef]
- Goshayeshi, H.R.; Safaei, M.R.; Goodarzi, M.; Dahari, M. Particle size and type effects on heat transfer enhancement of Ferro-nanofluids in a pulsating heat pipe. Powder Technol. 2016, 301, 1218–1226. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Safaei, M.R.; Goodarzi, M.; Alrashed, A.A.; Nguyen, T.K. New temperature, interfacial shell dependent dimensionless model for thermal conductivity of nanofluids. Int. J. Heat Mass Transf. 2017, 114, 207–210. [Google Scholar] [CrossRef]
- Peng, Y.; Zahedidastjerdi, A.; Abdollahi, A.; Amindoust, A.; Bahrami, M.; Karimipour, A.; Goodarzi, M. Investigation of energy performance in a U-shaped evacuated solar tube collector using oxide added nanoparticles through the emitter, absorber and transmittal environments via discrete ordinates radiation method. J. Therm. Anal. Calorim. 2020, 139, 2623–2631. [Google Scholar] [CrossRef]
- Shamshirband, S.; Malvandi, A.; Karimipour, A.; Goodarzi, M.; Afrand, M.; Petković, D.; Dahari, M.; Mahmoodian, N. Performance investigation of micro-and nano-sized particle erosion in a 90 elbow using an ANFIS model. Powder Technol. 2015, 284, 336–343. [Google Scholar] [CrossRef]
- Tian, Z.; Etedali, S.; Afrand, M.; Abdollahi, A.; Goodarzi, M. Experimental study of the effect of various surfactants on surface sediment and pool boiling heat transfer coefficient of silica/DI water nano-fluid. Powder Technol. 2019, 356, 391–402. [Google Scholar] [CrossRef]
- Zaidi, Z.A.; Mohyud-Din, S.T. Effect of joule heating and MHD in the presence of convective boundary condition for upper convected Maxwell fluid through wall jet. J. Mol. Liq. 2017, 230, 230–234. [Google Scholar] [CrossRef]
- Afify, A.A.; Elgazery, N.S. Effect of a chemical reaction on magnetohydrodynamic boundary layer flow of a Maxwell fluid over a stretching sheet with nanoparticles. Particuology 2016, 29, 154–161. [Google Scholar] [CrossRef]
- Mustafa, M. An analytical treatment for MHD mixed convection boundary layer flow of Oldroyd-B fluid utilizing non-Fourier heat flux model. Int. J. Heat Mass Transf. 2017, 113, 1012–1020. [Google Scholar] [CrossRef]
- Hayat, T.; Nawaz, S.; Alsaedi, A.; Rafiq, M. Influence of radial magnetic field on the peristaltic flow of Williamson fluid in a curved complaint walls channel. Results phys. 2017, 7, 982–990. [Google Scholar] [CrossRef]
- Khan, M.; Hamid, A. Influence of non-linear thermal radiation on 2D unsteady flow of a Williamson fluid with heat source/sink. Results phys. 2017, 7, 3968–3975. [Google Scholar] [CrossRef]
- Baron Fourier, J.B.J. Théorie Analytique de la Chaleur. In Landmark Writings in Western Mathematics 1640–1940; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Cattaneo, C. Sulla conduzione del calore. Atti Sem. Mat. Fis. Univ. Modena 1948, 3, 83–101. [Google Scholar]
- Christov, C.I. On frame indifferent formulation of the Maxwell–Cattaneo model of finite-speed heat conduction. Mech. Res. Commun. 2009, 36, 481–486. [Google Scholar] [CrossRef]
- Hayat, T.; Qayyum, S.; Imtiaz, M.; Alsaedi, A. Impact of Cattaneo-Christov heat flux in Jeffrey fluid flow with homogeneous-heterogeneous reactions. PLoS ONE 2016, 11, e0148662. [Google Scholar] [CrossRef]
- Mustafa, M. Cattaneo-Christov heat flux model for rotating flow and heat transfer of upper-convected Maxwell fluid. AIP Adv. 2015, 5, 047109. [Google Scholar] [CrossRef]
- Tibullo, V.; Zampoli, V. A uniqueness result for the Cattaneo-Christov heat conduction model applied to incompressible fluids. Mech. Res. Commun. 2011, 38, 77–99. [Google Scholar] [CrossRef]
- Han, S.; Zheng, L.; Li, C.; Zhang, X. Coupled flow and heat transfer in viscoelastic fluid with Cattaneo-Christov heat flux model. Appl. Math. Lett. 2014, 38, 87–93. [Google Scholar] [CrossRef]
- Ahmad Khan, J.; Mustafa, M.; Hayat, T.; Alsaedi, A. Numerical study of Cattaneo-Christov heat flux model for viscoelastic flow due to an exponentially stretching surface. PLoS ONE 2015, 10, e0137363. [Google Scholar] [CrossRef]
- Raptis, A.; Ram, P.C. Effects of hall current and rotation. Astrophys. Space Sci. 1984, 106, 257–264. [Google Scholar] [CrossRef]
- Das, S.; Maji, S.L.; Jana, R.N. Hall effects on unsteady hydromagnetic flow induced by a porous plate. Int. J. Comput. Appli. 2012, 57, 37–44. [Google Scholar]
- Jha, B.K.; Apere, C.A. Combined effect of hall and ion-slip currents on unsteady MHD couette flows in a rotating system. J. Phys. Soc. Jpn. 2010, 79, 1–9. [Google Scholar]
- Aurangzeeb, S.; Shafie, S. Effects of Soret and Dufour on unsteady MHD flow by mixed convection over a vertical surface in porous media with internal heat generation, chemical reaction and Hall current. Can. J. Sci. Eng. Math. 2011, 2, 153–162. [Google Scholar]
- Ferdows, M.; Jahan, E.; Hamad, M.M.; Masahiro, O.T.A. Effects of Hall and ion-slip currents on free convective heat transfer flow past a vertical plate considering slip conditions. Can. J. Sci. Eng. Math. 2011, 2, 70–76. [Google Scholar]
- Anwar Bég, O.; Sim, L.; Zueco, J.; Bhargava, R. Numerical study of magnetohydro-dynamic viscous plasma flow in rotating porous media with Hall currents and inclined magnetic field influence. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 345–359. [Google Scholar]
- Kumar, R.; Chand, K. Effect of slip conditions and hall current on unsteady MHD flow of a viscoelastic fluid past an infinite vertical porous plate through porous medium. Int. J. Eng. Sci. Technol. 2011, 3, 3124–3133. [Google Scholar]
- Li, X.; Faghri, A. Local entropy generation analysis on passive high concentration DMFCs (direct methanol fuel cell) with different cell structures. Energy 2011, 36, 403–414. [Google Scholar] [CrossRef]
- Hayat, T.; Rafiq, M.; Ahmad, B.; Asghar, S. Entropy generation analysis for peristaltic flow of nanoparticles in a rotating frame. Int. J. Heat Mass Transf. 2017, 108, 1775–1786. [Google Scholar] [CrossRef]
- Nouri, D.; Pasandideh-Fard, M.; Oboodi, M.J.; Mahian, O.; Sahin, A.Z. Entropy generation analysis of nanofluid flow over a spherical heat source inside a channel with sudden expansion and contraction. Int. J. Heat Mass Transf. 2018, 116, 1036–1043. [Google Scholar] [CrossRef]
- Dalir, N.; Dehsara, M.; Nourazar, S.S. Entropy analysis for magnetohydrodynamic flow and heat transfer of a Jeffrey nanofluid over a stretching sheet. Energy 2015, 79, 351–362. [Google Scholar] [CrossRef]
- Khan, M.I.; Qayyum, S.; Hayat, T.; Waqas, M.; Khan, M.I.; Alsaedi, A. Entropy generation minimization and binary chemical reaction with Arrhenius activation energy in MHD radiative flow of nanomaterial. J. Mol. Liq. 2018, 259, 274–283. [Google Scholar] [CrossRef]
- Khan, M.I.; Hayat, T.; Waqas, M.; Khan, M.I.; Alsaedi, A. Entropy generation minimization (EGM) in nonlinear mixed convective flow of nanomaterial with Joule heating and slip condition. J. Mol. Liq. 2018, 256, 108–120. [Google Scholar] [CrossRef]
- Hayat, T.; Kanwal, M.; Qayyum, S.; Khan, M.I.; Alsaedi, A. Entropy generation optimisation in the nanofluid flow of a second grade fluid with nonlinear thermal radiation. Pramana 2019, 93, 54. [Google Scholar] [CrossRef]

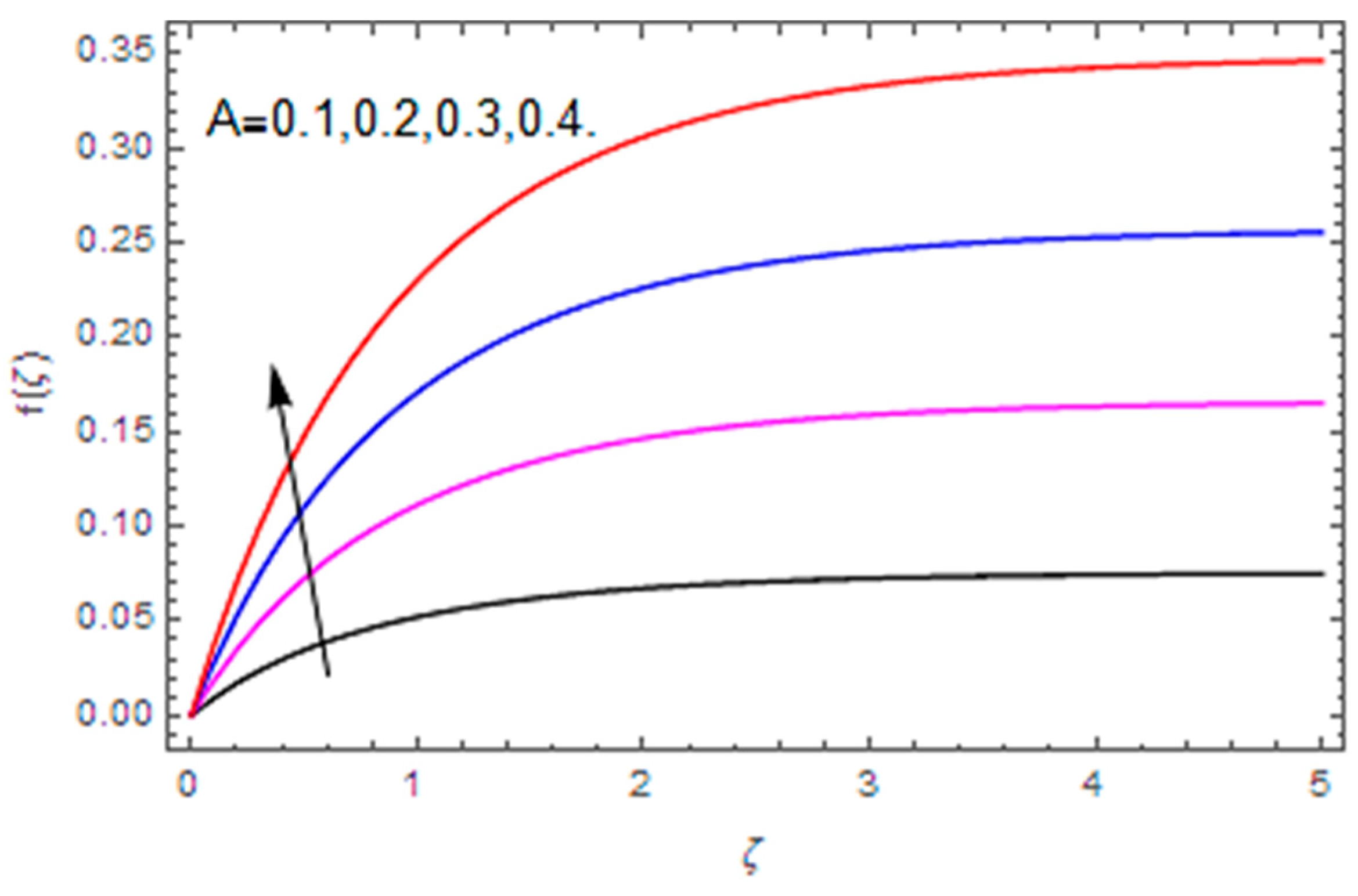
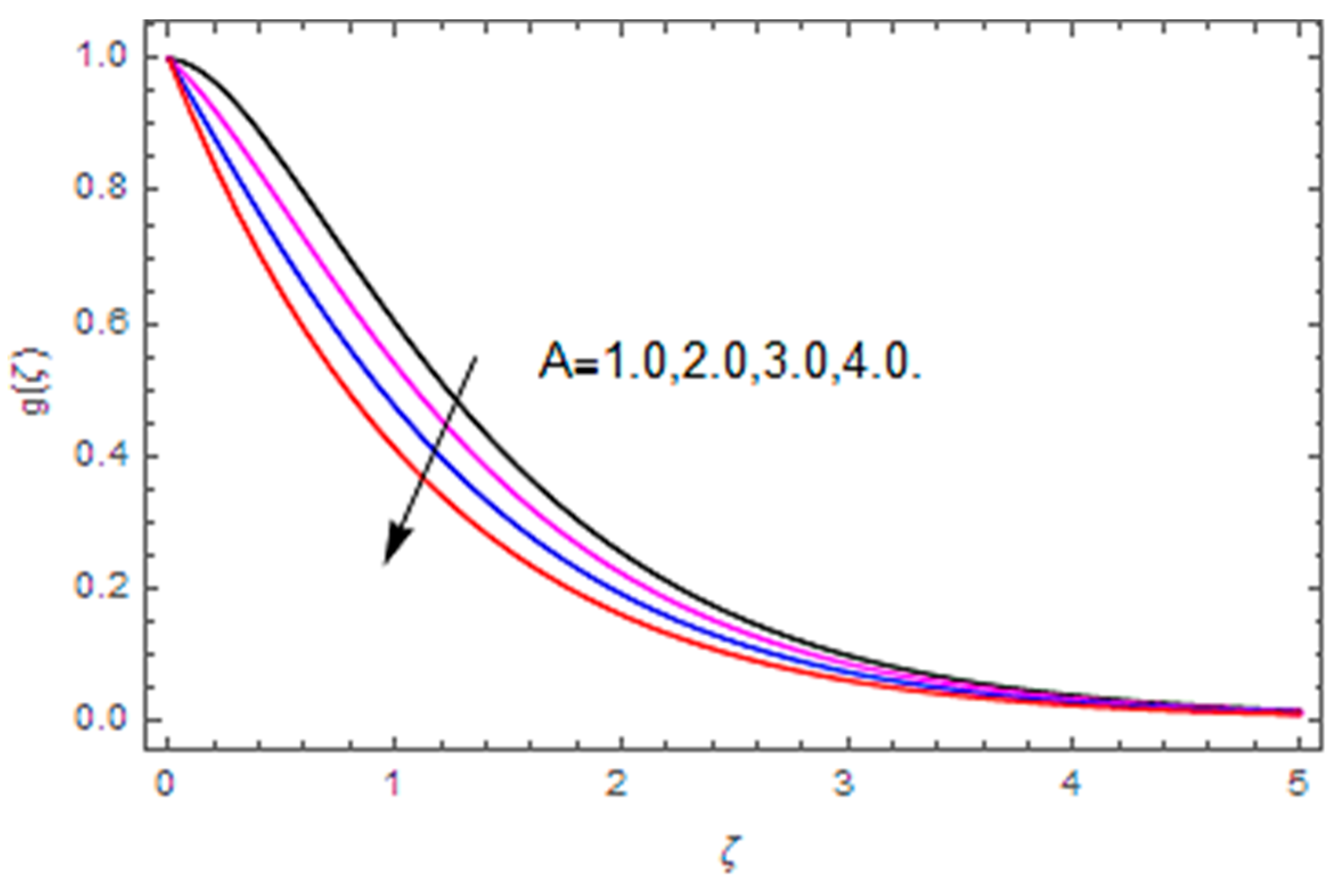
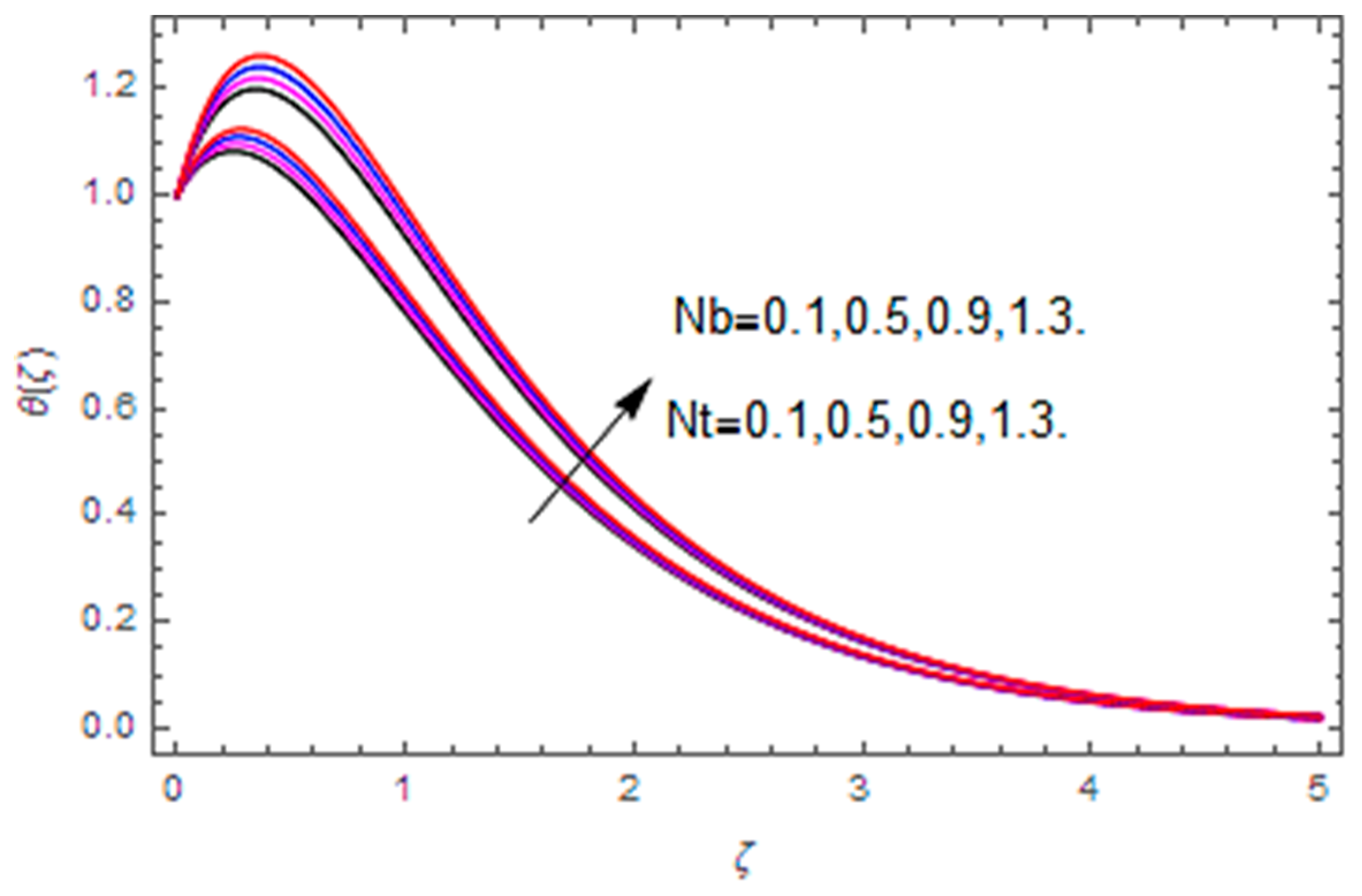
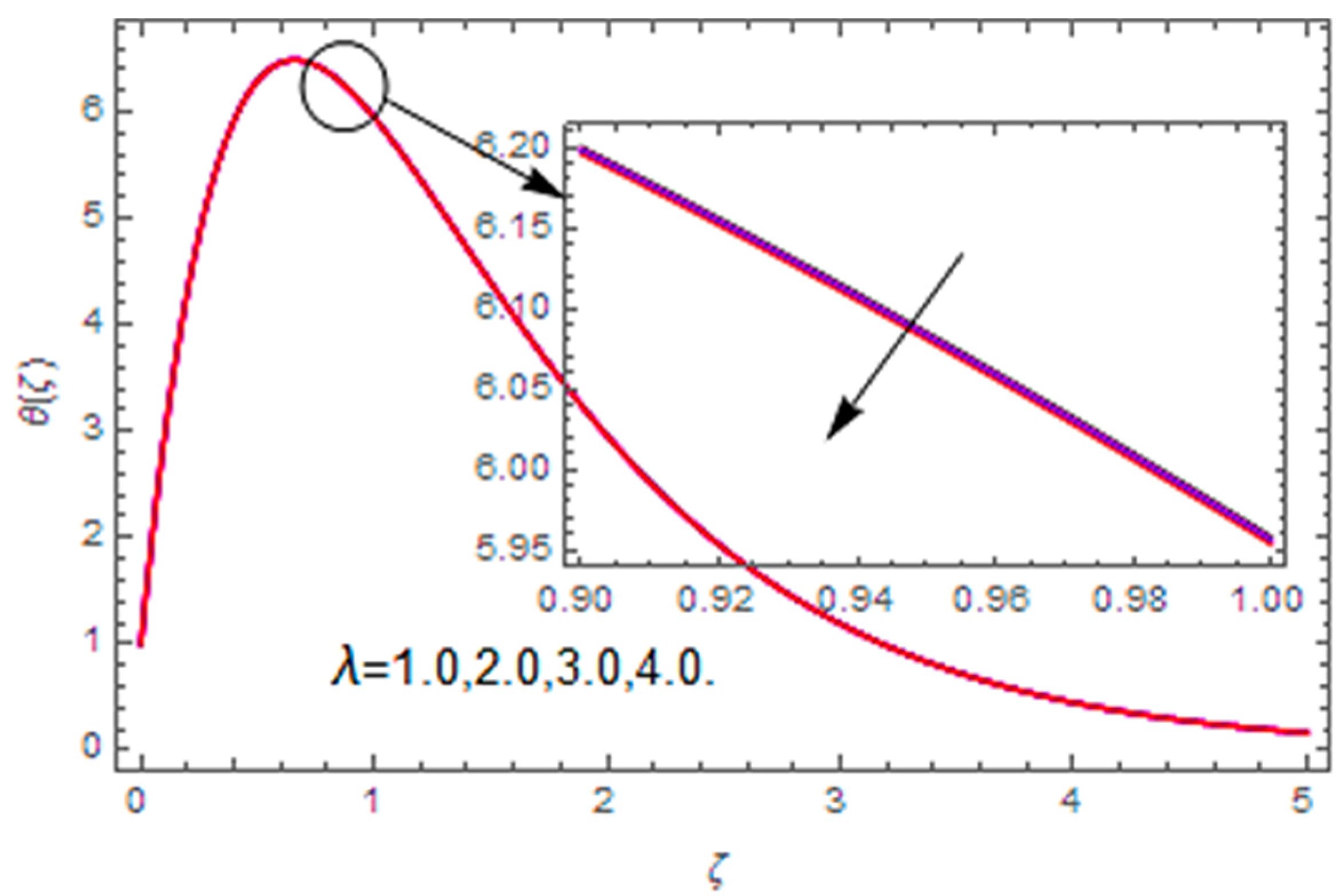


| We | Re | M | m | A | RerCfr | ReθCfθ |
|---|---|---|---|---|---|---|
| 0.2 | 0.5 | 0.3 | 0.2 | 0.1 | 0.076871 | −0.578141 |
| 0.3 | – | – | – | – | 0.109318 | −0.601784 |
| 0.4 | – | – | – | – | 0.126191 | −0.613634 |
| – | 0.0 | – | – | – | −0.073910 | −0.529679 |
| – | 1.0 | – | – | – | 0.349447 | −0.703740 |
| – | 1.5 | – | – | – | 0.595858 | −0.800002 |
| – | – | 0.0 | – | – | 0.608339 | −0.928553 |
| – | – | 0.2 | – | – | 0.600019 | −0.842866 |
| – | – | 0.5 | – | – | 0.587538 | −0.714335 |
| – | – | – | 0.3 | – | 0.588645 | −0.726248 |
| – | – | – | 0.5 | – | 0.539113 | −0.755780 |
| – | – | – | 0.7 | – | 0.521225 | −0.786661 |
| – | – | – | – | 0.2 | 0.536944 | −1.122600 |
| – | – | – | – | 0.4 | 0.531917 | −1.973220 |
| – | – | – | – | 0.5 | 0.514140 | −2.487880 |
| Re | Pr | q | Nb | Nt | λ | Ec | θw | Nux |
|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.72 | 0.3 | 0.4 | 0.4 | 0.1 | 0.2 | 0.3 | 0.436148 |
| 1.0 | – | – | – | – | – | – | – | 0.425559 |
| 1.5 | – | – | – | – | – | – | – | 0.420265 |
| – | 0.4 | – | – | – | – | – | – | 0.502356 |
| – | 0.8 | – | – | – | – | – | – | 0.399743 |
| – | 1.2 | – | – | – | – | – | – | 0.297129 |
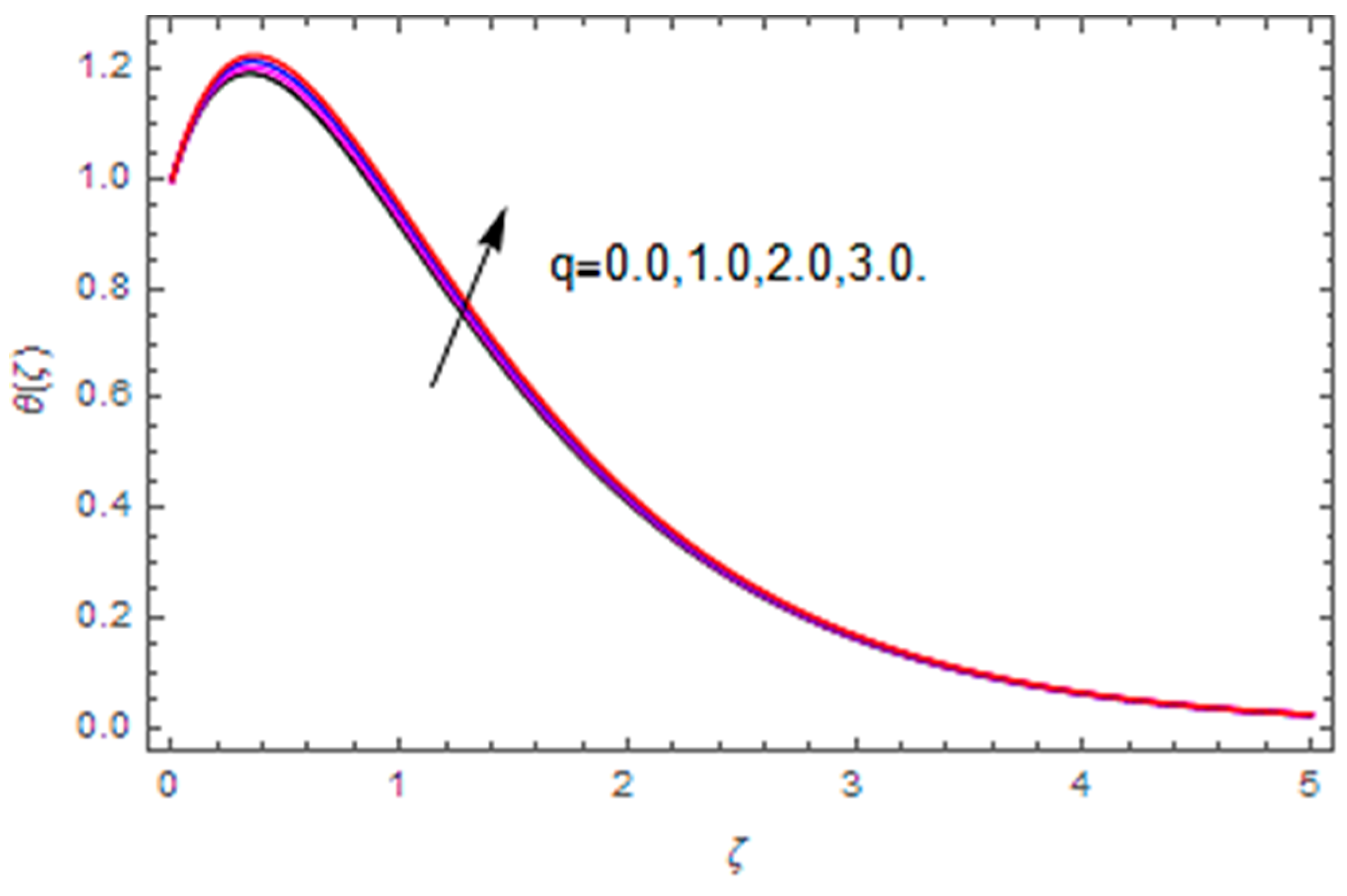
| – | – | 0.4 | – | – | – | – | – | 0.230951 |
| – | – | 0.5 | – | – | – | – | – | 0.164773 |
| – | – | 0.6 | – | – | – | – | – | 0.098594 |
| – | – | – | 0.5 | – | – | – | – | 0.065505 |
| – | – | – | 0.6 | – | – | – | – | 0.032416 |
| – | – | – | 0.7 | – | – | – | – | −0.000672 |
| – | – | – | – | 0.5 | – | – | – | −0.033761 |
| – | – | – | – | 0.6 | – | – | – | −0.066850 |
| – | – | – | – | 0.7 | – | – | – | −0.099939 |
| – | – | – | – | – | 0.3 | – | – | 0.111830 |
| – | – | – | – | –– | 0.5 | – | – | 0.125066 |
| – | – | – | – | – | 0.7 | – | – | 0.138302 |
| – | – | – | – | – | – | 0.3 | – | 0.129974 |
| – | – | – | – | – | – | 0.4 | – | 0.121646 |
| – | – | – | – | – | – | 0.5 | – | 0.113318 |
| – | – | – | – | – | – | – | 1.0 | 0.116974 |
| – | – | – | – | – | – | – | 1.5 | 0.041694 |
| – | – | – | – | – | – | – | 2.0 | −0.296988 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wakeel Ahmad, M.; McCash, L.B.; Shah, Z.; Nawaz, R. Cattaneo-Christov Heat Flux Model for Second Grade Nanofluid Flow with Hall Effect through Entropy Generation over Stretchable Rotating Disk. Coatings 2020, 10, 610. https://doi.org/10.3390/coatings10070610
Wakeel Ahmad M, McCash LB, Shah Z, Nawaz R. Cattaneo-Christov Heat Flux Model for Second Grade Nanofluid Flow with Hall Effect through Entropy Generation over Stretchable Rotating Disk. Coatings. 2020; 10(7):610. https://doi.org/10.3390/coatings10070610
Chicago/Turabian StyleWakeel Ahmad, Muhammad, Luthais B. McCash, Zahir Shah, and Rashid Nawaz. 2020. "Cattaneo-Christov Heat Flux Model for Second Grade Nanofluid Flow with Hall Effect through Entropy Generation over Stretchable Rotating Disk" Coatings 10, no. 7: 610. https://doi.org/10.3390/coatings10070610
APA StyleWakeel Ahmad, M., McCash, L. B., Shah, Z., & Nawaz, R. (2020). Cattaneo-Christov Heat Flux Model for Second Grade Nanofluid Flow with Hall Effect through Entropy Generation over Stretchable Rotating Disk. Coatings, 10(7), 610. https://doi.org/10.3390/coatings10070610






