Fluid Morphologies Governed by the Competition of Viscous Dissipation and Phase Separation in a Radial Hele-Shaw Flow
Abstract
:1. Introduction
2. Experiment
2.1. Solutions
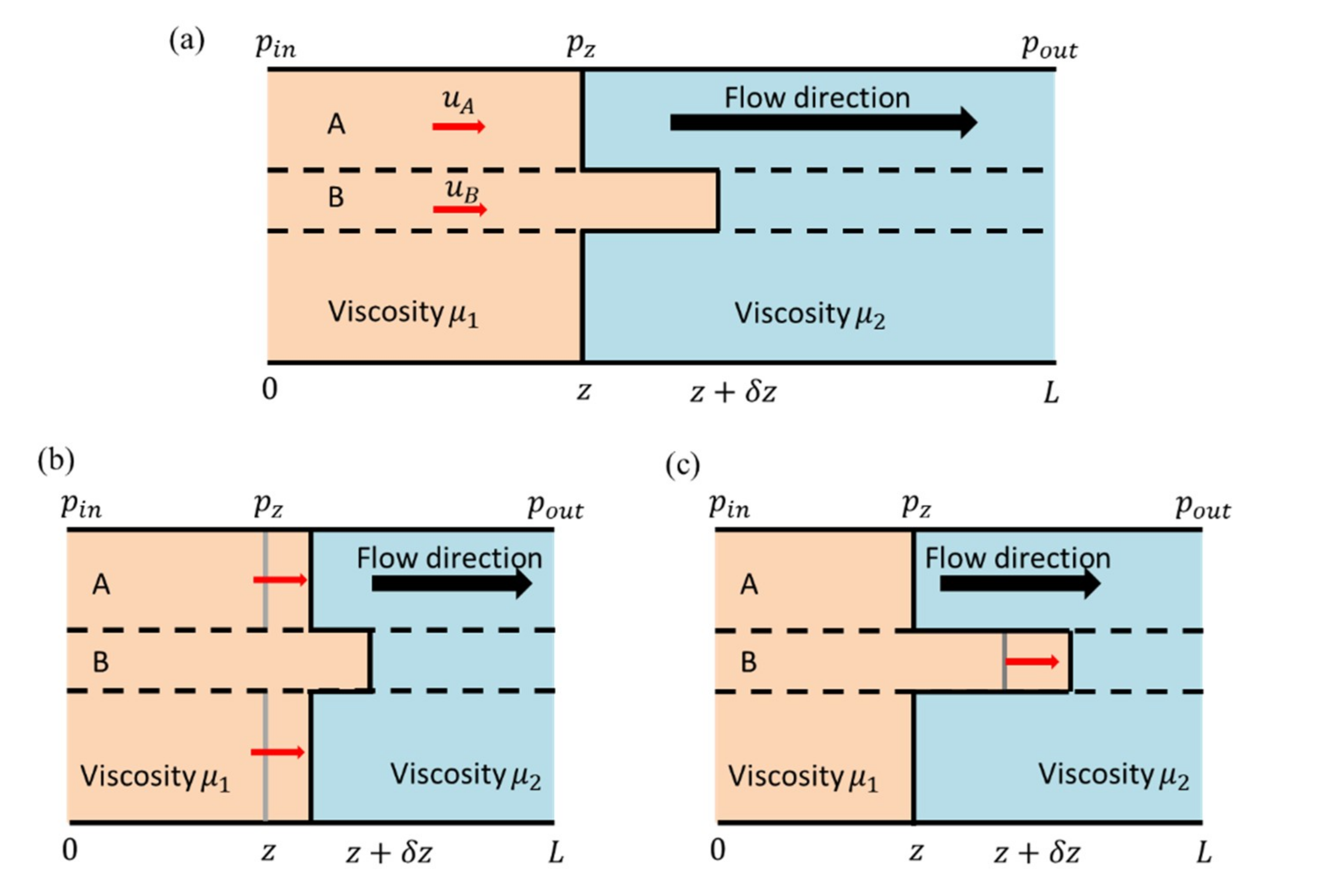
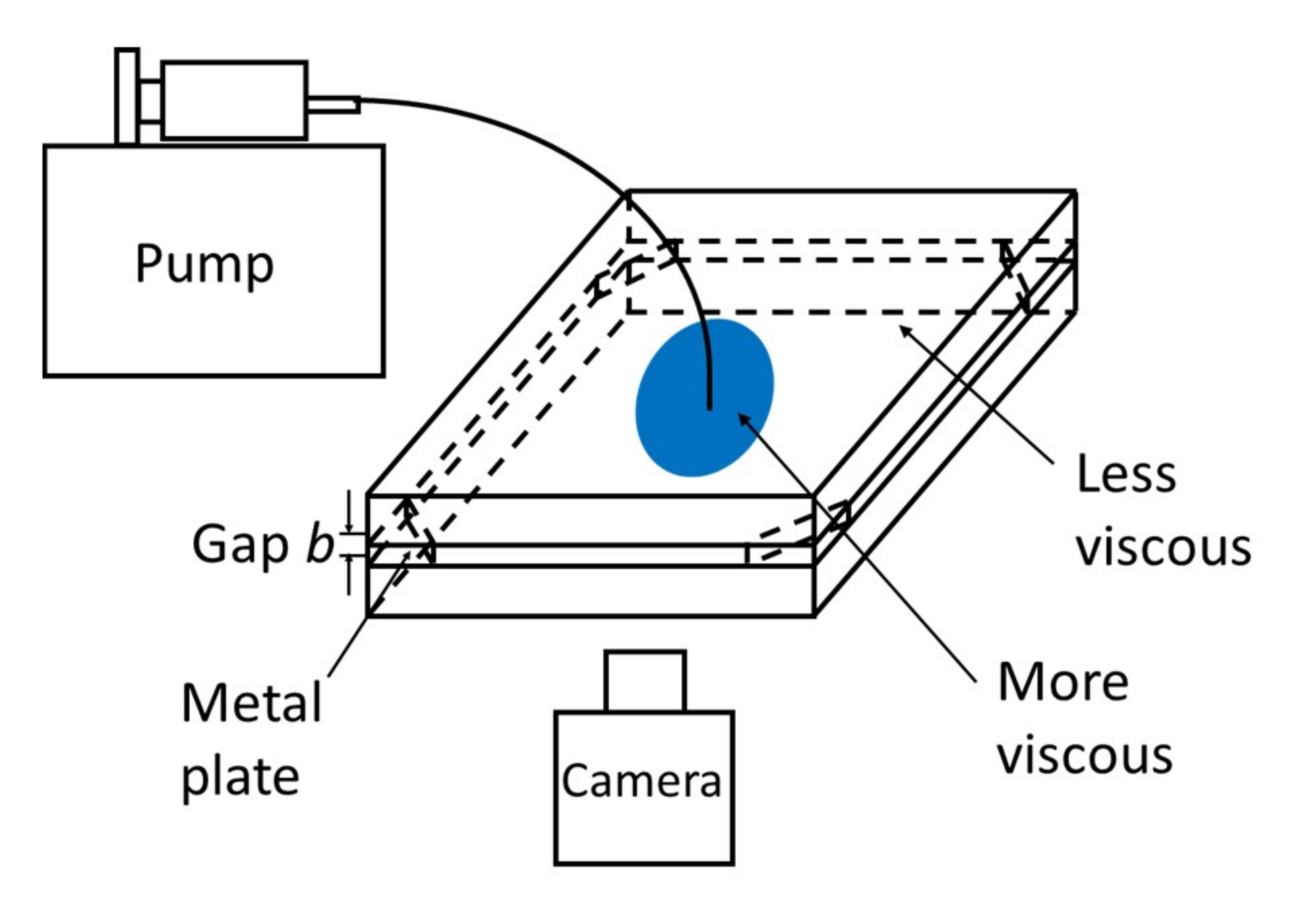
2.2. Displacement Experiment
2.3. Physical Property Measurements
3. Results and Discussion
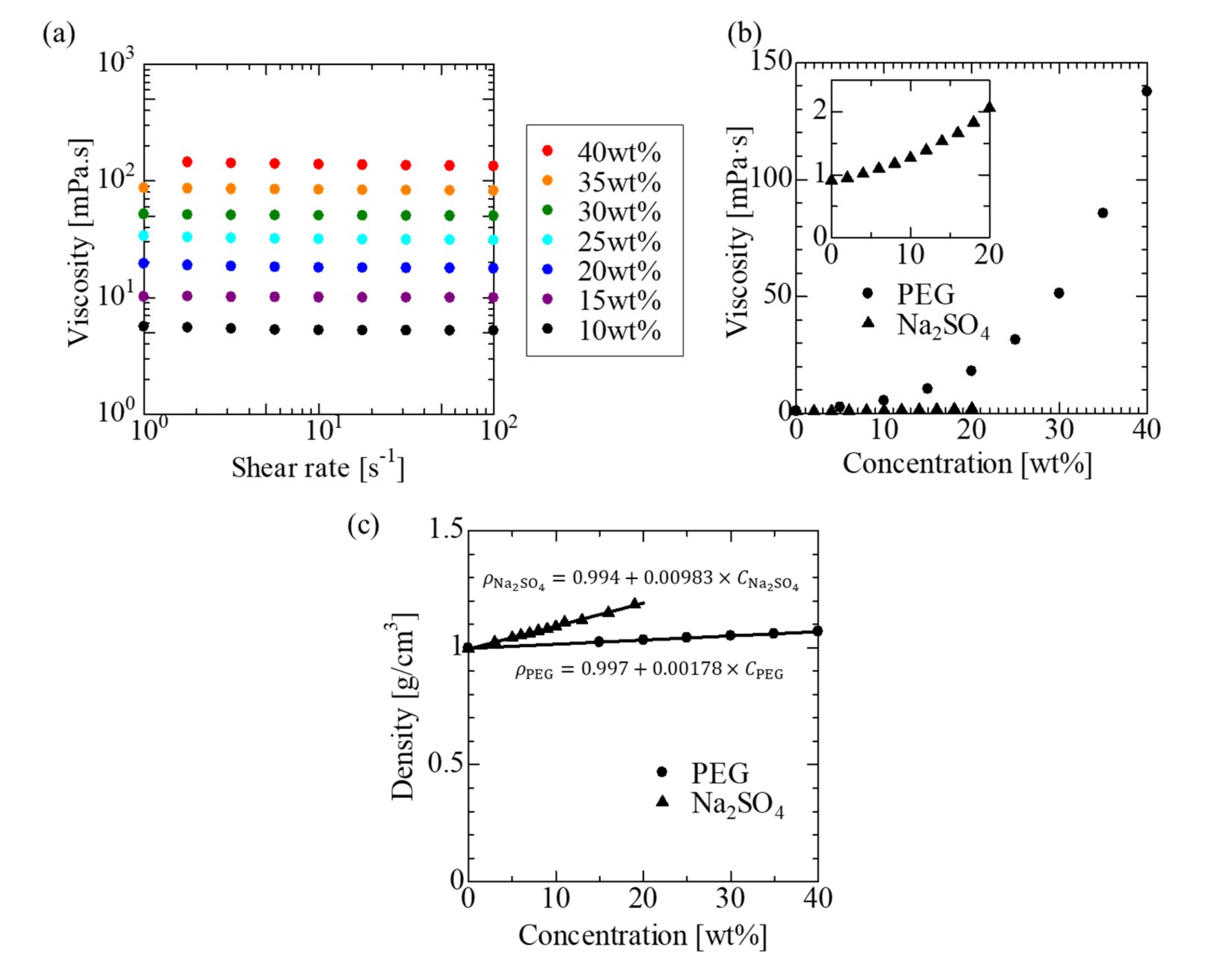
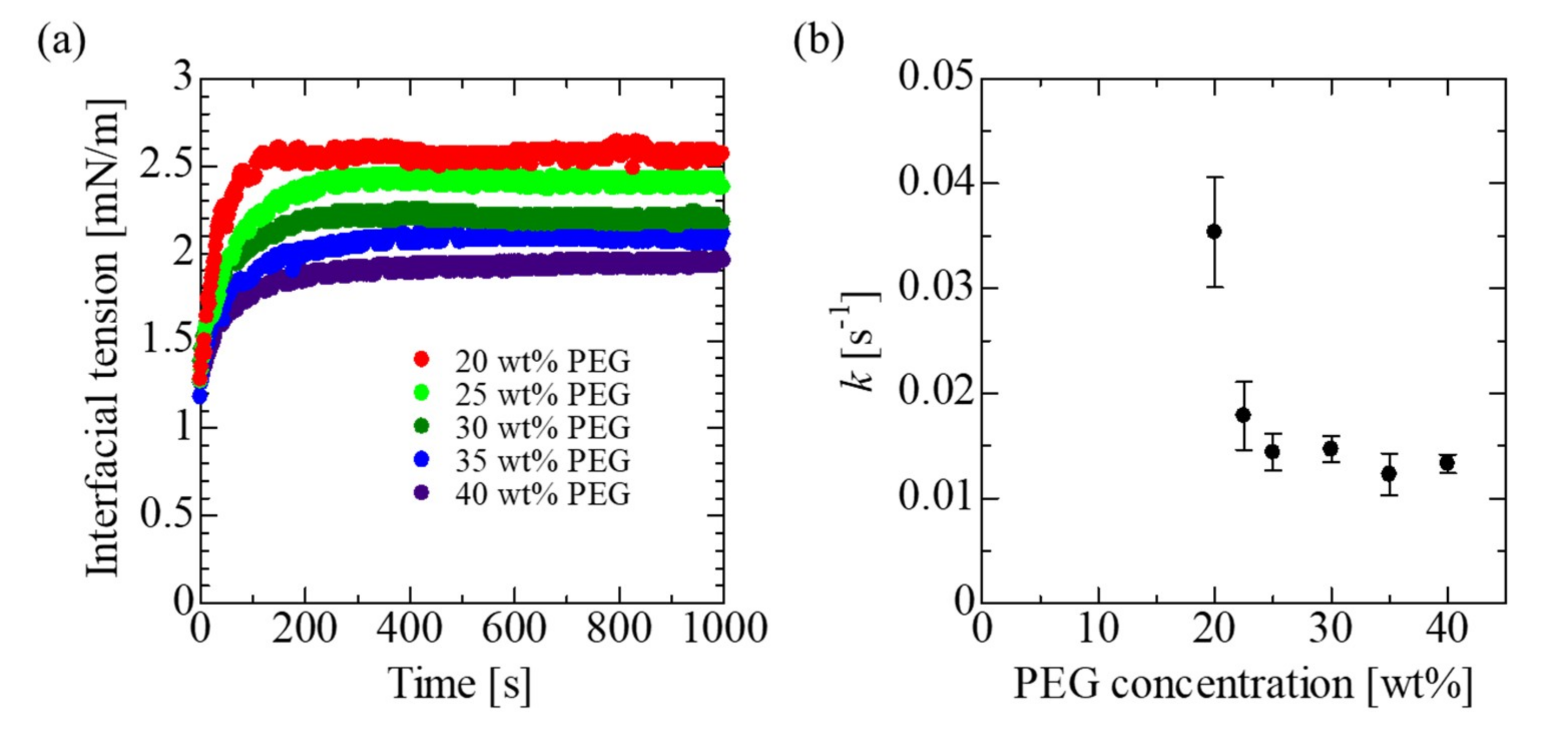
3.1. Physical Properties
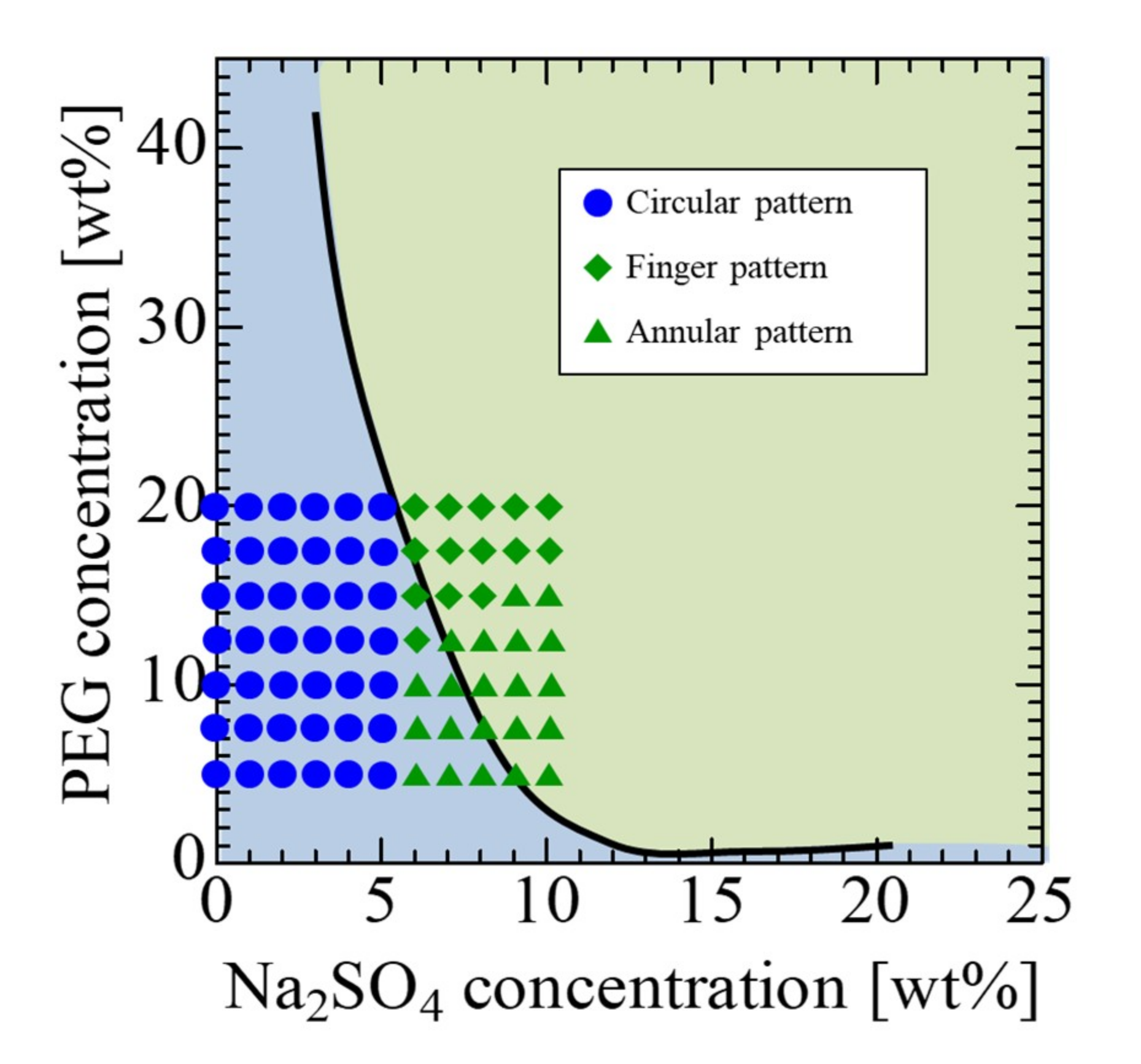
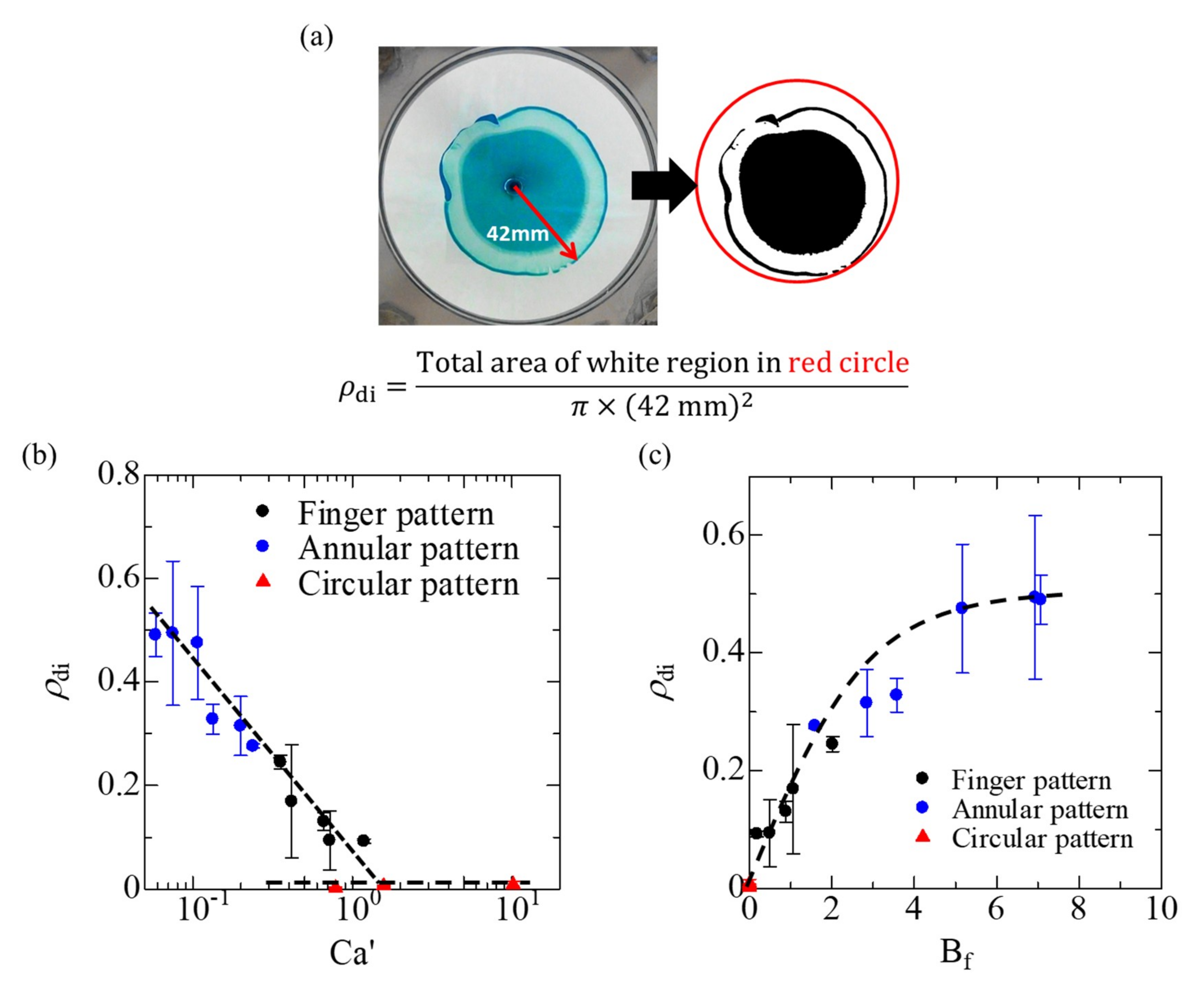
3.2. Fluid Displacements
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Broyles, B.S.; Shalliker, R.A.; Cherrak, D.E.; Guiochon, G. Visualization of viscous fingering in chromatographic columns. J. Chromatogr. A 1998, 822, 173–187. [Google Scholar] [CrossRef]
- Bhaskar, K.R.; Garik, P.; Turner, B.S.; Bradley, J.D.; Bansil, R.; Stanley, H.E.; LaMont, J.T. Viscous fingering of HCl through gastric mucin. Nature 1992, 360, 458–461. [Google Scholar] [CrossRef] [PubMed]
- Nordbotten, J.M.; Celia, M.A.; Bachu, S. Injection and storage of CO2 in deep saline aquifers: Analytical solution for CO2 plume evolution during injection. Transp. Porous Media 2005, 58, 339–360. [Google Scholar] [CrossRef]
- Pojman, J.A.; Gunn, G.; Patterson, C.; Owens, J.; Simmons, C. Frontal dispersion polymerization. J. Phys. Chem. B 1998, 102, 3927–3929. [Google Scholar] [CrossRef]
- Lake, L.W.; Johns, R.T.; Rossen, W.R.; Pope, G.A. Fundamentals of Enhanced Oil Recovery; Society of Petroleum Engineers: Richardson, TX, USA, 2014; ISBN 978-1-61399-328-6. [Google Scholar]
- Saffman, P.G.; Taylor, G. The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. A 1958, 245, 312–329. [Google Scholar] [CrossRef]
- Homsy, G.M. Viscous fingering in porous media. Annu. Rev. Fluid Mech. 1987, 19, 271–311. [Google Scholar] [CrossRef]
- Darcy, H.P.G. Les Fontaines Publiques de la Ville de Dijon; Victor Dalmont: Paris, France, 1856. [Google Scholar]
- Wyckoff, R.D.; Botset, H.G.; Muskat, M.; Reed, D.W. The measurement of the permeability of porous media for homogeneous fluids. Rev. Sci. Instrum. 1933, 4, 394–405. [Google Scholar] [CrossRef]
- Suzuki, R.X.; Nagatsu, Y.; Mishra, M.; Ban, T. Fingering pattern induced by spinodal decomposition in hydrodynamically stable displacement in a partially miscible system. Phys. Rev. Fluids 2019, 4, 104005. [Google Scholar] [CrossRef]
- McCloud, K.V.; Maher, J.V. Experimental perturbations to Saffman-Taylor flow. Phys. Rep. 1995, 260, 139–185. [Google Scholar] [CrossRef]
- Nagatsu, Y. Viscous fingering phenomena with chemical reactions. Curr. Phys. Chem. 2015, 5, 52–63. [Google Scholar] [CrossRef]
- De Wit, A. Chemo-hydrodynamic patterns in porous media. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150419. [Google Scholar] [CrossRef] [PubMed]
- De Wit, A. Chemo-hydrodynamic patterns and instabilities. Annu. Rev. Fluid Mech. 2020, 52, 531–555. [Google Scholar] [CrossRef] [Green Version]
- Chan, C.K.; Liang, N.Y. Observations of surfactant driven instability in a Hele-Shaw cell. Phys. Rev. Lett. 1997, 79, 4381–4384. [Google Scholar] [CrossRef]
- Krechetnikov, R.; Homsy, G.M. On a new surfactant-driven fingering phenomenon in a Hele-Shaw cell. J. Fluid Mech. 2004, 509, 103–124. [Google Scholar] [CrossRef] [Green Version]
- Fernandez, J.; Krechetnikov, R.; Homsy, G.M. Experimental study of a surfactant-driven fingering phenomenon in a Hele-Shaw cell. J. Fluid Mech. 2005, 527, 197–216. [Google Scholar] [CrossRef] [Green Version]
- Tang, H.; Grivas, W.; Homentcovschi, D.; Geer, J.; Singler, T. Stability considerations associated with the meniscoid particle band at advancing interfaces in Hele-Shaw suspension flows. Phys. Rev. Lett. 2000, 85, 2112–2115. [Google Scholar] [CrossRef]
- Bihi, I.; Baudoin, M.; Butler, J.E.; Faille, C.; Zoueshtiagh, F. Inverse Saffman-Taylor experiments with particles lead to capillarity driven fingering instabilities. Phys. Rev. Lett. 2016, 117, 034501. [Google Scholar] [CrossRef] [Green Version]
- Xu, F.; Kim, J.; Lee, S. Particle-induced viscous fingering. J. Nonnewton. Fluid Mech. 2016, 238, 92–99. [Google Scholar] [CrossRef]
- Kim, J.; Xu, F.; Lee, S. Formation and destabilization of the particle band on the fluid-fluid interface. Phys. Rev. Lett. 2017, 118, 074501. [Google Scholar] [CrossRef]
- Podgorski, T.; Sostarecz, M.C.; Zorman, S.; Belmonte, A. Fingering instabilities of a reactive micellar interface. Phys. Rev. E 2007, 76, 016202. [Google Scholar] [CrossRef] [Green Version]
- Gérard, T.; De Wit, A. Miscible viscous fingering induced by a simple A+B→C chemical reaction. Phys. Rev. E 2009, 79, 016308. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nagatsu, Y.; De Wit, A. Viscous fingering of a miscible reactive A + B → C interface for an infinitely fast chemical reaction: Nonlinear simulations. Phys. Fluids 2011, 23, 043103. [Google Scholar] [CrossRef] [Green Version]
- Riolfo, L.A.; Nagatsu, Y.; Iwata, S.; Maes, R.; Trevelyan, P.M.J.; De Wit, A. Experimental evidence of reaction-driven miscible viscous fingering. Phys. Rev. E 2012, 85, 015304. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nagatsu, Y.; Ishii, Y.; Tada, Y.; De Wit, A. Hydrodynamic fingering instability induced by a precipitation reaction. Phys. Rev. Lett. 2014, 113, 024502. [Google Scholar] [CrossRef] [Green Version]
- Mishra, M.; Trevelyan, P.M.J.; Almarcha, C.; De Wit, A. Influence of double diffusive effects on miscible viscous fingering. Phys. Rev. Lett. 2010, 105, 204501. [Google Scholar] [CrossRef] [Green Version]
- Fu, X.; Cueto-Felgueroso, L.; Juanes, R. Thermodynamic coarsening arrested by viscous fingering in partially miscible binary mixtures. Phys. Rev. E 2016, 94, 033111. [Google Scholar] [CrossRef] [Green Version]
- Amooie, M.A.; Soltanian, M.R.; Moortgat, J. Hydrothermodynamic mixing of fluids across phases in porous media. Geophys. Res. Lett. 2017, 44, 3624–3634. [Google Scholar] [CrossRef]
- Fu, X.; Cueto-Felgueroso, L.; Juanes, R. Viscous fingering with partially miscible fluids. Phys. Rev. Fluids 2017, 2, 104001. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, R.X.; Nagatsu, Y.; Mishra, M.; Ban, T. Phase separation effects on a partially miscible viscous fingering dynamics. J. Fluid Mech. 2020, 898, A11. [Google Scholar] [CrossRef]
- Korteweg, D.J. Sur la forme que prennent les équations du mouvement des fluides si l’on tient compte des forces capillaires cauśees par des variations de densité. Arch. Néerl. Sci. Exactes Nat. 1901, 6, 1–24. [Google Scholar]
- Molin, D.; Mauri, R. Enhanced heat transport during phase separation of liquid binary mixtures. Phys. Fluids 2007, 19, 074102. [Google Scholar] [CrossRef] [Green Version]
- Budroni, M.A.; Riolfo, L.A.; Lemaigre, L.; Rossi, F.; Rustici, M.; De Wit, A. Chemical control of Hydrodynamic instabilities in partially miscible two-layer systems. J. Phys. Chem. Lett. 2014, 5, 875–881. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Budroni, M.A.; Thomas, C.; De Wit, A. Chemical control of dissolution-driven convection in partially miscible systems: Nonlinear simulations and experiments. Phys. Chem. Chem. Phys. 2017, 19, 7936–7946. [Google Scholar] [CrossRef] [PubMed]
- Snyder, S.M.; Cole, K.D.; Sziag, D.C. Phase compositions, viscosities, and densities for aqueous two-phase systems composed of polyethylene glycol and various salts at 25 °C. J. Chem. Eng. Data 1992, 37, 268–274. [Google Scholar] [CrossRef]
- Rauseo, S.N.; Barnes, P.D.; Maher, J.V. Development of radial fingering patterns. Phys. Rev. A 1987, 35, 1245–1251. [Google Scholar] [CrossRef]
- Chen, J.D. Growth of radial viscous fingers in a Hele-Shaw cell. J. Fluid Mech. 1989, 201, 223–242. [Google Scholar] [CrossRef] [Green Version]
- Fernandez, J.; Homsy, G.M. Viscous fingering with chemical reaction: Effect of in-situ production of surfactants. J. Fluid Mech. 2003, 480, 267–281. [Google Scholar] [CrossRef]
- Tsuzuki, R.; Ban, T.; Fujimura, M.; Nagatsu, Y. Dual role of surfactant-producing reaction in immiscible viscous fingering evolution. Phys. Fluids 2019, 31, 022102. [Google Scholar] [CrossRef]
- Tsuzuki, R.; Tanaka, R.; Ban, T.; Nagatsu, Y. Deviation from capillary number scaling of nonlinear viscous fingering formed by the injection of Newtonian surfactant solution. Phys. Fluids 2019, 31, 042108. [Google Scholar] [CrossRef]




| Displacing More Viscous Liquid | Displaced Less Viscous Liquid |
|---|---|
| 0 wt % Na2SO4 solution | |
| 2 wt % Na2SO4 solution | |
| 10 wt % PEG solution | 4 wt % Na2SO4 solution |
| 15 wt % PEG solution | 6 wt % Na2SO4 solution |
| 20 wt % PEG solution | 8 wt % Na2SO4 solution |
| 25 wt % PEG solution | 10 wt % Na2SO4 solution |
| 30 wt % PEG solution | 12 wt % Na2SO4 solution |
| 35 wt % PEG solution | 14 wt % Na2SO4 solution |
| 40 wt % PEG solution | 16 wt % Na2SO4 solution |
| 18 wt % Na2SO4 solution | |
| 20 wt % Na2SO4 solution | |
| Phase L | Phase H |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suzuki, R.X.; Takeda, R.; Nagatsu, Y.; Mishra, M.; Ban, T. Fluid Morphologies Governed by the Competition of Viscous Dissipation and Phase Separation in a Radial Hele-Shaw Flow. Coatings 2020, 10, 960. https://doi.org/10.3390/coatings10100960
Suzuki RX, Takeda R, Nagatsu Y, Mishra M, Ban T. Fluid Morphologies Governed by the Competition of Viscous Dissipation and Phase Separation in a Radial Hele-Shaw Flow. Coatings. 2020; 10(10):960. https://doi.org/10.3390/coatings10100960
Chicago/Turabian StyleSuzuki, Ryuta X., Risa Takeda, Yuichiro Nagatsu, Manoranjan Mishra, and Takahiko Ban. 2020. "Fluid Morphologies Governed by the Competition of Viscous Dissipation and Phase Separation in a Radial Hele-Shaw Flow" Coatings 10, no. 10: 960. https://doi.org/10.3390/coatings10100960
APA StyleSuzuki, R. X., Takeda, R., Nagatsu, Y., Mishra, M., & Ban, T. (2020). Fluid Morphologies Governed by the Competition of Viscous Dissipation and Phase Separation in a Radial Hele-Shaw Flow. Coatings, 10(10), 960. https://doi.org/10.3390/coatings10100960





