Thin Film Flow of Couple Stress Magneto-Hydrodynamics Nanofluid with Convective Heat over an Inclined Exponentially Rotating Stretched Surface
Abstract
1. Introduction
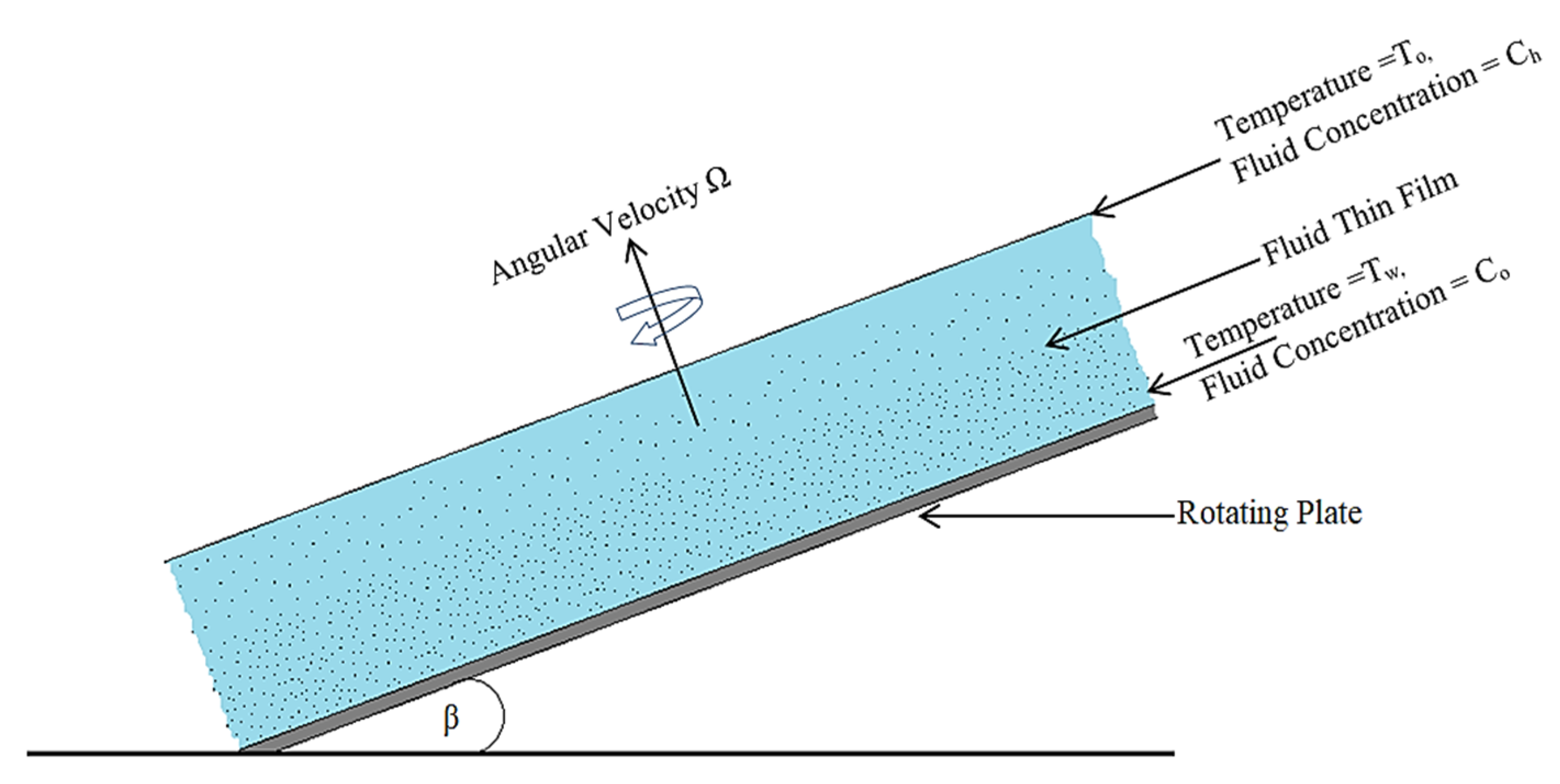
2. Problem Formulation
3. Solution by HAM
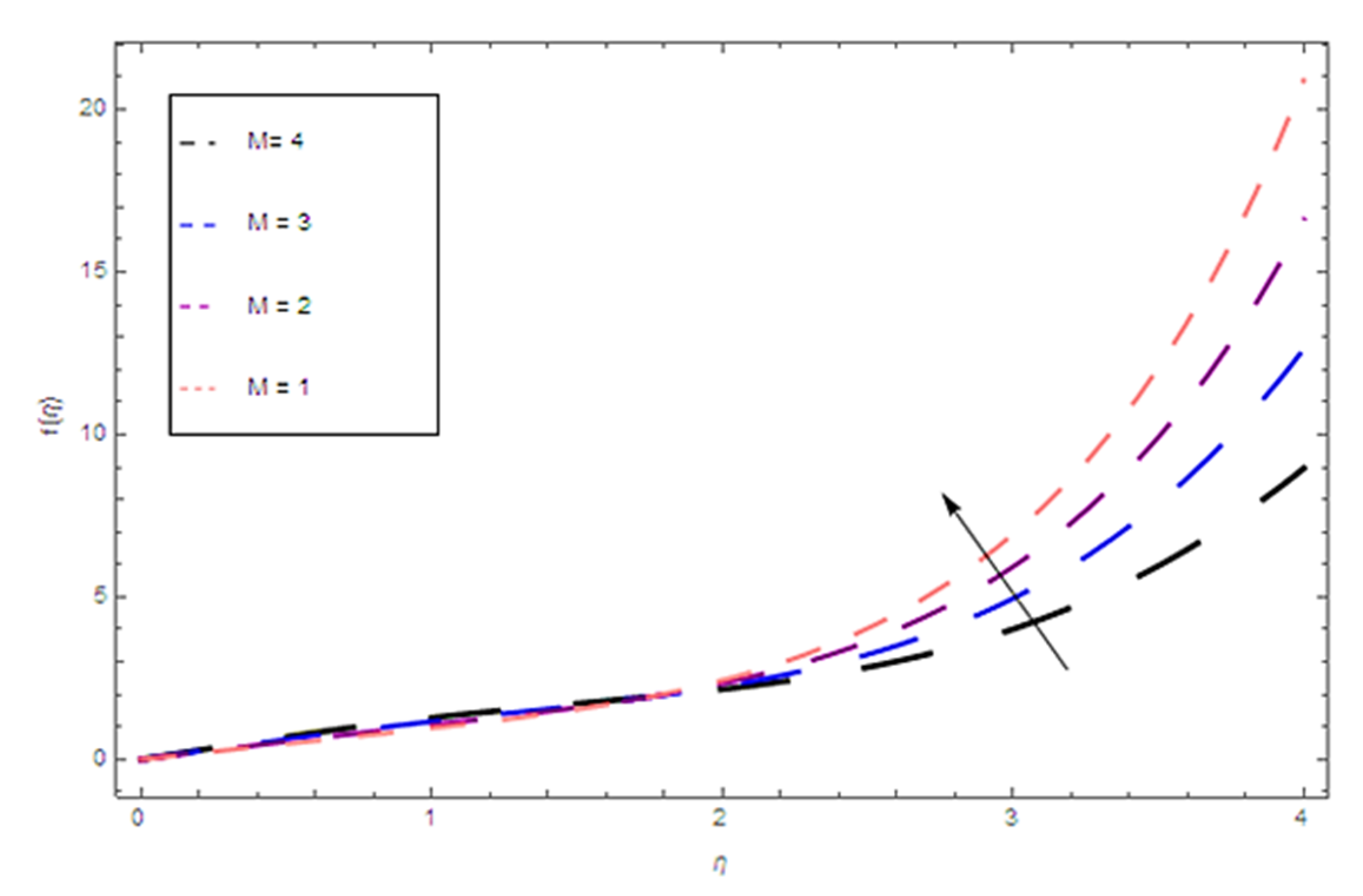
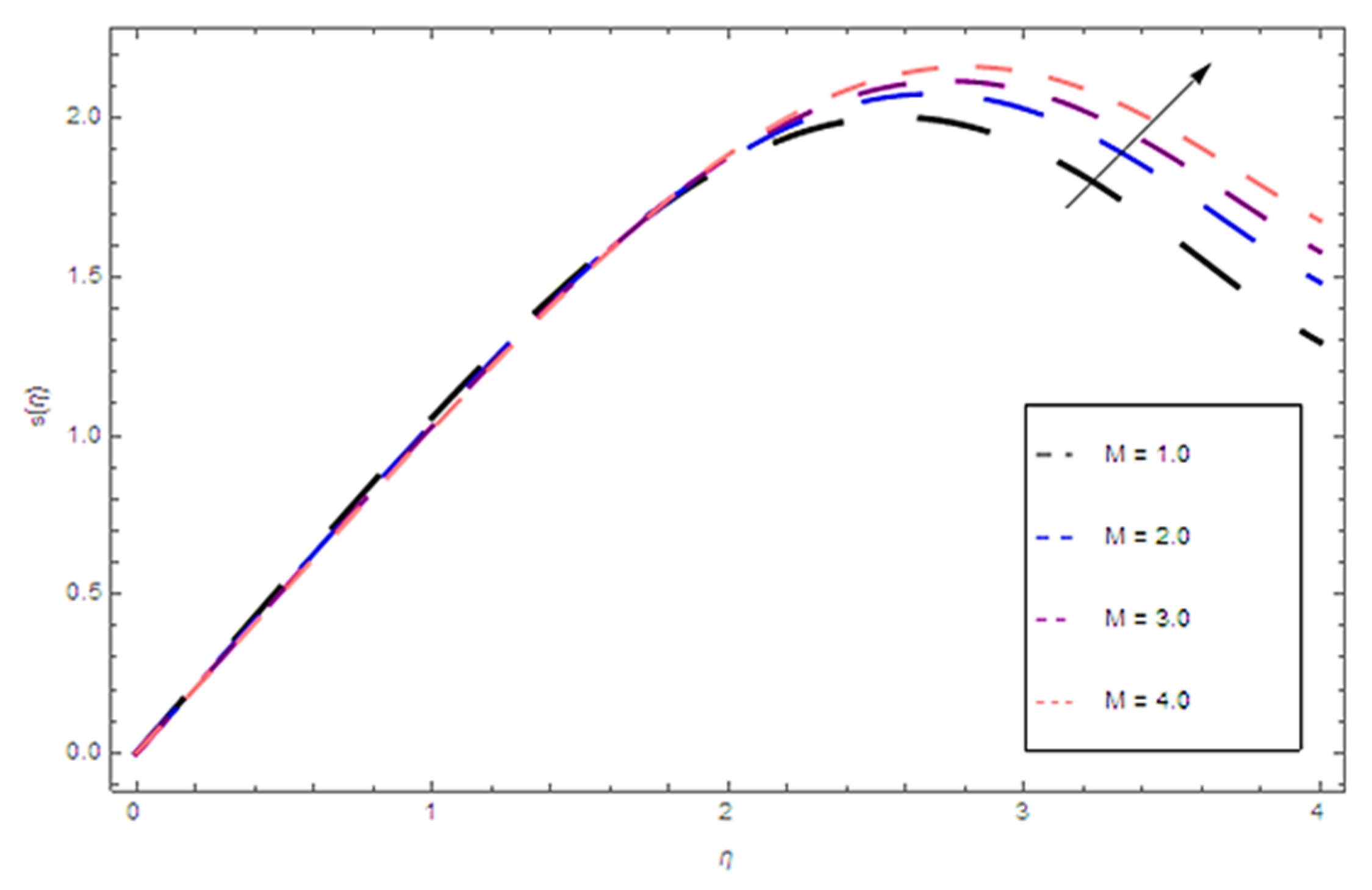
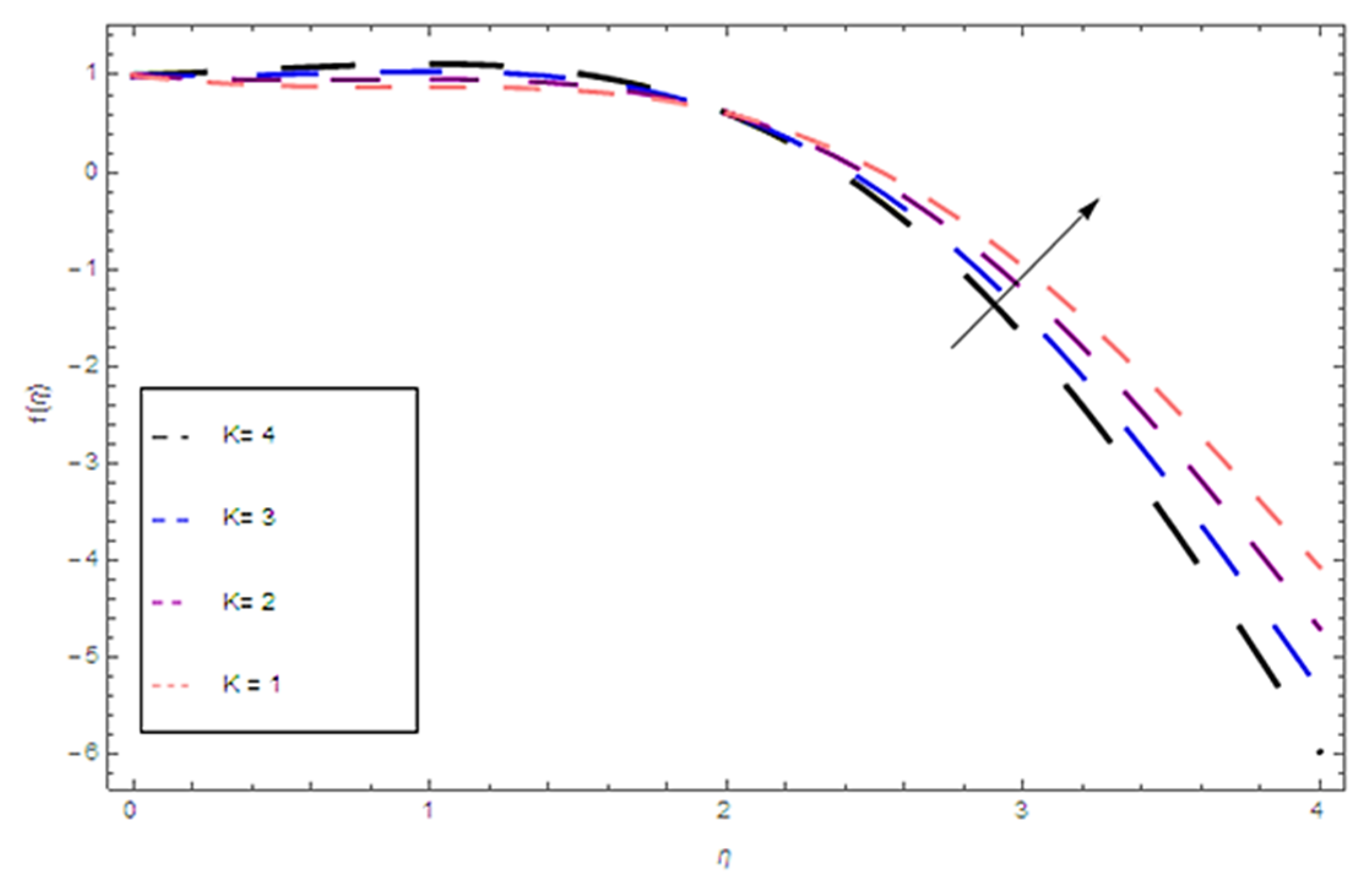
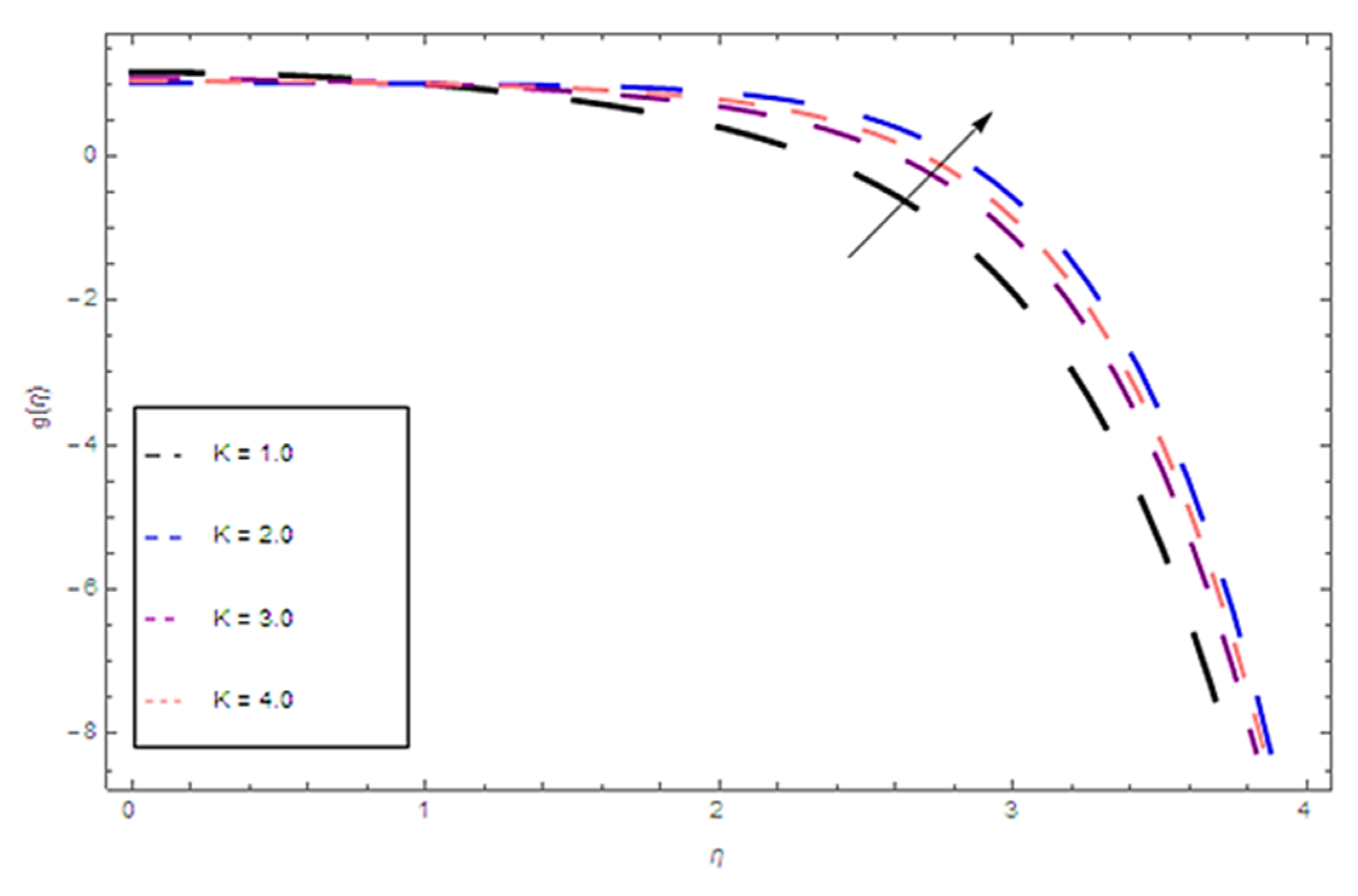
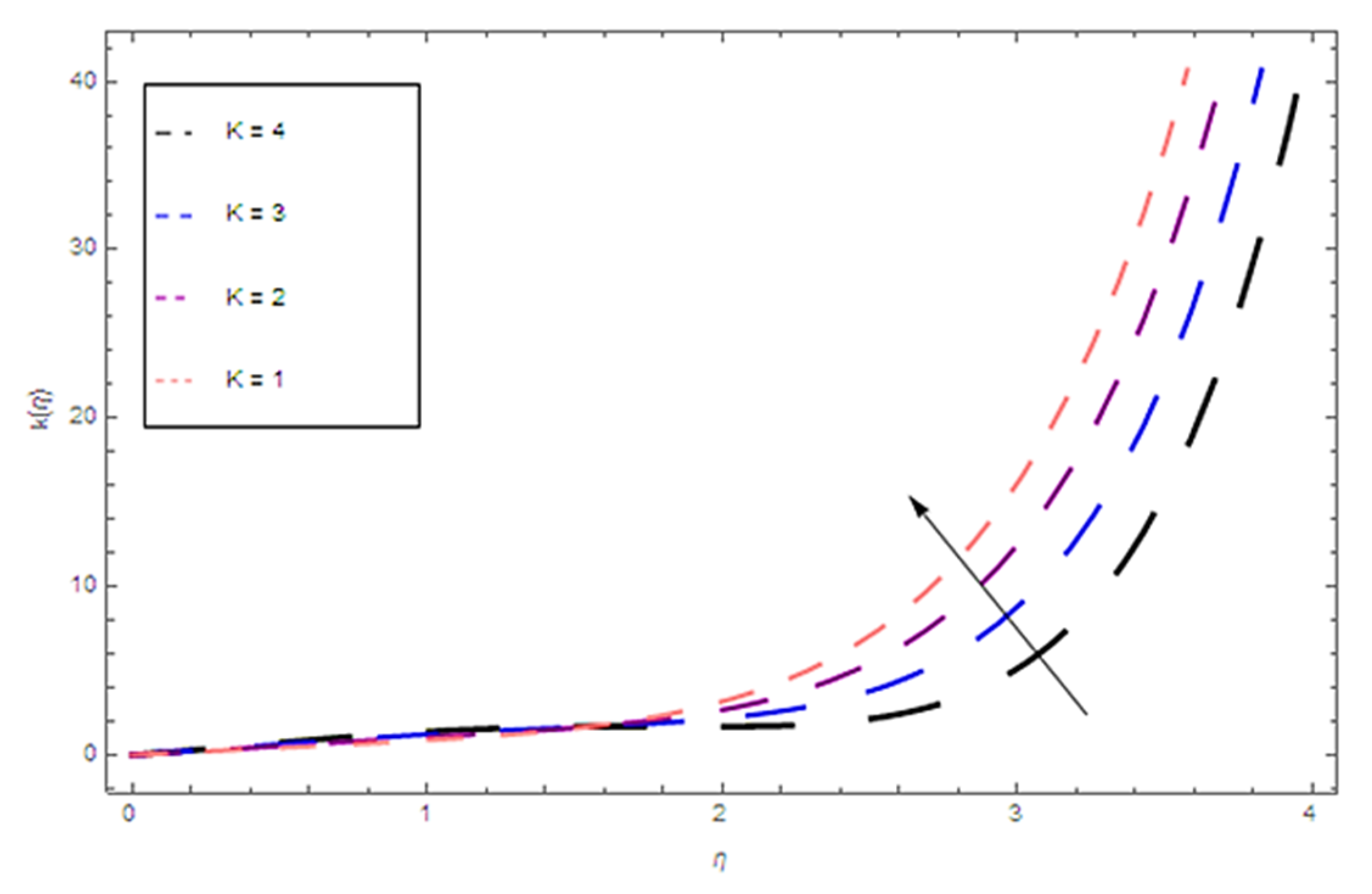
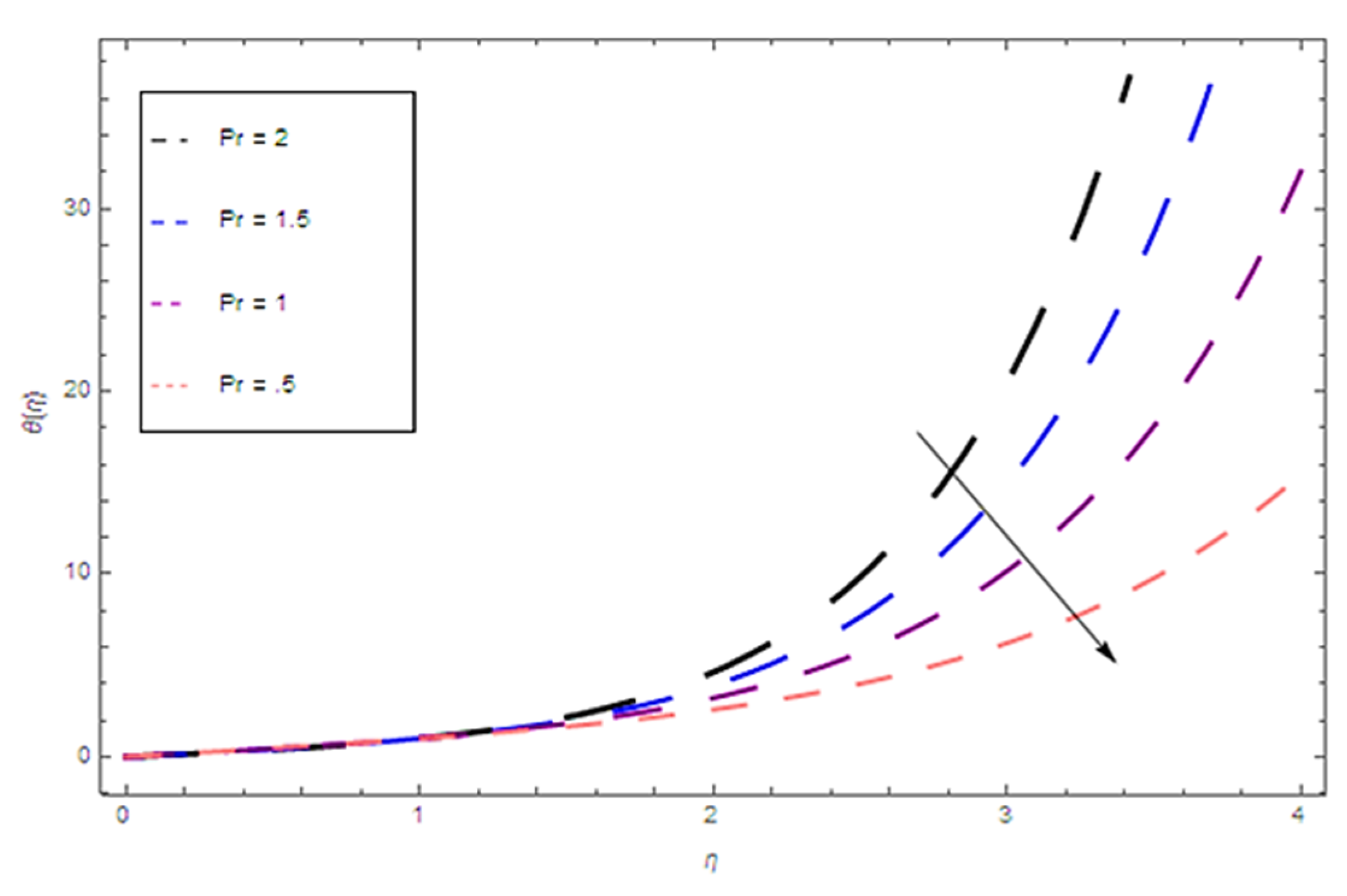
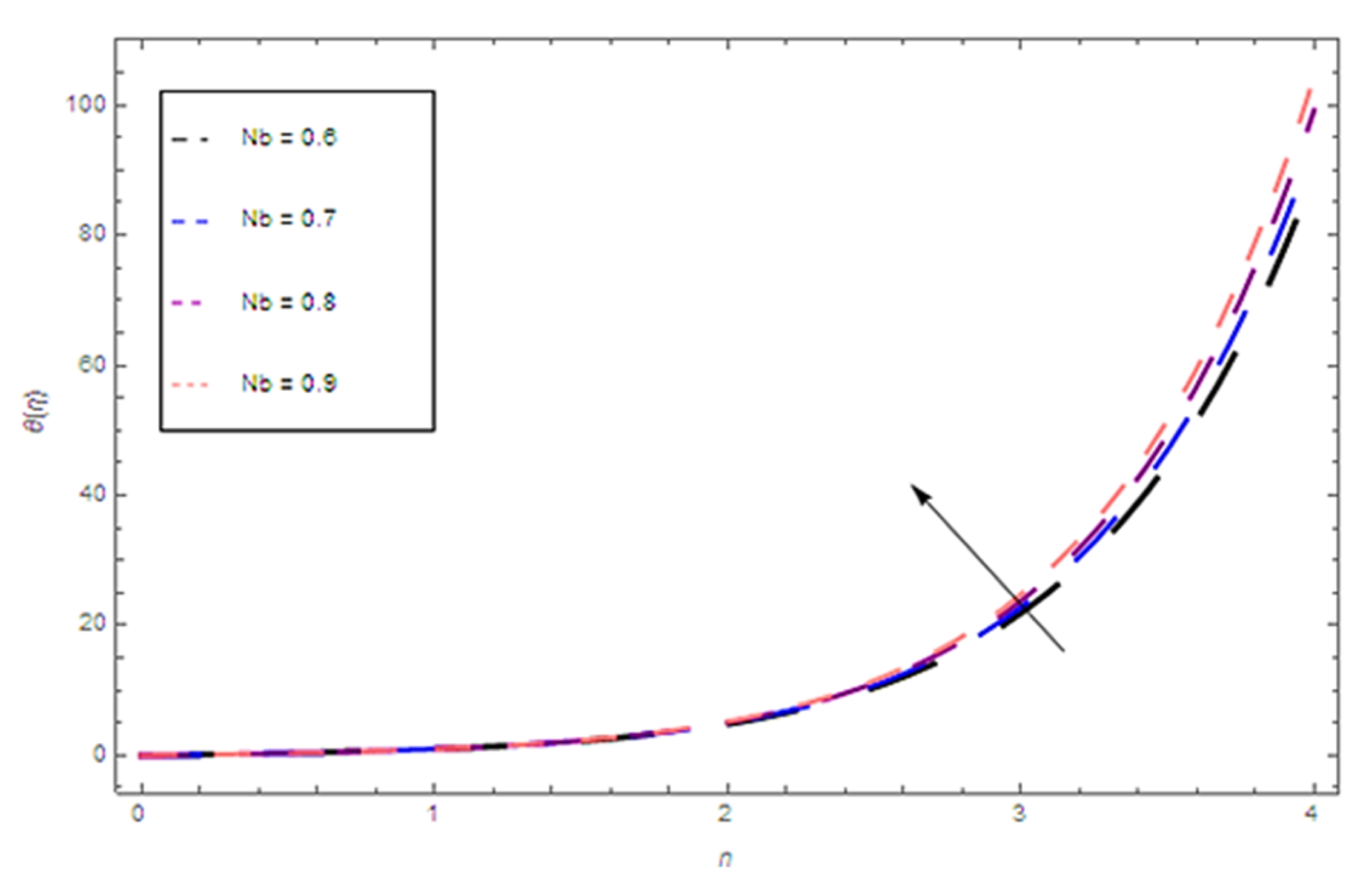
4. Results
5. Discussion
6. Conclusions
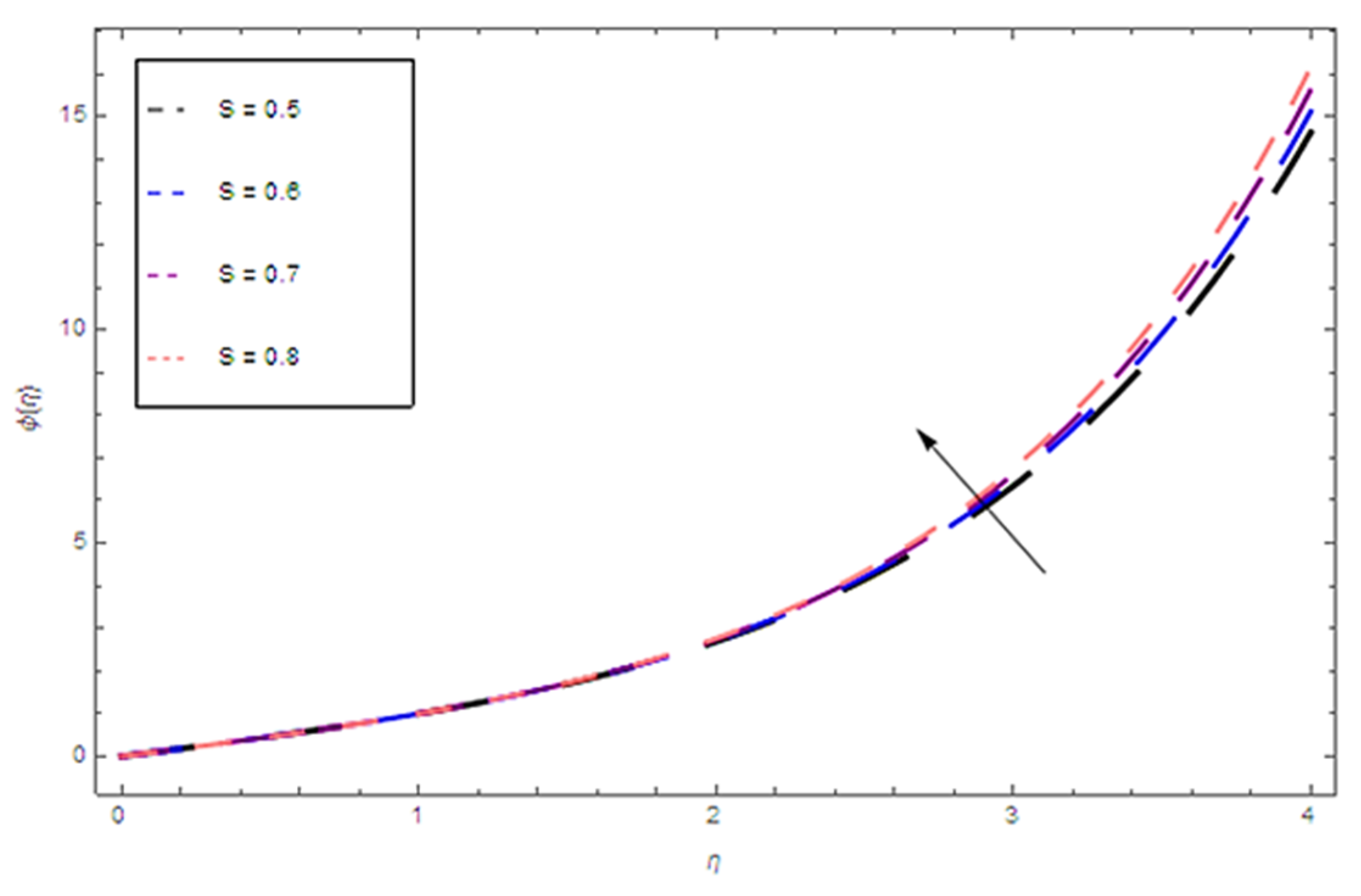
- Higher values of S provide coolness to the boundary layer, while Nu increases the profile.
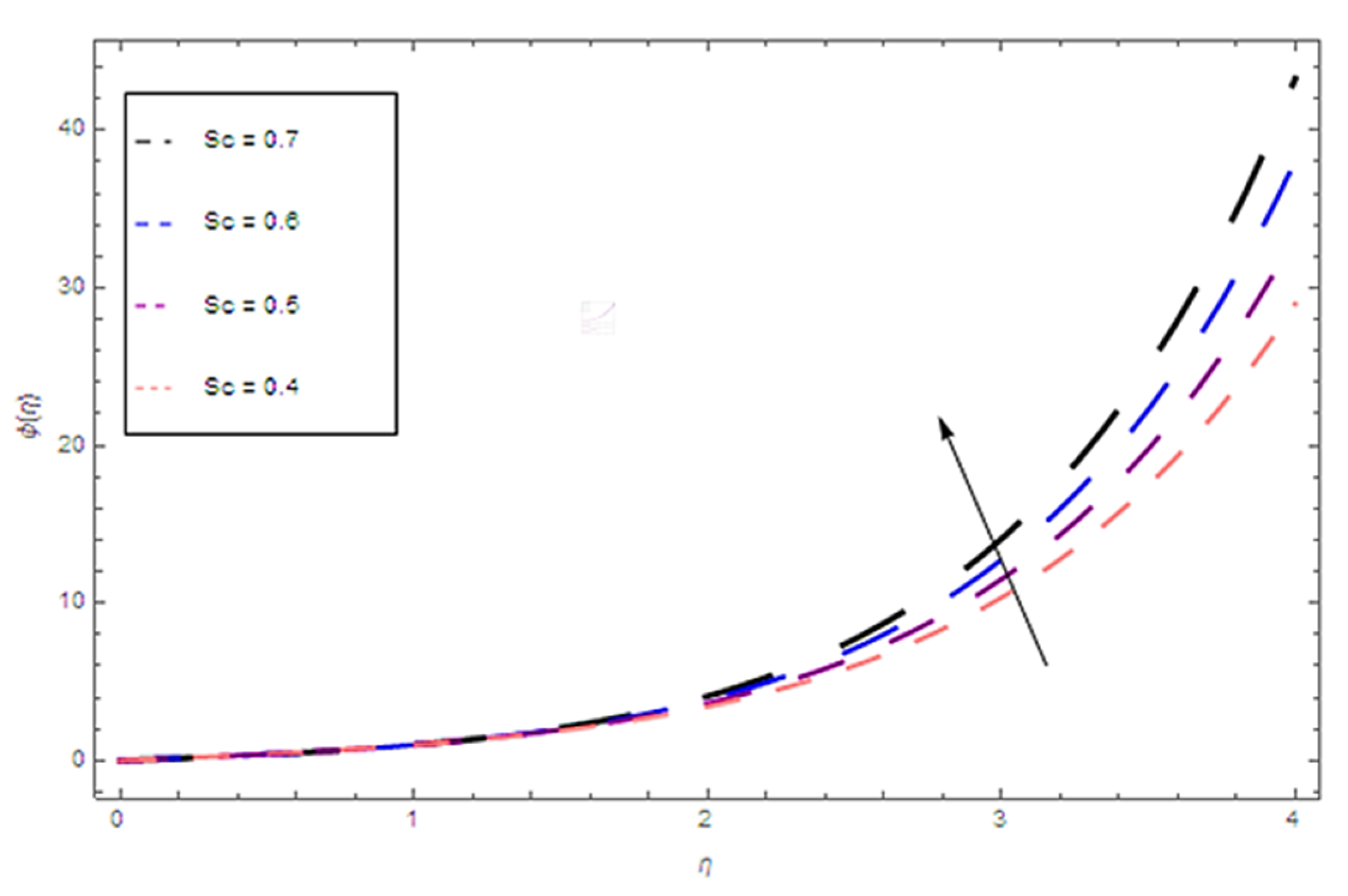
- A larger value of Sc reduces the Sherwood number, which as a result enhances the concentration and kinematic viscosity of the fluid.
- The higher values of the Prandtl number reduce the Nusselt number.
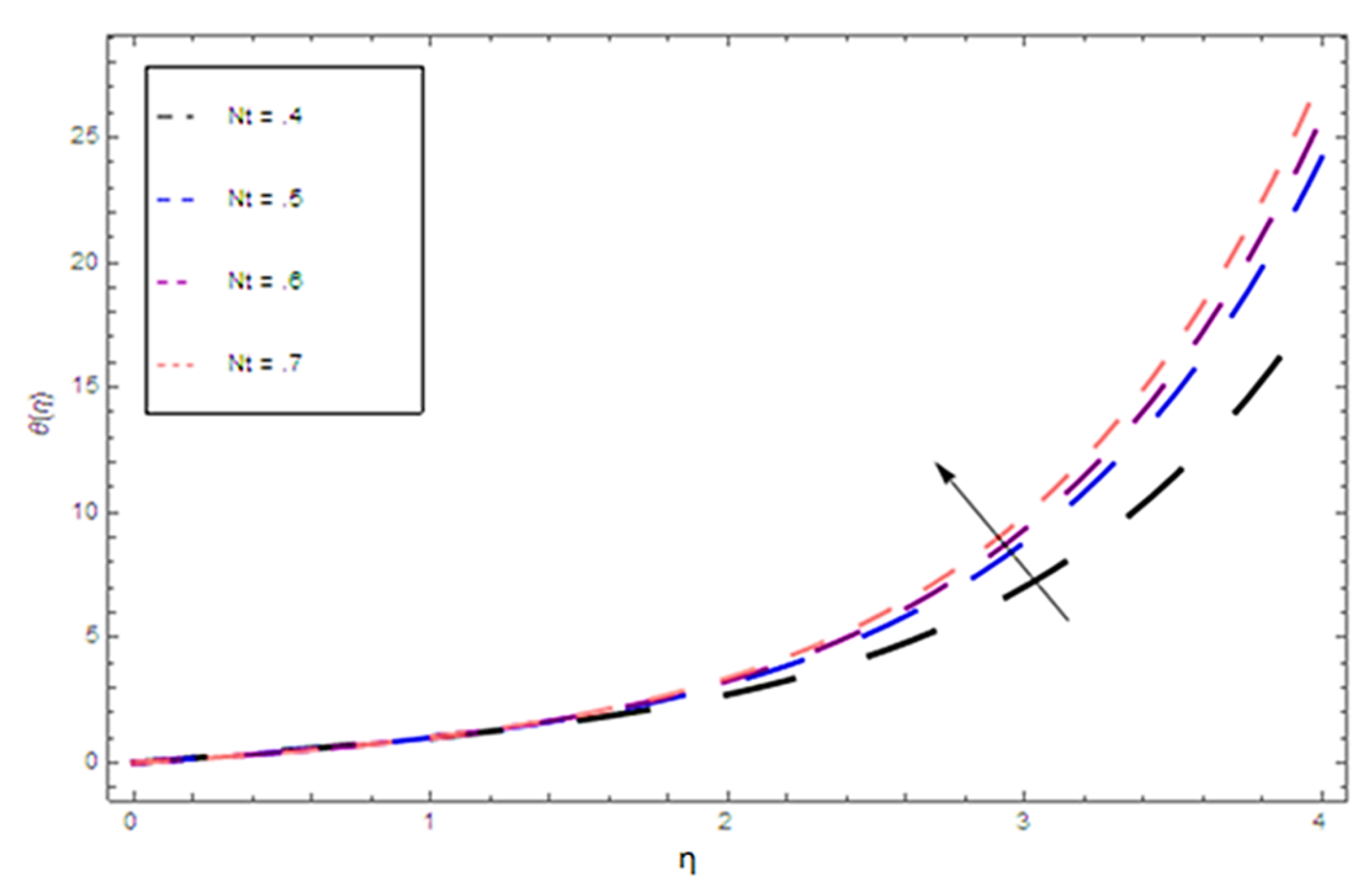
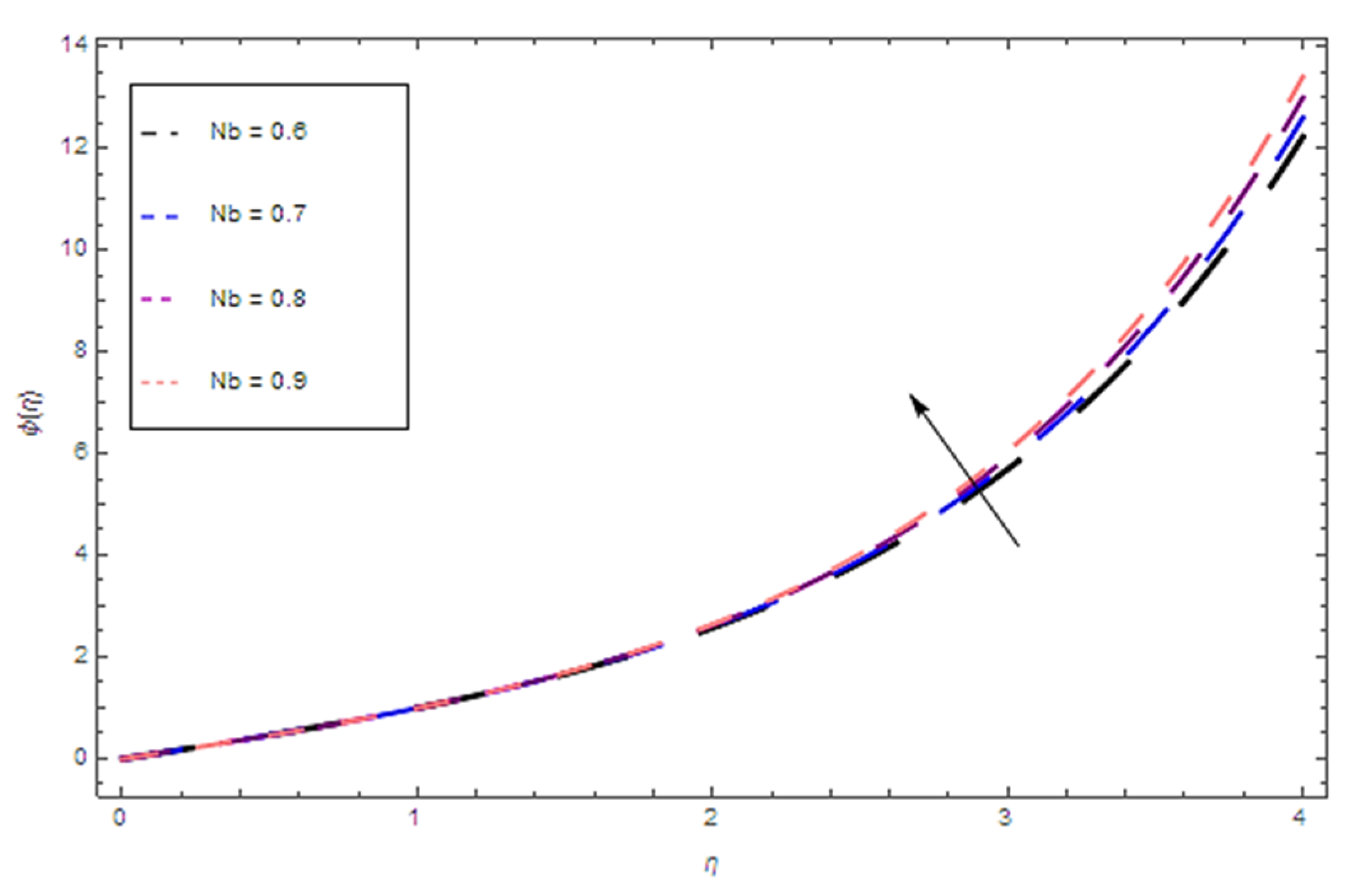
- The higher values of the Brownian motion parameter increase the concentration distribution and decline with increasing values of the thermophoresis parameters.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature:
| u, v, w | Velocity components in x, y, z directions (m/s) |
| x, y, z | Space coordinates (m) |
| T | Temperature of fluid (K) |
| Tw | Temperature at the surface (K) |
| T∞ | Ambient temperature (K) |
| B0 | Uniform magnetic field (Tesla) |
| C | Concentration of fluid (kg/m3) |
| Cw | Concentration at the surface (kg/m3) |
| DB | Brownian diffusion coefficient |
| DT | Thermophoresis diffusion coefficient |
| C∞ | Ambient concentration (kg/m3) |
| Uw | Stretching sheet velocity (m/s) |
| g | Gravity (m/s2) |
| α | Thermal diffusivity Coefficient (m2/s) |
| β | Angle of inclination |
| f | Dimensionless stream function |
| Nt | Thermophoresis parameter |
| Q | Heat generation/absorption coefficient (W/m2·K) |
| Sr | Soret number |
| δ | Electrical conductivity of the fluid (m/s) |
| K0 | Chemical reaction coefficient |
| CP | Specific heat at constant pressure (J/kg K) |
| Nb | Brownian motion parameter |
| Pr | Prandtl number |
| Cfx | Skin friction coefficient |
| Nux | Local Nusselt number |
| Re | Reynolds number |
| ρ | Fluid density (kg/m3) |
| qw | Surface heat flux |
| μ0 | Zero shear viscosity (s−1) |
| μ∞ | Infinite shear viscosity (s−1) |
| ν | Kinematic viscosity (m2/s) |
| μ | Dynamic viscosity (N s/m2) |
| Φ, θ | Dimensionless concentration and temperature |
| Subscripts | |
| ∞ | Condition for away from the surface |
| w | Condition at the sheet |
| Superscript | |
| ′ | Derivative with respect to η |
References
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab.: Lemont, IL, USA, 1995.
- Wang, X.-Q.; Mujumdar, A.S. Heat transfer characteristics of nanofluids: A Review. Int. J. Therm. Sci. 2007, 46, 1–19. [Google Scholar] [CrossRef]
- Eastman, J.A.; Phillpot, S.R.; Choi, S.U.S.; Keblinski, P. Thermal transport in nanofluids. Annu. Rev. Mater. Res. 2004, 34, 219–246. [Google Scholar] [CrossRef]
- Eastman, J.A.; Choi, S.U.S.; Li, S.; Yu, W.; Thompson, L.J. Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Appl. Phys. Lett. 2001, 78, 718–720. [Google Scholar] [CrossRef]
- Murshed, S.M.S.; Leong, K.C.; Yang, C. Enhanced thermal conductivity of TiO2—Water based nanofluids. Int. J. Therm. Sci. 2005, 44, 367–373. [Google Scholar] [CrossRef]
- Maïga, S.E.B.; Nguyen, C.T.; Galanis, N.; Roy, G. Heat transfer behaviours of nanofluids in a uniformly heated tube. Superlattices Microstruct. 2004, 35, 543–557. [Google Scholar] [CrossRef]
- Bianco, V.; Chiacchio, F.; Manca, O.; Nardini, S. Numerical investigation of nanofluids forced convection in circular tubes. Appl. Therm. Eng. 2009, 29, 3632–3642. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Kasaeian, A.; Daneshazarian, R.M.; Omid, K.; Lioua, C.A.J.; Wongwises, S.; Pop, I. Nanofluid flow and heat transfer in porous media: A review of the latest developments. Int. J. Heat Mass Transf. 2017, 107, 778–791. [Google Scholar] [CrossRef]
- Ramzan, M.; Chung, J.D.; Ullah, N. Radiative magnetohydrodynamic nanofluid flow due to gyrotactic microorganisms with chemical reaction and non-linear thermal radiation. Int. J. Mech. Sci. 2017, 130, 31–40. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Shehzad, S. RETRACTED: Magnetohydrodynamic Nanofluid Convective Flow in a Porous Enclosure by Means of LBM; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Jawad, M.; Shah, Z.; Islam, S.; Bonyah, E.; Khan, A.Z. Darcy-Forchheimer flow of MHD nanofluid thin film flow with Joule dissipation and Navier’s partial slip. J. Phys. Commun. 2018, 2, 115014. [Google Scholar] [CrossRef]
- Jawad, M.; Shah, Z.; Islam, S.; Majdoubi, J.; Tlili, I.; Khan, W.; Khan, I. Impact of nonlinear thermal radiation and the viscous dissipation effect on the unsteady three-dimensional rotating flow of single-wall carbon nanotubes with aqueous suspensions. Symmetry 2019, 11, 207. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Zeeshan, A.; Ellahi, R. Simultaneous effects of coagulation and variable magnetic field on peristaltically induced motion of Jeffrey nanofluid containing gyrotactic microorganism. Microvasc. Res. 2017, 110, 32–42. [Google Scholar] [CrossRef] [PubMed]
- Ellahi, R. The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe: Analytical solutions. Appl. Math. Model. 2013, 37, 1451–1467. [Google Scholar] [CrossRef]
- Hatami, M.; Ganji, D. Thermal and flow analysis of microchannel heat sink (MCHS) cooled by Cu–water nanofluid using porous media approach and least square method. Energy Convers. Manag. 2014, 78, 347–358. [Google Scholar] [CrossRef]
- Hatami, M.; Sheikholeslami, M.; Ganji, D. RETRACTED: Laminar Flow and Heat Transfer of Nanofluid between Contracting and Rotating Disks by Least Square Method; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Shah, Z.; Islam, S.; Ayaz, H.; Khan, S. Radiative heat and mass transfer analysis of micropolar nanofluid flow of Casson fluid between two rotating parallel plates with effects of Hall current. J. Heat Transf. 2019, 141, 022401. [Google Scholar] [CrossRef]
- Shah, Z.; Gul, T.; Islam, S.; Khan, M.A.; Bonyah, E.; Hussain, F.; Mukhtar, F.; Ullah, M. Three dimensional third grade nanofluid flow in a rotating system between parallel plates with Brownian motion and thermophoresis effects. Results Phys. 2018, 10, 36–45. [Google Scholar] [CrossRef]
- Shah, Z.; Alzahrani, E.O.; Alghamdi, W.; Ullah, M.K. Influences of electrical MHD and Hall current on squeezing nanofluid flow inside rotating porous plates with viscous and joule dissipation effects. J. Therm. Anal. Calorim. 2020. [Google Scholar] [CrossRef]
- Shah, Z.; Kumam, P.; Deebani, W. Radiative MHD Casson nanofluid flow with activation energy and chemical reaction over past nonlinearly stretching surface through Entropy generation. Sci. Rep. 2020, 10, 4402. [Google Scholar] [CrossRef]
- Ullah, A.; Alzahrani, E.O.; Shah, Z.; Ayaz, M.; Islam, S. Nanofluids thin film flow of Reiner-Philippoff fluid over an unstable stretching surface with Brownian motion and thermophoresis effects. Coatings 2019, 9, 21. [Google Scholar] [CrossRef]
- Ramzan, M. Influence of Newtonian heating on three dimensional MHD flow of couple stress nanofluid with viscous dissipation and joule heating. PLoS ONE 2015, 10, e0124699. [Google Scholar] [CrossRef] [PubMed]
- Hayat, T.; Imtiaz, M.; Alsaedi, A. Melting heat transfer in the MHD flow of Cu–water nanofluid with viscous dissipation and Joule heating. Adv. Powder Technol. 2016, 27, 1301–1308. [Google Scholar] [CrossRef]
- Van Dinh, Q.; Vo, T.Q.; Kim, B. Viscous heating and temperature profiles of liquid water flows in copper nanochannel. J. Mech. Sci. Technol. 2019, 33, 3257–3263. [Google Scholar] [CrossRef]
- Zhao, X.; E., J.; Zhang, Z.; Chen, J.; Liao, G.; Zhang, F.; Leng, E.; Han, D.; Hu, W. A review on heat enhancement in thermal energy conversion and management using Field Synergy Principle. Appl. Energy 2020, 257, 113995. [Google Scholar] [CrossRef]
- Zhao, X.; E., J.; Wu, G.; Deng, Y.; Han, D.; Zhang, B.; Zhang, Z. A review of studies using graphenes in energy conversion, energy storage and heat transfer development. Energy Convers. Manag. 2019, 184, 581–599. [Google Scholar] [CrossRef]
- E., J.; Jin, Y.; Deng, Y.; Zuo, W.; Zhao, X.; Han, D.; Peng, Q.; Zhang, Z. Wetting models and working mechanisms of typical surfaces existing in nature and their application on superhydrophobic surfaces: A review. Adv. Mater. Interfaces 2018, 5, 1701052. [Google Scholar] [CrossRef]
- E., J.; Zhang, Z.; Tu, Z.; Zuo, W.; Han, D.; Jin, Y. Effect analysis on flow and boiling heat transfer performance of cooling water-jacket of bearing in the gasoline engine turbocharger. Appl. Therm. Eng. 2018, 130, 754–766. [Google Scholar] [CrossRef]
- Khare, R.; Keblinski, P.; Yethiraj, A. Molecular dynamics simulations of heat and momentum transfer at a solid–fluid interface: Relationship between thermal and velocity slip. Int. J. Heat Mass Transf. 2006, 49, 3401–3407. [Google Scholar] [CrossRef]
- Soleimani, S.; Sheikhulislami, M.; Ganji, D.D.; Gorji-Bapanday, M. Natural convection heat transfer in a nanofluid filled semi-annulus enclosure. Int. Commun. Heat Mass Transf. 2012, 39, 565–574. [Google Scholar] [CrossRef]
- Rudraiah, N.; Barron, R.M.; Venkatachalappa, M.; Subbaraya, C.K. Effect of a magnetic field on free convection in a rectangular enclosure. Int. J. Eng. Sci. 1995, 33, 1075–1084. [Google Scholar] [CrossRef]
- Kandelousi, M.S.; Ellahi, R. Simulation of ferrofluid flow for magnetic drug targeting using the lattice Boltzmann method. Zeitschrift für Naturforschung A 2015, 70, 115–124. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Shehzad, S.A.; Alsaedi, A. Simultaneous effects of magnetic field and convective condition in three-dimensional flow of couple stress nanofluid with heat generation/absorption. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 1165–1176. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Alsaedi, A. On three-dimensional flow of couple stress fluid with Cattaneo–Christov heat flux. Chin. J. Phys. 2017, 55, 930–938. [Google Scholar] [CrossRef]
- Hayat, T.; Muhamamd, T.; Shehzad, S.A.; Alsaedi, A. Three-dimensional boundary layer flow of Maxwell nanofluid: Mathematical model. Appl. Math. Mech. 2015, 36, 747–762. [Google Scholar] [CrossRef]
- Malik, M.; khan, I.; Hussain, A.; Salahuddin, T. Mixed convection flow of MHD Eyring-Powell nanofluid over a stretching sheet: A numerical study. AIP Adv. 2015, 5, 117118. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Khan, Z. Numerical study of MHD boundary layer flow of a Maxwell fluid past a stretching sheet in the presence of nanoparticles. J. Taiwan Inst. Chem. Eng. 2014, 45, 121–126. [Google Scholar] [CrossRef]
- Raju, C.; Sandeep, N.; Malvandi, A. Free convective heat and mass transfer of MHD non-Newtonian nanofluids over a cone in the presence of non-uniform heat source/sink. J. Mol. Liq. 2016, 221, 108–115. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Rezaeianjouybari, B.; Darzi, M.; Shafee, A.; Li, Z.; Nguyen, T.K. Application of nano-refrigerant for boiling heat transfer enhancement employing an experimental study. Int. J. Heat Mass Transf. 2019, 141, 974–980. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Jafaryar, M.; Hedayat, M.; Shafee, A.; Nguyen, T.K.; Bakouri, M. Heat transfer and turbulent simulation of nanomaterial due to compound turbulator including irreversibility analysis. Int. J. Heat Mass Transf. 2019, 137, 1290–1300. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Jafaryar, M.; Shafee, A.; Li, Z.; Haq, R. Heat transfer of nanoparticles employing innovative turbulator considering entropy generation. Int. J. Heat Mass Transf. 2019, 136, 1233–1240. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Haq, R.; Shafee, A.; Li, Z. Heat transfer behavior of nanoparticle enhanced PCM solidification through an enclosure with V shaped fins. Int. J. Heat Mass Transf. 2019, 130, 1322–1342. [Google Scholar] [CrossRef]
- Sheikholeslami, M. New computational approach for exergy and entropy analysis of nanofluid under the impact of Lorentz force through a porous media. Comput. Methods Appl. Mech. Eng. 2019, 344, 319–333. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Numerical approach for MHD Al2O3-water nanofluid transportation inside a permeable medium using innovative computer method. Comput. Methods Appl. Mech. Eng. 2019, 344, 306–318. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Gerdroodbary, M.B.; Moraadi, R.; Shafee, A.; Li, Z. Application of Neural Network for estimation of heat transfer treatment of Al2O3-H2O nanofluid through a channel. Comput. Methods Appl. Mech. Eng. 2019, 344, 1–12. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Shah, Z.; Shafee, A.; Khan, I.; Tilili, I. Uniform magnetic force impact on water based nanofluid thermal behavior in a porous enclosure with ellipse shaped obstacle. Sci. Rep. 2019, 9, 1–11. [Google Scholar] [CrossRef]
- Li, Z.; Sheikhulislami, M.; Shah, Z.; Shafee, A.; Al-Qawasmi, A.; Tlili, I. Transient process in a finned triplex tube during phase changing of aluminum oxide enhanced PCM. Eur. Phys. J. Plus 2019, 134, 173. [Google Scholar] [CrossRef]
- Shah, Z.; Ullah, A.; Bonyah, E.; Ayaz, M.; Islam, S.; Khan, I. Hall effect on Titania nanofluids thin film flow and radiative thermal behavior with different base fluids on an inclined rotating surface. AIP Adv. 2019, 9, 055113. [Google Scholar] [CrossRef]
- Kumam, P.; Shah, Z.; Dawar, A.; Rasheed, H.; Islam, S. Entropy generation in MHD radiative flow of CNTs Casson nanofluid in rotating channels with heat source/sink. Math. Probl. Eng. 2019, 2019, 9158093. [Google Scholar] [CrossRef]
- Shah, Z.; Babazadeh, H.; Kumam, P.; Shafee, A.; Thounthong, P. Numerical simulation of magnetohydrodynamic nanofluids under the influence of shape factor and thermal transport in a porous media using CVFEM. Front. Phys. 2019, 7, 164. [Google Scholar] [CrossRef]
- Ameen, I.; Shah, Z.; Islam, S.; Nasir, S.; Khan, W.; Kumam, P.; Thounthong, P. Hall and ion-slip effect on CNTS nanofluid over a porous extending surface through heat generation and absorption. Entropy 2019, 21, 801. [Google Scholar] [CrossRef]
- Vo, D.D.; Shah, Z.; Sheikhulislami, M.; Shafee, A.; Nguyen, T.T. Numerical investigation of MHD nanomaterial convective migration and heat transfer within a sinusoidal porous cavity. Phys. Scr. 2019, 94, 115225. [Google Scholar] [CrossRef]
- Javed, T.; Sajid, M.; Abbas, Z.; Ali, N. Non-similar solution for rotating flow over an exponentially stretching surface. Int. J. Numer. Methods Heat Fluid Flow 2011, 21, 903–908. [Google Scholar] [CrossRef]
- Rosali, H.; Ishak, A.; Nazar, R.; Pop, I. Rotating flow over an exponentially shrinking sheet with suction. J. Mol. Liq. 2015, 211, 965–969. [Google Scholar] [CrossRef]
- Khan, N.S.; Gut, T.; Iskam, S.; Khan, A.; Shah, Z. Brownian motion and thermophoresis effects on MHD mixed convective thin film second-grade nanofluid flow with Hall effect and heat transfer past a stretching sheet. J. Nanofluids 2017, 6, 812–829. [Google Scholar] [CrossRef]





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tassaddiq, A.; Amin, I.; Shutaywi, M.; Shah, Z.; Ali, F.; Islam, S.; Ullah, A. Thin Film Flow of Couple Stress Magneto-Hydrodynamics Nanofluid with Convective Heat over an Inclined Exponentially Rotating Stretched Surface. Coatings 2020, 10, 338. https://doi.org/10.3390/coatings10040338
Tassaddiq A, Amin I, Shutaywi M, Shah Z, Ali F, Islam S, Ullah A. Thin Film Flow of Couple Stress Magneto-Hydrodynamics Nanofluid with Convective Heat over an Inclined Exponentially Rotating Stretched Surface. Coatings. 2020; 10(4):338. https://doi.org/10.3390/coatings10040338
Chicago/Turabian StyleTassaddiq, Asifa, Ibni Amin, Meshal Shutaywi, Zahir Shah, Farhad Ali, Saeed Islam, and Asad Ullah. 2020. "Thin Film Flow of Couple Stress Magneto-Hydrodynamics Nanofluid with Convective Heat over an Inclined Exponentially Rotating Stretched Surface" Coatings 10, no. 4: 338. https://doi.org/10.3390/coatings10040338
APA StyleTassaddiq, A., Amin, I., Shutaywi, M., Shah, Z., Ali, F., Islam, S., & Ullah, A. (2020). Thin Film Flow of Couple Stress Magneto-Hydrodynamics Nanofluid with Convective Heat over an Inclined Exponentially Rotating Stretched Surface. Coatings, 10(4), 338. https://doi.org/10.3390/coatings10040338





