Abstract
This research work deals with investigation of the thermal characteristics of the Darcy–Forchheimer hydromagnetic hybrid nanofluid (Al2O3-Cu/H2O) flow through a permeable stretching cylinder. The model equations, which consist of continuity, momentum, and energy equations, are converted to a set of coupled ordinary differential equations through similarity variables transformations and appropriate boundary conditions. Brownian motion and Thermophoresis effects are mainly focused in this work. The impacts of some interesting parameters over velocity, temperature, and concentrations profiles are graphically studied. The present study will be helpful in understanding the thermal characteristics of heat transfer liquids.
1. Introduction
The liquid coolants are mainly employed to keep the operating temperature of different equipment in the specified range by transferring heat from them. Presently, the investigations show that the thermal conductivities of different fluids used in liquid coolants are much smaller when compared to those of solid metals. The natural laminar and convective heat energy transfer is a significant process in engineering and industry due to its numerous applications. Currently, a lot of research is in progress to investigate the different heat energy transfer characteristics of the newly developed fluid called “hybrid nanofluid” due to an extensive range of engineering and technological uses, like medical manufacturing, microfluidics, transportation, generator cooling, naval structures, and solar heating. A hybrid nanofluid refers to a combination in a base fluid of two different types of nanoparticles. Therefore, if nanoparticles materials are correctly picked, then they will enhance each other’s positive aspects. The metallic nanoparticles, such as aluminum, copper, and zinc, have high thermal conductivities. However, the use of these metallic nanoparticles for nanofluid applications is limited because of their reactivity and stability. On the other hand, ceramic nanoparticles have lower thermal conductivity relative to metal nanoparticles, but they have many desirable possessions, such as chemical inertness and stability. In the case of closed cavities, heat transfer study appeared in several applications and has been widely deliberated in the literature [1,2,3]. In open cavities, the processes of natural convection give significant results by simulating more complex geometries at the open end. In open cavities natural convection is related to different engineering systems, such as the cooling of electrical equipment, room air conditioning, and solar thermal central receiver systems etc. [4,5,6]. Skok et al. [4] have undertaken an experimental survey of the open cavity natural convective flow numerically. They found some good agreements between the experimental data and the numerical results. For larger values, their results are very significant. Chan and Tien [7] studied the two-dimensional (2-D) natural convection flow in narrow open cavities and conducted relative studies while using open square cavities with protracted domains. The small thermal conductivities of the base fluids used in the natural convection are showed to be an essential obstacle for increasing the heat energy transformation rate beyond a definite limit. As a ground breaking work, Choi et al. added solid nanoparticles to the base fluid to enhance its thermal conduction, and called it nanofluids [8]. Mahmoudi et al. [9] numerically deliberated the enhancement of natural convective heat energy transfer flow. Sheremet et al. performed the numerical investigation of non-steady natural convection in a permeable open corrugated cavity through a two-phase model [10]. They showed that the Nusselt number reduces by enhancing the number of iterations. Presently, Tassaddiq et al. [11] investigated couple stress magneto-hydrodynamic nanofluid thin film flow over an exponential stretching sheet with joule heating and viscous dissipation. Tahar and Chamkha [12] discussed the flow of a hybrid nanofluid through horizontal and confocal elliptical cylinders with natural convection enhancement. Moreover, it has been determined that the key aim of including the nanomaterials in a transferor liquid is to augment its thermal conductivity. It shall also be noted that stable nanofluids have significant attributes, such as small nanoparticle concentration and higher thermal conductivities. Hence, the majority of the studies in the past have been carried out to attain high thermal conductivity through the use of a single nanomaterial [13,14,15,16]. Currently, many articles have considered the topic of hybrid nanofluids [17,18,19,20]. Mixed nanomaterials display important chemical and thermo-physical characteristics that do not happen in a single component. Hybrid nanomaterials are mainly categorized into three types [21,22,23]. In current years, numerous numerical and experimental works that are associated to hybrid nanofluids have been published, and their results display that they are more suitable than the conventional nanofluids. Suresh et al. [24] discussed a copper-alumina nanocomposite powder, which was mixed by using thermochemical method, and prepared a hybrid nanofluid through a two-step procedure. In another study, Suresh et al. [25] examined the heat energy transfer characteristics of hybrid nanofluid (alumina-copper)/water metal nanomaterials and polymer nanomaterials. Nadeem et al. [26] deliberated the MHD Maxwell nanofluid flow through a stretch sheet. Rockney et al. [27] studied the MHD nanofluid flow involving heat energy transfer through two plates. Shehzad et al. [28] investigated a nanofluidic flow by using the Jaffrey fluid model with MHD convective boundary conditions. Mahmood et al. discussed the flow of nanofluids for cooling purposes [29]. Nanofluid flow through a porous medium by incorporating the heat conduction through channels have explored by Fakour et al. [30]. Hatami et al. [31] described the laminar flow of nanofluids through rotating disks. Nadeem et al. [32] investigated the non-orthogonal and nanofluid non-Newtonian flows with heat energy transformation. Sheikholeshlami et al. [33] thoroughly investigated the nanofluid flow through a semi-porous channel. Akbar et al. [34] studied the viscosity and buoyancy impacts during the nanofluid MHD flow over a stretch surface. Fakour et al. [35] have undertaken the nanofluid flow through vertical channels. Maskeen et al. [36] have examined nanofluid flow by using water as base fluid and investigated the enrichment of heat energy transfer through the stretching sheet. Akilu et al. [37] deliberated the flow with the thermo-physical properties of water-based composite nanofluids. Hayat et al. [38] considered the Newtonian nanofluid flow through a cylinder along with the heating impacts. Further study can be read in [39,40,41,42].
Ceramic materials like alumina (Al2O3) have numerous excellent possessions, such as chemical inertness and good stability. Yet, alumina’s thermal conductivity is small when compared to metallic nanoparticles. Metallic nanoparticles, such as copper, have greater thermal conductivity. Yet, reactivity and stability are two significant factors that impede these metallic nanoparticles from being used. The inclusion of small quantities of copper particles in an alumina matrix will significantly increase the thermal possessions without affecting the nanofluid’s stability. Jena et al. [43] clarified the synthesis of Cu-Al2O3 nanocomposites while using hydrogen reduction techniques from chemically formulated Cu-Al2O3 mixtures. Niihara [44] and Oh et al. [45,46] revealed the manufacture of Al2O3-Cu nanocomposite made from fine powder mixtures of Al2O3 and CuO nanoscale. The proposed nanocomposites had a new concept of material design, thermal properties, and enhanced mechanical dramatically.
The Darcy–Forchheimer law is the law for porous media flows with Reynolds numbers more than approximately 1 to 10, and the inertial impacts can also become important. Sometimes a term of inertia is applied to the equation of Darcy, defined as the word Forchheimer. The non-linear behavior of the pressure difference vs. flow data can be taken into account by this term. In 1856, Hennery Darcy has developed the flow of a steady fluid through porous media, when he was carrying out his work of moving the water through sand bags. Though his outcome was not very much reliable at that time because he did not deliver a positive consequence. Yet, based on his research, a Dutch scientist, known as Forchheimer, came in 1901. Forchheimer, gave his ideas and expressions more extensive. Forchheimer added the velocity term square in the momentum equations for calculating inertial forces as well as limit layer flow [47]. Muskat later added the name ’Forchheimer term’ [48] Pal and Mondal [49] later investigated Darcy–Forchheimer’s model over a stretch face, where they defined that the value of the electric field parameter increases with a lessening in the nanoparticles concentration sketch. Ganesh et al. [50] conducted a study on the nanofluid flow of Darcy–Forchheimer MHD over a stretched/shrinking sheet and determined that the temperature value rises with the presence of viscous-dissipation effects. Hayat et al. [51] investigated the Darcy–Forchheimer flow with heat flux and variable thermal conductivity between Cattaneo and Christov. Muhammad et al. [52] an updated Darcy–Forchheimer flow of Maxwell nanofluid model due to convective boundary conditions. They used the pores medium, and found that the concentration and temperature-profile of nanoparticles increased with the value of the porosity parameter. Jawad et al. [53] have been studied MHD Nanofluid Darcy–Forchheimer thin film flow with Navier’s partial slip and joule dissipation. Uddin et al. [54] have been deliberated flow with nonlinear thermal Radiation of Darcy–Forchheimer Sisko nanomaterial. Mohamed et al. [55] have studied flow of Carreau nanofluid over a convectively heated nonlinear stretching surface in the presence chemically reactive species. Lahmar et al. [56] have investigated unsteady nanofluid squeezing flow with the effects of an inclined magnetic field and variable thermal conductivity. Mohamed et al. [57] have discussed FEM for blood-based SWCNTs flow with electromagnetic radiation through a circular cylinder in a porous medium. Mohamed et al. [58] have described SQLM for external yield stress effect on three-dimensional (3D) MHD nanofluid flow in a porous medium. Mohamed [59] has studied MHD boundary-layer flow of two-phase nanofluid model over an exponentially stretching sheet with a heat generation and Chemical reaction effect. Mohamed [60] has investigated unsteady flow of water-NPs over a stretching sheet in a saturated porous medium in the stagnation-point region with chemical reaction. Other related study can be read in [61,62,63].
The aim of this research work is the investigation of the thermal characteristics of the Darcy–Forchheimer hydromagnetic hybrid nanofluid flow through a stretching porous cylinder. The model equations with appropriate boundary conditions are solved analytically. Thermophoresis and Brownian motion impacts are mainly focused in this work. The impacts of modeled parameters over velocity, temperature, and concentrations profiles are graphically studied.
2. Mathematical Formulation
2.1. Flow Modelling
In the current work, we examine the steady and incompressible boundary layer hydro-magnetic flow of alumina-copper/water hybrid nanofluids through a permeable stretch cylinder. An external magnetic field is applied. The hybrid nanofluid flow is affected in the axial direction by the stretching of the elastic cylinder. The Darcy–Forchheimer impact is included in momentum equation. The coordinate system are selected in such a method that fluid flow is started due to elongating cylinder in the axial direction, where (x, r) shows axial and radial directions.
The energy, mass, and momentum conservation laws in boundary layer approximation can be represented as:
Boundary conditions are:
We employ the following transformations to convert the model equations into dimensionless form are [36]:
By using Equation (7) in Equations (1) to (6), we get:
We have defined the different parameters in Equations (8)–(10) as; is the permeability parameter, is the local Reynolds number, is the thermophoresis constraint, is the Prandtl number. represents the Brownian motion limitation, is the curvature parameter, and is the magnetic parameter. The Schmidt number is defined by , whereas represents the local inertia parameter.
2.2. Important Physical Quantities
The basic physical quantities of interest are the coefficient of friction () and Nusselt number (), which are defined by:
By using the similarity transformations as defined in Equation (7), the dimensionless forms of Equations (13)–(15) are:
In Equation (8), the different constant terms appearing are given by:
2.3. Hybrid Nanofluid Modelling
The density , viscosity , thermal expansion coefficient , thermal conductivity of the hybrid nanofluid, and heat capacity are given according to [18,19], as:
The subscripts and represent the nanoparticles of Al2O3 and Cu, whereas and represent the base fluid and hybrid nanofluid. The symbol is the fraction of whole volume, which is the combination of two different types of nanoparticles, Alumina–Copper dispersed in the transferor fluid in order to develop the hybrid nanofluid, which is: .
2.4. Solution by HAM
For solution process optimal approach is used. Equations (8)–(10) with boundary conditions (11 and 12) are solved by HAM. Basic derivations of the model equations through HAM are specified in details below.
Linear operators are signified as
The consistent non-linear operators are reasonably selected as and identify as:
For Equations (8)–(10) the 0th-order system is shown as
Whereas, BCs are
While the embedding constraint is , to regulate for the solution convergence , and are used. When , we have:
Expand the and through Taylor’s series for
Whereas, BCs are:
Now
While
3. Result and Discussion
We discuss in this section the effect produced by the different physical parameters of interest on the velocity profile (), temperature profile (), and concentration profile () during the hybrid nanofluid flow of a boundary layer through a stretching cylinder. Figure 1 describes the geometry of the nanofluid flow. We have plotted the effects that are produced by these different parameters in the Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14.
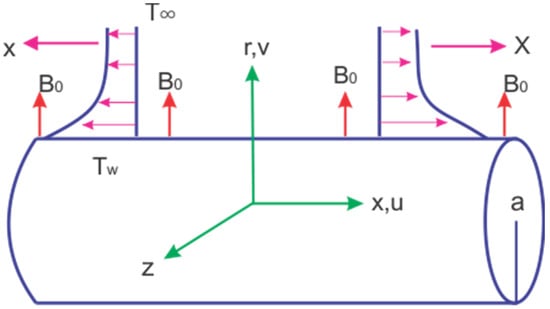
Figure 1.
Physical sketch of flow phenomena.
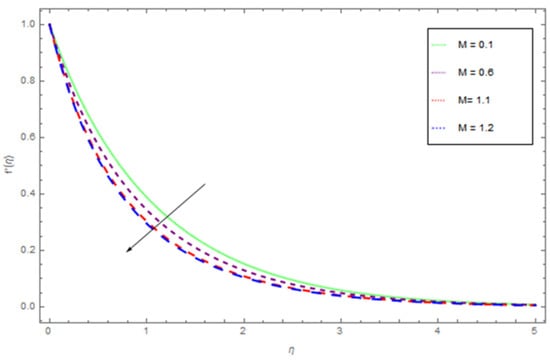
Figure 2.
The influence of on when .
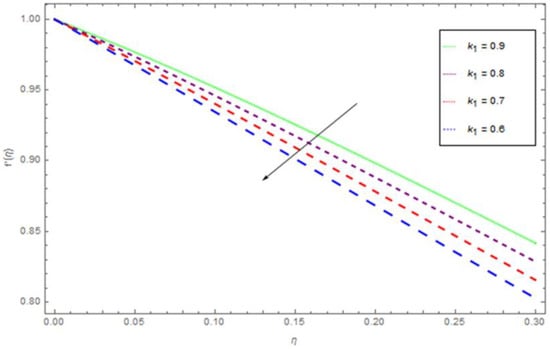
Figure 3.
The variation of with , for .
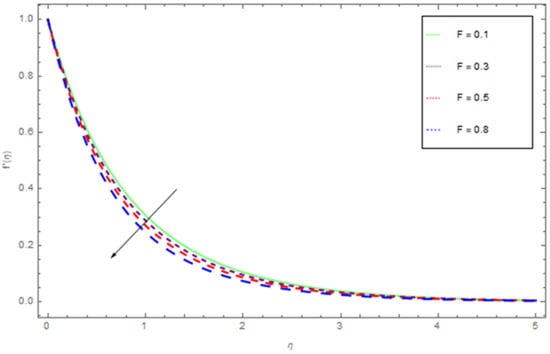
Figure 4.
The influence of on when .
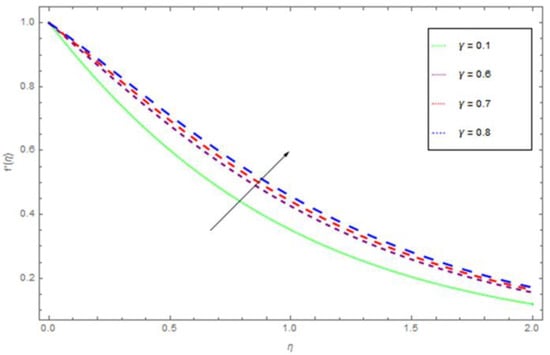
Figure 5.
The effect of on when .
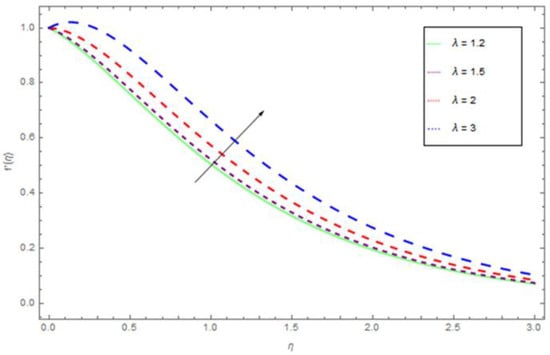
Figure 6.
The variation of with , when .
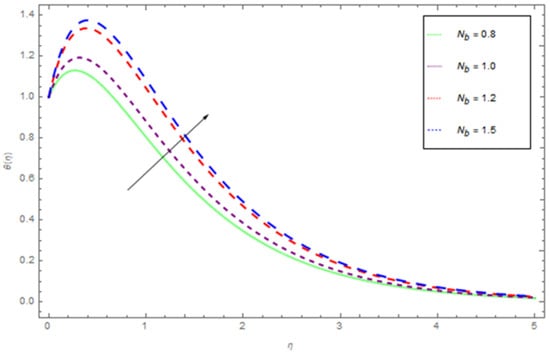
Figure 7.
The influence of on when .
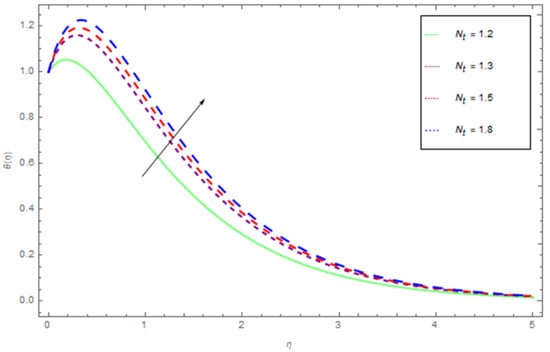
Figure 8.
The effect of on when .
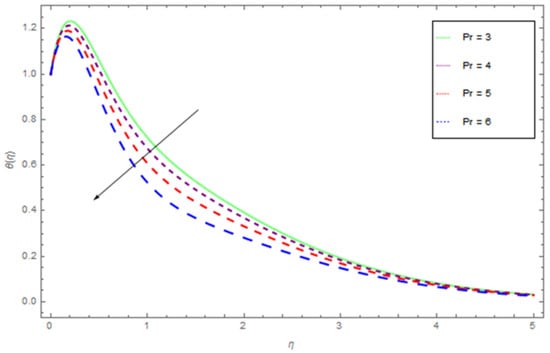
Figure 9.
The influence of on while .
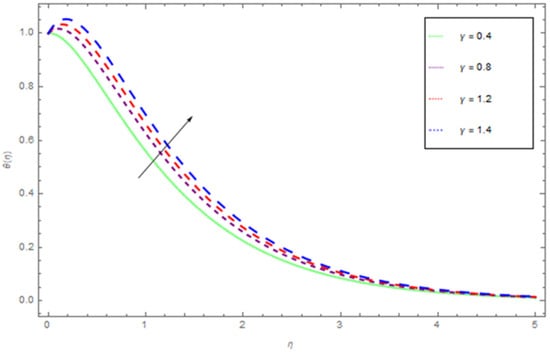
Figure 10.
The influence of on when .
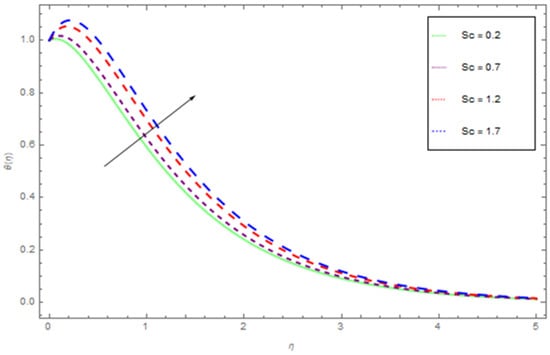
Figure 11.
The influence of on , while .
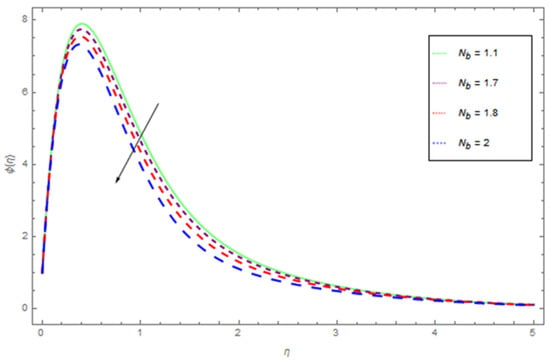
Figure 12.
The influence of on when .
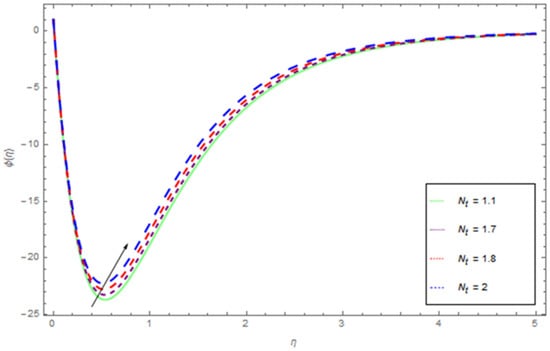
Figure 13.
The influence of on when .
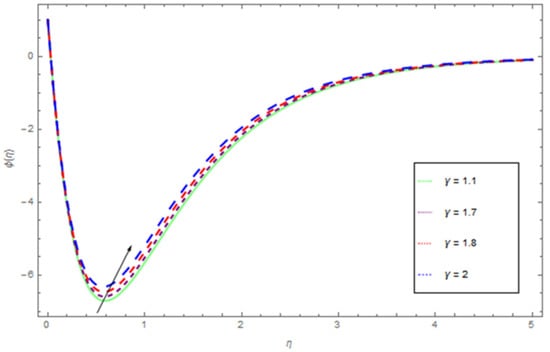
Figure 14.
The influence of on when .
3.1. Velocity
Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 display the variation of with respect to the variations in the magnetic parameter permeability parameter , inertial parameter , curvature parameter , and convection parameter . From Figure 2 it is observed that decreases almost exponentially with η at a given value of the M. The velocity profiler decreases with the higher values of M. This is because of the Lorentz force, which resists force that acts in the direction opposite to the flow direction. This opposes force slow down the fluid motion. Figure 3 represents the impact of the permeability parameter over the velocity profile . The higher value of permeability parameter decreases . Actually, an increasing permeability produces resistance in the flow path and that resistance reduces the fluid flow motion. Figure 4 show the influence of on velocity profile. Figure 4 illustrates that on rising , inner nanofluid fluid velocity is diminished, while there is no impact of on thickness of the fluid. There is hardly an influence of on free surface velocity, which is obvious from Figure 2. In state of porous gap with larger pores sizes, and porous medium expanded by fluid-solid interaction, which increases the viscous interference. Hence, an increase in causes a better flow resistance, so the velocity of fluid is reduced. We describe the effect of the curvature parameter on the velocity profile in Figure 5. From Figure 5, we demined that a higher value of curvature parameter augmented the fluid flow motion. The influence of convection parameter on velocity profile is illustrated in Figure 7. The increasing behavior for the motion of nanofluid is found with augmentation of convection parameter , because of the buoyancy impact.
3.2. Temperature
The variations of (Brownian motion parameter), (thermophoresis parameter), (Prandtl number), and (curvature parameter) on temperature profile are respectively shown in Figure 7, Figure 8, Figure 9 and Figure 10. We have shown the effect that is produced by the variation of Brownian motion on in Figure 7. Brownian motion is the arbitrary movement of small colloidal particles suspended in a fluid, brought about by the collision of the fluid atoms with the particles. An expansion in the Brownian motion impact yields noteworthy movement of nanoparticles, which offers ascend to the fluid kinetic energy and henceforth temperature increments. It is seen that, at fixed , initially the profile drops to the lowest value at around η = 0.4, and then rises and reaches to maximum at the largest value of η. By changing to larger values, there is an upshift in the temperature function from about η = 0.4 to η = 3.0. This shows that there is an enhancement in the average kinetic energy of the hybrid nanofluid with the higher values of . The influence of the thermophoresis parameter () on is displayed in Figure 8. It is initiated that rise in leads to augmenting both the liquid temperature. The augmented value of Shows stouter thermophoretic force due to temperature gradient, which transfers the nanoparticles from the warm surface to the quiescent fluid. Thermophoresis force is generated by temperature gradient, which fashions a degenerate flow away from the surface. Figure 9 depicts the effects that are produced by the variation of the Prandtl number over the temperature function . Figure 9 is portraying the declining behavior of temperature curves for growing values of Prantl number , since the thickness of the thermal boundary layer reduced by enhancing . Figure 10 illustrates the variation of with respect to the changing values of the curvature parameter . It is apparent that increases with increasing values of .
3.3. Concentration
The impacts of , , and on are presented in Figure 11, Figure 12, Figure 13 and Figure 14. Figure 11 shows the profile of for dissimilar values of . We observe that increases with the higher values of . The impact of and on the concentration profile is shown in Figure 12 and Figure 13. Figure 12 shows that the concentration profile reduced as the values of reduces. Enhancing thermophoresis process boosts the traveling of particles from higher to lower temperature deference, which results in maximizing the concentration of nanoparticles in the flow regime. Figure 13 show the influence of on the concentration profile. The higher values of corresponds increasing trends in concentration profile and related momentum boundary layer. Figure 14 shows that increases with the higher values of in quite the same manner.
3.4. Table Discussion
In Table 1, numerical calculation of surface drag force at different value of and with variation of magnetic parameter in range of 0 to 1 are shown. It is observed that the surface drag force is augmented in for all value of when is increases. The surface drag force reduces all values of when is segmented. In Table 2, numerical calculation of heat flux at different value of and with variation of magnetic parameter in range of 0 to 0.2 are shown. Increasing , and heat flux is decreases with variation of . The present results are compared with previous published results for validation. Both results are with good agreement. Table 3 shows the physical properties of some nanoparticles.

Table 1.
Computed numerical values of skin friction coefficient Cf for numerous values of k, M, and c, when .

Table 2.
Numerical computed values of Nusselt number for numerous values of .

Table 3.
Physical properties of water , alumina (Al2O3), and Copper (Cu).
4. Conclusions
We have investigated in this work the Darcy–Forchheimer hybrid nanofluid (Al2O3-Cu/H2O) boundary layer hydromagnetic flow over a stretch cylinder. The model equations are converted to a set of coupled ODEs by employing similarity transformations and appropriate boundary conditions. The impact of variation of dissimilar physical parameters over velocity profile, concentration, and temperature profile are graphically studied. We conclude the following:
- The higher value of permeability parameter decreases .
- Increase in causes a better flow resistance, so velocity of fluid is reduced.
- The velocity profile decreases exponentially with the increasing of , while it rises with the rising values of the permeability, inertial, curvature, and convection parameters.
- The augmented value of shows stouter thermophoretic force due to the temperature gradient, which transfers the nanoparticles from the warm surface to the quiescent fluid. Thermophoresis force is generated by temperature gradient, which fashions a degenerate flow away from the surface.
- The temperature profile of the hybrid nanofluid increases almost in the same manner with the increasing values of , Reynold number and convection parameter. The variation is more prominent for the intermediate values of the independent variable η.
- The temperature profile decreases with the higher values of the Prandtl number. The drop in is more significant from η = 0.2 to η = 3.6. Furthermore, the temperature function drops at a maximum rate for the highest value of , i.e., .
- The increases with the higher values of from η = 0.3 to η = 2.6, while it reduces with the rising values of Brownian motion parameter from η = 0.4 to η = 3.2.
Author Contributions
Conceptualization, methodology, software, validation, writing—original draft preparation, writing—review and editing, A.S., A.T., Z.S. and M.J.; conceptualization, methodology, software, visualization, writing—review and editing, W.D., A.K. and S.I.; writing—review and editing, visualization, project administration, funding acquisition, investigation, resources, A.T., W.D., A.S. and Z.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work is funded by the Deanship of Scientific Research at Majmaah University under Project Number (RGP-2019-28).
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research at Majmaah University for funding this work under Project Number (RGP-2019-28).
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Components of Velocity | |
| Axial and radial Coordinates | |
| Strength of Magnetic field | |
| Characteristic radius | |
| Temperature | |
| Dimensional velocity | |
| Dimensional temperature | |
| Eckert number | |
| Hear source/sink | |
| Thermal diffusivity | |
| Specific heat | |
| Density | |
| Local inertial parameter | |
| Stretching velocity | |
| Stephan-Boltzmann constant | |
| Mean absorption coefficient | |
| Volume fraction of the nanoparticles | |
| similarity variable | |
| Prandtl Number | |
| Skin friction coefficient | |
| Nusselt number | |
| Local Reynolds number | |
| Coefficients of mean absorption | |
| Radiative heat flux | |
| Starching rate | |
| Thermal conductivity | |
| Schimid number | |
| Temperature difference | |
| Kinematic viscosity | |
| Shear stress | |
| Curvature parameter | |
| Magnetic parameter | |
| Thermal radiation parameter | |
| Dynamic viscosity | |
| Electrical conductivity | |
| Convection parameter | |
| Subscripts | |
| Base fluid | |
| Nanofluid | |
| Ambient | |
| Hybrid nanofluid | |
| Wall | |
| particles | |
References
- Davis, G.d.V. Natural convection of air in a square cavity, a bench mark numerical solution. Int. J. Numer. Methods Fluids 1983, 3, 249–264. [Google Scholar] [CrossRef]
- Fusegi, T.; Hyun, J.M.; Kuwahara, K.; Farouk, B. A numerical study of three dimensional natural convection in a differentially heated cubical enclosure. Int. J. Heat Mass Transf. 1991, 34, 1543–1557. [Google Scholar] [CrossRef]
- Barakos, G.; Mistoulis, E. Natural convection flow in a square cavity revisited: Laminar and turbulent models with wall functions. Int. J. Numer. Method Heat Fluid Flow 1994, 18, 695–719. [Google Scholar] [CrossRef]
- Skok, H.; Ramadhyani, S.; Schoenhals, R.J. Natural convection in a side-facing open cavity. Int. J. Heat Fluid Flow 1991, 12, 36–45. [Google Scholar] [CrossRef]
- Cha, S.S.; Choi, K.J. An interferometric investigation of open-cavity natural convection heat transfer. Exp. Heat Transf. 1989, 2, 27–40. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Shah, Z.; Shafee, A.; Khan, I.; Tlili, I. Uniform magnetic force impact on water based nanofluid thermal behavior in a porous enclosure with ellipse shaped obstacle. Sci. Rep. 2019, 9, 1196. [Google Scholar] [CrossRef]
- Chan, Y.L.; Tien, C.L. A numerical study of two-dimensional laminar natural convection in shallow open cavities. Int. J. Heat Mass Transf. 1985, 28, 603–612. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the 1995 International Mechanical Engineering Congress and Exhibition, San Francisco, CA, USA, 12–17 November 1995. [Google Scholar]
- Mahmoudi, A.H.; Shahi, M.; Shahedin, A.M.; Hemati, N. Numerical mod-eling of natural convection in an open enclosure with two vertical thin heat sources subjected to a nanofluid. Int. Commun. Heat Mass Transf. 2011, 38, 110–118. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Pop, A.S.I. Unsteady free convection in a porous open wavy cavity filled with a nanofluid using Buongiorno’s mathematical model. Int. Commun. Heat Mass Transf. 2015, 67, 66–72. [Google Scholar] [CrossRef]
- Tassaddiq, A.; Amin, I.; Shutaywi, M.; Shah, Z.; Ali, F.; Islam, S.; Ullah, A. Thin Film Flow of Couple Stress Magneto-Hydrodynamics Nanofluid with Convective Heat over an Inclined Exponentially Rotating Stretched Surface. Coatings 2020, 10, 338. [Google Scholar] [CrossRef]
- Tayebi, T.; Chamkha, A.J. Free convection enhancement in an annulus between horizontal confocal elliptical cylinders using hybrid nanofluids. Numer. Heat Transf. Part A 2016, 70, 1141–1156. [Google Scholar] [CrossRef]
- Abbas, T.; Bhatti, M.M.; Ayub, M. Aiding and opposing of mixed convection Casson nanofluid flow with chemical reactions through a porous Riga plate. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2018, 232, 519–527. [Google Scholar] [CrossRef]
- Shah, Z.; Kumam, P.; Deebani, W. Radiative MHD Casson Nanofluid Flow with Activation energy and chemical reaction over past nonlinearly stretching surface through Entropy generation. Sci. Rep. 2020, 10, 4402. [Google Scholar] [CrossRef] [PubMed]
- Rashidi, S.; Akar, S.; Bovand, M.; Ellahi, R. Volume of fluid model to simulate the nanofluid flow and entropy generation in a single slope solar still. Renew. Energy 2018, 115, 400–410. [Google Scholar] [CrossRef]
- Akbarzadeh, M.; Rashidi, S.; Karimi, N.; Ellahi, R. Convection of heat and thermodynamic irreversibilities in two-phase, turbulent nanofluid flows in solar heaters by corrugated absorber plates. Adv. Powder Technol. 2018, 29, 2243–2254. [Google Scholar] [CrossRef]
- Shah, Z.; Alzahrani, E.O.; Alghamdi, W.; Ullah, M.Z. Influences of electrical MHD and Hall current on squeezing nanofluid flow inside rotating porous plates with viscous and joule dissipation effects. J. Therm. Anal. Calorim. 2020, 140, 1215–1227. [Google Scholar] [CrossRef]
- Takabi, B.; Shokouhmand, H. Effects of Al2O3–Cu/water hybrid nanofluid on heat transfer and flow characteristics in turbulent regime. Int. J. Mod. Phys. C 2015, 26, 1550047. [Google Scholar] [CrossRef]
- Shah, Z.; Babazadeh, H.; Kumam, P.; Shafee, A.; Thounthong, P. Numerical simulation of magnetohydrodynamic nanofluids under the influence of shape factor and thermal transport in a porous media using CVFEM. Front. Phys. 2019, 7, 164. [Google Scholar] [CrossRef]
- Minea, A.A. Hybrid nanofluids based on Al2O3, TiO2 and SiO2: Numerical evaluation of different approaches. Int. J. Heat Mass Transf. 2017, 104, 852–860. [Google Scholar] [CrossRef]
- Taylor, P.K.M.; Della, R.J.; Huxford, R.C.; Lin, W. Hybrid nanomaterials for biomedical applications. Chem. Commun. 2010, 46, 5832–5849. [Google Scholar] [CrossRef]
- Farahani, M.M.; Movassagh, J.; Taghavi, F.; Eghbali, P.; Salimi, F. Magnetite–polyoxometalate hybrid nanomaterials: Synthesis and characterization. Chem. Eng. J. 2012, 184, 342–346. [Google Scholar] [CrossRef]
- Mehryan, S.A.M.; Izadpanahi, E.; Ghalambaz, M.; Chamkha, A.J. Mixed convection flow caused by an oscillating cylinder in a square cavity filled with Cu-Al2O3/water hybrid nanofluid. J. Therm. Anal. Calorim. 2019. [Google Scholar] [CrossRef]
- Suresh, S.; Venkitaraj, K.P.; Selvakumar, P.; Chandrasekar, M. Synthesis of Al2O3–Cu/water hybrid nanofluids using two step method and its thermo physical properties. Colloids Surf. A 2011, 388, 41–48. [Google Scholar] [CrossRef]
- Suresh, S.; Venkitaraj, K.P.; Selvakumar, P.; Chandrasekar, M. Effect of Al2O3–Cu/water hybrid nanofluid in heat transfer. Exp. Fluid Sci. 2012, 38, 54–60. [Google Scholar] [CrossRef]
- Rokni, H.B.; Alsaad, D.M.; Valipour, P. Electro hydrodynamic nanofluid flow and heat transfer between two plates. J. Mol. Liq. 2016, 216, 583–589. [Google Scholar] [CrossRef]
- Shehzad, S.A.; Hayat, A.; Alsaedi, A. MHD flow of Jeffrey nanofluid with convective boundary conditions. Braz. Soc. Mech. Sci. Eng. 2014, 3, 873–883. [Google Scholar] [CrossRef]
- Mahmoodi, M.; Kandelousi, S.H. Kerosene∓alumina nanofluid flow and heat transfer for cooling application. J. Cent. South Univ. 2016, 23, 983–990. [Google Scholar] [CrossRef]
- Fakour, M.; Ganji, D.D.; Abbasi, M. Scrutiny of underdeveloped nanofluid MHD flow and heat conduction in a channel with porous walls. Int. J. Case Stud. Therm. Eng. 2014, 4, 202–214. [Google Scholar] [CrossRef]
- Fakour, M.; Rahbari, A.; Khodabandeh, E. Nanofluid thin film flow and heat transfer over an unsteady stretching elastic sheet by LMS. J. Mech. Sci. Technol. 2018, 32, 177–183. [Google Scholar] [CrossRef]
- Hatami, M.; Sheikholeslami, M.; Ganji, D.D. Laminar flow and heat transfer of nanofluid between contracting and rotating disks by least square method. Power Technol. 2014, 253, 769–779. [Google Scholar] [CrossRef]
- Nadeem, S.; Mehmood, R.; Akbar, N.S. Nonorthogonal stagnation point flow of a nano non-Newtonian fluid towards a stretching surface with heat transfer. Int. J. Heat Mass Transf. 2013, 57, 679–689. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Hatami, M.; Ganji, D.D. Analytical investigation of MHD nanofluid flow in a semi-porous channel. Powder Technol. 2013, 246, 327–336. [Google Scholar] [CrossRef]
- Akbar, N.S.; Tripathi, D.; Khan, Z.H.; Beg, O.A. A numerical study of magneto hydrodynamic transport of nanofluids over a vertical stretching sheet with exponential temperature-dependent viscosity and buoyancy effects. Chem. Phys. Lett. 2016, 661, 20–30. [Google Scholar] [CrossRef]
- Fakour, M.; Vahabzadeh, A.; Ganji, D.D. Scrutiny of mixed convection flow of a nanofluid in a vertical channel. Int. J. Case Stud. Therm. Eng. 2014, 4, 15–23. [Google Scholar] [CrossRef]
- Maskeen, M.M.; Zeeshan, A.; Mehmood, O.U.; Hassan, M. Heat transfer enhancement in hydromagnetic alumina–copper/water hybrid nanofluid flow over a stretching cylinder. J. Anal. Calorim. 2019, 138, 1127–1136. [Google Scholar] [CrossRef]
- Akilu, S.; Sharma, K.V.; Baheta, A.T.; Mamat, R. A review of thermophysical properties of water based composite nanofluids. Renew. Sustain. Energy Rev. 2016, 66, 654–678. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Waqas, M.; Alsaedi, A. Newtonian heating effect in nanofluid flow by a permeable cylinder. Result Phys. 2017, 7, 256–262. [Google Scholar] [CrossRef]
- Jamaludin, A.; Naganthran, K.; Nazar, R.; Pop, I. Thermal radiation and MHD effects in the mixed convection flow of Fe3O4–water ferrofluid towards a nonlinearly moving surface. Processes 2020, 8, 95. [Google Scholar] [CrossRef]
- Zaib, A.; Khan, U.; Khan, I.; Seikh, A.H.; Sherif, E.-S.M. Entropy generation and dual solutions in mixed convection stagnation point flow of micropolar Ti6Al4V nanoparticle along a riga surface. Processes 2020, 8, 14. [Google Scholar] [CrossRef]
- Saeed, A.; Islam, S.; Dawar, A.; Shah, Z.; Kumam, P.; Khan, W. Influence of Cattaneo–Christov heat flux on MHD Jeffrey, Maxwell, and Oldroyd-B nanofluids with homogeneous-heterogeneous reaction. Symmetry 2019, 11, 439. [Google Scholar] [CrossRef]
- Ahmad Farooq, A.; Shah, Z.; Alzahrani, E.O. Heat transfer analysis of a magneto-bio-fluid transport with variable thermal viscosity through a vertical ciliated channel. Symmetry 2019, 11, 1240. [Google Scholar] [CrossRef]
- Jena, P.K.; Brocchi, E.A.; Motta, M.S. In-situ formation of Cu–Al2O3 nano-scale composites by chemical routes and studies on their microstructures. Mater. Sci. Eng. A 2001, 313, 180–186. [Google Scholar] [CrossRef]
- Niihara, K. New design concept of structural ceramics–ceramic nanocomposites. J. Ceram. Soc. Jpn. 1991, 99, 974–982. [Google Scholar] [CrossRef]
- Oh, S.-T.; Sekino, T.; Niihara, K. Effect of particle size distribution and mixing homogeneity on microstructure and strength of alumina/copper composites. Nanostruct. Mater. 1998, 10, 327–332. [Google Scholar] [CrossRef]
- Oh, S.-T.; Sekino, T.; Niihara, K. Fabrication and mechanical properties of 5 vol% copper dispersed alumina nanocomposite. J. Eur. Ceram. Soc. 1998, 18, 31–37. [Google Scholar] [CrossRef]
- Forchheimer, P. Wasserbewegung Durch Boden; Zeitschrift des Vereins Deutscher Ingenieure: Düsseldorf, Germany, 1901; Volume 45, pp. 1782–1788. [Google Scholar]
- Muskat, M. The Flow of Homogeneous Fluids through Porous Media; JW Edwards: Edwards, MI, USA, 1946. [Google Scholar]
- Pal, D.; Mondal, H. Hydromagnetic convective diffusion of species in Darcy-Forchheimer porous medium with non-uniform heat source/sink and variable viscosity. Int. Commun. Heat Mass Transf. 2012, 39, 913–917. [Google Scholar] [CrossRef]
- Ganesh, N.V.; Hakeem, A.K.A.; Ganga, B. Darcy-Forchheimer flow of hydromagnetic nanofluid over a stretching/shrinking sheet in a thermally stratified porous medium with second order slip, viscous and Ohmic dissipations effects. Ain Shams Eng. J. 2016, 9, 939–951. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Al-Mezal, S.; Liao, S.J. Darcy-Forchheimer flow with variable thermal conductivity and Cattaneo-Christov heat flux. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 2355–2369. [Google Scholar] [CrossRef]
- Muhammad, T.; Alsaedi, A.; Shahzad, S.A.; Hayat, T. A revised model for Darcy-Forchheimer flow of Maxwell nanofluid subject to convective boundary condition. Chin. J. Phys. 2017, 55, 963–976. [Google Scholar] [CrossRef]
- Jawad, M.; Shah, Z.; Islam, S.; Bonyah, E.; Khan, A.Z. Darcy-Forchheimer Flow of MHD Nanofluid thin Film Flow with Joule dissipation and Navier’s partial slip. J. Phys. Commun. 2018, 2, 115014. [Google Scholar] [CrossRef]
- Uddin, I.; Akhtar, R.; Zhiyu, Z.; Islam, S.; Shoaib, M.; Raja, M.A.Z. Numerical treatment for Darcy-Forchheimer flow of Sisko nanomaterial with nonlinear thermal radiation by lobatto IIIA technique. Math. Probl. Eng. 2019, 2019. [Google Scholar] [CrossRef]
- Mohamed, R.E.; Mahny, K.L.; Dar, A.; Muhammad, T. Numerical study for Carreau nanofluid flow over a convectively heated nonlinear stretching surface with chemically reactive species. Physica A 2020, 540, 123063. [Google Scholar]
- Lahmar, S.; Kezzar, M.; Eid, M.R.; Sari, M.R. Heat transfer of squeezing unsteady nanofluid flow under the effects of an inclined magnetic field and variable thermal conductivity. Physica A 2020, 540, 123138. [Google Scholar] [CrossRef]
- Eid, M.R.; Al-Hossainy, A.F.; Zoromba, M.S. FEM for blood-based SWCNTs flow through a circular cylinder in a porous medium with electromagnetic radiation. Commun. Theor. Phys. 2019, 71, 1425–1434. [Google Scholar] [CrossRef]
- Al-Hossainy, A.F.; Eid, M.R.; Zoromba, M.S. SQLM for external yield stress effect on 3D MHD nanofluid flow in a porous medium. Phys. Scr. 2019, 94, 105208. [Google Scholar] [CrossRef]
- Mohamed, R.E. Chemical reaction effect on MHD boundary-layer flow of two-phase nanofluid model over an exponentially stretching sheet with a heat generation. J. Mol. Liq. 2016, 220, 718–725. [Google Scholar]
- Mohamed, R.E. Time-dependent flow of water-NPs over a stretching sheet in a saturated porous medium in the stagnation-point region in the presence of chemical reaction. J. Nanofluids 2017, 6, 550–557. [Google Scholar]
- Sheikholeslami, M. New computational approach for exergy and entropy analysis of nanofluid under the impact of Lorentz force through a porous media. Comput. Methods Appl. Mech. Eng. 2019, 344, 319–333. [Google Scholar] [CrossRef]
- Awais, M.; Shah, Z.; Parveen, N.; Ali, A.; Kumam, P.; Rehman, H.; Thounthong, P. MHD effects on ciliary-induced peristaltic flow coatings with rheological hybrid nanofluid. Coatings 2020, 10, 186. [Google Scholar] [CrossRef]
- Alsagri, A.S.; Nasir, S.; Gul, T.; Islam, S.; Nisar, K.; Shah, Z.; Khan, I. MHD thin film flow and thermal analysis of blood with CNTs nanofluid. Coatings 2019, 9, 175. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).