Molecular Dynamics Simulations of Vacancy Generation and Migration near a Monocrystalline Silicon Surface during Energetic Cluster Ion Implantation
Abstract
1. Introduction
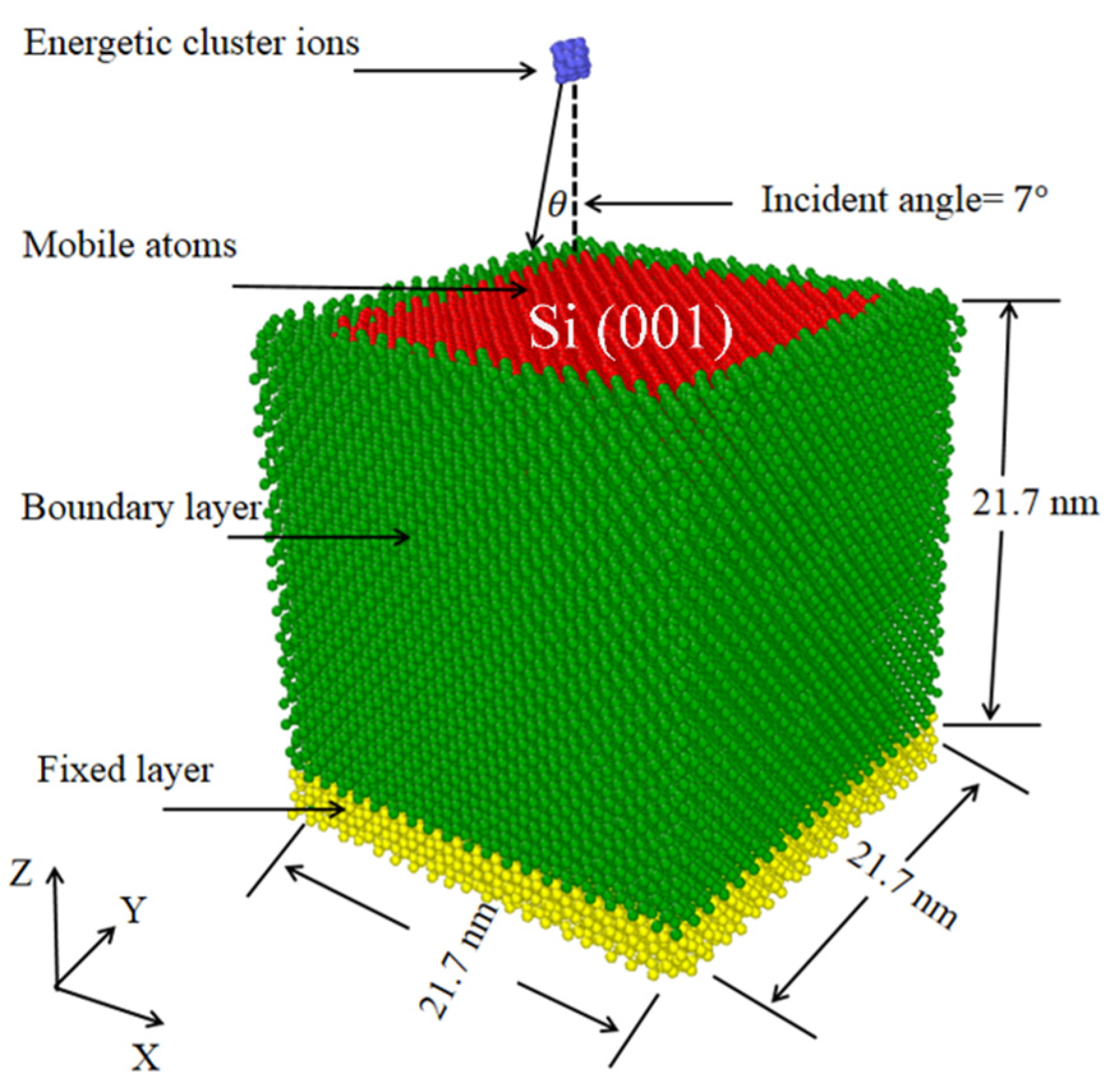
2. Simulation Method and Model
3. Results and Discussion
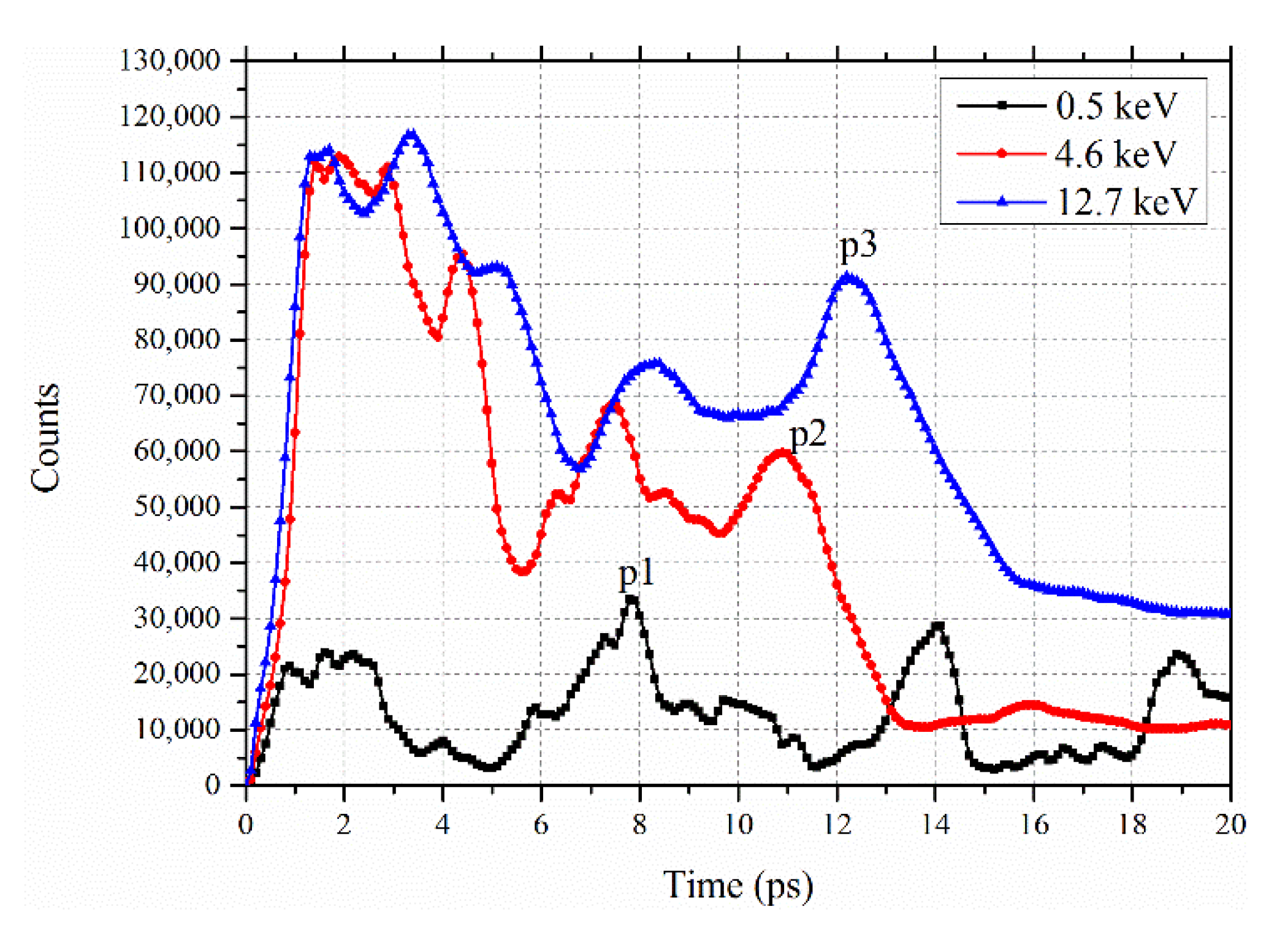
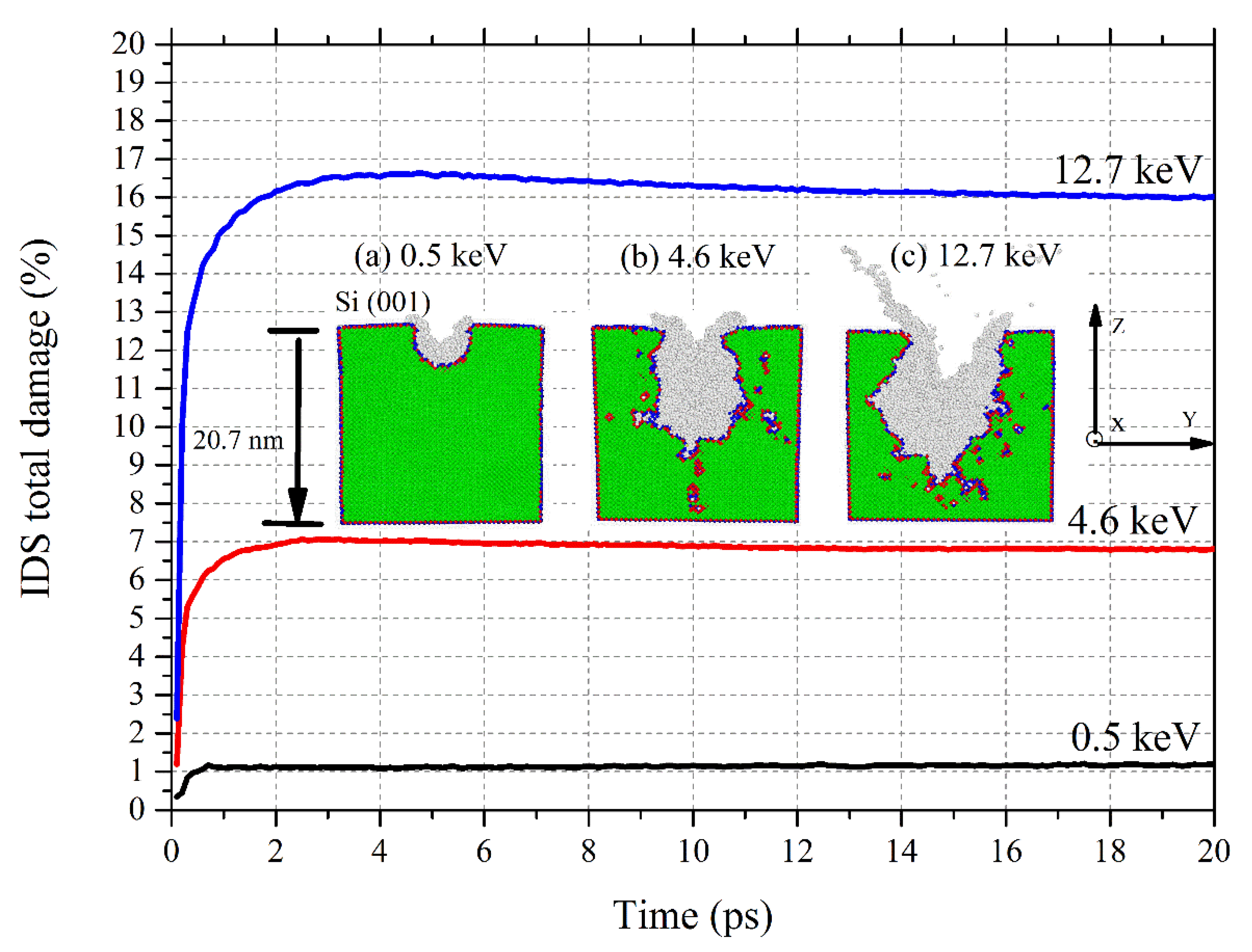
3.1. Silicon Target Surface Damage during Energetic Cluster Ion Implantation
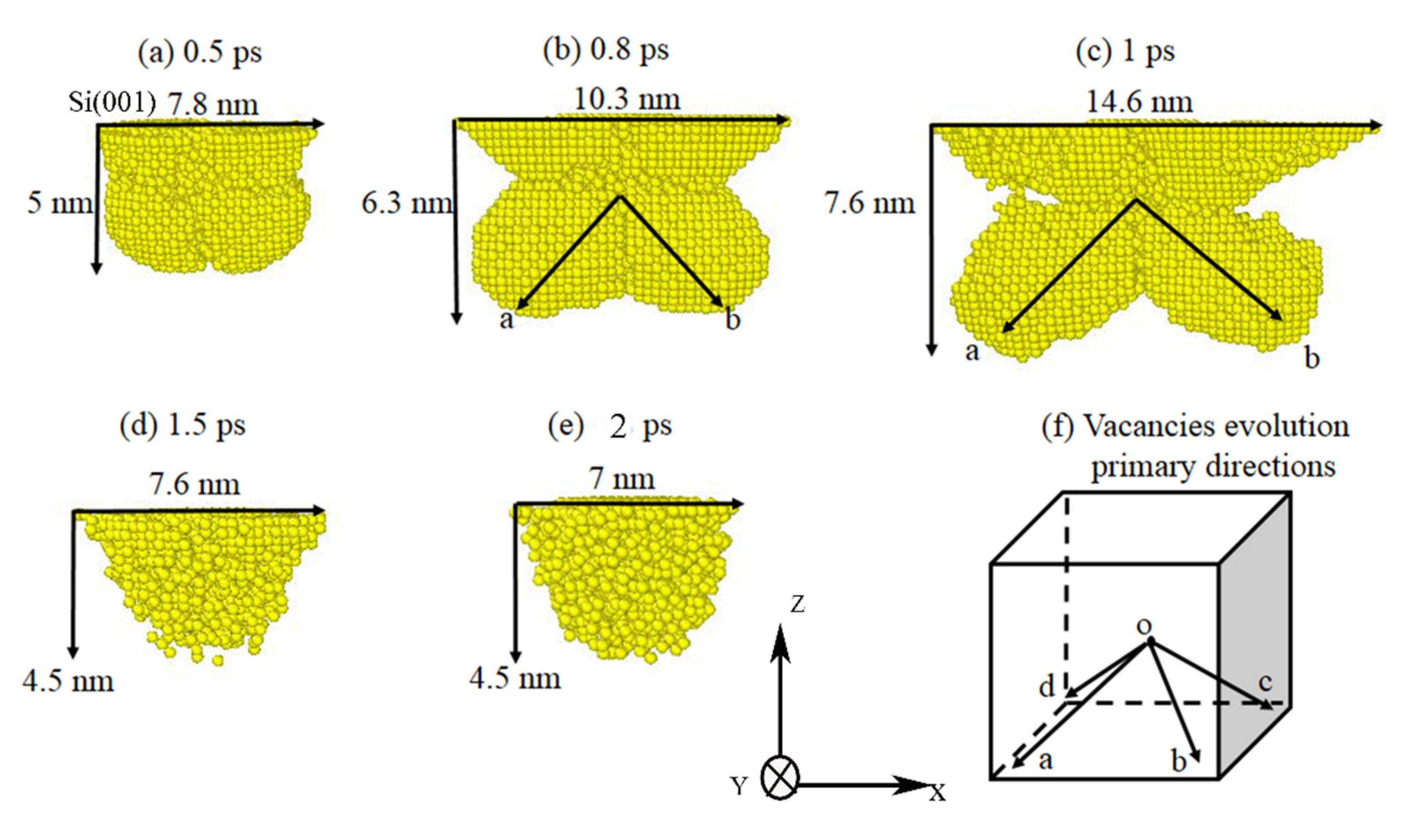
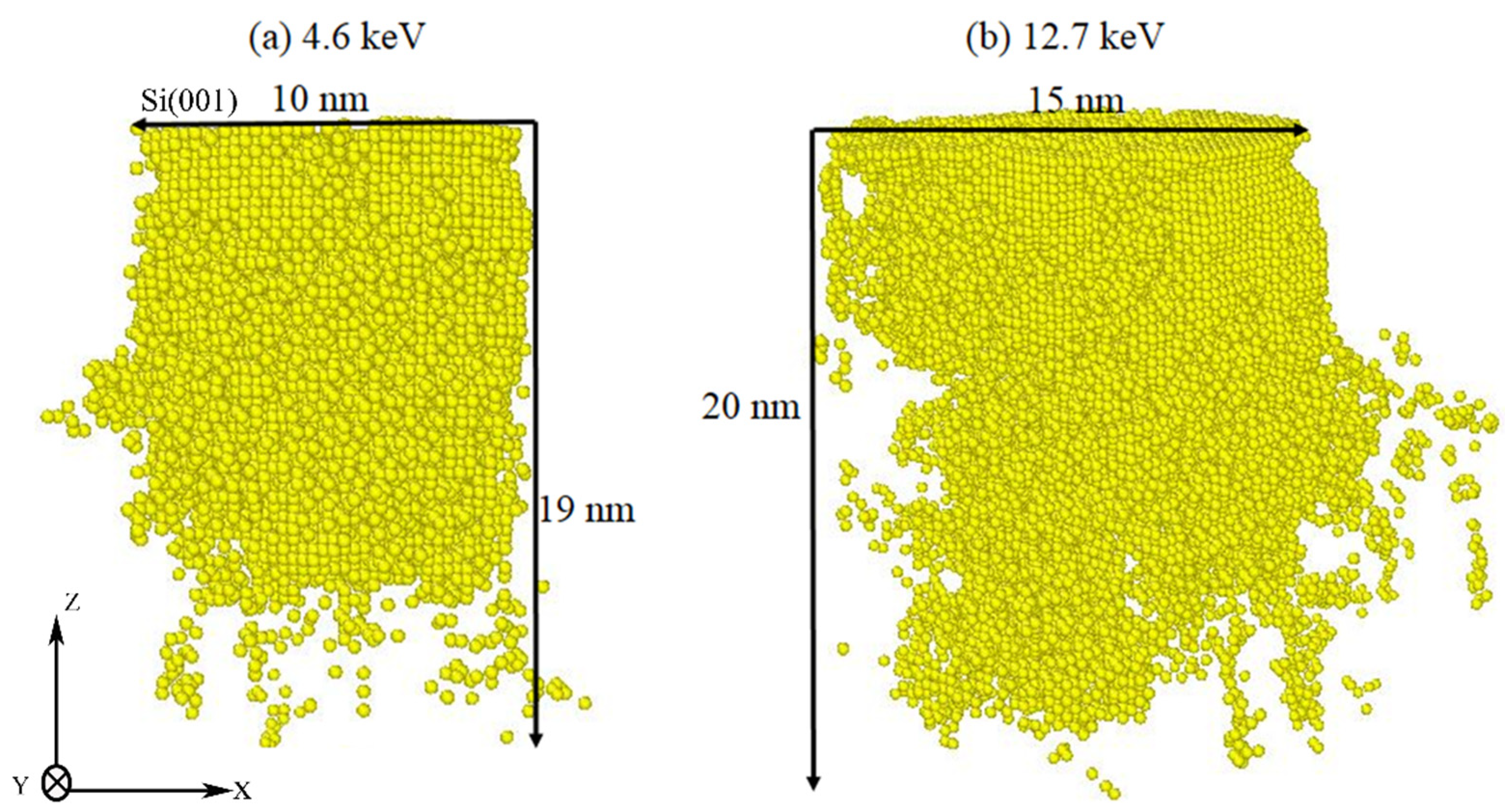
3.2. Vacancy Generation and Migration during Si35 Cluster Implantation
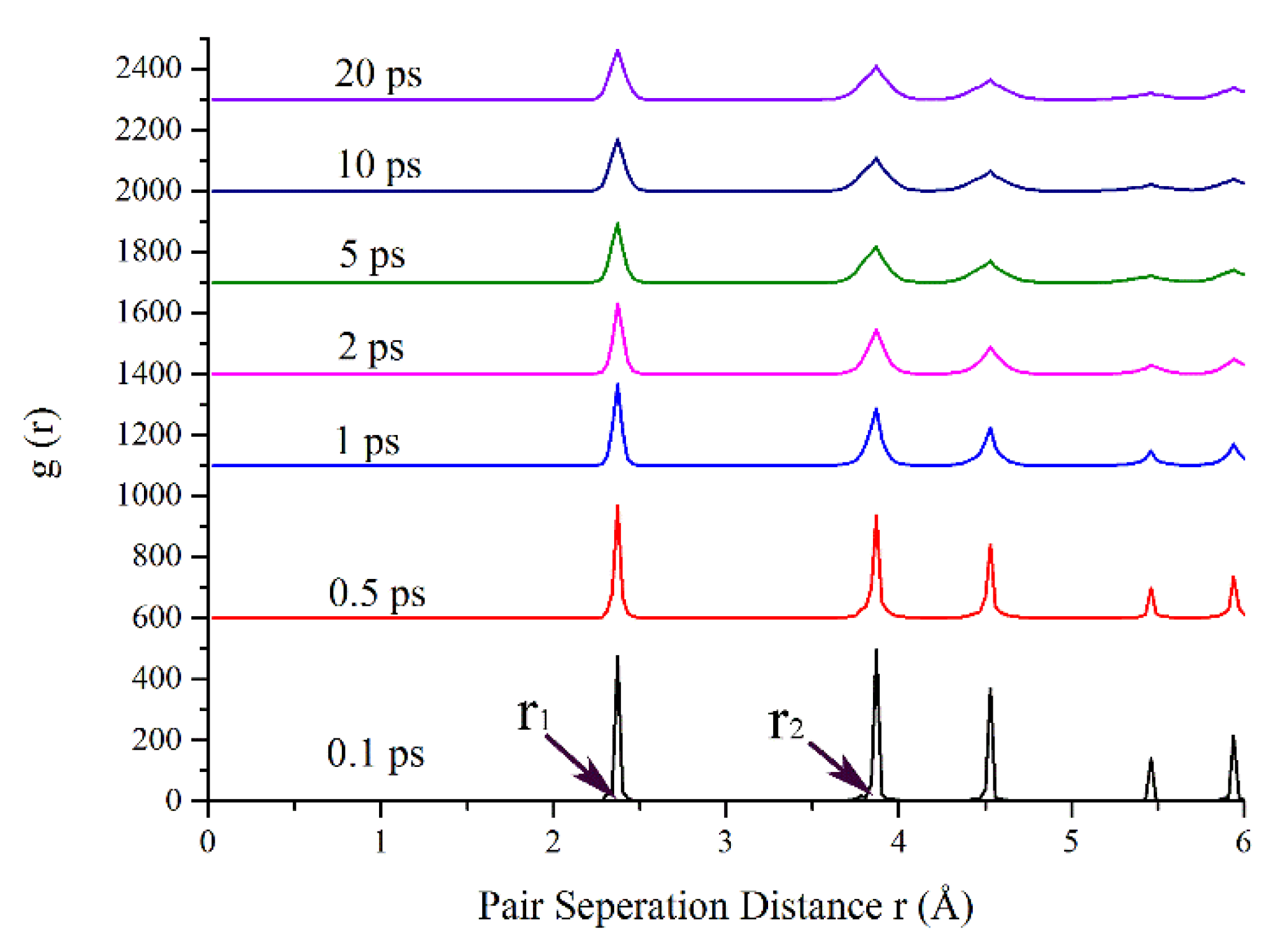
3.3. Identify Diamond Structure Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Current, M.I. Ion implantation of advanced silicon devices : Past, present and future. Mater. Sci. Semicond. Process. 2017, 62, 13–22. [Google Scholar] [CrossRef]
- Schultz, P.J.; Jagadish, C.; Ridgway, M.C.; Elliman, R.G.; Williams, J.S. Crystalline-to-amorphous transition for Si-ion irradiation of Si(100). Phys. Rev. Lett. 1991, 44, 9118–9121. [Google Scholar] [CrossRef] [PubMed]
- Pelaz, L.; Marqús, L.A.; Barbolla, J. Ion-beam-induced amorphization and recrystallization in silicon. J. Appl. Phys. 2004, 96, 5947–5976. [Google Scholar] [CrossRef]
- Wallace, J.B.; Bayu Aji, L.B.; Shao, L.; Kucheyev, S.O. Deterministic Role of Collision Cascade Density in Radiation Defect Dynamics in Si. Phys. Rev. Lett. 2018, 120, 216101. [Google Scholar] [CrossRef] [PubMed]
- Kempton, W.; Tomic, J. Vehicle-to-grid power fundamentals: Calculating capacity and net revenue. J. Power Sources 2005, 144, 268–279. [Google Scholar] [CrossRef]
- Baktash, A.; Sasani, A.; Alavizargar, A.; Mirabbaszadeh, K. First principle study of Nb defects in anatase (101) TiO2 surface. Mat. Sci. Semicon. Proc. 2016, 45, 45–50. [Google Scholar] [CrossRef]
- Nordlund, K.; Samela, J. Atomic flows, coronas and cratering in Au, Si and SiO2. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2009, 267, 1420–1423. [Google Scholar] [CrossRef]
- Lively, M.; Holybee, B.; Toriyama, M.; Allain, J. Massive-scale molecular dynamics of ion-irradiated III–V compound semiconductors at the onset of nanopatterning. Nucl. Instruments Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2017, 409, 282–287. [Google Scholar] [CrossRef]
- Osmani, O.; Alzaher, I.; Peters, T.; Ban d’Etat, B.; Cassimi, A.; Lebius, H.; Monnet, I.; Medvedev, N.; Rethfeld, B.; Schleberger, M. Damage in crystalline silicon by swift heavy ion irradiation. Nucl. Instruments Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2012, 282, 43–47. [Google Scholar] [CrossRef]
- Wallace, J.B.; Bayu Aji, L.B.; Shao, L.; Kucheyev, S.O. Fractal analysis of collision cascades in pulsed-ion-beam-irradiated solids. Sci. Rep. 2017, 7, 17574. [Google Scholar] [CrossRef]
- Aoki, T.; Seki, T.; Matsuo, J. Molecular dynamics simulation study of damage formation and sputtering with huge fluorine cluster impact on silicon. Nucl. Instruments Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2013, 303, 170–173. [Google Scholar] [CrossRef]
- Aoki, T. Molecular dynamics simulations of cluster impacts on solid targets: Implantation, surface modification, and sputtering. J. Comput. Electron. 2014, 13, 108–121. [Google Scholar] [CrossRef]
- Azarov, A.Y.; Titov, A.I.; Karaseov, P.A.; Hallén, A. Effect of collision cascade density on radiation damage in SiC. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2009, 267, 1247–1250. [Google Scholar] [CrossRef]
- Yu, X.; Shen, J.; Zhong, H.; Zhang, J.; Yan, S.; Zhang, G.; Zhang, X.; Le, X. Thermo-hydrodynamic process simulation of craters formation and evolution on metal surfaces caused by intense pulsed ion beams. Vacuum 2015, 120, 116–120. [Google Scholar] [CrossRef]
- Shen, J.; Yu, X.; Zhang, J.; Zhong, H.; Cui, X.; Liang, G.; Yu, X.; Huang, W.; Shahid, I.; Zhang, X.; et al. Anisotropy effect of crater formation on single crystal silicon surface under intense pulsed ion beam irradiation. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2018, 421, 7–12. [Google Scholar] [CrossRef]
- Xiao, Y.J.; Fang, F.Z.; Xu, Z.W.; Hu, X.T. Annealing recovery of nanoscale silicon surface damage caused by Ga focused ion beam. Appl. Surf. Sci. 2015, 343, 56–69. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Ziegler, J.; Biersack, J.; Littmark, U. The Stopping and Range of Ions in Solids; Pergamon Press: New York, NY, USA, 1985. [Google Scholar] [CrossRef]
- Tersoff, J. Modeling solid-state chemistry: Interatomic potentials for multicomponent systems. Phys. Rev. B 1989, 39, 5566–5568. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Liu, S.; Li, H.; He, Y.; Li, X.; Li, Y.; Wang, X. Pathway into the silicon nucleation on silicene substrate at nanoscale. Mater. Des. 2015, 85, 60–66. [Google Scholar] [CrossRef]
- Fang, K.C.; Weng, C.I.; Ju, S.P. An investigation into the structural features and thermal conductivity of silicon nanoparticles using molecular dynamics simulations. Nanotechnology 2006, 17, 3909–3914. [Google Scholar] [CrossRef]
- Peng, Q.; Meng, F.; Yang, Y.; Lu, C.; Deng, H.; Wang, L.; De, S.; Gao, F. Shockwave generates <100 > dislocation loops in bcc iron. Nat. Commun. 2018, 9. [Google Scholar] [CrossRef]
- Wigner, E.; Seitz, F. On the constitution of Metallic Sodium. Phys. Rev. 1933, 68, 804–810. [Google Scholar] [CrossRef]
- Bai, X.M.; Voter, A.F.; Hoagland, R.G.; Nastasi, M.; Uberuaga, B.P. Efficient annealing of radiation damage near grain boundaries via interstitial emission. Science 2010, 327, 1631–1634. [Google Scholar] [CrossRef] [PubMed]
- Maras, E.; Trushin, O.; Stukowski, A.; Ala-Nissila, T.; Jónsson, H. Global transition path search for dislocation formation in Ge on Si(001). Comput. Phys. Commun. 2016, 205, 13–21. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, G.; Zhong, H.; Wang, Y.; Zhang, S.; Xu, M.; Kuang, S.; Ren, J.; Zhang, N.; Yan, S.; Yu, X.; et al. Molecular Dynamics Simulations of Vacancy Generation and Migration near a Monocrystalline Silicon Surface during Energetic Cluster Ion Implantation. Coatings 2020, 10, 146. https://doi.org/10.3390/coatings10020146
Liang G, Zhong H, Wang Y, Zhang S, Xu M, Kuang S, Ren J, Zhang N, Yan S, Yu X, et al. Molecular Dynamics Simulations of Vacancy Generation and Migration near a Monocrystalline Silicon Surface during Energetic Cluster Ion Implantation. Coatings. 2020; 10(2):146. https://doi.org/10.3390/coatings10020146
Chicago/Turabian StyleLiang, Guoying, Haowen Zhong, Yinong Wang, Shijian Zhang, Mofei Xu, Shicheng Kuang, Jianhui Ren, Nan Zhang, Sha Yan, Xiao Yu, and et al. 2020. "Molecular Dynamics Simulations of Vacancy Generation and Migration near a Monocrystalline Silicon Surface during Energetic Cluster Ion Implantation" Coatings 10, no. 2: 146. https://doi.org/10.3390/coatings10020146
APA StyleLiang, G., Zhong, H., Wang, Y., Zhang, S., Xu, M., Kuang, S., Ren, J., Zhang, N., Yan, S., Yu, X., Remnev, G. E., & Le, X. (2020). Molecular Dynamics Simulations of Vacancy Generation and Migration near a Monocrystalline Silicon Surface during Energetic Cluster Ion Implantation. Coatings, 10(2), 146. https://doi.org/10.3390/coatings10020146



