Unraveling the Complex Interactions: Machine Learning Approaches to Predict Bacterial Survival against ZnO and Lanthanum-Doped ZnO Nanoparticles
Abstract
1. Introduction
2. Results and Discussion
2.1. Nanoparticle Characterization
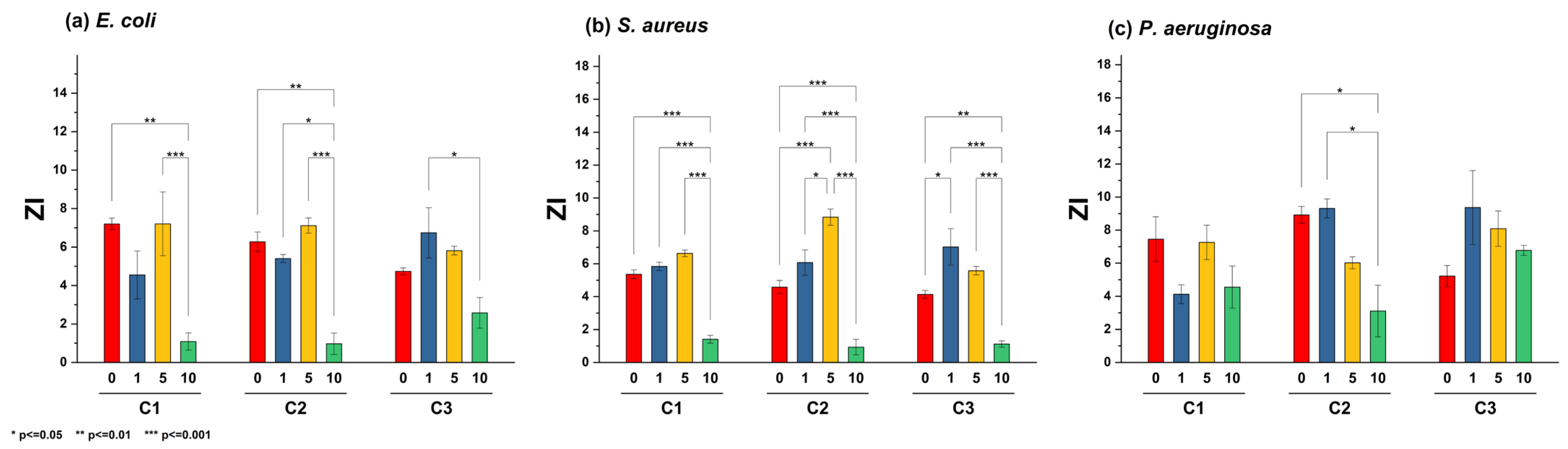
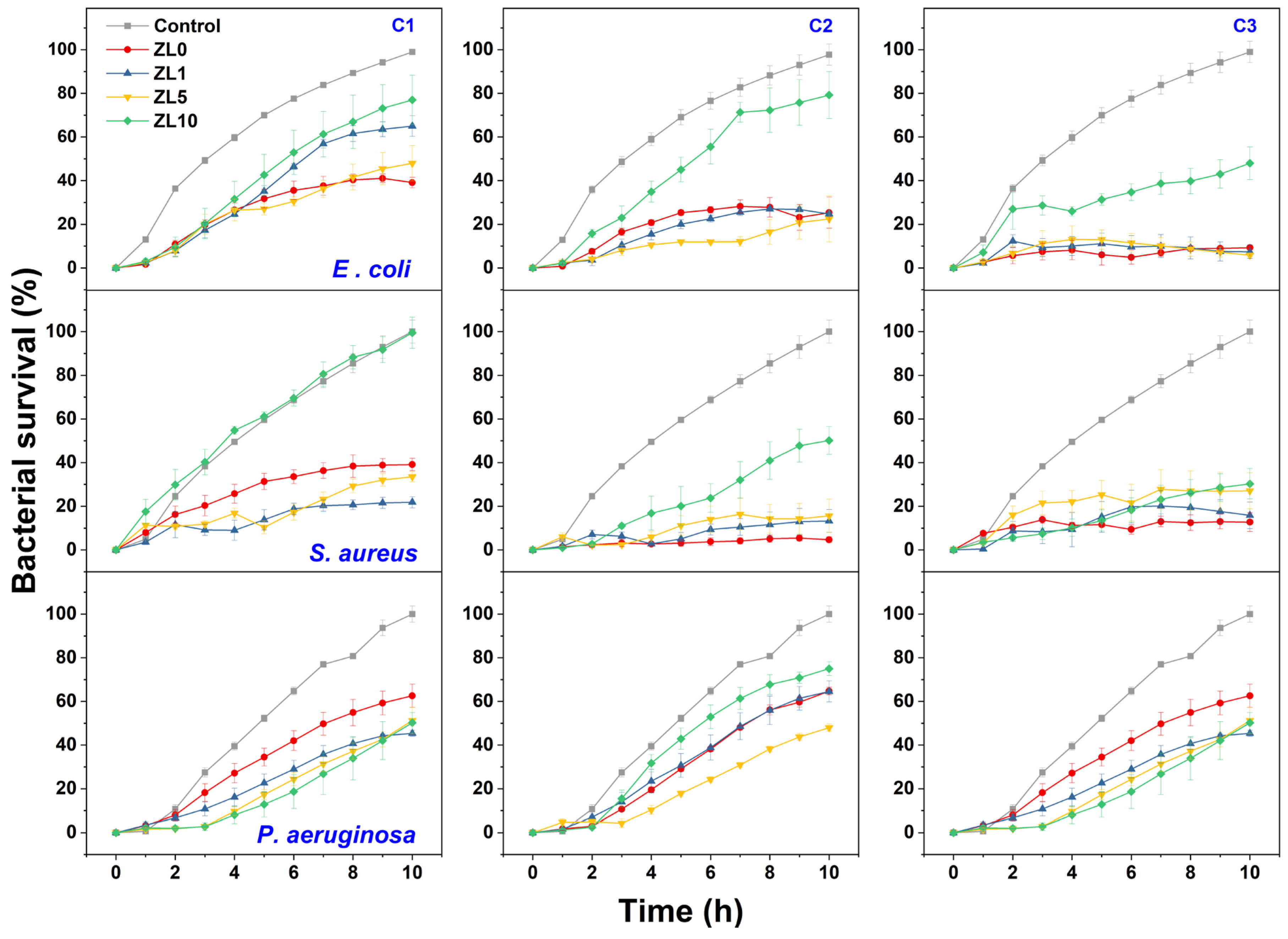
2.2. Potential Role of Particles as Nano-Antibiotics
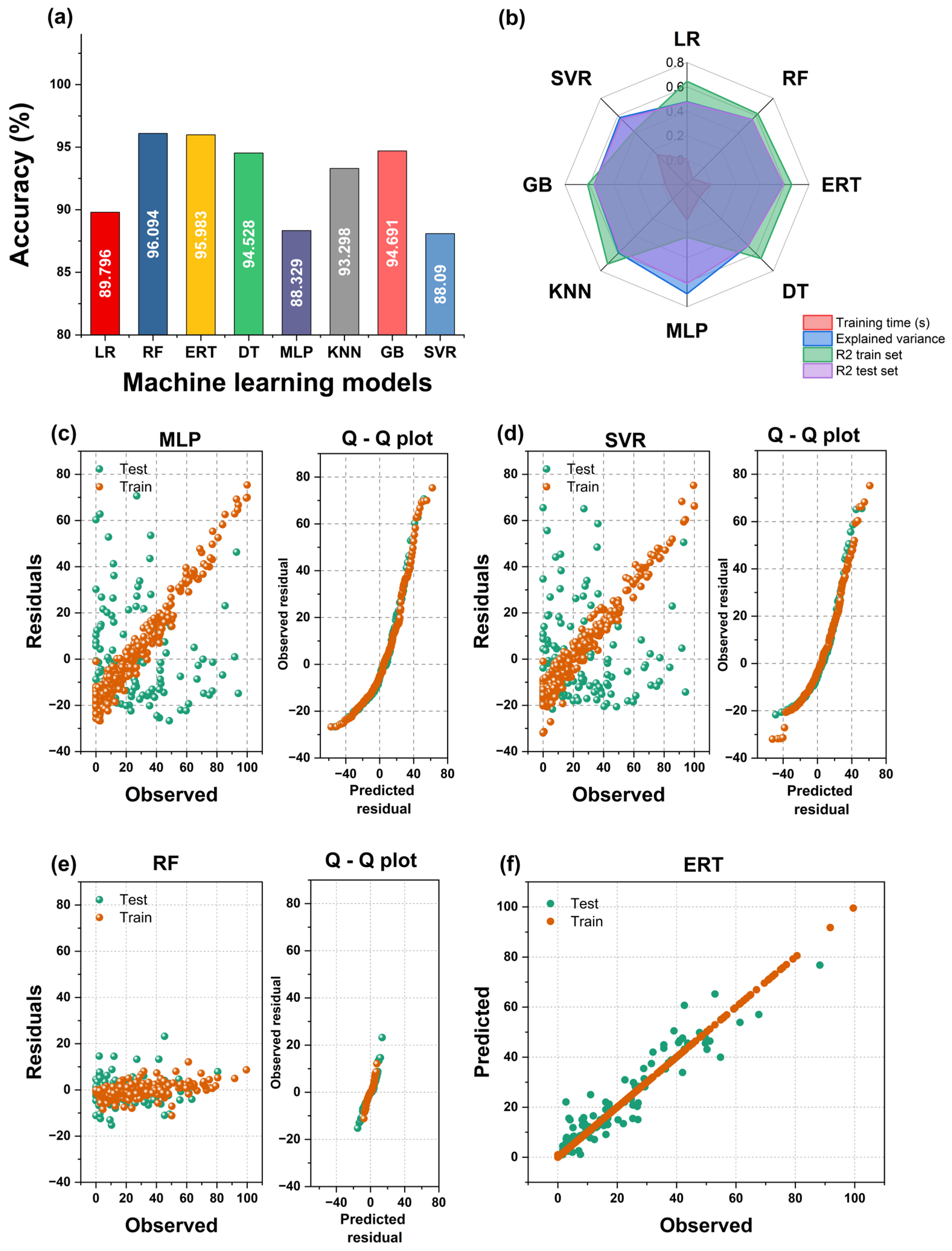
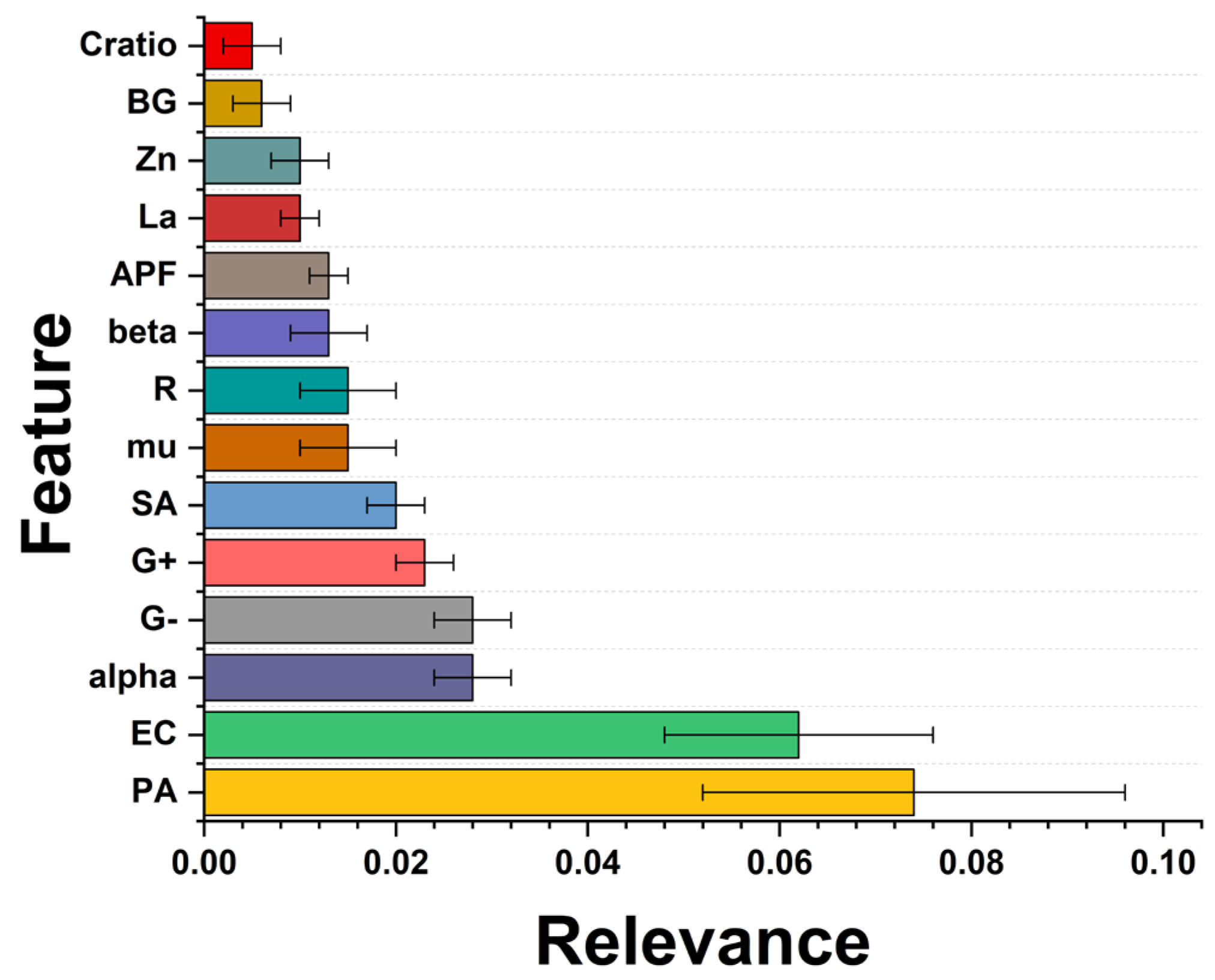
2.3. Machine Learning Modeling
2.4. Hyperparameter Optimization
- Define the hyperparameter search space: The first step is to define a range of values for each hyperparameter that will be optimized.
- Set the number of iterations: Next, determine how many iterations of the random search will be run. This will determine the number of combinations of hyperparameters that will be sampled.
- Sample hyperparameters: For each iteration, randomly sample a set of hyperparameters from the defined search space.
- Train the model: Train a model using the sampled hyperparameters.
- Evaluate the model on a validation set.
- Store the results: Store the hyperparameters and the corresponding performance metric (e.g., accuracy, F1 score) for each iteration.
- Select the best hyperparameters: After completing all iterations, select the set of hyperparameters that performed the best on the validation set.
3. Methods
3.1. Nanoparticles Synthesis
3.2. Nanoparticles Characterization Techniques
3.3. Effect of Nanoparticles on Bacterial Growth
3.4. Quantitative Determination of the Effect of Nanoparticles on Bacterial Growth
3.5. Statistical Data Analysis
3.6. Machine Learning Modeling
- Define the problem: The first step is clearly defining the problem you want to solve with the regression model. This includes identifying the input variables (features) and the output variable (target) that you want to predict.
- Collect and preprocess the data: Next, you need to collect and preprocess the data used to train and test the model. This involves cleaning the data, handling missing values, removing outliers, and splitting the data into training and testing sets.
- Choose a regression algorithm: There are several regression algorithms, such as linear regression, polynomial regression, and support vector regression. You need to select the appropriate algorithm based on the problem you are trying to solve and the characteristics of your data.
- Train the model: Once you have chosen the algorithm, you must train the model using the training data. This involves feeding the input data into the algorithm, which will adjust its internal parameters to produce the best possible predictions for the output variable.
- Evaluate the model: After training, you must evaluate its performance using the testing data. This involves measuring how well the model predicts the output variable on data it has not seen before. Standard evaluation metrics include mean squared error (MSE) and R-squared.
- Tune the model: If the model’s performance is unsatisfactory, you can try to improve it by tweaking its parameters or using a different algorithm. This process is called hyperparameter tuning, and involves testing different combinations of parameters to find the best-performing one.
- Deploy the model: Once satisfied with its performance, you can deploy it into production. This involves integrating the model into a software system or application that can use it to make predictions on new data.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adeniji, O.O.; Ojemaye, M.O.; Okoh, A.I. Antibacterial Activity of Metallic Nanoparticles against Multidrug-Resistant Pathogens Isolated from Environmental Samples: Nanoparticles/Antibiotic Combination Therapy and Cytotoxicity Study. ACS Appl. Bio Mater. 2022, 5, 4814–64826. [Google Scholar] [CrossRef]
- Frei, A.; Verderosa, A.D.; Elliott, A.G.; Zuegg, J.; Blaskovich, M.A.T. Metals to Combat Antimicrobial Resistance. Nat. Rev. Chem. 2023, 7, 202–224. [Google Scholar] [CrossRef] [PubMed]
- Deter, H.S.; Hossain, T.; Butzin, N.C. Antibiotic Tolerance Is Associated with a Broad and Complex Transcriptional Response in E. Coli. Sci. Rep. 2021, 11, 6112. [Google Scholar] [CrossRef] [PubMed]
- Ojkic, N.; Serbanescu, D.; Banerjee, S. Antibiotic Resistance via Bacterial Cell Shape-Shifting. mBio 2022, 13, e00659-22. [Google Scholar] [CrossRef]
- Huang, L.; Wu, C.; Gao, H.; Xu, C.; Dai, M.; Huang, L.; Hao, H.; Wang, X.; Cheng, G. Bacterial Multidrug Efflux Pumps at the Frontline of Antimicrobial Resistance: An Overview. Antibiotics 2022, 11, 520. [Google Scholar] [CrossRef] [PubMed]
- Yu, T.; Fu, Y.; He, J.; Zhang, J.; Xianyu, Y. Identification of Antibiotic Resistance in ESKAPE Pathogens through Plasmonic Nanosensors and Machine Learning. ACS Nano 2023, 17, 4551–4563. [Google Scholar] [CrossRef]
- Kachooei, A.; Karbalaie Niya, M.H.; Khales, P.; Sabaei, M.; Fard, S.R.; Hamidzade, M.; Tavakoli, A. Prevalence, Molecular Characterization, and Clinical Features of Human Bocavirus in Children under 5 Years of Age with Acute Gastroenteritis Admitted to a Specialized Children’s Hospital in Iran: A Cross-Sectional Study. Health Sci. Rep. 2023, 6, e1591. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhao, X.; Jiang, X.; Zhang, J.; Li, L.; Pei, C.; Zhou, Y.; Zeng, L.; Kong, X. Contribution of Flagellar Cap Gene in Virulence and Pathogenicity of Aeromonas Veronii. J. Fish Dis. 2023, 46, 247–259. [Google Scholar] [CrossRef]
- Sharmin, S.; Rahaman, M.M.; Sarkar, C.; Atolani, O.; Islam, M.T.; Adeyemi, O.S. Nanoparticles as Antimicrobial and Antiviral Agents: A Literature-Based Perspective Study. Heliyon 2021, 7, e06456. [Google Scholar] [CrossRef]
- Rabiee, N.; Ahmadi, S.; Akhavan, O.; Luque, R. Silver and Gold Nanoparticles for Antimicrobial Purposes against Multi-Drug Resistance Bacteria. Materials 2022, 15, 1799. [Google Scholar] [CrossRef]
- Sánchez-López, A.L.; Perfecto-Avalos, Y.; Sanchez-Martinez, A.; Ceballos-Sanchez, O.; Sepulveda-Villegas, M.; Rincón-Enríquez, G.; Rodríguez-González, V.; Garcia-Varela, R.; Lozano, L.M.; Eloyr Navarro-López, D.; et al. Influence of Erbium Doping on Zinc Oxide Nanoparticles: Structural, Optical and Antimicrobial Activity. Appl. Surf. Sci. 2022, 575, 151764. [Google Scholar] [CrossRef]
- Park, Y.; Lee, J.S. Bifunctional Silver-Doped ZnO for Reliable and Stable Organic-Inorganic Hybrid Perovskite Memory. ACS Appl. Mater. Interfaces 2021, 13, 1021–1026. [Google Scholar] [CrossRef]
- Wojnarowicz, J.; Chudoba, T.; Lojkowski, W. A Review of Microwave Synthesis of Zinc Oxide Nanomaterials: Reactants, Process Parameters and Morphoslogies. Nanomaterials 2020, 10, 1086. [Google Scholar] [CrossRef] [PubMed]
- Noman, M.T.; Amor, N.; Petru, M. Synthesis and Applications of ZnO Nanostructures (ZONSs): A Review. Crit. Rev. Solid. State Mater. Sci. 2022, 47, 99–141. [Google Scholar] [CrossRef]
- Shahzad, S.; Javed, S.; Usman, M. A Review on Synthesis and Optoelectronic Applications of Nanostructured ZnO. Front. Mater. 2021, 8, 613825. [Google Scholar] [CrossRef]
- Zheng, K.; Bai, J.; Yang, H.; Xu, Y.; Pan, G.; Wang, H.; Geng, D. Nanomaterial-Assisted Theranosis of Bone Diseases. Bioact. Mater. 2023, 24, 263–312. [Google Scholar] [CrossRef]
- Bian, D.; Chu, X.; Xiao, J.; Tong, Z.; Huang, H.; Jia, Q.; Liu, J.; Li, W.; Yu, H.; He, Y.; et al. Design of Single-Phased Magnesium Alloys with Typically High Solubility Rare Earth Elements for Biomedical Applications: Concept and Proof. Bioact. Mater. 2023, 22, 180–200. [Google Scholar] [CrossRef]
- Jakubowski, M.; Domke, A.; Ratajczak, M.; Szczuka, J.; Buchwald, T.; Ławniczak, Ł.; Homa, J.; Voelkel, A.; Sandomierski, M. Chitosan Hydrogel Modified with Lanthanum as a Drug Delivery System for Epigallocatechin Gallate: Investigation of Hydrogel—Drug Interaction by FT-IR and Raman Spectroscopy. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2023, 297, 122748. [Google Scholar] [CrossRef] [PubMed]
- Pęczkowski, P.; Szostak, E.; Pocheć, E.; Michalik, J.M.; Piętosa, J.; Tahraoui, T.; Łuszczek, M.; Gondek, Ł. Biocompatibility and Potential Functionality of Lanthanum-Substituted Cobalt Ferrite Spinels. J. Alloys Compd. 2023, 966, 171433. [Google Scholar] [CrossRef]
- Senthilkumar, G.; Sakthivelu, A.; Abdur Rahman, M.; Parameswari, P. Enhancement of Antibacterial and Anticancer Properties Lanthanum Insight into Zinc Oxide Nanoparticles Prepared via Coprecipitation Process. Inorg. Chem. Commun. 2023, 155, 111081. [Google Scholar] [CrossRef]
- Iqbal, T.; Masood, A.; Khalid, N.R.; Tahir, M.B.; Asiri, A.M.; Alrobei, H. Green Synthesis of Novel Lanthanum Doped Copper Oxide Nanoparticles for Photocatalytic Application: Correlation between Experiment and COMSOL Simulation. Ceram. Int. 2022, 48, 13420–13430. [Google Scholar] [CrossRef]
- Khalid, A.D.; Ur-Rehman, N.; Tariq, G.H.; Ullah, S.; Buzdar, S.A.; Iqbal, S.S.; Sher, E.K.; Alsaiari, N.S.; Hickman, G.J.; Sher, F. Functional Bioinspired Nanocomposites for Anticancer Activity with Generation of Reactive Oxygen Species. Chemosphere 2023, 310, 136885. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, X.; Cao, X.; Huang, C.; Liu, E.; Qian, S.; Liu, X.; Wu, Y.; Dong, F.; Qiu, C.W.; et al. Artificial Intelligence: A Powerful Paradigm for Scientific Research. Innovation 2021, 2, 100179. [Google Scholar] [CrossRef] [PubMed]
- Hart, G.L.W.; Mueller, T.; Toher, C.; Curtarolo, S. Machine Learning for Alloys. Nat. Rev. Mater. 2021, 6, 730–755. [Google Scholar] [CrossRef]
- Choudhary, K.; DeCost, B.; Chen, C.; Jain, A.; Tavazza, F.; Cohn, R.; Park, C.W.; Choudhary, A.; Agrawal, A.; Billinge, S.J.L.; et al. Recent Advances and Applications of Deep Learning Methods in Materials Science. NPJ Comput. Mater. 2022, 8, 59. [Google Scholar] [CrossRef]
- Sarker, I.H. Machine Learning: Algorithms, Real-World Applications and Research Directions. SN Comput. Sci. 2021, 2, 160. [Google Scholar] [CrossRef]
- Wang, A.Y.T.; Murdock, R.J.; Kauwe, S.K.; Oliynyk, A.O.; Gurlo, A.; Brgoch, J.; Persson, K.A.; Sparks, T.D. Machine Learning for Materials Scientists: An Introductory Guide toward Best Practices. Chem. Mater. 2020, 32, 4954–4965. [Google Scholar] [CrossRef]
- Mohtasham Moein, M.; Saradar, A.; Rahmati, K.; Ghasemzadeh Mousavinejad, S.H.; Bristow, J.; Aramali, V.; Karakouzian, M. Predictive Models for Concrete Properties Using Machine Learning and Deep Learning Approaches: A Review. J. Build. Eng. 2023, 63, 105444. [Google Scholar] [CrossRef]
- Bishara, D.; Xie, Y.; Liu, W.K.; Li, S. A State-of-the-Art Review on Machine Learning-Based Multiscale Modeling, Simulation, Homogenization and Design of Materials. Arch. Comput. Methods Eng. 2023, 30, 191–222. [Google Scholar] [CrossRef]
- Surucu, O.; Gadsden, S.A.; Yawney, J. Condition Monitoring Using Machine Learning: A Review of Theory, Applications, and Recent Advances. Expert. Syst. Appl. 2023, 221, 119738. [Google Scholar] [CrossRef]
- Chan, C.H.; Sun, M.; Huang, B. Application of Machine Learning for Advanced Material Prediction and Design. EcoMat 2022, 4, e12194. [Google Scholar] [CrossRef]
- Cotton, S.A.; Raithby, P.R.; Shield, A.; Harrowfield, J.M. A Comparison of the Structural Chemistry of Scandium, Yttrium, Lanthanum and Lutetium: A Contribution to the Group 3 Debate. Coord. Chem. Rev. 2022, 455, 214366. [Google Scholar] [CrossRef]
- Navarro-López, D.E.; Sánchez-Huerta, T.M.; Flores-Jimenez, M.S.; Tiwari, N.; Sanchez-Martinez, A.; Ceballos-Sanchez, O.; Garcia-Gonzalez, A.; Fuentes-Aguilar, R.Q.; Sanchez-Ante, G.; Corona-Romero, K.; et al. Nanocomposites Based on Doped ZnO Nanoparticles for Antibacterial Applications. Colloids Surf. A Physicochem. Eng. Asp. 2022, 652, 129871. [Google Scholar] [CrossRef]
- Rivera-Calderón, S.; Sepulveda-Villegas, M.; Ceballos-Sanchez, O.; Perfecto-Avalos, Y.; Tiwari, N.; Garcia-Varela, R.; Sánchez-López, A.L.; Eloyr Navarro-López, D.; López-Mena, E.R.; Sanchez-Martinez, A. Erbium-Doped ZnO Nanoparticles for Anode Materials: A Comparative Study Using Anthocyanin and Curcumin Dyes in DSSC. Mater. Lett. 2022, 315, 131988. [Google Scholar] [CrossRef]
- López-Mena, E.R.; Jiménez-Sandoval, S.J.; Jiménez-Sandoval, O. Samarium-Doped ZnO Thin Films Synthesized by Sol-Gel: Structural, Optical and Electrical Properties. Mater. Sci. Semicond. Process. 2021, 126, 105648. [Google Scholar] [CrossRef]
- Elboughdiri, N.; Iqbal, S.; Abdullaev, S.; Aljohani, M.; Safeen, A.; Althubeiti, K.; Khan, R. Enhanced Electrical and Magnetic Properties of (Co, Yb) Co-Doped ZnO Memristor for Neuromorphic Computing. RSC Adv. 2023, 13, 35993–36008. [Google Scholar] [CrossRef] [PubMed]
- Sahu, J.; Kumar, S.; Vats, V.S.; Alvi, P.A.; Dalela, B.; Kumar, S.; Dalela, S. Lattice Defects and Oxygen Vacancies Formulated Ferromagnetic, Luminescence, Structural Properties and Band-Gap Tuning in Nd3+ Substituted ZnO Nanoparticles. J. Lumin. 2022, 243, 118673. [Google Scholar] [CrossRef]
- Nishi, Y.; Kasai, Y.; Suzuki, R.; Matsubara, M.; Muramatsu, A.; Kanie, K. Gallium-Doped Zinc Oxide Nanoparticle Thin Films as Transparent Electrode Materials with High Conductivity. ACS Appl. Nano Mater. 2020, 3, 9622–9632. [Google Scholar] [CrossRef]
- Pandey, P.K.; Chauhan, V.; Dixit, P.; Pandey, P.C. Correlation of Enhanced Photocurrent with Structural and Optical Properties of Ag–ZnO Nanocomposites Synthesized by a Facile Chemical Route. Phys. B Condens. Matter 2021, 612, 412937. [Google Scholar] [CrossRef]
- Li, D.; Chen, Q.; Chun, J.; Fichthorn, K.; De Yoreo, J.; Zheng, H. Nanoparticle Assembly and Oriented Attachment: Correlating Controlling Factors to the Resulting Structures. Chem. Rev. 2023, 123, 3127–3159. [Google Scholar] [CrossRef]
- Consonni, V.; Lord, A.M. Polarity in ZnO Nanowires: A Critical Issue for Piezotronic and Piezoelectric Devices. Nano Energy 2021, 83, 105789. [Google Scholar] [CrossRef]
- Mendes, C.R.; Dilarri, G.; Forsan, C.F.; Sapata, V.d.M.R.; Lopes, P.R.M.; de Moraes, P.B.; Montagnolli, R.N.; Ferreira, H.; Bidoia, E.D. Antibacterial Action and Target Mechanisms of Zinc Oxide Nanoparticles against Bacterial Pathogens. Sci. Rep. 2022, 12, 2658. [Google Scholar] [CrossRef]
- Hastuti, E.; Subhan, A.; Amonpattaratkit, P.; Zainuri, M.; Suasmoro, S. The Effects of Fe-Doping on MnO2: Phase Transitions, Defect Structures and Its Influence on Electrical Properties. RSC Adv. 2021, 11, 7808–7823. [Google Scholar] [CrossRef]
- Li, S.; Chang, L.; Peng, J.; Gao, J.; Lu, J.; Zhang, F.; Zhu, G.; Hojamberdiev, M. Bi0 Nanoparticle Loaded on Bi3+-Doped ZnWO4 Nanorods with Oxygen Vacancies for Enhanced Photocatalytic NO Removal. J. Alloys Compd. 2020, 818, 152837. [Google Scholar] [CrossRef]
- Adimule, V.; Nandi, S.S.; Yallur, B.C.; Bhowmik, D.; Jagadeesha, A.H. Enhanced Photoluminescence Properties of Gd(x−1) SrxO: CdO Nanocores and Their Study of Optical, Structural, and Morphological Characteristics. Mater. Today Chem. 2021, 20, 100438. [Google Scholar] [CrossRef]
- Landi, S.; Segundo, I.R.; Freitas, E.; Vasilevskiy, M.; Carneiro, J.; Tavares, C.J. Use and Misuse of the Kubelka-Munk Function to Obtain the Band Gap Energy from Diffuse Reflectance Measurements. Solid State Commun. 2022, 341, 114573. [Google Scholar] [CrossRef]
- Kim, M.; Lee, H.; Krecker, M.C.; Bukharina, D.; Nepal, D.; Bunning, T.J.; Tsukruk, V.V. Switchable Photonic Bio-Adhesive Materials. Adv. Mater. 2021, 33, 2103674. [Google Scholar] [CrossRef] [PubMed]
- Shao, Q.; Lin, H.; Shao, M. Determining Locations of Conduction Bands and Valence Bands of Semiconductor Nanoparticles Based on Their Band Gaps. ACS Omega 2020, 5, 10297–10300. [Google Scholar] [CrossRef]
- Kusmierek, E. A CeO2 Semiconductor as a Photocatalytic and Photoelectrocatalytic Material for the Remediation of Pollutants in Industrial Wastewater: A Review. Catalysts 2020, 10, 1435. [Google Scholar] [CrossRef]
- Qin, S.; Xiao, W.; Zhou, C.; Pu, Q.; Deng, X.; Lan, L.; Liang, H.; Song, X.; Wu, M. Pseudomonas aeruginosa: Pathogenesis, Virulence Factors, Antibiotic Resistance, Interaction with Host, Technology Advances and Emerging Therapeutics. Signal Transduct. Target. Ther. 2022, 7, 199. [Google Scholar] [CrossRef] [PubMed]
- e Silva, R.F.; Longo Cesar Paixão, T.R.; Der Torossian Torres, M.; de Araujo, W.R. Simple and Inexpensive Electrochemical Paper-Based Analytical Device for Sensitive Detection of Pseudomonas aeruginosa. Sens. Actuators B Chem. 2020, 308, 127669. [Google Scholar] [CrossRef]
- Simoska, O.; Stevenson, K.J. Electrochemical Sensors for Detection of Pseudomonas aeruginosa Virulence Biomarkers: Principles of Design and Characterization. Sens. Actuators Rep. 2022, 4, 100072. [Google Scholar] [CrossRef]
- Alonso, B.; Fernández-Barat, L.; Di Domenico, E.G.; Marín, M.; Cercenado, E.; Merino, I.; de Pablos, M.; Muñoz, P.; Guembe, M. Characterization of the Virulence of Pseudomonas aeruginosa Strains Causing Ventilator-Associated Pneumonia. BMC Infect. Dis. 2020, 20, 909. [Google Scholar] [CrossRef]
- Jabłońska, J.; Dubrowska, K.; Augustyniak, A.; Wróbel, R.J.; Piz, M.; Cendrowski, K.; Rakoczy, R. The Influence of Nanomaterials on Pyocyanin Production by Pseudomonas aeruginosa. Appl. Nanosci. 2022, 12, 1929–1940. [Google Scholar] [CrossRef]
- Saleh, M.M.; Sadeq, R.A.; Abdel Latif, H.K.; Abbas, H.A.; Askoura, M. Zinc Oxide Nanoparticles Inhibits Quorum Sensing and Virulence in Pseudomonas aeruginosa. Afr. Health Sci. 2019, 19, 2043–2055. [Google Scholar] [CrossRef]
- Okeke, I.S.; Agwu, K.K.; Ubachukwu, A.A.; Madiba, I.G.; Maaza, M.; Whyte, G.M.; Ezema, F.I. Impact of Particle Size and Surface Defects on Antibacterial and Photocatalytic Activities of Undoped and Mg-Doped ZnO Nanoparticles, Biosynthesized Using One-Step Simple Process. Vacuum 2021, 187, 110110. [Google Scholar] [CrossRef]
- Perfecto-Avalos, Y.; Navarro-López, D.E.; Martínez-Beltrán, S.; Rojas-Torres, D.E.; Suárez Ávila, K.D.; Robles, T.I.; Zavala, A.; de Luna, M.A.; Sanchez-Martinez, A.; Ceballos-Sanchez, O.; et al. Data-Driven Machine Learning to Predict Antibacterial Activity of Cerium-Doped Nanoparticles. ACS Appl. Nano Mater. 2023, 6, 20719–20730. [Google Scholar] [CrossRef]
- Ghaffari, S.-B.; Sarrafzadeh, M.-H.; Salami, M.; Alvandi, A. A Comparative Study of the Action Mechanisms and Development Strategies of Different ZnO-Based Nanostructures in Antibacterial and Anticancer Applications. J. Drug Deliv. Sci. Technol. 2024, 91, 105221. [Google Scholar] [CrossRef]
- Munawar, T.; Yasmeen, S.; Mukhtar, F.; Nadeem, M.S.; Mahmood, K.; Saqib Saif, M.; Hasan, M.; Ali, A.; Hussain, F.; Iqbal, F. Zn0.9Ce0.05M0.05O (M = Er, Y, V) Nanocrystals: Structural and Energy Bandgap Engineering of ZnO for Enhancing Photocatalytic and Antibacterial Activity. Ceram. Int. 2020, 46, 14369–14383. [Google Scholar] [CrossRef]
- Navarro-López, D.E.; Garcia-Varela, R.; Ceballos-Sanchez, O.; Sanchez-Martinez, A.; Sanchez-Ante, G.; Corona-Romero, K.; Buentello-Montoya, D.A.; Elías-Zuñiga, A.; López-Mena, E.R. Effective Antimicrobial Activity of ZnO and Yb-Doped ZnO Nanoparticles against Staphylococcus Aureus and Escherichia Coli. Mater. Sci. Eng. C 2021, 123, 112004–112015. [Google Scholar] [CrossRef] [PubMed]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of Deep Learning: Concepts, CNN Architectures, Challenges, Applications, Future Directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef] [PubMed]
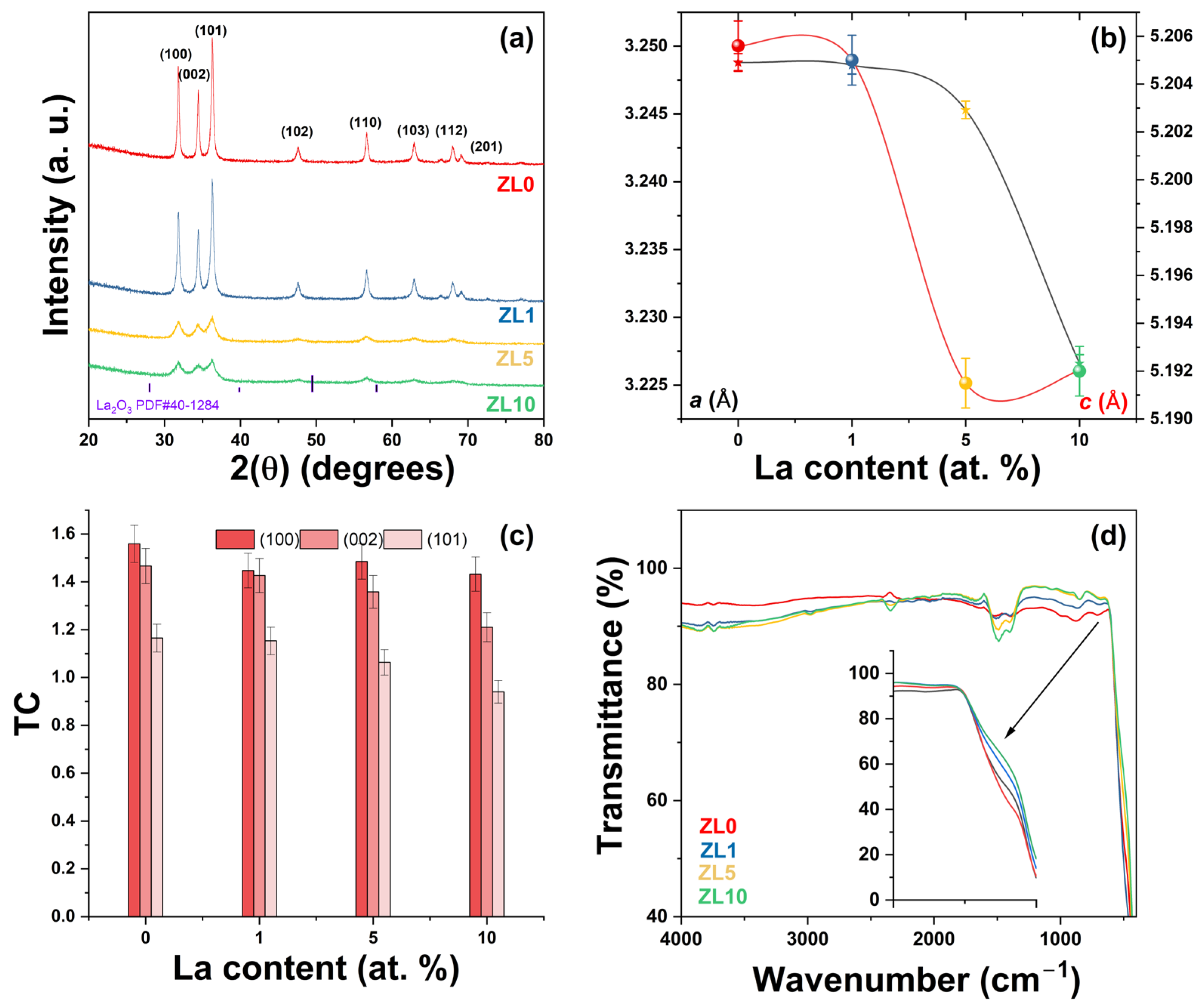
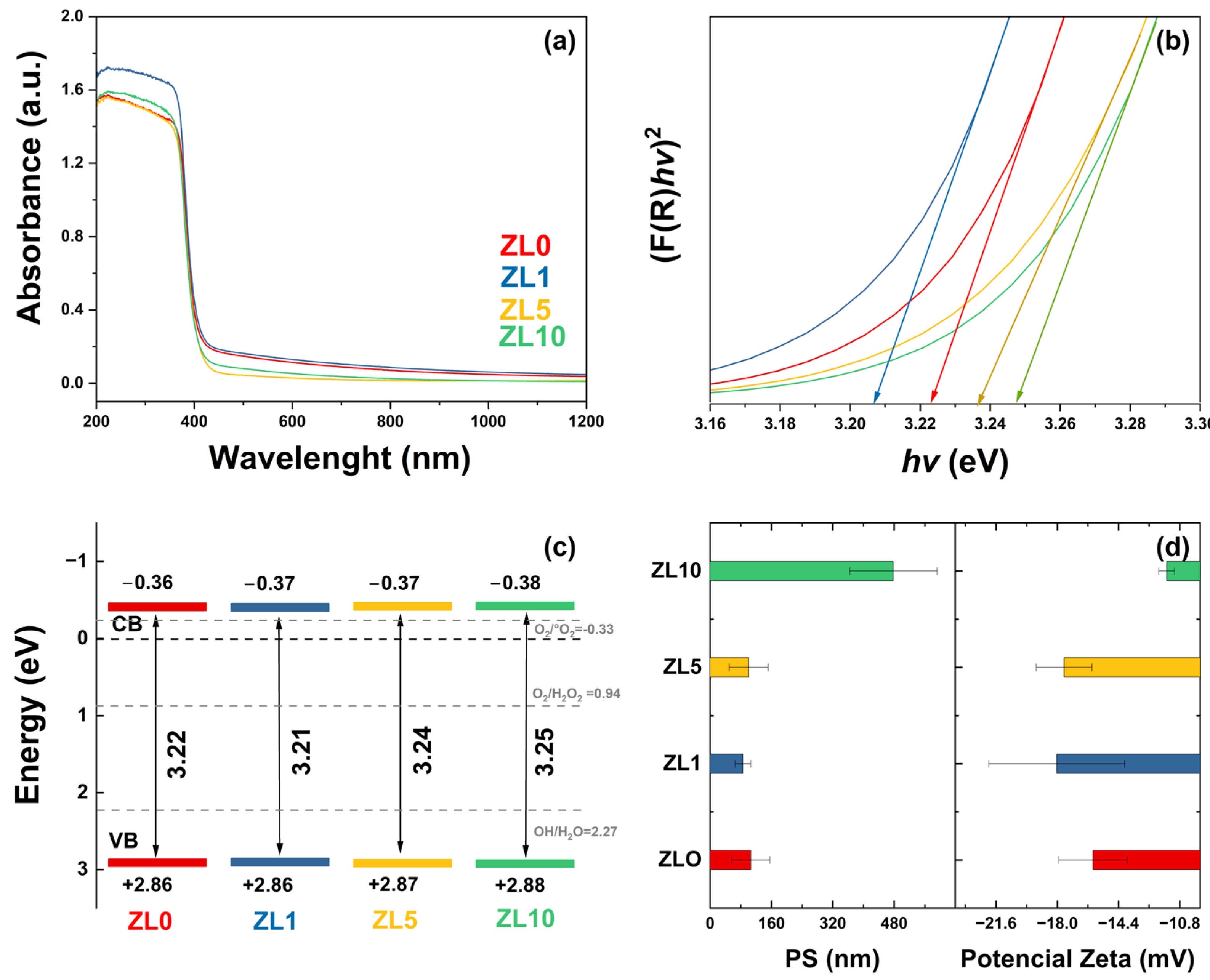
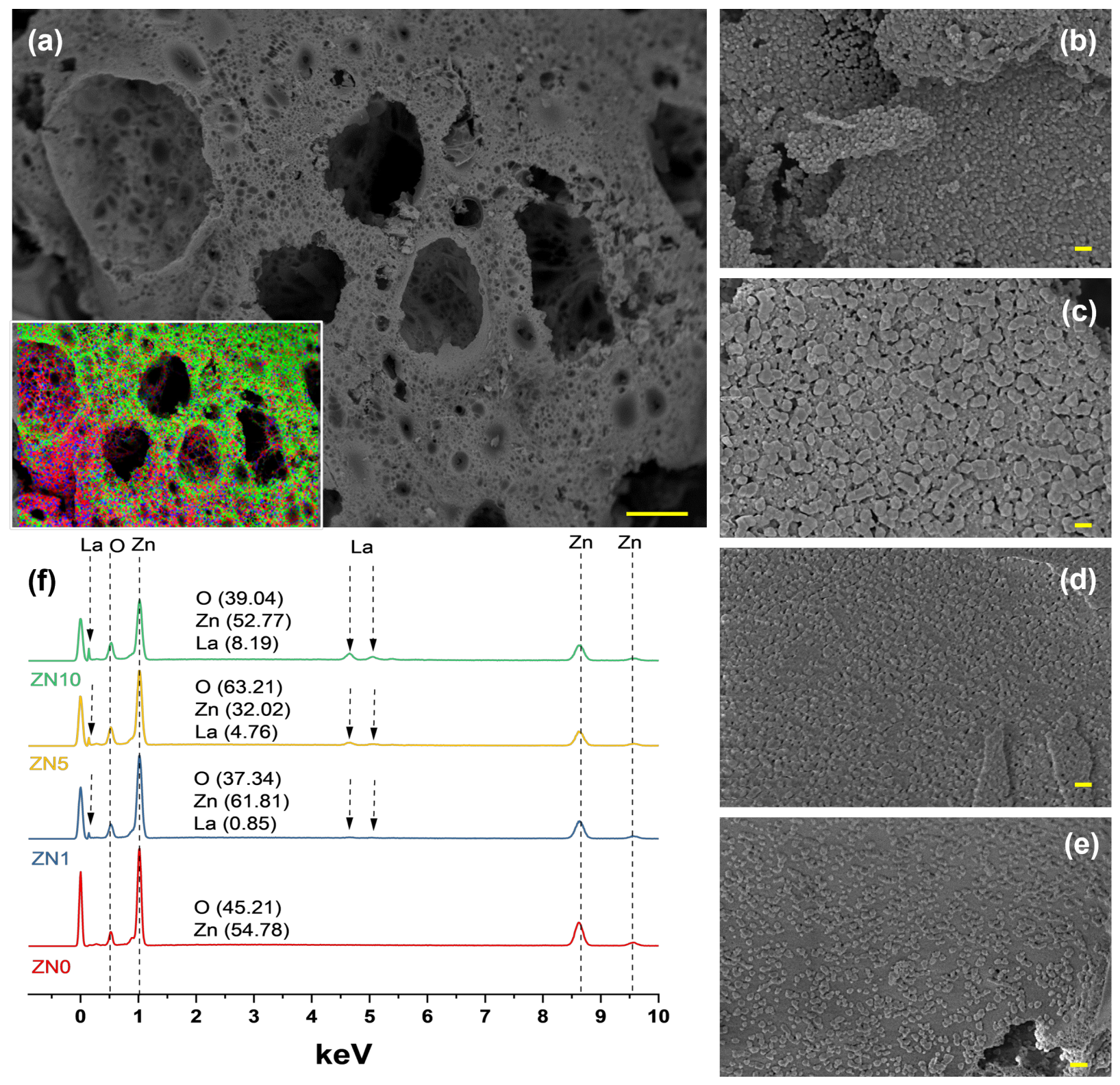



| Sample | 2(θ) (100) | 2(θ) (101) | c/a Ratio | Unit Cell Vol (Å3) | Distortion (R) | D (nm) |
|---|---|---|---|---|---|---|
| ZL0 | 31.778 | 36.277 | 1.602 | 47.58 | 1.019 | 27 |
| ZL1 | 31.780 | 36.280 | 1.602 | 45.57 | 1.019 | 24 |
| ZL5 | 31.813 | 36.267 | 1.600 | 47.35 | 1.020 | 6 |
| ZL0 | 32.002 | 36.405 | 1.609 | 46.81 | 1.015 | 5 |
| Model | Training Time (s) | Prediction Time (s) | Explained Variance | MAE | R2 Train Set | R2 Test Set |
|---|---|---|---|---|---|---|
| LR | 0.011 | 0.000 | 0.4785 | 10.204 | 0.6457 | 0.4722 |
| RF | 0.080 | 0.003 | 0.9046 | 3.906 | 0.9844 | 0.9022 |
| ERT | 0.069 | 0.003 | 0.9003 | 4.017 | 0.9999 | 0.9047 |
| DT | 0.001 | 0.000 | 0.7917 | 5.472 | 1.0 | 0.791 |
| MLP | 0.258 | 0.000 | 0.3787 | 11.671 | 0.2860 | 0.3619 |
| KNN | 0.001 | 0.081 | 0.7504 | 6.702 | 0.9037 | 0.7282 |
| GB | 0.048 | 0.001 | 0.862 | 5.309 | 0.9393 | 0.8595 |
| SVR | 0.008 | 0.004 | 0.2664 | 11.91 | 0.1689 | 0.2555 |
| Model | Parameters | MAE | Accuracy | R2 Score |
|---|---|---|---|---|
| Random Forest | Default | 3.96 | 58.16 | 0.90 |
| Random Forest * | {‘n_estimators’: 500, ‘min_samples_split’: 2, ‘min_samples_leaf’: 1, ‘max_features’: ‘sqrt’, ‘max_depth’: 60, ‘bootstrap’: False} | 3.98 | 58.80 | 0.91 |
| Extremely Randomized Trees | Default | 3.98 | 53.89 | 0.90 |
| Extremely Randomized Trees * | n_estimators: 522, min_samples_split: 2, min_samples_leaf: 1, max_features: sqrt, max_depth: 20, criterion: log2, bootstrap: False | 3.48 | 62.27 | 0.95 |
| Sample | PVA (g) | Sucrose (g) | Zn2+ Precursor | La3+ Precursor |
|---|---|---|---|---|
| ZL0 | 0.4 | 3.0 | 3.654 | 0 |
| ZL1 | 0.4 | 3.0 | 3.568 | 0.065 |
| ZL5 | 0.4 | 3.0 | 3.321 | 0.254 |
| ZL10 | 0.4 | 3.0 | 3.016 | 0.487 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Navarro-López, D.E.; Perfecto-Avalos, Y.; Zavala, A.; de Luna, M.A.; Sanchez-Martinez, A.; Ceballos-Sanchez, O.; Tiwari, N.; López-Mena, E.R.; Sanchez-Ante, G. Unraveling the Complex Interactions: Machine Learning Approaches to Predict Bacterial Survival against ZnO and Lanthanum-Doped ZnO Nanoparticles. Antibiotics 2024, 13, 220. https://doi.org/10.3390/antibiotics13030220
Navarro-López DE, Perfecto-Avalos Y, Zavala A, de Luna MA, Sanchez-Martinez A, Ceballos-Sanchez O, Tiwari N, López-Mena ER, Sanchez-Ante G. Unraveling the Complex Interactions: Machine Learning Approaches to Predict Bacterial Survival against ZnO and Lanthanum-Doped ZnO Nanoparticles. Antibiotics. 2024; 13(3):220. https://doi.org/10.3390/antibiotics13030220
Chicago/Turabian StyleNavarro-López, Diego E., Yocanxóchitl Perfecto-Avalos, Araceli Zavala, Marco A. de Luna, Araceli Sanchez-Martinez, Oscar Ceballos-Sanchez, Naveen Tiwari, Edgar R. López-Mena, and Gildardo Sanchez-Ante. 2024. "Unraveling the Complex Interactions: Machine Learning Approaches to Predict Bacterial Survival against ZnO and Lanthanum-Doped ZnO Nanoparticles" Antibiotics 13, no. 3: 220. https://doi.org/10.3390/antibiotics13030220
APA StyleNavarro-López, D. E., Perfecto-Avalos, Y., Zavala, A., de Luna, M. A., Sanchez-Martinez, A., Ceballos-Sanchez, O., Tiwari, N., López-Mena, E. R., & Sanchez-Ante, G. (2024). Unraveling the Complex Interactions: Machine Learning Approaches to Predict Bacterial Survival against ZnO and Lanthanum-Doped ZnO Nanoparticles. Antibiotics, 13(3), 220. https://doi.org/10.3390/antibiotics13030220