Exploring Orientation Invariant Heuristic Features with Variant Window Length of 1D-CNN-LSTM in Human Activity Recognition
Abstract
:1. Introduction
- How can sensor orientation be solved?
- What is the impact of window length on model accuracy?
- What is the impact of the inter-participant validation method in the case of a vast number of participants?
2. Materials and Methods
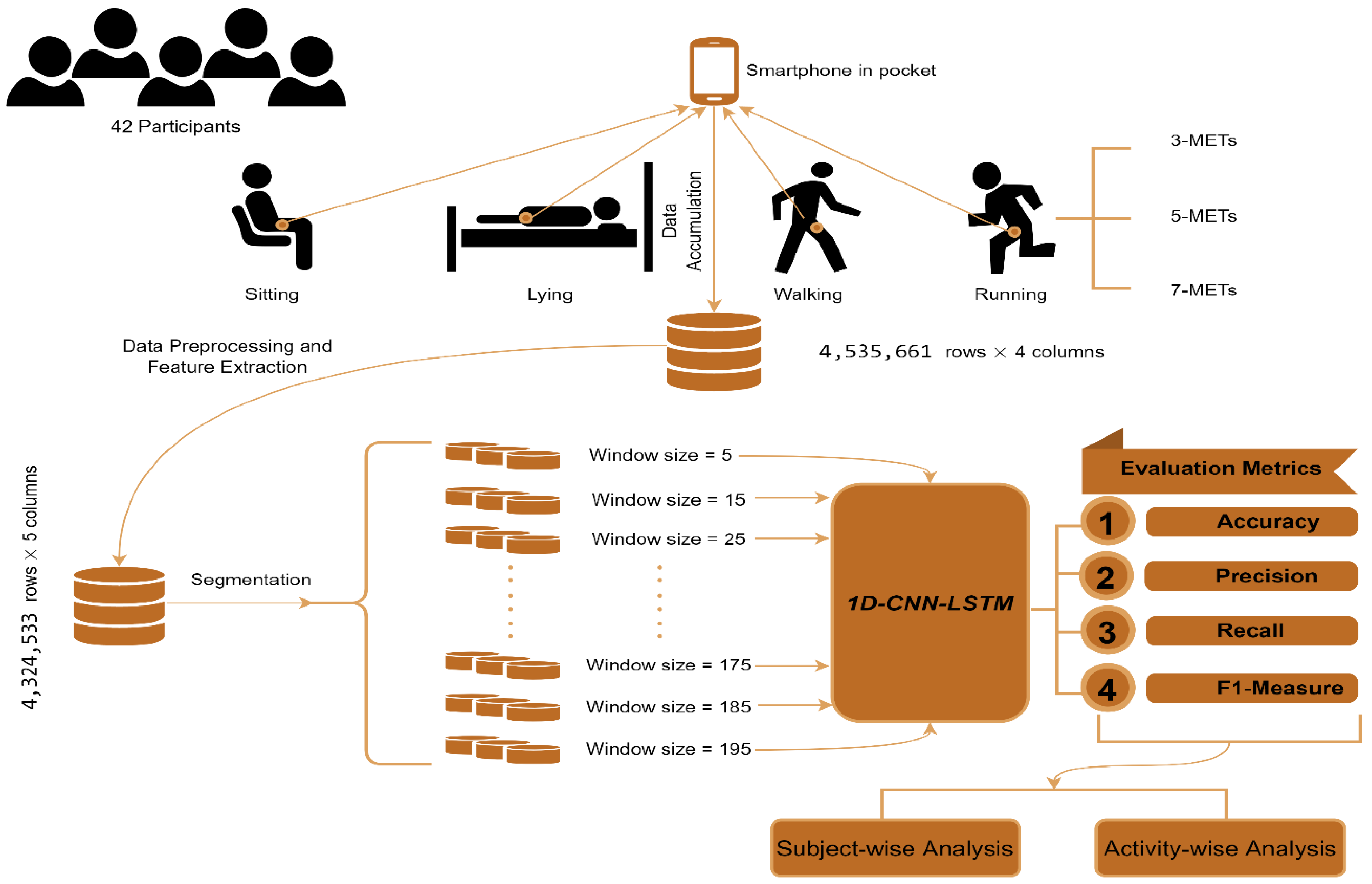
2.1. Data Accumulation
2.2. Data Preprocessing and Feature Extraction
2.2.1. Data Resampling and Data Imputation
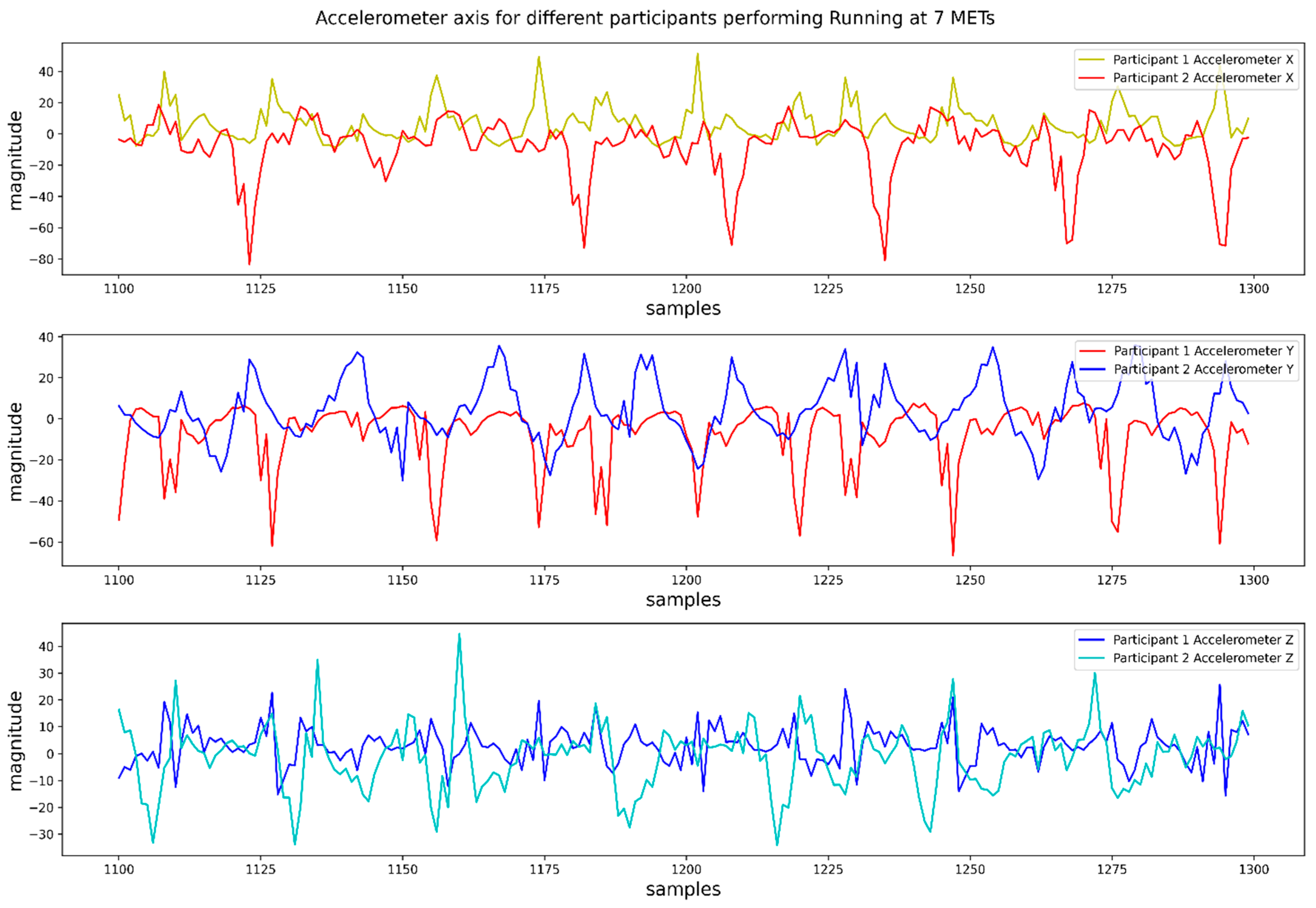
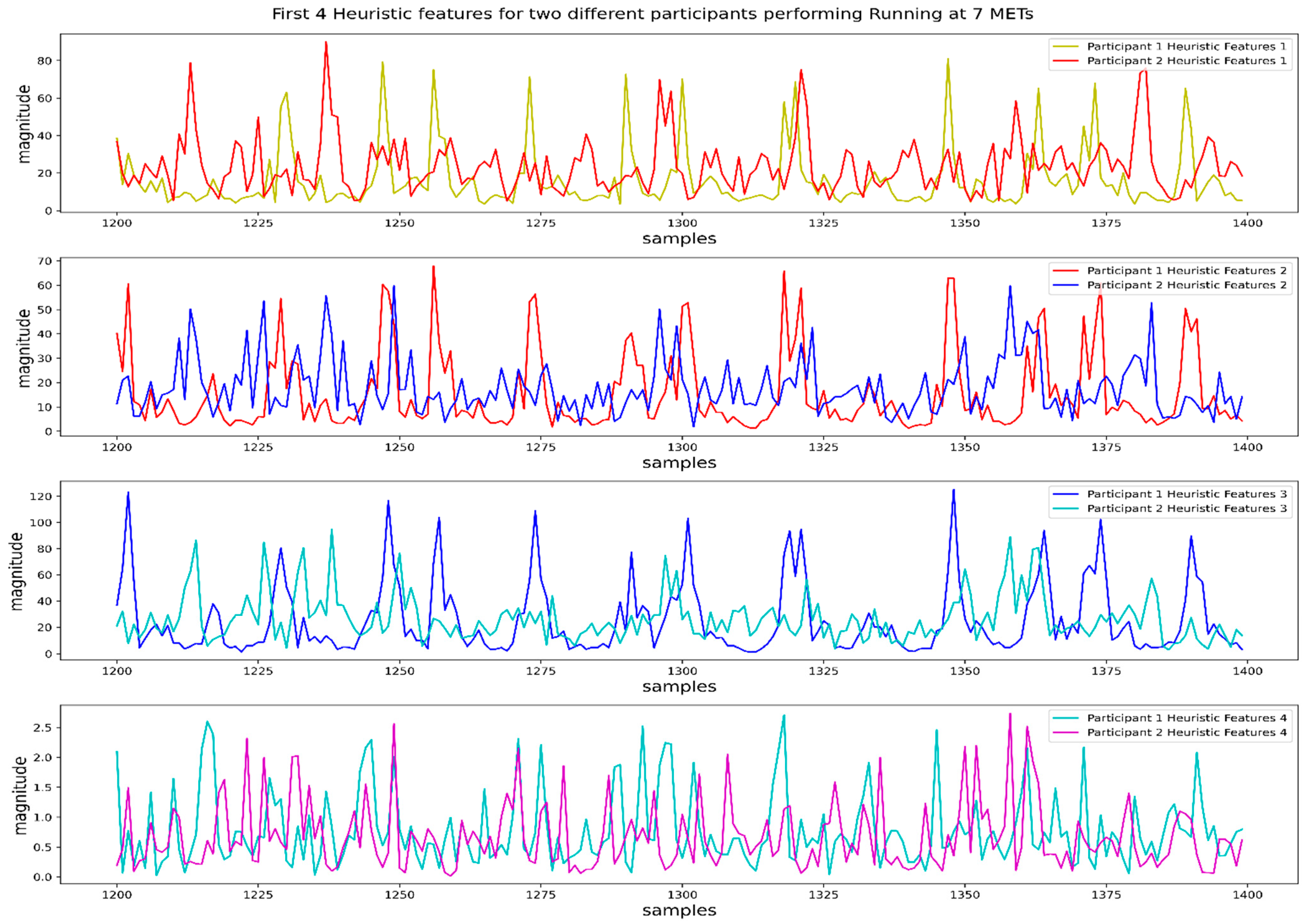
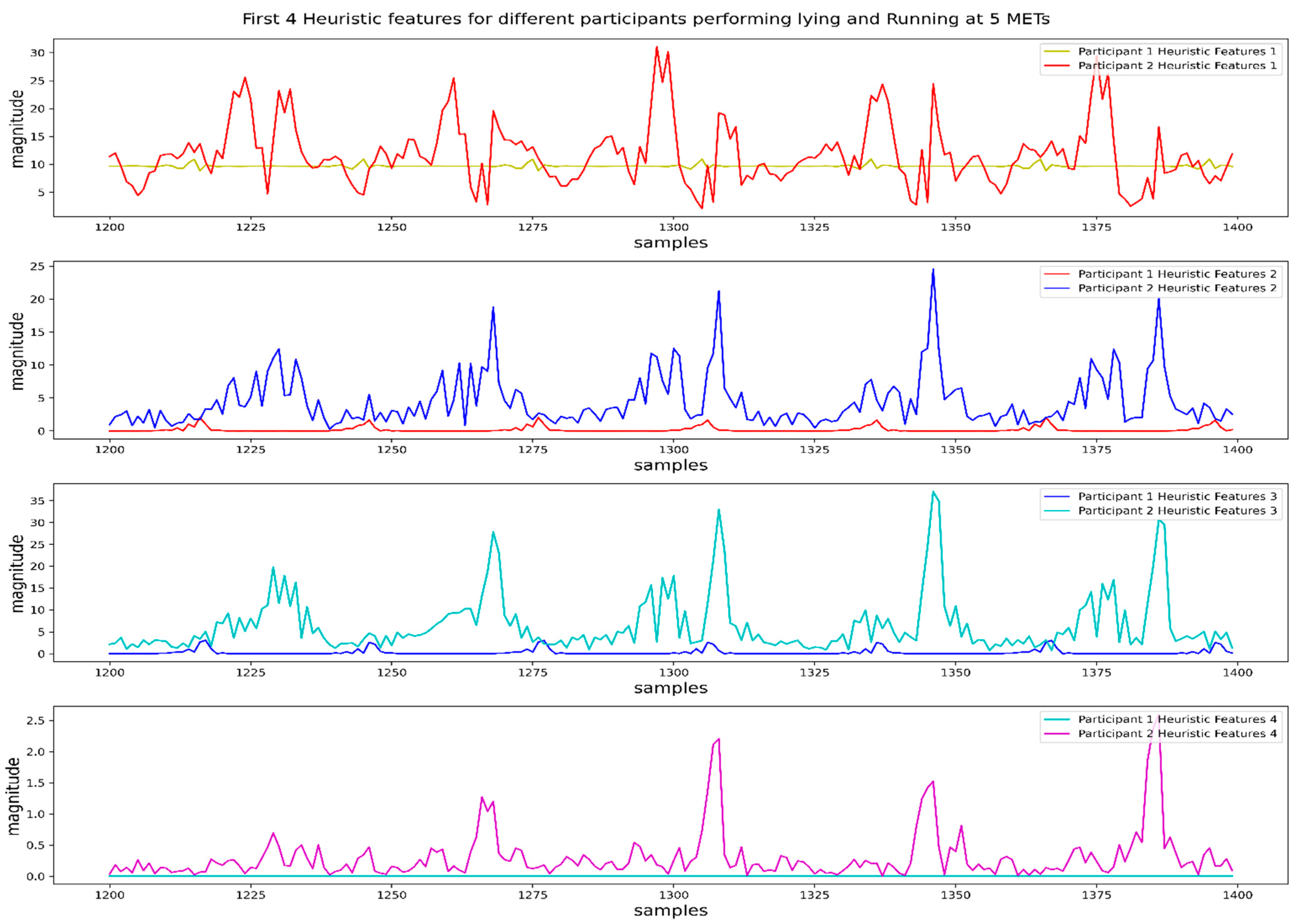
2.2.2. Feature Extraction and Selection
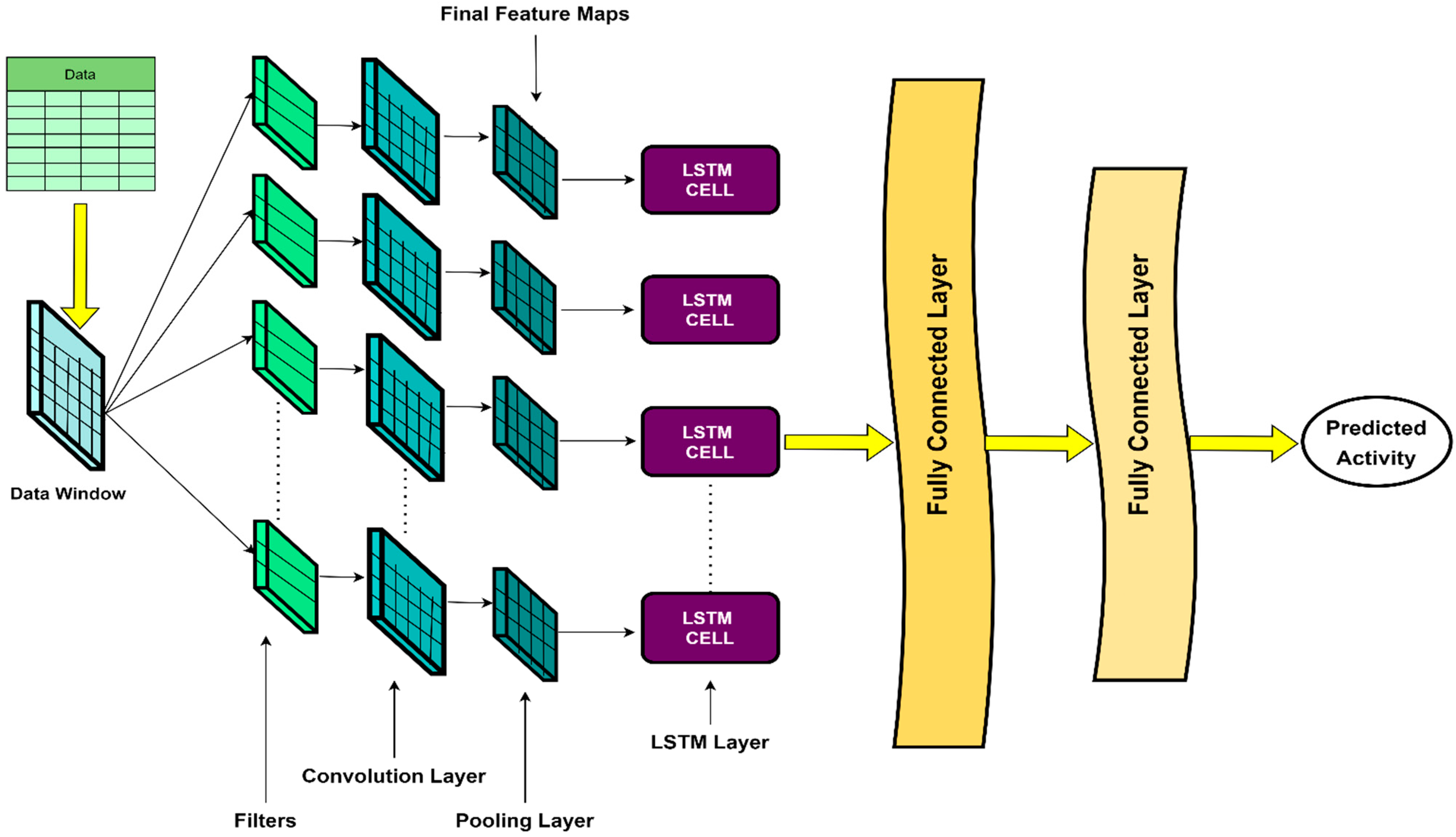
2.3. The Architecture of 1D-CNN-LSTM
3. Results
3.1. Validation Procedure
3.2. Evaluation Metrics
3.2.1. Accuracy
3.2.2. Precision
3.2.3. Recall
3.2.4. F1 Measure
3.3. Data Reshaping
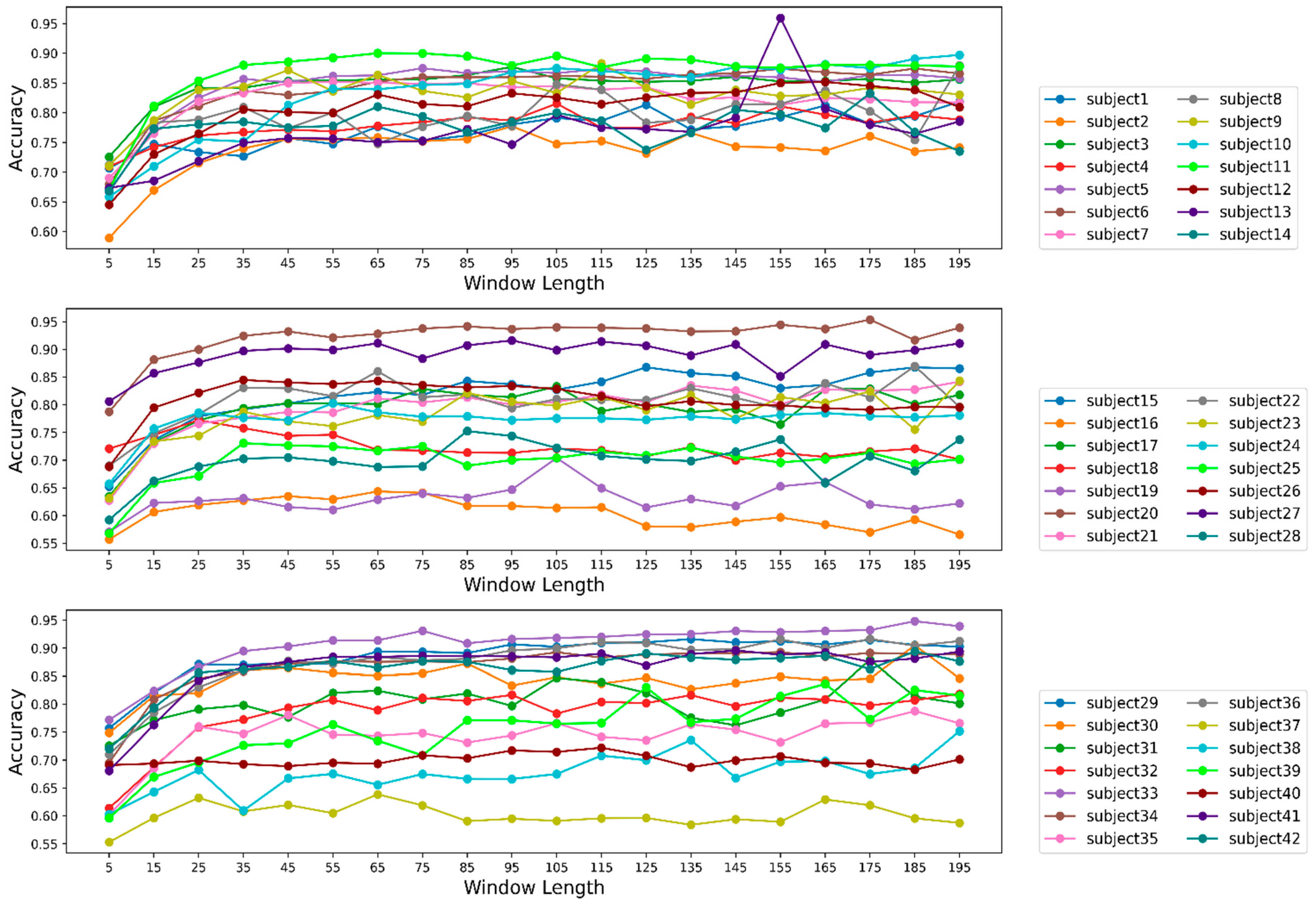
3.4. Effects of Window Length on the Overall Result
3.5. Effect of Window Length on Model Performance for Individual Participants
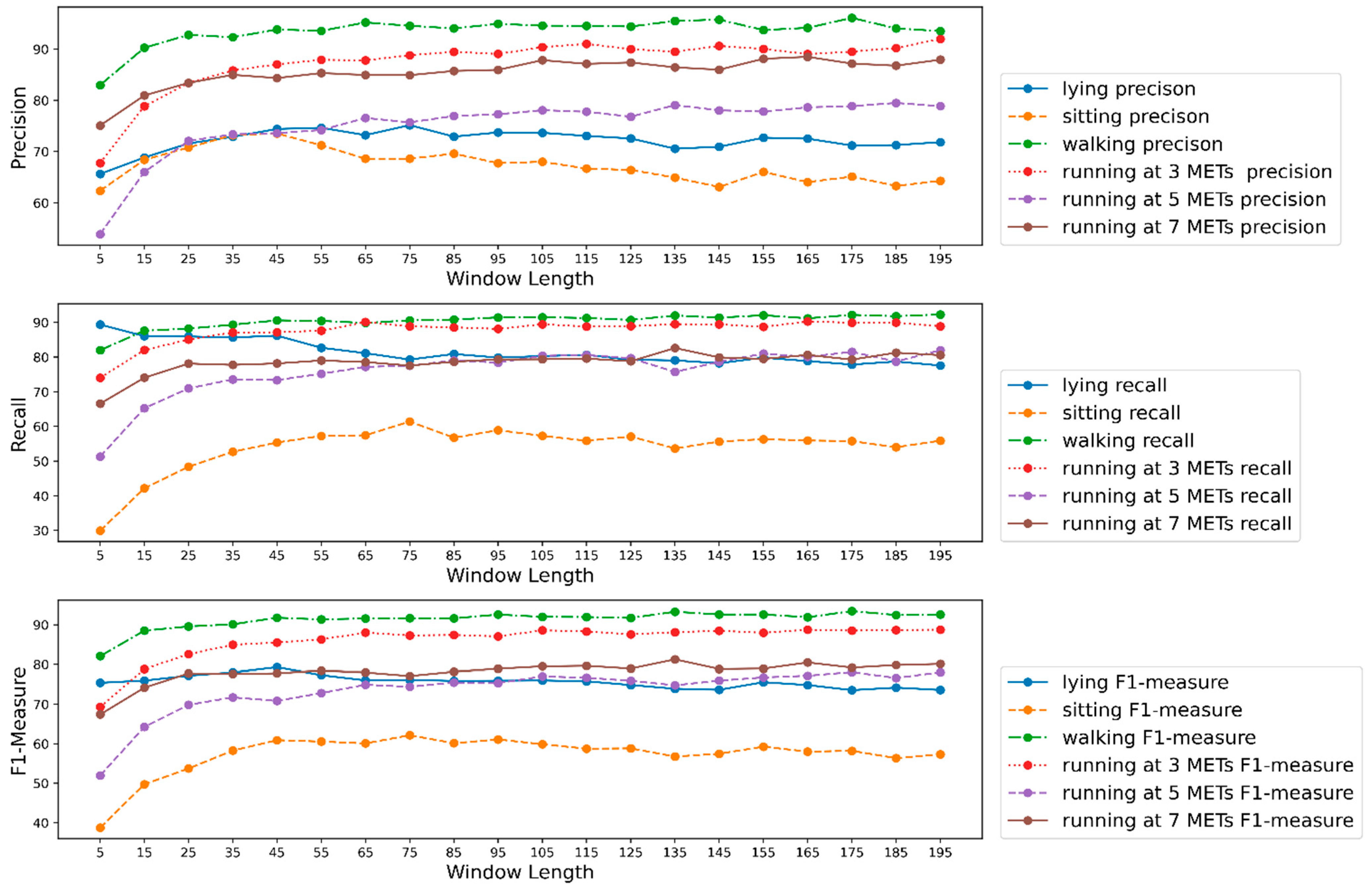
3.6. Effect of Window Length on Model Performance for Each Activity
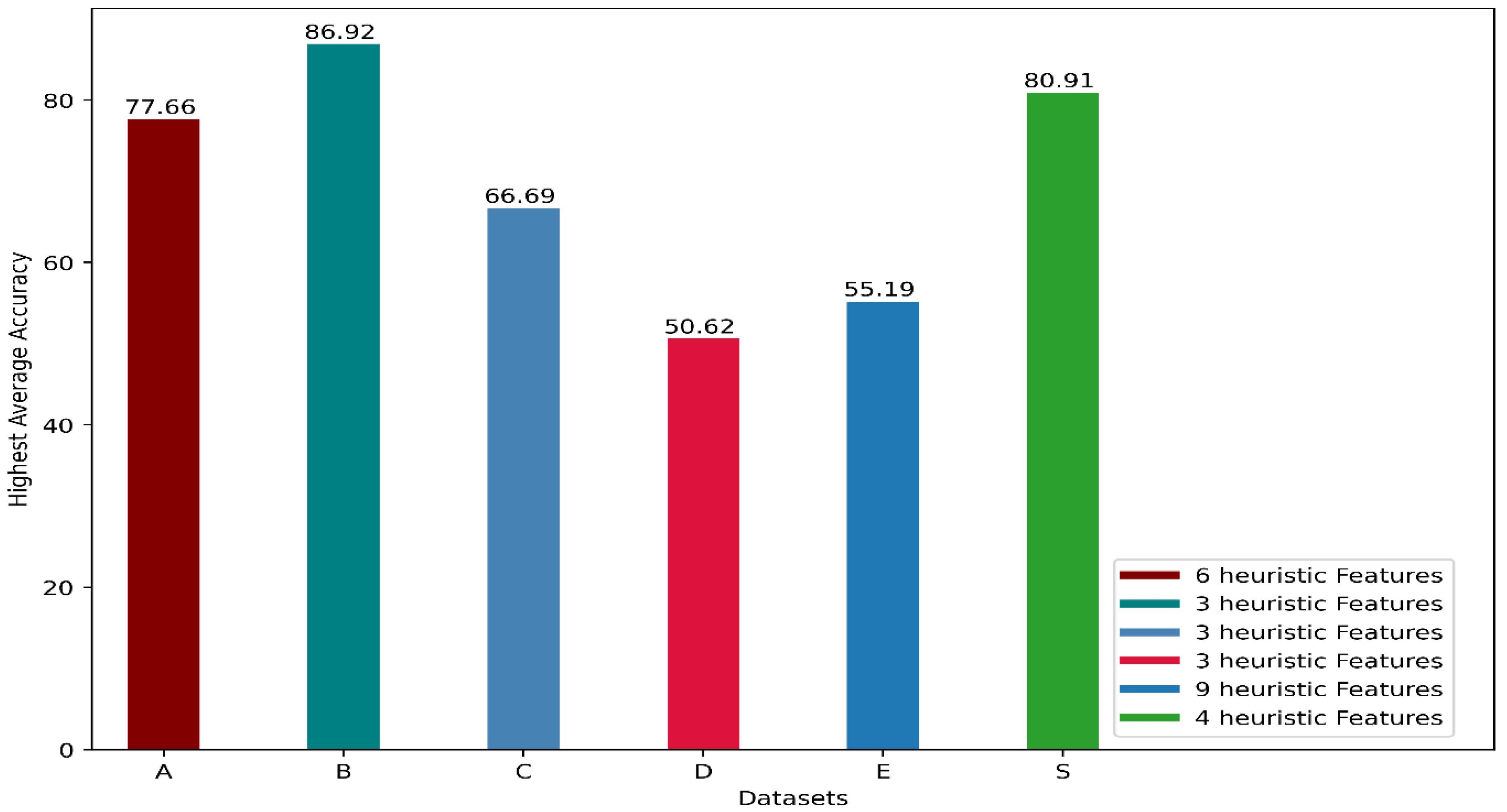
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mekruksavanich, S.; Jitpattanakul, A. Biometric user identification based on human activity recognition using wearable sensors: An experiment using deep learning models. Electronics 2021, 10, 308. [Google Scholar] [CrossRef]
- Zhou, X.; Liang, W.; Wang, K.I.-K.; Wang, H.; Yang, L.T.; Jin, Q. Deep-learning-enhanced human activity recognition for Internet of healthcare things. IEEE Internet Things J. 2020, 7, 6429–6438. [Google Scholar] [CrossRef]
- Barua, A.; Masum, A.K.M.; Bahadur, E.H.; Alam, M.R.; Chowdhury, M.A.U.Z.; Alam, M.S. Human activity recognition in prognosis of depression using long short-term memory approach. Int. J. Adv. Sci. Technol. 2020, 29, 4998–5017. [Google Scholar]
- Chelli, A.; Pätzold, M. A machine learning approach for fall detection and daily living activity recognition. IEEE Access 2019, 7, 38670–38687. [Google Scholar] [CrossRef]
- Nweke, H.F.; Teh, Y.W.; Al-Garadi, M.A.; Alo, U.R. Deep learning algorithms for human activity recognition using mobile and wearable sensor networks: State of the art and research challenges. Expert Syst. Appl. 2018, 105, 233–261. [Google Scholar] [CrossRef]
- Antar, A.D.; Ahmed, M.; Ahad, M.A.R. Challenges in sensor-based human activity recognition and a comparative analysis of benchmark datasets: A review. In Proceedings of the 2019 Joint 8th International Conference on Informatics, Electronics & Vision (ICIEV) and 2019 3rd International Conference on Imaging, Vision & Pattern Recognition, Spokane, WA, USA, 30 May–2 June 2019; pp. 134–139. [Google Scholar]
- Jobanputra, C.; Bavishi, J.; Doshi, N. Human activity recognition: A survey. Procedia Comput. Sci. 2019, 155, 698–703. [Google Scholar] [CrossRef]
- Ramamurthy, S.R.; Roy, N. Recent trends in machine learning for human activity recognition—A survey. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1254. [Google Scholar] [CrossRef]
- Yurtman, A.; Barshan, B.; Fidan, B. Activity recognition invariant to wearable sensor unit orientation using differential rotational transformations represented by quaternions. Sensors 2018, 18, 2725. [Google Scholar] [CrossRef] [Green Version]
- Yurtman, A.; Barshan, B. Activity recognition invariant to sensor orientation with wearable motion sensors. Sensors 2017, 17, 1838. [Google Scholar] [CrossRef] [Green Version]
- Yang, R.; Wang, B. PACP: A position-independent activity recognition method using smartphone sensors. Information 2016, 7, 72. [Google Scholar] [CrossRef] [Green Version]
- Wan, S.; Qi, L.; Xu, X.; Tong, C.; Gu, Z. Deep learning models for real-time human activity recognition with smartphones. Mob. Netw. Appl. 2019, 25, 743–755. [Google Scholar] [CrossRef]
- Mutegeki, R.; Han, D.S. A CNN-LSTM approach to human activity recognition. In Proceedings of the 2020 International Conference on Artificial Intelligence in Information and Communication (ICAIIC), Fukuoka, Japan, 19–21 February 2020; pp. 362–366. [Google Scholar]
- Ignatov, A. Real-time human activity recognition from accelerometer data using Convolutional Neural Networks. Appl. Soft Comput. 2018, 62, 915–922. [Google Scholar] [CrossRef]
- Micucci, D.; Mobilio, M.; Napoletano, P. Unimib shar: A dataset for human activity recognition using acceleration data from smartphones. Appl. Sci. 2017, 7, 1101. [Google Scholar] [CrossRef] [Green Version]
- Masum, A.K.M.; Hossain, M.E.; Humayra, A.; Islam, S.; Barua, A.; Alam, G.R. A statistical and deep learning approach for human activity recognition. In Proceedings of the 2019 3rd International Conference on Trends in Electronics and Informatics (ICOEI), Tirunelveli, India, 23–25 April 2019; pp. 1332–1337. [Google Scholar]
- Attal, F.; Mohammed, S.; Dedabrishvili, M.; Chamroukhi, F.; Oukhellou, L.; Amirat, Y. Physical human activity recognition using wearable sensors. Sensors 2015, 15, 31314–31338. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ahmed, N.; Rafiq, J.I.; Islam, R. Enhanced human activity recognition based on smartphone sensor data using hybrid feature selection model. Sensors 2020, 20, 317. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Zhu, Q.; Soh, Y.C.; Zhang, L. Robust human activity recognition using smartphone sensors via CT-PCA and online SVM. IEEE Trans. Ind. Inform. 2017, 13, 3070–3080. [Google Scholar] [CrossRef]
- Barna, A.; Masum AK, M.; Hossain, M.E.; Bahadur, E.H.; Alam, M.S. A study on human activity recognition using gyroscope, accelerometer, temperature and humidity data. In Proceedings of the 2019 International Conference on Electrical, Computer and Communication Engineering (ECCE), Cox’sBazar, Bangladesh, 7–9 February 2019; pp. 1–6. [Google Scholar]
- Anguita, D.; Ghio, A.; Oneto, L.; Parra-Llanas, X.; Reyes-Ortiz, J. A public domain dataset for human activity recognition using smartphones. In Proceedings of the 21th international European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning, Online, 5–7 October 2022; pp. 437–442. [Google Scholar]
- Reiss, A.; Stricker, D. Introducing a new benchmarked dataset for activity monitoring. In Proceedings of the 2012 16th International Symposium on Wearable Computers, Newcastle, UK, 18–22 June 2012; pp. 108–109. [Google Scholar]
- Ronao, C.A.; Cho, S.-B. Human activity recognition with smartphone sensors using deep learning neural networks. Expert Syst. Appl. 2016, 59, 235–244. [Google Scholar] [CrossRef]
- Yang, J.; Nguyen, M.N.; San, P.P.; Li, X.L.; Krishnaswamy, S. Deep convolutional neural networks on multichannel time series for human activity recognition. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Xia, K.; Huang, J.; Wang, H. LSTM-CNN architecture for human activity recognition. IEEE Access 2020, 8, 56855–56866. [Google Scholar] [CrossRef]
- Weiss, G.M.; Yoneda, K.; Hayajneh, T. Smartphone and smartwatch-based biometrics using activities of daily living. IEEE Access 2019, 7, 133190–133202. [Google Scholar] [CrossRef]
- Roggen, D.; Calatroni, A.; Rossi, M.; Holleczek, T.; Forster, K.; Troster, G.; Lukowicz, P.; Bannach, D.; Pirkl, G.; Ferscha, A.; et al. Collecting complex activity datasets in highly rich networked sensor environments. In Proceedings of the 2010 Seventh International Conference on Networked Sensing Systems (INSS), Kassel, Germany, 15–18 June 2010; pp. 233–240. [Google Scholar]
- Lv, T.; Wang, X.; Jin, L.; Xiao, Y.; Song, M. Margin-based deep learning networks for human activity recognition. Sensors 2020, 20, 1871. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mukherjee, D.; Mondal, R.; Singh, P.K.; Sarkar, R.; Bhattacharjee, D. EnsemConvNet: A deep learning approach for human activity recognition using smartphone sensors for healthcare applications. Multimed. Tools Appl. 2020, 79, 31663–31690. [Google Scholar] [CrossRef]
- Chen, Y.; Xue, Y. A deep learning approach to human activity recognition based on single accelerometer. In Proceedings of the 2015 IEEE International Conference on Systems, Man, and Cybernetics, Hong Kong, China, 9–12 October 2015; pp. 1488–1492. [Google Scholar]
- Murad, A.; Pyun, J.-Y. Deep recurrent neural networks for human activity recognition. Sensors 2017, 17, 2556. [Google Scholar] [CrossRef] [Green Version]
- Hammerla, N.Y.; Halloran, S.; Plötz, T. Deep, convolutional, and recurrent models for human activity recognition using wearables. arXiv 2016, arXiv:1604.08880. [Google Scholar]
- Xu, C.; Chai, D.; He, J.; Zhang, X.; Duan, S. InnoHAR: A deep neural network for complex human activity recognition. IEEE Access 2019, 7, 9893–9902. [Google Scholar] [CrossRef]
- Almaslukh, B.; Artoli, A.M.; Al-Muhtadi, J. A robust deep learning approach for position-independent smartphone-based human activity recognition. Sensors 2018, 18, 3726. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khataeipour, S.J.; Anaraki, J.R.; Bozorgi, A.; Rayner, M.; A Basset, F.; Fuller, D. Predicting lying, sitting and walking at different intensities using smartphone accelerometers at three different wear locations: Hands, pant pockets, backpack. BMJ Open Sport Exerc. Med. 2022, 8, e001242. [Google Scholar] [CrossRef]
- Ethica Data; Ethica [Mobile App]. 2020. Available online: https://ethicadata.com/ (accessed on 15 April 2022).
- Jetté, M.; Sidney, K.; Blümchen, G. Metabolic equivalents (METS) in exercise testing, exercise prescription, and evaluation of functional capacity. Clin. Cardiol. 1990, 13, 555–565. [Google Scholar] [CrossRef]
- Narayanan, A.; Desai, F.; Stewart, T.; Duncan, S.; Mackay, L. Application of raw accelerometer data and machine-learning techniques to characterize human movement behavior: A systematic scoping review. J. Phys. Act. Health 2020, 17, 360–383. [Google Scholar] [CrossRef]
- Sainath, T.N.; Vinyals, O.; Senior, A.; Sak, H. Convolutional, long short-term memory, fully connected deep neural networks. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, Australia, 19–24 April 2015; pp. 4580–4584. [Google Scholar]
- Tharwat, A. Classification assessment methods. Appl. Comput. Inform. 2020, 17, 168–192. [Google Scholar] [CrossRef]
- Sasaki, Y. The truth of the F-measure. Teach Tutor Mater 2007, 1, 1–5. [Google Scholar]
- Dehghani, A.; Sarbishei, O.; Glatard, T.; Shihab, E. A quantitative comparison of overlapping and non-overlapping sliding windows for human activity recognition using inertial sensors. Sensors 2019, 19, 5026. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barshan, B.; Yüksek, M.C. Recognizing daily and sports activities in two open source machine learning environments using body-worn sensor units. Comput. J. 2013, 57, 1649–1667. [Google Scholar] [CrossRef]
- Ugulino, W.; Cardador, D.; Vega, K.; Velloso, E.; Milidiú, R.; Fuks, H. Wearable computing: Accelerometers’ data classification of body postures and movements. In Brazilian Symposium on Artificial Intelligence; Springer: Berlin/Heidelberg, Germany; pp. 52–61.
- Zhang, M.; Sawchuk, A.A. USC-HAD: A daily activity dataset for ubiquitous activity recognition using wearable sensors. In Proceedings of the 2012 ACM conference on ubiquitous computing, Pittsburgh, PA, USA, 5–8 September 2012; pp. 1036–1043. [Google Scholar]
- Casale, P.; Pujol, O.; Radeva, P. Human activity recognition from accelerometer data using a wearable device. In Iberian Conference on Pattern Recognition and Image Analysis; Springer: Berlin/Heidelberg, Germany; pp. 289–296.
- Dua, N.; Singh, S.N.; Semwal, V.B. Multi-input CNN-GRU based human activity recognition using wearable sensors. Computing 2021, 103, 1461–1478. [Google Scholar] [CrossRef]
- Challa, S.K.; Kumar, A.; Semwal, V.B. A multibranch CNN-BiLSTM model for human activity recognition using wearable sensor data. Vis. Comput. 2021, 1–15. [Google Scholar] [CrossRef]
- Ullah, M.; Ullah, H.; Khan, S.D.; Cheikh, F.A. Stacked lstm network for human activity recognition using smartphone data. In Proceedings of the 2019 8th European Workshop on Visual Information Processing (EUVIP), Roma, Italy, 2 January 2020; pp. 175–180. [Google Scholar]
- Yu, T.; Chen, J.; Yan, N.; Liu, X. A multilayer parallel lstm network for human activity recognition with smartphone sensors. In Proceedings of the 2018 10th International Conference on Wireless Communications and Signal Processing (WCSP), Hangzhou, China, 18–20 October 2018; pp. 1–6. [Google Scholar]
- Tufek, N.; Yalcin, M.; Altintas, M.; Kalaoglu, F.; Li, Y.; Bahadir, S.K. Human action recognition using deep learning methods on limited sensory data. IEEE Sens. J. 2020, 20, 3101–3112. [Google Scholar] [CrossRef] [Green Version]
- Mekruksavanich, S.; Jitpattanakul, A. Deep convolutional neural network with rnns for complex activity recognition using wrist-worn wearable sensor data. Electronics 2021, 10, 1685. [Google Scholar] [CrossRef]



| Number of Participants | Age (Years) | Height (cm) | Weight (kg) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Male | Female | Average | Maximum | Minimum | Average | Maximum | Minimum | Average | Maximum | Minimum |
| 18 | 24 | 29 | 56 | 18 | 169.17 | 185 | 143 | 68.19 | 95.2 | 43 |
| Rank | Activity | Duration (Minutes) |
|---|---|---|
| 1 | Lying down | 5 |
| 2 | Sitting | 5 |
| 3 | Walking | 10 |
| 4 | Lying down | 5 |
| 5 | Running at 3-METs | 10 |
| 6 | Lying down | 5 |
| 7 | Running at 5-METs | 10 |
| 8 | Sitting | 5 |
| 9 | Running at 7-METs | 10 |
| Activity | Number of Data Points | Ratio to Total Dataset |
|---|---|---|
| Running at 7-METs | 926,606 | 21.43% |
| Running at 5-METs | 812,135 | 18.78% |
| Running at 3-METs | 815,498 | 18.86% |
| Walking | 609,406 | 14.09% |
| lying | 696,329 | 16.10% |
| sitting | 464,559 | 10.74% |
| Parts of Architecture | Components of Each Part (Blank Cell = Not Available for This Layer) | |||||||
|---|---|---|---|---|---|---|---|---|
| CNN | Layer’s Name | Number of Filters | Kernel Size | Activation Function | Dropout Ratio | Pooling Type | Pool Size | Padding Type |
| Convolution | 512 | 5 | relu | same | ||||
| Dropout | 0.3 | |||||||
| Pooling | Average | 3 | same | |||||
| Convolution | 256 | 3 | relu | same | ||||
| Dropout | 0.3 | |||||||
| Convolution | 64 | 3 | relu | same | ||||
| Pooling | Average | 3 | same | |||||
| Convolution | 128 | 3 | relu | same | ||||
| Convolution | 256 | 5 | relu | same | ||||
| Dropout | N/A | 0.3 | ||||||
| Convolution | 512 | 7 | relu | same | ||||
| Dropout | 0.3 | |||||||
| Pooling | Average | 3 | same | |||||
| LSTM | Layer’s Name | Number of Units | Activation Function | |||||
| LSTM | 512 | tanh | ||||||
| Fully Connected Network | Layer’s Name | Number of Neurons | Activation Function | |||||
| Dense | 100 | relu | ||||||
| Dense | 28 | relu | ||||||
| Dense | 64 | relu | ||||||
| Dense | 6 | softmax | ||||||
| Window Length | Overlapping Ratio (%) | No. of Windows in the Training Set ± Standard Deviation | No. of Windows in the Test Set ± Standard Deviation |
|---|---|---|---|
| 5 | 80.00 | 4,221,561 ± 31,399 | 102,959 ± 31,399 |
| 15 | 93.33 | 4,221,551 ± 31,399 | 102,949 ± 31,399 |
| 25 | 96.00 | 4,221,541 ± 31,399 | 102,939 ± 31,399 |
| 35 | 97.14 | 4,221,531 ± 31,399 | 102,929 ± 31,399 |
| 45 | 97.77 | 4,221,521 ± 31,399 | 102,919 ± 31,399 |
| 55 | 98.18 | 4,221,511 ± 31,399 | 102,909 ± 31,399 |
| 65 | 98.46 | 4,221,501 ± 31,399 | 102,899 ± 31,399 |
| 75 | 98.66 | 4,221,491 ± 31,399 | 102,889 ± 31,399 |
| 85 | 98.82 | 4,221,481 ± 31,399 | 102,879 ± 31,399 |
| 95 | 98.94 | 4,221,471 ± 31,399 | 102,869 ± 31,399 |
| 105 | 99.04 | 4,221,461 ± 31,399 | 102,859 ± 31,399 |
| 115 | 99.13 | 4,221,451 ± 31,399 | 102,849 ± 31,399 |
| 125 | 99.20 | 4,221,441 ± 31,399 | 102,839 ± 31,399 |
| 135 | 99.25 | 4,221,431 ± 31,399 | 102,829 ± 31,399 |
| 145 | 99.31 | 4,221,421 ± 31,399 | 102,819 ± 31,399 |
| 155 | 99.35 | 4,221,411 ± 31,399 | 102,809 ± 31,399 |
| 165 | 99.39 | 4,221,401 ± 31,399 | 102,799 ± 31,399 |
| 175 | 99.42 | 4,221,391 ± 31,399 | 102,789 ± 31,399 |
| 185 | 99.46 | 4,221,381 ± 31,399 | 102,779 ± 31,399 |
| 195 | 99.49 | 4,221,371 ± 31,399 | 102,769 ± 31,399 |
| Activities | Properties for the Highest Precision | Properties for the Lowest Precision | Properties for the Highest Recall | Properties for the Lowest Recall | Properties for the Highest F1 Measure | Properties for the Lowest F1 Measure | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Highest Value | Window Length | Lowest Value | Window Length | Highest Value | Window Length | Lowest Value | Window Length | Highest Value | Window Length | Lowest Value | Window Length | |
| Lying | 76.16 | 75 | 65.63 | 5 | 89.38 | 5 | 77.58 | 195 | 79.30 | 45 | 73.55 | 175 |
| Sitting | 73.53 | 45 | 62.34 | 5 | 61.41 | 175 | 29.91 | 5 | 62.15 | 75 | 38.74 | 5 |
| Walking | 96.10 | 175 | 82.99 | 5 | 92.29 | 195 | 82.00 | 5 | 93.46 | 175 | 82.07 | 5 |
| Running 3 METS | 91.98 | 195 | 67.73 | 5 | 90.26 | 165 | 74.04 | 5 | 88.76 | 195 | 69.30 | 5 |
| Running 5 METS | 79.48 | 185 | 53.87 | 5 | 81.99 | 195 | 51.30 | 5 | 78.08 | 175 | 51.95 | 5 |
| Running 7 METS | 88.49 | 165 | 75.08 | 5 | 82.62 | 135 | 66.57 | 5 | 81.26 | 135 | 67.39 | 5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barua, A.; Fuller, D.; Musa, S.; Jiang, X. Exploring Orientation Invariant Heuristic Features with Variant Window Length of 1D-CNN-LSTM in Human Activity Recognition. Biosensors 2022, 12, 549. https://doi.org/10.3390/bios12070549
Barua A, Fuller D, Musa S, Jiang X. Exploring Orientation Invariant Heuristic Features with Variant Window Length of 1D-CNN-LSTM in Human Activity Recognition. Biosensors. 2022; 12(7):549. https://doi.org/10.3390/bios12070549
Chicago/Turabian StyleBarua, Arnab, Daniel Fuller, Sumayyah Musa, and Xianta Jiang. 2022. "Exploring Orientation Invariant Heuristic Features with Variant Window Length of 1D-CNN-LSTM in Human Activity Recognition" Biosensors 12, no. 7: 549. https://doi.org/10.3390/bios12070549
APA StyleBarua, A., Fuller, D., Musa, S., & Jiang, X. (2022). Exploring Orientation Invariant Heuristic Features with Variant Window Length of 1D-CNN-LSTM in Human Activity Recognition. Biosensors, 12(7), 549. https://doi.org/10.3390/bios12070549






