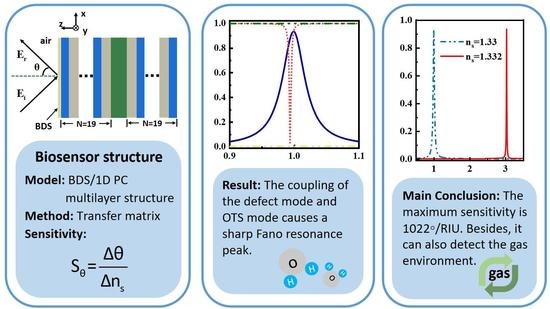
Terahertz Biosensor Based on Mode Coupling between Defect Mode and Optical Tamm State with Dirac Semimetal
Abstract
1. Introduction
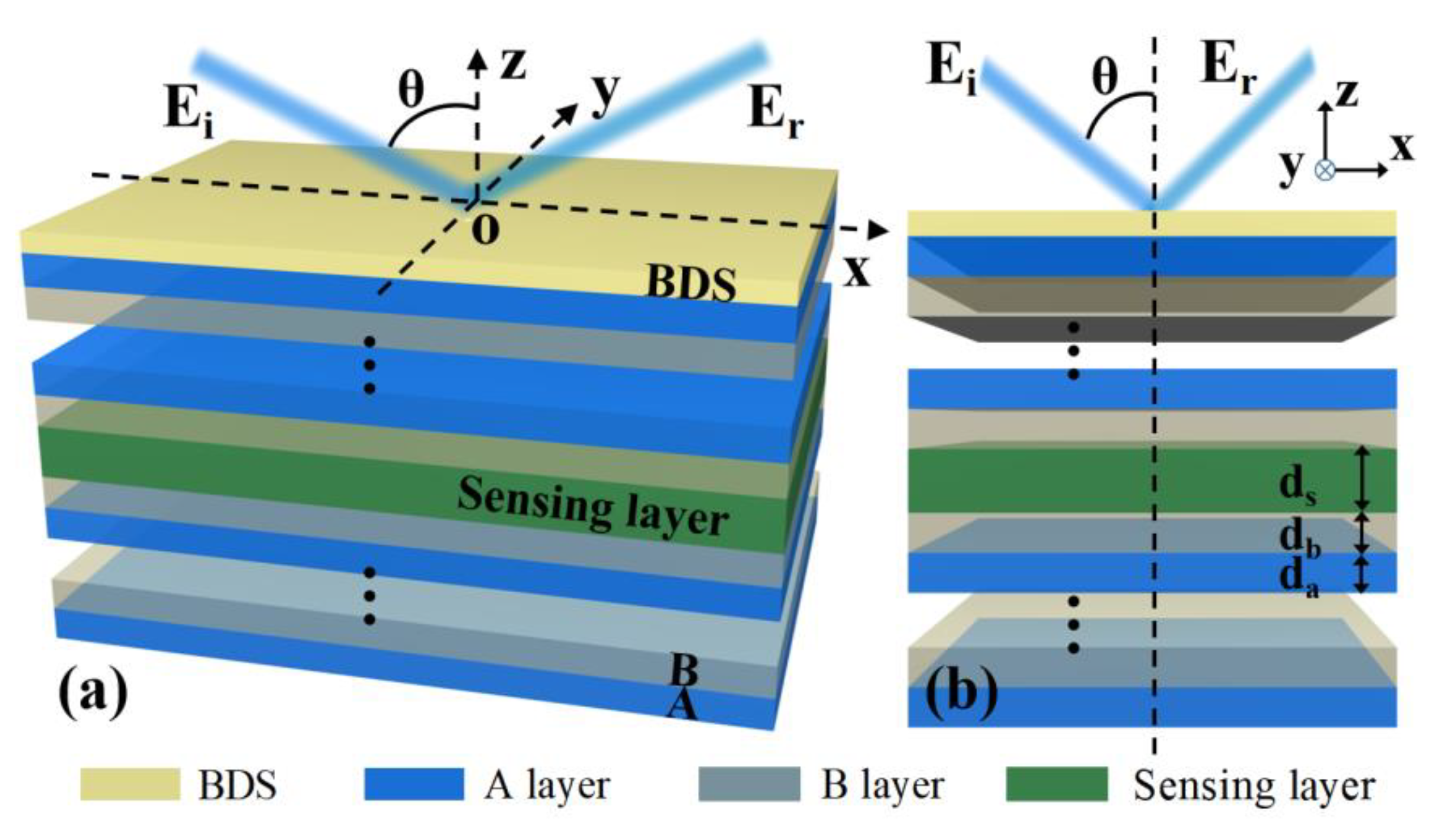
2. Theoretical Model and Method
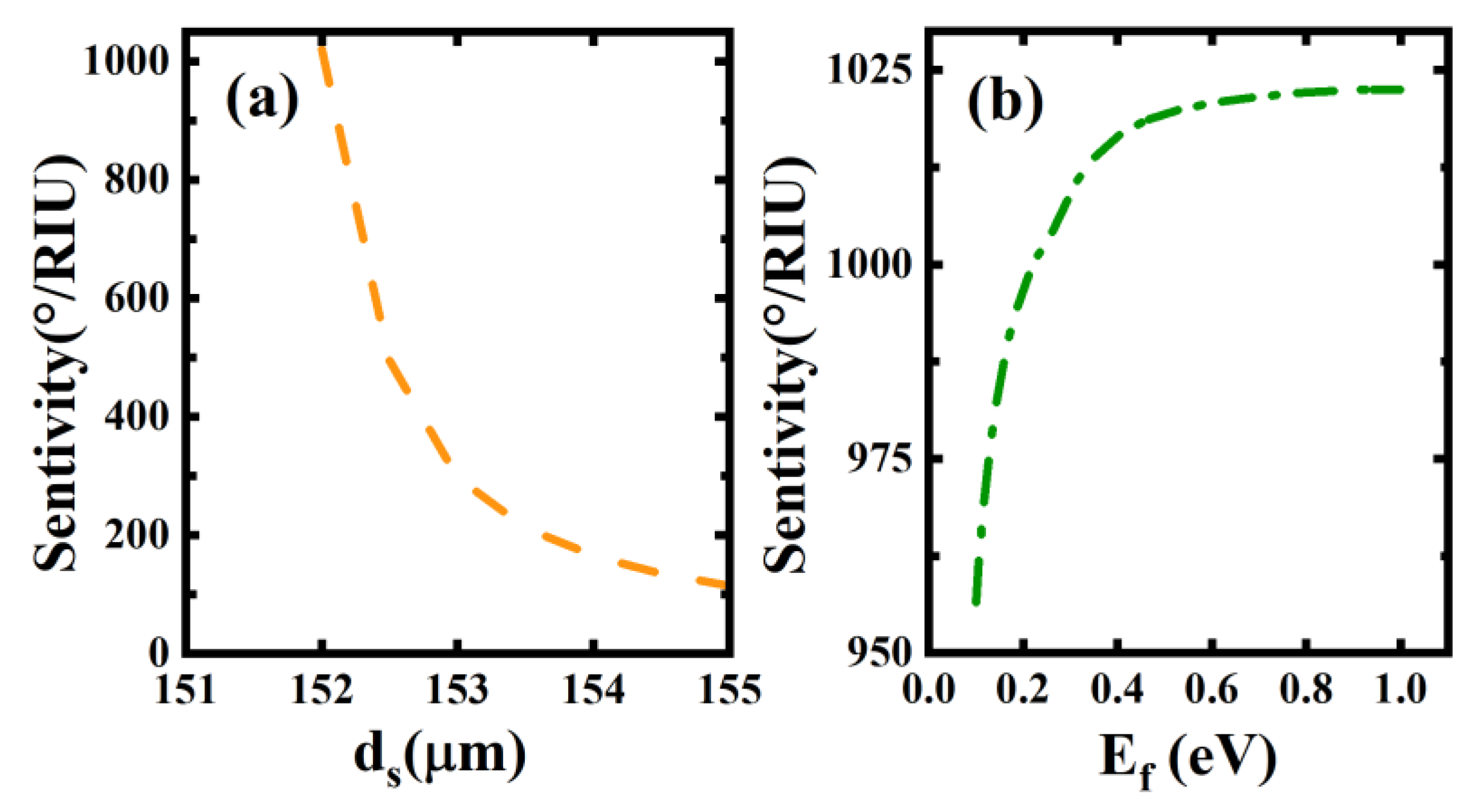
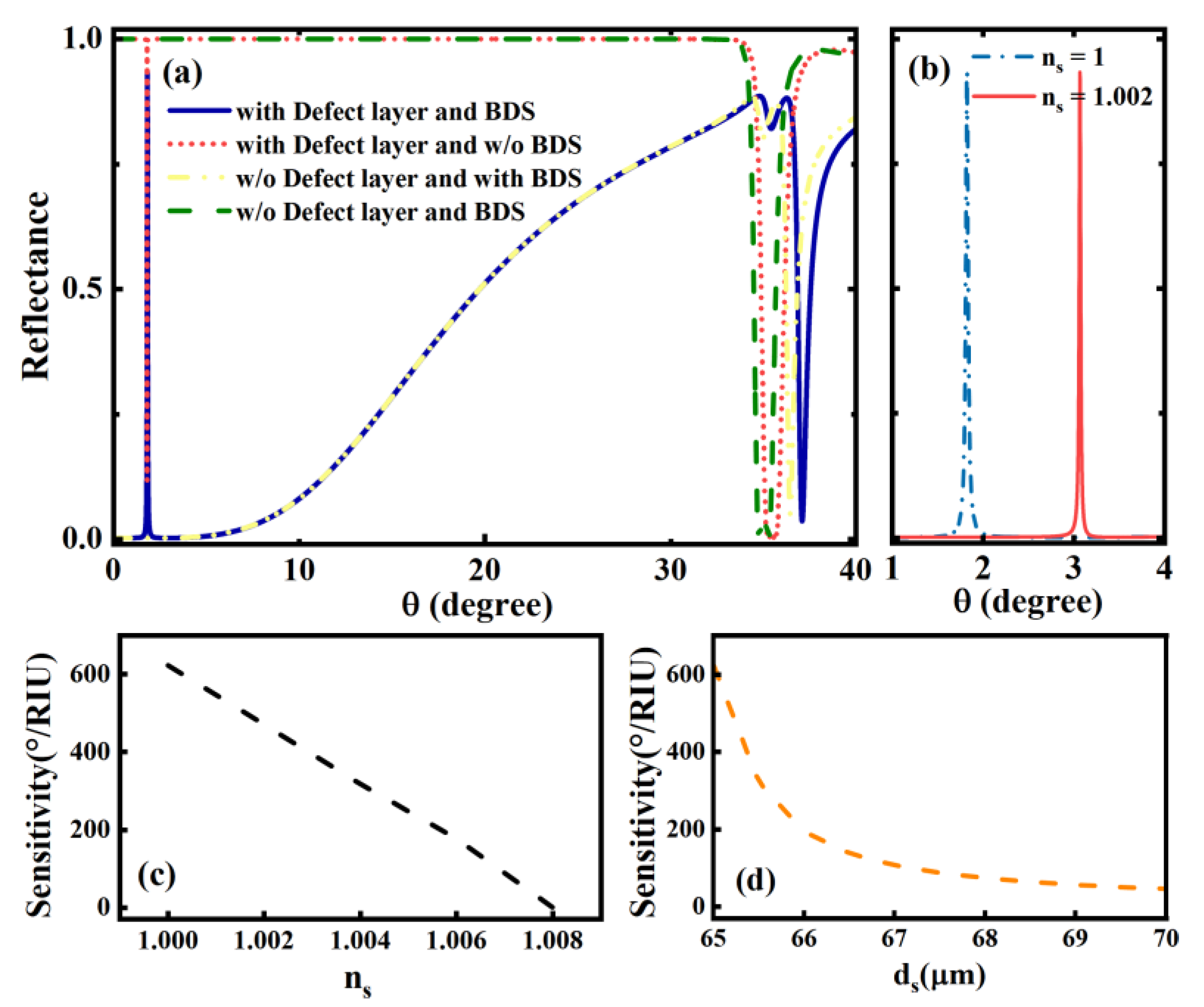
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Turner, A.P.F. Biosensors: Sense and sensibility. Chem. Soc. Rev. 2013, 42, 3184–3196. [Google Scholar] [CrossRef] [PubMed]
- Nooke, A.; Beck, U.; Hertwig, A.; Krause, A.; Krüger, H.; Lohse, V.; Negendank, D.; Steinbach, J. Onthe application of gold based SPR sensors for the detection of hazardous gases. Sens. Actuators B Chem. 2010, 149, 194–198. [Google Scholar] [CrossRef]
- Fernández, F.; Hegnerová, K.; Piliarik, M.; Sanchez-Baeza, F.; Homola, J.; Marco, M. A label-free and portable multichannel surface plasmon resonance immunosensor for on site analysis of antibiotics in milk samples. Biosens. Bioelectron. 2010, 26, 1231–1238. [Google Scholar] [CrossRef] [PubMed]
- Shankaran, D.R.; Gobi, K.V.; Miura, N. Recent advancements in surface plasmon resonance immunosensors for detection of small molecules of biomedical, food and environmental interest. Sens. Actuators B Chem. 2007, 121, 158–177. [Google Scholar] [CrossRef]
- Lamb, D.W.; Trotter, M.G.; Schneider, D.A. Ultra low-level airbornesensing of crop canopy reflectance: A case study using a CropCircle™ sensor. Comput. Electron. Agric. 2009, 69, 86–91. [Google Scholar] [CrossRef]
- Rau, C.; Torosyan, G.; Beigang, R.; Nerkararyan, K. Prism coupled Terahertz waveguide sensor. Appl. Phys. Lett. 2005, 86, 211119. [Google Scholar] [CrossRef]
- Yalcin, A.; Popat, K.C.; Aldridge, J.C.; Desai, T.A.; Hryniewicz, J.; Chbouki, N.; Little, B.E.; King, O.; Van, V.; Chu, S.; et al. Optical sensing of biomolecules using microring resonators. IEEE J. Sel. Top. Quantum Electron. 2016, 12, 148–155. [Google Scholar] [CrossRef]
- Song, K.; Kong, X.; Liu, X.; Zhang, Y.; Zeng, Q.; Tu, L.; Shi, Z.; Zhang, H. Aptamer optical biosensor without bio-breakage using upconversion nanoparticles as donors. Chem. Commun. 2012, 48, 1156–1158. [Google Scholar] [CrossRef]
- Rifat, A.A.; Ahmed, R.; Yetisen, A.K.; Butt, H.; Sabouri, A.; Mahdiraji, G.A.; Yun, S.H.; Adikan, F.R.M. Photonic crystal fiber based plasmonic sensors. Sens. Actuators B Chem. 2017, 243, 311–325. [Google Scholar] [CrossRef]
- Slavík, R.; Homola, J. Ultrahigh resolution long range surface plasmon-based sensor. Sens. Actuators B Chem. 2007, 123, 10–12. [Google Scholar] [CrossRef]
- Li, C.T.; Lo, K.C.; Chang, H.Y.; Wu, H.T.; Ho, J.H.; Yen, T.J. Ag/Au bi-metallic film based color surface plasmon resonance biosensor with enhanced sensitivity, color contrast and great linearity. Biosens. Bioelectron. 2012, 36, 192–198. [Google Scholar] [CrossRef] [PubMed]
- Zeng, S.; Sreekanth, K.V.; Shang, J.; Yu, T.; Chen, C.K.; Yin, F.; Baillargeat, D.; Coquet, P.; Ho, H.P.; Kabashin, A.V.; et al. Graphene-gold metasurface architectures for ultrasensitive plasmonic biosensing. Adv. Mater. 2015, 27, 6163–6169. [Google Scholar] [CrossRef] [PubMed]
- Piper, J.R.; Fan, S.H. Total absorption in a graphene monolayer in the optical regime by critical coupling with a photonic crystal guided resonance. ACS Photonics 2014, 1, 347–353. [Google Scholar] [CrossRef]
- Zhang, B.L.; Liu, Y.; Luo, Y.; Kusmartsev, F.V.; Kusmartseva, A. Perfect Impedance Matching with Meta-Surfaces Made of Ultra-Thin Metal Films: A Phenomenological Approach to the Ideal THz Sensors. Materials 2020, 13, 5417. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Zeng, W.; Sun, H.; Luo, S.; Chen, D.; Chan, V.; Liao, K. Inorganic/polymer-graphenehybrid gel as versatile electrochemical platform for electrochemical capacitor and biosensor. Carbon 2018, 132, 589–597. [Google Scholar] [CrossRef]
- Xu, S.; Zhan, J.; Man, B.; Jiang, S.; Yue, W.; Gao, S.; Guo, C.; Liu, H.; Li, Z.; Wang, J.; et al. Real-time reliable determination of binding kinetics of DNA hybridization using a multi-channel graphene biosensor. Nat. Commun. 2017, 8, 14902. [Google Scholar] [CrossRef]
- Wu, L.; Chu, H.S.; Koh, W.S.; Li, E.P. Highly sensitive graphene biosensors based on surface plasmon resonance. Opt. Express 2010, 18, 14395–14400. [Google Scholar] [CrossRef]
- Rodrigo, D.; Limaj, O.; Janner, D.; Etezadi, D.; García de Abajo, F.J.; Pruneri, V.; Altug, H. Mid-infrared plasmonic biosensing with graphene. Science 2015, 349, 165–168. [Google Scholar] [CrossRef]
- Xiao, B.G.; Wang, Y.C.; Cai, W.J.; Xiao, L.H. Design and prediction of PIT devices through deep learning. Opt. Express 2022, 30, 14985–14997. [Google Scholar] [CrossRef]
- Kavokin, A.V.; Shelykh, I.A.; Malpuech, G. Lossless interface modes at the boundary between two periodic dielectric structures. Phys. Rev. B 2005, 72, 233102. [Google Scholar] [CrossRef]
- Kaliteevski, M.; Iorsh, I.; Brand, S.; Abram, R.A.; Chamberlain, J.M.; Kavokin, A.V.; Shelykh, I.A. Tamm plasmon-polaritons: Possible electromagnetic states at the interface of a metal and a dielectric Bragg mirror. Phys. Rev. B 2007, 76, 165415. [Google Scholar] [CrossRef]
- Sasin, M.E.; Seisyan, R.P.; Kalitteevski, M.A.; Brand, S.; Abram, R.A.; Chamberlain, J.M.; Egorov, A.Y.; Vasil’ev, A.P.; Mikhrin, V.S.; Kavokin, A.V. Tamm plasmon polaritons: Slow and spatially compact light. Appl. Phys. Lett. 2008, 92, 251112. [Google Scholar] [CrossRef]
- Tsurimaki, Y.; Tong, J.K.; Boriskin, V.N.; Semenov, A.; Ayzatsky, M.I.; Machekhin, Y.P.; Chen, G.; Boriskina, S.V. Topological engineering of interfacial optical Tamm states for highly sensitive near-singular-phase optical detection. ACS Photonics 2018, 5, 929–938. [Google Scholar] [CrossRef]
- Brand, S.; Kaliteevski, M.A.; Abram, R.A. Optical Tamm states above the bulk plasma frequency at a Bragg stack/metal interface. Phys. Rev. B 2009, 79, 085416. [Google Scholar] [CrossRef]
- Maji, P.S.; Shukla, M.K.; Das, R. Blood component detection based on miniaturized self-referenced hybrid Tamm plasmon polariton sensor. Sens. Actuators B Chem. 2018, 255, 729–734. [Google Scholar] [CrossRef]
- Ye, Y.; Xie, M.; Tang, J.; Ouyang, J. Highly sensitive and tunable terahertz biosensor based on optical Tamm states in graphene-based Bragg reflector. Results Phys. 2019, 15, 102779. [Google Scholar] [CrossRef]
- Zaky, Z.A.; Aly, A.H. Modeling of a biosensor using Tamm resonance excited by graphene. Appl. Opt. 2021, 60, 1411–1419. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.K.; Jiang, J.; Zhou, B.; Wang, Z.J.; Zhang, Y.; Weng, H.M.; Prabhakaran, D.; Mo, S.-K.; Peng, H.; Dudin, P. A stable three-dimensional topological Dirac semimetal Cd3As2. Nat. Mater. 2014, 13, 677–681. [Google Scholar] [CrossRef]
- Kotov, O.V.; Lozovik, Y.E. Dielectric response and novel electromagnetic modes in three-dimensional Dirac semimetal films. Phys. Rev. B 2016, 93, 235417. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, H.; Dong, J.L.; Hu, S.Q.; Zhu, W.G.; Qiu, W.T.; Lu, H.H.; Yu, J.H.; Guan, H.Y.; Gao, S.C. Sensitivity-enhanced surface plasmon resonance sensor utilizing a tungsten disulfide (WS2) nanosheets overlayer. Photonics Res. 2018, 6, 485–491. [Google Scholar] [CrossRef]
- Tang, T.T.; Li, J.; Luo, L.; Sun, P.; Yao, J.Q. Magneto-Optical Modulation of Photonic Spin Hall Effect of Graphene in Terahertz Region. Adv. Opt. Mater. 2018, 6, 1701212. [Google Scholar] [CrossRef]
- Zhao, Y.T.; Gan, S.W.; Wu, L.M.; Zhu, J.Q.; Xiang, Y.J.; Dai, X.Y. GeSe nanosheets modified surface plasmon resonance sensors for enhancing sensitivity. Nanophotonics 2020, 9, 327–336. [Google Scholar] [CrossRef]
- Ooi, K.J.A.; Ang, Y.S.; Zhai, Q.; Tan, D.T.H.; Ang, L.K.; Ong, C.K. Nonlinear plasmonics of three-dimensional Dirac semimetals. APL Photonics 2019, 4, 034402. [Google Scholar] [CrossRef]
- Wang, H.L.; Wu, J.P.; Guo, J.; Jiang, L.Y.; Xiang, Y.J.; Wen, S.C. Low-threshold optical bistability with multilayer graphene-covering Otto configuration. J. Phys. D Appl. Phys. 2016, 49, 255306. [Google Scholar] [CrossRef]
- Xu, H.L.; Wu, L.M.; Dai, X.Y.; Gao, Y.X.; Xiang, Y.J. An ultra-high sensitivity surface plasmon resonance sensor based on graphene-aluminum-graphene sandwich-likestructure. J. Appl. Phys. 2016, 120, 053101. [Google Scholar] [CrossRef]
- Tang, J.; Ye, Y.Y.; Xu, J.; Zheng, Z.W.; Jin, X.L.; Jiang, L.Y.; Jiang, J.; Xiang, Y.J. High-Sensitivity Terahertz Refractive Index Sensor in a Multilayered Structure with Graphene. Nanomaterials 2020, 10, 500. [Google Scholar] [CrossRef]
- Liu, Y.M.; Zheng, Q.W.; Yuan, H.X.; Wang, S.P.; Yin, K.Q.; Dai, X.Y.; Zou, X.; Jiang, L.Y. High Sensitivity Terahertz Biosensor Based on Mode Coupling of a Graphene/Bragg Reflector Hybrid Structure. Biosensors 2021, 11, 377. [Google Scholar] [CrossRef]
- Xiang, Y.J.; Zhu, J.Q.; Wu, L.M.; You, Q.; Ruan, B.X.; Dai, X.Y. Highly sensitive terahertz gas sensor based on surface plasmon resonance with graphene. IEEE Photonics J. 2017, 10, 1–7. [Google Scholar] [CrossRef]
- Cai, D.; Lu, Y.; Lin, K.; Wang, P.; Ming, H. Improving the sensitivity of SPR sensors based on gratings by double-dips method (DDM). Opt. Express 2008, 16, 14597–14602. [Google Scholar] [CrossRef]
- Srivastava, T.; Purkayastha, A.; Jha, R. Graphene based surface plasmon resonance gas sensor for terahertz. Opt. Quantum Electron. 2016, 48, 1–11. [Google Scholar] [CrossRef]
- Goyal, A.K.; Saini, J. Performance analysis of Bloch surface wave-based sensor using transition metal dichalcogenides. Appl. Nanosci. 2020, 10, 4307–4313. [Google Scholar] [CrossRef]


| Ref. | Mechanism | Structure | Sensitivity | FOM (RIU−1) | Frequency Range |
|---|---|---|---|---|---|
| [36] | OTSs sensor | Graphene–Bragg reflector structure | 407.36°/RIU | 65 | THz |
| [26] | OTSs sensor | Graphene–Bragg reflector structure | 517.9°/RIU | 222.9 | THz |
| [38] | SPR sensor | Otto structure | 147°/RIU | / | THz |
| [39] | SPR sensor | Grating structure | 237°/RIU | 95 | Near Infrared |
| [40] | SPR sensor | Otto structure | 52.7°/RIU | 741 | THz |
| [41] | Bloch surface wave sensor | TMDC–Bragg reflector structure | 231°/RIU | 48,250 | Near Infrared |
| [37] | Mode couplingsensor | Graphene–Bragg reflector structure (with defect layer) | 1085°/RIU | 8482 | THz |
| This work | Mode coupling sensor | BDS–Bragg reflector structure (with defect layer) | 1022°/RIU | / | THz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, Y.; Ren, M.; Ji, C.; Dong, J.; Jiang, L.; Dai, X. Terahertz Biosensor Based on Mode Coupling between Defect Mode and Optical Tamm State with Dirac Semimetal. Biosensors 2022, 12, 1050. https://doi.org/10.3390/bios12111050
Bao Y, Ren M, Ji C, Dong J, Jiang L, Dai X. Terahertz Biosensor Based on Mode Coupling between Defect Mode and Optical Tamm State with Dirac Semimetal. Biosensors. 2022; 12(11):1050. https://doi.org/10.3390/bios12111050
Chicago/Turabian StyleBao, Yuwen, Mengjiao Ren, Chengpeng Ji, Jun Dong, Leyong Jiang, and Xiaoyu Dai. 2022. "Terahertz Biosensor Based on Mode Coupling between Defect Mode and Optical Tamm State with Dirac Semimetal" Biosensors 12, no. 11: 1050. https://doi.org/10.3390/bios12111050
APA StyleBao, Y., Ren, M., Ji, C., Dong, J., Jiang, L., & Dai, X. (2022). Terahertz Biosensor Based on Mode Coupling between Defect Mode and Optical Tamm State with Dirac Semimetal. Biosensors, 12(11), 1050. https://doi.org/10.3390/bios12111050