Nonlinear Optical Studies of Gold Nanoparticle Films
Abstract
1. Introduction
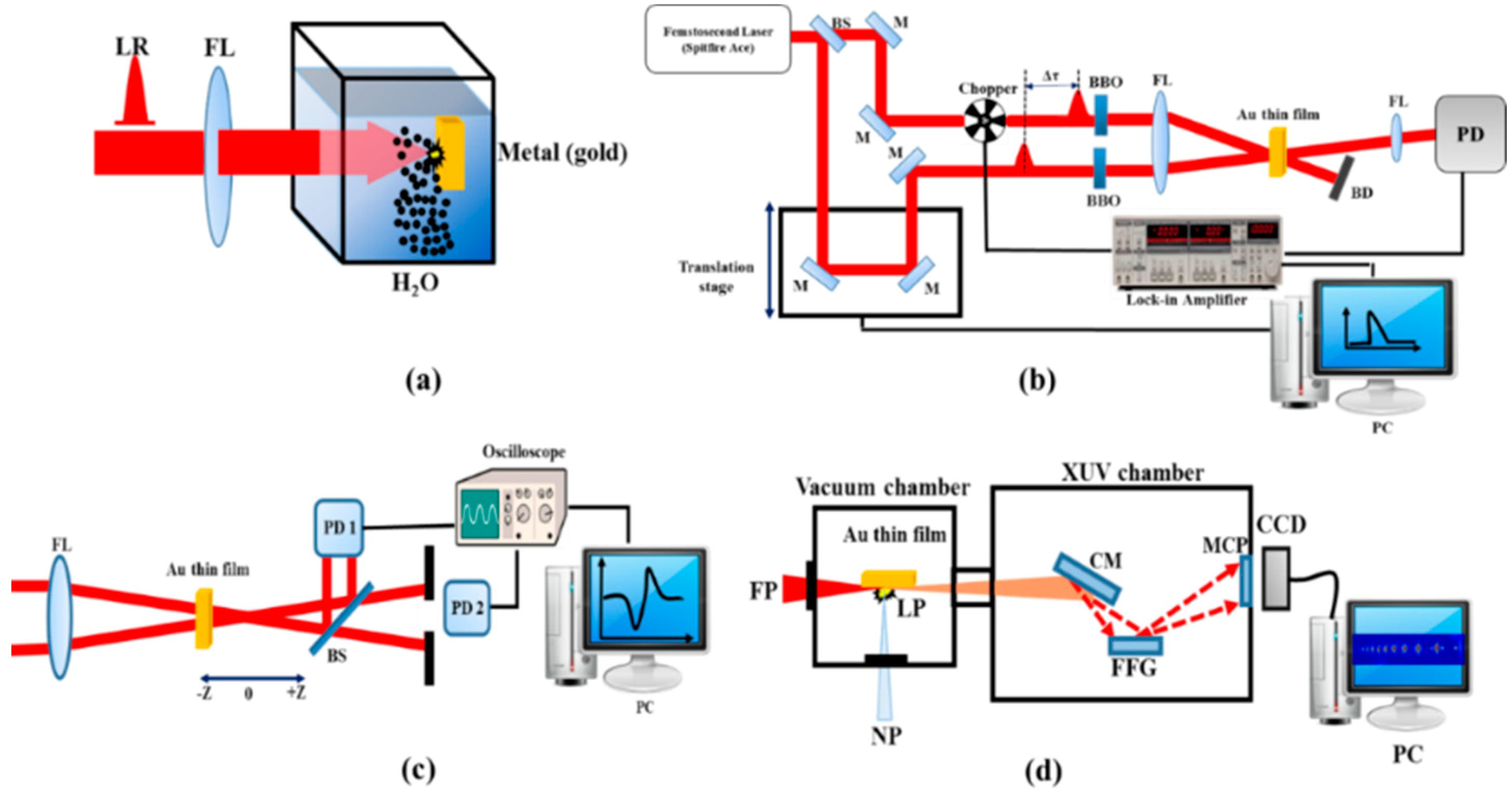
2. Experimental Arrangements
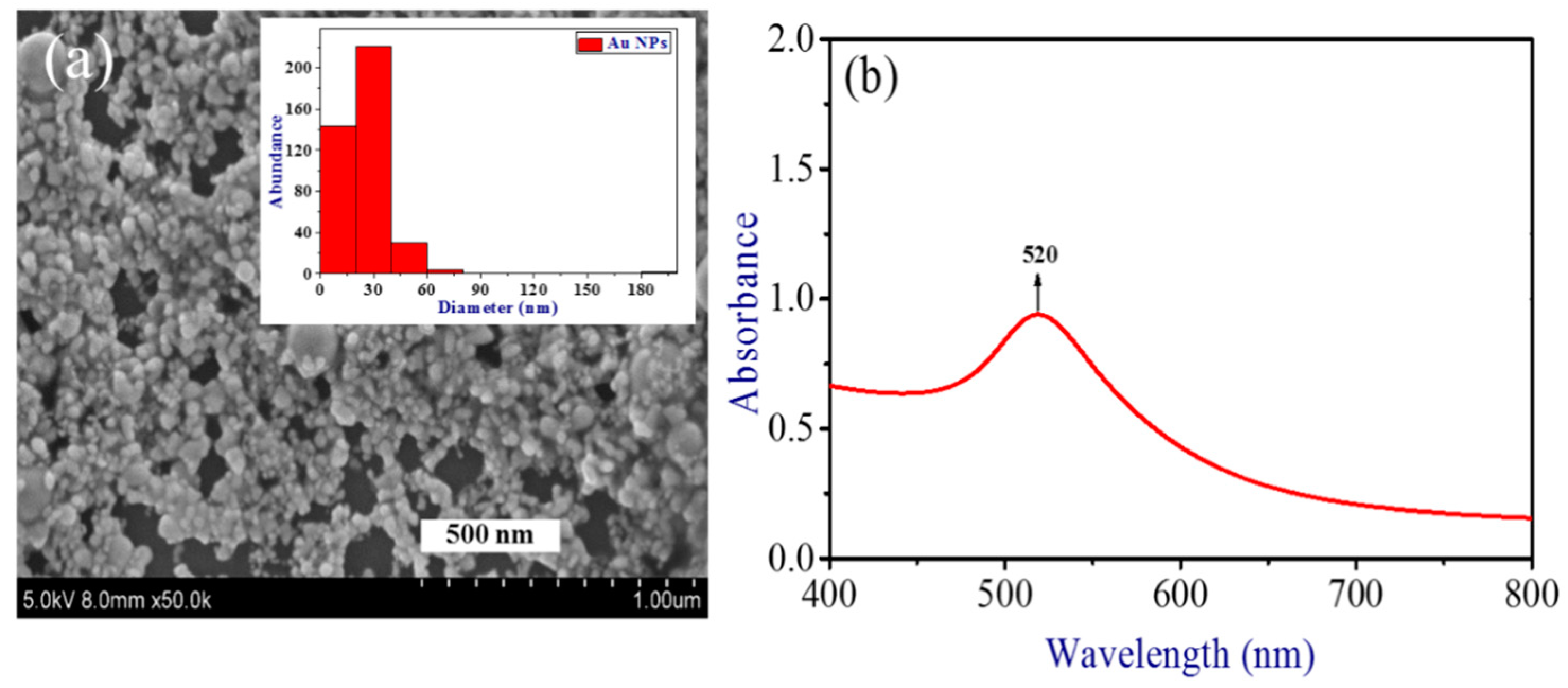
3. Results and Discussion
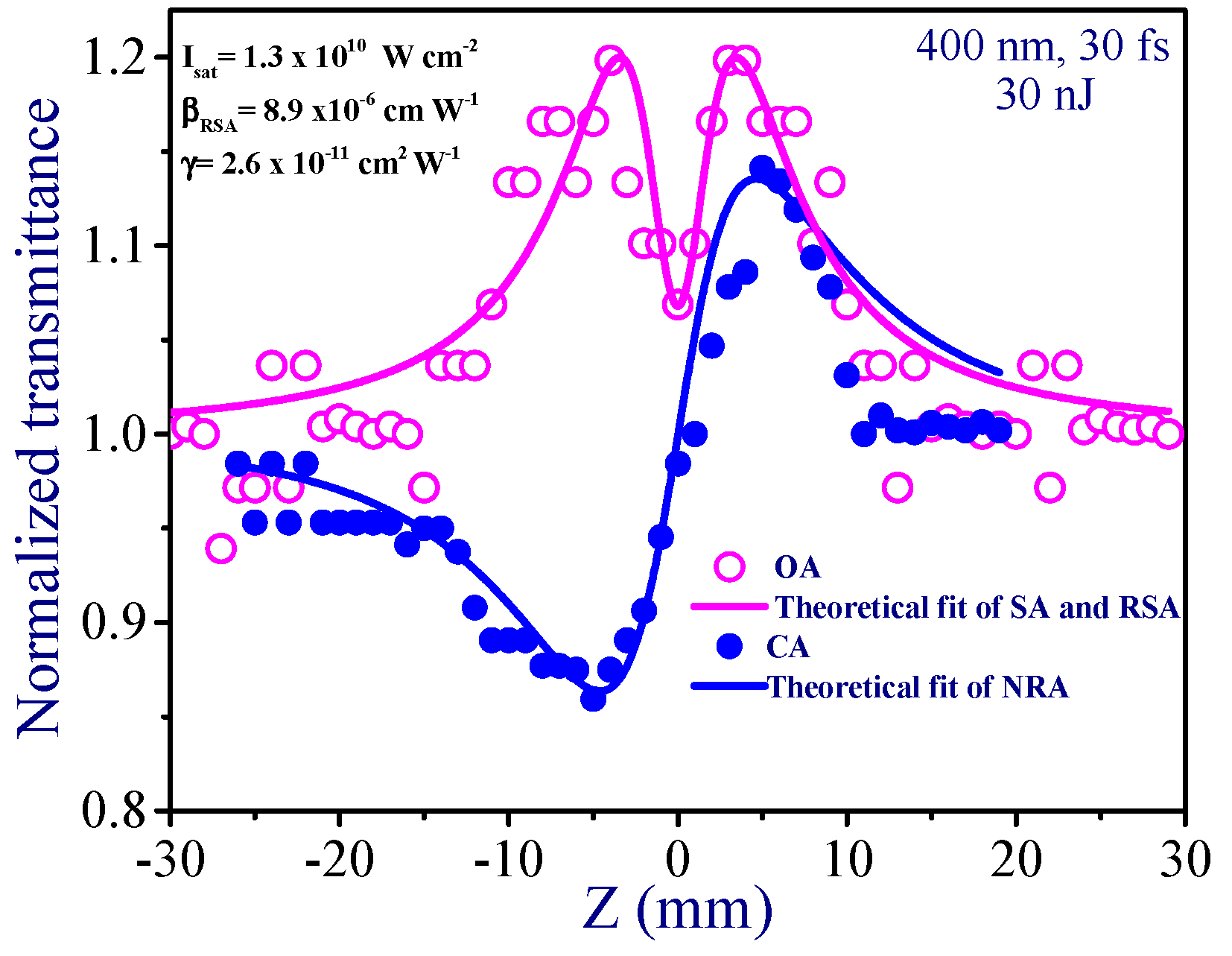
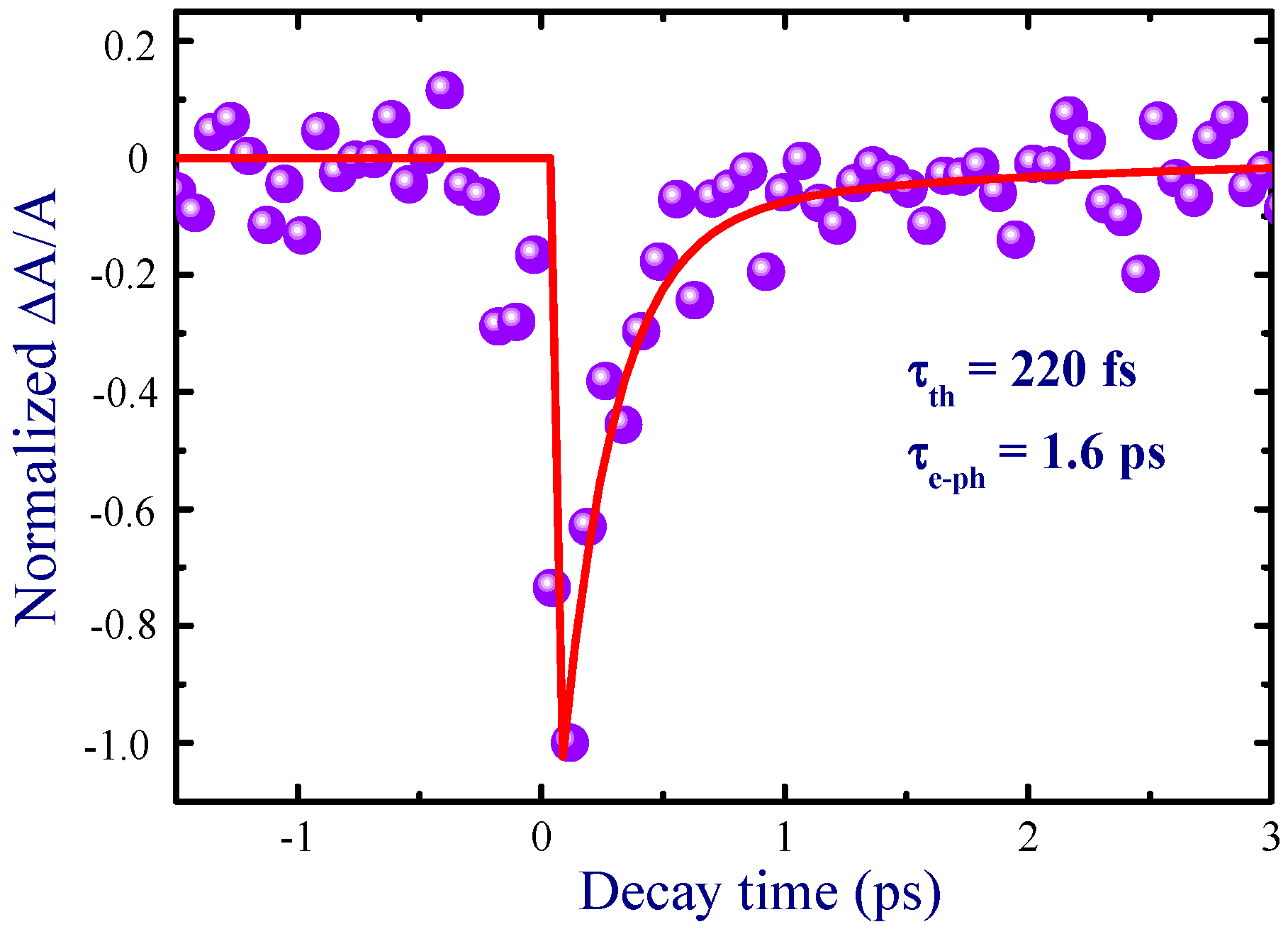
3.1. Low-order Nonlinearities of Au NP Film
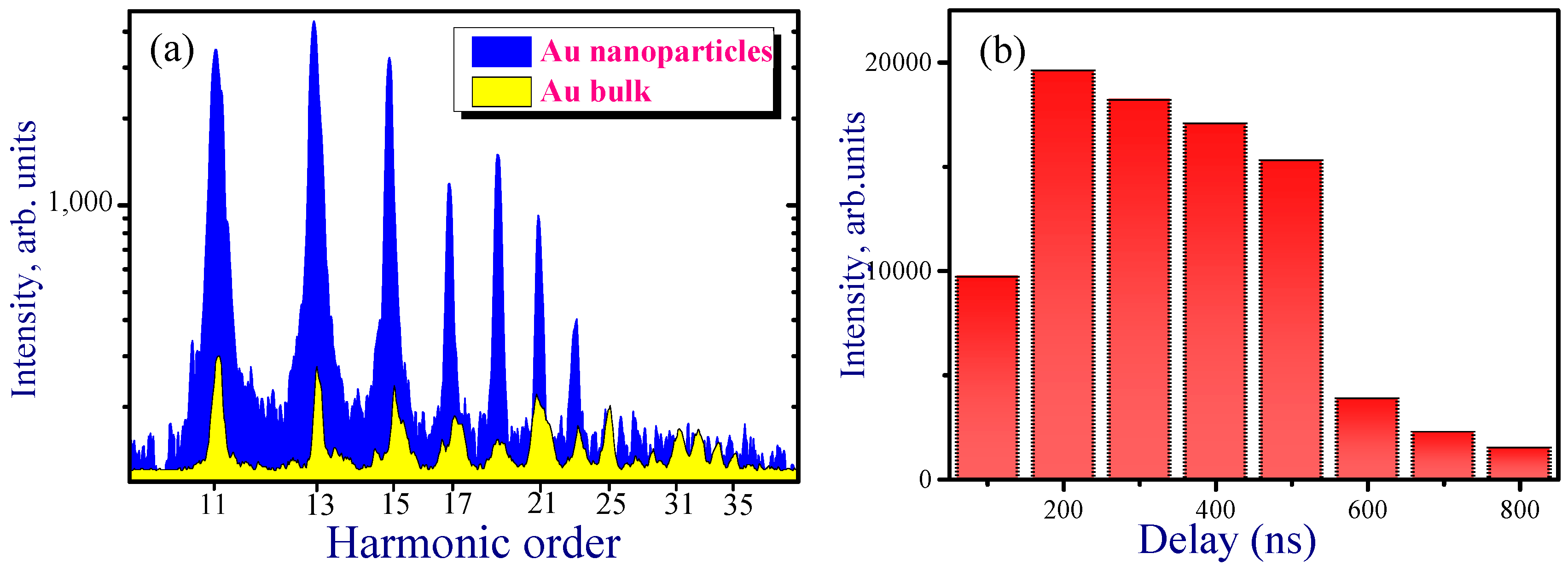
3.2. High-order Harmonic Generation in Au NP Plasmas
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ganeev, R.A.; Baba, M.; Ryasnyansky, A.I.; Suzuki, M.; Kuroda, H. Characterization of optical and nonlinear optical properties of silver nanoparticles prepared by laser ablation in various liquids. Opt. Commun. 2004, 240, 437–448. [Google Scholar] [CrossRef]
- Ganeev, R.A.; Ryasnyansky, A.I.; Stepanov, A.L.; Usmanov, T. Saturated absorption and nonlinear refraction of silicate glasses doped with silver nanoparticles at 532 nm. Opt. Quantum Electron. 2004, 36, 949–960. [Google Scholar] [CrossRef]
- Falconieri, M.; Salvetti, G.; Cattaruzza, E.; Gonella, F.; Mattei, G.; Mazzoldi, P.; Piovesan, M.; Battaglin, G.; Polloni, R. Large third-order optical nonlinearity of nanocluster-doped glass formed by ion implantation of copper and nickel in silica. Appl. Phys. Lett. 1998, 73, 288–290. [Google Scholar] [CrossRef]
- Ryasnyansky, A.; Palpant, B.; Debrus, S.; Ganeev, R.; Stepanov, A.; Can, N.; Buchal, C.; Uysal, S. Nonlinear optical absorption of ZnO doped with copper nanoparticles in the picosecond and nanosecond pulse laser field. Appl. Opt. 2005, 44, 2839–2845. [Google Scholar] [CrossRef] [PubMed]
- Debrus, S.; Lafait, J.; May, M.; Pinçon, N.; Prot, D.; Sella, C.; Venturini, J. Z-scan determination of the third-order optical nonlinearity of gold:silica nanocomposites. J. Appl. Phys. 2000, 88, 4469–4475. [Google Scholar] [CrossRef]
- Alvarez-Fregoso, O.; Mendoza-Alvarez, J.G.; Zelaya-Angel, O. Quantum confinement in nanostructured CdNiTe composite thin films. J. Appl. Phys. 1997, 82, 708–711. [Google Scholar] [CrossRef]
- Baskoutas, S.; Poulopoulos, P.; Karoutsos, V.; Angelakeris, M.; Flevaris, N.K. Strong quantum confinement effects in thin zinc selenide films. Chem. Phys. Lett. 2006, 417, 461–464. [Google Scholar] [CrossRef]
- Muller, E.A.; Johns, J.E.; Caplins, B.W.; Harris, C.B. Quantum confinement and anisotropy in thin-film molecular semiconductors. Phys. Rev. B 2011, 83, 165422. [Google Scholar] [CrossRef]
- Rao, C.N.R.; Kulkarni, G.U.; Thomas, P.J.; Edwards, P.P. Metal nanoparticles and their assemblies. Chem. Soc. Rev. 2000, 29, 27–35. [Google Scholar] [CrossRef]
- Fazio, E.; Hulin, D.; Chumash, V.; Michelotti, F.; Andriesh, A.M.; Bertolotti, M. On-off resonance femtosecond non-linear absorption of chalcogenide glassy films. J. Non. Cryst. Solids 1994, 168, 213–222. [Google Scholar] [CrossRef]
- Anshu, K.; Sharma, A. Study of Se based quaternary SePb(Bi,Te) chalcogenide thin films for their linear and nonlinear optical properties. Optik (Stuttg.) 2016, 127, 48–54. [Google Scholar] [CrossRef]
- Michelotti, F.; Bertolotti, M.; Chumash, V.; Andriesh, A. Chalcogenide glass thin films: Z-Scan measurements of refractive index changes. Proc SPIE 1992, 1773, 423–432. [Google Scholar]
- Dawar, A.L.; Shishodia, P.K.; Chauhan, G.; Joshi, J.C.; Jagadish, C.; Mathur, P.C. Effect of UV exposure on optical properties of amorphous as(2)s(3) thin films. Appl. Opt. 1990, 29, 1971–1973. [Google Scholar] [CrossRef] [PubMed]
- Olesiak-banska, J.; Gordel, M.; Kolkowski, R.; Matczyszyn, K.; Samoc, M. Third-order nonlinear optical properties of colloidal gold nanorods. J. Phys. Chem. C 2012, 116, 13731. [Google Scholar] [CrossRef]
- Lv, J.; Jiang, L.; Li, C.; Liu, X.; Yuan, M.; Xu, J.; Zhou, W.; Song, Y.; Liu, H.; Li, Y.; et al. Large third-order optical nonlinear effects of gold nanoparticles with unusual fluorescence enhancement. Langmuir 2008, 24, 8297–8302. [Google Scholar] [CrossRef] [PubMed]
- Storhoff, J.J.; Lucas, A.D.; Garimella, V.; Bao, Y.P.; Müller, U.R. Homogeneous detection of unamplified genomic DNA sequences based on colorimetric scatter of gold nanoparticle probes. Nat. Biotechnol. 2004, 22, 883–887. [Google Scholar] [PubMed]
- Philip, R.; Kumar, G.R. Picosecond optical nonlinearity in monolayer-protected gold, silver, and gold-silver alloy nanoclusters. Phys. Rev. B 2000, 62, 160–166. [Google Scholar] [CrossRef]
- Tajdidzadeh, M.; Zakaria, A.B.; Abidin Talib, Z.; Gene, A.S.; Shirzadi, S. Optical nonlinear properties of gold nanoparticles synthesized by laser ablation in polymer solution. J. Nanomater. 2017, 2017, 4803843. [Google Scholar] [CrossRef]
- Smith, D.D.; Yoon, Y.; Boyd, R.W.; Campbell, J.K.; Baker, L.A.; Crooks, R.M. z-scan measurement of the nonlinear absorption of a thin gold film. J. Appl. Phys. 1999, 86, 11. [Google Scholar] [CrossRef]
- West, R.; Wang, Y.; Goodson, T., III. Nonlinear absorption properties in novel gold nanostructured topologies. J. Phys. Chem. B 2003, 107, 15. [Google Scholar] [CrossRef]
- Wang, K.; Long, H.; Fu, M.; Yang, G.; Lu, P. Intensity-dependent reversal of nonlinearity sign in a gold nanoparticle array. Opt. Lett. 2010, 35, 1560–1562. [Google Scholar] [CrossRef] [PubMed]
- Ryasnyanskiy, A.I.; Palpant, B.; Debrus, S.; Pal, U.; Stepanov, A. Third-order nonlinear-optical parameters of gold nanoparticles in different matrices. J. Lumin. 2007, 127, 181–185. [Google Scholar] [CrossRef]
- Ganeev, R.A.; Suzuki, M.; Baba, M.; Ichihara, M.; Kuroda, H. Low- and high-order nonlinear optical properties of Au, Pt, Pd, and Ru nanoparticles. J. Appl. Phys. 2008, 103. [Google Scholar] [CrossRef]
- Sheik-bahae, M.; Said, A.A.; Van Stryland, E.W. High-sensitivity, single-beam n2 measurements. Opt. Lett. 1989, 14, 955. [Google Scholar] [CrossRef] [PubMed]
- Chapple, P.B.; Staromlynska, J.; Hermann, J.A.; Mckay, T.J.; Mcduff, R.G. Single-beam Z-Scan: Measurement techniques and analysis. J. Nonlinear Opt. Phys. Mater. 1997, 06, 251–293. [Google Scholar] [CrossRef]
- Liu, X.; Guo, S.; Wang, H.; Hou, L. Theoretical study on the closed-aperture Z-scan curves in the materials with nonlinear refraction and strong nonlinear absorption. Opt. Commun. 2001, 197, 431–437. [Google Scholar] [CrossRef]
- Link, S.; Burda, C.; Wang, Z.L.; El-Sayed, M.A. Electron dynamics in gold and gold-silver alloy nanoparticles: The influence of a nonequilibrium electron distribution and the size dependence of the electron-phonon relaxation. J. Chem. Phys. 1999, 111, 1255–1264. [Google Scholar] [CrossRef]
- Voisin, C.; Christofilos, D.; Loukakos, P.A.; Del Fatti, N.; Vallee, F.; Lerme, J.; Gaudry, M.; Cottancin, E.; Pellarin, M.; Broyer, M. Ultrafast electron-electron scattering and energy exchanges in noble-metal nanoparticles. Phys. Rev. B 2004, 69, 195416. [Google Scholar]
- Varnavski, O.P.; Goodson, T.; Mohamed, M.B.; El-Sayed, M.A. Femtosecond excitation dynamics in gold nanospheres and nanorods. Phys. Rev. B Condens. Matter Mater. Phys. 2005, 72, 1–9. [Google Scholar] [CrossRef]
- Guo, L.; Xu, X. Ultrafast spectroscopy of electron-phonon coupling in gold. J. Heat Transf. 2014, 136, 122401. [Google Scholar]
- Kolomenskii, A.A.; Mueller, R.; Wood, J.; Strohaber, J.; Schuessler, H.A. Femtosecond electron-lattice thermalization dynamics in a gold film probed by pulsed surface plasmon resonance. Appl. Opt. 2013, 52, 7352–7359. [Google Scholar]
- Bauer, C.; Abid, J.-P.; Girault, H.H. Role of adsorbates on dynamics of hot-electron (type I and II) thermalization within gold nanoparticles. C. R. Chim. 2006, 9, 261–267. [Google Scholar] [CrossRef]
- Masia, F.; Langbein, W.; Borri, P. Measurement of the dynamics of plasmons inside individual gold nanoparticlesusing a femtosecond phase-resolved microscope. Phys. Rev. B 2012, 85, 235403. [Google Scholar] [CrossRef]
- Ganeev, R.A.; Suzuki, M.; Baba, M.; Ichihara, M.; Kuroda, H. Ablation of boron carbide for high-order harmonic generation of ultrafast pulses in laser-produced plasma. Opt. Commun. 2016, 370, 6–12. [Google Scholar] [CrossRef]
- Ganeev, R.A.; Bom, L.B.E.; Wong, M.C.H.; Brichta, J.-P.; Bhardwaj, V.R.; Redkin, P.V.; Ozaki, T. High-order harmonic generation from C60-rich plasma. Phys. Rev. A 2009, 80, 043808. [Google Scholar] [CrossRef]
- Ganeev, R.A.; Naik, P.A.; Singhal, H.; Chakera, J.A.; Kumar, M.; Joshi, M.P.; Srivastava, A.K.; Gupta, P.D. High order harmonic generation in carbon nanotube-containing plasma plumes. Phys. Rev. A 2011, 83, 013820. [Google Scholar] [CrossRef]
- Donnelly, T.D.; Ditmire, T.; Neuman, K.; Perry, M.D.; Falcone, R.W. High-order harmonic generation in atom clusters. Phys. Rev. Lett. 1996, 76, 2472–2475. [Google Scholar] [CrossRef]
- Tisch, J.W.G.; Ditmire, T.; Fraser, D.J.; Hay, N.; Mason, M.B.; Springate, E.; Marangos, J.P.; Hutchinson, M.H.R. Investigation of high-harmonic generation from xenon atom clusters. J. Phys. B 1997, 30, L709–L714. [Google Scholar] [CrossRef]
- Vozzi, C.; Nisoli, M.; Caumes, J.-P.; Sansone, G.; Stagira, S.; De Silvestri, S.; Vecchiocattivi, M.; Bassi, D.; Pascolini, M.; Poletto, L.; et al. Cluster effects in high-order harmonics generated by ultrashort light pulses. Appl. Phys. Lett. 2005, 86, 111121. [Google Scholar] [CrossRef]
- Hu, S.X.; Xu, Z.Z. Enhanced harmonic emission from ionized clusters in intense laser pulses. Appl. Phys. Lett. 1997, 71, 2605–2607. [Google Scholar] [CrossRef]
- Ruf, H.; Handschin, C.; Cireasa, R.; Thiré, N.; Ferré, A.; Petit, S.; Descamps, D.; Mével, E.; Constant, E.; Blanchet, V.; Fabre, B.; Mairesse, Y. Inhomogeneous high harmonic generation in krypton clusters. Phys. Rev. Lett. 2013, 110, 083902. [Google Scholar] [CrossRef] [PubMed]
- Ganeev, R.A.; Suzuki, M.; Baba, M.; Ichihara, M.; Kuroda, H. High-order harmonic generation in Ag nanoparticle-containing plasma. J. Phys. B 2008, 41, 045603. [Google Scholar] [CrossRef]
- Ganeev, R.A.; Suzuki, M.; Baba, M.; Ichihara, M.; Kuroda, H. Low- and high-order nonlinear optical properties of BaTiO3 and SrTiO3 nanoparticles. J. Opt. Soc. Am. B 2008, 25, 325–333. [Google Scholar] [CrossRef]
- Singhal, H.; Ganeev, R.A.; Naik, P.A.; Chakera, J.A.; Chakravarty, U.; Vora, H.S.; Srivastava, A.K.; Mukherjee, C.; Navathe, C.P.; Deb, S.K.; Gupta, P.D. In-situ laser induced silver nanoparticle formation and high order harmonic generation. Phys. Rev. A 2010, 82, 043821. [Google Scholar] [CrossRef]
- De Nalda, R.; López-Arias, M.; Sanz, M.; Oujja, M.; Castillejo, M. Harmonic generation in ablation plasmas of wide bandgap semiconductors. Phys. Chem. Chem. Phys. 2011, 13, 10755–10761. [Google Scholar] [CrossRef] [PubMed]
- Ganeev, R.A.; Boltaev, G.S.; Kim, V.V.; Zhang, K.; Zvyagin, A.I.; Smirnov, M.S.; Ovchinnikov, O.V.; Redkin, P.V.; Wöstmann, M.; Zacharias, H.; et al. Effective high-order harmonic generation from metal sulfide quantum dots. Opt. Express 2018, 26, 35013–35025. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rout, A.; Boltaev, G.S.; Ganeev, R.A.; Fu, Y.; Maurya, S.K.; Kim, V.V.; Rao, K.S.; Guo, C. Nonlinear Optical Studies of Gold Nanoparticle Films. Nanomaterials 2019, 9, 291. https://doi.org/10.3390/nano9020291
Rout A, Boltaev GS, Ganeev RA, Fu Y, Maurya SK, Kim VV, Rao KS, Guo C. Nonlinear Optical Studies of Gold Nanoparticle Films. Nanomaterials. 2019; 9(2):291. https://doi.org/10.3390/nano9020291
Chicago/Turabian StyleRout, Anuradha, Ganjaboy S. Boltaev, Rashid A. Ganeev, Yue Fu, Sandeep Kumar Maurya, Vyacheslav V. Kim, Konda Srinivasa Rao, and Chunlei Guo. 2019. "Nonlinear Optical Studies of Gold Nanoparticle Films" Nanomaterials 9, no. 2: 291. https://doi.org/10.3390/nano9020291
APA StyleRout, A., Boltaev, G. S., Ganeev, R. A., Fu, Y., Maurya, S. K., Kim, V. V., Rao, K. S., & Guo, C. (2019). Nonlinear Optical Studies of Gold Nanoparticle Films. Nanomaterials, 9(2), 291. https://doi.org/10.3390/nano9020291







